Mapping the structural and functional network architecture of the medial temporal lobe using 7T MRI

Abstract

Medial temporal lobe (MTL) subregions play integral roles in memory function and are differentially affected in various neurological and psychiatric disorders. The ability to structurally and functionally characterize these subregions may be important to understanding MTL physiology and diagnosing diseases involving the MTL. In this study, we characterized network architecture of the MTL in healthy subjects (n = 31) using both resting state functional MRI and MTL‐focused T2‐weighted structural MRI at 7 tesla. Ten MTL subregions per hemisphere, including hippocampal subfields and cortical regions of the parahippocampal gyrus, were segmented for each subject using a multi‐atlas algorithm. Both structural covariance matrices from correlations of subregion volumes across subjects, and functional connectivity matrices from correlations between subregion BOLD time series were generated. We found a moderate structural and strong functional inter‐hemispheric symmetry. Several bilateral hippocampal subregions (CA1, dentate gyrus, and subiculum) emerged as functional network hubs. We also observed that the structural and functional networks naturally separated into two modules closely corresponding to (a) bilateral hippocampal formations, and (b) bilateral extra‐hippocampal structures. Finally, we found a significant correlation in structural and functional connectivity (r = 0.25). Our findings represent a comprehensive analysis of network topology of the MTL at the subregion level. We share our data, methods, and findings as a reference for imaging methods and disease‐based research.

1. INTRODUCTION

The medial temporal lobe (MTL) comprises hippocampal subfields and surrounding parahippocampal, perirhinal, and entorhinal cortices. In healthy humans, it serves as the anatomical locus for declarative memory (Squire and Zola‐Morgan, 1991) and is a key component of the default mode network (Buckner et al., 2009). The MTL is also affected in a number of neurological and psychiatric disorders, including Alzheimer's disease, temporal lobe epilepsy, schizophrenia, and depression (Mueller et al., 2009; Mueller et al., 2010; Posener et al., 2003; Schobel et al., 2009; Small, Schobel, Buxton, Witter, & Barnes, 2011).

Prior studies in humans and animal models suggest functional specialization of the various MTL subregions in memory processes, with left and right hemispheres mediating verbal and nonverbal memory, respectively (Guzowski, Knierim, & Moser, 2004; Leal and Yassa, 2015; Suthana, Ekstrom, Moshirvaziri, Knowlton, & Bookheimer, 2009; Suthana et al., 2015). For example, the dentate gyrus plays a role in pattern separation (Leutgeb, Leutgeb, Moser, & Moser, 2007), CA3 in pattern completion (Neunuebel and Knierim, 2014), CA1 in place memory and autobiographical memory retrieval (Bartsch et al., 2010; Bartsch, Dohring, Rohr, Jansen, & Deuschl, 2011), and entorhinal cortex in hippocampal‐neocortical communication (Lavenex and Amaral, 2000). Evidence from a range of modalities indicates that there are spatially non‐uniform structural and functional changes in the MTL in neurological diseases. Although many of these studies derive from neuroanatomical and neurophysiological data, more recent work uses noninvasive in vivo neuroimaging. For example, MRI and PET studies in Alzheimer's disease show hypometabolism of the entorhinal cortex (de Leon et al., 2001; Moreno et al., 2007; Small et al., 2011), volumetric changes in entorhinal cortex, subiculum, CA1, and the CA1–2 transition zones (Mueller et al., 2010), and atrophy localized to CA1 in early disease (de Flores, La Joie, & Chételat., 2015). The cortical thickness of Brodmann area 35 (a component of the perirhinal cortex) also discriminates between preclinical Alzheimer's disease and normal aging (Wolk et al., 2017). Semantic dementia patients exhibit atrophy of CA1 and subiculum, most prominently in the left hemisphere (La Joie et al., 2013). Patients with unilateral mesial temporal sclerosis and temporal lobe epilepsy demonstrate atrophy (Mueller et al., 2009) and decreased functional activation during memory encoding (Das et al., 2011) of several hippocampal subfields ipsilateral to seizure focus. MTL subregions are also implicated in psychiatric disorders where findings include volume loss in CA3/dentate gyrus subfields in post‐traumatic stress disorder (Wang et al., 2010), hippocampal atrophy and shape deformations localized to the subiculum in depression (Malykhin and Coupland, 2015; Posener et al., 2003; Sheline, Wang, Gado, Csernansky, & Vannier, 1996), and selective CA1 hypermetabolism in schizophrenia (Schobel et al., 2009).

Neuroanatomical studies elucidate intra‐MTL circuitry as a complex network of structural connections promoting information transfer (Lavenex and Amaral, 2000). A growing body of research from the field of network neuroscience highlights the importance of characterizing brain connectivity, though predominantly at the scale of a whole brain connectome. This network neuroscience approach involves applying methods from graph theory to describe functional and/or structural connectivity between pre‐defined brain regions (Bassett and Sporns, 2017; Bullmore and Sporns, 2009; Zalesky et al., 2010). Application of this approach reveals that whole‐brain network architecture is modulated during cognitive effort (Bassett et al., 2009; Braun et al., 2015; Kitzbichler, Henson, Smith, Nathan, & Bullmore, 2011; Stanley, Dagenbach, Lyday, Burdette, & Laurienti, 2014), and disrupted in various neurological and psychiatric diseases impacting cognition (Bassett, Nelson, Mueller, Camchong, & Lim, 2012; Bernhardt, Chen, He, Evans, & Bernasconi, 2011; Minkova et al., 2016; Supekar, Menon, Rubin, Musen, & Greicius, 2008; Zhang et al., 2011). In addition to whole‐brain networks, several studies suggest that network features within particular subregions of the brain can serve as useful biomarkers for neurological function and dysfunction (Khalsa, Mayhew, Chechlacz, Bagary, & Bagshaw, 2014; Ould Ismail, Amouzandeh, & Grant, 2016; Soto, Bassett, & Ashby, 2016), and may also reflect changes in larger‐scale brain patterns of functioning and behavior (Deco et al., 2014; Palop et al., 2007). This prior work lends evidence to the notion that characterizing the intra‐MTL network via non‐invasive neuroimaging can lead to a better understanding of MTL physiology and provide a baseline for studies of neurological diseases involving the MTL.

Functional networks in neuroimaging data are typically derived from resting state blood oxygenation level dependent (BOLD) functional MRI (fMRI) time series that show spontaneous, low‐frequency signal fluctuations (Biswal, Yetkin, Haughton, & Hyde, 1995). Structural brain networks can be derived from across‐subject covariance of MRI‐derived morphometric features such as cortical thickness or gray matter volume (Bassett et al., 2008; Mechelli, Friston, Frackowiak, & Price, 2005). These networks display some correspondence with known anatomical networks, perhaps because brain regions that strongly covary in size across subjects may experience common trophic influences (Alexander‐Bloch, Giedd, & Bullmore, 2013; Gong, He, Chen, & Evans, 2012; Lerch et al., 2006; Zielinski, Gennatas, Zhou, & Seeley, 2010). Whole‐brain functional and structural networks are correlated but also provide complementary information; for example, functional connectivity has been observed between regions with minimal structural connectivity, suggesting that functional connectivity can be mediated by indirect structural connections (Damoiseaux and Greicius, 2009; Hagmann et al., 2008; Honey et al., 2009; Koch, Norris, & Hund‐Georgiadis, 2002; Liang et al., 2017).

The primary goal of this study was to exploit recent developments in high‐resolution MRI and automated segmentation algorithms to investigate the network architecture of the MTL. Specifically, we carried out a multi‐atlas segmentation approach to identify MTL subregions in healthy adults, using sub‐millimeter 7 tesla (7T) T2‐weighted MRI data tailored for MTL subregion visualization, and used graph theoretic methods to characterize both structural and functional MTL subregion networks. We sought to address several key questions. First, to what extent are the structure and function of the MTL symmetric across hemispheres? Elucidating MTL symmetry in a normative population would be particularly useful to establish a baseline for future studies, given the existence of hemispheric lateralization of memory function and the possibility of unilateral MTL deficits in neurological diseases, most apparently temporal lobe epilepsy and semantic dementia. Second, which MTL subregions serve as network hubs that might facilitate information transfer within network? Third, what is the modular organization of the MTL subregion network? And finally, what is the interplay between structure and function within the network? Our findings represent a comprehensive in vivo analysis of intra‐MTL network topology in healthy subjects at the subregion level, and can serve as the basis for better understanding its physiological function in both health and disease.

2. METHODS

2.1. Subjects

We recruited 31 healthy adult subjects (mean age = 30.9, SD 10.2, 16 female) with no history of neurological or psychiatric disorders. All studies were conducted under an approved Institutional Review Board protocol of the University of Pennsylvania. We additionally recruited four adults with temporal lobe epilepsy and three adults with mild cognitive impairment for our atlas set of manually segmented structural MRI images to be used for the automated segmentation protocol (see Section 2.3 for details). The rationale for including subjects with neurological disease is to enhance usability of our atlas in future studies, with the hypothesis that such a representative atlas will allow for more accurate automated segmentations in both healthy and diseased brains.

2.2. Image acquisition

Whole‐brain images were acquired using a 7.0‐T whole‐body MRI scanner (Siemens Medical Systems) with a 32‐channel phased‐array head coil (Nova Medical Inc.). For all 31 healthy subjects and additional atlas subjects, we obtained 0.4 × 0.4 × 1.0 mm³ MTL‐tailored 7T T2‐weighted structural turbo spin‐echo MRI (0.4 × 0.4 mm in plane resolution, 1 mm slice thickness, 224 coronal slices, TR = 3,000 ms, TE = 388 ms, 6.16 ms echo spacing) with oblique coronal slices oriented perpendicular to the long axis of the hippocampus and 0.8 × 0.8 × 0.8 mm³ T1‐weighted MPRAGE (176 axial slices, TR = 2,800 ms, TE = 4.4 ms, TI = 1,500 ms, flip angle =7°). We also obtained 2 mm³ isotropic resting state fMRI in a subset of 24 healthy adult subjects (mean age = 31.7, SD 11.2, 14 female), using a gradient‐echo echoplanar (EPI) sequence (64 axial slices with 2 mm thickness prescribed in the superior–inferior direction starting from the apex of the brain; matrix size = 96 × 96; FOV = 192 mm; TR = 1 s; TE = 23.6 ms; multiband factor = 4; 420 volumes; 7 minutes) and a B0 field‐map sequence (TR = 1 s, TE1 = 3.24 ms, TE2 = 5.37 ms). This fMRI acquisition led to coverage of the entire cerebrum in all subjects.

2.3. MTL segmentation

To generate MTL segmentations for our dataset, we used the multi‐atlas automated segmentation pipeline, Automated Segmentation of Hippocampal Subfields (ASHS) (Yushkevich et al., 2015), which employs joint label fusion (Wang et al., 2013) and corrective learning (Wang et al., 2011) to automatically segment a target image based on a set of manually labeled atlas images. To allow for automated segmentation of our data, we first acquired our own atlas set of 19 subjects: 12 healthy adults (a subset of our 31 healthy adult dataset), 4 temporal lobe epilepsy patients, and 3 subjects with mild cognitive impairment. Structural MRI was acquired in these subjects using the protocol described in Section 2.2.

Manual segmentation of the MTL in these 19 subjects was carried out in ITK‐SNAP (Yushkevich et al., 2006) by a trained segmentation expert, using a protocol adapted from the ASHS 3T MRI study (Yushkevich et al., 2015). The protocol defines MTL subregion boundaries based on a combination of image intensity features and geometric rules using the oblique coronal slices of the T2‐weighted images. As illustrated in Figure 1, we segmented 10 subregions per hemisphere as follows: hippocampal subfields (CA1, CA2, CA3, DG, subiculum, tail) and cortical regions of the parahippocampal gyrus (entorhinal cortex, parahippocampal cortex (PHC), and perirhinal cortex divided into BA35 and BA36). The hilus (also sometimes called CA4 or included in CA3) was incorporated in the DG label, and the tail region was composed of the posterior‐most aspects of the hippocampus in which individual subfields cannot be discriminated.

Figure 1.

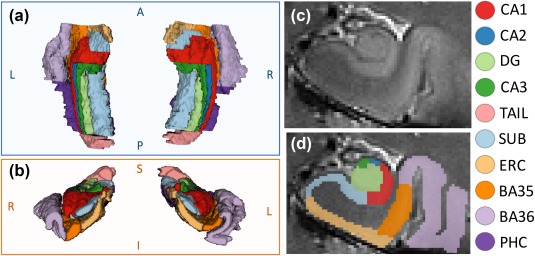
Example MTL manual segmentation: (a) superior and (b) anterior 3D views, (c) coronal T2 slice with (d) overlying segmentation. DG, dentate gyrus; SUB, subiculum; ERC, entorhinal cortex; BA35 + BA36, Brodmann areas 35 and 36 (perirhinal cortex); PHC, parahippocampal cortex

To evaluate the efficacy of the atlas, we used a leave‐one‐out approach to generate automated segmentations for each subject in the atlas. We then assessed for the degree of overlap between the automated and manual segmentations for each subject by computing the dice similarity coefficient (DSC). DSC ranges from 0 to 1 and is computed as follows:

$$\mathrm{D}\mathrm{S}\mathrm{C}\left(A,B\right)=\frac{2\hspace{0.17em}|A\cap B|}{\left|A\right|+\left|B\right|},$$ (1)

where A and B are, in our case, binary image segmentations. We computed mean DSCs between automated and manual segmentations in our atlas for each individual subregion. The computed DSCs were good across all subregions (range 0.61–0.83) (Table 1). Although all subregions had a mean DSC > 0.6, smaller subregions had lower overlap scores, likely because small, voxel‐level shifts between automated and manual segmentations can substantially penalize the DSC in smaller, thinner subregions (Pipitone et al., 2014; Wisse et al., 2016). Perirhinal cortical regions BA35 and BA36 also had slightly lower DSC values, likely due to some ambiguity in the maximal coronal extents of these regions. Our overlaps were comparable to those seen in the prior 3T ASHS MTL atlas (subregion‐level DSCs between 0.50 and 0.819) (Yushkevich et al., 2015) and higher in smaller subregions, perhaps as a result of the higher resolution images. The hippocampal subfield overlaps were also comparable with another recently published hippocampal atlas (DSCs between 0.54 and 0.85) which also used the ASHS protocol on 7T MRI but did not include all regions of the parahippocampal gyrus (Wisse et al., 2016). For a visual representation of the efficacy of the automated approach, Figure 2 illustrates the comparison between the manual and automated segmentation for a representative subject.

Table 1.

Atlas validation: DSCs (mean ± SDs) characterizing overlap between automated and manual segmentation for each subregion in the MTL atlas

	DSC (Auto vs. manual)
	Left	Right
CA1	0.79 ± 0.04	0.78 ± 0.07
CA2	0.60 ± 0.12	0.62 ± 0.15
CA3	0.62 ± 0.07	0.61 ± 0.09
DG	0.82 ± 0.04	0.83 ± 0.05
Tail	0.78 ± 0.06	0.78 ± 0.07
Sub	0.80 ± 0.02	0.78 ± 0.03
ERC	0.77 ± 0.04	0.76 ± 0.03
BA35	0.66 ± 0.07	0.65 ± 0.07
BA36	0.71 ± 0.04	0.70 ± 0.08
PHC	0.75 ± 0.06	0.75 ± 0.09

Figure 2.

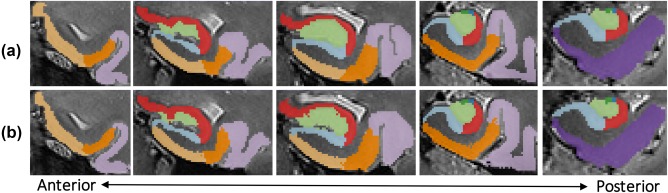
Coronal slices of left MTL in a representative subject with (a) manual segmentation and (b) corresponding automated segmentation

The study atlas was used to generate automated MTL segmentations of the 31 T2‐weighted images in our healthy adult dataset. We qualitatively assessed all resulting automated segmentations via visual inspection (by authors P.S., L.W.). The resulting segmented MTL subregions were used as regions of interest for all subsequent analysis, though for the 12 healthy adult subjects which were also in the atlas set, we used the manual rather than automated segmentations to maximize segmentation accuracy.

2.4. MTL volumetry

We first computed MTL subregion volumes to compare findings to prior studies and to relate our network findings to underlying volumetry. We calculated volumes and volumetric asymmetry indices ([Right – Left]/[Right + Left]) for each of the 10 subregions, as well as for the entire hippocampus and entire MTL.

2.5. Functional and structural network generation

We carried out several processing steps on the raw fMRI time series data. First, B0 maps were used to correct EPI distortion. Next, six‐parameter rigid body motion correction was implemented to account for head motion‐related artifacts (Friston, Frith, Frackowiak, & Turner, 1995). All included subjects experienced minimal head motion (<1 mm translation and < 0.5° rotation in any direction) at all times during acquisition. Following motion correction, the fMRI data were co‐registered to the high‐resolution structural MRI space (using rigid‐body transformation and a mutual information cost function), as there is evidence that analyzing fMRI data in higher resolution anatomical space improves spatial precision and reproducibility of measurements (Kang, Yund, Herron, & Woods, 2007). To reduce low‐frequency drift and high‐frequency noise (Biswal et al., 1995; Van Dijk et al., 2010), the fMRI data were temporally band‐pass filtered in the range of 0.008‐0.08 Hz. Physiological noise was eliminated via linear regression to factor out the global signal and mean signals from white matter and cerebrospinal fluid regions (Van Dijk et al., 2010). The Atropos method (Avants, Tustison, Wu, Cook, & Gee, 2011) was used for three‐tissue segmentation. We also regressed out the six parameters of head motion (obtained from motion correction) and their six temporal derivatives to minimize motion‐induced signal variation (Van Dijk, Sabuncu, & Buckner, 2012; Power, Barnes, Snyder, Schlaggar, & Petersen, 2012). To minimize mixing of BOLD signal between neighboring subregions, we did not apply any spatial smoothing, as is common in high‐resolution fMRI studies (Carr, Rissman, & Wagner, 2010; Das et al., 2011). Linear Pearson correlations between the average residual time‐series signals for each MTL subregion were used to generate functional connectivity matrices for each subject (Zalesky, Fornito, & Bullmore, 2012). The matrices were Fisher r‐z transformed for variance stabilization (Fisher, 1921) and then averaged across subjects to generate a group‐level functional connectivity matrix.

We carried out several extra processing steps on the volumetric data. First, consistent with the procedures in Yushkevich et al. (2015), we normalized the volumes of the extrahippocampal cortical regions (ERC, BA35&36, and PHC) by their the anterior‐posterior extents as follows:

$$\left[\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{d}\hspace{0.17em}\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\right]=\frac{\left[\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\right]}{\left[\mathrm{e}\mathrm{x}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{i}\mathrm{n} \mathrm{s}\mathrm{l}\mathrm{i}\mathrm{c}\mathrm{e}\mathrm{s}\right]\times \left[\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{c}\mathrm{e} \mathrm{t}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{k}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}\right]}.$$ (2)

Since the anterior–posterior slice boundaries of these regions were defined relative to the hippocampal head, this normalization step ensures that the volumes are not confounded by hippocampal head length. Additionally, we adjusted each subregion volume by total intracranial volume via linear regression, motivated by a prior study demonstrating that normalizing regional volumes by intracranial volume is necessary to accurately characterize the extent of disease‐driven regional atrophy (Voevodskaya et al., 2014), and consistent with other studies (Mueller et al., 2009; Yushkevich et al., 2015). We generated a group‐level structural covariance matrix using the Pearson correlations between these normalized MTL subregion volumes across subjects, as Pearson correlation between regional gray matter volumes has been found to be a useful measure of structural connectivity in prior studies (Hosseini, Hoeft, & Kesler, 2012; Wu et al., 2012). Similar to the functional networks, the matrix was then Fisher r‐z transformed.

Matrices were kept fully weighted, as there is evidence that connection strength carries important information about network architecture (Bassett and Bullmore, 2016) and that weak connections show potential as disease biomarkers (Bassett et al., 2012). In both the functional and structural networks, the matrices represent graphs in which subregions serve as nodes and the strength of correlation between pairs of subregions serve as edge weights. The procedure for generating both functional and structural networks from the MTL subregions is summarized in Figure 3.

Figure 3.

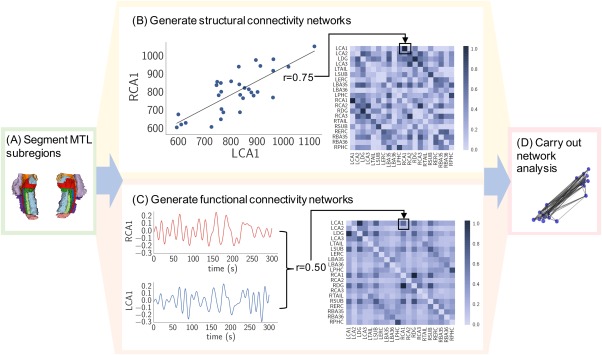
Network analysis approach: (a) MTL subregions were segmented. (b) Elements of the structural covariance matrix were equivalent to Pearson correlations between normalized MTL subregion gray matter volume pairs across subjects (each data point in the displayed plot represents one subject). (c) Elements of the subject‐specific functional connectivity matrices were equivalent to Pearson correlations of residual time series between MTL subregion pairs (these matrices were then averaged across subjects). (d) Matrices were further processed via Fisher r‐z transformation and analyzed using various graph‐theoretic measures

2.6. Functional and structural network analysis

2.6.1. Network symmetry and hubness

As described in Section 2.5, we characterized the MTL networks as graphs, which contain nodes and edges. Such graphs can contain heterogeneous structure that is important for the system's function. Although a number of graph statistics have been defined to understand this heterogeneous structure, many of them are correlated with one another, especially in brain networks (Li et al., 2011; Lynall et al., 2010). It is useful to choose a set of graph statistics that describe important dimensions of variation in brain networks but are not necessarily redundant. Historically, measures that have proven particularly useful in characterizing brain graphs include the connectivity strength, clustering coefficient, and efficiency (Bullmore and Sporns, 2009), largely due to their sensitivity to the markers of small‐world architecture (Bassett and Bullmore, 2016). We therefore computed local connectivity strength, clustering coefficient, and efficiency for both group‐level structural covariance and functional networks. Since the most widely‐applied definitions for these metrics require non‐negative edge weights (Rubinov and Sporns, 2010), and since the meaning of negative correlations is debatable and not well understood (Chai, Castañón, Öngür, & Whitfield‐Gabrieli, 2012; Fox, Zhang, Snyder, & Raichle, 2009; Murphy and Fox, 2016), we set negative edge weights to zero. The percentage of connections surviving this threshold was 85.3% of edges in the group structural network and 96.8% in the group functional network. We define the network metrics below.

1. Connectivity Strength: The local connectivity strength k_i at node i for a weighted network with a set of nodes, N, is the sum of the weights of all connections to node i as follows:

   $$k_i=\hspace{0.17em}\frac{1}{N}\sum _{j\hspace{0.17em}\in \hspace{0.17em}N}{w}_{ij},$$ (3)

   where w_ij is the edge weight between nodes i and j.
2. Clustering Coefficient: The local clustering coefficient c_i at node i can be conceptualized as the likelihood that the neighbors of i are interconnected. One way in which to quantify this concept for weighted networks is:

   $$c_i=\hspace{0.17em}\frac{2}{k_i(k-1)}\sum _{j,h\hspace{0.17em}\in \hspace{0.17em}N}{\left({\stackrel{\sim }{w}}_{ij}{\stackrel{\sim }{w}}_{ih}{\stackrel{\sim }{w}}_{jh}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.},$$ (4)

   where the weights are scaled by the largest weight in the network, i.e. ${\stackrel{\sim }{w}}_{ij}=w_{ij}/\mathrm{m}\mathrm{a}\mathrm{x}$( $w_{ij}$) (Onnela, Saramäki, Kertész, & Kaski, 2005).
3. Efficiency: The local efficiency e_i is often thought of as a measure of the capacity of node i for information transfer throughout the network (Latora and Marchiori, 2003, 2001) (although for caveats in this interpretation, see also Rubinov and Bassett, 2011). It can be defined as follows (Achard and Bullmore, 2007):

   $$e_i=\hspace{0.17em}\frac{1}{N-1}\sum _{i\hspace{0.17em}\ne j\hspace{0.17em}\in \hspace{0.17em}N}\frac{1}{L_{ij}},$$ (5)

   where L_ij is the shortest weighted path length between nodes i and j, where the length of each edge is the reciprocal of the edge weight, 1/w_ij.

To characterize the network symmetry, we computed the Pearson correlation coefficient between the network metrics for left and right hemispheres, as well as the asymmetry indices ([Right – Left]/[Right + Left]) for each subregion for each of the three network metrics. To summarize the degree of asymmetry in the network, we also defined a network asymmetry index $\mathrm{\nu }$ as the mean of the absolute value of the asymmetry indices across all subregions and across all three network metrics as follows:

$$\mathrm{\nu }\hspace{0.17em}=\hspace{0.17em}\frac{1}{3\ast N} \sum _{i=1}^{N/2}\left|\frac{k_{i+N/2}-\hspace{0.17em}{k}_i}{k_{i+N/2}+\hspace{0.17em}{k}_i}\right|+\hspace{0.17em}\left|\frac{c_{i+N/2}-\hspace{0.17em}{c}_i}{c_{i+N/2}+\hspace{0.17em}{c}_i}\right|+\hspace{0.17em}\left|\frac{e_{i+N/2}-\hspace{0.17em}{e}_i}{e_{i+N/2}+\hspace{0.17em}{e}_i}\right|,$$ (6)

where the first N/2 nodes correspond to the left MTL subregions and the last N/2 nodes correspond to the analogous right MTL subregions. Like a standard asymmetry index, $\mathrm{\nu }$ can range from 0 to 1.

We also used the local network metrics to identify network hubs that might serve as key facilitators of information transfer. Although there is no one agreed upon definition of a network hub (Zuo et al., 2012), it has been suggested that aggregating rankings across multiple network metrics is a robust approach to defining a hub (van den Heuvel and Sporns, 2013). We wanted to identify subregions with relatively high strength, clustering, and efficiency. Since the distributions of metric values were non‐Gaussian, we defined a network hub to be any subregion that had a local network metric value at least 25% higher than the median value across subregions, for all three computed metrics (strength, clustering, and efficiency).

2.6.2. Modular organization assessed by community detection

Although the previous analysis focused on node‐level network analysis, additional characterization of global network topology was needed to highlight the relationships between the MTL subregions. Therefore, we characterized modular organization, which is a network property that has previously been shown in whole‐brain studies to vary across development and in neurological diseases (Alexander‐Bloch et al., 2010; Doucet et al., 2014; Fair et al., 2009). Modules represent “communities” within networks (Fortunato, 2010; Porter, Onnela, & Mucha, 2009): subsets of nodes that are more strongly connected among themselves than they are to nodes in other modules. To quantify the degree to which a network can be partitioned into modules, one can define a modularity quality function as follows (Newman, 2004):

$$Q_0=\hspace{0.17em}\sum _{i\hspace{0.17em}\ne j\hspace{0.17em}\in \hspace{0.17em}N}{(A}_{ij}-\mathrm{\gamma }{P}_{ij}\left)\mathrm{\delta }\right(g_i,g_j),$$ (7)

where $A_{ij}$ is the weighted adjacency matrix, $\mathrm{\delta }(g_i,g_j)$ = 1 if nodes i and j are in the same module and 0 otherwise, and $\mathrm{\gamma }$ is a resolution parameter (chosen to be 1 as is standard). The element $P_{ij}$ is the expected weight of the edge connecting node i to node j under the Newman‐Girvan null model defined by:

$$P_{ij}=\hspace{0.17em}\frac{k_i{k}_j}{2m},$$ (8)

where m is the total weight of the edges in the matrix. The Louvain algorithm was used to partition the MTL into modules, as this method is computationally efficient and leads to higher modularity values compared with other approaches (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008).

2.6.3. Structure‐function correlation

Given prior work suggesting topological isomorphism between whole‐brain structural covariance networks and resting‐state fMRI networks (Bassett et al., 2008; Liao et al., 2013), we wanted to determine to what degree this finding is upheld in intra‐MTL networks. This information could clarify the degree to which structural and functional connectivity provide complementary vs. equivalent information. The normal structure–function correlation may also serve as an informative baseline for future studies, as prior whole‐brain studies have revealed changes in structure–function relationship during neurological disease (Liao et al., 2013) and in various cognitive states (Hermundstad et al., 2013; Hermundstad et al., 2014). To directly quantify the relationship between structure and function in the MTL network, we computed the Pearson correlation coefficient between the edges in the group level structural covariance matrix and the group‐level functional connectivity matrix. To minimize loss of information, we included anti‐correlations (edge weights less than zero) in this analysis. Furthermore, we repeated the analysis using only the 24 subjects who had both structural and functional scans (n = 24) to ensure robustness of findings over a common group of subjects.

2.7. Statistical analysis

2.7.1. MTL volumetry

Regions with significant volumetric asymmetry were determined using a one‐sample, two‐tailed t‐test, Bonferroni‐corrected for multiple comparisons over the 12 regions (10 MTL subregions + entire hippocampus + entire MTL).

2.7.2. Network analysis

To assess the variability of our findings for both functional and structural networks, we carried out a bootstrapping procedure by randomly sampling subjects with replacement. We generated 1,000 bootstrapped samples such that each sample had the same number of subjects as the original dataset (n = 31 for structural networks, n = 24 for functional networks). For each of 1,000 bootstrapped samples, we generated a functional and structural network as described in Section 2.5, leading to a set of 1,000 functional and 1,000 structural bootstrapped matrices. Variability in local network metrics and the network asymmetry measurements was assessed by repeating these computations across the bootstrapped networks. We determined the significance of network symmetry by comparing the computed $\mathrm{\nu }$‐values to a null distribution of $\mathrm{\nu }$‐values generated by randomly permuting the network nodes (1,000 permutations).

For modularity, we determined the significance of the partitions by comparing the modularity of the partitioned networks with that of random networks generated via random permutation of the network edges (10,000 permutations) (Bassett et al., 2013). To verify the replicability of the discovered modules, we also assessed modular organization using alternative approaches. First, for both functional and structural networks, we carried out modularity analysis for each of the 1,000 bootstrapped matrices. Specifically, we computed the partitions for each of the 1,000 bootstrapped matrices and identified a consensus partition (Bassett et al., 2013). The consensus partition is defined as the partition that is most similar to the rest (Doron, Bassett, & Gazzaniga, 2012), where similarity is defined as the z‐score of the Rand similarity coefficient (Traud, Kelsic, Mucha, & Porter, 2011). Second, for the functional networks, we computed the partitions for each of the subject‐specific functional matrices (prior to averaging across subjects) and identified a consensus partition.

Finally, we computed the significance of the structure–function Pearson correlation by comparing the true correlation to a null distribution of correlations generated via random permutation of the network edges (10,000 permutations).

We considered the possibility that subregion size and temporal signal‐to‐noise ratio (tSNR) could be confounding factors for our functional network findings. Therefore, we assessed the correlation between mean subregion size and mean subregion tSNR with functional node‐level metrics to assess the effect of these variables. Significance in these correlations was determined by permuting the nodes of the network (i.e., subregions) to generate a null distribution of correlations (1,000 iterations).

2.8. Reproducibility analysis

We carried out additional analyses to evaluate robustness of our findings to modifications in our analysis pipeline. First, we replicated our functional network analyses omitting global signal regression, as this pre‐processing step has been a topic of much debate (Murphy and Fox, 2016). Second, we replicated our entire analysis after replacing any manual segmentations with their corresponding automated segmentations. Third, since investigations of brain connectivity often utilize binary graphs as input, we carried out analogous analyses on binary networks derived using a range of thresholds (see Supporting Information for a detailed description), to enhance interpretability and applicability to future studies. Finally, since the CA2 and CA3 regions are quite small and may have unreliable signal on their own, we repeated analyses after combining them with CA1 to generate a “CA” region, as well as removing them altogether.

2.9. Software

Image processing and network analyses used a combination of SPM (Friston et al., 1994), FSL (Smith et al., 2004), ANTS (Avants, Tustison, & Song, 2009), the Brain Connectivity Toolbox (Rubinov and Sporns, 2010), and custom python scripts.

3. RESULTS

3.1. MTL volumetric analysis

Following atlas validation, we computed MTL subregion volumes (Table 2) and asymmetry indices (Figure 4) across our healthy adult dataset. Although normative MTL subregion volumes are unknown due to variation in subregion definitions and protocols, our volumes fall within the range of values from various prior neuroimaging and histological studies (Supporting Information Table S1). Our total hippocampal volumes are consistent with those of previous studies, including a meta‐analysis which incorporated data from 3,564 subjects (Pedraza, Bowers, & Gilmore, 2004).

Table 2.

Mean and SDs of computed volumes for each MTL subregion, entire hippocampus (CA1–3, DG, Tail, Sub) and entire MTL over the healthy adult dataset

	Computed volumes (mm3)
	Left	Right
CA1	821 ± 182	804 ± 160
CA2	26.2 ± 8.70	30.4 ± 11.3
CA3	107 ± 19	88.9 ± 26.3
DG	623 ± 123	740 ± 128
Tail	315 ± 83.0	296 ± 69.9
Sub	837 ± 93.3	853 ± 97.7
ERC	612 ± 85.4	588 ± 81.5
BA35	660 ± 90.0	608 ± 110
BA36	1816 ± 292	1646 ± 235
PHC	1093 ± 225	1047 ± 271
HIPP	2729 ± 347	2812 ± 344
MTL	6911 ± 787	6701 ± 690

Figure 4.

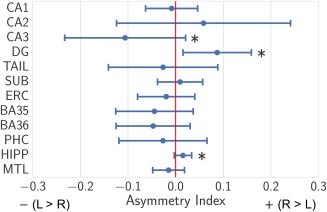
Mean and SDs of volumetric asymmetry indices [(Right – Left)/(Right + Left)] for each MTL subregion, entire hippocampus (CA1–3, DG, Tail, Sub) and entire MTL over the healthy adult dataset, *p < 0.001 (one‐sample, two‐tailed t test, Bonferroni corrected for multiple comparisons over 12 regions) [Color figure can be viewed at http://wileyonlinelibrary.com]

As expected, most subregions exhibited hemispheric volumetric symmetry; interestingly, we found significant asymmetries (p < .001) in the dentate gyrus (R > L), CA3 (L > R), and hippocampus (R > L), using a one‐sample, two‐tailed t‐test, Bonferroni‐corrected for multiple comparisons over the 12 regions.

3.2. MTL network findings

By relating the three subregion‐level functional network metrics (connectivity strength, clustering coefficient, and efficiency) between left and right hemispheres, we found that there is a strong degree of functional MTL symmetry, greater than what would be expected by chance (r = .97; $\mathrm{\nu }$ = 0.026, p < .0001) (Figure 5a). There is also a moderate degree of structural symmetry, greater than what would be expected by chance (r = .45–.67; $\mathrm{\nu }$ = 0.08, p = .002), though certain subregions—most notably the dentate gyrus—exhibit strong structural network asymmetry (Figure 5b). Mean and SDs of individual subregion‐level network metric values and asymmetries, based on the bootstrapped matrices, are presented in Supplementary Figure 1. As shown in Figure 5a, the bilateral CA1, subiculum, and DG subregions exhibit substantially higher functional connectivity as measured by all 3 metrics, and serve as clear functional network hubs. Using our definition of hubness, no subregions emerge as structural hubs.

Figure 5.

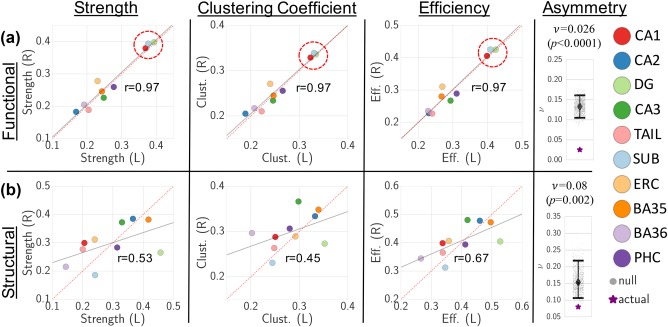
Functional (a) and structural (b) local strength, clustering coefficient (Clust.), and efficiency (Eff.) plotted for each MTL subregion between left (L) and right (R) hemispheres, along with correlation line (gray) and Pearson correlation values. Dotted red y = x line shown for comparison. Functional hubs (bilateral CA1, DG, and subiculum) are highlighted by dotted red circle. Overall network asymmetry ( $\mathrm{\nu })$ metric is also displayed for functional (a) and structural (b) networks in relation to null distributions (with associated median and 95% CIs), which demonstrates significantly lower network asymmetry compared with the null distribution (functional permutation p < .0001, structural permutation p = .002)

After analysis of subregion‐level network properties, our next analysis focused on the relationship between subregions via modularity detection. We found that both functional and structural networks organize into two modules, determined to be significant via permutation testing (structural p = .0006, functional p = .0241) (Figure 6). The functional networks subdivide into one module consisting of bilateral hippocampi and a second module consisting of bilateral parahippocampal regions. The structural networks subdivide into one module consisting of bilateral CA1, DG, subiculum, and tail, and a second module consisting of all remaining regions. Modularity detection and consensus partitioning on the bootstrapped networks yielded the identical functional and structural modules, as did modularity detection and consensus partitioning on the subject‐specific functional networks. These results highlight the reproducibility of our findings across a range of approaches for characterizing network modularity.

Figure 6.

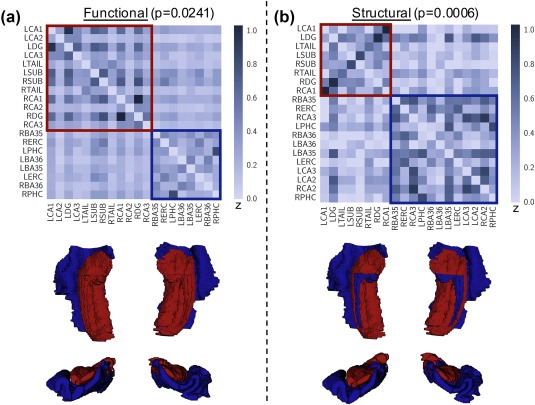
Detection of (a) functional and (b) structural modules within MTL connectivity matrices, along with visualization of modules mapped onto MTL segmentation. We find that both networks subdivide into two significant modules (structural p = .0241, functional p = .0006, permutation‐based testing), one consisting primarily of hippocampal subfields (red) and the second including all extrahippocampal subregions (blue)

Finally, we determined the relationship between function and structure by correlating the edge weights of the structural and mean functional matrices. We found a subtle but significant correlation (r = .25, p < .0005 via permutation testing) between the structural and functional networks (Figure 7). Re‐computing the structure–function correlation with only the 24 subjects who had both structural and functional scans (n = 24) yielded nearly identical results (r = .26, p < .0005).

Figure 7.

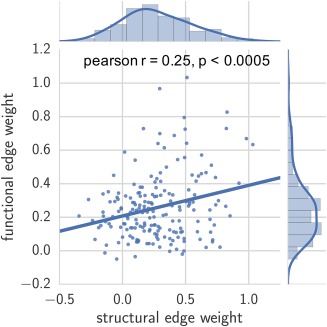
Relationship between functional and structural connectivity networks, measured by Pearson correlation of corresponding edge weights in group‐level functional and structural networks (Pearson r = .25, p < .0005, permutation‐based testing). Distribution of edge weights are also portrayed [Color figure can be viewed at http://wileyonlinelibrary.com]

Overall findings of network symmetry, hubness, modular organization, and structure–function correlation were consistent after replicating analysis with various modifications (omitting global signal regression, utilizing all manual segmentations, carrying out binary network analysis, and removing CA2/3 effects), with only minimal changes in results (Supporting Information Figures S2–S5). We found no significant correlation between mean subregion size and mean connectivity strength (r = .18, p = .60), clustering coefficient (r = .17, p = .62), or local efficiency (r = .130, p = .70). Similarly, we found no significant correlation between mean subregion tSNR and mean connectivity strength (r = .19, p = .59), clustering coefficient (r = .20, p = .57), or local efficiency (r = 0.20, p = .59).

4. DISCUSSION

The main goal of this study was to characterize the network architecture of the MTL in healthy adults using high‐resolution structural and functional MRI. Using local network metrics, we demonstrated functional and structural inter‐hemispheric symmetry, and identified functional and structural network hubs. We also found significant community structure in our networks which revealed inter‐hemispheric connectivity and a delineation between hippocampal and extra‐hippocampal structures. Finally, we observed a significant correlation in structural and functional network connectivity. Even with a moderate sample size, our findings are robust to variations in processing and analysis steps. Our findings provide an approach to characterizing MTL network structure and function that can be applied to future studies examining disease‐related changes in MTL networks.

4.1. MTL volumetric and network findings

We found that while functional connectivity was largely symmetric across hemispheres, there was considerably less symmetry in volume and structural connectivity. Structural asymmetry was driven by dentate gyrus and, less substantially, CA3. The volumetric asymmetry in dentate gyrus and CA3 also manifested as asymmetry in structural connectivity, which is likely at least partially due to the fact that volumetric information was used for structural network construction. Several prior studies have revealed that right hippocampi are subtly larger than left in healthy adults (Hou, Yang, & Yuan, 2013; Pedraza et al., 2004; Woolard and Heckers, 2012), though subregion‐level asymmetry has not been previously evaluated. Our findings suggest that this asymmetry is primarily localized to the dentate gyrus, though further studies should be carried out on larger datasets to support this finding. Though the underlying mechanism for hippocampal asymmetry is unknown, it may relate to the functional specialization of the hemispheres, as the left and right MTL are associated with verbal and nonverbal memory, respectively (Kelley et al., 1998; Kennepohl, Sziklas, Garver, Wagner, & Jones‐Gotman, 2007). Although the functional connectivity networks revealed a strong level of functional symmetry during the resting‐state, our methodology can be applied to memory task‐based data to assess the degree of hemispheric asymmetry based on known functional lateralization.

Our analysis revealed that CA1, DG, and subiculum serve as functional network hubs, suggesting that these subregions facilitate functional integration within the MTL network. Indeed, CA1, DG, and subiculum are implicated in a number of hippocampal pathways, including the mossy fiber pathway (DG → CA3), perforant path (entorhinal cortex → subiculum, DG, CA) and Schaffer collaterals (CA3 → CA1) (Lavenex and Amaral, 2000; Small et al., 2011; Zeineh et al., 2016). The subiculum also forms a key transition zone between CA1 and the entorhinal cortex (Stafstrom, 2005). Therefore, our finding of high functional connectivity in these regions is in accordance with existing knowledge of MTL physiology.

Community detection analyses revealed that the functional MTL network subdivides into two modules—one consisting of bilateral hippocampal subfields and the other consisting of bilateral parahippocampal regions. Since modules exhibit high intra‐modular statistical dependence and high inter‐modular statistical independence (Sporns, 2013), the modular organization suggests a functional segregation of neuronal processing within the MTL. Our finding is supported by a prior fMRI study which found a functional distinction between the hippocampus and adjacent MTL cortices (Lacy and Stark, 2012). The structural MTL covariance network subdivided similarly, although surprisingly, bilateral CA2/CA3 fell in the structural module consisting of otherwise parahippocampal structures. Given the relatively high variance and low DSCs of these smallest subregions, this analysis should be confirmed in future studies with larger and/or higher‐resolution datasets. Interestingly, we found that the bilateral CA1, DG, and subiculum, which formed a structural module, also were the functional network hubs. This highlights the complementary, yet indirect, relationship between structure and function within the MTL.

Our demonstration of a significant structure–function correlation further suggests that while MTL structure and function are clearly linked, there is also considerable variance between these MTL attributes that warrants further exploration. Our dual structural–functional approach is particularly relevant within the context of several recent studies which reveal that the relationship between whole‐brain structural and functional connectivity is implicated in both normal cognition and in disease (Goni et al., 2014; Hermundstad et al., 2013; van den Heuvel, Mandl, Kahn, & Hulshoff Pol, 2009; Honey et al., 2009; Liao et al., 2013; Wirsich et al., 2016; Zhang et al., 2011). Though a significant correlation in whole‐brain structural and functional connectivity is observed in these studies, differences in imaging techniques, parcellation schemes, and network methods prohibit direct quantitative comparisons in correlation strength.

Previous research in network neuroscience (Bassett and Sporns, 2017) has focused on mapping structural and functional “connectomes” in healthy adults by rigorously characterizing connectivity between regions of the cerebral cortex based on multi‐modal neuroimaging (Fornito, Zalesky, & Breakspear, 2013, 2015; Hagmann et al., 2007; Zuo et al., 2012). Such work to establish valid normative data has spawned an entire field of research mapping network changes across variables such as intelligence, gender, and age, as well as in various neurological and psychiatric diseases (Fair et al., 2009; Khambhati, Davis, Lucas, Litt, & Bassett, 2016; Li et al., 2009; Lynall et al., 2010; Supekar et al., 2008). In this study we extend this approach to map the MTL connectome, which should lead to new insights into brain–behavior relationships, particularly given the integral role of the MTL in cognition and the increasing availability of high resolution MRI datasets.

4.2. Methodological considerations and limitations

It is important to note that our measure of structural connectivity is not a measure of direct white matter paths connecting various MTL subregions, but rather a proxy for structural wirings based on covariance in gray matter volumes. Although several studies have found robust correlations between structural networks based on covariance of morphometric features and structural networks based on anatomical connections, there is no direct proof that correlations of gray matter volumes across subjects indicate axonal connectivity (Mechelli et al., 2005; Pezawas et al., 2005). Therefore, in our model, high structural connectivity between an MTL subregion and its contralateral counterpart does not necessarily support the presence of a direct inter‐hemispheric anatomical connection. In our case, such an approach is necessary because diffusion tractrography, the primary alternative approach to glean structural connectivity, does not have the resolution to isolate pathways within the MTL. However, recent advances in ultra‐high resolution diffusion‐weighted imaging (Modo, Hitchens, Liu, Richardson, & Modo, 2015; Yassa, Muftuler, & Stark, 2010) may allow researchers to employ our methods using diffusion tractography data in future studies.

Another consideration relates to the fMRI data resolution. Although most subregions have a substantial average number of voxels in the fMRI space (e.g., CA1: 203, DG: 170), the smaller subregions have relatively few voxels (CA2: 7, CA3: 24). Since neighboring voxels in fMRI data are known to be highly correlated, signal from neighboring subregions—particularly the smallest subregions—may be collinear. Our processing pipeline aimed to mitigate this effect by co‐registering to the higher‐resolution structural MRI space, which has been shown to help maintain the effective resolution of the measured functional activity (Kang et al., 2007) and is common in high‐resolution studies of hippocampal subfields (Carr et al., 2010; Das et al., 2013; Suthana et al., 2015). We also omitted spatial smoothing to maintain spatial specificity of the measured functional activity and minimize collinearity. Moreover, we regressed out ventricular CSF and white matter to minimize partial volume effects and ensure that the observed signals were not a result of neighboring non‐gray matter noise. Finally, we replicated our analysis after removal of CA2 and CA3, and after merging CA2 and CA3 with CA1, to ensure that partial volume effects in these two regions were not driving our overall findings. Further studies should be carried out on higher resolution fMRI data to confirm our findings related to the smallest subregions.

A related consideration is that functional connectivity networks were generated in this study using a different number of voxels per subregion, since there is inherently a large range of sizes across the 10 MTL subregions. This means that the measurements for smaller subregions are inherently noisier than larger subregions. We decided to keep all voxels rather than eroding the larger regions to more closely approximate the size of smaller regions, in order to minimize effects of biasing results based on the chosen voxels within each subregion. Also, while the small CA2 and CA3 hippocampal subfields had low connectivity strength, so did the larger PHC, indicating that the correlation strength is not merely a function of subregion size. It may also be possible that central, rounded structures, such as dentate gyrus, may have more reliable SNR ratio than a more peripheral cortical ribbon‐like structure such as PHC. However, we are reassured that subregion size and tSNR are not significant confounds, as they are not significantly correlated with the computed node‐level metrics.

A limitation of our 7T atlas set is that we were unable to include intra‐rater reliability measurements for validation. However, since our atlas protocol was directly derived from an existing extensively validated 3T protocol, and since MTL subregion DSCs were comparable to those of prior protocols, we believe it is of high reliability. Although our atlas yielded high‐quality automated segmentations, further studies should be carried out to optimize atlas composition—such as number and distribution of healthy vs. diseased subjects—for maximal applicability to future investigations.

Several prior fMRI studies reveal differential connectivity patterns along the gradient of the MTL's anterior–posterior axis (Das et al., 2015; Libby, Ekstrom, Ragland, & Ranganath, 2012; Maass et al., 2015). Although our study focused on network connectivity among MTL regions with clear anatomical delineations, further exploration of the intra‐MTL subregion connectivity along the anterior‐posterior gradient is warranted. Future higher‐resolution studies may also allow for the subdivision of the “tail” region into its component subfields to distinguish the detailed neuroanatomy in this region.

4.3. Conclusion

We present a comprehensive in vivo neuroimaging study characterizing intra‐MTL network connectivity in healthy adults by applying graph‐theoretical techniques to high‐resolution 7T MRI data. This study delineates a methodological approach and provides normative data for a range of future work involving neurological and psychiatric disorders involving the MTL, in which MTL network measures potentially provide insights into disease pathogenesis or serve as biomarkers.

Our network analysis scripts, associated visualizations, and raw data are publicly available at https://github.com/shahpreya/MTLnet.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supporting Information

Shah P, Bassett DS, Wisse LEM, et al. Mapping the structural and functional network architecture of the medial temporal lobe using 7T MRI. Hum Brain Mapp. 2018;39:851–865. 10.1002/hbm.23887