Abstract
As photoinhibition primarily reduces the photosynthetic light use efficiency at low light, sunfleck-induced photoinhibition might result in a fatal loss of carbon gain in the shade leaves within a canopy with barely positive carbon balance. We hypothesized that shade leaves at the lower canopy might retain a certain amount of leaf nitrogen (NL) to maintain energy consumption via electron transport, which contributes to circumventing photoinhibition during sunflecks to keep efficient utilization of low light during the rest period of daytime. We investigated excess energy production, a potential measure of susceptibility to photoinhibition, as a function of NL distribution within a Japanese oak canopy. Optimal NL distribution, which maximizes canopy carbon gain, may lead to a higher risk of photoinhibition in shade leaves during sunflecks. Conversely, uniform NL distribution would cause a higher risk of photoinhibition in sun leaves under the direct sunlight. Actual NL distribution equalized the risk of photoinhibition throughout the canopy indicated by the constant excess energy production at the highest light intensities that the leaves received. Such a homeostatic adjustment as a whole canopy concerning photoinhibition would be a key factor to explain why actual NL distribution does not maximize canopy carbon gain.
Introduction
Within a canopy, leaves acclimate to the growth light conditions, where sun-exposed leaves have a higher area-based leaf N pool (NL) and higher photosynthetic capacity than shaded leaves1–4. Such a gradient of leaf N along the canopy depth is considered as an efficient utilization of the limited N resource to maximize photosynthetic C gain over the canopy of an entire plant in response to the light gradient within a canopy5–7. However, the measured NL distribution is more uniform than the theoretically optimal NL distribution to maximize the canopy carbon gain8–10, which means that sun leaves show lower and shade leaves greater NL than the optimal value6,11. Furthermore, Hikosaka10 reported that the optimal NL distribution, considering both direct and diffuse light into account, was much steeper than that conventionally estimated under diffuse light only6,7. Several theoretical approaches have been conducted to explain the less steep declines in NL than the light gradient within canopies accounting other constraints than light, such as leaf morphological plasticity12, photosynthetic capacity at the top of the canopy limited by the maximum nutrient concentration13, and hydraulic conductance14.
Recently, the importance of direct light, i.e., sunflecks within a canopy, was emphasized both in photosynthesis and photoinhibition. Sunflecks can significantly improve C gain in shade leaves of the lower canopy, while shade leaves may suffer from photoinhibition by the high photosynthetic photon flux density (PPFD) of sunflecks15. Photosynthetic efficiency is reduced during the recovery from photoinhibition on the transition from sunflecks to shade, which would result in a considerable reduction in plant productivity16. The degree of photoinhibition has been empirically linked to average or integrated light intensity in photosynthetic plant production models17,18. However, recent studies have reported that plants grown under fluctuating light environments upregulated the photoprotective mechanisms and electron transport compared with those grown under constant light conditions in response to sunflecks, even when the amounts of daily total irradiance are comparable19,20. This suggests that leaves may well acclimate to sun flecks (brief and strong irradiance) rather than averaged irradiance, so as to circumvent transient photoinhibition.
Photoinhibition primarily reduces the photosynthetic light use efficiency at low PPFD, i.e. a reduction of the initial slope of the photosynthetic light-response curve rather than the light-saturated photosynthetic rate17. In this context, sunfleck-induced photoinhibition may result in a fatal loss of carbon gain in the shade leaves with barely positive carbon balance16. To prevent photoinhibition, electron transport, mainly involved in photosynthesis and photorespiration21, plays an important role in consuming absorbed light energy as well as thermal energy dissipation3,22,23. Excess energy, neither consumed by electron transport nor dissipated as heat, is known to have a close relationship to photoinactivation of PSII under the inhibition of PSII repair24,25.
Leaf N participation for the circumvention of photoinhibition is specifically involved in electron transport, but not in xanthophyll-related thermal energy dissipation, since xanthophyll pigments, violaxanthin (C40H56O4), antheraxanthin (C40H56O3), and zeaxanthin (C40H56O2), do not contain any N26. As for the fractions of leaf N in Rubisco, and in proteins related to linear electron transport, there can be little differences in the fractions between upper and lower canopy leaves27. In this context, leaf N gradient within the canopy can closely reflect the gradient of photosynthesis-related proteins. The capacity of electron transport depends on NL, which is varied through intra-canopy light gradients28,29. Thus, shade leaves at the lower canopy may retain a certain amount of NL to circumvent photoinhibition during sunflecks to keep efficient utilization of low PPFD during the rest period of daytime16.
We hypothesized that NL should be distributed within a canopy to prevent photoinhibition both in shade leaves during sunflecks and sun leaves under the direct sunlight, leading to the less steep NL distribution than the optimal NL distribution. To test this hypothesis, we determined how excess energy production, which could be a possible measure of the susceptibility to photoinhibition22,24,25,30, was distributed within a canopy when NL distribution was changed. We investigated photosynthetic traits in the leaves within a canopy of Japanese oak by gas exchange and chlorophyll fluorescence measurements, as well as light and N distribution within the canopy.
Results
Total leaf area index (LAI), FT, in the forest was estimated to be 5.91 m2 m−2 based on the stratified clipping method conducted in 2001 and 2003. Based on the LAI cumulated from the canopy top (F), the light extinction coefficient of the canopy (KL) was 0.739 in Eq. 6. Based on the relationship between the relative light intensity (I/I0) and F (Eq. 6), we derived F of 15 leaves used for the photosynthetic measurements in 2007 by using relative light intensity at each leaf position. The actual distribution of NL as a function of F in 2007 was revealed as follows:
Based on the integration of the actual NL distribution, total N per unit ground area (NT) was calculated as 8.59 g m−2. Optimal N distribution in the canopy was expressed as follows:
NL with uniform distribution was estimated to be 1.45 g m−2, estimated as NT/FT.
Actual and optimal NL distributions within the canopy are shown in Fig. 1. Optimal NL was higher than the actual value in the case of F < 1.7 m2 m−2, whereas it was lower than the actual value in the case of F > 1.7 m2 m−2. F of 1.7 m2 m−2 corresponds to the average integrated daily quantum flux density in June (Qint) of 12 mol m−2 day−1 (Eq. 6).
Figure 1.
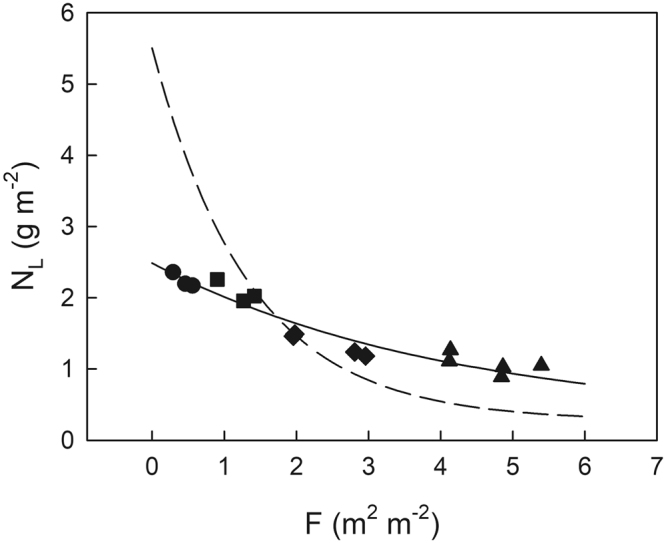
Actual leaf N (NL) distribution in the canopy of Japanese oak as a function of the leaf area index cumulated from the canopy top (F). Dashed line indicates optimal NL distribution. Leaves were classified into four types based on their growth light environments (Qint): (1) deep shade (triangle, 0 < Qint < 3 mol m−2 day−1), moderate shade (diamond, 3 < Qint < 15 mol m−2 day−1), moderate sun (square, 15 < Qint < 25 mol m−2 day−1), and typical sun leaves (circle, 25 < Qint < 35 mol m−2 day−1).
In the present study, we expediently classified the leaves into four types based on their growth light environments: (1) deep shade leaves (0 < Qint < 3 mol m−2 day−1, n = 5); (2) moderate shade leaves (3 < Qint < 15 mol m−2 day−1, n = 4); (3) moderate sun leaves (15 < Qint < 25 mol m−2 day−1, n = 3); and (4) typical sun leaves (25 < Qint < 35 mol m−2 day−1, n = 3). Hereafter, we often use “shade leaves” to refer to deep and moderate shade leaves and “sun leaves” to refer to moderate and typical sun leaves. Peak PPFD entering through the canopy (PPFDmax), i.e. sunflecks, was considerably high (>700 µmol m−2 s−1), even for the deep shade leaves (Fig. 2).
Figure 2.
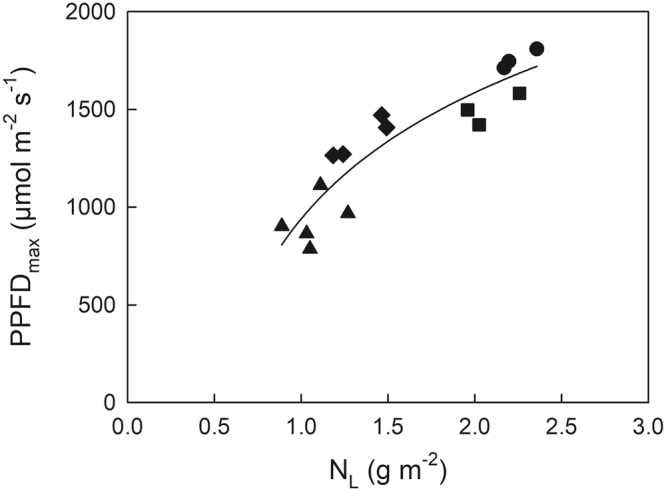
Maximal photosynthetic photon flux density (PPFDmax) in June at various leaf positions with various leaf N pool (NL) within the canopy of Japanese oak. PPFDmax was estimated as average daily peak PPFD at each leaf position using the five highest values daily in June. Symbols are the same as in Fig. 1.
Electron transport rate (ETR) with actual, optimal and uniform NL distribution showed similar relationships as a function of NL (Fig. 3a). Higher ETR in sun leaves but lower ETR in shade leaves was observed with optimal NL distribution when compared with those with actual NL distribution (Table 1). To investigate how ETR changed from the actual to the optimal and uniform NL distribution, we showed ETRopt/ETRact and ETRuni/ETRact as a function of Qint (Fig. 4a). Higher ETRopt/ETRact was observed in leaves grown under higher Qint, compared among leaf types (Fig. 4a, Table 2). When compared with ETR in leaves with actual NL distribution for each leaf type, relatively lower ETR in the deep shade leaves and relatively higher ETR in the typical sun leaves were observed with optimal NL distribution (Table 2). Conversely, with uniform NL distribution, higher ETRuni/ETRact was observed in the deep shade leaves than the other leaves, where relatively higher ETR in the deep shade leaves and lower ETR in sun leaves were observed when compared with those in leaves with actual NL distribution (Fig. 4a, Table 2).
Figure 3.
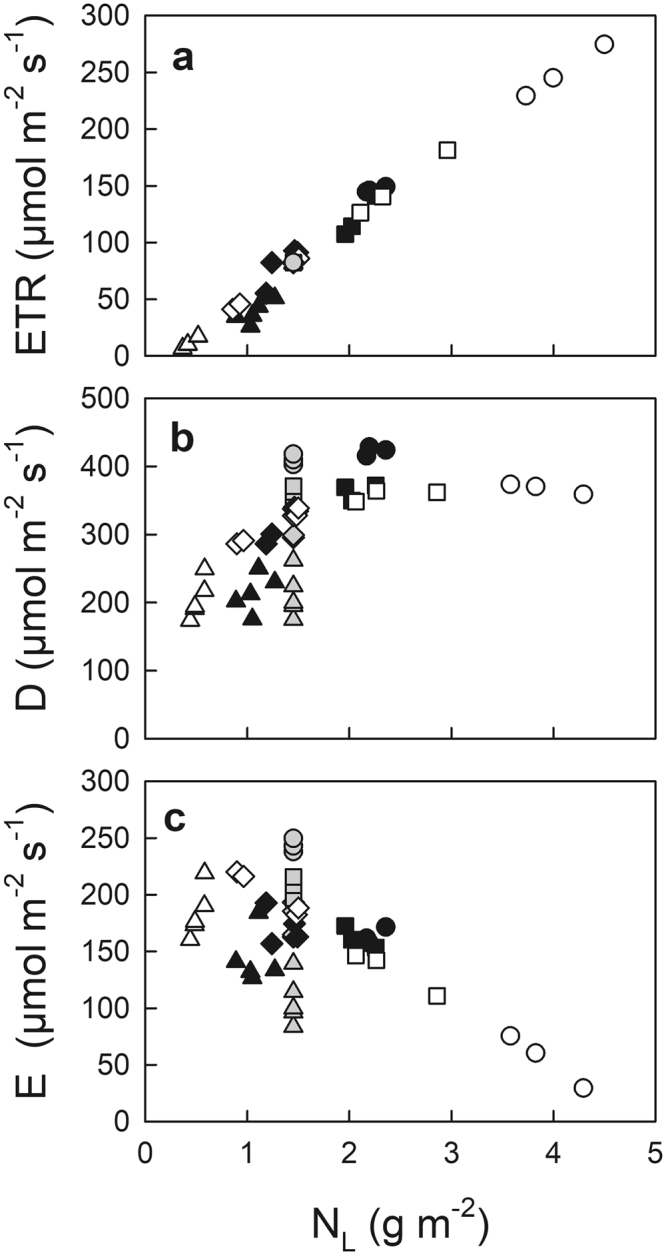
Electron transport rate (ETR) (a), thermal energy dissipation (D) (b), and excess energy (E) (c) at maximal photosynthetic photon flux density (PPFDmax) as a function of leaf N pool (NL) with actual (closed), optimal distribution (open), and uniform distribution (grey symbols) in the canopy of Japanese oak. Symbols are the same as in Fig. 1.
Table 1.
ETR, D and E (µmol m−2 s−1) in different leaf types of Q. mongolica at PPFDmax with actual, optimal and uniform NL distribution.
| Parameter | Leaf type | ANOVA | |||
|---|---|---|---|---|---|
| Deep shade | Moderate shade | Moderate sun | Typical sun | ||
| Actual NL | |||||
| ETR | 38 ± 4a | 80 ± 9b | 121 ± 10c | 147 ± 1d | F = 50.0 P < 0.001 |
| D | 214 ± 13a | 315 ± 13b | 364 ± 7c | 423 ± 4d | F = 60.8 P < 0.001 |
| E | 143 ± 10 | 172 ± 8 | 162 ± 6 | 163 ± 4 | F = 2.2 ns |
| Optimal NL | |||||
| ETR | 12 ± 2a | 64 ± 12b | 149 ± 17c | 250 ± 13d | F = 95.3 P < 0.001 |
| D | 205 ± 13a | 311 ± 13b | 358 ± 5bc | 368 ± 4c | F = 44.5 P < 0.001 |
| E | 184 ± 10c | 202 ± 10c | 133 ± 11b | 55 ± 14a | F = 32.9 P < 0.001 |
| Uniform NL | |||||
| ETR | 82 ± 0a | 82 ± 0b | 82 ± 0b | 82 ± 0b | F = 19.7 P < 0.001 |
| D | 211 ± 15a | 315 ± 10b | 360 ± 7c | 410 ± 4c | F = 51.3 P < 0.001 |
| E | 107 ± 9a | 177 ± 8b | 207 ± 5c | 244 ± 3d | F = 54.3 P < 0.001 |
Values are means ± SE for each leaf type. Different letters indicate significant differences among the leaf types at P < 0.05, according to Holm’s pairwise comparisons. ns indicates non-significant effect of leaf type.
Figure 4.
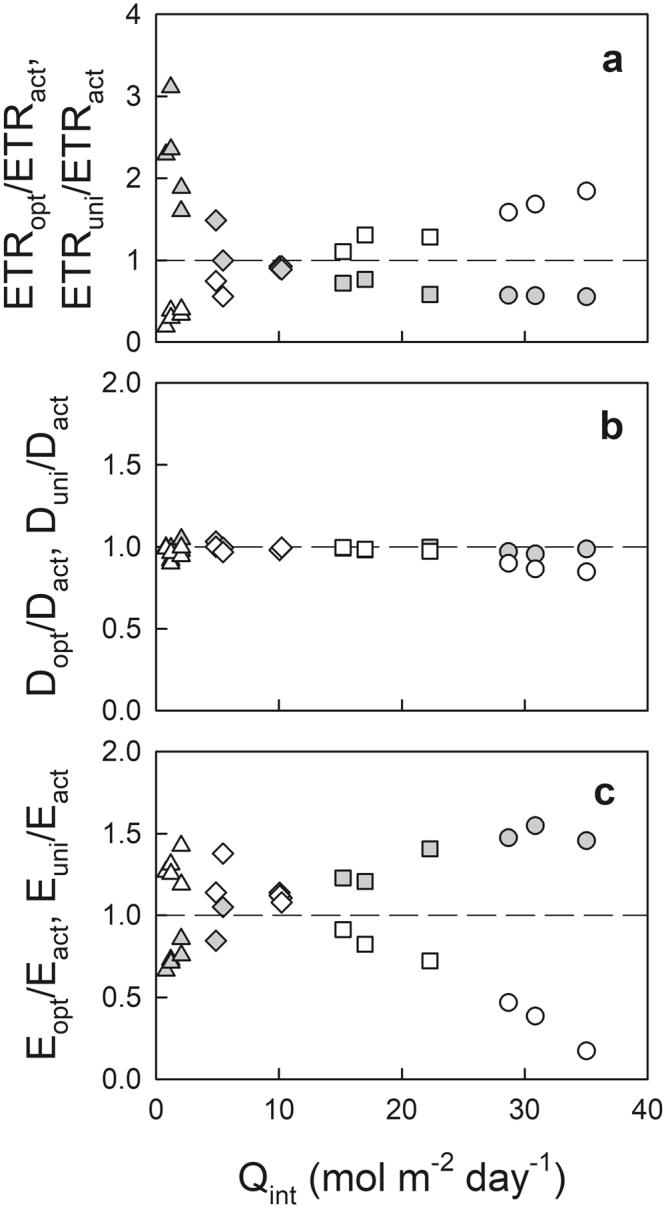
The ratio of ETR (a), D (b) and E (c) with optimal (open) and uniform NL distribution (grey symbols) (ETRopt, Dopt and Eopt; ETRuni, Duni and Euni) to those with actual NL distribution (ETRact, Dact and Eact, respectively) at PPFDmax for a given leaf as a function the daily mean of the integrated photon flux density during leaf development (Qint). Dashed line indicates the ratios = 1. Symbols are the same as in Fig. 1.
Table 2.
The ratio of ETR, D and E with optimal and uniform NL distribution (ETRopt, Dopt and Eopt; ETRuni, Duni and Euni) to those with actual NL distribution (ETRact, Dact and Eact, respectively) at PPFDmax in different leaf types of Q. mongolica. Values are means ± SE for each leaf type.
| Parameter | Leaf type | ANOVA | |||
|---|---|---|---|---|---|
| Deep shade | Moderate shade | Moderate sun | Typical sun | ||
| Optimal NL | |||||
| ETRopt/ETRact | 0.32 ± 0.04a,* | 0.79 ± 0.09b | 1.23 ± 0.06c | 1.70 ± 0.08d,* | F = 81.3 P < 0.001 |
| Dopt/Dact | 0.96 ± 0.02b | 0.99 ± 0.01b | 0.99 ± 0.01b | 0.87 ± 0.02a,* | F = 12.2 P < 0.001 |
| Eopt/Eact | 1.29 ± 0.04c,* | 1.18 ± 0.07c | 0.82 ± 0.06b | 0.34 ± 0.09a,* | F = 47.6 P < 0.001 |
| Uniform NL | |||||
| ETRuni/ETRact | 2.25 ± 0.26b,* | 1.07 ± 0.14a | 0.69 ± 0.06a,* | 0.56 ± 0.00a,* | F = 17.4 P < 0.001 |
| Duni/Dact | 0.98 ± 0.02 | 1.00 ± 0.01 | 0.99 ± 0.00 | 0.97 ± 0.01 | F = 0.54 ns |
| Euni/Eact | 0.74 ± 0.03a,* | 1.04 ± 0.07b | 1.28 ± 0.06c,* | 1.49 ± 0.03d,* | F = 43.4 P < 0.001 |
Different letters indicate significant differences among the leaf types at P < 0.05, according to Holm’s pairwise comparisons. ns indicates non-significant effect of leaf type. *Indicates significant differences in ETR, D and E from those of actual NL distribution in each leaf type at P < 0.05 with t-test.
Higher thermal energy dissipation (D) was generally observed in leaves grown under higher Qint with any NL distribution, whereas the slope become less steep in leaves with optimal NL than the actual, and uniform NL distribution (Fig. 3b, Table 1). With optimal NL distribution, the typical sun leaves showed lower Dopt/Dact than the other leaf types, and relatively lower D than that in the typical sun leaves with actual NL distribution. Conversely, there was no significant differences in Duni/Dact among leaf types with uniform NL distribution, and also there was no difference in D in leaves with uniform NL distribution from that in leaves with actual NL distribution within each leaf type (Fig. 4b, Table 2).
There was no difference in excess energy production (E) among leaf types with the actual NL distribution (Fig. 3c, Table 1). A significantly higher E was observed in shade leaves than in sun leaves with optimal NL distribution. Conversely, a significantly higher E was observed in sun leaves than in shade leaves with uniform NL distribution (Fig. 3c, Table 1). Similarly, higher Eopt/Eact was observed in shade leaves than in sun leaves with optimal NL distribution, whereas higher Euni/Eact was observed in sun leaves than in shade leaves with uniform NL distribution (Fig. 4c, Table 2). With optimal NL distribution, deep shade leaves showed relatively higher E, but typical sun leaves showed relatively lower E compared with those in actual NL distribution (indicated by the asterisks in Table 2). Conversely, with uniform NL distribution, deep shade leaves showed relatively lower E, but sun leaves showed relatively higher E compared with those in actual NL distribution.
Based on the relationship between variance in E (s2) and the leaf N distribution coefficient (Kn), the Kn minimizing s2 was estimated as 0.291 (Fig. 5), which was very close to the Kn in the actual NL distribution (0.241 in Eq. 7). We also found that the values of E at PPFDmax with the actual NL distribution within the canopy of Japanese oak were very similar to those with the NL distribution to maintain E constant, minimizing the variance in E (Kn = 0.291) (Fig. 6).
Figure 5.
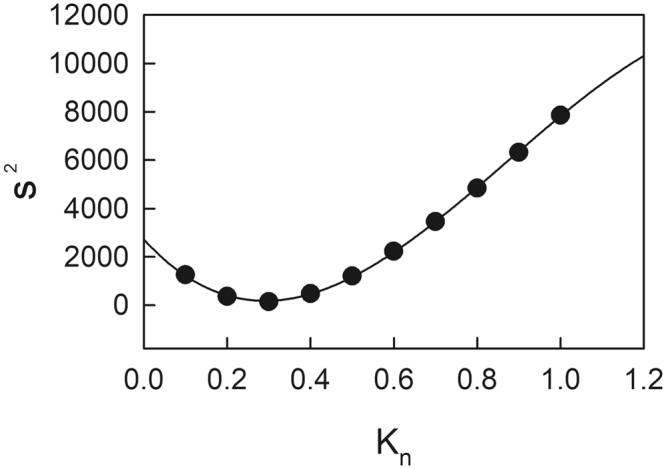
The relationship between the variance (s2) in excess energy production (E) at maximal photosynthetic photon flux density (PPFDmax) and variable leaf N distribution coefficient (Kn).
Figure 6.
Excess energy production (E) at maximal photosynthetic photon flux density (PPFDmax) as a function of leaf N pool (NL) with actual distribution (closed) and the distribution to minimize the variation in E (open symbols) in the canopy of Japanese oak. Symbols are the same as in Fig. 1.
Discussion
We investigated the fate of absorbed light energy (ETR, D, and E) in leaves with actual, optimal, and uniform N distribution within the canopy of Japanese oak. Excess energy is known to have a close relationship to photoinactivation of PSII under the inhibition of PSII repair24,25. There are two mechanisms involved in photoinhibition (defined as photoinactivation of PSII), i.e., an excess energy mechanism and a two-step mechanism25. As excess energy might be predominantly involved in photoinhibition in the field under visible light especially at the range of relatively high irradiance25,30,31, c.f. 700–1800 µmol m−2 s−1 during the sunflecks in the present study, we used the chlorophyll fluorescence parameter “excess energy,” as an empirical measure of the sensitivity of photoinhibitory damage based on the former mechanism. It is noteworthy that E during sunflecks for shade leaves or direct sunlight for sun leaves was stable among leaf types with the actual NL distribution at various canopy depths, whereas a significantly higher E was observed in the shade leaves than sun leaves with the optimal NL distribution; a significantly higher E in sun leaves than shade leaves with the uniform NL distribution (Fig. 3c, Table 1). As photoprotective D was not enhanced in the leaves with decreased ETR (Table 2)22, the decreases in ETR in the shade leaves with an optimal NL distribution, and in the sun leaves with a uniform NL distribution both resulted in the increases in E. This also suggests that the photoprotective thermal energy dissipation would not respond enough to set off the changes in ETR with different NL distributions as far as the present model prediction is concerned, partly because of the small variation in D in the fully acclimated leaves to their growth environments (Supplemental Fig. S1) as reported in long-term drought acclimated plants32,33.
In the present study, the optimal N distribution was estimated using the simple Beer’s law with an assumption that leaves received diffuse light only6,7. Hikosaka10 reported that the optimal N distribution under direct and diffuse light, a more realistic condition than diffuse light only6,7, was steeper than that under diffuse light only. However, from the viewpoint of photoinhibitory damage, the actual N distribution in the canopy of Japanese oak, which was less steep than the optimal distribution, might be inherently optimized to circumvent photoinhibitory damage at the whole-canopy level by maintaining excessive energy at a certain level under direct sunlight throughout the leaves grown at various light environments within a canopy.
We estimated canopy C gain based on light response curves built with different N distribution and incident PPFD with 1-min-intervals in July 2007 (details in Supplementary Information: Estimation of canopy C gain, Figs S2–S5). We used coefficients of light response curves measured at a leaf temperature of ≈27 °C, with no correction for the effects of air temperature, and air humidity on photosynthesis. Total canopy C gain was 24.9, 21.3, and 15.8 mol m−2 on the ground surface basis for optimal, even-E, which makes E constant throughout the canopy with Kn = 0.291 (Fig. 6), and uniform leaf N distribution, respectively. Even-E N distribution, showed a 15% decrease in canopy C gain integrated in July, during a photosynthetically most vigorous period, compared with optimal N distribution. Conversely, uniform N distribution resulted in a 36% decrease in canopy gain compared with the optimal N distribution. It is noteworthy, not only the sun leaves with higher leaf NL with optimal canopy N distribution, but also the shade leaves with lower NL compared with those with even-E N distribution contributed to the higher C gain as a consequence of reduced nighttime respiration rate (Supplementary Figure S5). In this estimation, a decrease in photosynthetic efficiency caused by photoinhibition under fluctuating light was not taken into account16,19,20. An enhanced recovery capacity from photoinhibition by bioengineering lead to an increase in biomass of tobacco plants by up to 20% in fluctuating light16. Thus, there is a possibility to reduce the difference in the canopy C gain between even-E and optimal N distribution, when the photoinhibitory effects on photosynthetic efficiency are accounted. In addition to an acclimation to short-term fluctuating light (sunflecks), as Japanese oak is a gap-dependent species, which needs a gap formation for its regeneration2,23, keeping relatively higher ETR in shade leaves than optimal would be a pre-conditioning for long-term fluctuating light (gap formation) for this species.
The cost of D1 protein turn-over, as a relevant process of PSII repair, is substantially low at most 0.5% of photosynthetic ATP production34, and the cost of relaxation of thermal energy dissipation is also reported to be substantially small, about 0.05% of the total photosynthetic electron flow under saturating light26. Therefore, the recovery cost from photoinhibition would be negligible for canopy C balance. Rather, reduced photosynthetic efficiency during the recovery from photoinhibition on transfer from sun flecks to shade may have a more significant adverse effect on canopy C gain16. In this context, circumvention of photoinhibition via an enhancement of ETR is essential to maintain the canopy C gain by preventing photoinhibition without any decrease in photosynthetic efficiency, in contrary to xanthophyll-related thermal energy dissipation.
Leaf photosynthetic capacity is closely related to leaf morphology such as leaf mass per area (LMA), where leaves with greater LMA generally have greater leaf area-based nitrogen contents and greater photosynthetic capacity3,35,36. During leaf maturation of Japanese oak, LMA reaches its maximum, accompanied with an increase in net photosynthetic rate, several weeks after the leaves are fully expanded and the light environment within a canopy is fixed (Tobita unpublished data37). Although the sun/shade anatomy of deciduous leaves is mainly determined by the light condition in the previous year38, less extent but some plasticity exists in leaf morphological change in response to current-year light environment39. For Japanese oak, LMA and net photosynthetic rate increased during June, after the leaf expansion had completed at the end of May (Tobita unpublished data). It was for this reason that we chose growth light environments (Qint, PPFDmax) in June as determining factors for photosynthetic traits. The equalized amount of excessive energy production observed across the various light environments within a canopy (Figs 5 and 6) could be explained if the developments of photosynthesis (involved in ETR) and photoprotection (involved in D) along with the increase in LMA would be continued until the excessive energy production during sunflecks or direct sunlight drops below a certain level both in shade and sun leaves19,20.
The hypothesis of the present study: higher NL than optimal is needed in the shade leaves to prevent photoinhibition during sunflecks, is partly similar to that proposed by Dewar et al.12, where a lower bound of LMA in the shade leaves exists, in relation to the limitation in leaf morphological plasticity23. Furthermore, the present study also proposes that the upper bound of NL in sun leaves would be regulated as the minimum required to circumvent photoinhibition under direct sunlight, which might be related to the upper-bound constraint on photosynthetic capacity at the top of the canopy proposed by Lloyd et al.13 to explain the less steep NL decline. In the present study, water stress during leaf development was considered to be negligible because of a considerable amount of spring snowmelt in the forest (mean maximum snow depth was 114 cm)40. Peltoniemi et al.14 proposed that limited hydraulic conductance for the sun leaves may result in a lower NL in sun leaves with actual NL distribution than the optimal one. In contrast, leaves acclimated to long-term drought often show higher NL accompanied with higher ETR, than leaves grown without drought stress, to prevent photoinhibition under lower intercellular CO2 concentration by stomatal closure32,33,41,42. In this context, water stress on sun leaves induced by the limited hydraulic conductance in the upper canopy43,44 would not necessarily decrease NL in sun leaves, but rather increase NL for preventing photoinhibition. Further investigation is needed on such environmental stresses during leaf development influencing excess energy production to predict leaf N distribution within a canopy.
Conclusion
The present study provides a novel insight into the canopy NL distribution with respect to circumvention of photoinhibitory damage at the whole-canopy level like a homeostatic adjustment, where plants follow a strategy through which NL distribution is not optimized for canopy C gain but rather regulated to prevent photoinhibition during sunflecks for shade leaves or direct sunlight for sun leaves. This regulation of NL distribution contributes to keeping an efficient light utilization capacity during the daytime at the whole-canopy level, by means of minimizing a time lag in the recovery from photoinhibition16, which indicates an important biological plasticity in the response to light environment, and may suggest genetically-driven adjustments for successful acclimation in a changing light environment. Revealing such a physiological coordination of individual leaves for the benefit of the whole canopy will contribute to advancing the understanding of carbon–nitrogen interactions45,46 and energy flow in terrestrial ecosystems. Further studies with different species and at different environmental conditions are needed to demonstrate that the regulation of NL distribution found in this study is an unequivocal biological mechanism occurring across species.
Methods
Study site
The present study was conducted in the experimental forest of the Hokkaido Research Center, Forestry and Forest Products Research Institute in Sapporo, Japan (43°N, 141°E; 180 m above sea level). Mean annual precipitation was approximately 900 mm and the mean annual temperature was 7.1 °C. The predominant species were Japanese white birch (Betula platyphylla Sukatchev var. japonica Hara) and Japanese oak (Q. mongolica Fisch. ex Ledeb. var. crispula (Blume) H. Ohashi), which comprised >75% of the plot basal area.
Estimation of the photosynthetic photon flux density (PPFD) at various leaf positions within the canopy
Leaf morphological and physiological traits are determined by light environments under which leaves are developed27. We considered that light conditions during leaf development in June were important for leaves of Q. mongolica because photosynthesis reached its maximum during this period (Tobita unpublished data). A hemispherical photograph was taken by a digital camera (Coolpix 4500, Nikon, Tokyo, Japan) with a fisheye lens (Fisheye Lens, FC-E8, Nikon) right above each of the leaves that were used for the photosynthetic gas exchange and chlorophyll fluorescence measurements at the summertime in 2007. Based on the photographs, we estimated the incident PPFD for each leaf by using a canopy analysis software (WinScanopy, Regent Instruments Inc., Quebec, Canada)47 combined with the data of direct and diffuse radiation from the open sky measured by a pyrheliometer (CH1, Kipp & Zonen, Delft, The Netherlands) combined with an automatic solar tracker (ASTX-1, Prede, Tokyo, Japan) and a pyrheliometer (CM21, Kipp & Zonen) with 1-min intervals placed above the canopy in the experimental forest. Instantaneous incident PPFD at each leaf position was estimated as below:
or
| 1 |
where ISF is the indirect (diffuse) site factor estimated by the WinScanopy software, penetration of the direct radiation is also assessed with the sun track simulated by the software. The average integrated daily quantum flux density at each leaf position in June (Qint; mol m−2 day−1) was calculated as a measure of growth light environment based on 1-min-interval PPFD from the 1st to 30th June, 2007. Average daily peak PPFD in June at each leaf position (PPFDmax) was estimated using the daily five highest values during June3.
Leaf area index (LAI), and light gradients within the canopy
We used the relationship between LAI and light gradients within the canopy of an inventory plot (50 × 50 m) of the experimental forest after Utsugi et al.48. The three predominant canopy tree species, B. platyphylla, Q. mongolica, and Kalopanax septemlobus, were used for the measurements of LAI during the summers of 2001 and 2003. Eight sample trees for each species (24 trees in total for each summer) were felled, and the gradient of LAI was determined by a stratified clipping method with 1-m strata intervals. PPFD within the canopy was also measured with PPFD sensors (Li-190SA, Li-Cor, NE, USA) with 1-m vertical intervals from 1 to 26 m along with permanent steel scaffolding within the canopy of B. platyphylla, Q. mongolica, and K. septemlobus in the area adjacent to the stratified clipping plot. The measurements were carried out under overcast conditions. Relative PPFD for each height was calculated as a mean of 200 replicates, with synchronized measurements of above and below canopy PPFD. The stand, consisting of B. platyphylla, Q. mongolica and K. septemlobus, was considered to be matured at that time since the age of the stand was about 90 years when the stratified clipping was conducted. We used the relationship between relative PPFD and LAI based on the pooled data for 2001 and 200348 to estimate LAI for each leaf measured in 2007 from the relative PPFD. Relative PPFD at each leaf used for the photosynthetic measurement in 2007 was estimated as (Qint at each leaf position)/(Qint above the canopy), where Qint above the canopy was 43.4 mol m−2 day−1 measured by the pyrheliometers placed above the canopy.
Measurements of gas exchange and chlorophyll fluorescence
Measurements of gas exchange and chlorophyll fluorescence were conducted at the summertime of 2007 on mature leaves of a Japanese oak (approximately 23 m height and 95-years-old as of 2007), surrounded by the scaffolding described above with a portable photosynthesis measuring system (Li-6400, Li-Cor, Lincoln, NE, USA) combined with a leaf chamber fluorometer (Li-6400-40, Li-Cor). We selected a total of 15 leaves grown at various positions within the canopy (4 to 23 m in height). The net photosynthetic rate (An), quantum yield of PSII electron transport (ΦPSII), photochemical efficiency of the open PSII (Fv′/Fm′) and excitation pressure adjusted for the efficiency of PSII photochemistry (1 − qP) Fv′/Fm′24,30 were measured at a photosynthetic steady state, where qP is photochemical quenching. The measurements were conducted under an ambient CO2 concentration of 360 µmol mol−1 and at various PPFD (0, 50, 100, 200, 300, 600, 1,000, 1,500, and 2,000 µmol m−2 s−1) provided by a red/blue LED array (Li-6400-40, Li-Cor), with blue light comprising 10% of the total PPFD. Leaf temperature was ≈27 °C during the measurements. After the measurements, the leaves were sampled and used for determination of NL by the combustion method using an analysis system composed of a N/C determination unit (SUMIGRAPH, NC 800, Sumika Chem. Anal. Service, Osaka, Japan), a gas chromatograph (GC 8 A, Shimadzu, Kyoto, Japan), and a data processor (Chromatopac, C R6A, Shimadzu).
Electron transport rate (ETR) was calculated as ETR = ΦPSII × leaf absorptance × light intensity × 0.522,49. Leaf absorptance was calculated from a calibration curve between SPAD readings (measured with a SPAD chlorophyll meter, SPAD 502, Minolta, Osaka, Japan) and leaf absorptance3. The responses of electron transport to incident irradiance were fitted by the convexity equations50 as below:
| 2 |
where ϕ is the initial slope (maximum quantum yield), θ the convexity of the curve, and ETRmax the maximum rate of electron transport.
The responses of Fv′/Fm′ and (1 − qP) Fv′/Fm′ to incident irradiance for each leaf were fitted as follows:
| 3 |
| 4 |
Analogous to ETR, thermal dissipation (D) and excess energy production (E) were estimated from (1 − Fv′/Fm′) × leaf absorptance × light intensity × 0.5 and ((1 − qP) Fv′/Fm′) × leaf absorptance × light intensity × 0.5, respectively22,24. Each coefficient in Eqs 2–4 was fitted as a function of NF defined as (NL – Nb) of the leaves used for the chlorophyll fluorescence measurements, where Nb is the x-intercept of the maximum rate of photosynthesis (Amax) − NL relationship, which can be regarded as non-photosynthetic leaf structural N content. Conversely, NF can be regarded as photosynthetically-functional leaf N content6,51. Amax was estimated from the light response of An based on the convexity equations50, as below:
| 5 |
where Rd is the dark respiration rate, ϕ the initial slope (maximum quantum yield), and θ is the convexity of the curve. The relationships between NF and photosynthesis-related coefficients are summarized in Supplemental Fig. S1. Based on the coefficients of light responses in ETR, Fv′/Fm′, and (1 − qP) Fv′/Fm′ as a function of NF, we extrapolated the light responses in leaves that have various NL content with optimal and uniform NL distribution.
Actual, optimal and uniform leaf N distribution
We derived the light extinction coefficient of the canopy, KL 52 as follows:
| 6 |
where F is the LAI cumulated from the canopy top, and I and I0 are PPFD at F and the canopy top, respectively. Actual NL distribution at depth F in the canopy is also described by an exponential function of F with a photosynthetic leaf N distribution coefficient (Kn):
| 7 |
where N0 is the NL of the leaves at the canopy top. Optimal NL distribution was derived after Anten et al.6 as follows:
| 8 |
With
| 9 |
where NTF is the total free nitrogen in the canopy and NT and FT are the total leaf N pool and LAI per unit ground area, respectively. NT is calculated based on the integration of Eq. 2 11. A NL distribution is defined as uniform when all leaves have the same NL irrespective of leaf position. Therefore, NL with uniform distribution is determined as:
| 10 |
Based on the estimated NL with optimal and uniform distribution, we calculated ETR, D, and E under the maximum PPFD during sunflecks for each leaf by using the NL-dependent photosynthetic coefficients (Supplemental Fig. S1) and Eqs 2–4.
We hypothesized that canopy N might be distributed to maintain E constant throughout the canopy during sunflecks, thus to keep an efficient light utilization capacity by preventing photoinhibition for all leaves across sun and shade environments. Therefore, we estimated the leaf N distribution coefficient (Kn) that minimized the variance in E at PPFDmax across the different leaf types within the canopy, using Eq. 8 with various Kn (0.1 to 1.0 with an interval of 0.1) instead of KL as follows:
| 11 |
Variance (s2) in E was estimated as follows:
| 12 |
Statistical analysis
We expediently classified the leaves into four types based on their growth light environments: (1) deep shade leaves (0 < Qint < 3 mol m−2 day−1, n = 5); (2) moderate shade leaves (3 < Qint < 15 mol m−2 day−1, n = 4); (3) moderate sun leaves (15 < Qint < 25 mol m−2 day−1, n = 3); and (4) typical sun leaves (25 < Qint < 35 mol m−2 day−1, n = 3). One-way analysis of variance (ANOVA) was used to test the differences among leaf types in ETR, D, and E with actual, optimal, or uniform NL distribution, and the ratio of ETR, D, and E with optimal or uniform to actual NL distribution53. Furthermore, when the ANOVA returned an overall significant effect of leaf type, the means were further tested using Holm’s pairwise comparisons. The threshold for statistical significance was predefined at an alpha level of 0.05.
Data availability
All data used in this manuscript are present in the manuscript and its supplementary information.
Electronic supplementary material
Acknowledgements
This study was partly supported by the project “Research on response to climate change for agriculture, forestry and fisheries” funded by Agriculture, Forestry and Fisheries Research Council, Japan, and by JSPS KAKENHI Grant Number JP17F17102. Evgenios Agathokleous is a JSPS International Research Fellow (ID No: P17102).
Author Contributions
M.K., H.T. and H.U. conceived the idea; M.K., S.K., H.H., H.T. and H.U. collected the data; S.K. conducted the leaf N analysis; H.H. analyzed hemispheric photographs; M.K. and E.A. led the writing of the manuscript with input from all co-authors; All authors contributed critically to the drafts and gave final approval for publication.
Competing Interests
The authors declare that they have no competing interests.
Footnotes
Electronic supplementary material
Supplementary information accompanies this paper at 10.1038/s41598-017-18766-0.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Björkman, O. Responses to different quantum flux densities. In Physiological Plant Ecology I: Responses to the Physical Environment (eds Lange, O. L., Nobel, P. S., Osmond, C. B. & Ziegler, H.) 57–107, 10.1007/978-3-642-68090-8_4 (Springer, 1981).
- 2.Kitao M, Lei TTT, Koike T, Tobita H, Maruyama Y. Susceptibility to photoinhibition of three deciduous broadleaf tree species with different successional traits raised under various light regimes. Plant, Cell Environ. 2000;23:81–89. doi: 10.1046/j.1365-3040.2000.00528.x. [DOI] [Google Scholar]
- 3.Kitao M, et al. Leaves of Japanese oak (Quercus mongolica var. crispula) mitigate photoinhibition by adjusting electron transport capacities and thermal energy dissipation along the intra-canopy light gradient. Physiol. Plant. 2012;146:192–204. doi: 10.1111/j.1399-3054.2012.01609.x. [DOI] [PubMed] [Google Scholar]
- 4.Pearcy, R. W. & Sims, D. A. Photosynthetic acclimation to changing light environments: Scaling from the leaf to the whole plant. In Exploitation of Environmental Heterogeneity by Plants: Ecophysiological processes above- and belowground (eds Roy, J., Caldwell, M. M. & Pearce, R. P.) 145–174, 10.1016/B978-0-12-155070-7.50010-X (Elsevier, 1994).
- 5.Field C. Allocating leaf nitrogen for the maximization of carbon gain: Leaf age as a control on the allocation program. Oecologia. 1983;56:341–347. doi: 10.1007/BF00379710. [DOI] [PubMed] [Google Scholar]
- 6.Anten NPR, Schieving F, Werger MJA. Patterns of light and nitrogen distribution in relation to whole canopy carbon gain in C3 and C4 mono-and dicotyledonous species. Oecologia. 1995;101:504–513. doi: 10.1007/BF00329431. [DOI] [PubMed] [Google Scholar]
- 7.Hirose T. Development of the Monsi-Saeki theory on canopy structure and function. Ann. Bot. 2005;95:483–494. doi: 10.1093/aob/mci047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Anten NPR. Optimal photosynthetic characteristics of individual plants in vegetation stands and implications for species coexistence. Ann. Bot. 2005;95:495–506. doi: 10.1093/aob/mci048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Niinemets Ü, Way D. Optimization of foliage photosynthetic capacity in tree canopies: Towards identifying missing constraints. Tree Physiol. 2012;32:505–509. doi: 10.1093/treephys/tps045. [DOI] [PubMed] [Google Scholar]
- 10.Hikosaka K. Optimal nitrogen distribution within a leaf canopy under direct and diffuse light. Plant, Cell Environ. 2014;37:2077–2085. doi: 10.1111/pce.12291. [DOI] [PubMed] [Google Scholar]
- 11.Hirose T, Werger MJA. Maximizing daily canopy photosynthesis with respect to the leaf nitrogen allocation pattern in the canopy. Oecologia. 1987;72:520–526. doi: 10.1007/BF00378977. [DOI] [PubMed] [Google Scholar]
- 12.Dewar RC, Tarvainen L, Parker K, Wallin G, McMurtrie RE. Why does leaf nitrogen decline within tree canopies less rapidly than light? An explanation from optimization subject to a lower bound on leaf mass per area. Tree Physiol. 2012;32:520–534. doi: 10.1093/treephys/tps044. [DOI] [PubMed] [Google Scholar]
- 13.Lloyd J, et al. Optimisation of photosynthetic carbon gain and within-canopy gradients of associated foliar traits for Amazon forest trees. Biogeosciences. 2010;7:1833–1859. doi: 10.5194/bg-7-1833-2010. [DOI] [Google Scholar]
- 14.Peltoniemi MS, Duursma RA, Medlyn BE. Co-optimal distribution of leaf nitrogen and hydraulic conductance in plant canopies. Tree Physiol. 2012;32:510–519. doi: 10.1093/treephys/tps023. [DOI] [PubMed] [Google Scholar]
- 15.Way DA, Pearcy RW. Sunflecks in trees and forests: From photosynthetic physiology to global change biology. Tree Physiol. 2012;32:1066–1081. doi: 10.1093/treephys/tps064. [DOI] [PubMed] [Google Scholar]
- 16.Kromdijk J, et al. Improving photosynthesis and crop productivity by accelerating recovery from photoprotection. Science. 2016;354:857–861. doi: 10.1126/science.aai8878. [DOI] [PubMed] [Google Scholar]
- 17.Werner C, Ryel RJ, Correia O, Beyschlag W. Effects of photoinhibition on whole-plant carbon gain assessed with a photosynthesis model. Plant, Cell Environ. 2001;24:27–40. doi: 10.1046/j.1365-3040.2001.00651.x. [DOI] [Google Scholar]
- 18.Niinemets Ü, Keenan T. Photosynthetic responses to stress in Mediterranean evergreens: Mechanisms and models. Environ. Exp. Bot. 2014;103:24–41. doi: 10.1016/j.envexpbot.2013.11.008. [DOI] [Google Scholar]
- 19.Alter P, Dreissen A, Luo FL, Matsubara S. Acclimatory responses of Arabidopsis to fluctuating light environment: Comparison of different sunfleck regimes and accessions. Photosynth. Res. 2012;113:221–237. doi: 10.1007/s11120-012-9757-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Miyata K, Ikeda H, Nakaji M, Kanel DR, Terashima I. Rate constants of PSII photoinhibition and its repair, and PSII fluorescence parameters in field plants in relation to their growth light environments. Plant Cell Physiol. 2014;56:1841–1854. doi: 10.1093/pcp/pcv107. [DOI] [PubMed] [Google Scholar]
- 21.Cornic G, Fresneau C. Photosynthetic carbon reduction and carbon oxidation cycles are the main electron sinks for photosystem II activity during a mild drought. Ann. Bot. 2002;89:887–894. doi: 10.1093/aob/mcf064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Demmig-Adams B, et al. Using chlorophyll fluorescence to assess the fraction of absorbed light allocated to thermal dissipation of excess excitation. Physiol. Plant. 2008;98:253–264. doi: 10.1034/j.1399-3054.1996.980206.x. [DOI] [Google Scholar]
- 23.Kitao M, Lei TT, Koike T, Tobita H, Maruyama Y. Tradeoff between shade adaptation and mitigation of photoinhibition in leaves of Quercus mongolica and Acer mono acclimated to deep shade. Tree Physiol. 2006;26:441–448. doi: 10.1093/treephys/26.4.441. [DOI] [PubMed] [Google Scholar]
- 24.Kato MC, Hikosaka K, Hirotsu N, Makino A, Hirose T. The excess light energy that is neither utilized in photosynthesis nor dissipated by photoprotective mechanisms determines the rate of photoinactivation in photosystem II. Plant Cell Physiol. 2003;44:318–325. doi: 10.1093/pcp/pcg045. [DOI] [PubMed] [Google Scholar]
- 25.Oguchi R, Terashima I, Kou J, Chow WS. Operation of dual mechanisms that both lead to photoinactivation of Photosystem II in leaves by visible light. Physiol. Plant. 2011;142:47–55. doi: 10.1111/j.1399-3054.2011.01452.x. [DOI] [PubMed] [Google Scholar]
- 26.Wilhelm C, Selmar D. Energy dissipation is an essential mechanism to sustain the viability of plants: The physiological limits of improved photosynthesis. J. Plant Physiol. 2011;168:79–87. doi: 10.1016/j.jplph.2010.07.012. [DOI] [PubMed] [Google Scholar]
- 27.Niinemets Ü, Kull O, Tenhunen JD. Within-canopy variation in the rate of development of photosynthetic capacity is proportional to integrated quantum flux density in temperate deciduous trees. Plant, Cell Environ. 2004;27:293–313. doi: 10.1111/j.1365-3040.2003.01143.x. [DOI] [Google Scholar]
- 28.Niinemets Ü, Bilger W, Kull O, Tenhunen JD. Acclimation to high irradiance in temperate deciduous trees in the field: Changes in xanthophyll cycle pool size and in photosynthetic capacity along a canopy light gradient. Plant, Cell Environ. 1998;21:1205–1218. doi: 10.1046/j.1365-3040.1998.00364.x. [DOI] [Google Scholar]
- 29.Niinemets Ü, Bilger W, Kull O, Tenhunen J. Responses of foliar photosynthetic electron transport, pigment stoichiometry, and stomatal conductance to interacting environmental factors in a mixed species forest canopy. Tree Physiol. 1999;19:839–852. doi: 10.1093/treephys/19.13.839. [DOI] [PubMed] [Google Scholar]
- 30.Kornyeyev D, Logan BA, Holaday AS. Excitation pressure as a measure of the sensitivity of photosystem II to photoinactivation. Funct. Plant Biol. 2010;37:943–951. doi: 10.1071/FP09276. [DOI] [Google Scholar]
- 31.Vass I. Role of charge recombination processes in photodamage and photoprotection of the photosystem II complex. Physiol. Plant. 2011;142:6–16. doi: 10.1111/j.1399-3054.2011.01454.x. [DOI] [PubMed] [Google Scholar]
- 32.Kitao M, Lei TT. Circumvention of over-excitation of PSII by maintaining electron transport rate in leaves of four cotton genotypes developed under long-term drought. Plant Biol. 2007;9:69–76. doi: 10.1055/s-2006-924280. [DOI] [PubMed] [Google Scholar]
- 33.Kitao M, et al. Interaction of drought and elevated CO2 concentration on photosynthetic down-regulation and susceptibility to photoinhibition in Japanese white birch seedlings grown with limited N availability. Tree Physiol. 2007;27:727–735. doi: 10.1093/treephys/27.5.727. [DOI] [PubMed] [Google Scholar]
- 34.Miyata K, Noguchi K, Terashima I. Cost and benefit of the repair of photodamaged photosystem II in spinach leaves: Roles of acclimation to growth light. Photosynth. Res. 2012;113:165–180. doi: 10.1007/s11120-012-9767-0. [DOI] [PubMed] [Google Scholar]
- 35.Evans JR. Photosynthesis and nitrogen relationship in leaves of C3 plants. Oecologia. 1989;78:9–19. doi: 10.1007/BF00377192. [DOI] [PubMed] [Google Scholar]
- 36.Keenan TF, Niinemets Ü. Global leaf trait estimates biased due to plasticity in the shade. Nat. Plants. 2016;3:16201. doi: 10.1038/nplants.2016.201. [DOI] [PubMed] [Google Scholar]
- 37.Harayama H, Ishida A, Yoshimura J. Overwintering evergreen oaks reverse typical relationships between leaf traits in a species spectrum. R. Soc. open Sci. 2016;3:160276. doi: 10.1098/rsos.160276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Eschrich W, Burchardt R, Essiamah S. The induction of sun and shade leaves of the European beech (Fagus sylvatica L.): anatomical studies. Trees. 1989;3:1–10. doi: 10.1007/BF00202394. [DOI] [Google Scholar]
- 39.Tobita H, et al. Variation in photoinhibition among Sasa senanensis, Quercus mongolica, and Acer mono in the understory of a deciduous broad-leaved forest exposed to canopy gaps caused by typhoons. Trees. 2010;24:307–319. doi: 10.1007/s00468-009-0400-6. [DOI] [Google Scholar]
- 40.Mizoguchi Y, Yamanoi K, Kitamura K, Nakai YSS. Meteorological observations at the Sapporo forest meteorology research site from 1999 to 2008, Hokkaido, Japan. Bull. For. For. Prod. Res. Inst. 2014;13:193–206. [Google Scholar]
- 41.Flexas J, Bota J, Galmés J, Medrano H, Ribas-Carbó M. Keeping a positive carbon balance under adverse conditions: Responses of photosynthesis and respiration to water stress. Physiol. Plant. 2006;127:343–352. doi: 10.1111/j.1399-3054.2006.00621.x. [DOI] [Google Scholar]
- 42.Sperdouli I, Moustakas M. A better energy allocation of absorbed light in photosystem II and less photooxidative damage contribute to acclimation of Arabidopsis thaliana young leaves to water deficit. J. Plant Physiol. 2014;171:587–593. doi: 10.1016/j.jplph.2013.11.014. [DOI] [PubMed] [Google Scholar]
- 43.Niinemets Ü, Sonninen E, Tobias M. Canopy gradients in leaf intercellular CO2 mole fractions revisited: Interactions between leaf irradiance and water stress need consideration. Plant, Cell Environ. 2004;27:569–583. doi: 10.1111/j.1365-3040.2003.01168.x. [DOI] [Google Scholar]
- 44.Ishii HR, Azuma W, Kuroda K, Sillett SC. Pushing the limits to tree height: Could foliar water storage compensate for hydraulic constraints in Sequoia sempervirens? Funct. Ecol. 2014;28:1087–1093. doi: 10.1111/1365-2435.12284. [DOI] [Google Scholar]
- 45.LeBauer DS, Treseder KK. Nitrogen limitation of net primary productivity in terrestrial ecosystems is globally distributed. Ecology. 2008;89:371–379. doi: 10.1890/06-2057.1. [DOI] [PubMed] [Google Scholar]
- 46.Coskun D, Britto DT, Kronzucker HJ. Nutrient constraints on terrestrial carbon fixation: The role of nitrogen. J. Plant Physiol. 2016;203:95–109. doi: 10.1016/j.jplph.2016.05.016. [DOI] [PubMed] [Google Scholar]
- 47.Chazdon RL, Field CB. Photographic estimation of photosynthetically active radiation: evaluation of a computerized technique. Oecologia. 1987;73:525–532. doi: 10.1007/BF00379411. [DOI] [PubMed] [Google Scholar]
- 48.Utsugi H, Tobita H, Maruyama Y, Ishizuka M. Spatial and seasonal variations in leaf mass per area and their relationship to leaf nitrogen in a secondary northern hardwood forest in Japan. Phyton. 2005;45:245–251. [Google Scholar]
- 49.Genty B, Briantais JM, Baker NR. The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. Biochim. Biophys. Acta - Gen. Subj. 1989;990:87–92. doi: 10.1016/S0304-4165(89)80016-9. [DOI] [Google Scholar]
- 50.Leverenz, J. W. Factors determining the nature of the light dosage response curve of leaves. In Photoinhibition of Photosynthesis: from Molecular Mechanisms to the Field (eds Baker, N. R. & Bowyer, J. R.) 239–254, (BIOS Scientific Publishers, 1994).
- 51.Hikosaka K, et al. A meta-analysis of leaf nitrogen distribution within plant canopies. Ann. Bot. 2016;118:239–47. doi: 10.1093/aob/mcw099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Monsi M, Saeki T. Über den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung für die Stoffproduktion. Japanese J. Bot. 1953;14:22–52. [Google Scholar]
- 53.R Development Core Team. R: A language and environment for statistical computing. R Found. Stat. Comput. Vienna, Austria. ISBN 3-900051-07-0 (2014).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data used in this manuscript are present in the manuscript and its supplementary information.


