Canopy nitrogen distribution is optimized to prevent photoinhibition throughout the canopy during sun flecks

Abstract

As photoinhibition primarily reduces the photosynthetic light use efficiency at low light, sunfleck-induced photoinhibition might result in a fatal loss of carbon gain in the shade leaves within a canopy with barely positive carbon balance. We hypothesized that shade leaves at the lower canopy might retain a certain amount of leaf nitrogen (N_L) to maintain energy consumption via electron transport, which contributes to circumventing photoinhibition during sunflecks to keep efficient utilization of low light during the rest period of daytime. We investigated excess energy production, a potential measure of susceptibility to photoinhibition, as a function of N_L distribution within a Japanese oak canopy. Optimal N_L distribution, which maximizes canopy carbon gain, may lead to a higher risk of photoinhibition in shade leaves during sunflecks. Conversely, uniform N_L distribution would cause a higher risk of photoinhibition in sun leaves under the direct sunlight. Actual N_L distribution equalized the risk of photoinhibition throughout the canopy indicated by the constant excess energy production at the highest light intensities that the leaves received. Such a homeostatic adjustment as a whole canopy concerning photoinhibition would be a key factor to explain why actual N_L distribution does not maximize canopy carbon gain.

Introduction

Within a canopy, leaves acclimate to the growth light conditions, where sun-exposed leaves have a higher area-based leaf N pool (N_L) and higher photosynthetic capacity than shaded leaves^1–4. Such a gradient of leaf N along the canopy depth is considered as an efficient utilization of the limited N resource to maximize photosynthetic C gain over the canopy of an entire plant in response to the light gradient within a canopy^5–7. However, the measured N_L distribution is more uniform than the theoretically optimal N_L distribution to maximize the canopy carbon gain^8–10, which means that sun leaves show lower and shade leaves greater N_L than the optimal value^6,11. Furthermore, Hikosaka¹⁰ reported that the optimal N_L distribution, considering both direct and diffuse light into account, was much steeper than that conventionally estimated under diffuse light only^6,7. Several theoretical approaches have been conducted to explain the less steep declines in N_L than the light gradient within canopies accounting other constraints than light, such as leaf morphological plasticity¹², photosynthetic capacity at the top of the canopy limited by the maximum nutrient concentration¹³, and hydraulic conductance¹⁴.

Recently, the importance of direct light, i.e., sunflecks within a canopy, was emphasized both in photosynthesis and photoinhibition. Sunflecks can significantly improve C gain in shade leaves of the lower canopy, while shade leaves may suffer from photoinhibition by the high photosynthetic photon flux density (PPFD) of sunflecks¹⁵. Photosynthetic efficiency is reduced during the recovery from photoinhibition on the transition from sunflecks to shade, which would result in a considerable reduction in plant productivity¹⁶. The degree of photoinhibition has been empirically linked to average or integrated light intensity in photosynthetic plant production models^17,18. However, recent studies have reported that plants grown under fluctuating light environments upregulated the photoprotective mechanisms and electron transport compared with those grown under constant light conditions in response to sunflecks, even when the amounts of daily total irradiance are comparable^19,20. This suggests that leaves may well acclimate to sun flecks (brief and strong irradiance) rather than averaged irradiance, so as to circumvent transient photoinhibition.

Photoinhibition primarily reduces the photosynthetic light use efficiency at low PPFD, i.e. a reduction of the initial slope of the photosynthetic light-response curve rather than the light-saturated photosynthetic rate¹⁷. In this context, sunfleck-induced photoinhibition may result in a fatal loss of carbon gain in the shade leaves with barely positive carbon balance¹⁶. To prevent photoinhibition, electron transport, mainly involved in photosynthesis and photorespiration²¹, plays an important role in consuming absorbed light energy as well as thermal energy dissipation^3,22,23. Excess energy, neither consumed by electron transport nor dissipated as heat, is known to have a close relationship to photoinactivation of PSII under the inhibition of PSII repair^24,25.

Leaf N participation for the circumvention of photoinhibition is specifically involved in electron transport, but not in xanthophyll-related thermal energy dissipation, since xanthophyll pigments, violaxanthin (C₄₀H₅₆O₄), antheraxanthin (C₄₀H₅₆O₃), and zeaxanthin (C₄₀H₅₆O₂), do not contain any N²⁶. As for the fractions of leaf N in Rubisco, and in proteins related to linear electron transport, there can be little differences in the fractions between upper and lower canopy leaves²⁷. In this context, leaf N gradient within the canopy can closely reflect the gradient of photosynthesis-related proteins. The capacity of electron transport depends on N_L, which is varied through intra-canopy light gradients^28,29. Thus, shade leaves at the lower canopy may retain a certain amount of N_L to circumvent photoinhibition during sunflecks to keep efficient utilization of low PPFD during the rest period of daytime¹⁶.

We hypothesized that N_L should be distributed within a canopy to prevent photoinhibition both in shade leaves during sunflecks and sun leaves under the direct sunlight, leading to the less steep N_L distribution than the optimal N_L distribution. To test this hypothesis, we determined how excess energy production, which could be a possible measure of the susceptibility to photoinhibition^22,24,25,30, was distributed within a canopy when N_L distribution was changed. We investigated photosynthetic traits in the leaves within a canopy of Japanese oak by gas exchange and chlorophyll fluorescence measurements, as well as light and N distribution within the canopy.

Results

Total leaf area index (LAI), F_T, in the forest was estimated to be 5.91 m² m⁻² based on the stratified clipping method conducted in 2001 and 2003. Based on the LAI cumulated from the canopy top (F), the light extinction coefficient of the canopy (K_L) was 0.739 in Eq. 6. Based on the relationship between the relative light intensity (I/I₀) and F (Eq. 6), we derived F of 15 leaves used for the photosynthetic measurements in 2007 by using relative light intensity at each leaf position. The actual distribution of N_L as a function of F in 2007 was revealed as follows:

$${\mathrm{N}}_{\mathrm{L}}=2.22\exp (-0.241\mathrm{F})+0.269\left(\mathrm{according}\mathrm{to}\mathrm{Eq}\mathrm{.}7\mathrm{in}\mathrm{Methods}\right).$$

Based on the integration of the actual N_L distribution, total N per unit ground area (N_T) was calculated as 8.59 g m⁻². Optimal N distribution in the canopy was expressed as follows:

$${\mathrm{N}}_{\mathrm{L}}=5.24\exp \left(-0.739\mathrm{F}\right)+0.269\left(\mathrm{according}\mathrm{to}\mathrm{Eq}\mathrm{.}8\mathrm{in}\mathrm{Methods}\right).$$

N_L with uniform distribution was estimated to be 1.45 g m⁻², estimated as N_T/F_T.

Actual and optimal N_L distributions within the canopy are shown in Fig. 1. Optimal N_L was higher than the actual value in the case of F < 1.7 m² m⁻², whereas it was lower than the actual value in the case of F > 1.7 m² m⁻². F of 1.7 m² m⁻² corresponds to the average integrated daily quantum flux density in June (Q_int) of 12 mol m⁻² day⁻¹ (Eq. 6).

Figure 1.

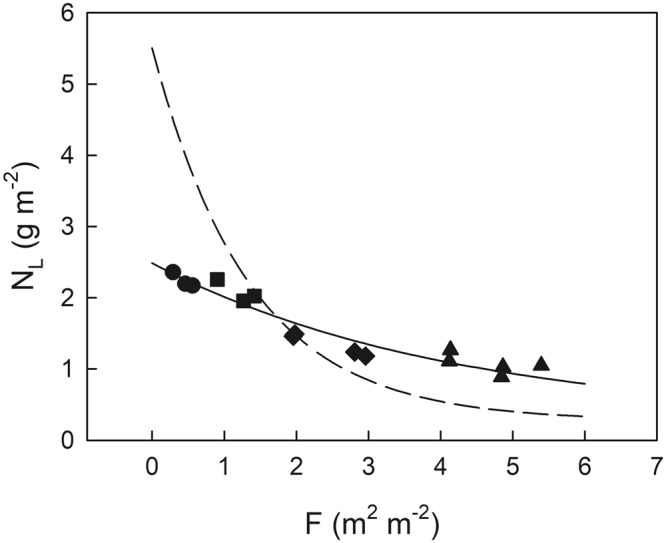
Actual leaf N (N_L) distribution in the canopy of Japanese oak as a function of the leaf area index cumulated from the canopy top (F). Dashed line indicates optimal N_L distribution. Leaves were classified into four types based on their growth light environments (Q_int): (1) deep shade (triangle, 0 < Q_int < 3 mol m⁻² day⁻¹), moderate shade (diamond, 3 < Q_int < 15 mol m⁻² day⁻¹), moderate sun (square, 15 < Q_int < 25 mol m⁻² day⁻¹), and typical sun leaves (circle, 25 < Q_int < 35 mol m⁻² day⁻¹).

In the present study, we expediently classified the leaves into four types based on their growth light environments: (1) deep shade leaves (0 < Q_int < 3 mol m⁻² day⁻¹, n = 5); (2) moderate shade leaves (3 < Q_int < 15 mol m⁻² day⁻¹, n = 4); (3) moderate sun leaves (15 < Q_int < 25 mol m⁻² day⁻¹, n = 3); and (4) typical sun leaves (25 < Q_int < 35 mol m⁻² day⁻¹, n = 3). Hereafter, we often use “shade leaves” to refer to deep and moderate shade leaves and “sun leaves” to refer to moderate and typical sun leaves. Peak PPFD entering through the canopy (PPFD_max), i.e. sunflecks, was considerably high (>700 µmol m⁻² s⁻¹), even for the deep shade leaves (Fig. 2).

Figure 2.

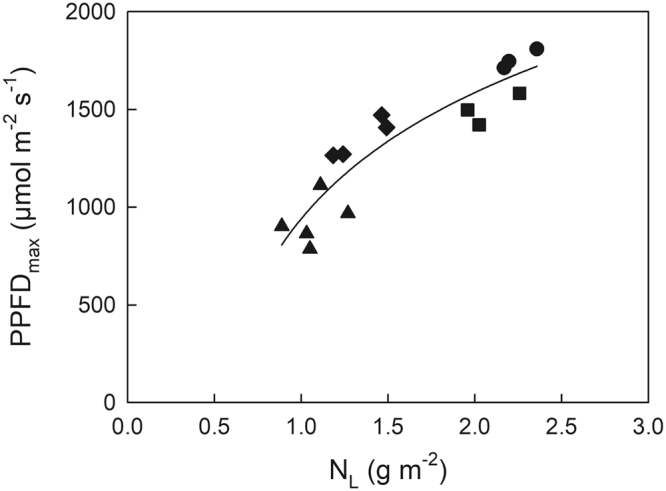
Maximal photosynthetic photon flux density (PPFD_max) in June at various leaf positions with various leaf N pool (N_L) within the canopy of Japanese oak. PPFD_max was estimated as average daily peak PPFD at each leaf position using the five highest values daily in June. Symbols are the same as in Fig. 1.

Electron transport rate (ETR) with actual, optimal and uniform N_L distribution showed similar relationships as a function of N_L (Fig. 3a). Higher ETR in sun leaves but lower ETR in shade leaves was observed with optimal N_L distribution when compared with those with actual N_L distribution (Table 1). To investigate how ETR changed from the actual to the optimal and uniform N_L distribution, we showed ETR_opt/ETR_act and ETR_uni/ETR_act as a function of Q_int (Fig. 4a). Higher ETR_opt/ETR_act was observed in leaves grown under higher Q_int, compared among leaf types (Fig. 4a, Table 2). When compared with ETR in leaves with actual N_L distribution for each leaf type, relatively lower ETR in the deep shade leaves and relatively higher ETR in the typical sun leaves were observed with optimal N_L distribution (Table 2). Conversely, with uniform N_L distribution, higher ETR_uni/ETR_act was observed in the deep shade leaves than the other leaves, where relatively higher ETR in the deep shade leaves and lower ETR in sun leaves were observed when compared with those in leaves with actual N_L distribution (Fig. 4a, Table 2).

Figure 3.

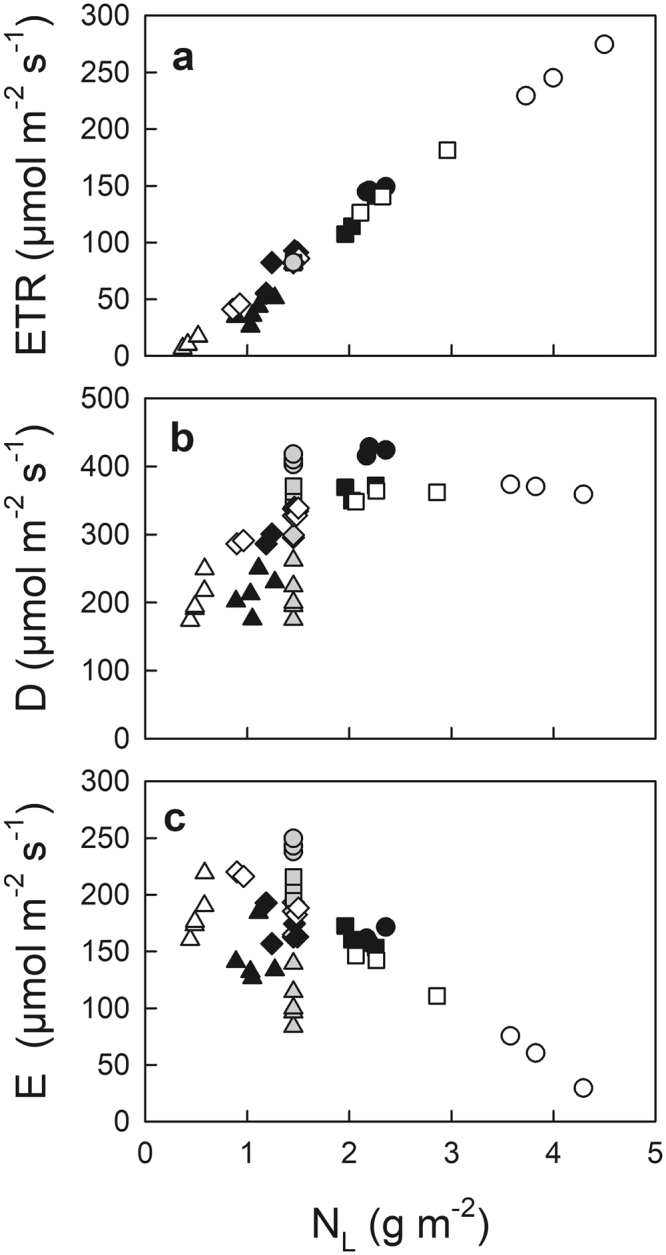
Electron transport rate (ETR) (a), thermal energy dissipation (D) (b), and excess energy (E) (c) at maximal photosynthetic photon flux density (PPFD_max) as a function of leaf N pool (N_L) with actual (closed), optimal distribution (open), and uniform distribution (grey symbols) in the canopy of Japanese oak. Symbols are the same as in Fig. 1.

Table 1.

ETR, D and E (µmol m⁻² s⁻¹) in different leaf types of Q. mongolica at PPFD_max with actual, optimal and uniform N_L distribution.

Parameter	Leaf type				ANOVA
	Deep shade	Moderate shade	Moderate sun	Typical sun
Actual NL
ETR	38 ± 4a	80 ± 9b	121 ± 10c	147 ± 1d	F = 50.0 P < 0.001
D	214 ± 13a	315 ± 13b	364 ± 7c	423 ± 4d	F = 60.8 P < 0.001
E	143 ± 10	172 ± 8	162 ± 6	163 ± 4	F = 2.2 ns
Optimal NL
ETR	12 ± 2a	64 ± 12b	149 ± 17c	250 ± 13d	F = 95.3 P < 0.001
D	205 ± 13a	311 ± 13b	358 ± 5bc	368 ± 4c	F = 44.5 P < 0.001
E	184 ± 10c	202 ± 10c	133 ± 11b	55 ± 14a	F = 32.9 P < 0.001
Uniform NL
ETR	82 ± 0a	82 ± 0b	82 ± 0b	82 ± 0b	F = 19.7 P < 0.001
D	211 ± 15a	315 ± 10b	360 ± 7c	410 ± 4c	F = 51.3 P < 0.001
E	107 ± 9a	177 ± 8b	207 ± 5c	244 ± 3d	F = 54.3 P < 0.001

Values are means ± SE for each leaf type. Different letters indicate significant differences among the leaf types at P < 0.05, according to Holm’s pairwise comparisons. ns indicates non-significant effect of leaf type.

Figure 4.

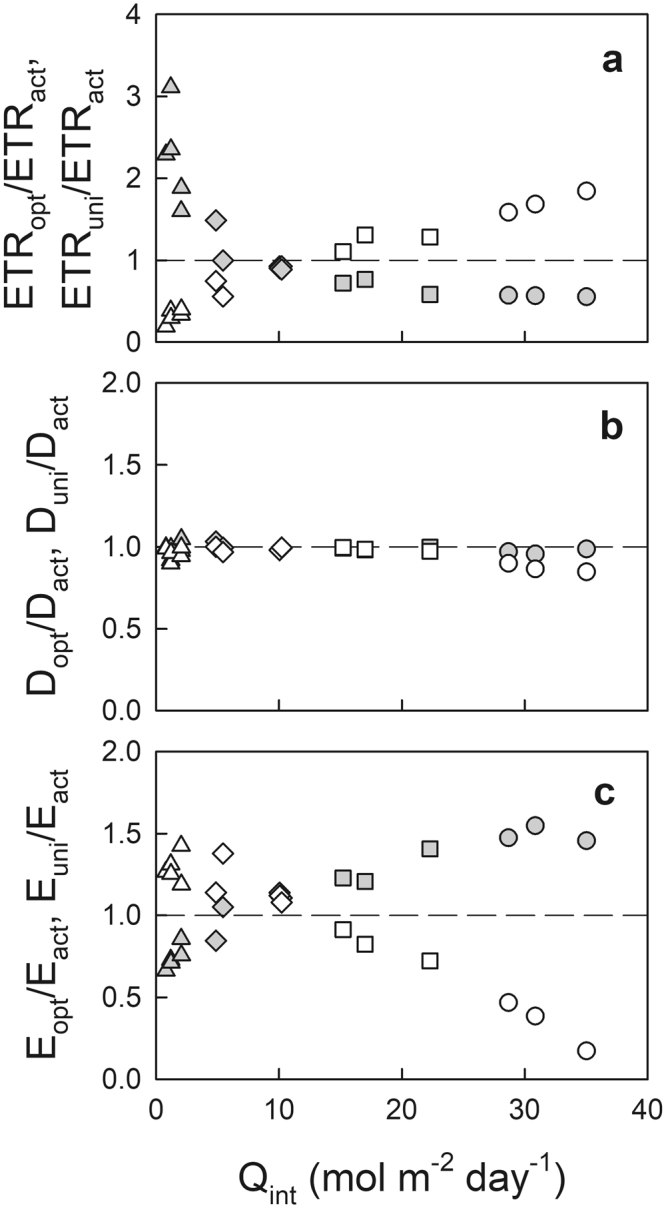
The ratio of ETR (a), D (b) and E (c) with optimal (open) and uniform N_L distribution (grey symbols) (ETR_opt, D_opt and E_opt; ETR_uni, D_uni and E_uni) to those with actual N_L distribution (ETR_act, D_act and E_act, respectively) at PPFD_max for a given leaf as a function the daily mean of the integrated photon flux density during leaf development (Q_int). Dashed line indicates the ratios = 1. Symbols are the same as in Fig. 1.

Table 2.

The ratio of ETR, D and E with optimal and uniform N_L distribution (ETR_opt, D_opt and E_opt; ETR_uni, D_uni and E_uni) to those with actual N_L distribution (ETR_act, D_act and E_act, respectively) at PPFD_max in different leaf types of Q. mongolica. Values are means ± SE for each leaf type.

Parameter	Leaf type				ANOVA
	Deep shade	Moderate shade	Moderate sun	Typical sun
Optimal NL
ETRopt/ETRact	0.32 ± 0.04a,*	0.79 ± 0.09b	1.23 ± 0.06c	1.70 ± 0.08d,*	F = 81.3 P < 0.001
Dopt/Dact	0.96 ± 0.02b	0.99 ± 0.01b	0.99 ± 0.01b	0.87 ± 0.02a,*	F = 12.2 P < 0.001
Eopt/Eact	1.29 ± 0.04c,*	1.18 ± 0.07c	0.82 ± 0.06b	0.34 ± 0.09a,*	F = 47.6 P < 0.001
Uniform NL
ETRuni/ETRact	2.25 ± 0.26b,*	1.07 ± 0.14a	0.69 ± 0.06a,*	0.56 ± 0.00a,*	F = 17.4 P < 0.001
Duni/Dact	0.98 ± 0.02	1.00 ± 0.01	0.99 ± 0.00	0.97 ± 0.01	F = 0.54 ns
Euni/Eact	0.74 ± 0.03a,*	1.04 ± 0.07b	1.28 ± 0.06c,*	1.49 ± 0.03d,*	F = 43.4 P < 0.001

Different letters indicate significant differences among the leaf types at P < 0.05, according to Holm’s pairwise comparisons. ns indicates non-significant effect of leaf type. *Indicates significant differences in ETR, D and E from those of actual N_L distribution in each leaf type at P < 0.05 with t-test.

Higher thermal energy dissipation (D) was generally observed in leaves grown under higher Q_int with any N_L distribution, whereas the slope become less steep in leaves with optimal N_L than the actual, and uniform N_L distribution (Fig. 3b, Table 1). With optimal N_L distribution, the typical sun leaves showed lower D_opt/D_act than the other leaf types, and relatively lower D than that in the typical sun leaves with actual N_L distribution. Conversely, there was no significant differences in D_uni/D_act among leaf types with uniform N_L distribution, and also there was no difference in D in leaves with uniform N_L distribution from that in leaves with actual N_L distribution within each leaf type (Fig. 4b, Table 2).

There was no difference in excess energy production (E) among leaf types with the actual N_L distribution (Fig. 3c, Table 1). A significantly higher E was observed in shade leaves than in sun leaves with optimal N_L distribution. Conversely, a significantly higher E was observed in sun leaves than in shade leaves with uniform N_L distribution (Fig. 3c, Table 1). Similarly, higher E_opt/E_act was observed in shade leaves than in sun leaves with optimal N_L distribution, whereas higher E_uni/E_act was observed in sun leaves than in shade leaves with uniform N_L distribution (Fig. 4c, Table 2). With optimal N_L distribution, deep shade leaves showed relatively higher E, but typical sun leaves showed relatively lower E compared with those in actual N_L distribution (indicated by the asterisks in Table 2). Conversely, with uniform N_L distribution, deep shade leaves showed relatively lower E, but sun leaves showed relatively higher E compared with those in actual N_L distribution.

Based on the relationship between variance in E (s²) and the leaf N distribution coefficient (K_n), the K_n minimizing s² was estimated as 0.291 (Fig. 5), which was very close to the K_n in the actual N_L distribution (0.241 in Eq. 7). We also found that the values of E at PPFD_max with the actual N_L distribution within the canopy of Japanese oak were very similar to those with the N_L distribution to maintain E constant, minimizing the variance in E (K_n = 0.291) (Fig. 6).

Figure 5.

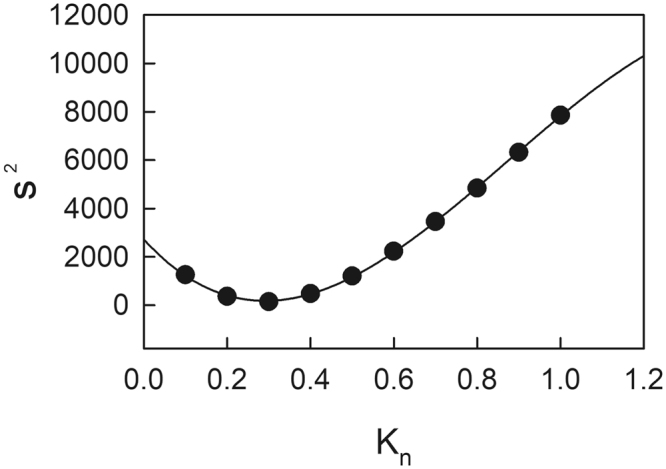
The relationship between the variance (s²) in excess energy production (E) at maximal photosynthetic photon flux density (PPFD_max) and variable leaf N distribution coefficient (K_n).

Figure 6.

Excess energy production (E) at maximal photosynthetic photon flux density (PPFD_max) as a function of leaf N pool (N_L) with actual distribution (closed) and the distribution to minimize the variation in E (open symbols) in the canopy of Japanese oak. Symbols are the same as in Fig. 1.

Discussion

We investigated the fate of absorbed light energy (ETR, D, and E) in leaves with actual, optimal, and uniform N distribution within the canopy of Japanese oak. Excess energy is known to have a close relationship to photoinactivation of PSII under the inhibition of PSII repair^24,25. There are two mechanisms involved in photoinhibition (defined as photoinactivation of PSII), i.e., an excess energy mechanism and a two-step mechanism²⁵. As excess energy might be predominantly involved in photoinhibition in the field under visible light especially at the range of relatively high irradiance^25,30,31, c.f. 700–1800 µmol m⁻² s⁻¹ during the sunflecks in the present study, we used the chlorophyll fluorescence parameter “excess energy,” as an empirical measure of the sensitivity of photoinhibitory damage based on the former mechanism. It is noteworthy that E during sunflecks for shade leaves or direct sunlight for sun leaves was stable among leaf types with the actual N_L distribution at various canopy depths, whereas a significantly higher E was observed in the shade leaves than sun leaves with the optimal N_L distribution; a significantly higher E in sun leaves than shade leaves with the uniform N_L distribution (Fig. 3c, Table 1). As photoprotective D was not enhanced in the leaves with decreased ETR (Table 2)²², the decreases in ETR in the shade leaves with an optimal N_L distribution, and in the sun leaves with a uniform N_L distribution both resulted in the increases in E. This also suggests that the photoprotective thermal energy dissipation would not respond enough to set off the changes in ETR with different N_L distributions as far as the present model prediction is concerned, partly because of the small variation in D in the fully acclimated leaves to their growth environments (Supplemental Fig. S1) as reported in long-term drought acclimated plants^32,33.

In the present study, the optimal N distribution was estimated using the simple Beer’s law with an assumption that leaves received diffuse light only^6,7. Hikosaka¹⁰ reported that the optimal N distribution under direct and diffuse light, a more realistic condition than diffuse light only^6,7, was steeper than that under diffuse light only. However, from the viewpoint of photoinhibitory damage, the actual N distribution in the canopy of Japanese oak, which was less steep than the optimal distribution, might be inherently optimized to circumvent photoinhibitory damage at the whole-canopy level by maintaining excessive energy at a certain level under direct sunlight throughout the leaves grown at various light environments within a canopy.

We estimated canopy C gain based on light response curves built with different N distribution and incident PPFD with 1-min-intervals in July 2007 (details in Supplementary Information: Estimation of canopy C gain, Figs S2–S5). We used coefficients of light response curves measured at a leaf temperature of ≈27 °C, with no correction for the effects of air temperature, and air humidity on photosynthesis. Total canopy C gain was 24.9, 21.3, and 15.8 mol m⁻² on the ground surface basis for optimal, even-E, which makes E constant throughout the canopy with K_n = 0.291 (Fig. 6), and uniform leaf N distribution, respectively. Even-E N distribution, showed a 15% decrease in canopy C gain integrated in July, during a photosynthetically most vigorous period, compared with optimal N distribution. Conversely, uniform N distribution resulted in a 36% decrease in canopy gain compared with the optimal N distribution. It is noteworthy, not only the sun leaves with higher leaf N_L with optimal canopy N distribution, but also the shade leaves with lower N_L compared with those with even-E N distribution contributed to the higher C gain as a consequence of reduced nighttime respiration rate (Supplementary Figure S5). In this estimation, a decrease in photosynthetic efficiency caused by photoinhibition under fluctuating light was not taken into account^16,19,20. An enhanced recovery capacity from photoinhibition by bioengineering lead to an increase in biomass of tobacco plants by up to 20% in fluctuating light¹⁶. Thus, there is a possibility to reduce the difference in the canopy C gain between even-E and optimal N distribution, when the photoinhibitory effects on photosynthetic efficiency are accounted. In addition to an acclimation to short-term fluctuating light (sunflecks), as Japanese oak is a gap-dependent species, which needs a gap formation for its regeneration^2,23, keeping relatively higher ETR in shade leaves than optimal would be a pre-conditioning for long-term fluctuating light (gap formation) for this species.

The cost of D1 protein turn-over, as a relevant process of PSII repair, is substantially low at most 0.5% of photosynthetic ATP production³⁴, and the cost of relaxation of thermal energy dissipation is also reported to be substantially small, about 0.05% of the total photosynthetic electron flow under saturating light²⁶. Therefore, the recovery cost from photoinhibition would be negligible for canopy C balance. Rather, reduced photosynthetic efficiency during the recovery from photoinhibition on transfer from sun flecks to shade may have a more significant adverse effect on canopy C gain¹⁶. In this context, circumvention of photoinhibition via an enhancement of ETR is essential to maintain the canopy C gain by preventing photoinhibition without any decrease in photosynthetic efficiency, in contrary to xanthophyll-related thermal energy dissipation.

Leaf photosynthetic capacity is closely related to leaf morphology such as leaf mass per area (LMA), where leaves with greater LMA generally have greater leaf area-based nitrogen contents and greater photosynthetic capacity^3,35,36. During leaf maturation of Japanese oak, LMA reaches its maximum, accompanied with an increase in net photosynthetic rate, several weeks after the leaves are fully expanded and the light environment within a canopy is fixed (Tobita unpublished data³⁷). Although the sun/shade anatomy of deciduous leaves is mainly determined by the light condition in the previous year³⁸, less extent but some plasticity exists in leaf morphological change in response to current-year light environment³⁹. For Japanese oak, LMA and net photosynthetic rate increased during June, after the leaf expansion had completed at the end of May (Tobita unpublished data). It was for this reason that we chose growth light environments (Q_int, PPFD_max) in June as determining factors for photosynthetic traits. The equalized amount of excessive energy production observed across the various light environments within a canopy (Figs 5 and 6) could be explained if the developments of photosynthesis (involved in ETR) and photoprotection (involved in D) along with the increase in LMA would be continued until the excessive energy production during sunflecks or direct sunlight drops below a certain level both in shade and sun leaves^19,20.

The hypothesis of the present study: higher N_L than optimal is needed in the shade leaves to prevent photoinhibition during sunflecks, is partly similar to that proposed by Dewar et al.¹², where a lower bound of LMA in the shade leaves exists, in relation to the limitation in leaf morphological plasticity²³. Furthermore, the present study also proposes that the upper bound of N_L in sun leaves would be regulated as the minimum required to circumvent photoinhibition under direct sunlight, which might be related to the upper-bound constraint on photosynthetic capacity at the top of the canopy proposed by Lloyd et al.¹³ to explain the less steep N_L decline. In the present study, water stress during leaf development was considered to be negligible because of a considerable amount of spring snowmelt in the forest (mean maximum snow depth was 114 cm)⁴⁰. Peltoniemi et al.¹⁴ proposed that limited hydraulic conductance for the sun leaves may result in a lower N_L in sun leaves with actual N_L distribution than the optimal one. In contrast, leaves acclimated to long-term drought often show higher N_L accompanied with higher ETR, than leaves grown without drought stress, to prevent photoinhibition under lower intercellular CO₂ concentration by stomatal closure^32,33,41,42. In this context, water stress on sun leaves induced by the limited hydraulic conductance in the upper canopy^43,44 would not necessarily decrease N_L in sun leaves, but rather increase N_L for preventing photoinhibition. Further investigation is needed on such environmental stresses during leaf development influencing excess energy production to predict leaf N distribution within a canopy.

Conclusion

The present study provides a novel insight into the canopy N_L distribution with respect to circumvention of photoinhibitory damage at the whole-canopy level like a homeostatic adjustment, where plants follow a strategy through which N_L distribution is not optimized for canopy C gain but rather regulated to prevent photoinhibition during sunflecks for shade leaves or direct sunlight for sun leaves. This regulation of N_L distribution contributes to keeping an efficient light utilization capacity during the daytime at the whole-canopy level, by means of minimizing a time lag in the recovery from photoinhibition¹⁶, which indicates an important biological plasticity in the response to light environment, and may suggest genetically-driven adjustments for successful acclimation in a changing light environment. Revealing such a physiological coordination of individual leaves for the benefit of the whole canopy will contribute to advancing the understanding of carbon–nitrogen interactions^45,46 and energy flow in terrestrial ecosystems. Further studies with different species and at different environmental conditions are needed to demonstrate that the regulation of N_L distribution found in this study is an unequivocal biological mechanism occurring across species.

Methods

Study site

The present study was conducted in the experimental forest of the Hokkaido Research Center, Forestry and Forest Products Research Institute in Sapporo, Japan (43°N, 141°E; 180 m above sea level). Mean annual precipitation was approximately 900 mm and the mean annual temperature was 7.1 °C. The predominant species were Japanese white birch (Betula platyphylla Sukatchev var. japonica Hara) and Japanese oak (Q. mongolica Fisch. ex Ledeb. var. crispula (Blume) H. Ohashi), which comprised >75% of the plot basal area.

Estimation of the photosynthetic photon flux density (PPFD) at various leaf positions within the canopy

Leaf morphological and physiological traits are determined by light environments under which leaves are developed²⁷. We considered that light conditions during leaf development in June were important for leaves of Q. mongolica because photosynthesis reached its maximum during this period (Tobita unpublished data). A hemispherical photograph was taken by a digital camera (Coolpix 4500, Nikon, Tokyo, Japan) with a fisheye lens (Fisheye Lens, FC-E8, Nikon) right above each of the leaves that were used for the photosynthetic gas exchange and chlorophyll fluorescence measurements at the summertime in 2007. Based on the photographs, we estimated the incident PPFD for each leaf by using a canopy analysis software (WinScanopy, Regent Instruments Inc., Quebec, Canada)⁴⁷ combined with the data of direct and diffuse radiation from the open sky measured by a pyrheliometer (CH1, Kipp & Zonen, Delft, The Netherlands) combined with an automatic solar tracker (ASTX-1, Prede, Tokyo, Japan) and a pyrheliometer (CM21, Kipp & Zonen) with 1-min intervals placed above the canopy in the experimental forest. Instantaneous incident PPFD at each leaf position was estimated as below:

$$\begin{array}{lll}\hfill \mathrm{PPFD}& \hfill =\hfill & \mathrm{ISF}\times \left[\mathrm{diffuse}\mathrm{radiation}\mathrm{from}\mathrm{the}\mathrm{open}\mathrm{sky}\right]+\left[\mathrm{direct}\mathrm{radiation}\right]\hfill \\ \hfill & \hfill & \left(\mathrm{if}\mathrm{not}\mathrm{interrupted}\mathrm{by}\mathrm{above}\mathrm{leaves}\right),\hfill \end{array}$$

or

$$\mathrm{PPFD}=\mathrm{ISF}\times \left[\mathrm{diffuse}\mathrm{radiation}\mathrm{from}\mathrm{the}\mathrm{open}\mathrm{sky}\right]\left(\mathrm{if}\mathrm{direct}\mathrm{radiation}\mathrm{was}\mathrm{interrupted}\right)$$ 1

where ISF is the indirect (diffuse) site factor estimated by the WinScanopy software, penetration of the direct radiation is also assessed with the sun track simulated by the software. The average integrated daily quantum flux density at each leaf position in June (Q_int; mol m⁻² day⁻¹) was calculated as a measure of growth light environment based on 1-min-interval PPFD from the 1st to 30th June, 2007. Average daily peak PPFD in June at each leaf position (PPFD_max) was estimated using the daily five highest values during June³.

Leaf area index (LAI), and light gradients within the canopy

We used the relationship between LAI and light gradients within the canopy of an inventory plot (50 × 50 m) of the experimental forest after Utsugi et al.⁴⁸. The three predominant canopy tree species, B. platyphylla, Q. mongolica, and Kalopanax septemlobus, were used for the measurements of LAI during the summers of 2001 and 2003. Eight sample trees for each species (24 trees in total for each summer) were felled, and the gradient of LAI was determined by a stratified clipping method with 1-m strata intervals. PPFD within the canopy was also measured with PPFD sensors (Li-190SA, Li-Cor, NE, USA) with 1-m vertical intervals from 1 to 26 m along with permanent steel scaffolding within the canopy of B. platyphylla, Q. mongolica, and K. septemlobus in the area adjacent to the stratified clipping plot. The measurements were carried out under overcast conditions. Relative PPFD for each height was calculated as a mean of 200 replicates, with synchronized measurements of above and below canopy PPFD. The stand, consisting of B. platyphylla, Q. mongolica and K. septemlobus, was considered to be matured at that time since the age of the stand was about 90 years when the stratified clipping was conducted. We used the relationship between relative PPFD and LAI based on the pooled data for 2001 and 2003⁴⁸ to estimate LAI for each leaf measured in 2007 from the relative PPFD. Relative PPFD at each leaf used for the photosynthetic measurement in 2007 was estimated as (Q_int at each leaf position)/(Q_int above the canopy), where Q_int above the canopy was 43.4 mol m⁻² day⁻¹ measured by the pyrheliometers placed above the canopy.

Measurements of gas exchange and chlorophyll fluorescence

Measurements of gas exchange and chlorophyll fluorescence were conducted at the summertime of 2007 on mature leaves of a Japanese oak (approximately 23 m height and 95-years-old as of 2007), surrounded by the scaffolding described above with a portable photosynthesis measuring system (Li-6400, Li-Cor, Lincoln, NE, USA) combined with a leaf chamber fluorometer (Li-6400-40, Li-Cor). We selected a total of 15 leaves grown at various positions within the canopy (4 to 23 m in height). The net photosynthetic rate (A_n), quantum yield of PSII electron transport (Φ_PSII), photochemical efficiency of the open PSII (Fv′/Fm′) and excitation pressure adjusted for the efficiency of PSII photochemistry (1 − qP) Fv′/Fm′^24,30 were measured at a photosynthetic steady state, where qP is photochemical quenching. The measurements were conducted under an ambient CO₂ concentration of 360 µmol mol⁻¹ and at various PPFD (0, 50, 100, 200, 300, 600, 1,000, 1,500, and 2,000 µmol m⁻² s⁻¹) provided by a red/blue LED array (Li-6400-40, Li-Cor), with blue light comprising 10% of the total PPFD. Leaf temperature was ≈27 °C during the measurements. After the measurements, the leaves were sampled and used for determination of N_L by the combustion method using an analysis system composed of a N/C determination unit (SUMIGRAPH, NC 800, Sumika Chem. Anal. Service, Osaka, Japan), a gas chromatograph (GC 8 A, Shimadzu, Kyoto, Japan), and a data processor (Chromatopac, C R6A, Shimadzu).

Electron transport rate (ETR) was calculated as ETR = Φ_PSII × leaf absorptance × light intensity × 0.5^22,49. Leaf absorptance was calculated from a calibration curve between SPAD readings (measured with a SPAD chlorophyll meter, SPAD 502, Minolta, Osaka, Japan) and leaf absorptance³. The responses of electron transport to incident irradiance were fitted by the convexity equations⁵⁰ as below:

$${\mathrm{\theta }\mathrm{ETR}}^2-\left(\mathrm{\phi }\mathrm{PPFD}+{\mathrm{ETR}}_{\max }\right)\mathrm{ETR}+\mathrm{\phi }\mathrm{PPFD}\times {\mathrm{ETR}}_{\max }=0$$ 2

where ϕ is the initial slope (maximum quantum yield), θ the convexity of the curve, and ETR_max the maximum rate of electron transport.

The responses of Fv′/Fm′ and (1 − qP) Fv′/Fm′ to incident irradiance for each leaf were fitted as follows:

$$\mathrm{Fv}\prime /\mathrm{Fm}\prime ={\mathrm{y}}_0+\mathrm{a}/(1+{\left(\mathrm{PPFD}/{\mathrm{x}}_0\right)}^{\mathrm{b}})$$ 3

$$\left(1-\mathrm{qP}\right)\mathrm{Fv}\prime /\mathrm{Fm}\prime =\mathrm{a}\left(1-\exp \left(-\mathrm{bPPFD}\right)\right)$$ 4

Analogous to ETR, thermal dissipation (D) and excess energy production (E) were estimated from (1 − Fv′/Fm′) × leaf absorptance × light intensity × 0.5 and ((1 − qP) Fv′/Fm′) × leaf absorptance × light intensity × 0.5, respectively^22,24. Each coefficient in Eqs 2–4 was fitted as a function of N_F defined as (N_L – N_b) of the leaves used for the chlorophyll fluorescence measurements, where N_b is the x-intercept of the maximum rate of photosynthesis (A_max) − N_L relationship, which can be regarded as non-photosynthetic leaf structural N content. Conversely, N_F can be regarded as photosynthetically-functional leaf N content^6,51. A_max was estimated from the light response of A_n based on the convexity equations⁵⁰, as below:

$$\theta {({\mathrm{A}}_{\mathrm{n}}+{\mathrm{R}}_{\mathrm{d}})}^2-(\phi \mathrm{P}\mathrm{P}\mathrm{F}\mathrm{D}+{\mathrm{A}}_{max})({\mathrm{A}}_{\mathrm{n}}+{\mathrm{R}}_{\mathrm{d}})+\phi \mathrm{P}\mathrm{P}\mathrm{F}\mathrm{D}\ast {\mathrm{A}}_{max}=0$$ 5

where R_d is the dark respiration rate, ϕ the initial slope (maximum quantum yield), and θ is the convexity of the curve. The relationships between N_F and photosynthesis-related coefficients are summarized in Supplemental Fig. S1. Based on the coefficients of light responses in ETR, Fv′/Fm′, and (1 − qP) Fv′/Fm′ as a function of N_F, we extrapolated the light responses in leaves that have various N_L content with optimal and uniform N_L distribution.

Actual, optimal and uniform leaf N distribution

We derived the light extinction coefficient of the canopy, K_L ⁵² as follows:

$$\mathrm{I}/{\mathrm{I}}_0=\exp \left(-{\mathrm{K}}_{\mathrm{L}}\mathrm{F}\right)$$ 6

where F is the LAI cumulated from the canopy top, and I and I₀ are PPFD at F and the canopy top, respectively. Actual N_L distribution at depth F in the canopy is also described by an exponential function of F with a photosynthetic leaf N distribution coefficient (K_n):

$${\mathrm{N}}_{\mathrm{L}}=({\mathrm{N}}_0-{\mathrm{N}}_{\mathrm{b}})\exp (-{\mathrm{K}}_{\mathrm{n}}\mathrm{F})+{\mathrm{N}}_{\mathrm{b}}$$ 7

where N₀ is the N_L of the leaves at the canopy top. Optimal N_L distribution was derived after Anten et al.⁶ as follows:

$${\mathrm{N}}_{\mathrm{L}}={\mathrm{K}}_{\mathrm{L}}{\mathrm{N}}_{\mathrm{TF}}/\left(1-\exp \left(-{\mathrm{K}}_{\mathrm{L}}{\mathrm{F}}_{\mathrm{T}}\right)\right)\exp \left(-{\mathrm{K}}_{\mathrm{L}}\mathrm{F}\right)+{\mathrm{N}}_{\mathrm{b}}$$ 8

With

$${\mathrm{N}}_{\mathrm{T}\mathrm{F}}={\mathrm{N}}_{\mathrm{T}}-{\mathrm{N}}_{\mathrm{b}}{\mathrm{F}}_{\mathrm{T}}$$ 9

where N_TF is the total free nitrogen in the canopy and N_T and F_T are the total leaf N pool and LAI per unit ground area, respectively. N_T is calculated based on the integration of Eq. 2 ¹¹. A N_L distribution is defined as uniform when all leaves have the same N_L irrespective of leaf position. Therefore, N_L with uniform distribution is determined as:

$${\mathrm{N}}_{\mathrm{L}}={\mathrm{N}}_{\mathrm{T}}/{\mathrm{F}}_{\mathrm{T}}$$ 10

Based on the estimated N_L with optimal and uniform distribution, we calculated ETR, D, and E under the maximum PPFD during sunflecks for each leaf by using the N_L-dependent photosynthetic coefficients (Supplemental Fig. S1) and Eqs 2–4.

We hypothesized that canopy N might be distributed to maintain E constant throughout the canopy during sunflecks, thus to keep an efficient light utilization capacity by preventing photoinhibition for all leaves across sun and shade environments. Therefore, we estimated the leaf N distribution coefficient (K_n) that minimized the variance in E at PPFD_max across the different leaf types within the canopy, using Eq. 8 with various K_n (0.1 to 1.0 with an interval of 0.1) instead of K_L as follows:

$${\mathrm{N}}_{\mathrm{L}}={\mathrm{K}}_{\mathrm{L}}{\mathrm{N}}_{\mathrm{TF}}/\left(1-\exp (-{\mathrm{K}}_{\mathrm{n}}{\mathrm{F}}_{\mathrm{T}})\right)\exp (-{\mathrm{K}}_{\mathrm{n}}{\mathrm{F})+\mathrm{N}}_{\mathrm{b}}$$ 11

Variance (s²) in E was estimated as follows:

$${\mathrm{s}}^2=\frac{1}{\mathrm{n}}\sum _{i=1}^{\mathrm{n}}{({\mathrm{E}}_{\mathrm{i}}-\overline{\mathrm{E}})}^2$$ 12

Statistical analysis

We expediently classified the leaves into four types based on their growth light environments: (1) deep shade leaves (0 < Q_int < 3 mol m⁻² day⁻¹, n = 5); (2) moderate shade leaves (3 < Q_int < 15 mol m⁻² day⁻¹, n = 4); (3) moderate sun leaves (15 < Q_int < 25 mol m⁻² day⁻¹, n = 3); and (4) typical sun leaves (25 < Q_int < 35 mol m⁻² day⁻¹, n = 3). One-way analysis of variance (ANOVA) was used to test the differences among leaf types in ETR, D, and E with actual, optimal, or uniform N_L distribution, and the ratio of ETR, D, and E with optimal or uniform to actual N_L distribution⁵³. Furthermore, when the ANOVA returned an overall significant effect of leaf type, the means were further tested using Holm’s pairwise comparisons. The threshold for statistical significance was predefined at an alpha level of 0.05.

Data availability

All data used in this manuscript are present in the manuscript and its supplementary information.

Author Contributions

M.K., H.T. and H.U. conceived the idea; M.K., S.K., H.H., H.T. and H.U. collected the data; S.K. conducted the leaf N analysis; H.H. analyzed hemispheric photographs; M.K. and E.A. led the writing of the manuscript with input from all co-authors; All authors contributed critically to the drafts and gave final approval for publication.

Competing Interests

The authors declare that they have no competing interests.