Standardised evaluation of medicine acceptability in paediatric population: reliability of a model

Abstract

Objectives

Our novel tool to standardise the evaluation of medicine acceptability was developed using observational data on medicines use measured in a paediatric population included for this purpose (0–14 years). Using this tool, any medicine may be positioned on a map and assigned to an acceptability profile. The present exploration aimed to verify its statistical reliability.

Methods

Permutation test has been used to verify the significance of the relationships among measures highlighted by the acceptability map. Bootstrapping has been used to demonstrate the accuracy of the model (map, profiles and scores of acceptability) regardless of variations in the data. Lastly, simulations of enlarged data sets (×2; ×5; ×10) have been built to study the model's consistency.

Key findings

Permutation test established the significance of the meaningful pattern identified in the data and summarised in the map. Bootstrapping attested the accuracy of the model: high RV coefficients (mean value: 0.930) verified the mapping stability, significant Adjusted Rand Indexes and Jaccard coefficients supported clustering validity (with either two or four profiles), and agreement between acceptability scores demonstrated scoring relevancy. Regarding enlarged data sets, these indicators reflected a very high consistency of the model.

Conclusions

These results highlighted the reliability of the model that will permit its use to standardise medicine acceptability assessments.

Introduction

Acceptability is the ‘overall ability of the patient and caregiver (defined as ‘user’) to use a medicinal product as intended (or authorised)’.1 To ensure treatment success, the European Medicine Agency (EMA) and the International Council for Harmonisation have highlighted in their guidelines2, 3 that acceptability assessment should be investigated during the development of medicines for paediatric use. A recently published review identified only 10 clinical studies comparing the appropriateness, acceptability or preference for different dosage form designs in paediatric populations, of which three studies used a validated methodology.4 This methodology, focusing on medicine swallowability, fails to incorporate the multidimensional aspect of medicine acceptability. In parallel, the EMA guideline has also identified the need for an internationally harmonised method to assess acceptability.

In Ruiz et al.,5 we described the development of a novel tool allowing standardised evaluation of medicine acceptability. Using a standardised questionnaire, multiple observational measures were collected in real‐life condition during medicine use in children (0–14 years). Mining this multivariate data set of 234 evaluations, exploratory analyses were performed to identify patterns and to develop an intelligible descriptive model defining our tool: an acceptability reference framework. A mapping process summarised the key information contained in the data onto an acceptability map. A subsequent cluster analysis gathered the evaluations plotted on the map into different groups defining distinct acceptability profiles.

Using this tool, acceptability scoring may be thus performed for any medicine assessed by at least 30 different users. The barycentre of those evaluations related to a particular medicine defines the medicine's position on the acceptability map. This barycentre was then assigned to a cluster, defining the medicine's acceptability profile. Additionally, the evaluations may be gathered according to factors of interest, for example patient age or country, or medicine dosage form or therapeutic group, and then analysed to score their acceptability. As such, this tool may be employed to explore each characteristic of patients, or medicines, on acceptability.

Due to the wide range of patients and medicines on the global market, an ongoing accumulation of data is required to improve knowledge on medicine acceptability. The present exploration has incorporated additional data, bringing the number of medicine use evaluations to 680 in total, and has aimed to demonstrate the reliability of the current descriptive model which was required to provide a valid evaluation of medicine acceptability in the paediatric population.

First, significance of relationships among elements highlighted by the acceptability map was established. Secondly, as the descriptive model fits with the set of evaluations collected at random, the influence of variations in source data on the modelling processes was explored to demonstrate the model's accuracy. Lastly, simulations were performed to verify the consistency of the tool to withstand the addition of further evaluations into the database.

Materials and Methods

Acceptability model

We followed the methodology previously published,5 as briefly described hereafter.

Data on medicines use

The observational study focused on medicines use in children (0–14 years) receiving any treatment. Infusion administered by a catheter already in place were, however, excluded from the analysis as catheter insertion was considered integral to the administration sequence. The study was conducted throughout France, in collaboration with a network of physicians and pharmacists based in both hospitals and community dispensaries. Patients and parents were recruited at random, on a voluntary basis.

The caregiver (parent, relative…) or healthcare professional (physician, nurse…) observing the first medicine use (following study inclusion) performed objective measures focused on observable content, then completed the web‐questionnaire.

The following variables linking to their categories were included in the analysis without weights in order to describe the acceptability: result of the intake (fully, partly or not taken), patient's reaction (positive, neutral or negative reaction), manipulation and administration time (short, medium or long time) and the use, or not, of the following methods to achieve administration: divided dose (use, or no divided dose), food/drink (use, or no food/drink), reward (use, or no reward) or restraint (use, or no restraint).

The data set was a table where the columns corresponded to these categorical variables listed above, and the rows corresponded to the evaluations of the use of distinct medicines by different users.

The combinations of categories obtained from each completed evaluation questionnaire reflect an individual user's behaviour. The number of distinct combinations observed over the course of data collection was continuously monitored. Curve fitting, using locally scatter plot smoothing, described the relationship between the size of the data set and the use of new relevant combinations of categories.

Data analysis

Multiple correspondence analysis (MCA) was used as the mapping process. This factorial method aims to summarise and to visualise in a three‐dimensional map, any similarities between combinations of categories, and the relationships between categories.6 Proximity on the map illustrated a similarity. To ensure constant mapping orientation, the coordinates of the extreme category ‘Not taken’ are maintained positive on all three dimensions of the map.

Cluster analysis was then used. This analysis gathered the evaluations into clusters according to their Euclidean distances on the map using hierarchical clustering on principal components then k‐means consolidation.7 The clusters, defining acceptability profiles, were characterised by the categories significantly over‐represented into their subset of evaluations. The categories over‐represented in the clusters had a v‐test value >1.96 (P‐value < 0.05), reflecting a significantly larger proportion of similar responses in those evaluations within the cluster than if the categories were to have been randomly distributed in the data set. The higher the v‐test value, the more strongly the measure was over‐represented into the cluster.

The barycentre of the evaluations of a particular medicine defined the medicine's position on the three‐dimensional acceptability map. The medicine was assigned to the cluster with the nearest barycentre using Euclidian distance, which defined the medicine's acceptability profile. Three confidence ellipses, surrounding the medicine's position for the dimensions 1–2, 1–3 and 2–3, defined an area containing the barycentre's true position with 90% probability if the experiment were to be repeated. Each ellipse was made of 1000 dots. Each dot was assigned to one of the clusters. The proportions of dots belonging to the different clusters were then recorded. The acceptability score was structured by the acceptability profile of the barycentre and the proportion of confidence ellipses belonging to it. Scoring may be performed for any medicine or characteristic that might be assessed by at least 30 evaluations.

Reliability of the model

Significance

Permutation testing is a non‐parametric statistical significance test.8 Statistical significance is reached when the test statistic is very unlikely to have occurred under the null hypothesis (H₀). According to H₀, rearrangement of labels among the observed data has no effect on the test statistic. Multiple rearrangements of data allow for the estimation of the sampling distribution of the test statistic when the null hypothesis is true.

We considered the inertia explained by the acceptability map, corresponding to the percentage of data set variance summarised by the three dimensions of the map, as the test statistic. Higher inertia value represented greater data set structure.

Rearrangement of the categories was performed at random among the 680 evaluations of the data set, for each variable independently. Based on the simulated data set, mapping was performed and the inertia explained by the newly created map was recorded. One million permutation rounds were performed to build the sampling distribution of inertia. The P‐value of the test corresponded to the proportion of rearrangement where the inertia of the new map is at least as extreme as the observed inertia value.

If the P‐value was less than the 5% significance level, the null hypothesis could be disproved. Thus, the relationships between categories summarised in the acceptability map could be considered significant.

Accuracy

As the model fits with the set of evaluations collected at random, the influence of variations in source data on modelling processes was explored to demonstrate the model's accuracy. As the empirical distribution of the observed data set was the only distribution information available, bootstrapping, which is based on a resampling method, was employed.9

Starting from the observed data set of 680 evaluations, we used random sampling with replacement to create simulated data sets of an equal size. One thousand rounds of resampling were performed. Mapping, clustering and scoring processes were performed for each simulated data set; then, statistical indicators measured variability among the results from the observed data set and those from the simulated data sets. We averaged the results for the indicators over all the iterations and computed the 95% confidence interval around the mean or the proportion to quantify the dispersion. This method, non‐parametric bootstrapping, provided measures of the model's outcomes’ accuracy regarding mapping, clustering and scoring processes.

The RV coefficient was used as the indicator for mapping process variability. The RV coefficient is a multivariate generalisation of the squared Pearson correlation coefficient measuring the closeness of two sets of points represented on a matrix.10 The coordinates, on the three dimensions of the maps, for the 17 categories of the categorical variables were represented on a matrix. The RV coefficient evaluated the likeness between both the matrix generated from the observed data set and those matrices generated from the simulated data sets. The coefficient values ranged from 0 (no correlation) to 1 (perfect correlation). An algorithm implemented in the package FactoMineR allowed us to test if the RV coefficient was significantly larger than 0.11

The adjusted Rand Index (ARI) was used as a statistical indicator to measure the degree of association between two complete partitions,12 yielding values between 0 (independent partitions) and 1 (perfect similarity). The ARI was used to compare the complete partitions from the observed and the simulated data sets. The statistical significance of the ARI was computed using the method proposed by Qannari et al.13

In addition, we used the Jaccard coefficient to study the stability of the original clusters as proposed by Henning.14 The Jaccard coefficient is a similarity measure between two subsets of data varying between 0 and 1 (similar). This coefficient was the ratio of the evaluations belonging to both subsets and the evaluations belonging to at least one of the subsets. For each original cluster, we computed the Jaccard coefficient between the subset of evaluations gathered into it and the distinct subsets of evaluations gathered into the clusters from the simulated data set. The calculation included the evaluations found in both the observed and simulated data sets. For each original cluster, the maximum Jaccard coefficients indicated the most similar cluster found among the clusters from the simulated data set. A value lower than 0.5 represents a ‘dissolution’ of the cluster and a value superior or equal to 0.75 denotes a ‘good recovery’ of the cluster.

Proportion of agreement between the observed medicine acceptability scores of the products assessed at least 30 times and their scores using the simulated data sets was the statistical indicator for the acceptability scoring reliability.

Consistency

As data collection is still ongoing, additional evaluations must not have a significant effect on the tool. Thus, we sought to demonstrate the consistency of the model over the course of data set enlargement.

We built 2, 5 and 10 times larger data sets, combining the 680 original evaluations of the observed data set to 680, 2720 and 6120 additional simulated evaluations. We used the previous methodology and the same statistical indicators to evaluate the consistency of the model.

Results

Acceptability model

Data on medicines use

Patients from less than one month to 14 years old were included in the study. Girls and boys were equally represented. Data on medicines use were collected at home or in hospital to maximise the evaluation of various users’ behaviours. The demographic characteristics of the 680 patients included in the study are presented in the Table S1.

There were 202 distinct medicines (particular brand name + strength + formulation) assessed in the study. They included 101 different active pharmaceutical ingredients (API) classified in 34 anatomical therapeutic groups (ATC2). Of the 14 main anatomical groups, corresponding to the first level of the code, all were represented with the exception of G (Genito‐urinary system and sex hormones) and L (Antineoplastic and immunomodulating agents). The 10 routes of administration and the 33 formulations highlight the wide variety of medicines assessed. The characteristics of the 202 medicines included in the study are presented in the Table S2.

Among these medicines, 46% were assessed more than once. Two medicines, anonymously labelled ‘X’ and ‘Y’, were assessed at least 30 times. These medicines are two distinct dosage forms of the same API. The medicine ‘X’ is an oral suspension, while the medicine ‘Y’ permits for higher dosage using a powder for oral solutions. The first medicine was administered to younger children (89% < 6 years), than the second (70% > 6 years).

These 680 evaluations were comprised of 138 distinct combinations of categories, of the 432 mathematically possibilities, and reflected existing users’ behaviours. The following combination of responses reflecting a medicine use without any problem was the most used (12% of the evaluations): ‘Fully taken’, ‘Positive reaction’, ‘Short time’, ‘No divided dose’, ‘No food drink’, ‘No reward’ and ‘No restraint’. For 11% of the evaluations, the following combination was used: ‘Fully taken’, ‘Neutral reaction’, ‘Short time’, ‘No divided dose’, ‘No food drink’, ‘No reward’ and ‘No restraint’. The most unfavourable combination was used twice: ‘Not taken’, ‘Negative reaction’, ‘Long time’, ‘Use divided dose’, ‘Use food drink’, ‘Use reward’ and ‘Use restraint’. Combinations such as ‘Not taken’, ‘Positive reaction’, ‘Long time’, ‘Use divided dose’, ‘No food/drink’, ‘No reward’ and ‘Use restraint’, reflecting improbable behaviours, were not observed.

The use of new combinations clearly decreased over the course of data collection. According to a curve fitting model, the relationship between the data set size and the use of new relevant combinations, the number of usable combinations tends to be stable (Figure S1).

Data analysis

The MCA summarised associations between the categories and relationships among the evaluations by placing them on the acceptability map. The first two dimensions structuring the map were the most important as they explained 37.9% of the total variance of the data set (Figure S2). The third dimension accounted for 11% of variance, and the inertia explained by the three‐dimensional map was 48.9%. Interpretation of the acceptability map was based on proximities between elements: response options that were often selected together in the evaluations, and evaluations completed in a similar manner, converged on the map.

The evaluations were thus gathered into clusters according to their proximities on the map. We partitioned the evaluations into either two or four clusters. Table 1 presents the coherent patterns of measures significantly over‐represented into the different clusters defining distinct acceptability profiles.

Table 1.

Acceptability profiles description using two or four clusters

Observational measures	2 Clusters		4 Clusters
	Positively accepted	Negatively accepted	Well‐accepted	Accepted	Poorly accepted	Not accepted
Dose fully taken	16.7	–	11.9	5.4	–	–
Dose partly taken	–	13.7	–	–	14.6	–
Dose not taken	–	8.1	–	–	–	14.7
Positive reaction	12.8	–	16.6	–	–	–
Neutral reaction	9.6	–	–	11.3	–	–
Negative reaction	–	20.5	–	–	17.2	7.7
Short time	10.4	–	17.7	–	–	–
Medium time	–	–	–	9.8	–	–
Long time	–	11.9	–	2.2	9.8	4.8
No divided dose	7.4	–	4.7	3.6	–	–
Use divided dose	–	7.4	–	–	9.7	–
No food/drink	7.2	–	12.8	–	–	–
Use food/drink	–	7.2	–	6.1	7.2	–
No reward	5.4	–	8.8	–	–	–
Use reward	–	5.4	–	5.2	2.3	3
No restraint	19.2	–	11.8	6.4	–	–
Use restraint	–	19.2	–	–	15.5	6.3

Values of the significant v‐test (>1.96).

Next, we scored the acceptability of the medicines ‘X’ and ‘Y’, which had been assessed at least 30 times. Using two clusters, the barycentres of the evaluations of these medicines were assigned to the acceptability profile ‘Positively accepted’. All the confidence ellipses fell within the same acceptability profile. Using four clusters, the barycentres of the evaluations of these medicines were assigned to the acceptability profile ‘Well‐accepted’. However, all the confidence ellipses of the medicine ‘X’ belonged to the cluster ‘Well‐accepted’, whereas a limited part of the confidence ellipses of the medicine ‘Y’ belonged to the cluster ‘Accepted’ (37% for dimensions 1–2, 24% for dimensions 1–3 and 24% for dimensions 2–3).

Reliability of the model

Significance

Figure 1 presents the sampling distribution of inertia explained by the map under the null hypothesis. One million permutation rounds were performed to build this sampling distribution. There was no rearrangement where the inertia explained by the new map was superior or equal to the observed value (48.9%). The mean inertia value under the null hypothesis was 34.1% with a standard deviation of 0.49.

Figure 1.

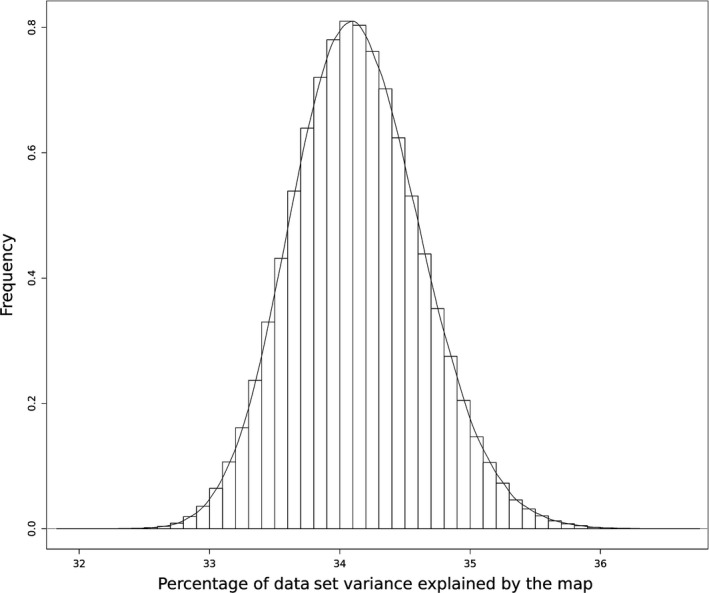
Inertia sampling distribution based on 1 000 000 permutation rounds.

According to the sampling distribution, the null hypothesis could thus be clearly disproved. Categories have not been found to be exchangeable among evaluations, so associations between categories were not due to chance.

Accuracy

We recorded the statistical indicators for each resampling round, averaged the results over all of the iterations and computed the 95% confidence interval around the mean or the proportion to quantify the dispersion.

The RV coefficient evaluated the likeness between the categories’ coordinates on the maps from the observed data set and the simulated data sets. The RV coefficient was significantly higher than 0 in all cases. The mean value of the RV coefficient was 0.930 ([0.926; 0.934]).

The ARI assessed similarity between complete clustering partitions from the observed data set and the simulated data sets. In addition, we computed for the original clusters the maximum Jaccard coefficient found in the simulated data set, corresponding to the most similar cluster.

The ARI values were significantly different from 0 (independent partitions) in all simulations. Using four clusters, the mean value of the ARI was 0.709 ([0.698; 0.720]). The averaged maximum Jaccard coefficient were 0.825 ([0.817; 0.834]) for the cluster ‘Well‐accepted’, 0.652 ([0.639; 0.664]) for the cluster ‘Accepted’, 0.850 ([0.843; 0.858]) for the cluster ‘Poorly accepted’ and 0.865 ([0.849; 0.881]) for the cluster ‘Not accepted’. Using two clusters, the mean value of the ARI was 0.960 ([0.958; 0.962]). The averaged maximum Jaccard coefficient were 0.987 ([0.986; 0.987]) for the cluster ‘Positively accepted’ and 0.966 ([0.965; 0.968]) for the cluster ‘Negatively accepted’.

There were more than 30 evaluations of the medicine ‘X’ in all the simulated data sets. The minimum number of evaluations of this medicine in a bootstrap iteration was 121, and the maximum was 190. There were 30, or more, evaluations of the medicine ‘Y’ in 50% of the simulated data sets. The maximum number of evaluations was 53.

Using four clusters, the barycentre of the evaluations of the medicine ‘X’ was assigned to the acceptability profile ‘Well‐accepted’ for 82.4% ([80.0; 84.8]) of the resampling rounds, and 67.0% ([62.8; 71.2]) for the barycentre of the evaluations of the medicine ‘Y’. In the others resampling rounds, the barycentres of the evaluations of these medicines were classified ‘Accepted’. Using two clusters, the barycentres of the evaluations of the medicines ‘X’ and ‘Y’ were classified ‘Positively accepted’ for all the simulation rounds.

Consistency

The statistical indicators for each size of the enlarged data sets and each iteration were recorded. Next, the results over all the resampling rounds were averaged and the 95% confidence interval around the mean or the proportion was computed. Percentages were used to express proportions.

The mean values of the RV coefficient were 0.982 ([0.981; 0.983]), 0.989 ([0.988; 0.990]) and 0.994 ([0.994; 0.994]) for the data sets 2, 5 and 10 times larger, respectively. These results denote the high mapping stability. The likeness between both the matrix generated from the observed data set and those matrices generated from the simulated data sets tended to be perfect with data set enlargement.

Using four clusters, the mean values of the ARI were 0.809 ([0.798; 0.820]), 0.826 ([0.815; 0.837]) and 0.832 ([0.821; 0.844]) for 2, 5 and 10 times larger data sets, respectively. Using two clusters, the mean values of the ARI were 0.980 ([0.979; 0.981]), 0.984 ([0.984; 0.985]) and 0.989 ([0.988; 0.989]) for 2, 5 and 10 times larger data sets, respectively.

For each cluster, Tables 2 and 3 present the maximum Jaccard coefficient averaged over all the bootstrap iterations for the enlarged data sets with four clusters and two clusters, respectively.

Table 2.

Four clusters consistency

	Enlarged data set ×2	Enlarged data set ×5	Enlarged data set ×10
Well‐accepted	0.877 [0.868; 0.885]	0.886 [0.878; 0.895]	0.887 [0.879; 0.896]
Accepted	0.788 [0.777; 0.799]	0.814 [0.804; 0.825]	0.824 [0.814; 0.834]
Poorly accepted	0.931 [0.928; 0.934]	0.941 [0.938; 0.944]	0.949 [0.946; 0.951]
Not accepted	0.973 [0.968; 0.979]	0.984 [0.981; 0.988]	0.995 [0.994; 0.996]

Maximum Jaccard coefficient averaged over all the sampling rounds and 95% confidence interval.

Table 3.

Two clusters consistency

	Enlarged data set ×2	Enlarged data set ×5	Enlarged data set ×10
Positively accepted	0.993 [0.993; 0.994]	0.995 [0.995; 0.995]	0.996 [0.996; 0.996]
Negatively accepted	0.983 [0.982; 0.984]	0.987 [0.986; 0.987]	0.990 [0.990; 0.991]

Maximum Jaccard coefficient averaged over all the sampling rounds and 95% confidence interval.

The barycentre of the 151 original evaluations of the medicine ‘X’ was well within the cluster ‘Well‐accepted’ for 95.1% ([93.8; 96.4]), 97.9% ([97.0; 98.8]) and 99.8% ([99.5; 100]) of the simulation rounds with 2, 5 and 10 times simulated larger data sets, respectively. For the case of medicine, ‘Y’, the barycentre of the 31 original evaluations was classified ‘Well‐accepted’ for 94.1% ([92.6; 95.6]), 98.1% ([97.3; 98.9]) and 99.5% ([99.1; 99.9]) of the simulation rounds for 2, 5 and 10 times larger data sets, respectively.

Using two clusters, the medicines ‘X’ and ‘Y’ were well within the cluster ‘Positively accepted’ for all the simulation rounds regardless of the size of the data sets.

Discussion

In the current study, we have continued the development of our tool that uses real‐life data on medicines use in children, collected for a wide range of medicines and patients using evaluations taken at home or in hospital, extending the number of medicine use evaluations to 680 in total.

We have collected data on medicines with new characteristics not included in our initial methodology publication containing a first set of 234 evaluations.5 Due to the wide range of patients and medicines on the global market, an ongoing accumulation of data is required to improve knowledge on medicine acceptability. At present, our extended data set contains evaluations of two new routes of administration (parenteral and topical), 15 new formulations (capsule, solution for injection, granules, solution for application, oral gel, rectal solution, chewable tablet…) and 11 new anatomical therapeutic subgroups of medicines (Drugs for constipation (A06), Digestives including enzymes (A09), Allergens (V01), Anthelmintics (P02), Anaesthetics (N01), Cardiac therapy (C01)…).

The variety of medicines and patients in the observed data set has allowed for the identification of relevant combinations of response options reflecting existing user behaviours. The current expanded data set is 190% larger than the observed data set collected in our initial publication [5], but only 45% more combinations of response options were observed. As the use of new combinations tended to decrease over the course of data collection, the key and influencing user behaviours were likely to have already been collected by earlier evaluations as captured by the model.

Correlation between the tool's assessments and user impressions has been demonstrated, but further validations were required. The acceptability map and the acceptability profiles have been quite consistent, as demonstrated by the successive communications: the poster presentation of the proof of concept with 66 evaluations at the 7th EuPFI conference,15, 16 the methodology publication with 234 evaluations5 and the poster presentation with 436 evaluations at the 8th EuPFI conference.17 However, even if variations in the data and data set enlargement seem to have no significant impact on the model, the reliability of the tool must be investigated.

In this study, we have sought to demonstrate the statistical reliability of the current descriptive model. The three following properties of the model were considered: significance, accuracy and consistency.

The significance of relationships among elements highlighted by the acceptability map was investigated using permutation test. None of the maps created from the 1 000 000 rearrangements had an inertia greater than or equal to the observed inertia value (48.9%).

According to this non‐parametric statistical significance test, categories are not exchangeable among evaluations; as such, associations between categories were not due to chance. The pattern identified in the set of evaluations and the relationships among elements highlighted by the acceptability map were found to be robust and significant. Thus, the observed data set appeared well‐structured and the map highly relevant.

The current descriptive model fits with the set of evaluations collected at random, so the influence of variations in the data on the model was explored using bootstrapping.

The original map from the observed data set demonstrated a highly coherent relationship among the 17 categories of the categorical variables: positively connotated categories were found in close proximity on the map, separate from the negatively connotated response. According to the RV coefficient, the positions on the acceptability map of the categories remained very similar regardless of variations in the data. A perfect correlation between two matrices of coordinates is related to a RV coefficient value of 1, so the mean value of the RV coefficient, 0.930, attested to a high stability among the original map and the maps from the simulated data sets.

Using partitions with either two or four clusters, we were able to establish coherent and understandable acceptability profiles from the observed data set. Using four clusters, the mean value of the ARI was 0.709; it was 0.960 using two clusters. A perfect correlation between two partitions is related to an ARI value of 1, so the similarity of partitions from the observed and the simulated data sets was satisfactory. Using two clusters, the partitions from the simulated data sets were even closer to the partition from the observed data set than with four clusters. The Jaccard coefficient was then employed to study the stability of the distinct original clusters. There was no ‘dissolution’ of clusters due to variation in the observed data set. The values from the Jaccard coefficient denoted a ‘good recovery’ of the original clusters, with the exception of the cluster ‘Accepted’, when using four clusters. For this cluster, the averaged maximum Jaccard coefficient was 0.652 ([0.639; 0.664]), just below the 0.75 threshold. So, although the cluster ‘Accepted’ captured a meaningful pattern in the data, there were nevertheless some slight variations in the evaluations gathered together, over all of the bootstrap iterations.

The current tool has allowed scoring for the acceptability of the medicines ‘X’ and ‘Y’ that assessed at least 30 times. The medicines labelled ‘X’ and ‘Y’ originally classified ‘Well‐accepted’ using four clusters and ‘Positively accepted’ using two clusters. Subsequently, both were defined as accepted in all bootstrap iterations, thus supporting the accuracy of acceptability scoring. Using two clusters, the medicines of interest were always assigned to the acceptability profile ‘Positively accepted’, despite variations in the observed data set and variations in the subset of evaluations for both medicines. Using four clusters, the medicine ‘X’, originally strongly classified as ‘Well‐accepted’, was more similarly classified ‘Well‐accepted’ across the resampling rounds than the medicine ‘Y’, which was originally straddling both ‘Well‐accepted’ and slightly ‘Accepted’ according to its confidence ellipses. Stability of the scoring depended on the confidence ellipses whose size was based on the sample size and homogeneity of the evaluations.

Taken together, these results attested to the accuracy of the model. Acceptability map, acceptability profiles and acceptability scores remained stable regardless of variations in the observed data set.

Due to the wide range of medicines available on the global market, catering to a large variety of different patients, further data will be needed to improve the knowledge on acceptability. As such, the influence of additional evaluations on the model was investigated.

The mean values of the RV coefficient were 0.982, 0.989 and 0.994 for the simulated data sets produced that were 2, 5 and 10 times larger than the observed one, respectively. These results demonstrated that stability among the maps was retained between the observed data set and the enlarged simulated data sets, emphasising the high consistency of the mapping process. Moreover, the larger the data set, the more stable the mapping process was found to be.

As with mapping consistency, similarity between partitions tended to be perfect with data set enlargement. Regarding the ARI, closeness between partitions was even greater with two clusters than with four clusters. The values of the Jaccard coefficient denoted a ‘good recovery’ for all of the original clusters regardless of the size of enlarged data sets. The cluster ‘Accepted’ was highly stabilised with data set enlargement.

Acceptability scoring has thus remained stable, independent of the simulated additional data. The medicines acceptability scores should be reliable over the course of ongoing data collection.

These results presented here have demonstrated the statistical reliability of the current descriptive model. The map, the profiles and the scores of acceptability have appeared to be both meaningful and stable. The main relationships among categories, as well as major similarities between evaluations, were already discovered and structured by the current model. Thus, this novel tool has been validated and standardised to provide an evaluation of medicine acceptability in the paediatric population. Furthermore, it facilitates the measurement of the acceptability profile of different dosage forms of an API during drug development, as well as permitting the comparison of final products (dosage form and packaging) to any comparator that might be present on the market.

Medicine acceptability is influenced by characteristics of both medicines and the patients to whom they are administered.1 Our tool allows for the explorations of factors affecting acceptability. For example, with regards to the API of the medicines ‘X’ and ‘Y’, a difference in acceptability scoring was observed in a specific patient subpopulation depending on the formulation. The oral suspension formulation tended to be better accepted than the powder for oral solution among children between 3 and 5 that had used both formulations at home. Similar explorations highlighting the influence on acceptability were observed for features such as the therapeutic group, the formulation type, the strength or the flavour of a medicine (Vallet T.).

Additional data on medicines use will facilitate these ongoing explorations of predictive factors of acceptability using this stable and consistent tool. As such, the relevant knowledge on medicines acceptability extracted from these data will participate to the continuous improvement of medicines and their administration to paediatric populations.

Finally, a similar study has been carried out in more than 1000 older patients using a similar questionnaire, data collection processes and statistical analyses. This study in patients over 65 years of age has allowed us to design a relevant acceptability reference framework in the elderly population ensuring the validity of our methodology (Ruiz F.).

Conclusions

Intended to validate the statistical reliability of our novel tool that permits the standardised evaluation of medicine acceptability, this study has built upon our previous work. Using our tool, any medicine may be positioned on an acceptability map and assigned to an acceptability profile. Similarly, this tool may be employed to explore the influence of each characteristic of patients, or medicines, on acceptability. According to the results of our present study, the acceptability map is robust and significant. The model remained stable regardless of simulations of variations in the set of observational data on medicines use. Furthermore, simulations of additional data showed an improvement of stability due to data set enlargement. New inclusions, which are required to improve knowledge on medicine acceptability, should not have any significant impact on mapping, clustering and scoring processes. Significance, accuracy and consistency of the model have attested to its statistical reliability. Our tool thus provides a method of reliable standardised acceptability scoring and allows extraction of relevant knowledge on predictive factors of acceptability.

Declarations

Funding

This research received no specific grant from any funding agency in the public, commercial or not‐for‐profit sectors.

Supporting information

Figure S1. The number of combinations of categories observed over the course of data collection.

Figure S2. Acceptability map using four clusters (dimensions 1 and 2).

Table S1. Demographic characteristics of the patients.

Table S2. Characteristics of the assessed medicines.