Using Bilateral Functional and Anthropometric Tests to Define Symmetry in Cross-Country Skiers

Abstract

The aim of this study was to evaluate the symmetry of anthropometry and muscle function in cross-country skiers and their association to vertical jumping power. Twenty cross-country skiers were recruited (21.7 ± 3.8 yrs, 180.6 ± 7.6 cm, 73.2 ± 7.6 kg). Anthropometric data was obtained using an iDXA scan. VO_2max was determined using the diagonal stride technique on a ski treadmill. Bilateral functional tests for the upper and lower body were the handgrip and standing heel-rise tests. Vertical jump height and power were assessed with a counter movement jump. Percent asymmetry was calculated using a symmetry index and four absolute symmetry index levels. At a group level the upper body was more asymmetrical with regard to lean muscle mass (p = 0.022, d = 0.17) and functional strength (p = 0.019, d = 0.51) than the lower body. At an individual level the expected frequencies for absolute symmetry level indexes showed the largest deviation from zero for the heel-rise test (χ2 = 16.97, p = 0.001), while the leg lean mass deviated the least (χ2 = 0.42, p = 0.517). No relationships were observed between absolute symmetry level indexes of the lower body and counter movement jump performance (p > 0.05). As a group the skiers display a more asymmetrical upper body than lower body regarding muscle mass and strength. Interestingly at the individual level, despite symmetrical lean leg muscle mass the heel-rise test showed the largest asymmetry. This finding indicates a mismatch in muscle function for the lower body.

Introduction

Cross-country skiing involves the upper and lower body for both classical and skating techniques. However, the skating technique relies more on asymmetrical strength while the diagonal stride of the classical technique demands more symmetrical use of the body. Therefore, for optimal performance during the diagonal stride, symmetrical use of the right and left side of both the upper and lower body should be important.

Functional screening could be one way to evaluate and detect any asymmetry in athletes. The unilateral standing heel-rise test and the handgrip strength test are relatively easy and practical tests for functional screening (Hébert-Losier et al., 2012; Mathiowetz et al., 1985; Svantesson et al., 1998, 2009). The standing heel-rise test has been proven to be useful for assessing the soleus and gastrocnemius muscles (Hebert-Losier et al., 2009). It has been shown that the gastrocnemius muscle is more affected by fatigue than the soleus muscle especially in the eccentric phase of the standing heel-rise test (Svantesson et al., 1998). Interestingly, the gastrocnemius muscle during the diagonal stride is highly activated and independent of exercise intensity (Björklund et al., 2010). In addition, the heel-rise test has been suggested to be an endurance rather than strength test (Österberg et al., 1998). Handgrip strength measures can be used to evaluate a treatment outcome or to assess an athlete’s ability to return to previous sporting activities (Mathiowetz et al., 1985). Additionally handgrip strength has been linked to swimming performance (Zampagni et al., 2008).

While these tests are useful to examine athletes physical function, it has been shown that the level of symmetry, or lack thereof, could be crucial (Nadler et al., 2000). To evaluate a possible deviation from a symmetrical right and left side, i.e. asymmetry, both delta values and symmetry indexes have been used in other sports using upper and lower unilateral and bilateral body performance (Bell et al., 2014; Czuba et al., 2014; Evershed et al., 2014; Stöggl et al., 2013). Although athletes strive to optimize a symmetrical muscular function, they can display imbalances regarding functional strength of the lower body (Newton et al., 2006). While these functional strength tests are useful, the lean mass symmetry of the athletes could also be of importance as shown in a study comparing the level of leg lean mass asymmetry and vertical jumping ability (Bell et al., 2014). These results are in contrast with a previous study on cross-country skiing performance using an asymmetrical skating technique (V1), in which no relationship between performance and anthropometric data among lean mass was found (Stöggl et al., 2013). Also no asymmetry regarding the left and right side could explain side preference using the V1 technique. However, the latter study used delta values expressed as percentages and not symmetrical indexes. In swimming, another sport using both the upper and lower body, it has been reported that asymmetry is common with the majority of swimmers evaluated using index scores (Ostrowski et al., 2012; Evershed et al., 2014). Therefore, studying asymmetry using index scores among cross-country skiers could be of interest for both training and rehabilitation purposes.

Hence, the overall aim was to determine the cross-country skiers’ symmetry with regard to the functional test as well as anthropometric characteristics. Furthermore, the study aimed to investigate whether symmetry or lack of it was associated with vertical jumping characteristics.

Methods

Participants

Twenty well-trained male cross-country skiers participated in the study (Table 1). The cross-country skiers were recruited at the end of the specific training period between September and November when the emphasis was on cross-country skiing on snow, before the start of the competitive season in November. The testing period was selected as cross-country skiers are prepared in the best possible way for skiing during this time. The current study consisted of 1) preliminary tests to establish the skier’s maximal oxygen uptake (VO_2max) and their anthropometric characteristics; and 2) functional tests to determine the skier’s functional capacity for lower and upper body muscles. The body composition and VO_2max test were carried out on the same day. Additionally, the cross-country skiers completed a series of functional tests during the second day of testing.

Table 1.

Descriptive data of the participants (n = 20)

Age (years)	21.7 ± 3.8	18	30
Body height (cm)	180.6 ± 7.6	169	192
Body mass (kg)	73.2 ± 7.6	62	89
Lean weight (kg)	61.3 ± 7.0	50.5	70.2
LLM%	32.6 ± 1.3	30.4	34.8
Body fat (%)	13.3 ± 2.9	9.5	19.3
VO2max (l·min-1)	5.3 ± 0.7	4.0	6.5
VO2max (ml·kg-1·min-1)	70.9 ± 4.4	64.3	77.9
CMJ (cm)	35.2 ± 6.1	23.1	50.6
CMJ (W)	3472 ± 518	2629	4440
CMJ (W·kg-1)	47.6 ± 6.3	35.9	63.2

LLM%, percent leg lean mass compared to total lean mass;

VO_2max, maximal oxygen uptake; CMJ, counter-movement jump

Design and Procedures

The subjects were instructed to perform only light exercise the day before both testing days as well as to maintain normal eating and drinking habits. The first session (Day 1) consisted of an anthropometric evaluation in the morning and a VO_2max test using the diagonal stride later during the day. The second session (Day 2) was performed on a separate day, within one week from the first session, and consisted of a counter-movement jump (CMJ), handgrip strength and heel-rise tests. A symmetry index was used for the anthropometric variables and functional tests as previously described (Bell et al., 2014). All cross-country skiers were notified of the potential risks of taking part in the study and provided written informed consent for participation. None of the subjects reported any injuries during the time of testing. The study was approved by the Regional Ethical Review Board (Dnr. T995 – 13).

Measurement of anthropometric characteristics

The cross-country skiers were subjected to whole-body dual-energy x-ray absorptiometry (iDXA) (Lunar iDXA, enCORE software version 13.60, General Electric Company, Madison, WI, USA). The subjects arrived in a fasting state before the scan and their body height and mass were measured on a separate scale (7014 SECA 764, Benson Avenue, CA, USA) in minimal clothing. Before the measurements, the iDXA was calibrated using a phantom model (Quality Control, QC). The coefficient of variation was below 0.20% for all QC performed during the study. The subject was thereafter placed in a supine position on the scanner bed for a whole body scan from head-to-toe. The whole body scan assessed all body tissues based on three different variables: lean body mass (g), bone mineral content (BMC) and fat tissue (g). Lean body mass and fat tissue were additionally expressed as a percentage for each different region of interest (ROI). Furthermore, the whole body was automatically divided for assessment of different body regions for evaluation also of right and left sides. These regions were additionally verified and examined by certified operators. The coefficient of variation for lean body mass using iDXA had been proven to be less than 1% in the athletic population (Bilsborough et al., 2014).

Measurement of VO2max

The skier’s VO_2max was evaluated using a roller ski test on a motor driven treadmill (Rodby, RL 3000, Rodby Innovation AB, Vänge, Sweden). The diagonal stride skiing technique employed used an incremental protocol starting at an inclination of 4° with a velocity of 11 km·h^-1. Thereafter the inclination increased by 1° each minute until volitional fatigue. Respiratory variables were measured using an ergo-spirometer system (AMIS 2001 model C, Innovision A/S, Odense, Denmark) calibrated as described elsewhere (Björklund et al., 2010). For determination of VO_2max in both absolute (l·min^-1) and relative values (ml·kg^-1·min^-1), the three highest values achieved were averaged, using 10 s sampling duration. Post testing values greater than 18 of the rating of perceived exertion (RPE) were used to indicate the maximal effort as well as respiratory exchange values above 1.15. The cross-country skier was secured with a safety harness suspended from the ceiling. Typical error for VO₂ was estimated to be 0.06 l·min^-1 in comparison with the Douglas bag method as reference.

Measurement of jumping performance

Prior to the jump test, the subject performed 5 min of a low intensity warm-up on their own on a stationary cycle ergometer (Monark 828e, Monark Exercise AB, Vansbro, Sweden) as well as practiced CMJs under guidance. The CMJ was performed using both legs on a three-dimensional force plate using a sampling frequency of 1000 Hz (Kistler, Winterthur, Switzerland). With a shoulder-width stance, the CMJ started from an upright position and without interruption, using approximately a 90° knee flexion followed by a maximal jump. Three maximal CMJs were performed with a 2-min break in between. Throughout the CMJs subjects used a hand-on-hips position to minimize arm movement. Maximum jump height (cm), peak power (W) and relative peak power (W·kg^-1) were evaluated using Kistler Measurement, Analysis and Reporting Software (MARS, 2012, S2P Ltd., Ljubljana, Slovenia). MARS had shown to have high reliability for the CMJ regarding jump height and relative power with an ICC of 0.94 and 0.96, respectively (Hebert-Losier and Beaven, 2014).

Measurement of handgrip strength

A digital handgrip dynamometer (Sagitta Gripmeter, Mariestad, Sweden) was used to assess isometric peak handgrip strength (N). First, the subjects were asked to identify which hand they preferred for writing to determine the dominant hand. Thereafter, the subject executed the test in a sitting position with their forearm resting on a table at a height similar to the inferior rib. The handgrip was fitted to the respective hand size and the forearm rested on the table, adducted and neutrally rotated with the elbow flexed at a 90° angle. The subject was verbally encouraged to squeeze the dynamometer as hard as possible for approximately 10 s. This procedure was repeated three times with a rest in between of 1 min to obtain the maximal static force of both the dominant and non-dominant hand. The highest achieved force registered was considered as the subject’s isometric peak handgrip strength (N). The handgrip strength test had been proven to be reliable displaying a high ICC between 0.87-0.95 (Svantesson et al., 2009).

Measurement of heel-rises

The heel-rise test was performed for the right and left leg in standardized shoes. Each subject performed a maximal number of repetitions during a single legged heel-rise test on a specially designed board with a 10° inclination. The number of performed heel-rises was documented for each leg separately and was defined as maximum heel-rise. For balance purposes, subjects were allowed to use their fingertips to touch the wall at a height of their own shoulder during the test. Throughout the test, a supervisor ensured the knee was straight and the correct range of motion was maintained, i.e. of dorsi-flexion of 10° (starting position) to full plantar flexion (final position). A metronome was used to keep track of the correct pace at 92 beats per minute (Österberg et al., 1998) and the test was terminated when the subject reached exhaustion and could no longer perform the task in a correct manner.

Symmetrical indexes

Two different limb symmetry indexes were used to evaluate asymmetry between the right (X_r)and left (X_l) side of the upper and lower body, respectively. For descriptive data the symmetry index (SI%) was used (Equation 1). The SI% displays the dominance of either the right or left side, where a positive value indicates right dominance, while a negative value left dominance. Equation 1:

$$\begin{array}{l}{\displaystyle SymmetryIndex(SI\text{\%})=\frac{X_r-X_l}{\frac{1}{2}(X_r-X_l)}\times 100\text{\%}}\end{array}$$

To evaluate how symmetric the right and left sides were, an absolute symmetry index (ASI%) was used for comparisons between the right and left side for both upper and lower body anthropometric characteristics as well as and for the functional tests (Karamanidis et al., 2003) (Equation 2).

Equation 2:

$$\begin{array}{l}{\displaystyle Absolutesymmetryindex(ASI\text{\%})=\frac{|X_r-X_l|}{\frac{1}{2}(X_r-X_l)}\times 100\text{\%}}\end{array}$$

All data were checked for normal distribution using the Shapiro-Wilk test along with Q-Q plots. A dependent Student’s t-test was used for comparisons between the right and left side. Cohen’s d effect size was further calculated and ranked as low (0.2), medium (0.5) and high (0.8+) (Thomas et al., 1991) to determine the meaningfulness of the differences between the right and left side. Symmetry was assessed using the absolute symmetry index (ASI%) divided in four levels (0 – 5, 5 – 10, 10 – 15 and > 15%). A Chi² test was used to check if there were differences in numbers of subjects between the defined four levels. Cross-tabulation of frequencies for hand dominance and handgrip strength was evaluated with a 2 x 2 Fisher’s exact test. Pearson correlation was used to evaluate the relationships between the ASI% and CMJ performance (cm, W and W·kg^-1). Multiple linear regression analyses were used to assess the functional tests and anthropometric data from the lower body with the CMJ (cm, W and W·kg^-1). G^*Power version 3.1.7. Software (Franz Faul, Universität Kiel, Germany) was used in advance for determination of the required sample size. Typical error for VO₂ was 0.06 l·min^-1 in comparison to the Douglas bag method, while the ICCs for CMJ variables were between 0.94 – 0.96. All data were processed using Statistical Package for the Social Sciences (SPSS v21.0, SPSS Inc., Chicago, IL). The α-level was set a priori at < 0.05. Values are presented as mean ± SD or median and interquartile range (IQR) when stated.

Results

Overall the cross-country skiers showed right side dominance in both mean handgrip strength and muscle mass (Table 2). Differences between BMC for both arms and legs were apparent (p < 0.05), however, the meaningfulness of these differences was trivial with an effect size close to a Cohen’s d value of 0.2 for BMC for arms and legs, respectively (Table 2). At an individual level (i.e. ASI% levels), the standing heel-rise showed the greatest deviation from 0% with a considerable amount of cross-country skiers (30%) displaying an ASI% larger than 15 (Table 3). The ASI% for the heel-rise test also had the highest median of 7.7 (IQR = 3.3 – 17.5) for all ASI% variables with the handgrip strength median of 5.8 (IQR = 2.3 – 11.5) (Figure 1). With regard to the ASI% for lean mass, arms and legs had medians of 3.4 (IQR = 1.9 – 6.4) and 2.5 (IQR = 0.6 – 5.3), respectively (Figure 1). Leg BMC showed the lowest number for all ASI% variables with a median of 1.8 (IQR = 1.1 – 3.9) versus the arms which had a median of 4.3 (IQR = 2.3 – 7.7) (Figure 1).

Table 2.

Comparison of mean values between right and left side

Variables	Right side	Left side	P	Cohen’s d
Arm
Peak handgrip (N)	520 ± 45	497 ± 47	0.019	0.51
Lean mass (g)	4066 ± 579	3967 ± 593	0.022	0.17
BMC (g)	235 ± 34	226 ± 34	0.0001	0.26
Leg
Maximum heel-rise (counts)	40 ± 10	39 ± 10	0.555	0.07
Lean mass (g)	10070 ± 1368	9948 ± 1240	0.172	0.09
BMC (g)	609 ± 88	599 ± 82	0.014	0.11

The values are presented as mean ± SD. N, newton; g, gram;

Cohen’s d = Trivial (0.2), Medium (0.5), High (0.8+).

Table 3.

Levels of absolute asymmetry for upper- and lower body (%)

	0 - 5	5 - 10	10 - 15	>15	χ2, p values
Upper body
Handgrip (N)	8 (40)	5 (25)	5 (25)	2 (10)	χ2(3, n=20) = 9.29, p=0.026
Arm lean (g)£	13 (65)	6 (30)	1 (5)	0 (0)	χ2(2, n=20) = 1.93, p=0.381
BMC arm (g)£	13 (65)	6 (30)	1 (5)	0 (0)	χ2(2, n=20) = 1.93, p=0.381
Lower body
Heel-rise (count)	9 (45)	3 (15)	2 (10)	6 (30)	χ2(3, n=20) = 16.97, p=0.001
Leg lean (g)$	14 (70)	6 (30)	0 (0)	0 (0)	χ2(1, n=20) = 0.42, p=0.517
BMC leg (g)$	19 (95)	1 (5)	0 (0)	0 (0)	χ2(1, n=20) = 8,79, p=0.003
Total	76 (63)	27 (22)	9 (8)	8 (7)

Number of subjects (% in brackets) falling into respectively asymmetry level divided in 0 – 5, 5 – 10, 10 – 15 and above 15 percent defined by the ASI (%).

Total is defined as the number of observations for each levels summated for all variables with observed observations for the different levels of asymmetry.

^£Three levels were compared with 10 – 15 and >15 merged.

^$Two levels were compared with 5 – 10, 10 – 15 and > 15 merged.

Figure 1.

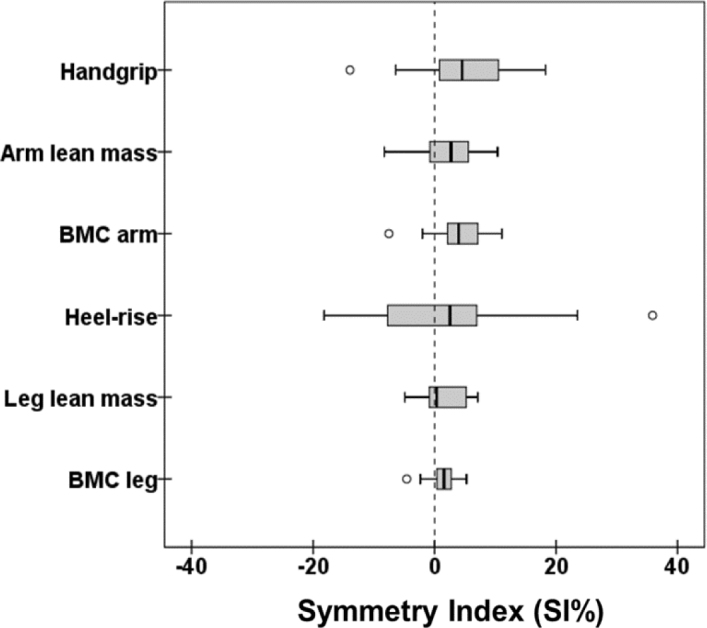
Box plots showing the symmetry index (SI%) for upper- and lower body characteristics. Positive numbers indicate right-sided dominance while negative numbers indicate left-sided dominance. Numbers are presented as median, quartiles, min and max values for respectively variable.

Percent leg lean mass compared to total lean mass (LLM%) was associated to CMJ absolute jump power (r = 0.534, p = 0.015). Multiple linear regression analysis was conducted to predict CMJ jump height, based on the ASI% for leg lean mass and heel-rise (F₂, ₁₈ = 0.362, p = 0.702) with R² of 0.041 for the CMJ.

Cross-tabulation between the stronger hand, i.e. generating the highest peak isometric force (N) and the dominant hand (right or left), showed that skiers with right hand dominance were strongest in the dominant hand (93.3%, 14 out of 15). In addition, the skiers with a dominant left hand proved to be stronger in the left hand (60%, 3 out of 5), but to a lesser degree than the right handed skiers. Hand strength (N) was related to lean arm mass (g) (r = 0.63, p = 0.003).

Discussion

The purpose of the study was to evaluate symmetry in cross-country skiers by measuring anthropometric characteristics and muscle function, using standard clinical tests for the lower and upper body, as well as to determine the association of symmetry to aerobic and vertical jumping power. The major finding of this study revealed that the upper body displayed asymmetrical features, i.e. lean mass and handgrip strength. However, when classifying the asymmetry level based upon the ASI%, the heel-rise test showed the largest asymmetry while lean mass of the lower body showed a low level of asymmetry. Interestingly this suggests that the muscle function in the lower body is less coupled to lean mass than it is for the upper body. These results provide an indication that it is beneficial to use symmetry indexes rather than mean values to evaluate the degree of dominance and asymmetry. Moreover, asymmetry measures were not related to vertical jumping power. However, a higher ratio of leg lean mass in relation to total lean mass was beneficial for vertical jumping power for the cross-country skiers.

This study showed a difference in mean handgrip strength between right and left sides. The difference in handgrip strength was related to the preferred use of the hand, i.e. dominance, which was demonstrated for both the right and left handed subjects. Moreover, this difference between the right and left side in mean values was also evident when evaluating asymmetry levels using the ASI%. This finding is in contrast with the results obtained from national level swimmers of similar age who did not demonstrate any differences in handgrip strength between the dominant and non-dominant hand (Garrido et al., 2012). Although the handgrip strength test examines mainly the distal parts of the arm, it has been shown that trained individuals display better isometric grip force than their untrained counterparts (Cortis et al., 2009). In swimming using the freestyle stroke, performance at the shorter distances has been linked to handgrip strength (Zampagni et al., 2008). Also the study by Garrido et al. (2012) found a strong relationship between handgrip strength for shorter swim freestyle events, such as the 100 m distance. Both of these studies imply that the majority of the propulsion during events <100 m is supplied primarily by the upper body. The freestyle stroke is characterized by using the arms interchangeably, but in a symmetrical pattern, similar to the diagonal stride. During the diagonal stride, the upper body muscles are highly activated (triceps brachii between 25-30% of MVC) for propulsion at high exercise intensities (Björklund et al., 2010). In addition, it was also demonstrated that muscle activation decreased during the poling phase, following double poling when using the diagonal stride (Björklund et al., 2015). This could indicate signs of fatigue in the upper body even for trained cross-country skiers. Also in general for cross-country skiing, the contribution of the upper body for power and propulsion is of high importance and could be a limiting factor (Hegge et al., 2015). In such a case, handgrip strength could definitely be of importance as shown in shorter swimming events (Garrido et al., 2012; Zampagni et al., 2008) and most likely as symmetrical propulsion. Therefore, handgrip strength could provide an indication of skiing performance during high intensity/short distance events using the diagonal stride.

Since there were no differences in mean heel-rises between the right and left leg, it could be interpreted that cross-country skiers’ gastrocnemius and soleus muscles are symmetrical with respect to muscular function. However, when using the absolute asymmetry index (ASI%), the heel-rise tests showed a large deviation from perfect symmetry, i.e. zero percentage. A large proportion of the group displayed a deviation greater than 15%, which was surprising when compared to other athletes and groups of the same age (Milne et al., 2003). However, differences in the ASI% could be alternatively explained by the variable itself as previously shown in a group of runners who showed kinematic variables with much larger asymmetries for angular velocity than for ground contact time (Karamanidis et al., 2003). The cross-country skiers also displayed similar heel-rises counts as runners and basketball players (approximately 40) (Madeley et al., 2007). This is an interesting finding because runners also use a symmetrical movement pattern with the gastrocnemius and soleus muscles contributing to propulsion, as in the diagonal stride (Ellis et al., 2014). Considering that the study involved only male cross-country skiers, it could be interpreted that female subjects could display a different number of completed cycles as shown in an earlier study (Svantesson et al., 1998); however, a later study showed no differences between matched groups of men and women (Hébert-Losier and Holmberg, 2013). Interestingly, in the latter study, a normal population completed an equal amount of heel-rises as the cross-country skiers in the current study. This finding is in line with previous data in elite cross-country skiers regarding no relationship between the magnitude of general strength and maximal speed (V_max) during various skiing techniques (Stöggl et al., 2011). However, in such a homogenous group of athletes, as in Stöggl et al. (2011) and in the present study, muscular strength might not be a limiting factor as there is rather an optimal strength level that needs to be converted to propulsion with greater timing. Therefore, although the cross-country skiers display asymmetries regarding the heel-rise test, which cannot be explained by leg lean mass, and considering that these athletes show rather similar counts of cycles, it might indicate that there is a minimum amount of heel-rises for maximal performance.

Although the heel-rise test has been proposed to be related to endurance rather than strength (Österberg et al., 1998), fatigue is also part of the outcome. Interestingly, it may be that the athletes could produce a higher peak torque which not necessarily is related to withstanding fatigue as shown in hip flexors (Jacobs et al., 2005). However, regarding symmetry, there was no difference between the dominant and non-dominant leg in heel-rise performance. Regarding the ASI% in relation to vertical jumping power, there was no such a relationship in the present study. Previous research had shown that strength imbalances between the legs could be a limiting factor for vertical jumping power (Newton et al.,2006). However, the current study only evaluated functional strength of distal muscles in the legs, which could possibly account for the diverging results. Yet it has been shown that calf muscles (m. gastrocnemius and soleus) are highly potentiated during a CMJ (Bosco et al., 1982). In accordance with previous results obtained from non-skiing subjects of different ages (Stephenson et al., 2015), the ratio between leg- and total lean mass in association to vertical jump power suggests that symmetry between the lower and upper body is an important measure for lower body explosiveness in cross-country skiers.

Limitations of the study include the use of a single force plate for jumping characteristics. A setup with dual force plates could provide information on timing and synchronization of the right and left leg. Furthermore, postural sway could be of interest as fatiguing exercise could impair control in the sagittal plane (Gribble and Hertel, 2004). This is of interest especially as cross-country skiing consists of a complex movement pattern where propulsion takes place in several directions for forward propulsion.

The study demonstrates a miss-match between the right and left sides regarding functional tests that cannot be explained by the amount of lean muscle mass especially for the lower body. The questions are whether or not these asymmetries are compensated for while cross-country skiing and if so how. Coaches should be aware that functional tests should be supplemented with anthropometric data. Minimum heel-rises could be of greater importance than the maximum amount of completed cycles. Possibly a minimum number close to 35 complete heel-rise cycles would be of importance. This study suggests that symmetry indexes are more relevant than mean delta values to screen for asymmetries.