Butterfly Sprint Swimming Technique, Analysis of Somatic and Spatial-Temporal Coordination Variables

Abstract

The aim of this study was to investigate somatic properties and force production of leg extensor muscles measured in the countermovement jump test (CMJ), as well as to analyse kinematic variables of sprint surface butterfly swimming. Thirty-four male competitive swimmers were recruited with an average age of 19.3 ± 1.83 years. Their average body height (BH) was 183.7 ± 5.93 cm, body fat content 10.8 ± 2.64% and body mass (BM) 78.3 ± 5.0 kg. Length measurements of particular body segments were taken and a counter movement jump (CMJ) as well as an all-out 50 m butterfly speed test were completed. The underwater movements of the swimmers’ bodies were recorded with a digital camera providing side-shots. We registered a significant relationship between body mass (r = 0.46), lean body mass (r = 0.48) and sprint surface butterfly swimming (VSBF). The anaerobic power measured in the CMJ test, total body length (TBL) as well as upper and lower extremity length indices did not influence swimming speed significantly. The temporal entry-kick index (the time ratio between the first kick and arm entry) significantly influenced VSBF (r = -0.45). Similarly, medium power of the coefficient was indicated between a) stroke rate kinematics (SR), b) duration of the first leg kick (LP1), c) air phase duration of arm recovery (Fly-arm), and VSBF (r = 0.40; r = 0.40 and r = 0.41, respectively). The entry-kick temporal index showed that, in the butterfly cycle, an appropriately early executed initial kick when compared to arm entry was associated with a longer arm propulsion phase, which in turn was associated with minimizing resistive gliding phases and enabled relatively longer and less resistive air arm recovery (higher value of the fly-arm index). The higher value of SR kinematic was another important element of the best butterfly results in this study.

Introduction

In competitive butterfly swimming, athletes should strive to improve their technique in order to achieve high propulsion force and avoid substantial intra-cycle variation in displacement of the centre of mass in cyclic limb and body movements. The swimmer does not move at a constant velocity, because variations in the action of arms, legs and trunk lead to changes in swimming velocity in each stroke cycle. These movements are aimed at overcoming inertia and hydrodynamic drag, which enables efficient locomotion (Barbosa et al., 2005, 2006; Barthels and Adrian, 1975; Mason et al., 1992; Toussaint et al., 1988; Ostrowski et al., 2012).

Researchers point out that swimmers may reduce energy expenditure by assuming particular positions during certain phases of a butterfly cycle (Louro et al., 2010; Seifert et al., 2008; Taïar et al., 1999, 2005), with significant interrelationships between swimming movements, passive drag and swimmer’s performance (Kolmogorov et al., 1997). In butterfly technique, coordinated arm, leg and trunk movements must be combined with undulation of the whole body. Forward motion is transmitted caudally through the adjacent body segment wave, which may contribute to a propulsive “whip-like” action (Persyn et al., 1983; Sanders et al., 1995; Ungerechts, 1982).

A butterfly swimming race contains various important components, including the start and turns with underwater dolphin movement locomotion and full stroke surface butterfly technique (Arellano et al., 2002; Mason et al., 2002; Tourny-Chollet et al., 2002). It could be argued that the effectiveness of full stroke surface swimming technique, which is not immediately apparent, depends on appropriate motor control, i.e., the coordinated movement of body parts. According to Chollet et al. (2006), synchronization at key motor points of the arm and leg actions may significantly affect butterfly technique.

The existing literature on the subject acknowledges the importance of somatic traits such as body length and composition which must be taken into consideration when analysing the bodies of swimmers who compete in the butterfly event (Chollet, 1990; Mazza et al., 1993; Silva, et al., 2007). Generation of higher muscle strength as well as endurance of swimmers who prefer butterfly to other styles have been less studied. However, the requirements of forceful 50 m sprinting and speed tolerance exhaustion over 100 m and 200 m butterfly distances seem to be well recognized by swimmers (Garrido et al., 2012; Morouço et al., 2011). It must also be stated that there are some well-controlled studies which contain data useful for improving butterfly performance, notably Seifert et al. (2008). After comparing more- and less-skilled swimmers the authors advised applying arm to leg coordination strategy along with short intervals of cyclic non-propulsive gaps, rather than gliding strategies. An earlier study conducted by Boulesteix et al. (2003) suggested that limb coordination with reduced temporal gaps of gliding between arms and legs propulsive actions enabled the swimmer to dedicate more time to execute propulsion in the butterfly cycle, which meant greater continuity in these actions.

This work was aimed at:

1. analysing the influence of selected body features (body height – BH, total body length – TBL, upper and lower extremities length, body mass – BM and lean body mass – LBM) on sprint surface butterfly swimming;

2. examining how force production of leg extensor muscles (measured in CMJ test) affected sprint surface butterfly swimming;

3. quantitative video analysis of basic stroke kinematics and coordination indices of the movement of each pair of limbs during sprint surface butterfly swimming. Differences in the stroke rate, variability of gliding, body movement coordination (Boulesteix et al., 2003) and the percentage of propulsion actions in the stroke cycle should influence swimming speed in the researched group of competitive athletes (Chollet et al., 2006).

The influence of somatic features and anaerobic power on sprint surface butterfly swimming was examined. It was assumed that swimming performance was also related to both higher propulsion continuity and simultaneously minimizing non-propulsive upper body gliding phases. These variables were also considered in this research.

Methods

Participants

A group of thirty-four male swimmers was recruited (19.3 ± 1.83 years) from two university swimming clubs. Each participant (or his parents) signed an informed consent form (approved by the Ethics Committee in Cracow). The youth swimmers, who specialized in the butterfly or in individual medleys, had competed either at regional (3 subjects), national (26 subjects) or international level (5 subjects). Their personal best results in 50 m butterfly races corresponded to 77%, 83.1% and 90.7% of elite swimming world records, respectively, which accounted for 457.3, 579.1 and 745.1 FINA points for regional, national and international swimmers. All of them had licenses from the Polish Swimming Federation and trained twice a day, six days a week.

Anthropometry

In youth swimmers anthropometric variables play an important role in enhancing the production of energy and propulsion (Strzała et al., 2009). Therefore anthropometric measurements included body height (BH) (183.7 ± 5.93 cm), body fat content (10.8 ± 2.64%) and body mass (78.3 ± 5.0 kg). Lean body mass (LBM) of the athletes was calculated according to Slaughter et al. (1988) after the measurement of skin-fold thickness using a Harpenden Skinfold Caliper (Holtain Ltd., UK) with constant pressure (10g·mm^-2), and body mass measurement with a Sartorius scale, Germany. The swimmers’ total body length (TBL) was measured in a lying position, from the tips of the fingers (with arms stretched up above the head) down to the pointed toes, foot plantar flexion. Upper extremity length was measured from the acromion to the fingertips of straightened hands. Lower extremity length was measured in a recumbent position from the trochanter major to the pointed toes. The measurements of particular body segments were completed using appropriate anthropometric instruments (Sieber Hegner Maschinen AG, Switzerland). The anthropometric measurements were conducted with reliability of – ICC_(3,1): 0.9994; 95% lower; upper CI: 0.9977 and 0.9998, respectively.

Dry-land maximal power test

The counter movement jump (CMJ) test was performed with the use of a force plate (JBA Staniak, Poland). The athlete stood upright on the platform with body mass evenly distributed over both feet. Hands were placed on the hips throughout the test to eliminate them from contributing to the generation of power. Work [W (J)] generated in the concentric muscle contraction phase of the jump (being a result of the CMJ test) was taken as an indicator of force production of leg extensor muscles. Elevation of the centre of mass [h (cm)] was considered an indicator of leg extensor muscles’ force production relative to body mass. The best result of the three attempts was registered for further analysis (Cormack et al., 2008).

Swimming test and kinematic analysis

The all-out 50 m butterfly speed test using an automatic timing device (Omega, Switzerland) was conducted in a 25 m pool that met FINA standards. The times achieved by swimmers in this test were used to calculate swimming speed. In order to eliminate personal advantage coming from more-skilled block starts and underwater dolphin kicks which result in less fatigue, the participants were asked to perform in-the-water starts and shorten the underwater swimming phase to 10 m only (also after the turn). The test was preceded by a self-selected warm-up, similar to the one performed before a competition, including at least 1000 m of swimming using butterfly as well as other swimming techniques. The underwater movements of the swimmers’ bodies were recorded with a digital camera (Sony HDR-AZ1, Japan) in a waterproof case, at the sampling rate of 60 Hz. The camera was installed on a portable trolley which moved along the edge of the swimming pool, parallel to the swimmer’s path, providing side-shots. The camera’s optical axis was kept between two virtual lines by the trolley operator. These lines were determined by the fingertips of the straightened arms of the swimmer at the front and by the toes of the outstretched legs at the back. The underwater camera was mounted to the lower arm of the trolley and submerged in water approximately 1 m below the surface, at a distance of approximately 3.5 m from the swimmer’s lane.

Analysis of butterfly surface swimming (V_SBF) was based on the data gathered in a 10 m sector during the second lap (specifically between the 35^th and 45^th m) of the 50 m distance. Measurement of V_SBF on the second lap was justified after analysis of the literature where it was reported that over short distances, the second half of the whole race determined the final result more than the first half (Arellano et al., 1994; Dybińska and Haljand 2007; Robertson et al., 2009; Thompson et al., 2000). Kinematic variables were calculated on the basis of video recording by two Canon Legria HV40 (Japan) camcorders (sampling rate of 50 Hz) which were located on tripods standing on the pool deck. Recordings from these two cameras were synchronized with a flash light triggered by the Omega electronic starting device. The Canon camcorders filmed each swimmer’s head crossing the 35 and 45 m lines. The recordings enabled calculation of the time needed to complete the 10 m sector (Δt_i), which in turn served as a basis for the calculation of average swimming speed: V_SBF =10m/Δt_i. For surface swimming analysis the number of cycles was counted, excluding the first cycle after the turn and the last two cycles before touching the contact plate. Swimmers performed their own breathing pattern, as they did in competition; yet, considering that breath and nonbreath butterfly cycles may differ as far as their kinematic quantities are concerned, two representative cycles (one breath and one nonbreath) were taken from the middle part of the 10 m sector. For every kinematic and temporal index, weighted average was calculated on the basis of the following formula:

$$\begin{array}{l}{\displaystyle \overline{x}=\frac{x_b{n}_b+x_{nb}{x}_{nb}}{n_b+n_{nb}}}\end{array}$$

where: x − weighted average of particular quantity (calculated for each of the basic kinematic and temporal indices in a cycle); x_b − value of particular quantity measured in the breath cycle; x_nb − value of particular quantity measured in the non-breath cycle; n_b − number of breath cycles; n_nb − number of non-breath cycles.

The stroke rate (SR_i) was calculated as the reciprocal of average duration of the swimming cycle: SR_i = 1/T_i, [cycle·min^-1], where T_i [min] – cycle duration; stroke length (SL_i) was calculated as the average speed to SR_i ratio: SL_i = V_i/SR_i [m]. Analysis of the video recordings involved identification of propulsive and non-propulsive phases of butterfly cycles of the arms and legs. Arm total propulsion phase (AP) was defined as starting from the beginning of the arm’s outside movement with the hands twisted out in pronation (Arm Propulsion Phase Beginning -APB), through the catch and backward arm pull, with hands moving inwards, and then outwards until the hands released water (Arm Propulsion Phase End - APE), (t_AP = t_APE - t_APB). Arm total recovery phase (AR) was defined as starting from the end of the AP phase (APE), through the hand water entry, until the beginning of the next AP in the following cycle (NAPB), (t_AR = t_NABP – t_APE). Leg total propulsion phase (Total LP) was the sum of the two kicks in the cycle (first kick closest to hand water entry and second closest to hand water release). Kicks were defined as starting when the feet began to move backwards and/or downwards (First/Second Leg Propulsion Phase Beginning – FLPB/SLPB), through the knee straightening, until the end of the feet’s downward movement (First/Second Leg Propulsion Phase End – FLPE/SLPE), (t_LP = t_FLPE − t_FLPB + t_SLPE − t_SLPB). Leg total recovery phase (Total LR) was the sum of two phases: first (LR1) was defined as starting from the end of the first LP phase (FLPE) until the beginning of the second LP phase (SLPB); second as starting from the end of the second LP phase (SLPE) until the beginning of the first LP of the following cycle (NFLPB) (t_LR = t_SLPB – t_FLPE + t_NFLPB – t_SLPE). The intraclass correlation coefficient (ICC) estimations for collected kinematic data were conducted with reliability of measurements – ICC_(3,1): 0.9955; 95% lower; upper CI: 0.9820 and 0.9989, respectively.

The collected data served as a basis for calculating four phase indices, expressed as the percentage of phase time in the butterfly cycle duration:

1. Entry-kick – cycle percentage of the period between the beginning of LP1 and hand water entry. If LP1 occurred first, the index had a negative value. When the hands entered the water before LP1, its value was positive.

2. 2^nd kick – cycle percentage of the period between the beginning of the hand water entry and beginning of LP2.

3. TTG – total time gap - cycle percentage of total non-propulsive phases. There was mostly only one such a phase; however, some athletes had two non-propulsive phases: 1^st from the end of AP or the end of LP2, whichever occurred last, until the beginning of LP1; 2^nd (not always occurring) – was a lag time (glide) between the end of the LP1 phase and before the beginning of AP (Chollet et al., 2005).

4. Fly-arm – cycle percentage of the air arm recovery phase (between the hand water release and entry).

Statistical analysis

Basic descriptive statistics were calculated and all variables were examined for normal distribution using the Shapiro-Wilk test. For data comparisons, a Student’s t-test was used for normally distributed data and equal variances, a Student’s t-test with Cochran-Cox adjustment in the case of normally distributed data yet unequal variances, and a U-Mann Whitney test for abnormally distributed data with statistically significant p value <0.05.

To exclude individual swimmers’ features of power production, experience and ability to shape butterfly cycles, partial correlations (controlled for age) were computed between VSBF and all indicators, i.e., (i) somatic indices (ii) indices of propulsive and non-propulsive phases of the butterfly cycle, and (iii) basic stroke kinematic quantities. Additionally, linear correlations were computed between two indices directly influencing butterfly swimming speed (SR and Entry-kick) as well as all other kinematic and coordination indices. The tests were performed using STATISTICA ver. 12 software (StatSoft, Inc.).

Results

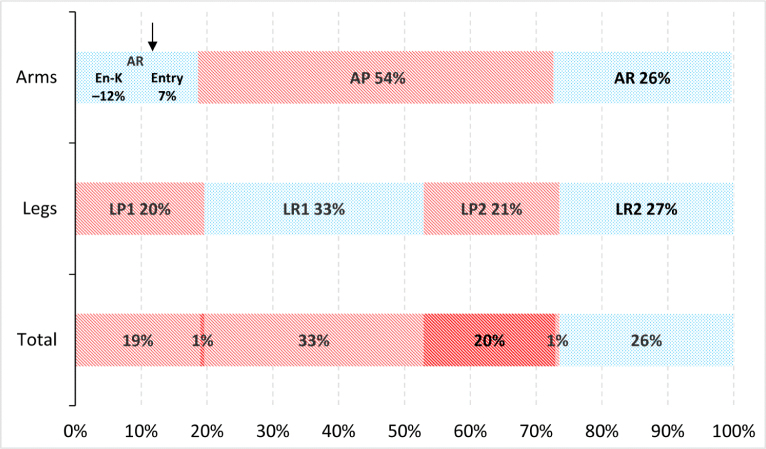
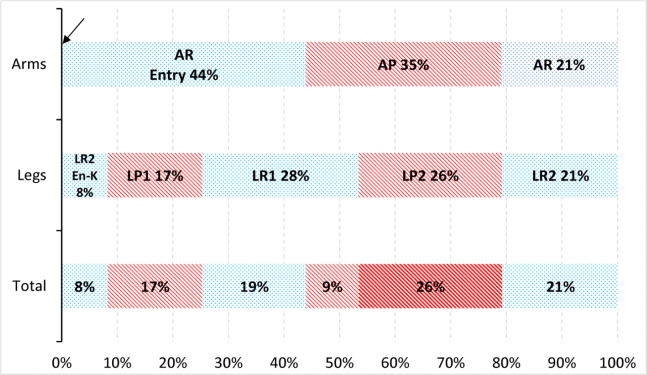
Figures 1 and 2 present butterfly cycles of swimmers A and B using extremely different strategies of limb coordination. Other observed swimmers used a combination of the coordination strategies outlined in these figures with the entry-kick index between -12% (swimmer A) and 8% (swimmer B).

Figure 1.

Swimmer A’s butterfly cycle with an early first kick and a single non-propulsive phase

Figure 2.

Swimmer B’s butterfly cycle with a late first kick and a double non-propulsive phase

Swimmer A (Figure 1) began the cycle with a kick. After 12% of the cycle time, his hands immersed, thus beginning the entry phase (marked with an arrow). The next 7% of the cycle time was taken up by gripping (stretching) hands until the beginning of the AP phase (backward movement). In the case of swimmer B (Figure 2), hands immersed first (marked with an arrow), and after 8% taken up by the arm and body glide, the swimmer performed a kick, thus beginning the LP1 phase.

Swimmer A started the AP phase while ending the first LP phase (1% of overlap; Figure 2); his AP phase was longer than the one of swimmer B, and by its conclusion his legs had gone through LR1 and LP2 phases (LP2 phase ended only 1% after hands had released water). Such coordination of movements in the cycle helped generate greater propulsion continuity with a single nonpropulsive gap, where TTG was only 26%, which was below the average for this group (Table 2).

Table 2.

Cycle basic kinematics (SR [cycle⋅min^-1] and SL [m]) and percentage of butterfly cycle temporal indices [%]. Line (34 x ) breath and non-breath cycles of whole swimmers group; line (28 Br) breath cycles of 28 swimmers; line (28 Nb) non-breath cycles of 28 swimmers; line (6 Br) breath cycle indices of 6 swimmers. Significant differences between breath and non-breath cycles indices in 28 swimmers are marked with #. Significant differences between breath cycle indices of 28 swimmers and 6 swimmers are marked with ǂ.

	SR	SL	AP	AR	LP1	LR1	LP2	LR2	Entry-kick	2nd-kick	TTG	Fly-arm
34 x	55.2 ± 3.86	1.75 ± 0.11	52.4 ± 0.07	47.6 ± 0.07	19.3 ± 0.02	32.5 ± 0.04	21.2 ± 0.03	27.0 ± 0.03	-1.9 ± 0.05	49.6 ± 0.04	30.5 ± 0.06	29.5 ± 0.04
28 Br	54.6 ± 3.89	-	51.8 ± 0.08	48.2 ± 0.08	18.4 ± 0.02	33.5 ± 0.05	21.5 ± 0.03	26.6 ± 0.03	-2.7 ± 0.05	49.2 ± 0.05	30.08 ± 0.07	27.2 ± 0.07
28 N b	56.4 ± 4.42	-	53.5 ± 0.07	46.5 ± 0.08	19.3 ± 0.02	32.0 ± 0.04	21.2 ± 0.03	27.5 ± 0.03	-1.3 ±0.05	50.1 ± 0.05	30.6 ± 0.05	30.7 ± 0.05
	#		-	-	#	#	-	#	#	-	-	#
6 Br	53.3 ± 2.47	1.84 ± 0.09	50.8 ± 0.07	49.2 ± 0.07	21.1 ± 0.02	32.0 ± 0.04	20.1 ± 0.02	26.8 ± 0.02	-3.2 ± 0.03	49.7 ± 0.04	30.0 ± 0.05	30.8 ± 0.03
	-	-	-	-	ǂ	-	-	-	-	-	-	-

##p<0.01

^#p < 0.05

^ǂp < 0.05

The whole body glide of swimmer B was conducted in two parts. The first part started 8% before the first LP phase (entry-kick index value was above 0), and the second part ended 19% after the LP1 phase. During the AP phase (which was shorter than the average of the group), the second kick was imposed (Figure 2 and Table 2). Such limb movement coordination and propulsive phase duration resulted in the presence of two nonpropulsive gaps, where TTG was 48%.

The 50 m butterfly speed for the whole group was 1.74 ± 0.07 m·s⁻¹, and clear surface swimming VSBF amounted to 1.64 ± 0.06 m·s⁻¹ with significant difference between those speeds (t33 = – 21.74, p < 0.001). Table 1 shows correlations between the main somatic indices of functional variables and VSBF. A significant relationship between BM, LBM and VSBF was found. Neither force production of leg extensor muscles (measured in the CMJ test), BH nor TBL (Table 1) significantly influenced either VSBF, or similarly upper (81.7 ± 2.94 cm) and lower (116.7 ± 4.92) extremity length indices (non-significant, very low dependences).

Table 1.

Partial correlation measurements with age control between somatic, functional (CMJ) indices and V_SBF.

Age control	BH [cm]	BM [kg]	LBM [kg]	TBL [cm]	CMJ [cm]	CMJ [J]
n 34	183.7 ± 5.93	78.3 ± 5.00	69.8 ± 4.59	2.55 ± 8.65	43.12 ± 5.34	334.2 ± 42.34
VSBF	0.05	0.46*	0.48*	0.06	-0.19	-0.02

^*p ≤ 0.01

Table 2 shows butterfly technique weighted average results for all 34 swimmers. Breath and non-breath cycle indices were compared, yet in 28 of the 34 swimmers only, as 6 swimmers presented solely breath cycles in the analysed swimming sector. Significant differences were found between LP1, LR1, LR2, Entry-Kick and Fly-arm. A comparison of breath cycles between the groups of 28 and 6 swimmers showed significant difference only for the LP1 index. It was not possible to reliably measure SL for breath or non-breath cycles separately in 28 swimmers, because they used both cycle types in the measured swimming sector.

Table 3 shows that out of all the indices calculated for the swimming cycle, one basic kinematic index (SR) and three temporal indices: Entry-kick, Fly arm and LP1 were significantly associated with VSBF.

Table 3.

Partial correlations with age control between basic kinematics, temporal indices and V_SBF.

34 x	SR	SL	AP	AR	LP1	LR1	LP2	LR2	Entry-kick	2nd-kick	TTG	Fly-arm
VSBF	0.40	-0.19	0.19	-0.19	0.40	0.06	-0.18	-0.19	-0.45	-0.23	-0.32	0.41
	*	-	-	-	*	-	-	-	**	-	-	*

^*p < 0.05

^**p < 0.01

The stroke kinematic SR was significantly negatively correlated with SL, TTG and AR, although positively correlated with the percentage of AP duration (Table 4).

Table 4.

Interrelationship between SR and basic kinematic (SL) and temporal indices.

34 x	SL	AP	AR	LP1	LR1	LP2	LR2	Entry-kick	2nd-kick	TTG	Fly-arm
S R	-0.85**	0.43*	-0.43*	0.27	0.30	-0.25	-0.36*	-0.31	0.10	-0.53**	0.33

^**p < 0.01

^*p < 0.05

The temporal entry-kick index at its higher positive values was negatively inter-correlated with AP (r = -0.50, p = 0.002) and Fly-arm (r = -0.75, p < 0.001) indices, and at the same time it was positively correlated with the TTG index (r = 0.42, p = 0.013).

Discussion

The results of this study indicate that temporal and coordination indices gathered on the basis of video analysis influence sprint butterfly performance – VSBF. The relationship between kinematic (SR), spatial-temporal indices (Entry-kick, Fly-arm, LP1) and VSBF variables indicates that optimal performance depends on the swimmer’s ability to achieve a suitably coordinated and more continuous high rate of stroking. In our study, the higher SR value implicated a lower percentage of LR2 and nonpropulsive gaps (TTG), which resulted in an increasing percentage of propulsive arm phases (AP). Deeper insight into the issue can be achieved when considering inter-correlations between the temporal indices. The entry-kick temporal index shows that the higher its value (which means that the first kick was performed later than the hand entry), the shorter the AP phase (r = -0.50). It seems that execution of the kick and arm entry (in this sequence) enabled less slipping of arm propulsion, a more fluent catch and pull of water, together with a quick, high range of body segment undulation. An alternative theory put forward by Haljand (2016) argues that a shorter AP phase could mean that arms work relatively alone, “breaking” water with high power because of weak support from the second leg kick. Furthermore, the delayed execution of LP1 (higher value of the entry-kick index) results in a higher TTG value in the butterfly cycle, which has a detrimental effect as far as VSBF performance is concerned. It should be noted that TTG, apart from one or two glide phases also covers arm air recovery, which, with longer duration and flight is positively correlated with VSBF. However, it is during the fly-arm phase that a lack of feeling in bringing the arms forward and momentum from quick arm recovery act against the forward momentum of the body (Haljand, 2016). In TTG, it is precisely this gliding part of a cycle that is most detrimental, because it is a resistive part of the cycle and causes a decrease of intra-cyclic speed. The longer the glide phase, the stronger the retardation effect is (Barbosa et al., 2005; Chollet et al., 2006; Nigg, 1983). Additionally, Barbosa et al. (2008) suggest that butterflyers should develop strategies to minimize segmental actions that impose increases of intra-cycle velocity variations, such as in the case of extensive lateral movements during hand entry which might increase wave drag, thus decelerating the swimmer’s body.

Indeed, it is true that sprint (50 m) butterfly swimmers achieve high speed with very high SR, usually exceeding 60 cycles per minute, as was the case during the European short course swimming championships, Eindhoven 2010 (Haljand, 2010). Our study, as well as others, shows that such effective powerful swimming requires fast coordination with an early kick opening the cycle (Boulesteix et al., 2003). Such synchronisation, combined with substantial undulation (flexion of the wrist and the high elbow together with shoulder extension behind the head and with undulation of lower segments of the body), enables a flexible swimmer to pull his hands without unnecessary glide, which can be achieved with body flexion support coming from a timely executed first kick (LP1). Maglischo (2003) emphasizes that “the downbeat of the first kick should begin during the second half of the arm recovery and should continue through the entry and stretch of the arms” and “the major propulsive phase of the kick should take place during the entry, stretch, and the first part of the outsweep of the arms”. Additionally, he argues convincingly that gain from the downbeat of the first dolphin kick (which is more propulsive than the second one) is absolutely essential for fast butterfly swimming. According to Barbosa et al. (2002) the increase of vertical velocity during the first downbeat plays an important role in reducing the deceleration and negative body impulse due to hand entry.

At the design stage of this study, the possibility that breathing action may change some variables of a breath cycle when compared to a non-breath cycle was considered (Alves et al., 1999; Barbosa et al., 2003; Hahn and Krug, 1992). Data of this study, which was obtained for every kinematic and temporal index, is presented as weighted average of breath and non-breath cycles, but further comparison of breath and non-breath cycles showed differences of indices influencing VSBF. Non-breath cycles were executed with a significantly higher rate (SR), relatively longer LP1 and longer fly-arm which was beneficial. The disadvantage of non-breath cycles was associated with a significantly higher (less beneficial) entry-kick index (-1.3 vs. -2.7). Contrarily, six insignificantly faster (higher speed of 0.03 m·s⁻¹) swimmers with only breath cycles showed that it was possible to execute better coordination with lesser entry-kick, lesser SR, but with simultaneously longer SL. A similar effect was found in the study of Seifert et al. (2008) where more-skilled butterflyers had greater velocity, stroke length, and stroke rate as well as better synchronization of the arm and leg stroke phases than the less-skilled swimmers. Nevertheless, our results and noted benefits of non-breath cycles provide information as to why swimmers include them in their self-selected patterns of breathing in sprint butterfly swimming.

Our study explicitly shows that synchronisation between specific motor points of arm and leg actions is the key factor of fast butterfly swimming. It is especially the case when we consider the initial kick of the cycle (lowering the value of entry-kick), which noticeably avoids unnecessary gliding before and after the kick. This corresponds to the study conducted by Chollet et al. (2005), where it is argued, contrary to the conventional way of thinking, that the butterfly stroke does not primarily require a great force, but rather a high degree of arm-to-leg coordination. It is shown in that study that swimmers often compensate for coordination deficiencies by applying greater force. Our study is consistent with that conclusion because the descriptive statistics reveal that the coefficient of variability of the main coordination index (entry-kick) was widely distributed (239%). For instance, it was possible to find swimmers achieving the same speed (VSBF) but using better (entry-kick -7% less strength) or poorer (entry-kick 4% more strength) coordination. It could imply, however, that in cases where a larger number of swimmers have appropriate temporal movement coordination, the ability of power production will result in higher swimming speed (Tanaka et al., 1993). Seifert et al. (2008) insist that in the butterfly stroke a high degree of arm–leg coordination ensures the propulsive continuity between the arm and leg actions and induces fewer instantaneous fluctuations in velocity. It was demonstrated in another study (Craig and Pendergast, 1979) that the simultaneous strokes (breaststroke and butterfly) were characterized by higher instantaneous velocity fluctuations (45–50%) than front and back crawl strokes (15–20%). High intracycle variation in the displacement of the centre of mass was observed to be associated with less efficient butterfly swimming and causing early fatigue over a longer distance (200 m) (Barbosa et al., 2005).

In swimming, generating propulsion depends on a personal hydrodynamic profile (Barbosa et al., 2012, 2014) which could be assessed by analysis of swimmers’ drag force (passive and active drag), and mechanical power and their relationships with anthropometrics. Swimming kinematics is associated with anthropometric characteristics in the front crawl as evidenced by the results of studies conducted in youth swimmers (Morais et al., 2012, 2013; Maszczyk et al., 2012; Stanula et al., 2012). In those and further studies of Morais et al. (2016) and Barbosa et al. (2015), it was shown that a significant relationship existed between the arm span and propelling efficiency or performance in youth swimmers. In our study conducted in junior and youth swimmers, a relationship between limb length and SL was not found; and other somatic traits (body length, length of upper and lower extremities) did not reveal an impact on VSBF, but according to the literature on the subject (Bulgakova, 1978, cited in: Chollet, 1990) competitive butterfly swimmers are not as tall as backstrokers or sprint freestyle swimmers, although the amount of data on this issue is scarce.

In our study assessment of interplay between dry-land anaerobic work generation (performed in the CMJ test) and VSBF was attempted. The obtained results turned out to be non-significant (Table 1). Strzała et al. (2009) noted strong relationships between results of anaerobic generation of arms and legs as well the CMJ and front crawl swimming speed, but that study focused on swimmers between 12 and 14 years of age. Chollet et al. (2006) argued that swimming speed did not depend exclusively on swimmer’s power. However, in our study an active component of the researched swimmers’ bodies (LBM) turned out to be significantly (0.48) associated with VSBF. The CMJ test proved to be a reliable test for the lower limbs and overall power in several sport disciplines, including swimming, but in this case it was not a good indicator of swimming performance.

Study limitations and conclusions

Based on the presented data, butterfly performance may depend less on anthropometrics (in comparison to freestyle), and more on technical variables (mainly motor coordination). Therefore, other studies should increase and update knowledge about the relationship between anthropometrics and butterfly performance, as well as power indexes and butterfly performance.

Our analysis of sprint butterfly swimming shows the importance of suitable matching of the upper and lower limb movements, which need to be coordinated with body undulation in repeated cycles. The entry-kick temporal index indicates that an appropriately timed initial kick when compared to arm entry (LP1) results in a longer arm propulsion phase, a longer first kick in the cycle and minimizing the most resistive gliding phases, which, in turn, enables relatively longer and less resistive air arm recovery (higher value of the fly-arm index). Higher value of the basic kinematic variable (SR) turned out to be another important element determining butterfly results. The results of this study are a prerequisite for use in the development of youth swimmers’ butterfly technique and the coordinating structure which affects the efficiency of swimming.