Hydroxyl-radical footprinting combined with molecular modeling identifies unique features of DNA conformation and nucleosome positioning

Abstract

Nucleosomes are the most abundant protein–DNA complexes in eukaryotes that provide compaction of genomic DNA and are implicated in regulation of transcription, DNA replication and repair. The details of DNA positioning on the nucleosome and the DNA conformation can provide key regulatory signals. Hydroxyl-radical footprinting (HRF) of protein–DNA complexes is a chemical technique that probes nucleosome organization in solution with a high precision unattainable by other methods. In this work we propose an integrative modeling method for constructing high-resolution atomistic models of nucleosomes based on HRF experiments. Our method precisely identifies DNA positioning on nucleosome by combining HRF data for both DNA strands with the pseudo-symmetry constraints. We performed high-resolution HRF for Saccharomyces cerevisiae centromeric nucleosome of unknown structure and characterized it using our integrative modeling approach. Our model provides the basis for further understanding the cooperative engagement and interplay between Cse4p protein and the A-tracts important for centromere function.

INTRODUCTION

Nucleosomes are the elementary building blocks of chromatin comprising a segment of DNA associated with an octamer of histone proteins (H3, H4, H2A, H2B—two copies of each) (1). The core of the nucleosome (named, nucleosome core particle or NCP) consists of 145–147 bp of DNA wrapped in ∼1.7 left-handed superhelical turns around the octamer (2) (Figure 1). Although the generic structure of the nucleosome has been well characterized (3), each particular nucleosome can be significantly different from its counterparts through variations in DNA sequence, incorporation of alternative histone variants (4,5), their post-translational modifications (6) and interactions with other proteins (7,8). These alterations and variations often affect DNA accessibility and conformation, which in turn modulate basic chromatin processes, such as transcription, replication, DNA repair, etc. (9,10). Shifting the position of DNA in nucleosome by only 1 bp leads to the changes in its rotational positioning of around 36°, which might be enough to affect the binding of many proteins to nucleosomes that read out DNA sequence (e.g. pioneer transcription factors (11,12)). Hence, detailed structural characterization of nucleosomes is of high importance. Atomic level structures of nucleosomes have been so far obtained through X-ray crystallography (3). However, this technique is very time-consuming and in many cases is severely limited by crystallization restraints on the composition and conformation of the nucleosome, potentially yielding conformations different from those adopted in solution. Precise and versatile techniques to characterize nucleosome structures are therefore in high demand.

Figure 1.

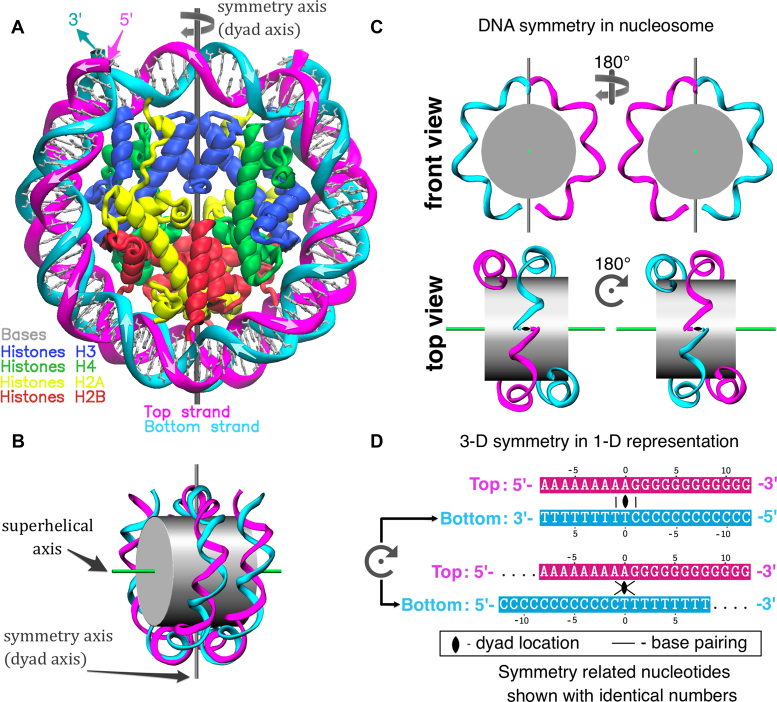
Nucleosome structure and pseudo-symmetry of top and bottom DNA strands. (A) Representation of the X-ray nucleosome core particle (NCP) structure (PDB ID: 1KX5 (50)). (B) Schematic representation of the nucleosome showing the locations of the 2-fold pseudo-symmetry axis and the superhelical axis. (C) Illustration of the pseudo-symmetry relation between top and bottom DNA strands in nucleosome (only parts of DNA strands are shown). (D) Representation of spatial DNA symmetry on planar sequence diagrams: conventional representation (top) and co-directional (bottom). In the latter representation two strands are aligned by placing the ‘dyad nucleotides’ of the top and the bottom DNA strands one under the other; consequently all symmetry related nucleotide pairs of the top and the bottom DNA strands are also in alignment (one under the other). Base pairing between selected nucleotides is shown on both representations.

In the laboratory, certain biochemical methods are widely used to quickly characterize the accessibility and positioning of DNA on nucleosomes in solution. These methods make use of DNA ‘footprinting’—cutting the DNA with enzymes or chemicals. These methods allow for mapping of protein–DNA interactions and characterization of DNA conformation along the DNA sequence. The hydroxyl-radical footprinting (HRF) method is recognized as the one providing the highest resolution due to the small size, neutral and non-discriminating nature of radicals yielding base-independent DNA cleavage (13). The DNA strand scission during HRF is believed to proceed primarily through the abstraction of the deoxyribose hydrogen atoms (Figure 2A) (14). HRF is usually performed in several steps: (i) each DNA strand is labeled on one end with a radioactive (or fluorescent) probe; (ii) protein–DNA complex (or free DNA) is treated with hydroxyl-radicals that cleave DNA at the exposed locations in the single hit kinetics regime (one cut per strand); (iii) the protein–DNA complex can be again purified; (iv) the DNA is then purified from proteins, denatured and subjected to high resolution denaturing polyacrylamide gel electrophoresis (PAGE); (v) the intensity of each band (i.e. base position) on the gel should then be proportional to the frequency of DNA cleavage during the footprinting reaction at a particular nucleotide site (13). Mapping of each band to a particular position along the DNA sequence can be easily accomplished by running products of DNA sequencing reactions (e.g. Maxam–Gilbert reactions) on adjacent lanes.

Figure 2.

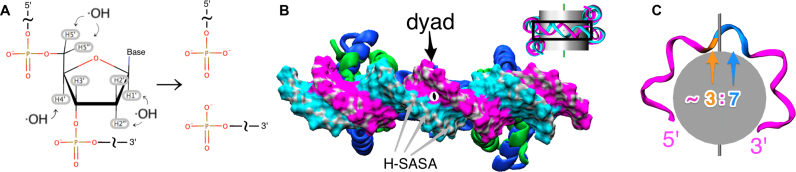
Details of hydroxyl–radical interactions with the nucleosomal DNA. (A) Chemical reaction of hydroxyl-radicals with DNA backbone: deoxyribose hydrogen atoms (highlighted in gray) are abstracted leading to the destruction of deoxyribose residue and DNA cleavage. Only major phosphate-terminated cleavage products are shown. (B) A segment of nucleosome viewed from the top (see inset) in solvent accessible surface area (SASA) representation. Patches of SASA belonging to deoxyribose hydrogen atoms (H-SASA) are colored in gray. (C) The asymmetry of histone–DNA contacts with respect to the dyad axis location leads to its manifestation on DNA cleavage profiles. The dyad splits the segment of a DNA strand between the two adjacent binding sites into unequal parts with ∼3:7 ratio when counted in 5′-3′ direction.

The application of HRF to nucleosomes was pioneered by Hayes et al. well before the first atomic resolution X-ray structures of nucleosomes became available (15–18). These authors were able to assess the helical periodicity of DNA in the nucleosome and their work has since served as a reference for many other studies that have used HRF to characterize nucleosomes. The latter studies employed nucleosomes with alternative DNA sequences (19–21), intrastrand crosslinks introduced by chemotherapeutic agents (20), nucleosomes interacting with remodelers (22) or other proteins (23). Although HRF of nucleosomes undoubtedly has helped to characterize nucleosome positioning, DNA geometry and interaction sites with the nucleosome binding proteins, there is additional potential of HRF to be tapped.

This potential lies in quantification of HRF data and combining this data with integrative molecular modeling techniques to obtain atomic level nucleosome models. The molecular modeling of nucleosomes is a challenging task since it requires not only the modeling of a histone octamer but also involves finding the correct rotational and translational positioning of DNA with respect to the octamer. Previous studies indicated that certain nucleosomes in yeast are well-positioned especially the centromeric ones (24) and therefore sliding of nucleosomal DNA by only 1 bp can result in significant changes in its exposure. The DNA cleavage frequencies extracted from the HRF solution experiments are usually at single base pair resolution and may provide data on relative DNA accessibility for cleavage that is affected by interactions with proteins and/or DNA conformation (e.g. narrow minor groove). Experimental HRF data can provide a convenient source for validating and refining the nucleosomal models.

The basis for linking experimental HRF footprinting data with molecular modeling has been formulated by Balasubramanian et al. who suggested that the frequencies of DNA strand breaking by hydroxyl-radicals were proportional to the solvent accessible surface area (SASA) of deoxyribose hydrogen atoms calculated from known structures (25). It facilitated the interpretation of HRF profiles in terms of the quantitative measures of DNA backbone solvent accessibility, DNA major and minor groove widths and other DNA geometrical characteristics (26,27). To our knowledge this approach has not yet been systematically applied to nucleosomes. Alternatively, Begusova et al. have proposed a sophisticated hybrid modeling approach based on Monte-Carlo simulations of hydroxyl-radical diffusion combined with reactivity parameters obtained from fitting models to experimental data (28,29).

The limited progress in using HRF data for constructing robust nucleosome models is partially due to the lack of studies that attempt to directly relate hydroxyl-radical footprints of nucleosomes to the high-resolution X-ray structures and dynamics of nucleosomes. Another reason is the deficiency of methodologies to quantify the experimental footprint profiles of nucleosomes and to understand the potential sources of biases and variations in experimental data.

In the current study, we try to address the above issues with an aim to provide a robust way to construct nucleosome models based on HRF data and to understand potential differences between nucleosome structures as seen in X-ray crystal structures and in solution. The first part of our work is devoted to the theoretical estimation of HRF profiles from 3D structures and their rationalization in terms of DNA conformation and protein–DNA interactions. Particularly, this analysis allowed us to establish a link between the pseudo-symmetry of nucleosome and similarity between HRF profiles of complimentary DNA strands. In the second part of our work we performed high-resolution HRF in solution for two different systems based on in vitro assembled Saccharomyces cerevisiae centromeric nucleosomes containing the Cse4/CENP-A histone variant with different DNA sequences: centromeric DNA sequence from chromosome III (CEN3) and 601TA nucleosome positioning sequence. Based on the experimental and modeling data we propose a new straightforward integrative method for determining DNA positioning in nucleosomes (both rotational and translational) at single base pair resolution. Our method uses experimental HRF data for both DNA strands and exploits the pseudo-symmetry of nucleosomes. Finally, we applied our method to determine DNA positioning in nucleosomes (nucleosome positioning) and built a structural model of an in vitro assembled centromeric nucleosome of S. cerevisiae, which has DNA unusually rich in A-tracts that are known to be critical for centromere function. We discuss the implications of our structural model for centromere function.

MATERIALS AND METHODS

Experimental procedures

Preparation of DNA fragments

The 601-TA DNA was first polymerase chain reaction (PCR) amplified with an asymmetric AvaI restriction site, CTCGGG, at both ends and cloned into a modified pUC19 vector that contains an engineered asymmetric AvaI site. However, PCR-amplification of the highly AT-rich (∼90%) budding yeast centromere DNA was problematic. Thus, the CEN3 DNA fragment was chemically synthesized with the asymmetric AvaI site and cloned into the pUC57 vector (Genscript USA Incorporated, Piscataway, NJ, USA). The asymmetric AvaI site was used to ligate DNA fragments into tandem arrays. Such tandem arrays of the 601-TA and centromere DNA fragments were then cloned in the modified pUC19 vector with the engineered asymmetric AvaI site. For large scale preparation of DNA fragments, plasmids that contain the tandem arrays were transformed into DH5-a or XL1-Blue cells for stable propagation of the long tandem arrays of DNA fragments. Purified plasmids were digested with restriction enzyme AvaI, and fragments were purified by agarose gel electrophoresis and ethanol precipitation. The base composition of the four-base overhang of the asymmetric AvaI site is different between the top strand (TS) and the bottom strand (BS), and thus can be used to label the DNA fragments strand-specifically at the 3′-end, using radioactive or fluorescent-labeled nucleotides in Klenow polymerase filling-in reactions. Because PCR is problematic for the production of AT-rich centromere fragment, 5′-labeling of either end would have necessitated chemical re-synthesis of centromere DNA with additional flanking restriction sites and generation of tandem arrays for large-scale DNA production; for this reason 5′-labeling was not pursued.

Nucleosome preparation and reconstitution

Expression and purification of S. cerevisiae core histones were as described previously (7,30,31). Core histone octamers were reconstituted using established protocols (30). Briefly, equimolar amounts of purified recombinant histones (H2A, H2B, Cse4 and H4) were dissolved in unfolding buffer (7M guanidine-HCl, 20 mM Tris-Cl, pH 7.5, 10 mM dithiothreitol (DTT)) at 2 mg/ml. The mixtures were dialyzed against four changes of 2 liters each of refolding buffer (10 mM Tris-Cl, pH 7.5, 1 mM ethylenediaminetetraacetic acid (EDTA), 5 mM beta-mercaptoethanol, 0.1 mM phenylmethylsulfonyl fluoride (PMSF)) containing 2M NaCl for 2 days at 4°C. The mixture was then centrifuged at 15 000 rpm in a Tomy MX-300 micro-centrifuge to remove any insoluble material. Soluble octamers were purified by size fractionation on a Superdex 200 gel filtration column. The 157 bp 601TA DNA fragment (32) and 136 bp CEN3 DNA fragment were prepared as previously described (7). Their full-length sequences are presented on the sequence axis on all corresponding figures.

To reconstitute nucleosomes, purified core histone octamers and DNA were mixed in 50 μl of high salt buffer (2M NaCl, 10 mM Tris-Cl, pH 7.5, 1 mM EDTA, 0.02% NP-40, 5 mM beta-mercaptoethanol) supplemented with BSA at 400 μg/ml. The mixture was transferred to a Slide-A-Lyzer MINI dialysis unit (Thermo Scientific). The dialysis unit was placed in a container with 600 ml of high salt buffer, and dialyzed for 30–60 min, followed by salt gradient dialysis, during which a low salt buffer (100 mM NaCl, 10 mM Tris-Cl, pH 7.5, 1 mM EDTA, 0.02% NP-40, 2 mM beta-mercaptoethanol) was pumped into the container at 3.5 ml/min for 16 h. The dialysis unit was then transferred to low salt buffer and dialyzed for 60 min. The dialysis was done at room temperature, and samples were further treated at 65°C overnight.

Hydroxyl-radical footprinting

Nucleosomes were reconstituted with DNA fragments end-labeled at 3′ with ³³P-dTTP for the TS and ³³P-dATP for the bottom strand by filling in the asymmetrical AvaI site using Klenow polymerase. HRF of nucleosomes was performed on reconstituted nucleosomes with iron (II)-EDTA as described previously (22).

The reaction products were resolved on a 1.3% native agarose gel, bands containing the free nucleosomes were visualized by SYBR Green staining and excised from the gel. DNA was recovered from the gel slices and resolved on an 8% DNA sequencing gel (National Diagnostics, cat# EC-833). DNA mobility markers were G+A and C+T sequencing reactions of the same ³³P-labeled DNA fragments performed as described in Molecular Cloning, CSHL. Gels were run on a 40 cm glass plate at 1500–1600V for ∼70 min with a gel temperature of about 55°C, then transferred to a DEAE filter paper (Whatman Grade DE81 ion exchange chromatography paper from GE Life Sciences) and dried under vacuum. Radioactive signals were captured using PhosphorImager (Fuji Photo Film Co., Ltd) and a Typhoon scanner (Typhoon 9410, Amersham Biosciences).

Computational analysis

Quantification of gel images from hydroxyl-radical footprinting experiments

The 1D lane intensity profiles for every lane in the gel were extracted using ImageJ v. 1.51f (33). A line or a segmented line was manually drawn through the centers of all bands in the lane. The line width was set to approximately half of the band width, and the signal profile along the lane was extracted and saved to a separate file for further processing. This standard procedure automatically triggered image straightening for every lane and data averaging across the lane width as implemented in ImageJ.

The lane intensity profiles corresponding to hydroxyl-radical experiments were further analyzed with the help of our newly developed HYDROID Python package (available at https://github.com/ncbi/HYDROID) (publication in preparation) in order to obtain values of DNA cleavage intensities at every position in DNA sequence. Although our methodology builds on the ideas proposed in earlier works (34–36), it has several novel aspects.

First, the initial locations of intensity peaks corresponding to the gel bands were semi-automatically assigned and mapped to positions along the DNA sequence by comparing them with the bands produced by Maxam–Gilbert reactions (13). The data range on each HRF profile was set to the region where continuous set of individual band locations could be identified (either directly by the presence of a peak or otherwise unambiguously inferred from the position of the neighboring peaks or corresponding band positions on other gel lanes).

Next, the analytical function was used to fit the experimental HRF profile. It represented a linear combination of Gaussian functions each intended to describe the shape of a specific band on the experimental profile. The Levenberg–Marquardt least square-fitting algorithm was employed to solve this optimization problem. The width parameters of Gaussian functions were constrained to ensure the monotonic width decrease with increased molecular weight of cleaved DNA fragments corresponding to the gel bands. Such regularization was shown to increase the accuracy of fitting procedure and was performed by a function implemented in HYDROID. Previously, Lorentzian instead of Gaussian functions were used as empirical approximation to alleviate signal distortions due to autoradiographic detection ((34) and appendix therein). In our case modeling with Lorentzian functions yielded slightly worse fitting results as measured by root-mean-square deviation between fitted and experimental curves, thus warranting the use of Gaussian functions for our analysis. As a result, the DNA cleavage frequencies for every position on the DNA sequence were derived from values of coefficients (obtained by integrating over intensities for each band) in front of Gaussian functions describing the corresponding band.

It should be mentioned, that the DNA cleavage intensity profiles usually differ in an absolute magnitude due to their dependence on many experimental conditions (sample load, exposure time, etc.). In order to enable an adequate comparison between two experimental profiles they have to be on the same scale. To this end we performed a linear regression describing one HRF profile as a linear function (without an intersect) of another profile. Latter intensity profile values were then rescaled by the obtained linear regression coefficient and were normalized from zero to one by dividing by the maximum intensity value of two profiles. For the comparison of experimental and theoretical (H-SASA, see below for definition) profiles, a simple normalization of each profile by its maximum value was used.

Molecular modeling and molecular dynamics simulations of nucleosomes

The molecular dynamics (MD) simulations of various NCP were performed according to our protocol described in ref. (37) if not noted otherwise. The initial models were based on X-ray structures obtained from the Protein Data Bank or on homology models. Structures were initially oriented in the nucleosomal reference frame as defined previously (37), so that Z-axis corresponded to the DNA super-helical axis (Figure 1B). Simulations were run for 80 ns and snapshots were saved every 1 ns, first 30 ns of MD simulation were discarded as a relaxation period. N1 and N9 atoms of bases in DNA were constrained to their initial positions via harmonic restraints of 6 kcal/mol/Ų. Additionally we compared the MD trajectories to a microsecond trajectory of nucleosome with the full histone tails and no restraints on the DNA published earlier (38). Structures were visualized and analyzed using Visual Molecular Dynamics (VMD) (39).

The initial structure of S. cerevisiae Cse4p-containting centromeric nucleosome with 601TA DNA sequence (601TA-NUC) was built based on Xenopus laevis nucleosome structure with 601 DNA (PDB ID: 3LZ0) using Modeller (40) and 3DNA (41). Histone sequences were obtained from HistoneDB 2.0 database (4). The model of yeast centromeric nucleosome on CEN3 DNA sequence (CEN3-NUC) was built using the same methods based on X. laevis nucleosome structure with α-satellite DNA (PDB ID: 1KX5). Since there is no data on DNA positioning for this nucleosome, we determined it using our dyad identification method applied to HRF experimental data on CEN3-NUC (see below). In both models DNA was modeled using the central 120 bp fragment (60 bp from the dyad in each direction)—the fragment known to be unambiguously organized by centromeric nucleosomes (42).

Theoretical estimation of DNA cleavage frequency profiles from atomic structures

As suggested in ref. (25), the cleavage frequency profiles for nucleosomal DNA were theoretically estimated as the sum of solvent accessible solvent areas (SASA) for all deoxyribose hydrogen atoms of a given nucleotide, called H-SASA profiles hereafter. SASA calculations were performed using NACCESS program (43) with a probe radius of 1.4 Å, slice width set to 0.005 Å and atom radii set to rmin parameters of the CHARMM36 force field (44). For the systems with truncated histone tails, tails were truncated at the following N-terminal (H3G44, H4D24, H2A16T and H2BR33) and C-terminal (H2AK118) positions (the residue numbering is given in the reference frame of X. laevis canonical histones). By default the H-SASA profiles were averaged over 50 MD snapshots (spaced every 1 ns) of fully hydrated structures (for reasons described in ‘Results section’). For MD simulations the hydrogen atoms were added as a regular part of system preparation and in cases of direct analysis of X-ray structures the hydrogen atom positions were generated by REDUCEv.3.14 from AmberTools13 (45). Plots of profiles together with sequences were generated by ggplot (46) and TexShade (47). Truncation of histone tails and structure relaxation and averaging provided by MD simulations were instrumental to obtain H-SASA profiles that reflected the DNA periodicity in nucleosome (see ‘Results’ section, Supplementary Figures S1 and 2). The contribution of DNA–protein contacts to H-SASA profiles was estimated by calculating H-SASA profiles for nucleosomal DNA with histones removed (Supplementary Figure S1, bottom panel). It can be seen that H-SASA model is sensitive to DNA minor groove narrowing at certain sites of DNA–histone interactions, where DNA is bent toward the minor groove. However, histone–DNA contacts are the main contributor to H-SASA minima at these sites.

Calculating parameters of DNA geometry

Parameters that represent the spatial orientation, conformation and periodicity of nucleosomal DNA as 1D profiles are instrumental to our analysis. As the main parameter representing the orientation of DNA base pairs in the nucleosomal superhelix, we used the value of nucleosomal DNA relative twist (rTw). Two types of twist parameters to characterize supercoiled DNA in nucleosome were defined previously: intrinsic twist (iTw) and rTw (or local twist) (48,49). The latter is assumed to be measured in HRF or enzymatic digestion experiments, because it highlights the geometrically equivalent positions along the DNA superhelix. The DNA iTw on the other hand highlights only the intrinsic rotation of base pairs with respect to each other along the DNA. However, rTw and iTw values are known to be related via the superhelical pitch of the nucleosomal DNA (49). The iTw values for every base pair step were calculated using 3DNA (41); summing this value along the DNA sequence yielded a cumulative iTw (ciTw).

To characterize the rTw, we introduce here a new quantity—the base pair orientation angle (BPOA), designed to reflect the local orientation of nucleotides with respect to histone octamer. BPOA was calculated from atomistic structures of nucleosomes as follows: (i) the nucleosome superhelical axis (Figure 1B) was defined as described in ref. (37); (ii) for every nucleotide a base pair vector (BPV) was defined as the vector pointing from the glycosidic nitrogen atom of the current nucleotide to the corresponding atom of the complimentary nucleotide (thus connecting N1 and N9 atoms); (iii) for every nucleotide its corresponding base pair center (BPC) was defined as the mid-point of BPV; (iv) the BPOA was then defined as the angle between BPV and the perpendicular pointing from the nucleosome superhelical axis to BPC (the radial vector in cylindrical coordinate system). The values of BPOA served as a measure of rTw ranging from 0 to 180°. Per analogy with ciTw the cumulative rTw (crTw) was implemented by following the rotation of BPV along the sequence and adding 180° every time the value of BPOA would start a new 180 interval. The relative (local) periodicity of nucleosomal DNA at each particular position was calculated based on the difference of crTw values between sites 5 bp upstream and downstream of the selected position. An alternative way to calculate rTw using BPOA defined as an angle between the BPV and the plane perpendicular to superhelical axis yielded almost identical results (Supplementary Figure S3A) thus validating our choice of BPOA as a measure of rTw. The difference between crTw and ciTw was observed in accordance with the theoretical expectations (Supplementary Figure S3B).

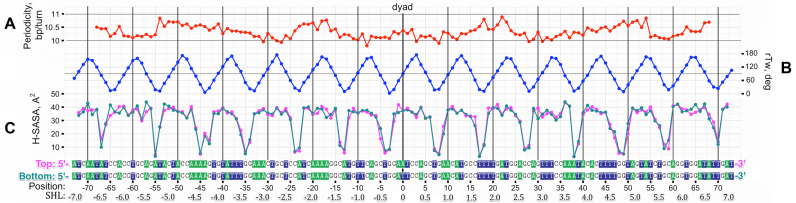
We employed the rTw parameter to characterize DNA path in atomistic structures of NCPs and to calculate local periodicity along the DNA sequence. This allowed us to analyze in detail the rotational positioning of DNA in nucleosomes and to identify geometrically equivalent positions with respect to the surface of the octamer. The minima of the rTw curve correspond to the positions where the corresponding base pairs are oriented almost perpendicular to the superhelical axis and the TS nucleotide interacts with the octamer primarily via its backbone atoms. The local periodicity of the DNA for the analyzed structures (Figures 3A and 4) fluctuates between 10 and 11 bp/turn and the DNA is over-twisted around positions ±20 and ±50 (SHLs ±2 and ±5), which is in agreement with previous analyses (3).

Figure 3.

DNA structure and H-SASA profiles in the highest resolution X-ray structure of NCP (NCP147). (A) Local DNA rotational periodicity in nucleosome calculated from relative twist (rTw). (B) rTw of nucleosomal DNA along the sequence, plotted in 5′-3′ direction of the top strand (TS). (C) H-SASA profiles for TS (magenta) and bottom strand (cyan), both profiles and sequences beneath are given in 5′-3′ direction. The H-SASA profiles calculated from MD trajectory of NCP147 without histone tails (see ‘Materials and Methods’ section).

Figure 4.

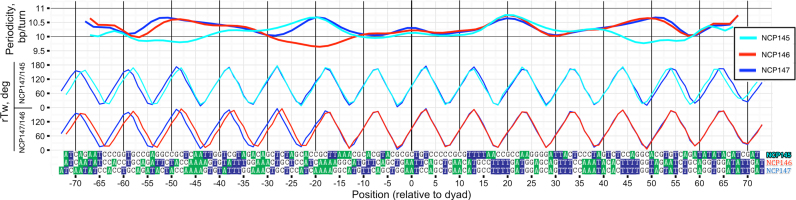
DNA structure variation between different X-ray structures of NCPs. Top: same as Figure 3A, but smoothed with B-spline (with 30 degrees of freedom). Bottom: pairwise comparison of rTw profiles.

RESULTS

Analysis of theoretical DNA cleavage frequency profiles for different nucleosomes

The calculation of theoretical HRF cleavage frequency profiles is based on the assumption that it is governed by the H-SASA profiles (see ‘Materials and Methods’ section) (13). This is certainly only an approximation to the complex diffusion and interaction processes happening during the hydroxyl-radical reaction. However, there are certain considerations in favor of such an approach. It allows to estimate in a robust way single nucleotide resolution theoretical profiles from the atomic nucleosome structures or from the accurate structural models and draw important conclusions about the expected shape and similarity of the experimental profiles. We argue here that the nucleosome symmetry can be exploited to provide a way to validate and advance the accuracy of theoretical profiles, to facilitate the interpretation of experimental HRF profiles and to allow the identification of the nucleosome dyad from HRF experimental data. Indeed, nucleosomes have 2-fold pseudo-symmetry (Figure 1B–D) that relates the top and bottom strands of the nucleosomal DNA in a way that, if a nucleosome is rotated by 180° around the dyad axis, the TS would almost exactly coincide with the position of the bottom strand and vice versa. In particular, the 5′-end of the TS will be superimposed with the 5′-end of the bottom strand.

As a reference, we first examined the highest resolution structure of a conventional NCP (PDB ID: 1KX5 (50)) where the 2-fold symmetry of the histone octamer is complimented by the symmetry of a quasi-palindromic DNA sequence: the central base pair at the dyad splits the nucleosome and two-stranded DNA into two identical halves. In case of known structures, the exact dyad position can be directly seen as the single base pair located on the pseudo-symmetry axis (2). Figure 3 shows a clear pattern of periodicity in H-SASA profiles calculated from this structure for both DNA strands. This shape and periodicity is very similar for both DNA strands, respecting the symmetry of the system. The dyad axis divides the segment between two minima on the H-SASA plot into non-equal parts (approximately at 3:7 ratio) with the dyad location closer to the 5′ end of the DNA strand. This is a consequence of the nucleosome geometry and is illustrated in Figure 2B and C.

In Figure 3C, the H-SASA profile has distinct sharp minima at every position where DNA is oriented perpendicular to the octamer surface and rather plateau-like areas of high values of exposure to potential hydroxyl-radical attack between these positions. The distance between the minima on H-SASA profile follows 10–11 bp periodicity but the positions of H-SASA minima do not always correspond exactly to the positions of rTw minima—they are usually off by 1 or 2 nt in either direction. The latter highlights the fact that not only twisting of the DNA is responsible for the exact shape of H-SASA profiles, but also the differences of protein-DNA interactions at various DNA binding sites on nucleosome influence local positions of H-SASA minima.

To get insights into these variations we calculated individual contributions of amino acids to the DNA protection from hydroxyl-radicals calculated as changes in total H-SASA upon removal of one specific amino acid residue (Supplementary Figure S4). A good example of local H-SASA shape variation is the increased protection in profiles at position −43 manifested as a local minimum on Figure 3C that is caused by an interactions of DNA with αN-helix, unique to H2A. Despite the presence of local spikes, the overall H-SASA profiles of the two DNA strands show a good superposition. As mentioned earlier, this is the result of the almost perfect 2-fold symmetry of the reference conventional nucleosome both at the protein and DNA levels.

HRF experiments are performed in solution on an ensemble of nucleosomes that collectively represent the conformational space accessible to individual nucleosomes over long periods of time, therefore it is appropriate to assume that two identical copies of histones and histone tails should sample indistinguishable ensembles of conformations. Hence, the symmetry rule introduced above should still pertain. Flexible histone tails, which are often found in the trapped non-native conformations in X-ray nucleosome structures (if resolved), may introduce irregularities into H-SASA profile (Supplementary Figure S1) and may provide considerable additional protection to the DNA cleavage (Supplementary Figure S2). We found that the best match between H-SASA profiles corresponding to two DNA strands was attained when flexible histone tails were omitted and ensemble averaging and relaxation of DNA backbone were performed by MD simulations (Figure 3C versus Supplementary Figure S1). For that reason, we implemented a protocol using systems with truncated histone tails and MD ensemble averaging, which we used throughout this study.

Next we analyzed the influence of variations in DNA sequence on the DNA geometry and theoretical H-SASA profiles. Figure 4 and Supplementary Figure S5 summarize the differences in DNA geometry and periodicity for three available NCP X-ray structures with different DNA sequences (Table 1): 146 bp α-satellite DNA (‘NCP146’) (2), modified 147 bp α-satellite DNA (‘NCP147’) (50) and 145 bp 601 Widom high-affinity sequence (‘NCP145’) (51,52). In all these structures 1 bp is located strictly at the dyad and DNA covers the same superhelical path despite the differences in their lengths. This is achieved by DNA stretching/compression at sites located ±20 or ±50 bp from the dyad. This is illustrated by the relative periodicity and rTw parameters proposed in this study (Figure 4, top plot). While DNA molecules from NCP147 and NCP145 adopt very similar conformations on both sides of the nucleosome, DNA from NCP146 is stretched by 1 bp on one side with respect to the other. Almost identical DNA conformation on both sides of the dyad in NCP147 and NCP145 results in a very good superposition between H-SASA profiles for both DNA strands (Pearson correlation coefficient = 0.97, Figure 3 and Supplementary Figure S6). As to NCP146, despite a slight asymmetry of the two halves of nucleosomal DNA, H-SASA profile similarity between two strands is maintained within ±20 bp vicinity of the dyad (Supplementary Figure S6). However, the slight asymmetry of NCP146 H-SASA profiles would not be manifested on HRF profiles for an ensemble of nucleosomes in solution. Indeed, NCP146, having a purely palindromic DNA sequence, in solution would have no preference as to which side of the nucleosomal DNA to stretch or extend, because the two halves of the DNA are completely identical.

Table 1. Key nucleosome structures analyzed and their composition.

Identifier	DNA	Histone content	PDB ID, Ref.
NCP147	147 bp, modified α-satellite	canonical histones from X. laevis	1KX5, (50)
NCP146	146 bp, α-satellite, palindromic		1AOI, (2)
NCP145	145 bp, 601 Widom high-affinity sequence (51)		3LZ0, (52)
601TA-NUC modela	145 bp, 601TA modified 601 high-affinity sequence (32)	Cse4p, H4, H2A, H2B from S. cerevisiae

^aHomology model based on PDB ID: 3LZ0.

Quantifying experimental HRF profiles and their comparison to theoretical H-SASA profiles

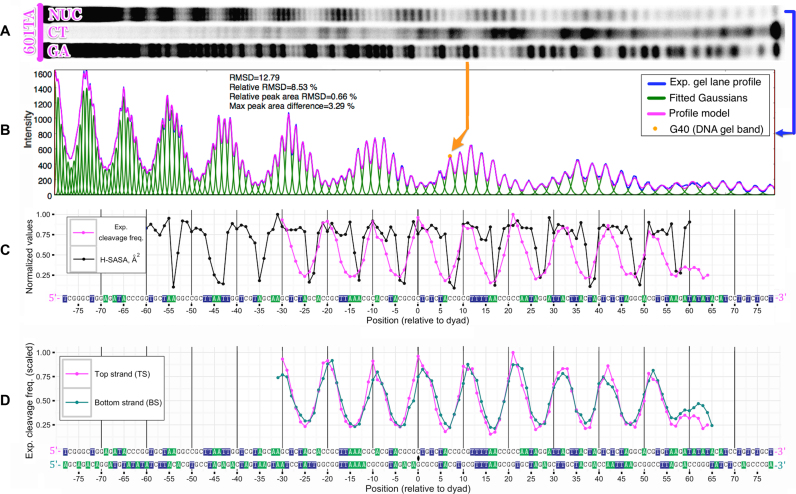
We have undertaken a set of HRF experiments for in vitro reconstituted octameric nucleosomes based on centromere histones of S. cerevisiae and two different DNA sequences: a high-affinity 601TA sequence and a yeast chromosome III centromere DNA sequence CEN3 (601TA-NUC and CEN3-NUC). In addition, we analyzed the free CEN3 DNA (CEN3-free). All analyzed systems are summarized in Table 2. According to our computational framework, every position in DNA sequence can be assigned a relative hydroxyl-radical cleavage frequency value by quantifying experimentally obtained PAGE gel image of HRF reaction products (Figures 5 and Supplementary Figure S7). As a proof of concept, in Figure 5C and Supplementary Figure S8 the experimental HRF profile of 601TA-NUC is compared to the theoretical H-SASA profile derived from a high quality model with the precise dyad position known from X-ray crystallography studies (‘Materials and Methods’ section). The overall periodicity of experimental and theoretical profiles are in good agreement with each other. A noticeable decrease in signal amplitude toward the 3′ end of DNA is likely attributed to the decreased propensity of short DNA fragments to get precipitated during the purification step. Experimental profiles for the top and bottom strands, when superimposed in 5′ to 3′ directions (Figure 5D), are very similar in shape reflecting the 2-fold pseudo-symmetry of the nucleosome as illustrated in a previous section.

Table 2. Systems subjected to HRF analysis (in vitro reconstituted nucleosomes or free DNA).

Identifier	DNA	Histone content
601TA-NUC	601TA	H4, H2A, H2B − canonical histones + Cse4p (centromeric variant of H3), all from S. cerevisiae
CEN3-NUC_1b	CEN3c
CEN3-NUC_2
CEN3-NUC_3
CEN3-free	CEN3	free DNA

^bThree independent experiments.

^cCentromere DNA sequence of Chromosome III in S.cerevisiae, 136 bp long.

Figure 5.

Quantification of HRF experiments and comparison with theoretical profiles derived from atomic structure (for 601TA-NUC nucleosome). (A) Original PAGE gel image of DNA segments produced by HRF of nucleosomes reconstituted on 601TA sequence (NUC) and corresponding Maxam–Gilbert reaction products (CT, GA). Data are shown for TS only. (B) Corresponding raw HRF lane intensity profile extracted from the gel image and its deconvolution into individual band intensities by fitting of Gaussian functions; root-mean-square-deviation (RMSD) and relative RMSD between the original profile and the fitted model are reported; RMSD for peak area also reported, peak areas calculated as the areas under the curve between adjacent minima. (C) Superposition of quantified experimental DNA cleavage frequencies and H-SASA profiles calculated from an atomistic structure; both profiles are normalized to their maximum values. (D) Superposition of experimental DNA cleavage frequencies for top and bottom DNA strands in 601TA-NUC nucleosome.

The location of minima at the DNA—histone interactions sites on H-SASA and experimental profiles coincide within the precision of ± 1 bp, in the majority of cases experimental minima are shifted toward the 5′-end of the strand with respect to the H-SASA minima. A potential explanation is that during hydroxyl-radical cleavage of 3′-labeled DNA strand in addition to major 5′-phosphate-terminated product, a minor alternative product is known to be present—a strand terminated by 5′-aldehyde group (25). The 5′-aldehyde product, which results from abstraction of a 5′-hydrogen atom, is 1 nt longer than the 5′-phosphate-terminated strand mentioned above, lacks the negative charge of the phosphate group, and thus has gel mobility 2–3 nt slower if compared with the corresponding Maxam–Gilbert product (53). Thus, in the actually measured DNA cleavage frequency profile, some portion of the signal is expected to be shifted by 2–3 toward the 5′-end. This may result in a slight shift of the minima on the measured profile with respect to the true profile (approximated by H-SASA profile). The mentioned effect should be considerably reduced if the DNA strand is radiolabeled at the 5′-end (25), but generation of 5′-labeled fragments of the highly AT-rich centromere DNA is technically challenging (‘Materials and Methods’ section).

There are other important differences between the theoretically estimated H-SASA and experimental profiles. The latter exhibit much smoother variation of cleavage frequency values along the sequence, while H-SASA profiles have sharp 1–2 bp wide minima flanked by regions of high cleavage frequency values (Figure 5C). Furthermore, while at certain positions H-SASA values are close to zero, pointing to the high protection of DNA from cleavage, experimental data support a minimum cleavage frequency of at least 25% relative to maximum values. In addition to that, experimental HRF profiles have distinct local maxima that correspond to the DNA facing away from the octamer, while H-SASA profiles have plateau-like shape in the corresponding regions. Potential reasons for these discrepancies are outlined in the ‘Discussion’ section below.

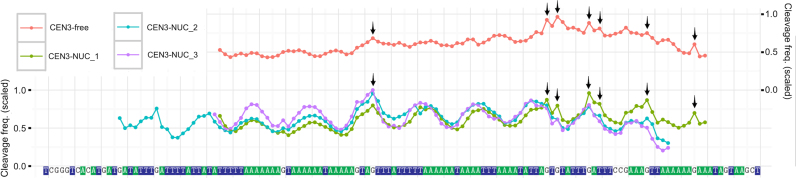
We observed that an overall sinusoidal-like HRF profile of DNA in nucleosomes has spikes at certain base pair positions, their magnitude varies from experiment to experiment. These spikes are best illustrated on CEN3-NUC nucleosome data sets (Supplementary Figures S9 and 10) and are highlighted by arrows in Figure 6. Interestingly, the locations of these spikes correspond very well to those of the free DNA. The HRF of free DNA is determined mainly by its geometry, which is sequence dependent. The unusual nature of CEN3 sequence, which is very rich in A-tracts (defined as four or more consecutive A⋅T base pairs without a TpA step (54)) manifests itself as spikes at locations where these A-tracts are disrupted by guanines or cytosines. The locations of major peaks observed experimentally for free CEN3 DNA is in corroboration with predictions from the ORCHID web server, which predicts the HRF profiles by averaging over existing HRF measurements for all possible free trinucleotides (55) (Supplementary Figure S11). Yet one should not expect a perfect correspondence between these two methods, since A-tracts are characterized by non-local bifurcating hydrogen bonds that may lead to non-additive long range rather than local effects manifested in trinucleotides (56). The appearance of ‘free DNA’ spikes in HRF of DNA in nucleosome is likely due to the interplay between intrinsic geometry and dynamics of free DNA and geometry imposed onto DNA by binding to histones. Our modeling of theoretical cleavage profiles using MD simulations suggests that H-SASA values are rather sensitive to small fluctuations in the dihedral angles of the DNA backbone, which may be triggered by only small displacements of the base pair positions. This provides one potential clue on how small changes in nucleosome structure and dynamics due to DNA sequence variation might manifest on HRF profiles.

Figure 6.

HRF DNA cleavage frequency profiles for CEN3-NUC nucleosomes and CEN3-free DNA. Data from several experiments for the TS are combined, arrows indicate minor spikes visible on both free and nucleosomal DNA profiles attributed to sequence-dependent contributions.

A novel method to determine nucleosomal DNA positioning from hydroxyl-radical footprinting data

The analysis of both experimental and H-SASA profiles described in the previous sections revealed several key relationships between the shape of HRF profiles and positioning of DNA on nucleosome. The method of dyad identification described below relies on these relationships. First, the 2-fold pseudo-symmetry of a nucleosome (Figure 1) relates the top and bottom strands of the nucleosomal DNA so that if a nucleosome is rotated 180° around the dyad axis the TS is superposed to the symmetrical position of the bottom strand and vice versa (Figure 1C). This observation implies that HRF profiles for the top and bottom DNA strands should match (or be very similar depending on the degree of pseudo-symmetry, as discussed earlier) if both are compared in the same direction (5′ to 3′ in our case). Second, based on the H-SASA or experimental HRF profiles and supported by the analysis of the geometry of the nucleosome structure, one can see that the dyad position is located asymmetrically between the two local minima on the corresponding profiles of either DNA strands dividing the segment between the minima approximately at a 3:7 ratio (referred to as ‘3:7 ratio rule’ hereafter) (Figure 2C).

An important aspect is the choice of the correct reference frames for comparison of the top and bottom strand profiles. It is especially relevant since HRF profiles typically lack data near the ends of the nucleosomal DNA because of the limited PAGE resolution making it impossible to identify the nucleosomal boundary on each profile and use it as an anchor for their alignment. However, if the dyad position on the DNA is known, the positions of the corresponding dyad nucleotides on each profile are also known. In this case, due to geometrical reasons and strand base pairing considerations, the correct choice of reference frames can be achieved by placing the dyad nucleotide positions of each profile at 0 as shown in Figure 1D. This is illustrated by the example of 601TA-NUC system (Figure 5D) where the known position of the dyad from structure (see ‘Materials and Methods’ section) is used to plot experimental HRF profiles for top and bottom strands of the same system in their respective reference frames. The two profiles appear to be perfectly aligned (Pearson correlation coefficient = 0.94), thus validating the correct choice of the dyad position.

If we now envision the situation when the position of the dyad is not known, but one has HRF experiments for both DNA strands, the above described approach can be readily generalized to identify the dyad position and therefore overall DNA positioning (also called nucleosome positioning). Since each intensity value of HRF profile corresponds to a specific base on a DNA strand, profile alignment defines the alignment of sequences of two strands plotted in 5′ to 3′ direction. A corresponding dyad position on the sequence alignment between top and bottom DNA strands can then be identified as the only position where the aligned bases form a base pair in the structure of the two-stranded nucleosomal DNA.

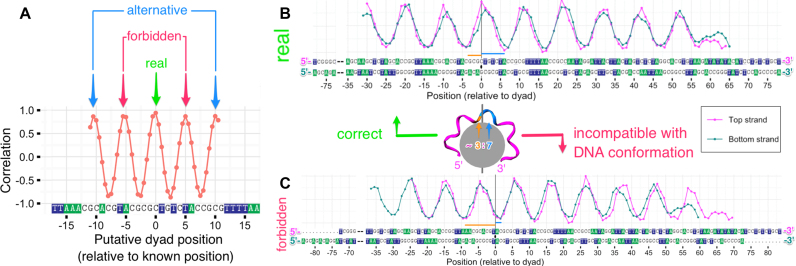
In practice, different alignments of HRF profiles for the top and bottom strands are sampled and the quality of their match is assessed by calculating the correlation coefficient between the two aligned HRF profiles (only the overlapping parts of the profiles are used to calculate the coefficient at any given alignment). This is inspired by the signal processing theory where the similarity between two processes is assessed by calculating the cross-correlation function. The dyad position should correspond to the maximum (at least local maximum) of the correlation coefficient. An animation of this approach for the 601TA-NUC HRF profiles is provided in Supplementary movie SM1. The correlation between the two HRF profiles as a function of putative dyad position for 601TA-NUC data is shown in Figure 7A. In this figure, there are several correlation coefficient maxima spaced periodically ∼5 bp apart and in some cases there might be an ambiguity as to which maximum corresponds to the true position of the dyad. Applying the ‘3:7 rule’ is useful, since half of these correlation maxima can be discarded as stereochemically ‘forbidden’ dyad positions helping to identify the ‘real’ dyad position (Figure 7). The mentioned periodicity and potential ambiguity is the consequence of (i) the quasi-periodic nature of the DNA conformation in nucleosome and (ii) the limited range of positions on DNA sequence for which the DNA cleavage profile was measured. However, in a practical setting the approximate dyad position (for example, found by locating nucleosomal boundaries via MNase digestion or MNase-seq) can be used to resolve the ambiguity. Alternatively, longer HRF profiles that cross the nucleosomal boundaries can be used.

Figure 7.

Explanation of the dyad identification algorithm as applied to 601TA-NUC nucleosome with known dyad position. (A) Pearson correlation coefficient between top (TS) and (BS) strand experimental HRF profiles as a function of putative dyad position used for the alignment of these profiles. The real dyad position corresponds to one of the local maxima. Only every other local maxima is compatible with a stereochemically allowed solution (‘3:7 rule’). (B) Superposition of TS and BS profiles aligned using the real (known) position of the dyad. (C) Superposition of TS and BS profiles aligned using a stereochemically forbidden putative dyad position.

The accuracy of our method clearly depends on the quality and signal-to-noise ratio of the data. For example, for the 601TA-NUC nucleosomes from the data obtained in this study the dyad position could be reproduced with an accuracy of 0.5 bp (Figure 7A). The higher than single base pair resolution accuracy stems from the fact that dyad could be potentially located not only at a certain base pair position but also between two adjacent base pairs, although the latter possibility has not been seen in the X-ray structures so far. However, it is worth noting that the position of the dyad in nucleosomes in solution is an intrinsically statistical characteristic, and for palindromic sequences it is expected that an average position would be between the two base pairs (as discussed earlier for NCP146).

It is important to note that our dyad identification approach is robust with respect to systematic experimental biases, for example, those originating from minor DNA cleavage products as described in the previous section. These biases are usually the same for the top and bottom strands and the similarity of DNA conformation in nucleosome due to pseudo-symmetry should still translate to the similarity of experimentally measured cleavage profiles.

Modeling of yeast CEN3 nucleosome by an integrative approach

We employed the method outlined in the previous section to determine the dyad position in an in vitro reconstituted S. cerevisiae centromeric nucleosome from chromosome III (CEN3-NUC) and to build its structural model. To this end HRF profiles for both DNA strands resulting from three independent experiments were analyzed (Figures 6; Supplementary Figures S9 and 10) following our proposed method. We illustrate the application of our approach to this dataset below.

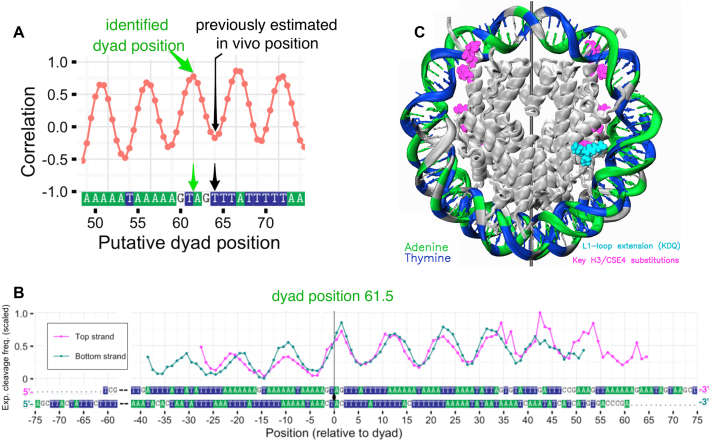
Various putative positions of the nucleosome dyad were sampled and tested as described previously. The specific region of interest was located in the vicinity of position 64, which was suggested in earlier MNase-seq experiments to be the center of the MNase resistant region occupied by corresponding centromere nucleosome in vivo (24). The correlation analysis (Figure 8A and B; Supplementary Figure S12) revealed several candidate dyad positions with high correlation between the aligned profiles (positions 61.5, 67 and 72). Position 67 was discarded as violating the ‘3:7 ratio rule’ as is evident after looking at the HRF profiles’ alignment (Supplementary movie SM2). There were two other candidate positions 61.5 and 72 with the same correlation coefficient of R = 0.78. However, position 61.5 provided a better match between DNA top and bottom strand profiles in the region around the dyad (and thus it may be considered a better candidate for the dyad). Importantly position 61.5 is located much closer to our original region of interest based on in vivo estimated position of the dyad (position 64).

Figure 8.

Dyad identification algorithm applied to CEN3-NUC nucleosome with unknown dyad position. (A) Pearson correlation coefficient between top (TS) and (BS) strand experimental HRF profiles as a function of putative dyad position; the position of the dyad consistent with HRF data (green arrow) and previously in vivo estimated position from the center of MNase-resistant region (24) (black arrow) are shown. (B) Superposition of TS and BS profiles aligned using the newly identified position of the dyad. (C) Model of CEN3-NUC nucleosome constructed using the DNA positioning identified from HRF experiments (dyad set at position 61). DNA strands are colored according to their sequence highlighting AT-tracts: A—green, T—blue, G or C—gray.

All available X-ray structures of nucleosomes support the dyad position at a specific nucleotide and not between them. At the same time, as discussed earlier, the average location of the dyad at a half-integer position is possible for an ensemble of nucleosomes in solution especially in the case of palindromic sequences. Correlation coefficient analysis favored position 61 as the primary one (Figure 8A) and it was further used to construct a precise model of CEN3-NUC nucleosome (Figure 8C and Supplementary movie SM3).

The knowledge of the precise location of the dyad allows for the first time to view the spatial relationship between the key DNA and protein elements that define the function of centromeric nucleosomes in yeast. Both A-tracts of the DNA and key residues of the Cse4p histone were shown previously to be crucial for the function of centromere in yeast, however, their collective engagement remains elusive (57,58).

DISCUSSION

In this work, we performed HRF experiments on two nucleosome systems and developed a computational framework: to analyze HRF data obtained from experiments on nucleosomes in solution; to interpret HRF data by comparison with theoretical H-SASA profiles; and to identify the precise DNA positioning from the HRF data. Using the advanced analysis of nucleosome structures combined with quantification of HRF experimental data we were able to rationalize the interpretation of HRF experiments at a conceptually new level. This in turn led to a development of the straightforward method for determining the nucleosome dyad position with single base pair resolution. We employed this method to determine the dyad position in an in vitro reconstituted centromeric nucleosome of S. cerevisiae and to build its structural model.

The dyad identification algorithm proposed in this study is based on the symmetry relationship between the two strands of nucleosomal DNA. We showed that this symmetry requirement translates directly into the similarity between HRF profiles of the top and bottom DNA strands. Using this criterion and experimental data for two DNA strands improves the accuracy and robustness of the dyad identification method as compared to the situation when HRF profile for each strand is analyzed separately. The latter approach has so far been used in several previous studies, which mainly resorted to reporting approximate dyad locations (15,19,21,59,60). The identification of the dyad position at single base pair resolution was previously achieved by site-directed hydroxyl-radical scission or site-specific photochemical cross-linking (61,62). However, these methods require chemical incorporation of specific probes into a histone octamer at symmetric positions and the dyad is then determined as the midpoint between the reaction sites. The method outlined in this paper provides a single base pair resolution using conventional HRF experimental data without the need for costly histone modifications.

As a proof of concept we estimated the DNA positioning in an in vitro CEN3-NUC nucleosome, which was found to be ∼3 bp away from the previously estimated in vivo position of the center of the MNase-resistant region (24). The precisely determined dyad position enabled us to build a model of this nucleosome and revealed the spatial relationship between the orientation of DNA sequence and key protein motifs on Cse4p (Figure 8). Our model can serve as the basis for the future studies aimed at understanding the cooperative engagement and interplay between Cse4p protein and the A-tracts of CEN sequences.

Currently, it is known that the CEN sequences are not conserved between different chromosomes in yeast, but their A-tract composition is crucial for viability (57). However, the molecular mechanism(s) of A-tract engagement in yeast centromere function remain unclear. One aspect might be the specific geometry of DNA conferred by A-tracts that are known for their conformational rigidity and narrow minor grooves both in free DNA (56) and in the nucleosome (63). Unlike conventional histone H3, variant Cse4p lacks arginine residue (substituted with serine R63S153) that in the case of H3 is inserted into the DNA minor groove around position ±15 (Supplementary movie SM3). This position is known to be adjacent to a unique histone motif, which enforces an extremely narrow minor groove via a hydrophobic ‘sugar clamp’ (64). On the other hand, it is known that TnAn motifs (as opposed to A_nT_n and contrary to A-tracts) display widened minor grooves at TpA dinucleotides (54). Highly AT-rich CEN sequences usually have several A-tracts that are separated by TpA dinucleotides and thus CEN sequences also contain several T_nA_n–like motifs. These motifs may contribute to functionally important widening of the minor groove at the respective sites.

Interestingly, according to our structural model of centromeric nucleosome, the CEN3 sequence is quasi-palindromic near the determined 61.5 dyad position. The AAAGTAGTTT sequence found at the dyad can be converted into a perfect palindrome with only 1 nt substitution. Further, the 4 nt at the dyad (GTAG) are flanked with DNA segments exclusively consisting of A or T rich in A-tracts (Figure 8). These structural data might further provide understanding of the centromeric nucleosome structure and functional binding to key kinetochore proteins such as yeast Mif2 (human CENP-C), which binds preferentially to AT-rich DNA of yeast centromeric nucleosomes (Xiao et al., unpublished data).

Apart from identification of the dyad position, HRF experiments can be used to further advance our understanding of DNA conformation in nucleosomes. The possibility to do this, however, depends on our ability to map the shape of HRF profiles to the structural details of the nucleosome. Understanding the discrepancies between theoretically derived H-SASA and experimental HRF profiles for known structures is an important step in this direction. Our comparative analysis of H-SASA and experimental HRF profiles revealed that, while their overall periodicities are similar, the experimental profiles are much smoother and might have different magnitude and/or exact locations of maxima and minima. The difference between theoretical and experimental profiles have also been seen in a previous study of DNA–TBP complex: the H-SASA values for certain nucleotides were close to zero, while a certain amount of cleavage was still detected experimentally (27). A considerable probability of DNA cleavage at DNA-binding sites might be the result of non-linear dependence of cleavage frequency on solvent accessibility. In fact, previous studies showed detectable cleavage probabilities through abstraction of hydrogen atoms with the vanishingly small SASA (25). However, the substantial contribution likely comes from nucleosomal dynamics and conformational heterogeneity (65,66). The nucleosomal DNA in solution has been suggested to occupy a number of DNA twist-defect states (67). In the course of HRF experiments, an ensemble of nucleosomes in solution with different conformations will be available to hydroxyl-radical attack at any given moment. Additional conformational variations may also result from differences in DNA positioning captured during the nucleosome reconstitution process (68).

One important aspect is the appearance of identifiable local maxima on the experimental profile spaced 10–11 bp apart—one per turn of nucleosomal DNA whereas in H-SASA profiles 7–8 nt DNA turn are almost equally accessible. The possible explanation may come from the imperfections of H-SASA model to approximate the complex physics and chemistry of DNA scission. In particular, as highlighted by Begusova et al. the diffusion controlled nature of the hydroxyl-radical attack reaction and rapid decay of radicals due to interaction with other atoms should make the scission probability dependent not only on the local accessibility of hydrogen atoms, but also on the overall shape of the molecule, which will govern the flux of the radicals that can reach a given site on DNA from solution (28,29). Moreover, electron density distribution of the target molecule has to be considered to correctly describe the reaction of hydroxyl-radical attack. Various multistage reaction pathways might also contribute to the chemical complexity, for instance, mechanisms of DNA scission through secondary histone radicals have also been reported (69).

Since the pioneering studies of the Wolffe and Tullius laboratories in the early 1990's on nucleosomal DNA periodicity in solution based on HRF experiments (15–17,70) high resolution X-ray structures of NCP have become available (2). The periodicity of the DNA in nucleosomes is an important parameter due to its implications in DNA supercoiling as exemplified by the ‘linking number paradox’ (71). Our study, through the simultaneous analysis of rTw, H-SASA and experimental HRF profiles allows examining the theoretical basis of using HRF experiments to determine DNA periodicity. The results of our analysis currently warrants caution in using the locations of maxima or minima on the experimental DNA cleavage frequency profiles to measure the nucleosomal DNA periodicity with the high precision (better than 1 bp/turn). As we showed, profile minima on rTw and H-SASA profiles are not in register and the locations of minima can differ by ±1/±2 bp due to the variations in local histone–DNA interactions (Figure 3). The maxima, on the other hand, on the experimental DNA cleavage frequency profiles might be affected by local dynamics of DNA, the nature of the allowed twist defects, other dynamic effects as well as some sequence specific cleavage irregularities (local spikes as seen in Figure 6). Additionally, minor slowly migrating DNA cleavage products might skew the shape of the profiles (see ‘Results’ section). Further research might deconvolute contributions from these effects to the fine details of the shape of HRF profiles.

Taken together our study provides a new robust approach to the analysis and interpretation of data from DNA hydroxyl-radical cleavage experiments of nucleosomes, the determination of DNA positioning at single base pair resolution and the construction of high-precision molecular models of unknown nucleosomes. Such models reveal the unique spatial arrangement between histone and DNA sequence features and may form the rational basis for structural understanding of interactions between nucleosomes and other chromatin proteins. Given the analogy between HRF and oxidative DNA damage in cells, results of this study can be further used to rationalize the influence on nucleosomes on DNA damage at single base pair resolution.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Intramural Research Programs of the National Library of Medicine and the National Cancer Institute, National Institutes of Health; Russian Science Foundation [14–24-00031] (agreement number 14-24-00031-p, development of nucleosome visualization algorithms); Howard Hughes Medical Institute Janelia Research Campus (to C.W.); Johns Hopkins University Bloomberg Distinguished Professorship (to C.W.); US–Russia Collaboration in the Biomedical Sciences National Institutes of Health visiting fellows′ program (to A.S.). Funding for open access charge: Intramural Research Program of the National Library of Medicine. This work utilized the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov).

Conflict of interest statement. None declared.