Enhanced estimations of post‐stroke aphasia severity using stacked multimodal predictions

Abstract

The severity of post‐stroke aphasia and the potential for recovery are highly variable and difficult to predict. Evidence suggests that optimal estimation of aphasia severity requires the integration of multiple neuroimaging modalities and the adoption of new methods that can detect multivariate brain‐behavior relationships. We created and tested a multimodal framework that relies on three information sources (lesion maps, structural connectivity, and functional connectivity) to create an array of unimodal predictions which are then fed into a final model that creates “stacked multimodal predictions” (STAMP). Crossvalidated predictions of four aphasia scores (picture naming, sentence repetition, sentence comprehension, and overall aphasia severity) were obtained from 53 left hemispheric chronic stroke patients (age: 57.1 ± 12.3 yrs, post‐stroke interval: 20 months, 25 female). Results showed accurate predictions for all four aphasia scores (correlation true vs. predicted: r = 0.79–0.88). The accuracy was slightly smaller but yet significant (r = 0.66) in a full split crossvalidation with each patient considered as new. Critically, multimodal predictions produced more accurate results that any single modality alone. Topological maps of the brain regions involved in the prediction were recovered and compared with traditional voxel‐based lesion‐to‐symptom maps, revealing high spatial congruency. These results suggest that neuroimaging modalities carry complementary information potentially useful for the prediction of aphasia scores. More broadly, this study shows that the translation of neuroimaging findings into clinically useful tools calls for a shift in perspective from unimodal to multimodal neuroimaging, from univariate to multivariate methods, from linear to nonlinear models, and, conceptually, from inferential to predictive brain mapping. Hum Brain Mapp 38:5603–5615, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Each year, stroke affects 800,000 people in the United States and 15 million people worldwide [Mackay et al., 2004; Mozaffarian et al., 2015]. An estimated one third of stroke survivors are left with permanent language deficits, commonly known as aphasia. Given the dramatic consequences of aphasia on life quality, tools that permit the prediction of aphasia severity and the potential for therapeutic intervention represent a major clinical goal.

The initial discovery that lesions of specific brain areas cause specific aphasic symptoms [Broca, 1861] has led to careful investigation of the relationship between lesion location and the severity of aphasia deficits. The importance of lesion location as a determinant of post‐stroke aphasia is also reflected in translational models that aim to predict aphasia severity [Basilakos et al., 2014; Hope et al., 2013; Seghier et al., 2015; Wang et al., 2013; Yourganov et al., 2015]. However, there is evidence that lesion location provides only a partial picture of the factors that contribute to cognitive performance after stroke [Carter et al., 2012; Hope et al., 2016; Kuceyeski et al., 2016; Willmes and Poeck, 1993]. This is likely because performance does not depend solely on the “missing” parts of the brain, but also on the structural and functional integrity of the remaining tissue, which can support the functional reorganization of language processes [Carter et al., 2012; Corbetta et al., 2005; Crofts et al., 2011; Rorden and Karnath, 2004; Saur et al., 2006; Siegel et al., 2016; Turkeltaub et al., 2011; Wu et al., 2015a]. Consequently, proper prediction of aphasia scores requires the integration of multiple neuroimaging modalities, each describing a different property, spanning from lesion maps to structural disconnections, and from pairwise connections to network properties [Carter et al., 2012; Crofts et al., 2011; Duncan and Small, 2016; Grefkes and Fink, 2014].

Although rich multimodal datasets are becoming increasingly available, the creation of predictive tools is hampered by methodological limitations. For example, neuroimaging data are often analyzed with a mass‐univariate approach, in which individual voxels (or brain regions) are tested for a relationship with behavior. This strategy increases type I errors [Bennett et al., 2009; Eklund et al., 2016] and ignores the hodologic properties of the brain, that is, interactions. In principle, no area of the brain acts in isolation without sending or receiving signals to or from other areas. This means that cognitive processes are likely to emerge from multivariate signal interactions that cannot be captured when considering each area in isolation [Medaglia et al., 2015; Price et al., 2016; Turken and Dronkers, 2011]. In voxel‐based lesion‐to‐symptom (VLSM) analyses, the mass‐univariate approach not only misses the interaction between lesioned brain areas but also produces displaced results along the vascular anatomy [Mah et al., 2014]. This may lead to wrong theoretical conclusions, and add to the current irreproducibility crisis in science [Collins and Tabak, 2014; Open Science Collaboration, 2015].

The linear models used for analyses (i.e., t‐tests, linear regressions, ANOVAs) pose another limitation since they rely on the assumption that brain behavior relationship must be linear. Examples from the literature suggest that brain‐behavior relationships are not necessarily linear. For example, Wang et al. [2013] performed curve estimation on patients with post‐stroke aphasia and found a nonlinear relationship between lesion load and aphasia severity. Similarly, Saur at al. [2006] found that the contralesional healthy hemisphere follows a nonlinear activation pattern during recovery. To detect these nonlinear relationships new analyses methods should be adopted which do not make strong assumptions on brain‐behavior relationships.

The creation of predictive models from neuroimaging data is also limited by the large number of predictors (i.e., voxels or brain regions) and the small number of subjects. This scenario increases dramatically the risk of overfitting; that is, the model cannot generalize well to new cases. To avoid overfitting, researchers use data reduction strategies such as preselection of relevant variables. However, many studies use statistical significance as a proxy for predictive power, a strategy that may produce poor predictive models since the most significant variables are not necessarily the best predictors [Lo et al., 2015].

The limitations mentioned above demonstrate a legitimate need for new approaches that can achieve multimodal integration, multivariate analyses, nonlinear modeling, and minimal overfitting. We propose a predictive framework of aphasia scores that utilizes data from three imaging modalities (lesion maps, structural connectivity, and functional connectivity) and produces a combined multimodal prediction; we refer to this approach as stacked multimodal prediction (STAMP). Two key elements characterize the STAMP framework: random forests (RF) and prediction stacking. RF is particularly well‐suited for our purpose because it overcomes the limitations of traditional statistical methods. RF can (1) detect linear and nonlinear relationships, (2) detect variable interactions, and (3) utilize a large number of variables with minimal overfitting [Kuhn and Johnson, 2013]. Prediction stacking is an enhancement method through which preliminary predictions from different sources are combined together in a final prediction [Breiman, 1996; Wolpert, 1992]. Using these tools on a sample of 53 chronic stroke subjects with aphasia, we found that multimodal integration yields more accurate predictions than any single modality alone.

METHODS

Subjects

Subjects were part of an ongoing project investigating the mechanisms of language disruption and recovery following left hemispheric chronic stroke [Mirman et al., 2015; Schwartz et al., 2011, 2012; Zhang et al., 2014]. Only subjects with available neuroimaging data were included in the study, consisting in a sample of 53 subjects (age: 57.1 ± 12.3 yrs, post‐stroke interval: 20 ± 21 months [range: 2–76], 25 female). The project was approved by the authorized Institutional Review Board, and all subjects gave informed consent. At the time of testing, all subjects were medically stable, without major psychiatric disorders, premorbidly right‐handed, native English speakers, and tested for adequate hearing and vision abilities.

Aphasia Batteries

Language performance was assessed with: (1) the Philadelphia naming test (PNT) [Roach et al., 1996], a 175‐item test of picture naming widely used to measure naming accuracy and error patterns in aphasia [Schwartz et al., 2009]; and (2) the Western aphasia battery (WAB) [Kertesz, 1982], a popular clinical assessment that yields a number of measures of language performance. For the present study we used the number of correctly named pictures (PNTcorrect), the global rating of aphasia severity (aphasia quotient: WABAQ), the repetition score (WABrep), and the comprehension score (WABcomp). The four aphasia scores showed medium to strong correlation with each other (range: 0.53–0.87). The mean, range, and distribution of these scores are displayed in Figure 1B.

Figure 1.

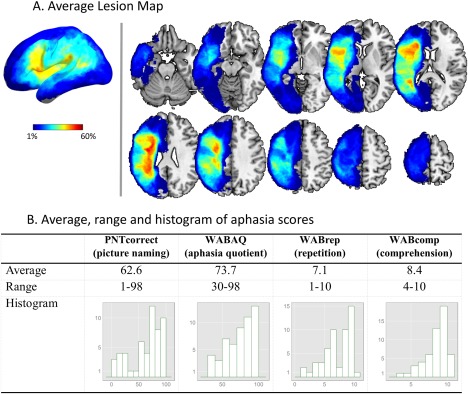
(A) Surface and slice views of the average lesion map. (B) Average, range, and histogram, of true aphasia score measured from patients. [Color figure can be viewed at http://wileyonlinelibrary.com]

Image Acquisition

Neuroimaging data were collected during an 8‐year span (2007–2015) using a Siemens Trio 3T scanner. Two acquisition sequences were collected for this study: a structural T1‐weighted and a functional resting BOLD (blood oxygenation level dependent). A third modality was imputed by generating virtual tractography lesions (see paragraph “virtual tractography lesions”). The T1 volume was acquired with a 3D inversion recovery sequence, 160 axial slices, TR = 1,620 ms, flip = 15°, inversion time = 950 ms, TE = 3.87 ms, FOV = 192 × 256 mm², voxel size = 0.98 × 0.98 × 1 mm. The BOLD sequence was acquired with a 2D sequence, consisting of 48 axial slices acquired with a TR = 3 s, TE = 30 ms, FOV = 192 × 192 mm², flip = 90°, voxel size = 3 × 3 × 3 mm, 100 volumes, 5 min acquisition. The BOLD sequence was repeated twice for each subject, and the two runs were later concatenated during preprocessing. Visual inspection was performed an all imaging data and no subject with excessive head motion was allowed in the study.

Manual Lesion Drawing

Lesions were drawn slice by slice on the T1 image using MRIcron software (http://www.mricro.com/mricron/) in multiview mode, such that the shape of the lesion could be understood from multiple orientations. A single expert (HBC) drew the lesions or reviewed the tracings completed by individuals he had trained. Figure 1A displays the average lesion map of the 53 patients.

Image Processing

Image processing was performed on a server cluster using ANTs and ANTsR software [Avants et al., 2011, 2015]. T1‐weighted images were skull‐stripped (“antsBrainExtraction.sh”) and registered to the template using a multi stage nonlinear registration (“antsRegistrationSyN.sh”). During the registration, cost function masking was applied to remove the lesioned area from computations. The template of reference was derived from 208 elderly individuals and is publicly available [Pustina et al., 2016b].

A publicly available template was used to parcellate the brain in 268 areas. The parcellation was achieved by grouping voxels with similar functional connectivity in a dataset of 45 healthy individuals [Finn et al., 2015].

The overview of the analysis pipeline is shown in Figure 2.

Figure 2.

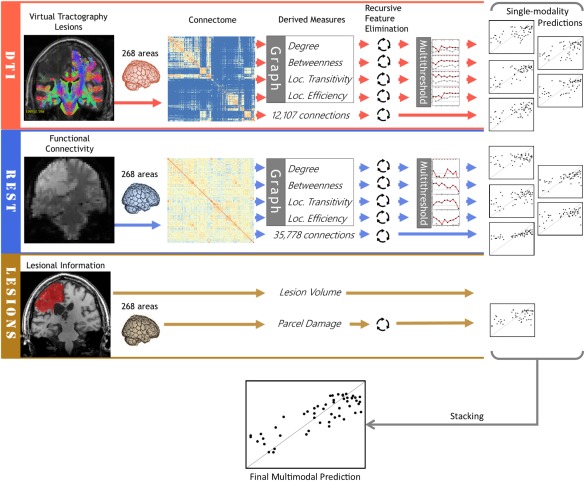
Overview of the analyses pipeline. [Color figure can be viewed at http://wileyonlinelibrary.com]

Lesion Load

Lesion load in each of the 268 brain parcels was computed by counting the number of lesioned voxels in each region and dividing by the total number of voxels in the region. Healthy regions that were not damaged in any subject were removed, reducing the number of regions to 72. The array of lesion load values was used to obtain a single prediction of aphasia for each score.

Virtual Tractography Lesions

All tractography computations were performed in MRtrix3 [Tournier et al., 2012] using the IIT HARDI template [Varentsova et al., 2014]. The template provides a fiber orientation distribution map derived from 72 healthy individuals. Since diffusion data were not available for our patients, we performed virtual tractography lesions using the following two steps. First, whole brain tractography was performed on the IIT HARDI template by seeding 70 million streamlines in the GM/WM border (“‐act” option, max angle = 45°, step size = 1 mm, min length = 2 mm, max length = 250 mm, method = iFOD2). The original number of streamlines was reduced to 10 million by applying an algorithm which eliminates tractography artifacts and guarantees a better match of the tractogram with the underlying diffusion signal (SIFT, spherical‐deconvolution informed filtering of tractograms) [Smith et al., 2013]. In a second step, the tractogram obtained from the template was virtually lesioned for each subject individually by removing the streamlines that entered the respective lesion mask. This procedure simulates the disconnections caused by stroke lesions (for a similar approach, see [Hope et al., 2016]). Once the virtually lesioned tractogram was obtained, a 268 × 268 connectome matrix was computed by counting the number of streamlines connecting each pair of regions in the parcellation template. In the following sections, this modality is named DTI (diffusion tractography imaging).

Resting State Connectivity

Resting BOLD data were preprocessed with a dedicated ANTsR pipeline to account for stroke lesions (available at https://github.com/dorianps/strokeRest). Preprocessing involved: (i) removal of the first 4 volumes to allow for steady state stabilization of the BOLD signal, (ii) motion correction using the average subject‐specific bold signal as reference (repeated twice to improve calculation of the bold average), (iii) fusion of the two runs in a single timeseries using a fourth order polynomial, (iv) motion scrubbing to eliminate volumes with frame displacement over 0.3 mm, (v) nuisance regression to remove spurious signals (white matter, CSF, motion parameters, global intensity), (vi) nuisance regression based on the CompCor algorithm with four components [Behzadi et al., 2007], (vii) band‐pass frequency filtering (0.009–0.08 Hz), and (viii) 5 mm Gaussian smoothing. The area under the lesion was removed during the calculation of nuisance regressors to account for uncertainties during the tissue segmentation process (i.e., WM can be assigned to GM). After preprocessing, a 268 × 268 connectome matrix was created by computing Pearson correlations between the average signals in each region pair of the parcellation template. In the following sections, the functional resting state data is named “resting BOLD” or “REST.” Quality control sheets were created for each subject, and visually inspected by two authors (DP and JDM). Three cases were excluded from the initial pool of available subjects (N = 56) because of severe motion artifacts that clearly affected the connectome matrices.

Graph Theory Measures

Weighted undirected graphs were obtained from DTI and REST connectomes, and four measures were extracted from each modality: (1) degree, (2) betweenness, (3) local transitivity, and (4) local efficiency [for an explanation of graph measures see Bullmore and Sporns, 2009]. Each of the graph measures obtained from each modality was used to derive a separate prediction of aphasia scores. These predictions were named by concatenating the modality and the measure names (e.g., DTI_deg, DTI_bwn, DTI_loc, DTI_eff, REST_deg, etc.).

Raw Connectivity

Beside graph measures, a separate prediction of aphasia severity was derived from raw pairwise connectivity values (i.e., the upper triangle of the connectome matrix). For REST, the number of pairwise connections was 35,778. For DTI, the connections that were not lesioned in any subject were removed, leaving 12,107 pairwise connections. The resulting aphasia predictions were named by appending the word “mat” to each modality: DTI_mat and REST_mat.

Variable Selection and Predictive Models

All predictive models were built using random forests [Breiman, 2001]. RF rely on an ensemble of decision trees. Within each tree, simple decisions are made to split the sample into groups with similar outcome (e.g., if Broca's area is lesioned above 50%, then subjects fall in a group with average fluency score of 30). Splits are performed recursively to create smaller groups with more refined averages, until the full relationship between input variables and the output variable is captured. Each tree is presented with a random subset of subjects (typically 2/3, sampled with replacement), and splits are made using a random subset of the variables (typically, 1/3, randomly selected). This creates slightly different decision trees, and, therefore, different predictions of new cases. However, the predictions from all trees are averaged together into a powerful forest prediction. We used the “randomForest” R package with default parameters (500 trees, mtry = 1/3 variables, nodesize = 5).

While RF is robust to overfitting, the prediction accuracy may suffer from the presence of many irrelevant variables. To remove irrelevant variables we utilized the recursive feature elimination (RFE) procedure [Kuhn and Johnson, 2013]. RFE gradually removes variables in steps predefined by the user. The variables to remove are determined by their “variable importance” (VI) score within random forests. VI is computed on out‐of‐bag data, that is, data that were not used during the creation of the branch/tree, and therefore VI is inherently crossvalidated. However, RFE adds another layer of crossvalidation by running a 10‐fold split, such that variable selection is performed on 90% of the subjects. Once all elimination steps are performed on this 90%, the remaining 10% is used to obtain the prediction error for each step. The step with least prediction error identifies the optimal number of variables. The identity of the winning variables is finally obtained by ranking the variables by their VI scores from all folds. To further enhance stability, we repeated the above procedure 10 times, each time with a different 10‐fold split, and performed variable selection from average scores of all repetitions. We also allowed a tolerance of 4% on the prediction error, such that, a step with fewer variables could be selected if the error did not increase more than 4% from the step with minimal error.

We applied RFE to three types of data: lesion data (P = 72 variables), graph measures (P = 268 variables), and raw pairwise connectivity (P = 35,778 for REST, and P = 12,107 for DTI). The steps used during RFE were larger at the beginning (i.e., in the thousands for pairwise connections) and gradually smaller as the number of variables was reduced (i.e., in the hundreds and tens, see exact steps in “Supporting Information—RFE steps”).

Predictive Brain Mapping

Variable selection allows both the optimization of the predictive model and the identification of topologic information about the brain regions participating in the prediction. Such “predictive” brain mapping can be used to understand functional specialization in the brain in a similar way “inferential” brain mapping is used (i.e., VLSM maps). To assess whether predictive brain mapping produces congruent information with more traditional methods we compared RFE maps with VLSM maps. RFE maps were obtained by using lesion load information to select which brain regions from the 72 available participated in the prediction. VLSM was performed on the same four behavioral scores using typical parameters found in earlier studies from our group [Mirman et al., 2015; Schwartz et al., 2009]. Specifically, massive t‐tests were run, one at each voxel, to create a whole brain t‐map. Voxels lesioned in less than 10% of the subjects were excluded from the analyses [Sperber and Karnath, 2017], and results were thresholded at α = 0.05 (FDR corrected for multiple comparisons) [Benjamini and Hochberg, 1995]. Note, VLSM and RFE analyses are very different in nature: one on voxels, the other on regions; one univariate, the other multivariate; one using linear t‐tests, the other using nonlinear random forests, etc. However, as the underlying data are the same, we expected some spatial congruency.

From Unthresholded to Multithreshold Graph Predictions

Current research standards assume that weighted graphs do not require thresholding of connectome matrices [van den Heuvel et al., 2010]. We ran preliminary tests to establish whether thresholding has an effect on the predictive power of graph measures. Ten predictions were obtained for each graph measure, each with connectomes thresholded between 10% and 100% in steps of 10%. For each threshold, RFE was performed and predictions were obtained with a 10‐fold crossvalidation. These preliminary tests showed that more accurate predictions could be obtained with thresholded graph measures (see “Supporting Information—Graph Thresholds”). Hoewever, we could not identify a single threshold to optimize all measures; for example, one measure benefitted from a threshold of 0.9, while another benefitted from a threshold of 0.3. Instead of using the “winning” threshold for each measure, we performed multithreshold prediction stacking. That is, we used the predictions obtained from each threshold as inputs to a second RF model that combined them in a multithreshold prediction. This procedure eliminated the need for determining optimal thresholds. Compared to the optimal threshold, the multithreshold prediction showed minor decreases in accuracy, while many REST graph theory measures showed more accurate predictions with multithreshold stacking than with the best single‐threshold prediction (see “Supporting Information—Multithreshold Results”).

Final STAMP Predictions

Single‐modality measures yielded 11 preliminary predictions: five from DTI (four from graph theory, one from pairwise connectivity), five from REST (four from graph theory, one from pairwise connectivity), and one from lesion patterns. Given the numerous reports of a strong relationship between lesion size and aphasia scores [Dell et al., 2013; Fridriksson et al., 2016; Hope et al., 2013; Kertesz et al., 1979; Schwartz et al., 2009; Wu et al., 2015b], we added lesion size as a twelfth predictor. These 12 variables were submitted to a final RF model to create a single final stacked multimodal prediction (STAMP, or “Final_All”). Age and post‐stroke duration were not included as predictors because earlier work on the same data showed no appreciable benefit [Pustina et al., 2016a]. Beside the “Final_All” prediction, another prediction was obtained by running RFE on the 12 predictors and selecting the most useful ones (“Final_RFE”). The entire process, from deriving preliminary predictions to the final STAMP combination was repeated 20 times, each time with a different 10‐fold split. Pearson correlations were computed between predicted and true values for single‐modality and multimodal predictions. The correlation scores of the 20 runs were Fisher‐z transformed and submitted to paired Wilcoxon tests (single tailed) to assess whether the combined multimodal prediction showed a systematic advantage over the best single modality prediction. We also assessed whether the difference in correlation was significant at each individual run (comparison with the Fisher method, “paired.r” function in R). This test is usually more conservative and requires large increases in “r” to become significant because it relies on single observations.

Full Separation of Training‐Test Groups

Although we kept training and test subjects separate at most stages, variable selection was performed using the whole sample (albeit with two layers of cross validation). Proper assessment of the generalizability of results requires a complete separation of the training/testing groups during all stages, including variable selection. The computational costs to achieve this validation were very high for the our pipeline; that is, a single behavioral score with a 10‐fold split requires ∼830 RFEs. However, we performed a single 10‐fold crossvalidation of picture naming, where training and test subjects were never mixed at any stage.

Computational and time considerations

All computations were performed on a computing cluster using Xeon E4–2450, 2.1 GHz CPUs. Most of the steps were performed separately with dedicated scripts (i.e., image preprocessing, feature selection, training, and testing). Each computation was submitted as a single job using one CPU core. Beside the image preprocessing steps, recursive feature elimination was the most time consuming step. RFE required ∼1 h of computations for a single graph theory measure (268 variables), and ∼6–10 h for a single full connectome (∼34,000 variables). The final step which performed 20 different training‐test predictions required ∼1 h per aphasia score. Most of the time in the final step was spent on accessing RFE files from the disk—our pipeline relied heavily on disk files. The above times are only approximate, and depended on the research needs of this project. In practice, a trained STAMP model can be used to predict aphasia scores in just a few minutes.

RESULTS

Figure 3 displays boxplots of the preliminary and final predictions for the four behavioral scores (see also individual predictions in “Supporting Information—Scatterplots”). Overall, STAMP predictions (indicated with an arrow) correlated with true scores in the range r = 0.79–0.88. Table 1 shows the comparison of STAMP with the best single modality prediction. Crucially, STAMP predictions were systematically more accurate than the best single modality prediction. For three of the four behavioral scores (PNTcorrect, WABAQ, WABcomp) the advantage was statistically significant (P < 0.001), while the fourth showed a trend toward significance (WABrep, P = 0.06). The three significant behavioral scores showed also above chance improvements at each run (15–20% of individual runs were significant as opposed to a 5% chance level). Results for each behavioral score are as follows.

Figure 3.

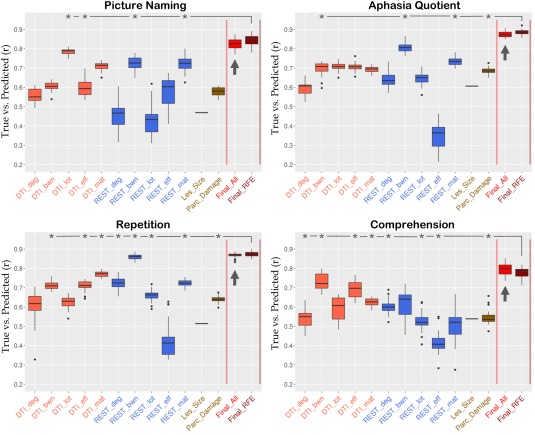
Correlations between true and predicted scores for four aphasia measures. Whisker plots show the distribution of correlations from 20 repetitions with different 10‐fold splits. Boxes extend from 25 th to 75 th percentiles. Whiskers extend to the closest value up to 1.5 times the length of the box itself. Values beyond the whiskers are shown as outliers (single dots). Arrows point to the STAMP predictions. Lesion size shows a single line corresponding to the correlation with the behavioral score (converted to positive for plotting purposes). Asterisks denote the measures selected for the Final_RFE prediction. [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 1.

Predictions results for all four aphasia scores

	STAMP		Best predictor			Paired t‐test (20 runs)	No. single run significants (5%=chance)
	Corr.	RMSE		Corr.	RMSE
Naming PNTcorrect	0.82 (0.03)	15.6 (1.2)	DTI_lot	0.78 (0.02)	17.9 (0.6)	<0.001	20%
Aph. Quotient WABAQ	0.88 (0.02)	9.5 (0.5)	REST_bwn	0.81 (0.03)	11.4 (0.6)	<0.001	20%
Repetition WABrep	0.87 (0.02)	1.16 (0.06)	REST_bwn	0.86 (0.02)	1.3 (0.05)	0.06	0%
Comprehension WABcomp	0.79 (0.03)	0.9 (0.06)	DTI_bwn	0.73 (0.05)	1.02 (0.07)	<0.001	15%

Values show Pearson's “r” and root mean square error (RMSE) of predicted versus true scores. The values in parenthesis show standard deviation of the 20 runs.

For picture naming, the most accurate single‐modality prediction was derived from DTI_lot (r = 0.78). The STAMP predictions produced a small but systematic improvement in accuracy (r = 0.82, P < 0.001). Four single‐modality predictors were selected in Final_RFE (DTI_lot, DTI_eff, REST_bwn, and REST_mat) which yielded another slight increase in accuracy (Final_RFE: r = 0.85 ± 0.03, RMSE = 15.6 ± 1.2). Among the 72 lesion load regions, RFE selected four regions as predictive of picture naming, including the post‐central gyrus and supramarginal gyri and extending into the temporoparietal junction and inferior angular gyrus (Fig. 4A). Visual comparison showed close proximity of RFE regions with peak clusters in the VLSM map (see Fig. 4A). Raw pairwise connections produced highly accurate predictions (DTI: r = 0.71 ± 0.02, REST: r = 0.72 ± 0.04). These scores relied on 160 DTI and 800 REST connections.

Figure 4.

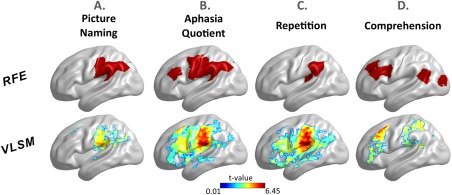
Comparison of RFE and VLSM maps. RFE shows the brain regions used to predict the respective aphasia score, while VLSM shows t‐maps. The results are projected on the brain surface and rendered with BrainNet Viewer [Xia et al., 2013]. [Color figure can be viewed at http://wileyonlinelibrary.com]

For the aphasia quotient, the most accurate single‐modality prediction was derived from REST_bwn (r = 0.81). The STAMP predictions produced a systematic increase in accuracy (r = 0.88, P < 0.001). Four single‐modality measures were selected in Final_RFE (DTI_bwn, REST_bwn, REST_mat, Parc_Damage; r = 0.89 ± 0.02, RMSE = 9.0 ± 0.5). Among the 72 lesion load regions, RFE selected eight regions as predictive of aphasia quotient, which were distributed in the temporo‐parietal junction, pre‐ and post‐central gyri, and inferior frontal cortex (Fig. 4B). These areas were similar to the heatmap distribution of VLSM, with a small displacement in the frontal lobe (Fig. 4B). Raw pairwise connections showed again high predictive accuracy: 50 connections were selected from DTI (r = 0.7 ± 0.02) and 20 connections were selected from resting BOLD (r = 0.74 ± 0.02).

For repetition, the most accurate single‐modality prediction was derived from REST_bwn (r = 0.86). The STAMP predictions produced only a marginal gain in accuracy which did not reach significance (r = 0.87, P = 0.06). Eight single‐modality predictors were selected in Final_RFE (DTI_bwn, DTI_eff, DTI_mat, REST_deg, REST_bwn, REST_lot, REST_mat, Parc_Damage; r = 0.87 ± 0.02, RMSE = 1.13 ± 0.06). Among the 72 lesion load regions, RFE selected two regions as predictive of repetition, both located in the temporo‐parietal junction (Fig. 4C). The VLSM map showed peaks in a similar area, with a slight anterior displacement (Fig. 4C). Raw pairwise connections showed high predictive accuracy, which was achieved from 10 DTI (r = 0.77 ± 0.01, RMSE = 1.5 ± 0.03) and 5 REST (r = 0.72 ± 0.02, RMSE = 1.64 ± 0.03) connections.

For comprehension, the most accurate single‐modality prediction was derived from DTI_bwn (r = 0.73). The STAMP predictions produced a systematic improvement in accuracy (r = 0.79, P < 0.001). Eight single‐modality predictors were selected in Final_RFE (DTI_deg, DTI_bwn, DTI_eff, DTI_mat, REST_deg, REST_lot, REST_eff, Parc_Damage; r = 0.78 ± 0.03, RMSE = 0.95 ± 0.05). Among the 72 lesion load regions, RFE selected five regions as predictive of comprehension, which were distributed in anterior (prefrontal cortex) and posterior (angular gyrus, lateral occipital lobe) areas of the brain (Fig. 4D). The VLSM map showed peaks in close proximity to the prefrontal and temporo‐parietal junction regions, while the occipital region found with RFE was not found with VLSM, and, vice versa, a peak located in the superior parietal lobe with VLSM was not found with RFE. Raw connections were still successful at predicting comprehension, albeit less than with other measures. Five DTI and 5,000 REST connections were selected, which yielded r = 0.62 ± 0.02 (RMSE = 1.17 ± 0.02) and r = 0.5 ± 0.01 (RMSE = 1.38 ± 0.03), respectively.

Connectome‐Based Predictions

The “mat” scores from REST and DTI, which is the raw connectivity score, showed relatively high predictive power for every measurement with the exception of the “comprehension.” This observation raises the question whether STAMP predictions using only these two measurements (DTI_mat and REST_mat) would be equally accurate, without the need to compute graph theory scores. To answer this question, we reran the STAMP pipeline and added a prediction that used only DTI_mat and REST_mat scores. Results showed that, although the combination of the *_mat predictions produced a small boost compared to each individual mat‐score, the combined prediction was less accurate than the Final_ALL prediction which used all single‐modality scores (boxplots are shown in “Supporting Information—STAMP from raw connectivity”).

Fully Separated Training‐Test Groups

A single crossvalidation was performed to obtain picture naming scores from fully separate training‐test groups. Initially, we noticed a major drop in the accuracy of the final STAMP prediction (from r = 0.82 to r = 0.52, Δr = 0.3). Upon decreasing the tolerance value used during variable selection from 4% to 2% (i.e., steps with more variables were selected), predictions improved, yielding a STAMP prediction accuracy of r = 0.66 (a drop of Δr = 0.16 from previous results). Importantly, even in this single run the accuracy of the final STAMP prediction (r = 0.66) was higher than the best single modality prediction (DTI_mat: r = 0.63).

DISCUSSION

We tested a framework for the prediction of aphasia scores from multimodal datasets. Our results showed that the combination of preliminary single‐modality predictions into a stacked multimodal prediction (STAMP) can produce aphasia estimates that systematically exceed the accuracy obtained from each separate modality. These results suggest that superior behavioral predictions can be achieved by combining modern connectomic approaches with a multimodal perspective. Importantly, our results showed that a predictive framework can also be utilized to recover topological information that can be used to make inferences about the functional organization of cognitive systems.

Previous work on post‐stroke aphasia has focused on the relationship between lesion location and language deficits [Basilakos et al., 2014; Bates et al., 2003; Dronkers et al., 2004; Mirman et al., 2015; Schwartz et al., 2009, 2012; Thothathiri et al., 2011]. This relationship, however, may carry only partial information about the factors that contribute to cognitive performance. For example, aphasia deficits have been found frequently to correlate with white matter damage [Dronkers et al., 2007; Forkel et al., 2014; Fridriksson et al., 2013; Marchina et al., 2011; Mirman et al., 2015]. This indicates that interruptions in structural networks might play an important role in aphasia. However, disconnections can occur at any segment along WM tracts, and, consequently, lesions apparently unrelated to each other can cause disruption of the same tract, producing similar symptoms. Supporting this rationale, recent studies have shown that structural disconnections can predict cognitive performance more accurately than lesion location [Hope et al., 2016; Kuceyeski et al., 2015, 2016]. Nonoverlapping lesions can also affect the same functional network, leading to similar clinical syndromes [Boes et al., 2015]. Thus, evidence from the literature shows that lesions of a focal nature can impact brain networks well beyond the lesion itself. In this scenario, cognitive deficits and the potential for recovery depend on factors that go beyond lesion location, such as, disruption of functional networks, disruption of structural networks, functional compensation by domain‐general systems, and plastic reorganization of networks that subserve alternative routes of cognitive processing. In our study, we found that structural and functional networks were frequently more powerful than lesion information at predicting aphasia scores; that is, the best predictors were consistently derived from connectome data rather than lesion size or location (see Fig. 3). From this perspective, our results confirm the advantage of adopting a network perspective [Boes et al., 2015; Carter et al., 2012]. However, STAMP findings go beyond this comparison in showing that multimodal integration has the potential to improve the prediction accuracy beyond any modality and beyond a simple connectomic approach. In this context, the separate predictive power of each modality is not directly informative of the contribution of that modality in the final outcome, because a less accurate prediction can interact with other predictors to yield an enhanced result (i.e., note the selection of DTI_eff over DTI_mat for Picture Naming in Fig. 3). Our results, therefore, suggest that neuroimaging modalities carry complementary information potentially useful for the prediction of behavioral deficits, and that, rather than comparing modalities with each other or selecting the best one, the key choice for enhancing aphasia predictions might be the combination of all information sources.

Although many studies have identified potential biomarkers for the prediction of aphasia, few have attempted to build rigorous predictive models. Among these, Hope et al. [2013] created a model of speech production from 270 subjects and achieved a correlation of r = 0.77 between true and predicted scores. More recently, Yourganov et al. [2016] created predictive models of several aphasia scores from 90 subjects using either lesion or structural connectivity information, and achieved correlation scores in the range r = 0.52–0.72. In another study, Kuceyeski et al. [2016] predicted future cognitive abilities in post‐stroke subjects using virtual tractography lesions, achieving an accuracy of r = 0.75. Compared to the above literature, STAMP showed higher predicted vs. true correlation (r = 0.79–0.88) by integrating multimodal information. The advantage of STAMP might derive from the introduction of prediction stacking, an approach which has been recently shown to improve the predictive accuracy over predictions derived from a single model [Rahim et al., 2017].

One result that requires particular consideration is the drop in accuracy from full‐split validations. This finding shows that variable selection can be a critical step. Broadly speaking, we found that brain regions which are powerful at predicting 90% of the subjects are not equally powerful at predicting the remaining 10%. The use of multiple layers of crossvalidation during variable selection excludes the possibility that this might be caused by analyses choices. The reason, instead, might be interindividual variability [Price et al., 2016]. In the healthy population, substantial individual differences have been shown in cytoarchitectonic maps [Amunts et al., 1999] and resting state networks [Finn et al., 2015]. Interindividual differences in activation maps are so prominent that Fedorenko and coworkers have proposed the use of subject‐specific functional localizers [Fedorenko et al., 2010; Mahowald and Fedorenko, 2016]. The large interindividual variability is also reflected in multimodal parcellations of each subject [Glasser et al., 2016]. Adding to these differences, stroke lesions are very different in size and location from one subject to another. Moreover, recovery from post‐stroke aphasia is different from subject to subject [Hope et al., 2013]. Considering the above evidence, it is not surprising that brain regions of 90% of the subjects might be less powerful at predicting the remaining 10%. This limitation does not undermine the power of multimodal integration since the STAMP prediction was more accurate than the best single modality prediction even after full‐split crossvalidation. Future studies might focus at addressing the problem of interindividual variability with new tools [Chai et al., 2016; Glasser et al., 2016; Wu et al., 2015a]. A large sample size may also increase the chances that similar brain architectures exist in the training and test groups [Price et al., 2010]. It is important to note that all previous studies have performed variable selection on the whole group [Hope et al., 2013; Kuceyeski et al., 2016]. An exception to this trend is the study of Yourganov et al. [2016], who selected the variables only from the training group. However, even in this case variables were first filtered based on group statistics, before running full‐split crossvalidation. Our findings, therefore, raise the possibility that, similar to our main analyses, existing methods described in the literature might be overly optimistic.

Besides providing aphasia predictions, STAMP revealed topological information about the brain areas participating in the prediction. Although an interpretation of topological findings is beyond the scope of this article, it is important to note that the information obtained with RFE was largely congruent with VLSM maps. This finding lays groundwork for the potential replacement of mass‐univariate lesion‐to‐symptom analyses, whose limitations have been articulated by several authors [Kimberg et al., 2007; Mah et al., 2014], with multivariate methods that can capture interactions between brain regions.

In this study we used a novel approach to combine multithreshold graph theory measures. The identification of appropriate thresholds when constructing graph theory measures is an ongoing challenge that has led some authors to propose the use of multithreshold graph measures [Drakesmith et al., 2015]. Our approach, which relies on multithreshold prediction stacking, may offer an alternative solution to the search for threshold‐free graph theory analyses.

Several limitations affect the present study. First, we acknowledge that the results from our main analyses might be overoptimistic, as shown in the full‐split validation. Part of this limitation may have derived by the limited sample size. Note, this does not necessarily undermine the advantage of multimodal integration. Our findings, however, indicate the full‐split validation is a necessary step to assess the true translational value of predictive models. Second, the ultimate aim of any predictive model is longitudinal prediction, which we did not achieve for lack of longitudinal data. The approach described here, however, can be easily extended to longitudinal predictions, either by including baseline neuroimaging data or by including baseline cognitive scores. Based on the work of Hope et al. [2013] the inclusion of baseline cognitive scores can be expected to boost the predictive accuracy. Third, lesion load was computed mainly from cortical areas, while the lesion load of specific white matter tracts was not computed. This might have decreased the predictive value of lesion load compared to the other two modalities. The study, however, aimed at integrating rather than comparing modalities.

In conclusion, we found that the adoption of a multimodal perspective might be key for the successful translation of neuroimaging research into clinical tools. More generally, our findings indicate the necessity of considering brain diseases in their entire complexity through the combination of information from different sources to achieve potentially useful clinical models. To help researchers start with the concepts presented in this article, we have made publicly available the R code used in this study (https://github.com/dorianps/STAMP).

Supporting information

Supporting Information