Predicting Locations of High-Risk Plaques in Coronary Arteries in Patients Receiving Statin Therapy

Abstract

Features of high-risk coronary artery plaques prone to major adverse cardiac events (MACE) were identified by intravascular ultrasound (IVUS) virtual histology (VH). These plaque features are: Thin-cap fibroatheroma (TCFA), plaque burden PB≥70%, or minimal luminal area MLA≤4mm². Identification of arterial locations likely to later develop such high-risk plaques may help prevent MACE. We report a machine learning method for prediction of future high-risk coronary plaque locations and types in patients under statin therapy. Sixty-one patients with stable angina on statin therapy underwent baseline and one-year follow-up VH-IVUS non-culprit vessel examinations followed by quantitative image analysis. For each segmented and registered VH-IVUS frame pair (n=6341), location-specific (≈0.5mm) vascular features and demographic information at baseline were identified. Seven independent support vector machine (SVM) classifiers with seven different feature subsets were trained to predict high-risk plaque types one year later. A leave-one-patient-out cross-validation was used to evaluate the prediction power of different feature subsets. The experimental results showed that our machine learning method predicted future TCFA with correctness of 85.9%, 81.7%, and 77.0% (G-mean) for baseline plaque phenotypes of TCFA, thick-cap fibroatheroma, and non-fibroatheroma, respectively. For predicting PB≥70%, correctness was 80.8% for baseline PB≥70% and 85.6% for 50%≤PB<70%. Accuracy of predicted MLA≤4mm² was 81.6% for baseline MLA≤4mm² and 80.2% for 4mm²<MLA≤6mm². Location-specific prediction of future high-risk coronary artery plaques is feasible through machine learning using focal vascular features and demographic variables. Our approach outperforms previously-reported results and shows the importance of local factors on high-risk coronary artery plaque development.

I. Introduction

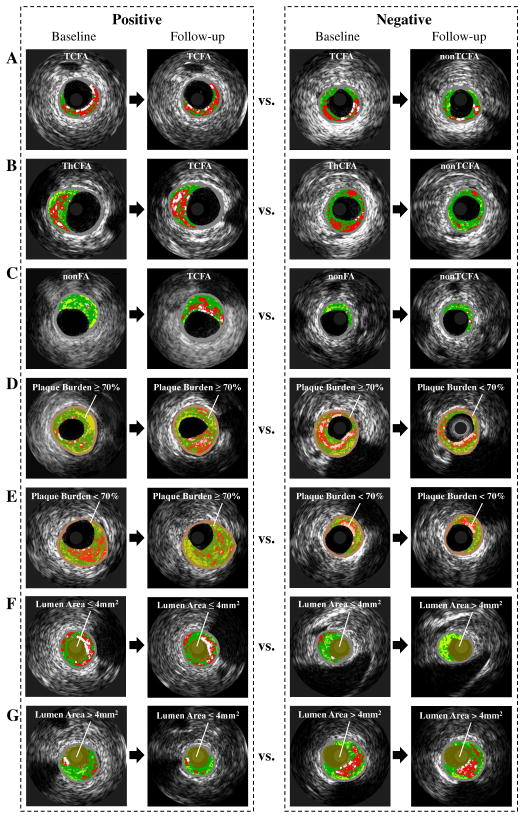
Identification of patients at risk of major adverse cardiac events (MACE) is challenging but has an enormous medical impact [1], [2]. Trials as PROSPECT [3], VIVA [4] and ATHEROREMO-IVUS [5] found that high-risk plaques exhibiting thin-cap fibroatheroma (TCFA), plaque burden (PB) ≥ 70%, and/or minimal luminal area (MLA) ≤ 4.0 mm² are predictors of MACE, as determined by virtual histology intravascular ultrasound (VH-IVUS) [6]–[8]. Although systemic pharmacologic therapies (mostly statins) contribute to regression of coronary plaques [9], [10] (“Negative” panel in Fig. 1 (A), (D), (F)), high-risk plaques (such as TCFA [11], [12]) still remain (“Positive” panel in Fig. 1 (A), (D), (F)). Additionally, some less-advanced plaques continue to progress to more advanced high-risk plaques even under statin therapy (“Positive” panel in Fig. 1 (B), (C), (E), (G)). These residual and newly-occuring high-risk plaques remain responsible for MACE in the future. Early identification of locations, in which high-risk plaques will likely develop in the future, is highly desirable as it will enable patient-specific preemptive strategies (such as more intensive pharmacological treatment in high-risk patients or attempting focal plaque stabilization [13]) to avert MACE.

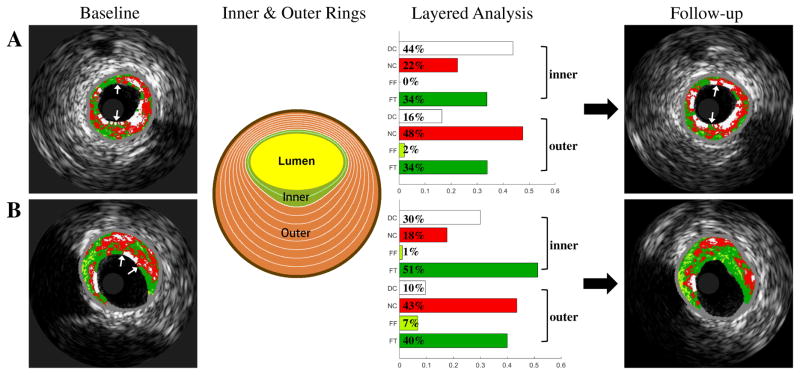
Fig. 1.

Evolution of high-risk plaques, including progression, regression and quiescence of: (A), (B), (C) TCFA; (D), (E) PB≥70%; (F), (G) MLA≤4mm². Plaque tissue compositions are color-coded by virtual histology: dense calcium [DC] (white), necrotic core [NC] (red), fibrofatty [FF] (light green), and fibrotic tissue [FT] (dark green). ThCFA: thick-cap fibroatheroma; nonFA: non-fibroatheroma.

Coronary atherosclerosis is a dynamic process during which focal plaque undergoes progression, regression, or quiescence in an independent manner [14]. Such a dynamic behavior is influenced by many systemic factors and by local vascular factors. Utilizing in vivo vascular imaging tools including VH-IVUS and angiography, efforts have been undertaken to enable the prediction of treated or untreated outcomes of plaques by correlating local vascular factors to plaque progression and vulnerability [11], [12], [14]–[17]. Only a very limited number of studies have reported successful prediction of high-risk plaques showing significant correlation between angiography-IVUS-derived features and TCFA outcome (healed or remaining) [11], [12]. Clearly, predicting whether, and if so, where high-risk plaques (TCFA, PB≥70%, MLA≤4mm²) will remain unchanged or will newly occur remains very challenging.

In order to learn how to prospectively predict high-risk plaques, frame-to-frame registration of baseline and follow-up VH-IVUS pullback data is necessary to facilitate location-specific quantitative comparisons between the two time points. Most previous studies assessed plaque progression in the entire lesions or over long vessel segments [3]–[5], [11], [12], [14], in part because accurate frame-to-frame registration of IVUS pullbacks at two time points was not available [16]. Using such long coronary segments fails to reflect the focal nature of clinical events and leads to excessive averaging of focal plaque morphology/composition indices [17]. Recently, we reported a highly-automated approach for frame-to-frame registration of baseline and follow-up IVUS pullback pairs based on 3D graph-based optimization [18]. Validation on 29 IVUS pullback pairs demonstrated registration performance statistically identical to that of human experts [18], [19]. This registration method is employed here, enabling focal studies of coronary atherosclerosis development. Such focal character of high-risk plaques has not been previously investigated.

Historically, prediction of plaque progression relied on statistical modeling, such as logistic regression [14], [17], generating interpretable results but suffering from lower accuracy compared to algorithmic models employing large numbers of mutually interacting variables [20], [21]. Algorithmic modeling, or machine learning [20], [22] allows estimation of prediction accuracy via cross-validation. Machine learning has been effective in coronary plaque component classification [23], classifying plaque erosion against intact fibrous plaques [24], and predicting disease recurrence or survival [21]. We have previously demonstrated a potential of machine learning for predicting subsequent development of TCFAs [19], [25]. Therefore, we hypothesized that machine learning approaches applied to serial studies of multimodality intravascular imaging data and clinical characteristics from patients allow prediction of future high-risk plaque locations and types. Besides TCFA [19], [25], the current study enables the prediction of PB≥70% and MLA≤4mm², provides more sophisticated methodology including prediction task splitting, uses new VH-IVUS-based features and brings more comprehensive evaluation considering several feature selection and imbalance learning techniques in a larger number of patients with more accurate frame-level registration.

II. Materials and Methods

A. Study Patients and Protocol

61 patients fulfilling inclusion criteria were selected from a database of 121 patients with stable angina pectoris enrolled in one of 2 studies comparing statin therapy for atherosclerosis progression (HEAVEN [26] and PREDICT (NCT01773512), Charles University Hospital, Prague, Czech Republic). Patients were treated with lipid lowering therapy ranging from bnormal intensityb to bhigh-intensityb to cover plaque behavior for the full range of treatment strategies. The inclusion criteria were: (1) R-wave gated VH-IVUS image pullback performed in a native coronary artery with angiographically-determined maximum stenosis ≤ 50% at baseline with no indication for either percutaneous coronary intervention (PCI) or coronary artery bypass grafting (CABG), (2) both baseline and follow-up IVUS-VH pullbacks of good quality, without noticeable pullback speed discontinuity and/or extended regions of calcification shadowing preventing wall boundary detection, at least 30mm long, with at least 25mm of the arterial image overlap between baseline and follow-up pullbacks. The main motivation of choosing 25mm was not to lose too many baseline/follow-up pairs while having a long-enough arterial segment. Major reason for patient exclusion was missing data, including loss of follow-up, damaged/unreadable VH data, and loss of ECG. Additionally, two patients were excluded after baseline/follow-up registration, since no corresponding vessel structures could ensure reliable registration. As such, 61 of 121 enrolled patients satisfied the inclusion criteria. The study protocol conforms to the ethical guidelines of the Declaration of Helsinki, was approved by the Institutional Review Board of Charles University, and all patients provided written informed consent.

IVUS imaging was performed using the phased-array probe (Eagle Eye 20MHz 2.9F monorail, Volcano Corporation, San Diego, CA), IVUS InVision console for the HEAVEN study and s5 console for the PREDICT study, InVision Gold software, and motorized pullback at 0.5mm/s (research pullback device, model R-100, Volcano Corporation) were used in all acquisitions. For each patient baseline/follow-up pair, the same IVUS console was used. After administration of 200μg of intracoronary nitroglycerin, the IVUS catheter was inserted into the target vessel beyond a distal fiduciary point and then pulled back to the aorto-ostial junction. The proximal fiduciary point was the left main bifurcation in the left coronary artery and the first branch or a well-defined calcification in the right coronary artery. Patients underwent repeated angiography with VH-IVUS of the same coronary artery after 8–14 months (mean: 12 ± 2.1 months).

B. Study Design

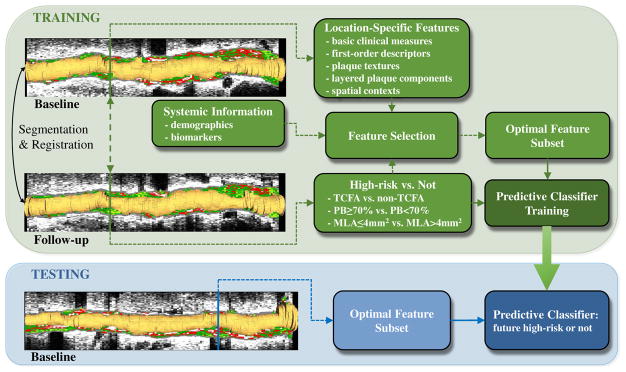
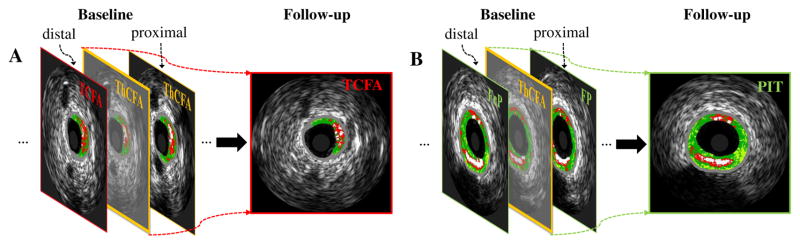
The overall design of training and use of the predictive classifier is shown in Fig. 2. Baseline and follow-up VH-IVUS pullback data are first segmented and mutually registered. The location-specific (frame-level) features and systemic/demographic information at baseline undergo feature selection [27], [28] to form an optimal feature subset. A set of Support Vector Machine classifiers [SVM] [29], [30] is trained to predict focal plaque type at follow-up. To predict three high-risk plaque forms (TCFA, PB≥70%, MLA≤4mm²) at follow-up, seven binary classifiers are trained (Fig. 1):

Fig. 2.

Prediction of future high-risk plaque locations. Lumen shown in orange, plaque tissue composition color-coded by VH. Seven separate classifiers are trained to predict high-risk plaques.

• Three classifiers predict whether focal plaque types (1) TCFA, (2) thick-cap fibroatheroma [ThCFA], and (3) non fibroatheroma [nonFA] at baseline transition to TCFA plaque type or not at follow-up (Fig. 1 (A), (B), (C));

• Two classifiers predict the follow-up plaque burden PB≥70% or not for local plaques with (4) PB≥70% or (5) 50%≤PB<70% at baseline (Fig. 1 (D), (E));

• For plaques with (6) MLA≤4mm² or (7) 4mm²<MLA≤6mm² at baseline, two classifiers predict whether MLA≤4mm² or not at follow-up (Fig. 1 (F), (G)).

In all cases, training and testing sets were disjoint in a leave-one-patient-out (LOPO) cross-validation manner. Each of the 61 training/validation sessions had a different patient bleft outb resulting in a complete separation of training and validation at the patient level and allowing validation on a sufficiently large set b-classification success therefore assessed as average performance of these 61 independently trained classifiers.

C. Segmentation and Registration of Baseline and Follow-Up IVUS Pullbacks

Lumen and external elastic membrane (EEM) borders (surfaces) were automatically segmented in R-wave gated baseline and follow-up IVUS pullbacks using our fully three-dimensional graph-search approach followed by a highly efficient interactive refinement step [31]. The obtained lumen and EEM surfaces/contours were fed into Volcano’s offline VH-IVUS computation software (Volcano Corp., San Diego, CA). A geometrically correct fully 3D representation of the vascular wall surfaces was obtained using our validated two-plane angiography and IVUS data fusion [32]. This 3D model served as a basis for quantitative morphologic analysis and quantitative assessment of plaque composition in every frame of the imaged vessel.

Our validated IVUS pullback registration method established one-to-one correspondences of baseline and follow-up IVUS frame pairs by globally optimizing the registered B-mode image similarity in a geometrically feasible manner [18], [19]. To ensure high registration accuracy for frame-level prediction, we have added a step of semi-automated editing by expert cardiologist. Evaluation on 383 landmarks on 61 patients demonstrated an average registration error of 0.45mm±0.78mm. The registration produced 6,341 registered IVUS frame pairs (46 to 191 frame pairs per patient) with 0.23 to 0.70mm frame-to-frame separation distances between adjacent frames depending on the heart rate. Quantitative indices of plaque morphology and composition were computed in every frame of the registered pullbacks [33] and all registered frames (locations) including those labeled as no lesion (plaque burden < 40%) were included in the prediction experiment.

D. Location-Specific and Patient-Specific Feature Extraction

Two categories of features including location-specific features (m=236) and systemic information (m=18) [3], [14], [34] were extracted to be used for training the prediction classifier (Table I). The location-specific features further contain four sub-types including basic clinical measurements (m=21), first-order descriptors (m=9), plaque textures (m=16), layered plaque components (m=72), and spatial contextual features (m=118). Among them, basic clinical measurements reflect local vascular disease severity and/or plaque development [3], [6], [8], [35], others were inspired by feature descriptors successfully used in computer-aided diagnosis applications (first-order descriptors, plaque textures) [36], [37] or incorporated spatial information in circumferential and axial directions (layered plaque components, spatial contextual features).

TABLE I.

Location-specific features and systemic information used in this study.

Local	Basic Clinical Measures (F1–F21)	Plaque composition: Plaque phenotype, DC/NC/FF/FT [CSA], DC/NC/FF/FT [%], max. confluent NC, max. NC angle, # NC abutting. Plaque morphology: Lumen/EEM/PM [CSA], PB, remodeling index, distance to ostium, mean plaque thickness, std. plaque thickness, eccentricity.
	First-Order Descriptors (F22–F30)	Plaque grayscale intensity: mean, median, std., max, min, mode. Plaque intensity histogram: first, median, third quartiles.
	Plaque Textures (F31–F46)	Contrast, correlation, energy, homogeneity [θ = 0°, 45°, 90°, 135°].
	Layered Plaque Components (F47–F118)	DC/NC/FF/FT [%] in 10%~90% inner & outer rings.
	Spatial Contextual Features (F119–F236)	Average feature value of one adjacent distal and one adjacent proximal frames. Calculate for all F1~F118.
Systemic	Demographics & Biomarkers (F237–F254)	Age, gender, weight, BMI, family history, smoking history, current smoker, hypertension, diabetes, hyperlipidemia, pervious MI, beta-blockers, ACE inhibitors, previous statin treatment, total cholesterol, LDL cholesterol, HDL cholesterol, triglycerides.

DC: dense calcium; NC: necrotic core; FF: fibrofatty; FT: fibrotic tissue; BMI: body mass index; MI: myocardial infarction; ACE: angiotensin-converting enzyme; LDL: low-density lipoprotein; HDL: high-density lipoprotein.

1) Basic Clinical Measurements

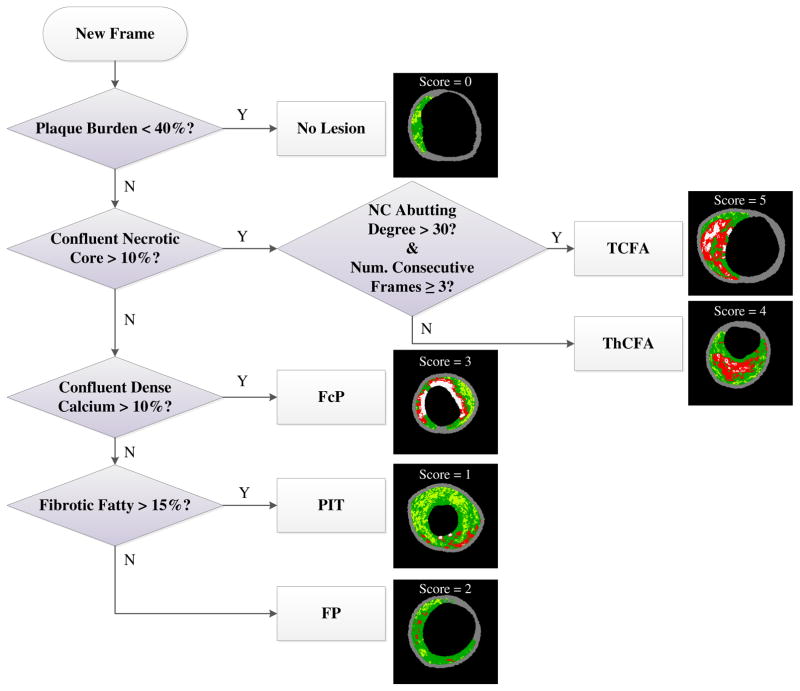
Using quantitative assessment of VH tissue types and lesion classification description [3], phenotypes of all frames were automatically classified into 6 categories (Fig. 3): no lesion [NL], pathological intimal thickening [PIT], fibrous plaque [FP], fibrocalcific plaque [FcP], ThCFA, and TCFA, according to the definitions of American Heart Association’s Committee on Vascular Lesions [38]. Each phenotype was assigned a vulnerability score in the range 0–5 (NL score=0, PIT =1, FP =2, FcP =3, ThCFA =4, TCFA score=5) (Fig. 3) [34]. Confluent NC>10% and NC abutting the lumen>30° in at least 3 consecutive frames defined the TCFA category b same as in the PROSPECT study [3]. The cross-sectional areas (CSAs) and percentages of each plaque component (dense calcium [DC], necrotic core [NC], fibrofatty [FF], and fibrotic tissue [FT]) were determined for each frame. Considering that large NC component and existence of a thin fibrous cap <65μm indicate instability of plaque [39], three NC- and NC-lumen-related features were introduced, i.e., percentage of the maximal confluent NC region, angle and size (number of pixels) of NC-region abutting the vessel lumen. IVUS-based measurements of CSAs of lumen, EEM, plaque (defined as EEM minus lumen CSA), plaque burden (plaque divided by EEM CSA), remodeling index (current frame EEM divided by mean reference EEM CSA) [35] and distance to current frame (from the coronary ostium, as derived from the reconstructed 3D vessel model) [32] were obtained for all frame locations. The mean and standard deviation of plaque thickness (defined as the distance between lumen and EEM borders at 360 circumferential wedges centered at the lumen centroid) were calculated. Eccentricity (defined as the ratio of minimal to maximal plaque thickness) [35] was determined to quantify the asymmetric distribution of plaque.

Fig. 3.

Automated determination of VH-IVUS plaque phenotypes.

2) First-Order Descriptors

To represent the first-order statistics of plaque, the grayscale intensity based mean, standard deviation, median, maximum, minimum, and mode values; and the intensity histogram based first, median, and third quartiles in the plaque region were calculated for each IVUS frame.

3) Plaque Textures

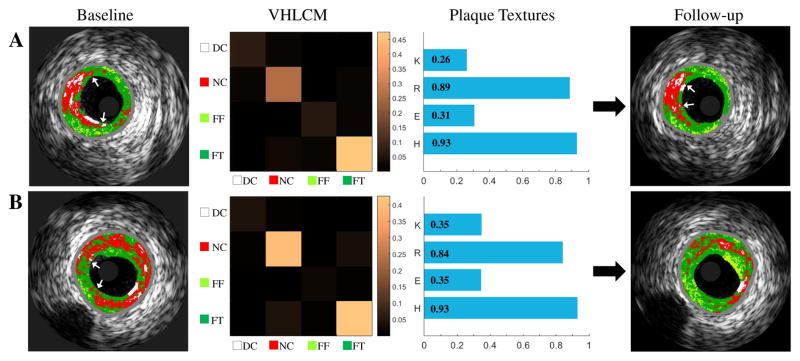
To describe the texture distribution of plaque, the gray level co-occurrence matrix [40] was computed. The 4-color-coded VH map of plaque (DC/NC/FF/FT) was used as a quantization of gray levels within the plaque, and four directions (θ = 0°, 45°, 90°, 135°) were used to generate 4 VH level co-occurrence matrices (VHLCMs) for each frame. Note that only VH-pixels from the plaque regions were included in the construction of texture indices. Second-order statistical texture features including contrast, correlation, energy, and homogeneity were calculated from each VHLCMs. Fig. 4 shows examples of extraction of plaque textures in TCFA.

Fig. 4.

Baseline VH-IVUS images (first column), corresponding VHLCMs (second column), plaque textures (third column), and follow-up VH-IVUS Images (fourth column). (A) TCFA unchanged. (B) TCFA regresses to PIT. K: contrast, R: correlation, E: Energy, H: homogeneity.

4) Layered Plaque Components

To enable a more detailed examination of plaque components, a layered analysis of different plaque depths in circumferential direction was performed in wall rings with adaptive radii of 10%, 20%, ..., 90% distance between the lumen and EEM borders. Percentages of DC/NC/FF/FT in the 10%~90% inner and outer rings were calculated, and therefore 72 layered plaque components features were obtained for each plaque. Fig. 5 shows examples of analysis of layered plaque components in a remaining TCFA and a healed TCFA, in which the schema and resulting features of the 20% adaptive ring are shown.

Fig. 5.

Baseline VH-IVUS images (first column), inner (green) and outer (orange) rings (second column), layered plaque components (third column), and follow-up VH-IVUS images (fourth column). (A) TCFA unchanged. (B) TCFA healed (regressed to ThCFA, 20% ring used).

5) Spatial Contextual Features

To incorporate spatial context between adjacent locations in axial direction and also to limit the impact of noise (e.g., potentially inaccurate frame-to-frame registration), we further extended the above four feature sets by computing the average values of features in the adjacent distal and proximal frames, resulting in 118 spatial contextual features. An example is shown in Fig. 6, where the spatial context features (e.g., plaque phenotype context) reflect disease severity in adjacent locations/frames, which potentially indicate future development of plaques (e.g., ThCFA progression or not). This hypothesis has been validated in a preliminary fashion by our previous studies of TCFA prediction [19], [25], where the plaque phenotype context shows superior performance.

Fig. 6.

Spatial context features. A: ThCFA progressed to TCFA. B: ThCFA regressed to PIT. Bounding box color: red: TCFA, orange: ThCFA, green: nonFA. Context feature of plaque phenotype is shown in this example.

E. Feature Selection and Predictive Classification

With the above feature set, feature selection was performed to increase the predictor performance and provide better understanding of the underlying factors/features that contribute to development of high-risk plaque. Specifically, features from the complete feature set (M=254) were ordered by a support vector machine recursive feature elimination (SVM RFE) method according to the discrimination ability of feature subset [27]. SVM RFE is an application of RFE using the weight magnitudes of features in SVM [29], [30] training as the ranking criterion, and is very effective for discovering/ranking informative features while overfitting is prevented [27], [36]. In our implementation, each feature was first preprocessed/normalized by subtracting its minimum and dividing the result by its maximum minus minimum, then linear SVMs (parameter C=1) were trained followed by the iterative chunk-based elimination approach [27] to produce a final feature subset of 50 features. Because of the imbalance in the class labels in our study (e.g., 55 TCFA remained while 353 TCFA healed), a different error costs (DEC) method [41] was utilized in SVM training, in which the individual class weights in the SVM model were assigned to be inversely proportional to the imbalance ratio.

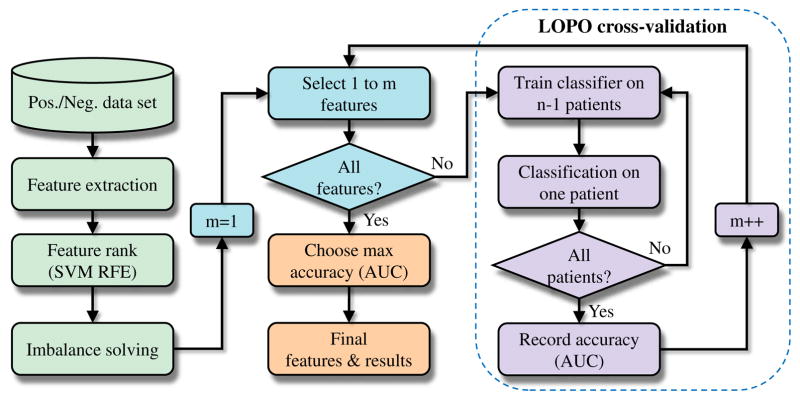
After obtaining the 50 best-ranked features, an incremental leave-one-patient-out (LOPO) cross validation with incrementally increasing numbers of features was repeatedly performed until all 50 features were considered. During SVM (linear kernel with C=1, as in SVM RFE) training, in order to account for the imbalance problems of our specific tasks, several different imbalanced data learning approaches [42] including random undersampling, DEC, synthetic minority oversampling technique (SMOTE), and SMOTE with different costs (SDC) were compared and the one that yielded the best performance was selected. The prediction performance including sensitivity (SEN), specificity (SPE), and the area under a receiver operating characteristic curve (AUC) were calculated and recorded after testing all n patients. In addition, as is widely accepted in class imbalance learning literature [42], G-mean metric ( $G-\mathit{mean}=\sqrt{\mathit{sensitivity}\times \mathit{specificity}}$) was used to quantify the prediction accuracy. Finally, the feature subset with the highest AUC was chosen as the final feature set, and the final prediction rates were obtained. We chose AUC because it is a good measure of classifier’s average performance and is insensitive to data distribution (Section 4.2 in [42]). The feature selection and predictive model validation procedure is shown in Fig. 7. Note that other combinations of feature selection (minimal-redundancy-maximal-relevance [mRMR] based on mutual information [43]) and classification methods (random forests, RF [44]; multilayer perceptron, MLP [45]) were also examined (section III-D).

Fig. 7.

Feature selection and predictive model validation.

The prediction strategy was designed to predict the future type of plaque for each IVUS frame location. Considering that a usual TCFA definition requires TCFA-frame presence in at least 3 consecutive frames, a post-processing step adjusts the local TCFA type labeling accordingly [25]. To take the current clinical practice scenario into account, we generalize our frame-level prediction to lesion- and patient-levels. A lesion was defined as at least three consecutive IVUS frames with PB≥40% [3], and lesions were considered separate if there was ≥5mm segment with PB<40% between them [12]. A lesion-/patient-level prediction would be labeled as TCFA, PB≥70%, or MLA≤4mm² only if at least 3 consecutive frames in a lesion/patient were predicted to be labeled as TCFA, PB≥70%, or MLA≤4mm².

III. Results

A. Prediction of TCFA vs. Non-TCFA

At baseline, 61 VH-IVUS pullbacks from the 61 enrolled patients exhibited 408 TCFA, 1068 ThCFA, and 4865 nonFA locations. At follow-up, 55 (13.5%) TCFAs remained TC-FAs, 36 (3.4%) ThCFAs and 33 (0.7%) nonFAs progressed to TCFAs. During this period, 353 (86.5%) TCFAs healed (transformed to non-TCFA), while 1032 (96.6%) ThCFAs and 4832 (99.3%) nonFAs did not progress to TCFA at follow-up (Table II). Note that the numbers of TCFA, ThCFA and nonFA reported here and also the PB and MLA in the following sections are per image frame. If per lesion, our assessments are actually comparable with previously reported values. For example, at follow-up, our assessment yields 19 TCFA lesions from 61 patients, comparable with 17 TCFA lesions from 99 patients in Kubo et al.’s study [11].

TABLE II.

Plaque phenotype changes (frame-level).

Baseline		Follow-up
		TCFA	ThCFA	FcP	FP	PIT	NL
TCFA	408 (6%)	55	148	13	109	71	12
ThCFA	1068 (17%)	36	390	59	205	277	101
FcP	140 (2%)	2	45	32	12	35	14
FP	826 (13%)	4	108	19	314	279	102
PIT	2005 (32%)	17	128	20	719	881	240
NL	1894 (30%)	10	51	18	86	196	1533
Total	6341	124 (2%)	870 (14%)	161 (3%)	1445 (23%)	1739 (27%)	2002 (32%)

Values are n or n (%). Plaque phenotypes were automatically labeled as given in [34].

TCFA: virtual histology-derived thin-cap fibroatheroma; ThCFA: thick-cap fibroatheroma; FcP: fibrocalcific plaque; FP: fibrous plaque; PIT: pathological intimal thickening; NL: No lesion.

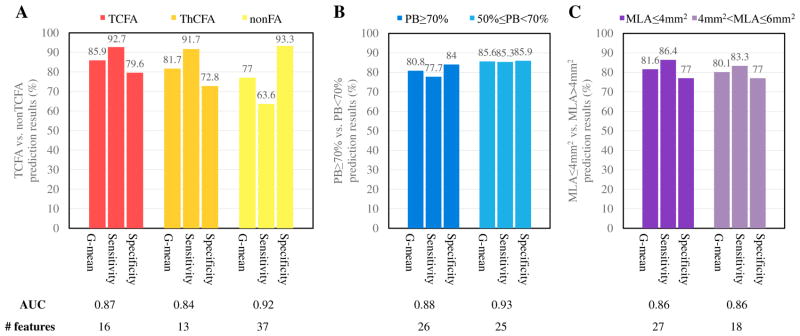
Our models predict (1) TCFA, (2) ThCFA, and (3) nonFA plaque types at follow-up with high G-mean values of 85.9%, 81.7%, and 77.0%, respectively (sensitivities and specificities ranging from 63.6% to 93.3%, Fig. 8(A)), employing 16, 13, and 37 optimal-feature-selection sets, respectively (Table III).

Fig. 8.

LOPO cross-validation results (frame-level). (A) TCFA vs. ThCFA vs. nonFA; (B) PB≥70% vs. PB<70%; (C) MLA≤4mm² vs. MLA>4mm². For imbalanced learning, SDC (SMOTE with different costs) and DEC (different error costs) have similar performance. Finally, SDC with 100% oversampling was used in baseline TCFA prediction, and DEC was used in other predictions.

TABLE III.

Final feature subsets in the seven predictors.

Task (1): TCFA→TCFA vs. TCFA→nonTCFA (m=16)

LPC/0.2outerDC%C, SYS/BMI, SYS/bl-choltotal, SYS/family-history, SYS/hypertension, SYS/bl-cholldl, PT/contrast135C, SYS/statins, LPC/0.5innerFF%C, FOD/modec, LPC/0.1outerDC%C, PT/energy0, SYS/acinhibitors, LPC/0.3innerNC%, SYS/age, LPC/0.6innerFT%C

Task (2): ThCFA→TCFA vs. ThCFA→nonTCFA (m=13)

PT/contrast135, LPC/0.2innerNC%, LPC/0.7innerNC%, PT/correlation45, LPC/0.6outerNC%C, LPC/0.2innerDC%C, LPC/0.3innerDC%C, BASIC/phenotypeC, FOD/mean, BASIC/DC-CSA, BASIC/#NC-abutting-lumen, SYS/BMI, SYS/statins

Task (3): nonFA→TCFA vs. nonFA→nonTCFA (m=37)

PT/homogeneity0C, PT/homogeneity90C, PT/homogeneity90, PT/homogeneity45C, PT/homogeneity45, BASIC/eccentricity, SYS/current-smoker, BASIC/lumen-CSA, BASIC/NC-CSA, BASIC/PBC, SYS/bl-tag, PT/homogeneity135C, FOD/maxC, FOD/3rdQC, BASIC/mean-plaque-thickness, LPC/0.8outerFT%, SYS/bl-cholldl, SYS/bl-choltotal, BASIC/confluentNCC, LPC/0.7outerDC%, BASIC/lumen-CSAC, BASIC/FT-CSA, FOD/1stQ, BASIC/PB, LPC/0.5innerFTC, LPC/0.2innerFFC, BASIC/mean-plaque-thicknessC, FOD/3rdQ, FOD/meanC, FOD/median, PT/contrast90C, LPC/0.1innerFT%C, SYS/acinhibitors, LPC/0.5outerFF%, SYS/BMI, FOD/mean, BASIC/max-NC-angle

Task (4): PB≥70%→PB≥70% vs. PB≥70%→PB<70% (m=26)

BASIC/PB, SYS/bl-cholldl, BASIC/PBC, SYS/hypertension, BASIC/NC-CSAC, BASIC/confluentNCC, LPC/0.1innerNC%, FOD/1stQ, BASIC/phenotypeC, SYS/current-smoker, BASIC/std-plaque-thickness, BASIC/lumen-CSA, FOD/medianC, LPC/0.8outerFF%, LPC/0.2innerFF%C, SYS/bl-choltotal, SYS/bl-tag, BASIC/eccentricityC, LPC/0.1innerDC%C, FOD/mode, SYS/betablockers, LPC/0.1innerFF%C, BASIC/std-plaque-thicknessC, BASIC/max-NC-angleC, LPC/0.7outerDC%, LPC/0.9outerDC%C

Task (5): PB<70%→PB≥70% vs. PB<70%→PB<70% (m=25)

BASIC/lumen-CSAC, BASIC/mean-plaque-thicknessC, PT/energy135, FOD/std, BASIC/PB, BASIC/eccentricityC, LPC/0.7outerDC%, FOD/3rdQ, BASIC/RIC, PT/correlation135, PT/energy90, PT/contrast45, PT/homogeneity90C, PT/contrast45C, LPC/0.6outerFT%C, SYS/age, SYS/acinhibitors, FOD/modeC, BASIC/PBC, LPC/0.9outerFT%, PT/correlation90C, LPC/0.9outerFF%C, LPC/0.3innerFT%C, LPC/0.6outerNC%C, SYS/statins

Task (6): MLA≤4mm2→MLA≤4mm2 vs. MLA≤4mm2→MLA>4mm2 (m=27)

BASIC/lumen-CSAC, PT/correlation0C, SYS/bl-cholhdl, LPC/0.1innerNC%C, LPC/0.1innerFT%C, SYS/acinhibitors, BASIC/confluentNCC, BASIC/lumen-CSA, LPC/0.5outerFF%, LPC/0.8outerNC%, SYS/hyperlipidemia, SYS/BMI, PT/correlation135C, FOD/1stQC, LPC/0.1innerNC%, FOD/3rdQ, SYS/bl-cholldl, SYS/betablockers, LPC/0.5innerNC%C, FOD/mode, LPC/0.2innerDC%C, LPC/0.4innerDC%C, LPC/0.5innerFT%C, LPC/0.2innerDC%, LPC/0.4innerDC%, LPC/0.9outerNC%, PT/contrast90

Task (7): MLA>4mm2→MLA≤4mm2 vs. MLA>4mm2→MLA>4mm2 (m=18)

PT/energy0, FOD/std, FOD/1stQ, BASIC/lumen-CSA, FOD/min, LPC/0.8outerDC%C, BASIC/confluentNCC, LPC/0.1innerDC%C, LPC/0.4innerDC%C, SYS/hypertension, PT/contrast90, SYS/bl-cholhdl, LPC/0.9outerNC%C, LPC/0.5innerDC%, BASIC/FF-CSAC, BASIC/PBC, PT/energy135C, LPC/0.2innerDC%

Features are denoted in the following notation: category/feature.

BASIC: basic clinical measures; FOD: first-order descriptors; LPC: layered plaque components; PT: plaque textures; SYS: systemic information;

^C: contextual features.

B. Prediction of Plaque Burden ≥70% vs. <70%

There were 206 (3.2%) locations of (PB) ≥70% at baseline. The total number of frames with PB≥70% at follow-up decreased to 173 (2.7%): 112 locations (64.7%) with PB≥70% at baseline and 61 frames (35.3%) with PB<70%, despite lipid-lowering therapy (Table IV). Frames with baseline PB<50% never progressed to PB≥70% at follow-up, so were not considered in our experiment.

TABLE IV.

Plaque burden changes (frame-level).

Baseline		Follow-up
		PB≥70%	PB<70%
PB≥70%	206 (3%)	112	94
50%≤PB<70%	2391 (38%)	61	2330
PB<50%	3744 (59%)	0	3744
Total	6341	173 (3%)	6168 (97%)

Values are n or n (%).

PB: plaque burden.

Our models predict the plaque burden categories (1) PB≥70% and (2) 50%≤PB<70% with high correctness (G-mean) of 80.8% and 85.6%, respectively (sensitivities and specificities ranging from 77.7% to 85.9%, Fig. 8(B)), employing 26 and 25 optimal features, respectively (Table III).

C. Prediction of MLA≤4mm² vs. >4mm²

There were 303 (4.8%) frames with MLA≤4mm² at baseline, decreasing to 267 frames (4.2%) at follow-up: 177 frames (66.3%) maintained MLA≤4mm² and 90 frames (33.7%) progressed to MLA≤4mm² (Table V). Frames with baseline MLA>6mm² never regressed to MLA≤4mm² at follow-up, so were not considered in our experiment.

TABLE V.

Lumen area changes (frame-level).

Baseline		Follow-up
		MLA≤4mm2	MLA>4mm2
MLA≤4mm2	303 (5%)	177	126
4mm2<MLA≤6mm2	1324 (21%)	90	1234
MLA>6mm2	4714 (74%)	0	4714
Total	6341	267 (4%)	6074 (96%)

Values are n or n (%).

MLA: minimal luminal area.

Our models predict the lumen area (1) MLA≤4mm² and (2) 4mm²<MLA≤6mm² at follow-up with high G-mean values of 81.6% and 80.2%, respectively (sensitivities and specificities ranging from 77.0% to 86.4%, Fig. 8(C)), employing 27 and 18 optimal features, respectively (Table III).

D. Comparison with Other Feature Selection and Classification Methods

Table VI compares different feature selection and classification methods. For imbalanced data learning in mRMR+SVM and RF, random undersampling and DEC were compared and the one yielding the best performance was selected. For MLP, random undersampling was used. The built-in RF feature selection was utilized in RF classification. The parameters of MLP and RF are listed in Table VI. We tested other settings in an earlier preliminary study, but they did not improve performance. Overall, the reported setup SVM recursive feature elimination + SVM classifier performed best.

TABLE VI.

Comparison of three different feature selection and classification methods.

Baseline		G-mean (%)	SEN (%)	SPEC (%)	AUC	#F
TCFA	SVM RFE+SVM	85.9	92.7	79.6	0.87	16
	mRMR+SVM	74.3	76.4	72.2	0.77	12
	SVM RFE+MLP	83.1	85.5	80.7	0.88	15
	mRMR+MLP	71.9	76.4	67.7	0.75	27
	RF	77.9	70.9	85.6	0.82	16
ThCFA	SVM RFE+SVM	81.7	91.7	72.8	0.84	13
	mRMR+SVM	66.3	58.3	75.4	0.77	14
	SVM RFE+MLP	79.6	83.3	76.0	0.85	17
	mRMR+MLP	75.4	88.9	64.0	0.82	20
	RF	68.0	58.3	79.2	0.77	7
nonFA	SVM RFE+SVM	77.0	63.6	93.3	0.92	37
	mRMR+SVM	78.7	75.8	81.8	0.87	12
	SVM RFE+MLP	83.7	97.0	72.3	0.87	12
	mRMR+MLP	81.9	90.9	73.9	0.88	6
	RF	78.7	75.8	81.7	0.89	7
PB≥70%	SVM RFE+SVM	80.8	77.7	84.0	0.88	26
	mRMR+SVM	70.3	75.0	66.0	0.81	16
	SVM RFE+MLP	74.8	74.1	75.5	0.83	10
	mRMR+MLP	72.4	79.5	66.0	0.82	12
	RF	78.9	77.1	80.8	0.87	9
PB<70%	SVM RFE+SVM	85.6	85.3	85.9	0.93	25
	mRMR+SVM	76.0	70.5	82.0	0.87	37
	SVM RFE+MLP	82.4	88.5	76.7	0.89	22
	mRMR+MLP	76.2	72.1	80.5	0.88	8
	RF	78.6	75.4	81.9	0.89	10
MLA≤4mm2	SVM RFE+SVM	81.6	86.4	77.0	0.86	27
	mRMR+SVM	73.5	75.7	71.4	0.81	17
	SVM RFE+MLP	77.9	81.4	74.6	0.86	8
	mRMR+MLP	76.3	75.7	77.0	0.81	21
	RF	76.0	77.4	74.6	0.83	11
MLA>4mm2	SVM RFE+SVM	80.1	83.3	77.0	0.86	18
	mRMR+SVM	71.4	77.8	65.6	0.78	3
	SVM RFE+MLP	74.6	74.4	74.8	0.83	17
	mRMR+MLP	72.4	72.2	72.6	0.77	2
	RF	73.3	70.0	76.8	0.80	20
Average	SVM RFE+SVM	81.8	83.0	81.4	0.88	23
	mRMR+SVM	72.9	72.8	73.5	0.81	16
	SVM RFE+MLP	79.4	83.5	75.8	0.86	14
	mRMR+MLP	75.2	79.4	71.7	0.82	14
	RF	75.9	72.1	80.1	0.84	11

mRMR (minimal-redundancy-maximal-relevance): based on mutual information.

MLP (multilayer perceptron): 1 hidden layer with the number of neurons = (# features + # classes) / 2, epochs = 500, and learning rate = 0.01.

RF (random forests): 100 trees with the size of features for node splitting $=\sqrt{\#\mathit{features}}$

E. Visualization of Future High-Risk Plaque Locations

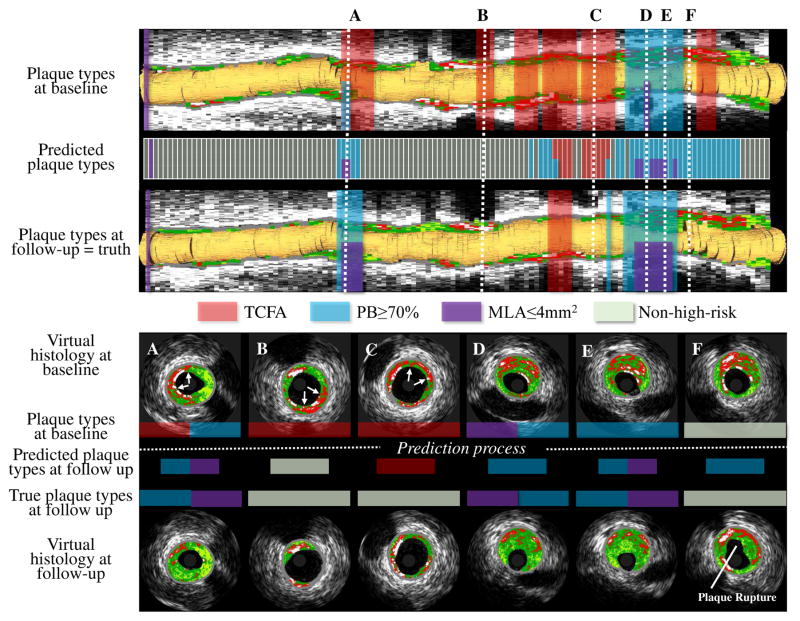
Fig. 9 shows our prediction method determining locations of future high-risk plaques. The baseline risk-plaque properties and follow-up predicted risk-plaque properties (TCFA, PB≥70%, and MLA≤4mm²) are overlaid on the baseline VH-IVUS rendering in red, blue, and purple.

Fig. 9.

Future high-risk plaque locations. Upper panel: Baseline VH-IVUS pullback with high-risk plaque risk locations (first row), predicted follow-up high-risk plaque locations (second row), and ground-truth at follow-up (third row). TCFA in red; PB≥70% blue; MLA≤4mm² purple. Lower panel: Cross-sectional VH-IVUS frames at the six locations marked in the upper panel. A: TCFA healed, PB≥70% unchanged, and new MLA≤4mm² occurred. B: TCFA healed. C: TCFA healed. D: PB≥70% and MLA≤4mm² unchanged. E: PB≥70% unchanged while new MLA≤4mm² present. F: No high-risk plaque with plaque rupture at follow-up.

F. Lesion- and Patient-Level Prediction

At follow-up, there were 19 TCFA, 18 PB≥70%, and 22 MLA≤4mm² lesions. The corresponding per-patient numbers were 19, 17, and 21. We obtained G-mean values for lesion-level correctness of 82.9%, 83.8%, and 90.0% for prediction of future TCFA, PB≥70%, and MLA≤4mm², respectively (Table VII). The corresponding G-mean for patient-level prediction correctness were 78.6%, 81.2%, and 84.5%, respectively (Table VII).

TABLE VII.

HIGH-RISK PLAQUE PREDICTION RESULTS IN LESION- AND PATIENT-LEVEL.

	# TP/P	# TN/N	G-mean (%)	SEN (%)	SPEC (%)
Lesion-level
TCFA	17/19	53/69	82.9	89.5	76.8
PB≥70%	17/18	52/70	83.8	94.4	74.3
MLA≤4mm2	21/22	56/66	90.0	95.5	84.8
Patient-level
TCFA	17/19	29/42	78.6	89.5	69.0
PB≥70%	17/17	29/44	81.2	100.0	65.9
MLA≤4mm2	20/21	30/40	84.5	95.2	75.0

TP: true positive; P: positive samples; TN: true negative; N: negative samples.

IV. Discussion

This work represents a novel pilot effort to develop a high-risk-plaque prediction approach with substantial clinical relevance. Our predictive models represent the first and –to the best of our knowledge – the only highly automated method to predict future locations of high-risk MACE-causing plaque properties (TCFA, PB≥70%, MLA≤4mm²) [3] with quantitatively assessed prediction performance. The only step that requires user interaction is the IVUS segmentation refinement, which only requires 6 minutes of expert time on average (note that the registration step would not be needed in clinical setting once the predictive models are trained). Location-specific prediction of the development and healing of high risk plaques expands on our previous effort to predict healing or development of TCFA alone [19], [25], yielding a more accurate prediction model.

A. Comparison with Other Studies, Advantage of Our Approach

Our study predicts future MACE-related plaques phenotypes (TCFA, PB≥70%, MLA≤4mm²) with high sensitivity and specificity, unlike previous studies [11], [12], [14], [16], [17], which focused on relationships between baseline predictors and plaque progression/regression. The proposed approach achieved a more precise and frame-location-specific prediction (≈0.5mm) compared to the segment level (≈3mm) [14] or lesion level (≈10mm) [11], [12] locational accuracy. Therefore, our approach avoids analysis of heterogeneous changes of plaque phenotypes [11], [12], and excessive averaging over longer distances while using a larger patient cohort (n=61) compared to past studies with typically enrolled about 20 patients [16], [17]. Although nearly half of the enrolled patients were excluded in our study, most of the exclusion criteria (e.g., loss or unreadable follow-up data, co-registration problem) do not detract from the applicability of our method since only the baseline data will be needed for the prediction purpose in the clinical setting. Information context from the immediately adjacent frames is contributing to our prediction model. As a justification of the use of this spatial context, our frame-level model with spatial context generalizes well on lesion- and patient-level prediction tasks (Table VII). Our work also provides an insight into local and systemic factors combined that influence plaque behavior over time. Finally, our method is general, as it can predict three different plaque-type characteristics by employing the same machine learning approach for all of these three tasks (DEC performs better than other imbalance learning techniques in almost all tasks, except for task 1 with a G-mean=85.1%, slightly lower than SDC with a G-mean=85.9%). This characteristic makes our approach easily extendible to other plaque development prediction tasks, such as prediction of longitudinal remodeling patterns or — once larger datasets become available — prediction of cardiovascular events. Equally important, while we have developed and evaluated our predictive models using data from patients with stable angina, our strategy is not limited to this patient group.

Previous research on TCFA prediction by our group treated the prediction of whether existing TCFA will remain, heal, or whether a new TCFA plaque will occur a single task [19], [25]. Such a strategy results in a nearly perfect accuracy for predicting that TCFA remains but a very low predictive accuracy for locations with healed TCFA. This is because the majority of future TCFAs originate from remaining TCFAs but only a small number of future non-TCFA are coming from healed TCFAs. With such imbalanced data, the classifier tends to learn a decision boundary close to the healed TCFAs (classifies most of the healed TCFAs as remaining TCFAs). Actually, accurate prediction of TCFA healing might be more important than TCFA remaining since the identification of high-risk individuals that would benefit from a pharmaceutical treatment is desired. Our new strategy splits the single task into multiple sub-tasks, which help balance the positive and negative samples and therefore yield a more accurate prediction.

The proposed learning method mainly relies on SVM. Besides its strong theoretical foundations [29] and efficiency in implementation, SVM is especially fit for our specific imbalanced data learning problems for the following reasons: (1) It builds the decision function based only on those instances that are close to the “borderline” (i.e., support vectors), thus naturally avoiding the influence of the large number of majority instances. (2) There are well-established imbalanced data learning approaches for SVM, i.e., the DEC and SDC are demonstrated to be more theoretically-correct and practically-effective [42] than undersampling, which was used in our previous study [19], [25]. (3) The SVM RFE based feature selection approach has built-in regularization mechanism that prevent overfitting in its selection of feature subsets [27]. Our experiments demonstrated that by incorporating DEC into the SVM RFE based feature selection process, the selected optimal feature sets performed best in all the seven prediction tasks in comparison with other two feature-selection approaches (mRMR and RF, Table VI).

B. Factors Leading to Development of High-Risk Plaques

Feature selection (Table III) showed that different optimal feature sets are suitable for different prediction tasks. For each prediction task, about 23 features were selected for each predictor and these features varied across the classification tasks. While we started with a large number (254) of features on 6341 images, the features were subjected to a feature selection step identifying the most discriminative feature subset for each given task. Feature selection resulted in a dramatic feature-set size reduction that preceded each training process. Consequently, the predictive classifiers always utilized a relatively small set of features (23 on average) thus minimizing the risk of overfitting. Similar ratio between images and features can be found in [36] when using SVM in medical imaging: 3443 CT images using 5–50 features.

There are 162 features involved in all the seven predictors. Out of these 162 features, 9.3% reflect basic clinical measures, 8.6% first-order descriptors, 11.7% layered plaque components, 7.4% plaque textures, 42.6% spatial contexts, and 20.4% systemic/demographic information. The spatial context of plaque characteristics in adjacent IVUS-frame locations indicates that the cumulative plaque-risk severity derived from adjacent locations at baseline potentially determines the development of future high-risk plaques in that location. We also observed that local vascular factors must be combined with systemic risk factors. On average, the prediction G-mean values obtained by our method with local factors only and systemic factors only are 73.2% and 68.8%, respectively. Combining local and systemic factors improves the G-mean-assessed performance to 81.8%. For example, half of the optimal features to predict whether TCFA will remain or heal come from systemic risk factors, including BMI, baseline total/LDL cholesterol, family history, hypertension, statins during baseline, ACE inhibitors, and age (Table III).

Kubo et al. [11] and Zhao et al. [12] found distance from ostium to lesion and lumen/vessel/plaque CSA predictive at the lesion/segment level to predict whether TCFA will remain or heal. Interestingly, none of these features were identified as important in our image-frame-based optimal feature set. By training an SVM classifier that was based on these four features only, the reached G-mean correctness was only 17.5% compared to 85.9% achieved using our method. There may be several reasons for this observation. First, Kubo et al. [11] and Zhao et al. [12] included patients with acute myocardial infarction while no such patients were enrolled in our study. Second, their lesion-level analysis over-averaged vessel features and plaque phenotypes, therefore, the derived significant features were not discriminative in our local-image-frame-level prediction. In addition, Kubo et al. [11] found no difference between baseline VH-IVUS plaque components for TCFA phenotypes that remained or healed at follow-up. In agreement with their findings, our optimal feature set did not include any traditional VH plaque components either. However, our five layered-plaque component features contributed substantially, demonstrating the prediction value of tissue components distributed at different plaque depths.

When predicting changes in PB and MLA, Stone et al. [14] identified endothelial shear stress (ESS), MLA, PB, distance from ostium, and vessel remodeling as useful indices. While ESS was not included in our study, our feature-selection-based predictors employ all of these features except ostial distance. By training SVM classifiers based on the Stone-identified features (except ESS), the G-mean values were 60.6%, 77.7%, 57.8%, and 68.7% for our tasks (4), (5), (6), and (7), respectively. In comparison, our G-mean values were unquestionably higher at 80.8%, 85.6%, 81.6%, and 80.1%, respectively.

To demonstrate the effects of the newly designed VH-IVUS-based features (F22–F236, Table I), we compared the performance of our method with that of using only basic clinical measures and demographics & biomarkers (F1–F21, F237–F254, Table I). The G-mean values were: 75.0%, 80.5%, 85.9%, 76.0%, 82.0%, 72.9%, and 69.6%, from task (1) to task (7), respectively, or 77.4% on average. Adding the newly-designed features improves the average G-mean to 81.8%. These results clearly show that our feature-selection-based, algorithmically-designed features help improve predictive accuracy in this difficult plaque-risk prediction task.

C. Limitations

Limited resolution of VH-IVUS does not allow direct measurement of thin fibrous caps (<65μm), and recent study questions the accuracy of the histological correlation of VH-IVUS characterization [46]. Nevertheless, we have clearly demonstrated that VH-IVUS-derived local plaque features combined with patient-specific systemic/demographic information can predict future high-risk plaques (VH-TCFA, PB≥70%, MLA≤4mm²) that may be later responsible for MACE [3]–[5]. Although our analysis uses nearly three-fold larger number of patients than other similar studies, the study size remains a limiting factor. Moreover, due to the lack of clinical follow-up, we are unable to directly assess MACE prediction. While our methodology utilizes one of the most advanced and accurate intravascular image co-registration approaches [18], it is still possible that co-registration may not be perfect. Having added the expert-approval of co-registration to the analysis sequence for each pullback minimized this limitation. In addition, our prediction model is based on relatively short-term follow-up (approximately one year) in lesions of moderate severity with all patients receiving high intensity statin agents. Furthermore, our current framework is not predicting MACE-associated quantitative indices as continuous variables, this remains a task for future work. Note however that our approach provides a continuous probability value of location-specific plaquebs future risk. Finally, our model reached a promising accuracy in prediction of future MACE indices and location-specific risk-plaque properties under LOPO evaluation only (a popular error estimation procedure when sample size is small); K-fold cross-validation and bootstrap method may be considered in future work.

V. Conclusion

Our machine-learning approach demonstrated that location-specific prediction of future plaque phenotypes related to MACE is feasible, thus improving risk stratification in patients with established coronary artery disease. The newly designed IVUS-VH-based features improve the prediction accuracy compared to only-employing clinical measures. The useful features mainly describe local vascular characteristics in spatial context (42.6%) and systemic/demographic information (20.4%). The SVM-based feature selection and imbalanced-data learning approaches predict high-risk plaque locations better than the previously clinical predictors and underline the importance of local factors on development of high-risk plaques.