Shear-Induced Diffusion of Red Blood Cells Measured with Dynamic Light Scattering-Optical Coherence Tomography

Abstract

Quantitative measurements of intravascular microscopic dynamics, such as absolute blood flow velocity, shear stress, and the diffusion coefficient of red blood cells (RBCs), are fundamental to understanding the blood flow behavior within the microcirculation, and for understanding why diffuse correlation spectroscopy (DCS) measurements of blood flow are dominantly sensitive to the diffusive motion of RBCs. Dynamic Light Scattering-Optical Coherence Tomography (DLS-OCT) takes the advantages of using DLS to measure particle flow and diffusion within an OCT resolution-constrained 3D volume, enabling the simultaneous measurements of absolute RBC velocity and diffusion coefficient with high spatial resolution. In this work, we applied DLS-OCT to measure both RBC velocity and the shear-induced diffusion coefficient within penetrating venules of the somatosensory cortex of anesthetized mice. Blood flow laminar profile measurements indicate a blunted laminar flow profile, and the degree of blunting decreases with increasing vessel diameter. The measured shear-induced diffusion coefficient was proportional to the flow shear rate with a magnitude of ~ 0.1 to 0.5 × 10⁻⁶ mm². These results provide important experimental support for the recent theoretical explanation for why DCS is dominantly sensitive to RBC diffusive motion.

Graphical abstract

1. Introduction

Quantitative high resolution measurements of intravascular dynamics, including blood flow velocity and its radial profile over the vessel cross-section, shear stress and the shear-induced diffusion of red blood cells (RBCs), are fundamental to understanding the intravascular blood flow behavior in the microcirculation.[1–3] The flow shear-induced diffusion phenomenon was quantified in vitro by a particle tracking approach by Goldsmith et al.[4], who reported a random walk-like motion of ghost cells within a shear flow. We have been particularly interested in establishing the microscopic relation between blood flow velocity and the shear-induced diffusion of RBCs in living animals in order to explain the routine observation that the diffuse correlation spectroscopy (DCS) measurement of blood flow is dominantly sensitive to the diffusive motion of RBCs and not the flow motion [5–7]. In addition, the quantitative measurement of shear-induced diffusion in vivo can serve invaluably for understanding interactions between the blood vessel wall and endothelium and hemodynamic forces governing blood flow and how these interactions are affected in pathological conditions like hypertension[8], diabetes[9], hyperlipidemia/atherosclerosis[10,11], stroke and many other common disease conditions [12,13]. However, no in vivo quantitative characterization at the microscopic level has been reported so far for these phenomena.

Several optical imaging techniques, such as laser Doppler flowmetry (LDF) [14], laser speckle velocimetry[15], Doppler Optical Coherence Tomography [16], and Doppler Photoacoustic Imaging [17], are all able to measure the blood flow velocity but have not been shown to detect diffusive motion. Particle imaging velocimetry (PIV)[18], dynamic light scattering (DLS)[19], and DCS [7,20] are capable of quantifying flow and diffusion simultaneously. However, PIV and DLS suffer from an unknown optical path-length distribution of the scattered light resulting in limited depth differentiability, while DCS has low spatial resolution (usually on the scale of millimeters or greater). The combination of DLS with optical coherence tomography (OCT) [21,22] exploits the advantages of using DLS to measure particle flow and diffusion within an OCT resolution-constrained 3D volume, enabling the simultaneous measurements of absolute RBC velocity and diffusion with high spatial resolution in 3D.

Using the novel Dynamic Light Scattering – Optical Coherence Tomography (DLS-OCT) technique [21,23] developed in our group, we were able to simultaneously acquire absolute particle velocity and diffusion coefficient with high spatial resolution, allowing us to quantify the relation between blood flow velocity and shear-induced diffusion of RBCs, for the first time, in living animals. In this work, we applied DLS-OCT to simultaneously measure RBC velocities and diffusion coefficients in cerebral blood vessels of anesthetized mice. We calculated the bluntness of the laminar profile of blood flow with respect to the vessel diameter, analyzed the relation between the measured diffusion coefficient and the blood flow shear rate, and experimentally confirmed that the shear induced RBC diffusion dynamics is sufficiently fast relative to the RBC flow velocity to dominate the DCS measurement of RBC dynamics.

2. Materials and Methods

2.1. Animal Preparation

CD1 mice (23–26 g, female, n=7) were used in this study. During surgery, mice were anesthetized with isoflurane (2–3% for induction and 1–2% for maintenance) and supplied with 25% oxygen in air. A tracheotomy was utilized for mechanical ventilation and the femoral artery was catheterized for continuous blood pressure measurements. A cranial window (3 mm × 3 mm) was prepared over the right somatosensory cortex with dura being carefully removed without damaging the cortex. The exposed brain was covered with clear agarose gel (1% in saline, without adding scattering particles) and sealed with a glass cover slip. The use of agarose gel and the glass cover slip was to protect the exposed brain from the environment. Agarose gel is a good choice of material that matches the refractive index between the brain tissue and the glass cover slip, in addition, it can effectively maintain moisture of the brain compared to saline which may be absorbed by the brain tissue. The animal was then placed under the OCT system for DLS-OCT imaging. To minimize the reflection from the glass cover slip we carefully aligned the sample so that the angle between the glass cover slip and the optical axis is around 84°–87°. For the duration of the experiments the animals were mechanically ventilated, blood pressure was continuously monitored, and the body temperature was maintained at 37±0.1 ° C with a homeothermic blanket control unit. Imaging was performed during the resting state while the dose of isoflurane was maintained for stable anesthesia. For each experiment, 3-to-4 regions of interest (ROI, 600 μm×600 μm) were selected for imaging, and the total imaging time for one animal was less than 1.5 hours.

All animal experimental procedures were reviewed and approved by the Massachusetts General Hospital Subcommittee on Research Animal Care.

2.2. DLS-OCT imaging system

We used a spectral domain OCT system (Thorlabs Inc.) optimized for DLS-OCT data acquisition (Figure 1A). A large spectral bandwidth near-infrared light source (center wavelength:1310 nm, bandwidth: 170 nm) composed with two superluminescent diodes (SLDs) was employed. With the long center wavelength and large bandwidth, our OCT system achieved an imaging depth of ~1 mm and an axial resolution of 3.5 μm in the brain tissue. The interference of light from the sample and reference arms was captured by a 1024-pixel InGaAs line scan camera operating at a sampling rate of 47,000 frames/s. In this study, a 10X objective (NA=0.26) was used and the transverse resolution in tissue was 3.5 μm. Therefore, the resolution voxel was isotropic and h=h_t was used for the DLS-OCT calculations. For more information regarding the OCT system please refer to our previous publication [24].

Figure 1.

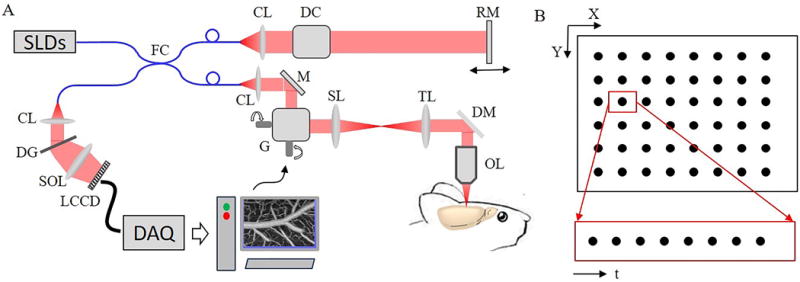
(A) Spectral domain OCT imaging system. SLD: superluminescent diode; FC: fiber coupler; CL: collimating lens; DC: dispersion compensation; RM: reference mirror; M: mirror; G: XY galvanometers; SL: scan lens; TL: tube lens; DM: dichroic mirror; OL: objective lens; DG: diffraction grating; SOL: spectrometer objective lens; LCCD: line CCD. (B) Four dimensional (XYZ and t) DLS-OCT data acquisition.

Figure 1B illustrates the data acquisition strategy of DLS-OCT. For each scanning position (x, y), 100 A-scans were repeated to permit calculation the temporal field autocorrelation functions along the depth axis. In this study, a field of view of 600×600 $\mu m^2$(x × y) was imaged in a raster scan manner containing 400 points in x and 400 points in y. Thus, the total acquired A-scans for each DLS-OCT image were 100×400×400 (t × x × y). The number of time data points per location was selected to be 100 because our fitting algorithm worked well when the autocorrelation function had more than 25 time lag points. In addition, the acquisition time for 100 A-scans was ~2.2 ms which was short enough to avoid motion artifacts primarily resulting from cardiac pulse (71–194 ms[25]) and respiration (261–750 ms[26]). The total time to acquire one volumetric image of DLS-OCT data is ~6.5 min.

2.3. DLS-OCT Autocorrelation Function and Fitting Algorithm

Offline data processing was performed with MATLAB (Mathworks Inc.) on a 200-core cluster system provided by the Martinos Center for Biomedical Imaging. Data extending 350 μm beneath the brain surface was extracted from each A-line. Experimental electric field autocorrelation functions ( $g_{1exp}$) were calculated for each voxel (x, y, z). Then, $M_S,M_F$, $v_t$, $v_z$, and D were obtained for each voxel (x, y, z) by fitting the theoretical electric field temporal autocorrelation function $g_1\left(\tau \right)$ given by Equation 1[21] to the measured $g_{1exp}\left(\tau \right)$.

$g_1\left(\tau \right)=E\left[\frac{R_1^{\ast }\left(t\right)R_1{\left(t+\tau \right)}_t}{R_1^{\ast }\left(t\right)R_1{\left(t\right)}_t}\right]=M_S+M_F{e}^{-h_t^2{v}_{t}2{\tau }^2-h^2{v}_{z}2{\tau }^2}\cdot e^{-q^{2}D\tau }\cdot e^{iq{v}_z\tau }+M_E\delta \left(\tau \right)$ (1)

where, $M_S$ is the composition ratio of static particles; $M_F$ and $M_E=\left(1-M_S-M_F\right)$ is that of flowing/diffusing particles and entering/exiting particles, respectively; $v_t$ is the transverse component of the flow velocity, $v_z$ is the axial component of the flow velocity, and D is the diffusion coefficient.

We improved our previously described fitting algorithm [21] to reduce uncertainty in the fitting parameters. Briefly, we noticed a strong crosstalk between $v_t$ and D when fitting the experimental autocorrelation function since both $v_t$ and D can affect the decay of the amplitude of the autocorrelation function ( $g_1\left(\tau \right)$). To reduce this crosstalk, we constrained $v_t$ within a reasonable region according to $v_z$ and $M_F$. We justify these constraints because 1) the total velocity ( $\sqrt{v_t^2+v_z^2}$) of cerebral blood flow is typically less than 12 mm/s[27], 2) $v_z$ could be accurately obtained according to the OCT signal phase change, and 3) flowing particles result in a higher value of $M_F$. In contrast, D was unconstrained. In addition, we noticed that an appropriate initial guess for $M_S$ and $M_F$ is very important to optimally find the global minimum in our fitting routine. We set $M_S$ to the value given by the center of rotation of the last half of the temporal autocorrelation function when $v_z\ge$1 mm/s; and $M_F$ equal to the difference in the autocorrelation function between the first and last time lags when $v_z$<1 mm/s. We used the relationship of $M_S=1-M_F$ for the initial guesses. This was empirically demonstrated to provide better fitting results (results not shown).

2.4. Data Processing and Statistical Analysis

We selected ascending venules with diameters greater than 30 μm for analysis since blood flow in arterioles have a higher axial velocity gradient within a voxel which exerts influence on the autocorrelation function as indicated by Uribe-Patarroyo and his colleagues.[28] Our DLS-OCT model doesn’t consider this axial velocity gradient, and therefore using the venules for analysis minimizes confounding effects. In addition, the reason we analyze penetrating vessels (ascending venules) instead of transverse vessels is that a ‘shadow’ beneath transverse vessels, which commonly exists in OCT imaging, can bias the estimate of the blood flow velocity profile, further resulting in inaccurate estimation of the magnitude between the shear-induced diffusion coefficient and the shear rate. Although such ‘shadow’ may also exist in penetrating vessels in deep layers, there should be no such bias in the z-plane cross section. In addition, the measured vessel sections were mostly extracted in the range of 40–80 $\mu m$ deep from brain surface, in which range single scattering should be in domination.

Equation 2 describes a general form of the blood flow velocity profile[2], and it was used to fit the blood flow radial velocity profile obtained with DLS-OCT,

$$V\left(r\right)=V_{\mathit{max}}(1-{|a\left(\frac{r}{R}\right)+b|}^K)$$ (2)

where, V(r) is the velocity at radial position r; R is the blood vessel radius; $V_{\mathit{max}}$ is the maximum velocity at the center; a is a scale factor accounting for a non-zero velocity at the vessel wall; b is a parameter accounting for a radial shift of the peak of the laminar profile; and K is the bluntness of the laminar profile. We calculated the coefficient of determination of blood flow velocity, $R_v^2$, to estimate the accuracy of fitting. Please note that r ranges from -R to R in describing the radial profile along a line bisecting the center of the vessel from the vessel wall on one side to the vessel wall on the other side.

Previous studies[3,4,29] have revealed that the shear-induced diffusion of red blood cells is linearly proportional to the shear rate (velocity radial gradient, $\frac{\partial V_{\mathit{RBC}}}{\partial r}$) with a proportionality constant ${\alpha }_{\mathit{shear}}$. We used Equation 3 to quantify ${\alpha }_{\mathit{shear}}$ based on the experimentally measured diffusion coefficient (D) and fitted RBC velocity $V_{\mathit{fit}}\left(r\right)$, where the fitted RBC velocity $V_{\mathit{fit}}\left(r\right)$ was obtained by fitting Equation 2 against the experimental blood flow velocity measured with DLS-OCT. The coefficient of determination of shear-induced diffusion， $R_{D-\partial v/\partial r}^2$, was used to estimate the fitting accuracy.

$$D\left(r\right)={\alpha }_{\mathit{shear}}\left|\frac{\partial V_{\mathit{RBC}}}{\partial r}\right|$$ (3)

Ascending venules (n=47) with a diameter greater than 30 μm were chosen from seven mice (3-to-4 DLS-OCT regions for each), and 2-to-3 horizontal cross sections at different depths in each venule were used for analysis. To minimize the blood vessel direction dependent bias resulting from the angle between blood flow direction and the optical axis, we selected the vessel section, which has 6 z-planes (corresponding to an ~20 um thickness), so that the center of the vessel shifted no more than 3 um over approximately 20 um in depth between the top z-plane and the bottom z-plane (as illustrated by Supplemental Figure 2 in Supplementary Figures). Blood flow velocities and diffusion coefficients for each vessel measured were estimated from 10 radial profiles with an angular interval of 18° for each horizontal cross section and initially grouped based on the averaged diameter of the 10 radial profiles (a total of 1,130 radial profiles extracted). Data was grouped into 5 diameter-groups: 30 $\pm 2.5\mu m$, 35 $\pm 2.5\mu m$, 40 $\pm 2.5\mu m$, 45 $\pm 2.5\mu m$, and 50 $\pm 2.5\mu m$. The individual diameter of each radial profile was calculated for each group, and profiles with a diameter exceeding the defined diameter range were omitted. This resulted in a total of 713 out of 1,130 radial profiles. After omitting the poor velocity fitting results ( $R_v^2<$0.5, n=123), data was further grouped according to velocity for each vessel size group for statistical analysis as shown in Table 1.

Table 1.

Statistical results of blood flow fitting accuracy $R_v^2$, relative velocity at vessel wall to peak velocity 1-a, bluntness K, and ${\alpha }_{\mathit{shear}}$ with respect to blood flow velocity for each vessel size group. ‘n’ indicates the number of radial profiles analyzed.

d ±2.5 μm		30	35	40	45	50
n	vavg∈[1 3] mm/s	28	54	26	0	0
	vavg∈(3 4] mm/s	28	16	25	37	0
	vavg∈(4 5] mm/s	49	20	27	10	28
	vavg∈(5 6] mm/s	27	32	18	16	32
	vavg∈(6 9] mm/s	9	19	42	16	31
	All velocities	141	141	138	79	91
$R_v^2$	vavg∈[1 3] mm/s	0.70±0.03	0.73±0.02	0.77±0.02
	vavg∈(3 4] mm/s	0.79±0.02	0.79±0.02	0.85±0.02	0.88±0.01
	vavg∈(4 5] mm/s	0.74±0.02	0.77±0.03	0.78±0.01	0.81±0.03	0.85±0.02
	vavg∈(5 6] mm/s	0.77±0.03	0.76±0.02	0.76±0.03	0.82±0.03	0.79±0.02
	vavg∈(6 9] mm/s	0.78±0.05	0.77±0.03	0.85±0.01	0.9±0.013	0.89±0.01
	All velocities	0.75±0.01	0.76±0.01	0.81±0.01	0.87±0.01	0.85±0.01
1-a	vavg∈[1 3] mm/s	0.31±0.02	0.35±0.01	0.34±0.02
	vavg∈(3 4] mm/s	0.31±0.02	0.28±0.02	0.26±0.02	0.25±0.01
	vavg∈(4 5] mm/s	0.33±0.01	0.31±0.02	0.29±0.02	0.27±0.03	0.25±0.01
	vavg∈(5 6] mm/s	0.33±0.02	0.32±0.02	0.29±0.02	0.28±0.02	0.31±0.01
	vavg∈(6 9] mm/s	0.32±0.03	0.34±0.02	0.28±0.01	0.30±0.02	0.29±0.01
	All velocities	0.32±0.01	0.33±0.01	0.28±0.01	0.26±0.01	0.27±0.01
K	vavg∈[1 3] mm/s	3.3±0.13	2.5±0.11	1.98±0.13
	vavg∈(3 4] mm/s	2.8±0.14	2.6±0.22	2.3±0.1	2.0±0.07
	vavg∈(4 5] mm/s	2.9±0.1	3.4±0.12	2.4±0.16	2.7±0.21	2.0±0.1
	vavg∈(5 6] mm/s	2.9±0.17	2.7±0.14	2.8±0.18	2.4±0.22	1.9±0.09
	vavg∈(6 9] mm/s	3.1±0.23	2.8±0.19	2.4±0.13	1.8±0.08	1.9±0.07
	All velocities	3.1±0.07	2.8±0.07	2.5±0.07	2.1±0.07	2.0±0.06
αshear, 10−6 mm2	vavg∈[1 3] mm/s	0.38±0.03	0.36±0.02	0.34±0.02
	vavg∈(3 4] mm/s	0.27±0.02	0.27±0.02	0.24±0.01	0.21±0.01
	vavg∈(4 5] mm/s	0.23±0.01	0.26±0.02	0.24±0.01	0.24±0.03	0.21±0.01
	vavg∈(5 6] mm/s	0.21±0.01	0.22±0.01	0.24±0.02	0.23±0.02	0.28±0.01
	vavg∈(6 9] mm/s	0.17±0.02	0.2±0.01	0.14±0.01	0.14±0.01	0.16±0.01
	All velocities	0.26±0.01	0.29±0.01	0.23±0.01	0.21±0.01	0.22±0.01

To account for the non-ideal-circular cross-section (varying vessel diameter) of blood vessels, we fit the RBC velocity along each radial profile directly with Equation 2 (without averaging across profiles). The bluntness (K) of the blood laminar flow profile and ${\alpha }_{\mathit{shear}}$ were statistically analyzed for each group. Measured data were compared among blood flow velocity and vessel size groups. The post-hoc Tukey test was performed after One-Way ANOVA to correct the family wise error. P<0.05 was accepted as statistically significant. All statistical results were expressed as mean±s.e.m. (standard error of the mean).

3. Results

The total blood flow velocity and diffusion coefficient were obtained with DLS-OCT, and the vascular structures indicated by the total blood flow velocity map and diffusion coefficient map were spatially aligned with the vascular anatomy measured with the OCT angiogram (Figure 2). Laminar blood flow and diffusion coefficient distributions within single blood vessels were observed from single plane en-face velocity and diffusion coefficient maps as shown in Supplemental Figures 1 and 2.

Figure 2.

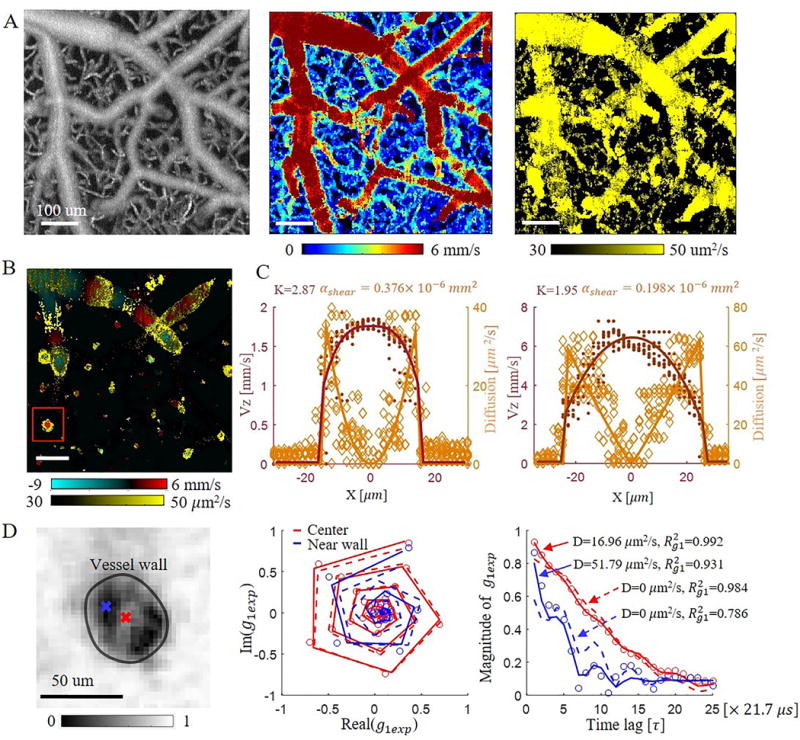
Representative DLS-OCT result. (A) Maximum Intensity Projection (MIPs) of an OCT angiogram (left), total blood flow velocity (middle), and diffusion coefficient (right) over 0–350 μm in depth. Scale bar, 100 μm. (B) En face single plane axial velocity overlapped with diffusion coefficient at a depth of 100 $\mu m$. Scale bar, 100 μm. (C) Axial blood flow profile and diffusion coefficient profile of ascending venules with a vessel diameter of 31 $\mu m$ (left) and 51 $\mu m$ (right). Solid lines are the fitted laminar blood flow profile and diffusion coefficient profile of the averaged $v_z$ and D along 10 profiles for each vessel section. Dark-red dots and orange diamonds represent the measured RBC velocity and diffusion coefficient along all 10 profiles, respectively. (D) Left: Experimental autocorrelation function ( $g_{1exp}$) map at the 10^th time lag for the ascending venule marked in (B); middle: complex plane autocorrelation function curve at the center (red) and near wall (blue) positions within the vessel; right: magnitude change of $g_{1exp}$ versus time lag for the center (red) and near wall (blue) positions. Red and blue circles are the experimental $g_{1exp}$. Solid curves are the fitted results when considering both convective and diffusive motions of RBCs. The dashed curves illustrate the fitted results when only considering convective motion of RBCs (diffusion coefficient was set to 0). $R_{g1}^2$ is the coefficient of determination, representing fitting accuracy.

The overlapped image of the axial velocity and the diffusion coefficient at a depth of 100 $\mu m$ shows that a higher diffusion coefficient near the vessel wall was observed for both penetrating and transverse vessels (Figure 2B). Further elaboration of this phenomenon is provided by the experimental autocorrelation function image shown in Fig. 2D. Note that the experimental autocorrelation function ( $g_{1exp}$) decays faster near the vessel wall (blue) than in the center (red) which already implies a high shear-induced diffusion coefficient of red blood cells near the vessel wall^3,4,9,14 since we know that RBC speed is the lowest at the vessel wall. To verify this hypothesis, we compared the fitting results when only considering convective motion (D=0) to that of considering both convective and diffusive motions. It turned out that the fitting accuracy ( $R_{g1}^2$, coefficient of determination) deteriorated for both locations ( $R_{g1}^2$ decreased from 0.992 to 0.984 for the center position, and from 0.931 to 0.786 for the near-wall position). In addition, we noticed that the fitted transverse velocities ( $v_t$) increased from 0.1 mm/s and 1.9 mm/s (convective and diffusive motion) to 5.6 mm/s and 8.0 mm/s (convective motion only) for the center and near-wall positions, respectively; while the axial velocities ( $v_z$) didn’t change ( $v_z$=4.7 mm/s and 4.2 mm/s, respectively). However, since a penetrating venule was being analyzed and the axial angle of the vessel was ~85°, the transverse velocity should not be greater than the axial velocity. Thus, $v_t$ was likely trying to compensate for the decay of the correlation function due to shear induced diffusion when the diffusion coefficient was fixed to 0. This indicates that in addition to convective motion, RBCs within the blood vessel also have diffusive motion; and that the diffusive motion is likely stronger (i.e. D is higher) near the vessel wall compared to that in the vessel center.

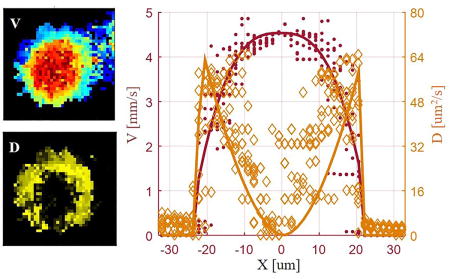
Figure 2C shows representative results of the radial blood flow velocity and shear-induced diffusion coefficient profiles of two ascending venules with vessel diameters of 31 $\mu m$ and 51 $\mu m$. A blunted laminar blood flow profile was observed from the fitted results. The measured bluntness (K) was 2.87 $\pm 0.22$ ( $R_v^2=0.73\pm 0.04,$n=10) and 1.95 $\pm 0.07$ ( $R_v^2=0.84\pm 0.03,$n=10) for vessels with diameters of 31 $\mu m$ and 51 $\mu m$, respectively. In addition, we also noticed a good agreement between the DLS-OCT measured diffusion coefficient and the shear-induced diffusion coefficient calculated from the velocity profile with Equation 3. The coefficient ${\alpha }_{\mathit{shear}}$ relating the shear-induced diffusion to the measured one was determined to be 0.376 $\pm 0.041\times {10}^{-6}m{m}^2$( $R_{D-\partial v/\partial r}^2=0.55\pm 0.05,$n=10) and 0.198 $\pm 0.007\times {10}^{-6}m{m}^2$ ( $R_{D-\partial v/\partial r}^2=0.65\pm 0.05,$n=10) for the vessels with a diameter of 31 $\mu m$ and 51 $\mu m$, respectively.

We analyzed the blood flow bluntness and ${\alpha }_{\mathit{shear}}$ as functions of the vessel diameter and blood flow velocity within each vessel size group. Data satisfying the criteria specified in the Methods were grouped with respect to the diameter with 5 μm intervals. Figure 3 presents the distribution of radial blood flow bluntness K and ${\alpha }_{\mathit{shear}}$ versus the radial velocity fitting accuracy $R_v^2$ (Figure 3A and Figure 3B, respectively), ${\alpha }_{\mathit{shear}}$ versus blood flow velocity (Figure 3C), and ${\alpha }_{\mathit{shear}}$ versus radial blood flow bluntness K (Figure 3D) for each vessel size group. Note that the radial velocity fitting accuracy ( $R_v^2$) is much better for large vessels compared to smaller ones as shown in Table 1, Figure 3A and B, and Figure 4B.

Figure 3.

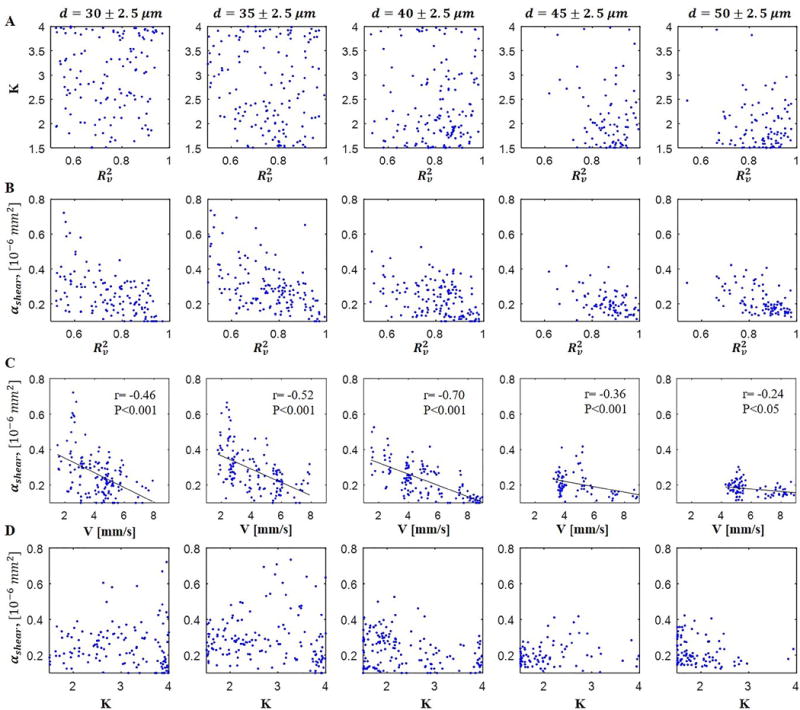
Scatter plot showing the distribution of (A) radial blood flow bluntness K versus radial velocity fitting accuracy $R_v^2$, (B) ${\alpha }_{\mathit{shear}}$ versus radial velocity fitting accuracy $R_v^2$, (C) ${\alpha }_{\mathit{shear}}$ versus average velocity, and (D) ${\alpha }_{\mathit{shear}}$ versus bluntness K for each vessel size group.

Figure 4.

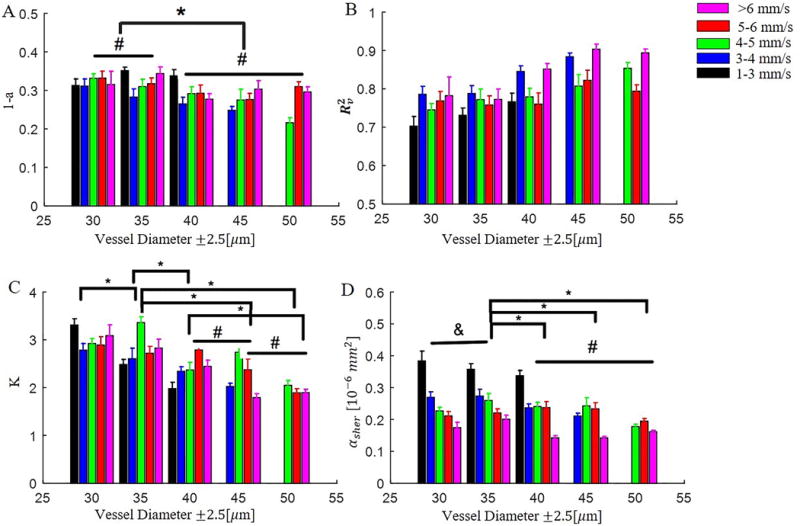
Distribution of (A) relative blood flow velocity (1-a) at the vessel wall (a: scale factor in Equation 2), (B) radial velocity fitting accuracy $R_v^2$, (C) bluntness of blood flow velocity, and (D) ${\alpha }_{\mathit{shear}}$ among vessel groups with different diameters and blood flow velocities. Significant differences between diameter groups are reported: * P<0.05, & P=0.07, # nonsignificant. Note that significant differences amongst velocity sub-groups are not reported.

One can note from Figure 3A that, for big vessels (d>40 μm), $R_v^2$ is better when the bluntness (K) is small. In addition, the bluntness was found to be decreasing with increasing vessel diameter (Table 1 and Figure 4C). Together, these data suggest that the smaller the vessel the blunter the blood flow, which is in agreement with previous reports[2,30,31]. The lack of significance between vessel groups d=40 μm and 45μm, and groups d=45 μm and 50 μm as shown in Figure 4C may suggest that the bluntness was gradually reaching a stable level (parabolic flow) as vessel size increased. We also analyzed the relationship between bluntness K and blood flow velocity v but found no significant correlation, suggesting that vessel diameter is the dominate factor that determines the blood flow radial profile in the cerebral microvasculature (vessel diameter<55 $\mu m$).

Figure 3B shows the distribution of ${\alpha }_{\mathit{shear}}$ versus $R_v^2$ and vessel size. Firstly, one can note that the larger the vessel size the narrower the distribution of ${\alpha }_{\mathit{shear}}$, and that ${\alpha }_{\mathit{shear}}$ was slowly decreasing with increasing vessel size (Figure 3C and Figure 4D). Another observation was that ${\alpha }_{\mathit{shear}}$ was decreasing to ~0.2 $\times {10}^{-6}m{m}^2$ as $R_v^2$ increased to greater than 0.8 for all vessel sizes. We don’t understand the significance of this observation, but it gives us more confidence in the lower values of ~0.2 $\times {10}^{-6}m{m}^2$ estimated for ${\alpha }_{\mathit{shear}}$. A weak negative correlation between ${\alpha }_{\mathit{shear}}$ and blood flow velocity was noticed, as shown in Figure 3C. The low correlation coefficient between ${\alpha }_{\mathit{shear}}$ and velocity for vessel groups d= 45 $\mu m$ and d=50 $\mu m$ may be due to the lack of slow velocity values for the two groups. We also compared the distribution of ${\alpha }_{\mathit{shear}}$ with respect to bluntness K (Figure 3D) but found no significant correlation.

4. Discussion

In this study, we have shown the shear-induced diffusion of RBCs as measured with DLS-OCT. We first tested the repeatability of DLS-OCT for RBC velocity and diffusion imaging in living animals as shown in Supplemental Figure 1. While variations were observed which may result from the physiological regulation of the animal, the measured values of blood flow velocity, radial profile bluntness, and ${\alpha }_{\mathit{shear}}$ were consistent in general. Representative en-face single plane images of a penetrating venule (Supplemental Figure 2) show the measured velocities, diffusion coefficients and fitted radial velocity and RBC shear-induced diffusion coefficient at adjacent depths. We compared the measured values of the 6 adjacent depths of this venule. We note that across the depths that (1) the vessel center remained constant indicating that the method we used to select ascending venule segments for data extraction can minimize any direction dependent bias, (2) laminar blood flow was observed in the velocity map for all depths (Supplemental Figure 2A), (3) a higher diffusion coefficient was detected in the peripheral region of the lumen (Supplemental Figure 2B), and (4) the measured velocities and diffusion coefficients were similar (Supplemental Figure 2C). We also compared the estimated diameter, fitted radial velocity at the center line, radial profile bluntness, and ${\alpha }_{\mathit{shear}}$ of the 6 adjacent planes as shown in Supplemental Figure 2D. It was noted that, with increasing depth, the velocity at the center line was increasing while the bluntness (k) of the radial profile was decreasing slightly. This may be a result of the blood vessel lumen becoming narrower in the deeper layers, as shown in the right panel of Supplemental Figure 2D. In contrast, the ${\alpha }_{\mathit{shear}}$ didn’t show any trend with changing depth.

We noted that a laminar blood flow profile (i.e. K=2) was commonly observed in bigger vessels (d>40 μm) while there was more blunted flow in small vessels (d<35 μm), as shown in Supplemental Figure 3. This is consistent with previous observations of more blunted flow in smaller diameter vessels [2,30,31], and is likely a result of the vessel diameter approaching the scale of the RBC diameter. This also results in a lower radial velocity fitting accuracy for smaller vessels. Interestingly, we also noticed lower scale factor ‘a’ values (Table 1 and Figure 4A) in smaller blood vessels compared to bigger vessels, indicating a higher relative velocity (1-a) near the vessel wall in smaller vessels. Therefore, the higher ${\alpha }_{\mathit{shear}}$ for smaller vessels may be due to the small velocity gradient (i.e. shear rate) that resulted from the higher relative velocity to the centerline velocity and the larger bluntness of the radial blood flow profile.

It’s worth noting that our measured value of ${\alpha }_{\mathit{shear}}$ is lower than the previously reported value of around 1 $\times {10}^{-6}$ mm² [4], which may be due to differences in experimental methodologies. Ex-vivo experiments performed by Goldsmith et al. [4] measured the parameters of ghost red blood cells flowing in a glass tube. In contrast, we measured the blood flow velocity and diffusion coefficient directly in the vasculature of a living animal brain. The differences in the dynamics of natural RBCs versus ghost RBCs may contribute in part to the smaller ${\alpha }_{\mathit{shear}}$. Also, the elasticity of blood vessels compared to the rigid glass tube may also affect the result. The blood vessel experiences normal physiological variations on the time scale of seconds while there was no such motion in the ex-vivo experiment. Nonetheless, the measured values of ${\alpha }_{\mathit{shear}}$ from in vivo and ex-vivo are of a comparable magnitude, adding confidence to our procedure for estimating shear induced RBC diffusion in vivo.

Isoflurane was used in this study for animal anesthetization. It is a well-known vasodilator of the cerebral vasculature, including pial and penetrating vessels and it is likely that it had an effect on the measured velocity and diffusion parameters. Since we had no data on another anesthetic or without anesthesia, we are not able to compare the effect of anesthesia on the same vessels within the same imaging area. Nonetheless, we don’t expect anesthesia to impact our general observation of blunted laminar blood flow and the RBC shear-induced diffusion.

The hemodynamic properties of blood flow are continuously sensed by the endothelium, which is the innermost layer of the blood vessels with direct contact with the blood flow[32]. The mechanical interactions have been suggested to play a role in physiological adaptive dilatation and vascular remodeling[33]. The measurement of the shear induced diffusion using DLS-OCT has the potential to serve as a biomarker for assessing vascular dysfunction. It could also be a valuable tool for studying the mechanical forces of blood flow interacting with the vessel wall and endothelium.

Finally, our experimental results provide direct experimental evidence explaining why the observations that non-invasive diffuse correlation spectroscopy (DCS) measurements of blood flow reveal an “apparent” diffusion of red blood cells and not the velocity of RBCs. From the earliest measurements of blood flow with DCS in 2001[34], it was noted that the “the diffusion model fits the data better than the random flow model” and that the reason was not known “We suspect that this may be due to the tortuous nature of the capillary bed, and to the peculiarities of a pulsatile complex fluid flow.” Other explanations for the diffusive nature of the motion detected in DCS experiments have also been discussed in the literature, such as the complexity of the RBC motions and RBC spatial distribution (rolling, tumbling, aggregation)[6], extravascular tissue shearing effects due to pulsatile flow[35], averaging of correlation curves corresponding to different points in the cardiac cycle[36], and averaging of signals from a heterogeneous mix of vessels with varied dimensions and flow rates[37]. The direct experimental evidence of shear-induced diffusion of RBCs is provided by Fig 2D which shows that the correlation function decays faster near the vessel wall where velocity is a minimum than in the center where velocity is a maximum. This faster decay can only happen because of other dynamics of the RBCs. The model fitting of the decay of the correlation function indicates that the diffusion model fits the experimental data well and produces a diffusion coefficient that is consistent with the phenomenon of shear induced diffusion of red blood cells [4–7]. This model fitting is particularly strong evidence for shear induced diffusion as the laminar flow profile produces a radial shear that well predicts the radial distribution of the RBC diffusion coefficient. Our experimental measurements of ${\alpha }_{\mathit{shear}}$ and the potential dependency on RBC velocity will guide future efforts to improve the quantitative accuracy of DCS measurements of blood flow.

5. Conclusion

In this work, we applied the DLS-OCT imaging technique to study the radial profiles of the cerebral blood flow velocity and shear-induced diffusion within ascending venules in the mouse cerebral cortex in vivo. Our data represents the first in-vivo measurement of shear-induced diffusion of red blood cells in the microvasculature. With this optimized DLS-OCT technique, we were able to simultaneously measure both absolute blood flow velocity and the diffusion coefficient in vivo. We estimated the bluntness in the measured blood flow velocity profile, and noticed that the smaller the vessel diameter the blunter the radial flow profile. Our study also suggested that the faster decay of the autocorrelation function near the vessel wall is due to a high diffusion coefficient resulting from the shear-induced diffusion of red blood cells. The coefficient of proportionality ( ${\alpha }_{\mathit{shear}}$) between the shear rate and the diffusion coefficient was measured to be 0.1 to 0.5 $\times {10}^{-6}$ mm² which is smaller than the value of 1 $\times {10}^{-6}$ mm² measured in an ex-vivo study[4]. Importantly, the observation that the shear induced diffusion of red blood cells causes a faster decay of the temporal field autocorrelation function than the RBC velocity provides experimental support for the observation that non-invasive measurements of cerebral blood flow by diffuse correlation spectroscopy is dominantly sensitive to the diffusion of red blood cells, not the velocity.