Tuning Low-Voltage-Activated A-Current for Silent Gain Modulation

Abstract

Modulation of stimulus-response gain and stability of spontaneous (unstimulated) firing are both important for neural computation. However, biologically plausible mechanisms that allow these distinct functional capabilities to coexist in the same neuron are poorly defined. Low-threshold, inactivating (A-type) K⁺ currents (I_A) are found in many biological neurons and are historically known for enabling low-frequency firing. By performing simulations using a conductance-based model neuron, here we show that biologically plausible shifts in I_A conductance and inactivation kinetics produce dissociated effects on gain and intrinsic firing. This enables I_A to regulate gain without major changes in intrinsic firing rate. Tuning I_A properties may thus represent a previously unsuspected single-current mechanism of silent gain control in neurons.

1. Introduction

The ability of neurons to alter their gain, that is, to change the steepness of the relationship between input stimulus and output firing rate, is considered crucial for neural computation (Salinas & Thier, 2000; Salinas & Sejnowski, 2001). However, effective neural processing is also thought to rely on the ability to maintain stable electrical activity in the absence of stimuli (Turrigiano & Nelson, 2000; Davis & Bezprozvanny, 2001; Marder & Prinz, 2002). Thus, it is of interest to elucidate biologically feasible mechanisms that allow modulation of stimulus-response gain independently of intrinsic neuronal activity. Hitherto proposed mechanisms of achieving such “silent” gain modulation (i.e., changing stimulus responsiveness without changing neural activity in the absence of stimuli) rely on elaborate balancing of electrically opposite sets of synaptic inputs (Chance, Abbott, & Reyes, 2002) or somatic voltage-gated currents (Burdakov, 2005). While this can, in theory, achieve silent gain modulation, there is little evidence to suggest that such balanced changes in coincident and opposing sets of currents can be triggered by biologically relevant stimuli.

On the other hand, there is a large body of experimental evidence showing that endogenous stimuli (such as second messengers and neuromodulators) can tune the properties of individual voltage-gated currents. However, little is known about whether changes in a single current can enable silent gain modulation. Here we have focused on a subthreshold current expressed in diverse types of neurons, the low-voltage-activated (LVA) transient A-type K⁺ current (I_A) (Birnbaum et al., 2004). We explored the extent to which experimentally reported variations in LVA I_A properties can produce silent gain modulation.

2. Methods

To study the effects of I_A on neuronal gain, we used a previously published single-compartment, Hodgkin-Huxley-type model neuron that comprises an LVA I_A, six other membrane currents (I_Na, I_CaS, I_KCa, I_Kd, I_H, and I_leak), and an intracellular calcium buffer (Prinz, Thirumalai, & Marder, 2003). All maximal conductances, channel kinetics, and reversal potentials (E_rev) were as in the tonically firing model neuron in Prinz et al. (2003), except those for the LVA I_A, which were changed as indicated. The membrane area was constant at 0.628 × 10⁻³ cm² for all simulations. For simplicity of analysis, changes to parameters were constrained to keep the firing pattern tonic and regular and to avoid silence or bursts. Simulations were performed using Matlab stiff systems numerical integrator ode23s at a time resolution of 25 μs.

Input-output gain was measured as the average gradient of the relationship between neuronal firing rate and driving current (as presented in Hz per nA) in the range of 0 to 0.4 nA driving current. In practice, this captured the steepest part of the tuning curve. The firing frequency plotted in these graphs was assessed 1 second after a change in the driving stimulus to avoid any confounding effects of adaptation.

We focused on two types of input stimulus: a sustained driving stimulus of variable intensity in the form of current, as occurs in a large class of biological neurons (Cowley et al., 2001; Burdakov et al., 2006) (see Figures 1 and 2), and a current-based synaptic input model (see Figure 3). The synaptic model was designed to introduce a series of impulses of 0.75 nA magnitude, each lasting 2 ms, at random intervals distributed by the Poisson distribution (see Figure 3A). The intensity of synaptic input was varied by changing the mean interpulse interval (λ) between 1 and 30 ms.

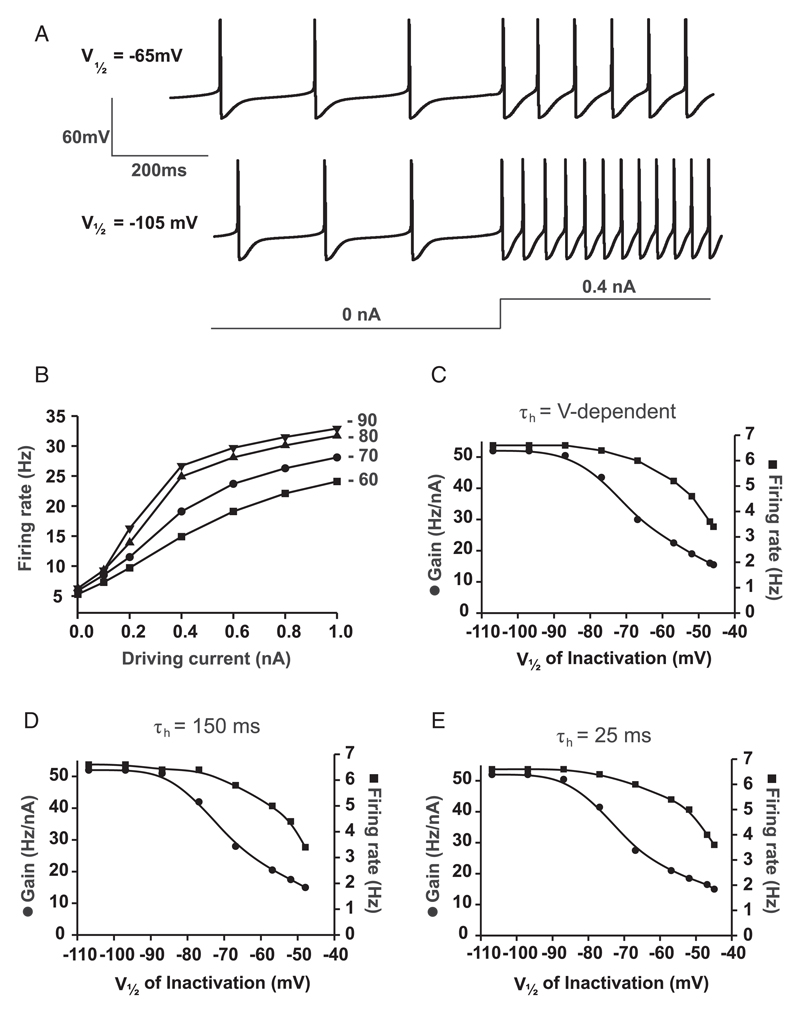
Figure 1.

(A) Input-output curves of the model neuron with different values of g_A (A-current conductance; values are given near corresponding datasets). (B) Relationship between g_A and gain (left y-axis) and between g_A and resting firing rate (right y-axis), where τ_h is intermediate and voltage-dependent (as in Prinz et al., 2003). (C) Same as in panel B but with slow voltage-independent τ_h(150 ms). (D) Same as in panel B, but with fast voltage-independent τ_h (25 ms). (E) Relationship between τ_h of inactivation and gain (left y-axis) and between τ_h of inactivation and baseline firing rate (right y-axis), where τ_h is voltage-independent. V_1/2 of inactivation is at baseline level (−56.9 mV, as in Prinz et al., 2003). (F) Same plot as in panel E, but where V_1/2 of inactivation is −100 mV.

Figure 2.

(A) Examples of firing responses of the model neuron with different values of V_1/2 of inactivation. τ_h is intermediate and voltage-dependent. (B) Input-output relationships of the model neuron with different values of V_1/2 of inactivation (V_1/2 values given near corresponding datasets). (C) Relationship between V_1/2 of inactivation and gain (left y-axis) and between V_1/2 of inactivation and baseline firing rate (right y-axis), where τ_h is intermediate and voltage-dependent (as in Prinz et al., 2003). (D) Same as in panel C, but with slow voltage-independent τ_h (150 ms). (E) Same as in panel C but with fast voltage-independent τ_h (25 ms).

Figure 3.

(A) Example of noisy membrane potential generated by the synaptic model (upper trace) where impulses were generated by the Poisson distribution (lower trace) with a mean interimpulse interval of 20 ms. (B) Input-output relationships of the model neuron with different values of g_A (g_A values given near the corresponding dataset). Av. I_syn is the average synaptic current, which is driven by modulating the mean interimpulse interval (λ) between 1 and 30 ms. (C) Examples of firing responses of the model neuron with different values of g_A using a model synaptic input (as demonstrated in panel A). g_A values are given near the corresponding dataset. λ is the mean interval between impulses generated by the Poisson distribution. (D) Input-output relationships of the model neuron with different values of V_1/2 of inactivation (V_1/2 values given near corresponding datasets). Av. I_syn is the average synaptic current, which is again driven by changes in λ. (E) Examples of firing responses of the model neuron with different values of V_1/2 of inactivation using the synaptic input model (as in panel C). Values of inactivation V_1/2 are given near the corresponding dataset. λ is the mean interval between impulses, generated by the Poisson distribution.

3. Results

We examined three types of biologically plausible changes in LVA I_A properties. First, we varied I_A conductance (g_A). Increasing g_A progressively reduced both the gain and the spontaneous firing rate (see Figures 1A–D). Given that the speed (τ_h) and voltage dependence of LVA I_A inactivation can vary in biological neurons (Lozovaya, Vulfius, Ilyin, & Krasts, 1993; Muller, Hallermann, & Swandulla, 1999; Burdakov & Ashcroft, 2002), we next examined the relationship between g_A, gain, and firing rate at (1) intermediate and voltage dependent τ_h (from Prinz et al., 2003) (see Figure 1B); (2) slow voltage-independent τ_h (150 ms) (see Figure 1C); and (3) fast voltage-independent τ_h (25 ms) (see Figure 1D). Increasing g_A progressively reduced both gain and baseline unstimulated firing rate under all of these conditions. Thus, g_A can modulate gain, but this modulation is not entirely silent, as the spontaneous firing rate is also affected.

Second, we explored the effects of changes in the speed of I_A inactivation. For simplicity, in these simulations we made τ_h voltage independent, as reported for some biological neurons (Burdakov & Ashcroft, 2002). Varying τ_h within a biologically plausible range of values had little effect on our measure of gain or on tonic firing rate, irrespective of whether the V_1/2 of inactivation was depolarized (see Figure 1E) or hyperpolarized (see Figure 1F).

Third, we varied the voltage dependence of I_A inactivation. Shifting the voltage at which inactivation is half-maximal (V_1/2) toward positive potentials reduced both gain and baseline firing rate (see Figures 2B–2E; see Figure 2A for an example of how the neuron processed the same input for different values of V_1/2). However, the changes in gain and intrinsic firing rate occurred at different ranges of V_1/2. In the hyperpolarized range (V_1/2 < −75 mV), as reported experimentally for some neuronal subtypes (Song et al., 1998; Starodub & Wood, 2000; Schone, Venner, Knowles, Karnani, & Burdakov, 2011), there were large effects on gain but not baseline firing (see Figures 2C–2E). This differential modulation of gain versus firing rate persisted at the three different types of τ_h, as described above: (1) intermediate and voltage-dependent τ_h (from Prinz et al., 2003) (see Figure 2C); (2) slow voltage-independent τ_h (150 ms) (see Figure 2D); and (3) fast voltage-independent τ_h (25 ms) (see Figure 2E). This suggests that changing the voltage dependence of I_A inactivation can lead to near-silent gain modulation regardless of the speed of inactivation within a biologically plausible range of inactivation V_1/2 (see Figure 2A for an example of raw data).

To explore whether these findings hold true under a noisy input, as well as under sustained current inputs, as examined in Figures 1 and 2, we also simulated the effects of changing g_A and V_1/2 of inactivation on firing driven by a fluctuating, synaptic-like, excitatory input (see Figure 3A and section 2). Similar to the simulations using a sustained driving input (see Figure 1), these simulations showed that increasing g_A progressively reduced both gain and baseline firing rate, but this was not entirely silent (see Figures 3B and 3C). On the other hand, again in concordance with the sustained-input simulations (see Figure 2), shifting the V_1/2 of inactivation to more hyperpolarized potentials increased gain with little or no effect on baseline firing (see Figures 3D and 3E).

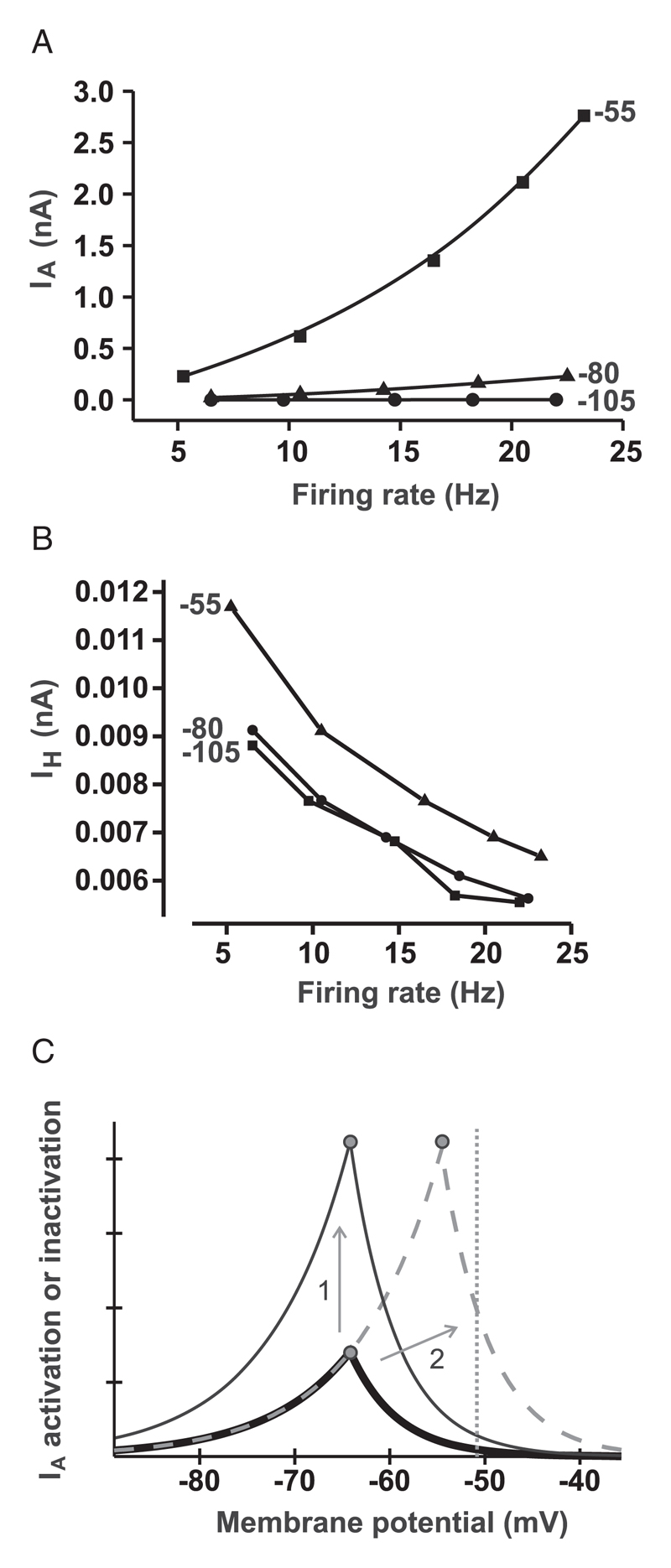
In view of these results, we next analyzed I_A current data in order to determine whether we could elucidate a mechanism of differential gain modulation. We measured the average I_A current per action potential, (averaged over 10 action potentials) under three physiological conditions: I_A inactivation V_1/2 of −55 mV (baseline), −80 mV, and −105 mV (see Figure 4A). We found that the relationship between average I_A current per spike and firing rate was considerably steeper for depolarized V_1/2 than for hyperpolarized V_1/2 (see Figure 4A). In contrast, the current-frequency relationship for I_H (an electrophysiological opponent of I_A) was similarly steep for all three values of V_1/2 (see Figure 4B). Thus, depolarizing shifts in inactivation V_1/2 would affect high-frequency firing more than lower frequency firing. This would account for the silent-like gain modulation we observe in Figures 2A and 2B.

Figure 4.

(A) Relationship between average I_A current (averaged over 10 spikes) and firing rate. Values at end of curves are V_1/2 of I_A used to generate those curves. (B) Same as in panel B, but for I_H (values near corresponding datasets are V_1/2 of I_A values). (C) Schematic of permissive voltage window of I_A. Left sides of peaks are steady-state activation curves (m); right sides of peaks are steady-state inactivation curves (h). The complete m and h curves upward of the m-h intercepts (peaks) are not shown for visual clarity. The thick solid line is the control; the thin solid line represents increased g_A; the dashed line represents inactivation V_1/2 shifted to positive potentials. The vertical dotted line shows the average membrane potential at the spontaneous firing rate (∼5 Hz) of the model neuron.

4. Discussion

Our results show that both g_A and I_A inactivation V_1/2 are capable of modulating gain and intrinsic (baseline) firing differentially, to produce either non-silent (g_A; see Figures 1A–1D), or near-silent (V_1/2 of inactivation; see Figure 2) gain modulation. These effects were consistent across a range of biologically plausible shifts in the voltage dependence and speed of inactivation (Lozovaya et al., 1993; Muller et al., 1999; Burdakov & Ashcroft, 2002), and also for two types of driving stimulus: a sustained current input, such as that triggered by certain neuromodulators (Cowley et al., 2001; Burdakov et al., 2006) (see Figures 1 and 2), and a fluctuating synaptic-like input (see Figure 3). We found τ_h itself incapable of controlling the gain or baseline firing rate at either depolarized or hyperpolarized potentials (see Figures 1E and 1F). This suggests that while the speed of I_A inactivation presumably modulates temporal summation of phasic inputs, it modulates neither firing nor gain under the conditions studied here (tonic firing, tonic driving current).

We propose that the differential effects of changes in I_A parameters (demonstrated for inactivation V_1/2) on gain versus intrinsic firing arise because the effects of I_A on firing depend on the average membrane potential of the neuron, which becomes more positive as the firing rate increases from a low (intrinsic) value to higher (stimulus-driven) values. Depolarizing I_A V_1/2 of inactivation affects the stimulus-driven (higher frequency) firing more that the intrinsic (lower frequency) firing (see Figure 4A). In our model, this steepening of the frequency dependence of I_A (see Figure 4A) was not accompanied by a corresponding steepening in its interspike opponent, I_H (see Figure 4B), showing that the kinetics of the two currents do not necessarily ensure coupled changes in their frequency dependencies.

We speculate that the I_A V_1/2 of inactivation could be more capable of silent gain modulation than g_A because these parameters cause different transformations in the I_A “permissive voltage window” (see Figure 4C). Shifts in g_A (1 in Figure 4C) will enhance I_A at all potentials at which it is active. However, shifts in the I_A V_1/2 of inactivation (2 in Figure 4C) would differentially enhance I_A at positive, but not negative, potentials because it moves the right-side (inactivation-set) boundary but not the left-side (activation-set) boundary of the I_A voltage window (see Figure 4C).

In summary, these results suggest that changes in I_A kinetics, especially in I_A inactivation V_1/2, can produce silent-like gain modulation without a requirement for any balancing changes in other currents. To the best of our knowledge, such a cellular mechanism of silent gain control has not previously been described. This mechanism is biologically plausible and could be of general physiological importance, especially considering that the LVA I_A is widely expressed in many biological neurons and that its voltage dependence of inactivation has been reported to be tunable by a number of neuromodulators (Lozovaya et al., 1993; Muller et al., 1999; Birnbaum et al., 2004).