Abstract
The evolution of solution aggregates of the anionic form of the native monorhamnolipid (mRL) mixture produced by Pseudomonas aeruginosa ATCC 9027 is explored at pH 8.0 using both experimental and computational approaches. Experiments utilizing surface tension measurements, dynamic light scattering, and both steady-state and time-resolved fluorescence spectroscopy reveal solution aggregation properties. All-atom molecular dynamics simulations on self-assemblies of the most abundant monorhamnolipid molecule, L-rhamnosyl-β-hydroxydecanoyl-β-hydroxydecanoate (Rha-C10-C10), in its anionic state explore the formation of aggregates and the role of hydrogen bonding, substantiating the experimental results. At pH 8.0, at concentrations above the critical aggregation concentration of 201 μM but below ~7.5 mM, small premicelles exist in solution; above ~7.5 mM, micelles with hydrodynamic radii of ~2.5 nm dominate, although two discrete populations of larger lamellar aggregates (hydrodynamic radii of ~10 and 90 nm) are also present in solution in much smaller number densities. The critical aggregation number for the micelles is determined to be ~26 monomers/micelle using fluorescence quenching measurements, with micelles gradually increasing in size with monorhamnolipid concentration. Molecular dynamics simulations on systems with between 10 and 100 molecules of Rha-C10-C10 indicate the presence of stable premicelles of seven monomers with the most prevalent micelle being ~25 monomers and relatively spherical. A range of slightly larger micelles of comparable stability can also exist that become increasing elliptical with increasing monomer number. Intermolecular hydrogen bonding is shown to play a significant role in stabilization of these aggregates. In total, the computational results are in excellent agreement with the experimental results.
Graphical abstract
INTRODUCTION
Surfactants are used extensively in a wide array of products including foods, drugs, detergents, cosmetics, and paints.1,2 Glycolipid surfactants are of emerging interest due to their potential as alternatives to surfactants derived from petroleum feedstocks.3 Rhamnolipids, glycolipid biosurfactants produced predominantly by Pseudomonas aeruginosa, are of particular note within this class due to their attractive surfactant properties and production in relatively large quantities, making them increasingly viewed as green alternatives to conventional synthetic surfactants.4–6
Rhamnolipids possess either a mono- or dirhamnose headgroup coupled to a (R,R)-β-hydroxyalkanoyl-β-hydroxyalkanoic acid tail (see Figure 1). Although the native material is generally a complex mixture of congeners in which the headgroups are preserved and the tails vary in alkyl chain length and unsaturation, the most abundant congeners are typically L-rhamnosyl-β-hydroxydecanoyl-β-hydroxydecanoate (Rha-C10-C10) and L-rhamnosyl-L-rhamnosyl-β-hydroxydecanoyl-β-hydroxydecanoate (Rha-Rha-C10-C10). Most bacterial strains make mixtures of both monorhamnolipids and dirhamnolipids,7 although at least one strain has been identified as a natural mutant that is an exclusive producer of mRLs.8
Figure 1.
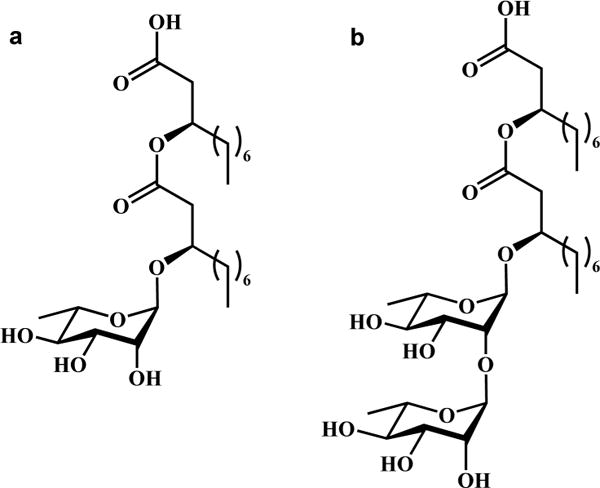
Molecular structure of (a) (R,R)-Rha-C10-C10 and (b) (R,R)-Rha-Rha-C10-C10.
Numerous previous studies have reported the behavior of rhamnolipids at the air–water interface.9–12 Given the potential of rhamnolipids as green surfactants, a thorough understanding of both their interfacial and bulk solution aggregation properties is needed to advance their utilization.
This work focuses on the evolution of aggregate structure for monorhamnolipids, since, of the two classes of rhamnolipids, monorhamnolipids are known to exhibit stronger surface activity.10,13–15 Although multiple researchers have reported critical micelle concentration (CMC) values in the micromolar regime from surface tensiometry,14,16,17 and dynamic light scattering (DLS) has provided insight into solution aggregate size, with aggregates of hydrodynamic radii ranging from several nanometers to a few hundred nanometers reported,10,14,17 detailed information about the early stages of aggregation and the growth of aggregate size as solution concentration increases is missing. Although small-angle neutron scattering (SANS) studies have provided some definitive information about aggregate size and shape, results have only been reported for solutions 20 mM and higher in concentration,9,10,15,18,19 with aggregates of ~47 monomers reported for 20 mM monorhamnolipids in pH 9 aqueous borax buffer.10 The results at 20 mM are consistent with the small micelles observed using cryo-TEM in solutions of basic pH;20 at higher concentrations, SANS results indicate the presence of lamellar structures.10 Work investigating the early stages of aggregation, and a detailed, systematic analysis of the evolution of aggregate structure with concentration is lacking in the literature.
Moreover, the published literature contains notable inconsistencies about rhamnolipid aggregation behavior, some of which arise from the use of widely varying solution conditions (ionic strength and pH) as well as rhamnolipid congener mixtures grown and harvested from different bacterial strains using different extraction procedures.10,14,16,17,20 Thus, a need still exists to fully characterize the aggregation properties of these surfactants in solution as well as to probe the chemical microenvironments within these aggregates, especially at concentrations below ~20 mM. Toward this end, we report the combined use of surface tensiometry, fluorescence spectroscopy,21,22 fluorescence quenching,23,24 and DLS combined with all-atom molecular dynamics (MD) simulations to better understand the aggregation properties of anionic monorhamnolipids in aqueous solution at basic pH. Reported here are aggregate morphology and size data on the deprotonated native mixture of monorhamnolipids produced by and harvested from the strain Pseudomonas aeruginosa American Type Culture Collection (ATCC) 9027, chosen because it is known to be an exclusive producer of monorhamnolipids.8
EXPERIMENTAL SECTION
Materials
Hexanes (EMD Chemicals, 98.5%), ethyl acetate (EMD Chemicals, 99.5%), dichloromethane (EMD Chemicals, 99.5%), chloroform (EMD Chemicals, 99.5%), methanol (J.T. Baker, ≥99.9%), glacial acetic acid (EMD Chemicals, 99.5%), sulfuric acid (EMD Chemicals, 95%), anthrone (Sigma-Aldrich, >93%) hydrochloric acid (EMD Chemicals, 36.5–38%), sodium hydroxide (J.T. Baker, 98%), ethanol (Decon Laboratories, Inc., absolute), sodium phosphate monobasic monohydrate (EMD, 98%), sodium dibasic anhydrous phosphate (EMD Chemicals, 99%), 6-propionyl-2-dimethylaminonaphthalene (prodan, Molecular Probes), 6-dodecanoyl-2-dimethylaminonaphthalene (laurdan, Molecular Probes), toluene (EMD Chemicals, 99.5%), pyridine (Sigma-Aldrich, ≥99%), and (tridecafluoro-1,1,2,2-tetrahydrooctyl)triethoxysilane (Gelest) were used as received. Pyrene (Sigma-Aldrich, ≥99.0%) and benzophenone (BP, Alfa Aesar, 99%) were further purified by recrystallization from an ethanol (1–2 vol %) in water solution. Water was purified using a Milli-Q UV system to a resistivity of 18.2 MΩ (Millipore Corp.) with a total organic carbon content <6 ppb.
Surfactant Stock Solution Preparation
The native monorhamnolipid mixture (mRL) was harvested from cultures of P. aeruginosa ATCC 9027 using procedures described previously25 and further purified using column chromatography on silica (Sigma-Aldrich, 60 Å). Eluted mRLs were detected on silica-coated, aluminum-backed thin layer chromatography (TLC) sheets (EMD Millipore). Dichloromethane solutions of the purified mRLs were then filtered through Whatman Anapore 0.02 μm filters prior to triple rotoevaporation followed by lyophilization. A combination of reversed-phase HPLC and LC-MS was used to assess native mRL mixture purity after this combined harvesting–purification protocol. These mRL mixtures are routinely in excess of 98% purity based on identifiable monorhamnolipid structures (i.e., single rhamnose unit with variable lipid tail length and saturation) in the reversed-phase HPLC analysis. More information about the composition of this mRL congener mixture is provided in Table S1 of the Supporting Information.
mRL solutions were prepared by dissolving purified and freshly lyophilized mRL in the appropriate buffer and stirring in a Teflon vial (VWR) with a Teflon-coated stir bar for a minimum of 12 h. Teflon is necessary to minimize strong surface adsorption of these materials. Buffers were prepared with appropriate amounts of sodium phosphate monobasic monohydrate, sodium dibasic anhydrous phosphate, and sodium hydroxide using Milli-Q water and then filtered sequentially through Acrodisc 25 mm syringe filters with 0.45, 0.2, and 0.1 μm Supor membranes.
Instrumentation and Measurement Procedures
Surface tension measurements were performed to ±0.5 mN/m on a Fisher Scientific model 21 Surface Tensiomat using a Pt–Ir du Noüy ring (Fisher Scientific) or a Biolin Scientific model Sigma 701 Attension surface tensiometer. Tensiometers were calibrated with pure water at ~72 mN/m before each experiment. Three independently prepared samples were tested for each solution condition studied.
Dynamic light scattering (DLS) measurements were taken on a Viscotek model 802 instrument, equipped with a 50 mW fiber-optic coupled diode laser at 830 nm, using a 150 μL sample aliquot in a submicro quartz fluorometer cuvette (Starna Cell) held at 20 °C. Autocorrelation functions were analyzed using OmniSIZE 3.0 software or through cumulants analysis26,27 by fitting the average correlation functions using Origin 7.5. The DLS instrument was validated daily using polystyrene particle standard solutions of 0.2 and 0.05 μm diameter, 2.5% (w/w) suspended in water (Alfa Aesar).
A Photon Technologies, Inc. (PTI), Quanta Master 40 spectrofluorometer was used for steady-state and time-resolved fluorescence measurements. Samples were prepared by subjecting them to a freeze–pump–thaw (FPT) cycle to eliminate dissolved O228 in an environmental control box purged with Ar and N2 and then stirred for an additional 2 h before being transferred to a sealed 0.4 cm cuvette (Starna Cell) that had been previously silanized with a fluorinated silane to prevent mRL adsorption (as described in the Supporting Information) and purged with N2. Pyrene fluorescence was excited at 337 nm with emission observed at 373 nm. Fluorescence experiments were performed at 20 °C. Three independently prepared surfactant/probe/quencher samples at each concentration were measured, and three instrumental replicates of data for each sample were acquired and averaged. Fluorescence intensities were corrected for the inner filter effect using the method of Gauthier et al.29
Molecular Dynamics Simulations
Force field parameters for the anionic Rha-C10-C10 mRL were first generated with charge groups defined according to the functional groups present in the molecule. Parameters for Rha-C10-C10 were obtained from the CHARMM (Chemistry at HARvard Macromolecular Mechanics) General Force Field (version 2b8)30 and optimized according to the CHARMM force field parameterization procedure to better reproduce the properties of Rha-C10-C10 of the high level ab initio calculations. It is noted that the set of parameters obtained for Rha-C10-C10 is compatible with the CHARMM36 force field,31,32 and it could also be used in combination with any force field parameters for other molecules.
The initial coordinates of the simulation were obtained by randomly placing Rha-C10-C10 molecules in a cubical box using PACKMOL software.33 These randomly distributed Rha-C10-C10 molecules were explicitly solvated using a cubic box of pre-equilibrated TIP3P water.34 The size of the water box was chosen to be 10 × 10 × 10 nm3 to ensure a minimal distance of at least 1 nm between the boundary water and the closest atom of the Rha-C10-C10 molecule in all directions. Solvent molecules were removed if they were within 0.28 nm of any heavy atoms of Rha-C10-C10. Equal numbers of Na+ were added to the system to neutralize the total net charge.
MD simulations were conducted in periodic boundary conditions using NAMD 2.9.35 A direct cutoff for nonbonded interactions of 1 nm, a switch function starting at 0.8 nm for the van der Waals interactions, and particle mesh Ewald36 for long-range electrostatics were applied. The SHAKE algorithm37 was used to constrain all bonds involving hydrogen atoms, and a time step of 1 fs was used for the MD integration. The temperature and pressure were controlled by the Langevin thermostat and the Nosé–Hoover Langevin barostat38,39 as implemented in NAMD, respectively. The system was first energy minimized, then heated to 300 K, and finally equilibrated under constant 1 atm pressure and temperature. During minimization, heating, and equilibration, no constraints were applied. To avoid computationally expensive long relaxation times and large systems, a method of simulated annealing was employed.40 The following protocol, used to obtain unbiased initial conformations, consists of a three-stage, simulated annealing: (i) temperature rise from 300 to 400 K in 200 ps; (ii) constant high temperature equilibration at 400 K for 800 ps; and (iii) slow cooling back to 300 K in 1 ns.
As a test of the MD simulation methods used here, the aggregation behavior of sodium dodecyl sulfate (SDS), which is known to produce aggregates of ~60 monomers, was tested. Starting with 120 anionic SDS molecules with 120 Na+ in a 10 × 10 × 10 nm3 box of water, two micelles form of ~59 SDS molecules each. This aggregation number is consistent with multiple measures of aggregation number for SDS reported in numerous papers in the literature,24,41 thereby validating the methods used here. These results are shown in Figure S11 in the Supporting Information.
RESULTS AND DISCUSSION
Critical Aggregation Concentration and Solution Aggregate Populations
Surface tension measurements on this mRL mixture at pH 8.0 in phosphate buffer (to ensure complete deprotonation of the carboxylic acid moiety42), pH 7.0, and pH 6.8 are reported in Table 1. They indicate critical aggregation concentrations (CACs) of 201 μM at pH 8.0, 130 μM at pH 7.0, and 108 μM at pH 6.8 (Figure S1), decreasing rapidly with decreasing pH as has been previously observed.10,12–14,43,44 These concentrations are termed critical aggregation concentrations, as it is believed based on results described below to be the concentration at which premicellar aggregates form, with full micelles not observed until higher concentrations. Further justification for this assertion is provided below in the fluorescence spectroscopy discussion.
Table 1.
Surface Physiochemical Properties of MRLs
| solution conditions | CAC (μM) | γmin (mN/m) | S (Å2) | Γ (mol/cm2) | reference |
|---|---|---|---|---|---|
| pH 8 in 10 mM phosphate buffera | 201 ± 12 | 29.0 ± 0.5 | 86 ± 2 | (1.94 ± 0.04) × 10−10 | this work |
| pH 7 in 0.063 M KH2PO4/0.037 M NaOHa | 130 ± 6 | 26.3 ± 0.3 | 109 ± 5 | (1.52 ± 0.07) × 10−10 | this work |
| pH 6.8 in a minimal amount of NaOHa | 108 ± 7 | 25.2 ± 0.2 | 98 ± 5 | (1.70 ± 0.09) × 10−10 | this work |
| pH 9 in 0.023 M borax/0.008 M HCl | 360 ± 20 | 31.2 | 77 | 2.2 × 10−10 | 10 |
| pH 7.4 in 5 mM HEPES/0.10 M NaCl | 70 | ~33 | 57 | 2.9 × 10−10 | 12 |
| pH 7 in 0.063 M KH2PO4/0.037 M NaOH | 180 ± 20 | 28.7 | 66 | 2.5 × 10−10 | 10 |
| pH 7, 0.1 M phosphate buffer | 79 | 29 | 46 | ||
| H2O | 40 ± 20 | 27.8 | 53 | 3.1 × 10−10 | 10 |
| 0.5 M NaCl | 30 ± 20 | 27.8 | 52 | 3.2 × 10−10 | 10 |
| pH 6.8 in 59.5 μM NaHCO3/0.01 M NaCl | 120 | 27.6 | 66 | 2.1 × 10−10 | 14 |
| pH 6.8 in a minimal amount of NaOH | 100 | 30.0 | 135 | 1.2 × 10−10 | 13 |
| pH 6.8, no electrolyte added | 150 | 29.7 | 44 | ||
| pH 5 in a minimal amount of CH3COOH | 40 | 28.2 | 59 | 2.8 × 10−10 | 13 |
Errors reported as standard deviations from measurements on a minimum of three independently prepared samples for each solution condition.
It is noted that the native mRL mixture is composed of a complex array of almost 40 congeners at varying relative abundances, with the Rha-C10-C10 congener the most abundant at typically 70–85%. Any given batch of purified mRLs has slightly different ratios of congeners, leading to small variances in measured CAC values.
The CAC values determined here along with a summary of previously reported CAC values and other parameters extracted from the surface tension results for mRLs are reported in Table 1. Of these values, none have been reported previously for mRLs collected from P. aeruginosa ATCC 9027. The values determined in this work are consistent in all cases with the values collected under generally similar solution conditions as shown in the table. In general, the CAC values decrease with pH due to the increasing protonation of the carboxylic acid moiety whose pKa has been reported to be 5.5.42
Minimum surface tension (γmin) values decrease from 29 mN/m at pH 8.0 to 26 mN/m at pH 7.0 to 25 mN/m at pH 6.8 with cross-sectional areas (S) calculated from the surface coverage (Γ) values of ranging from 86 to 109 Å2 as extracted from the surface tension data by fitting it to the Gibbs equation:2,10,13,45
| (1) |
where dγ is the change in surface tension, n is the Gibbs prefactor (here = 2), R is the gas constant, T is temperature, (d ln C1) is the change in surfactant concentration, and Γ is the surface coverage. All values calculated for the monorhamnolipid mixture used here are comparable to those measured previously for monorhamnolipid systems when accounting for differences in solution pH, ionic strength, and monorhamnolipid mixture composition.
The packing parameter (P)47,48 for the most abundant Rha-C10-C10 congener of native mRL as a representative model for the mixture is 0.48, which suggests ellipsoidal aggregates. DLS was used here to assess the aggregate populations present in solutions of these monorhamnolipids at pH 8.0. In seven separate instrumental replicates performed on three replicate solutions at pH 8.0, three aggregate populations with average Rh values of ~2.4, 10, and 90 nm were reproducibly observed at all mRL concentrations. Based on the DLS number distributions (see Figures S2 and S3), the predominant population under all mRL concentration conditions at pH 8.0 is micelles or premicelles (vida infra) with an average Rh of ~2.4 nm, with very small numbers of the two populations of larger aggregates. This conclusion is consistent with the results from fluorescence spectroscopy and MD simulations described below.
For the micelle population, another estimate of shape comes from comparing the average Rh values from the DLS data to the molecular length (plus a variable hydration layer) calculated with molecular modeling.49 With no free volume in the micelle interior, the radius of a perfectly spherical micelle (the so-called short axis) would be the length of one surfactant molecule. If the ratio of Rh to the short axis is 1, the micelle is predicted to be spherical; if this ratio is >1, the micelle is predicted to be ellipsoidal. From the DLS data, the Rh of mRL micelles is ~2.4 nm and the short axis is calculated to be 1.6 nm. Thus, the ratio of these values is >1, leading to the prediction of an ellipsoidal micellar shape. This method is in good agreement with the aggregate shapes predicted by the MD simulations below that indicate an ellipsoidal structure for micelles of larger monomer numbers. Indeed, for Rha-C10-C10 micelles, the MD simulation results suggest a slight increase in aggregate radius as monomer number increases; 2.4 nm falls approximately in the middle of all computationally determined micellar sizes.
Importantly, the DLS results are wholly consistent with our previously published cryo-TEM work on this native mRL mixture from P. aeruginosa ATCC 9027.20 The cryo-TEM results showed the presence of three populations of solution aggregates whose number densities are strongly dependent on solution pH. Micelles are clearly the predominant solution aggregate at pH 8.0, a conclusion consistent with the fluorescence spectroscopy results (vida infra); the TEM images also substantiate identification of the aggregates of ~10 nm radius as unilamellar vesicles and ~90 nm radius as multilamellar vesicles. Further, the cryo-TEM images show that the number densities of both types of vesicles drop drastically over the pH range from 7.0 to 8.0, with no vesicles of either type visible in a TEM image covering an approximate 800 nm × 800 nm region, consistent with the very low abundance of vesicles in the DLS number distribution data (Figure S3). Obviously, DLS samples a much larger volume of solution than cryo-TEM, and thus, the probability of detecting vesicles is much larger. Indeed, using the number densities of each aggregate type reported by DLS, one can develop a rough estimate of the cryo-TEM volume that would need to be sampled to see even one unilamellar or multilamellar vesicle. This analysis suggests that 50 or 50 000 images of an approximate 800 nm × 800 nm size would be needed to be analyzed to see just one unilamellar or one multilamellar vesicle, respectively. Thus, it is not surprising that neither of these vesicle structures is observed in the cryo-TEM results at pH 8.0.20 Finally, at these very low vesicle number densities, it is noted that the fraction of monorhamnolipid monomers consumed in forming these aggregates at pH 8.0 is also negligible at all concentrations greater than the CAC.
Previously reported results for mRLs suggest a growth in aggregate size as surfactant concentration increases.9,14 Thus, mRLs were studied with DLS across a range of concentrations between 0.1 and 100 mM to further explore this behavior. The size and population abundance of aggregates observed as a function of mRL concentration are shown in Figure S3. The relative abundances of these populations exhibit essentially no change within this concentration range; similarly, the observed micelle radii range from 2 to 3 nm with little to no systematic growth. Discussed below is experimental evidence from fluorescence spectroscopy measurements that supports a slight growth in aggregation number across this concentration range. This growth is believed to be primarily elongation along one axis of the micelle; the Rh determined from fitting the DLS autocorrelation function is less sensitive to such anisotropic growth. Thus, given the assumption of spherical shape in the analysis of the DLS data, the absolute sizes derived from DLS measurements should be considered only estimates.
The micelle population exhibits number densities 108 and 1011 times more prevalent than the next largest (Rh ~ 10 nm) and largest aggregates (Rh ~ 90 nm). Despite the potential error introduced in conversion of light scattering intensities to number densities by the assumption of spherical shape (up to 104 difference by the most conservative estimate50), the micelle population clearly dominates under all solution conditions studied here, with larger aggregates only present in trace quantities. Nonetheless, the presence of even small numbers of these larger aggregates strongly influences the light scattering behavior. This is manifest not only in the clear observation of these larger aggregates in the DLS intensity distributions but also in the polydispersity index calculated from the combined correlation function using cumulants analysis.26,27 Figure S4 shows the polydispersity index (PdI) as a function of mRL concentration. On the basis of these values, we conclude that the aggregate population at mRL concentrations just above the CAC is slightly polydisperse (PDI = 0.1–0.2) but increases steadily to be moderately polydisperse (PDI ~ 0.4) at higher mRL concentrations.
Previously reported Rh values for mRLs at pH 9 in borax buffer include the observation of micelles at lower concentrations (~20 mM) and lamellar structures at higher concentrations (up to 100 mM),9 lamellar structures for concentrations above the CMC at pH 7.4 in 5 mM HEPES/100 mM NaCl,12 and premicelles at low concentrations (0.06 mM), with both micelles and lamellar structures present at higher concentrations (up to 5.0 mM) at pH 6.8 in 59.5 μM sodium bicarbonate/10 mM NaCl.14 Our results are consistent in that they indicate the presence of both micelles and lamellar structures, but at pH 8.0 in 10 mM phosphate buffer, the propensity for micelle formation is high. The differences between this work and previous studies suggest that micelle and lamellar populations are highly sensitive to pH and electrolyte concentration.
Aggregate Type, Aggregate Microenvironment, and Aggregation Number
Insight into the predominant aggregate type and microenvironment in these mRL solutions is provided by the emission behavior of two hydrophobic probes, pyrene and prodan (solution emission spectra shown in Figure S5). Both probes are known to partition into hydrophobic regions of surfactant aggregates,21,51,52 and their emission intensities or wavelength maxima (λmax) depend sensitively on polarity of the aggregate microenvironment.22 Prodan exhibits a blue-shift in λmax from its free solution value of ~525 nm as its environment becomes more nonpolar, with distinct maxima observed for micelle (~500 nm) versus lamellar (~440 nm) aggregate types.21 In addition, a common measure of microenvironment polarity is the intensity ratio of the third (III) to first (I) vibronic bands of pyrene; this ratio ranges from values >1 in more nonpolar environments to ~0.5 in extremely polar environments.53
Figure 2a shows normalized fluorescence spectra for prodan as a function of mRL concentration in pH 8.0 solutions with the emission maxima plotted in Figure 2b. Prodan dissolved in octylglucoside aggregates has been shown previously to fluoresce at a λmax of ~500 nm with its corresponding emission in a lamellar phase at a much lower wavelength.22 Prodan in mRL micelles fluoresces at a λmax of ~500 nm while prodan in the mRL lamellar phase emits at the much lower wavelength of ~445 nm. At pH 8.0, prodan emission is more intense with increasing mRL concentration with the λmax shifting from that of free prodan dissolved in water (525 nm) to prodan dissolved in micelles (500 nm) as the concentration increases. A less intense shoulder is also observed at 445 nm, indicating the presence of small quantities of lamellar structures. Parasassi et al. have shown that the quantum efficiencies of prodan in micelle and lamellar environments are similar.21 Thus, these spectra allow an estimation of the relative amounts of the two phases in solution under a given set of conditions. Noteworthy about these spectra, therefore, is the dominance of the micelle form of the mRL aggregates at all concentrations at pH 8.0, consistent with the DLS results. This is in contrast to the prodan behavior at pH 4.0 (see Figure S6) in which lamellar aggregates clearly dominate at almost all concentrations.
Figure 2.
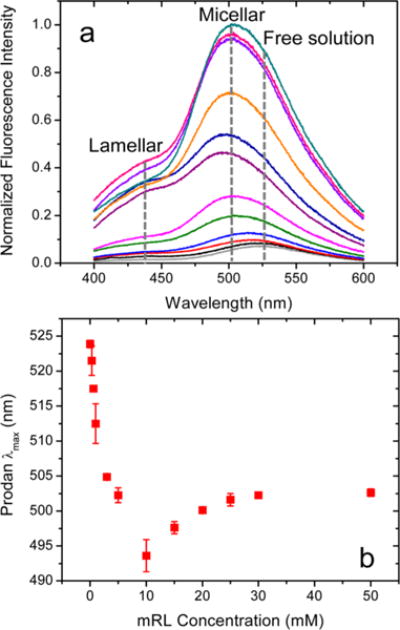
(a) Normalized prodan fluorescence spectra and (b) prodan λmax values as a function of mRL concentration at pH 8.0. Prodan concentration 250 nM; λex = 340 nm. Error bars on λmax values represent standard deviations from three independently prepared samples.
Normalized pyrene spectra are shown in Figure 3a, and the pyrene III/I intensity ratios as a function of mRL concentration are shown in Figure 3b. The pyrene ratio increases quickly up to ~7.5 mM before leveling off. In the same concentration regime <7.5 mM, the λmax for prodan (Figure 2b) decreases from its aqueous solution value of 525 to 495 nm indicative of aggregate formation.22 The rapid change in the pyrene and prodan indicators in this concentration regime suggests loosely packed premicellar aggregates that grow in size, creating increasingly more nonpolar environments. The MD simulations discussed below confirm the existence of loosely packed premicelles into which water significantly penetrates with the emergence of more spherical and ellipsoidal micelles at higher concentrations. At mRL concentrations >10 mM, the pyrene III/I intensity ratio levels off while the λmax for prodan quite surprisingly increases slightly before leveling off at >30 mM. This surprising red-shift with increasing aggregate size may arise from prodan residing progressively outside the hydrophobic core of the micelles, experiencing more polarity from the hydrated rhamnose headgroup region of the micelles. This probe emission behavior is indicative of a transition in this region in which water penetration of the aggregates decreases as fully formed micelles emerge at ~10 mM mRL with elongation of the micelles at higher concentrations. Elongation of the mRL micelles is observed in the MD simulation results at similar effective concentrations.
Figure 3.
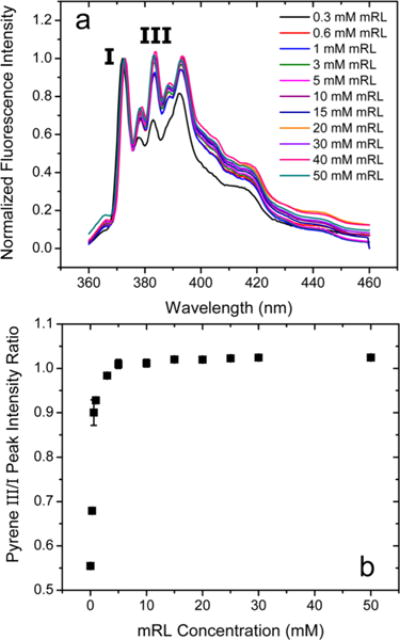
(a) Normalized pyrene fluorescence spectra and (b) pyrene III/I intensity ratios as a function of mRL concentration at pH 8.0. Pyrene concentration 250 nM; λex = 340 nm. Error bars on III/I intensity ratios represent standard deviations from three independently prepared samples.
A more accurate estimate of aggregate size for the micelle population can be obtained through determination of the aggregation number (Nagg), the number of monomers in the average micelle, at any given concentration. These values can be readily obtained from steady-state (SS) fluorescence quenching measurements using the method of Turro and Yekta.24 Using a probe and quencher pair that have a high affinity for the micelle, Nagg can be determined from a decrease in probe fluorescence with increasing quencher concentration.24 Fluorescence intensities measured as a function of quencher concentration allow development of a modified Stern–Volmer plot from
| (2) |
where I0 is the fluorescence intensity of the probe in the micelles in the absence of quencher, I is the fluorescence intensity at a given quencher concentration, and [S] is the total surfactant concentration. More detailed discussion about this method is provided in the Supporting Information.
This method is predicated on several assumptions: (1) that the probe and quencher follow a Poisson distribution within the micelles,23,24 (2) that the dynamic quenching rate constant (kq) is large relative to the fluorescence rate of the probe (k0) such that kq/k0 > 10,41,54 (3) that the probe and quencher have a high affinity for the micelle interior,24,55 (4) that the micelles are relatively monodisperse and small (Nagg < 500),55,56 and (5) that the probe residence time is ≫τ0.55,56 The experiments conducted here utilized quenching of a pyrene fluorescent probe with benzophenone (BP); this probe–quencher pair has been used extensively to identify Nagg values for multiple surfactants,28,51 and hence, their adherence to these assumptions with mRLs is likely. However, potential effects from changes in microenvironment and polydispersity of the mRLs are explored herein. Solution concentrations of fluorescent probe and quencher are chosen to ensure a Poisson distribution such that no more than one probe occupies a micelle; for this, [P]/[M] must be <0.05.41 If [Q]/[M] is then varied between 0 and 2, a Poisson distribution exists validating the method.28,51,57 Also, a zeroth-order assumption is that kq/k0 > 10 over the mRL concentration range studied; the validity of this assumption is addressed in more detail below. Finally, the association constants of the probe (KP) and quencher (KQ) for the micelle interior (Figures S7 and S8) were estimated to be 1.94 × 104 and 1.47 × 104 M−1, respectively, at concentrations >7.5 mM. Therefore, minimal error should be incurred when using eq 2 to estimate Nagg using SS fluorescence measurements at concentrations >7.5 mM. Below 7.5 mM, not all assumptions are fully valid, as will be discussed more below. Therefore, the SS fluorescence quenching method is applied here only to determine aggregation numbers for mRL concentrations >7.5 mM.
It is noted that using the Tanford method to predict micelle shape also allows estimation of Nagg.49 Using the most abundant congener (Rha-C10-C10) in the native mRL mixture as representative, Nagg is estimated to be 25–45 monomers/micelle.49
Using the fluorescence method of Turro and Yekta, Nagg values as a function of mRL concentration are shown with the black symbols in Figure 4. This plot exhibits an approximately linear change in Nagg with mRL concentration. The smallest stable true micelle is defined herein as the critical aggregation number (Nagg,crit), which for the native mRL mixture is ~26 monomers/micelle at mRL concentrations of ~10 mM. Although for anionic surfactants this value is quite small, it matches well with the values predicted by the Tanford model of ~25–45 monomers/micelle.49 This value is also consistent with the results of MD simulations described below as well as with the relatively small size of the major mRL congener in the mixture, Rha-C10-C10.
Figure 4.
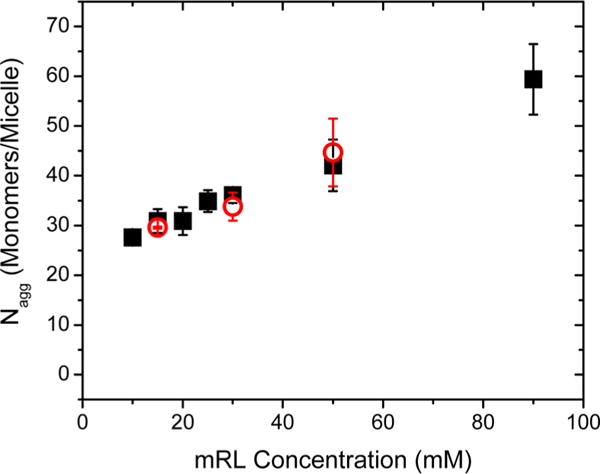
Nagg values from steady-state fluorescence (black squares) and time-resolved (red circles) fluorescence quenching of pyrene with BP as a function of mRL concentration in 10 mM phosphate buffer at pH 8.0.
The association constant (KQ) of the quencher for the micelle interior can be determined using the method of Tachiya that more fully describes the fluorescence quenching behavior according to58
| (3) |
In fact, the method of Turro and Yekta using eq 2 is an approximation in which the 1/KQ term is assumed to be negligible. Defining α to be the slope of a plot of n versus [Q], a plot of 1/α vs [S] – cmc (Figure S8) can be used to estimate KQ and Nagg from the intercept and slope of a fit of the linear portion of the values, respectively. The results suggest that at concentrations <7.5 mM the KQ value for BP (~5 × 103 M−1) is about an order of magnitude lower than at concentrations >7.5 mM, as might be expected for relatively loosely packed premicellar structures. The formation of premicelles from multiple monomers prior to the formation of full micelles has been postulated previously for multiple surfactant systems59,60 and proposed previously for native mixtures of mono- and dirhamnolipids.14 The premicellar mRL aggregates implicated here likely take on a loosely packed structure of several monomers as further validated by the MD simulations described below. Premicellar aggregation of mRLs is facilitated by the possibility of not only hydrophobic interactions between mRL chains but also hydrogen bonding between rhamnose headgroups. These arguments are strengthened by the large partition coefficients for pyrene and BP as well as the spectral behavior of pyrene and prodan which report on aggregate microenvironment polarity as discussed above.
For mRL concentrations >7.5 mM, fully formed micelles exist which then exhibit a continual slight increase in Nagg with increasing mRL concentration. Further evidence for the formation of true micelles at mRL concentrations >7.5 mM comes from the data shown in Figure S8; tangents to this curve for mRL concentrations near 10 mM begin to have smaller intercepts, indicating larger values of KQ for BP as would be expected for true micelles. Polydispersity may also occur along with the increase in Nagg arising from elongation of micelles and/or formation of lamellar structures as corroborated by the computations below.
Chen et al. reported an aggregation number of 47 mRL monomers/micelle using SANS for a mRL concentration of 20 mM at pH 9 in 0.023 M borax/0.008 M HCl; larger lamellar structures were reported at higher mRL concentrations.10,18 Our Nagg value from SS fluorescence quenching measurements at 20 mM mRL is ~31 monomers/micelle. This difference in aggregation number is likely due to the higher ionic strength in the work of Chen, which is known to increase aggregation number for anionic surfactants.61,62
The Nagg values determined using SS fluorescence quenching, along with the attendant assumptions, can be further validated using the Infelta–Tachiya method of time-resolved fluorescence quenching (TRFQ)54,63 under similar probe and quencher conditions. In this method, eq 4 is used to relate the intensity at time 0, I0, and at some time t after excitation, I(t), to parameters A1, A2, and A3 that are a function of the rate constants for the various processes leading to time-dependent changes in fluorescent signal intensity:54,63,64
| (4) |
| (5) |
| (6) |
| (7) |
Here, k− is the exit rate of the quencher from the micelle, kq is the rate constant for quenching, k0 is the fluorescence rate constant of the pyrene probe, and n, as defined by eq 3, is related to quencher and micelle concentrations and KQ. By fitting the pyrene lifetime decay curves (representative intensity–time curves are shown in Figure S9) to these equations, Nagg can be determined if the quencher concentration is known. Additional assumptions to those discussed above for the SS fluorescence measurements are that kq/k0 is >10 and static quenching contributions are minimal. Past work suggests that the benzophenone–pyrene quenching kinetics satisfy these conditions.50
Time-resolved fluorescence measurements were made on solutions of 15, 30, and 50 mM mRL. Pyrene concentrations of 250 nM were used and BP concentrations were maintained at a [Q]/[M] of ~1, for which the [M] concentration is approximated using Tanford’s method49 and the SS data above. The Nagg values observed for these three mRL concentrations are shown as the red symbols in Figure 4. They are in excellent agreement with the Nagg values determined in the SS experiments, further validating the above results.
The time-resolved fluorescence method also provides insight into kq and k− values, allowing validation of the kq/k0 and minimal migration (i.e., small k−) assumptions above. Values of kq/k0, k−, and τres (BP quencher residence time) at different mRL concentrations are given in Table S2. Negligible k− values (large τres values) for BP suggest the same for the more nonpolar pyrene, as it has a greater association with the hydrophobic aggregate interior. For mRL concentrations >7.5 mM wherein fully formed micelles are observed, the kq/k0 values are all >10, thereby validating use of the Turro–Yekta SS method. However, as noted, for mRL concentrations <7.5 mM, these values are <10, indicating that errors in Nagg values are likely. The kq/k0 value is as low as ~2 at a concentration of 1 mM mRL increasing to a value of 10 between 5 and 10 mM mRL. The impact of this assumption not being strictly met can be evaluated using the previous work of Alargova.41 According to this previous work, because the pyrene probe is not wholly engulfed by the premicellar aggregates for concentrations <7.5 mM, making the kq/k0 ratios in this concentration regime <10, exact Nagg values are likely to be underestimated by amounts ranging from 70% at mRL concentrations of ~1 mM, decreasing to ~25% by mRL concentrations of ~5 mM, and decreasing to zero by 10 mM. Even with errors of this magnitude, Nagg values for concentrations <7.5 mM are still considerably smaller (data not shown) than the critical aggregation number of ~26 determined here, consistent with premicellar aggregates as postulated above.
Finally, for concentrations >7.5 mM, the polydispersity of the aggregates can be assessed by varying quencher concentration in fluorescence quenching measurements to confirm the DLS, cryo-TEM, and prodan fluorescence spectroscopy results of a predominantly micellar system. The Nagg values reported above represent average values across all aggregate populations occupied by the quencher. Therefore, in a system of aggregates with multiple populations (i.e., micelle and lamellar), the aggregation number varies as a function of ⟨Q⟩ = [Q]/([S] – cmc).50 If a system has a population that is polydisperse, the quencher will first load into aggregates with more total mass, the lamellar aggregates,65,66 and then at higher ⟨Q⟩, quenchers will occupy aggregates with less total mass, here the micelles.50,65,66 By varying quencher concentration, a weighted average aggregation number (Nagg,w) can be calculated, and if significant polydispersity exists, then Nagg and Nagg,w will differ. The basis of this relationship is described in more detail in the Supporting Information. By plotting Nagg as a function of ⟨Q⟩, as shown in Figure S10a for a 15 mM native mRL solution, it can be seen that although there is scatter in the data, Nagg does not change significantly with ⟨Q⟩, indicating minimal polydispersity. To evaluate polydispersity further, the kinetics of the quenching rates are determined through fitting eq 4 in the fluorescence lifetime measurements above. If significant polydispersity exists, then the A3 fitting term in eq 4 will vary with ⟨Q⟩ due to the loading of larger aggregates by quencher first.57,65–67 Figure S10b shows the A3/A3,min ratio as a function of ⟨Q⟩ along with the fraction of micelles (fm = number of micelles/total number of aggregates) to generate a quantitative value for polydispersity. This plot shows a fraction of micelles of ~1 across the entire mRL concentration range studied here, confirming negligible polydispersity. These fluorescence spectroscopy results are consistent with the DLS, cryo-TEM, and prodan fluorescence spectroscopy data, indicating a system dominated by micelles at pH 8.0.
Molecular Dynamics Simulations
In order to gain more insight into the properties of aggregate structures formed from rhamnolipids, computer simulations were employed. Experimental results provide ensemble measurements of static properties. In order to elucidate the dynamic nature of rhamnolipid aggregates, we embarked on a MD investigation of micelle formation and structural evolution. Table S3 presents the list of systems studied in this work, comprising 10–100 molecules of the most common congener in the native mRL mixture, the Rha-C10-C10, in their anionic state. This range of monomer numbers was chosen as one that bracketed the range of possibly reasonable structures based on existing experimental evidence. A simulation box of size 10 × 10 × 10 nm3 was used to solvate the Rha-C10-C10 molecules. An initial starting structure for the aggregate is needed; simply beginning MD simulations on the monodisperse solution will not result in the formation of micelles or other aggregates in accessible computational times, and so another approach is needed. Simulated annealing was used to create all starting structures as described in the Experimental Section. Computations were started from an initial configuration of the Rha-C10-C10 molecules homogeneously solvated in the simulation box. The cycles of heating and cooling described above formed the initial aggregates. The aggregates were equilibrated by constant temperature MD with the equilibrium condition identified by stable total energy and temperature. A production run was performed on the fully equilibrated system to analyze the properties of the aggregates formed.
Aggregation Number
Table 2 presents the size of aggregates formed in each system considered in the simulation. More than one starting system was considered for 20, 25, and 30 Rha-C10-C10 molecules to ensure that final aggregation is not dependent on starting state and to find the most probable aggregates as a function of monomer number. The smallest aggregate size observed is N = 7. The most prevalent aggregate sizes are ~20–25. Systems consisting of 40, 70, and 80 Rha-C10-C10 molecules form aggregates of sizes 39, 55, and 44, respectively, in addition to smaller aggregates and monomers. The largest system with 100 Rha-C10-C10 molecules forms smaller aggregates of ~25 monomers, and further simulations show that all smaller aggregates (those formed by <25 monomers) interact with each other in such fashion as to merge to form a larger aggregate. These observations suggest that an aggregation number of ~25 is the most probable micelle, in agreement with the experimental observations of critical aggregation number reported above. Representative structures of aggregates composed of 25, 39, 55, and 95 monomers are shown in Figure 5.
Table 2.
Aggregation Information from Simulation
| starting no. of Rha-C10-C10 molecules
|
no. of Rha-C10-C10 molecules in aggregates observed
|
|||
|---|---|---|---|---|
| simulation 1 | simulation 2 | simulation 3 | major aggregate sizes | minor aggregate sizes |
| 10 | 7 | 1s | ||
| 20 | 20 | 20 | 20 | 7, 4, and 1s |
| 25 | 25 | 25 | 20 and 25 | 5 |
| 30 | 30 | 30 | 20 and 29 | 10 and 1s |
| 40 | 39 | 1 | ||
| 70 | 55 | 7, 4, 3, 2, and 1s | ||
| 80 | 24 and 44 | 4, 3, 2, and 1s | ||
| 100 | 95 | 1s | ||
Figure 5.
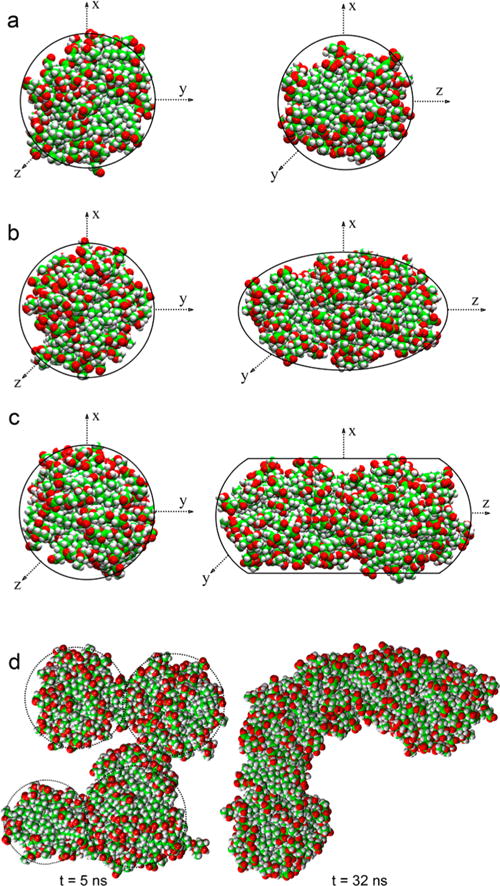
Representative structures of aggregates composed of (a) 25, (b) 39, (c) 55, and (d) 95 monomers. Water omitted for clarity. C atoms are green, H atoms are white, and O atoms are red. Aggregates 25, 39, and 55 are shown in two views. The 95-mer aggregate structure is shown at two different simulation times.
Micelle Size
A characteristic measurement of the micelle size is its radius, rm. The radius of the micelle can be calculated using the following equations:
| (8) |
| (9) |
where Rg is the radius of gyration and ⟨r⟩ is the mean distance of the heavy atoms (ri) from the micelle center of mass (COM). Rg is defined as the root-mean-square distance of the object’s parts from its center of mass. Figure 6 presents the calculated rm (with error bars) for all micellar aggregates by taking the average over all frames. Such calculations are necessary because as the snapshots in Figure 5 demonstrate, these Rha-C10-C10 micellar aggregates are far from spherical and highly dynamic in shape. These data show that the largest aggregate has a radius of ~4.0 nm and the smallest micelles have a radius of ~1.0 nm. It should be noted that these values are an average of radii across the ensemble of aggregate structures, and it is unclear from these calculations alone whether these aggregates take on a spherical or ellipsoidal shape. In total, the size of these micelles is generally consistent with the DLS results reported above in which the vastly predominant aggregate has a hydrodynamic radius (Rh) of 2–3 nm.
Figure 6.
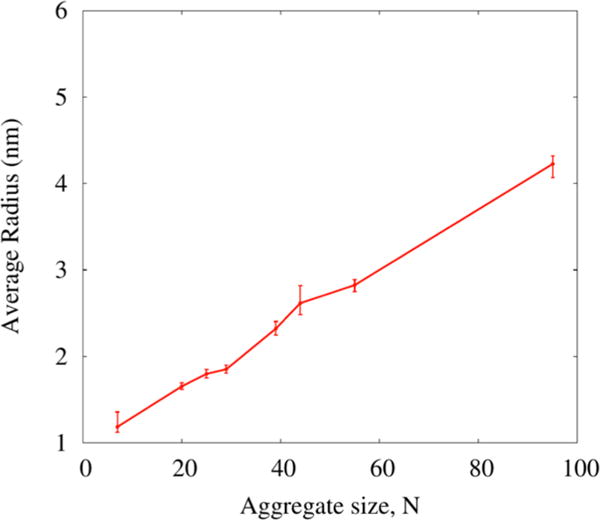
Calculated radii (with error bars) of all aggregates observed in the simulations. Radii chosen by averaging the maximum and minimum radius calculated for all structures along the trajectory for a given aggregate size.
Micelle Shape
The shape of the micelle can be characterized by examining the eccentricity (e), defined as
| (10) |
where Imin is the moment of inertia along the x-, y-, or z-axis with the smallest magnitude and Iavg is the average of all three moments of inertia. Figure S12 shows the eccentricity as a function of simulation time for all micellar aggregates. For a perfect spherical object, the value of e is zero, so deviation from sphericity can be quantified by examining the eccentricity in addition to visual inspection of system snapshots. It is evident from the results that the eccentricity of the 7-monomer aggregate is less stable in shape over the 1 ns period of the simulation, suggesting it acts as a premicellar aggregate. Aggregates formed from N ≥ 20 Rha-C10-C10 molecules can be classified as stable micelles, since they show modest deviation in eccentricity over this time period. The eccentricity data show further that 20, 25, and 29 molecules form aggregates close to spherical in shape.
The next biggest aggregate of 39 monomers is more of an ellipse. At higher concentrations, the aggregate shape predicted by the Tanford model is an elongated ellipsoid, which grows primarily along one direction. These trends are clearly evident in the representative structures shown in Figure 5 and are consistent with the Nagg values deduced from fluorescence quenching measurements as described above.
The structures shown in Figure 5 indicate that the alkyl chains are relatively disordered, likely due to their restricted motion because of their linkage via the ester group. This is especially true of the larger structures that are expected to be most representative of emerging lamellar properties. In general, lamellar structures of amphiphilic molecules are reasonably well ordered in which the alkyl chain axes are all parallel to each other and perpendicular to the lamellar axis. In contrast, the larger structures exhibit alkyl chains that appear oriented in relatively random directions, albeit in largely all-trans configurations.
Accessible Surface Area
Structural properties of these micelles can be analyzed by quantifying the accessible surface area (ASA) according to the method of Lee and Richards.68 In this technique, with all water molecules removed from the system, a probe molecule is rolled across the surface of the micelle and the contact area summed to quantify the total accessible area. A 1.6 Å diameter theoretical probe was utilized in order to mimic a water molecule. With this method, it is also possible to separate the contact area contribution from the hydrophilic headgroup and the hydrophobic tails. The results of this analysis are presented in Figure S13. For the micellar aggregates, the ASA of the hydrophilic group exposed to water is about ~4 times more abundant than the hydrophobic group, indicating that little of the hydrophobic micellar core is exposed to water (but critically, it is not zero). An additional analysis that analyzes the radial number density of various components from the micelle’s COM is shown in Figure S14; this analysis also suggests very slight interaction of the hydrophobic core with water. Thus, only minor penetration of water into the hydrophobic core of these aggregates occurs, largely due to the dynamic nature of the hydrophilic surface of the micelle.
In the case of the premicellar aggregate with N = 7, the ASA of the hydrophobic group exposed to water is ~50% of the hydrophilic group exposed to water. This highlights the loose packing of the premicellar aggregate with easy water access to the hydrophobic core. This behavior is consistent with the behavior of the prodan emission maximum reported above in the mRL concentration regime in which premicellar aggregates predominate (i.e., <7.5 mM). It should be noted that the ASA per molecule decreases with an increase in aggregate size, likely due to closer packing of both the Rha-C10-C10 headgroups and the alkyl chains. An interesting observation is that the ASA becomes constant from N ~ 55 to 95, which suggests that additional monomers are added in this regime with an insignificant change in size. This could only be accommodated by an increase in packing order of Rha-C10-C10 molecules, although none of our experimental measures to date are sensitive enough to validate this assertion.
Conformational Preference
To understand the importance of the hydrophobic tails in the formation of aggregates, the average tail length, the average distance between the terminal carbon atom of a single alkyl chain and the sixth carbon from it, was calculated for each chain separately in all frames along the trajectory and plotted (Figure S15). For all aggregates, the average tail length is ~6.8 Å, with no strong dependence on aggregate size observed. This value is slightly less than the 7.6 Å expected for a linear alkane of this length in an all-trans conformation, suggesting some slight twisting along the chain axis.
The intramolecular hydrogen bonding distance between the carboxylate and rhamnose groups was also measured to understand the conformational preference of Rha-C10-C10 in aggregates. The carboxylate oxygens were chosen as hydrogen bond acceptors, and the hydroxyl hydrogens of the rhamnose group were hydrogen bond donors. All possible hydrogen-bonding combinations consistent with these definitions were considered, and the shortest distance of each monomer was used for the purposes of this analysis. Figure 7 shows the distribution of the intramolecular hydrogen bonding distances of all molecules for three micelle sizes. The region of intramolecular distances of ~6 to 10 Å for anionic Rha-C10-C10 is more populated than a second, narrower peak in the distribution between ~10 and 13 Å. These data indicate that the probability of the partially folded conformation is higher in micelles than the open and the fully folded conformations.
Figure 7.
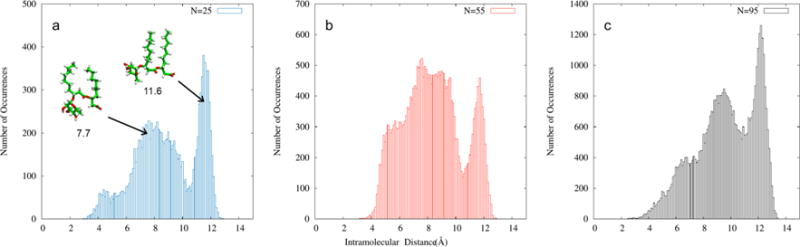
Conformational distribution of all the mRLs calculated based on the intramolecular distance between rhamnose group and carboxylic group for aggregates of (a) 25 molecules, (b) 55 molecules, and (c) 95 molecules. The representative monomer structures corresponding to peaks at 7.7 and 11.6 Å are also shown.
This observation is not true in the case of a single Rha-C10-C10 molecule; gas phase quantum chemical calculations on the open and folded conformations of Rha-C10-C10 showed that the folded conformation is more stable than the open conformation by 25.8 kcal/mol. The density functional theory (DFT) calculated structures and relative energies are shown in Figure S16.
Hydrogen-Bonding Interactions
Rha-C10-C10 molecules have polar carboxylic, hydroxyl, and ester moieties that have a tendency to form intra- as well as intermolecular hydrogen bonds (H-bonds). Given that both hydrophobic and hydrophilic interactions are expected to be major factors in micellar aggregate stabilization in these systems, the numbers of intra- and intermolecular (H-bonds) within and between Rha-C10-C10 molecules were calculated to elucidate the role of H-bonds in stabilization of these micelles. H-bonds were identified using the cutoff conditions that H-bond distances with oxygen are ≤3.5 Å, and H-bond oxygen–oxygen–hydrogen angles are ≤30°. Figure 8 presents the average intermolecular H-bonds per surfactant for all the aggregates. It is interesting to see that premicellar aggregates of N = 7 have only 0.3 H-bonds per molecule. However, this value gradually increases with increasing numbers of monomers in the aggregates, which supports the observation from Figure S13 that the headgroups are packed more closely in larger aggregates. The calculated average number of H-bonds per Rha-C10-C10 in each aggregate is ~0.5 H-bonds per molecule for N = 20 and 25 and ~0.7 H-bonds per molecule for N = 29, 44, 55, and 95. The N = 39 aggregate has the highest value of 0.9 H-bonds per molecule.
Figure 8.
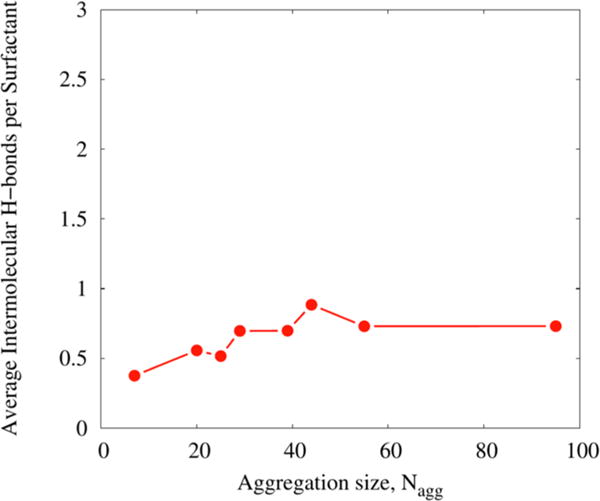
Average intermolecular hydrogen bonds per monomer for all the aggregates.
It is further observed that intramolecular H-bonds are few in number compared to intermolecular H-bonds. Therefore, the dominant form of H-bonds in the aggregates is intermolecular supporting the assertion that the head groups are not arranged randomly across the surface of the aggregate, but instead form H-bonded chains that help stabilize the structure.
Micelle–Water Interfacial Region and Water Penetration into Micelle
The nature of interaction between micelle and bulk water can be studied by investigating the interface between them. Figure 9 shows radial density plots for water constructed by calculating the distance of water molecules from the micelle center of mass (COM) and counting the number of water molecules in 0.1 Å wide shells around the COM. It can be seen that radial density of water appears much closer to the COM and reaches the maximum most sharply for premicellar aggregate N = 7. However, water density in the micellar aggregates starts to appear at ~10 Å from the COM and takes a longer distance to reach the maximum than in the premicelle. This behavior is strong proof that the hydrophobic core is densely packed and relatively impermeable to water. It is also seen that the nearly spherical aggregates (N = 20, 25, and 29) have radial densities that all rise with a similar slope, becoming constant much closer to the COM than in ellipsoidal aggregates (N = 39, 44, and 55). This observation is easily rationalized on the basis that ellipsoidal aggregates are not symmetric; therefore, the water radial density approaches a constant value only after reaching the long axis distance.
Figure 9.
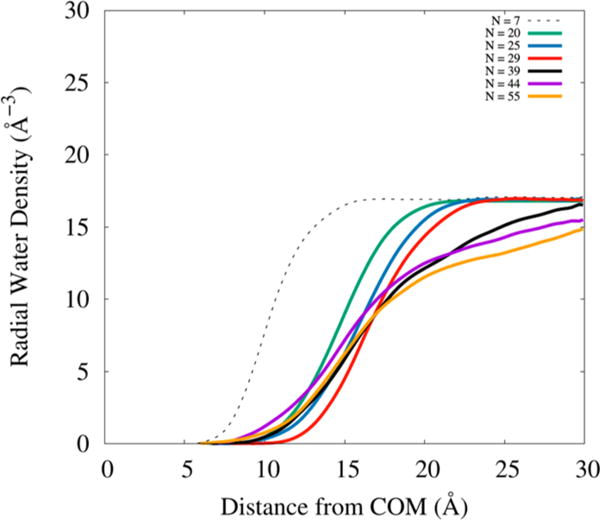
Radial water density for all aggregates considered in this study.
Additional insight into the interfacial distribution of Na+ at the aggregate–solution interface is described in the Supporting Information. Figure S17 shows radial distribution plots for Na+ relative to the carboxylate and rhamnose hydroxyl groups, and Figure S18 shows representative structures defining the range of Na+–monomer interactions.
CONCLUSIONS
This work represents a detailed, systematic exploration of the early stage aggregation behavior of mRLs. The results show that the solution aggregation behavior of mRLs is surprisingly complex. Purified native mRL produced by P. aeruginosa ATCC 9027 in its anionic state exhibits a critical aggregation concentration (CAC) of 201 μM, but at this concentration, only premicellar aggregates form; fully formed micelles do not form until mRL concentrations >7.5 mM are reached. At pH 8.0, micelles predominate in solution at all concentrations between the CAC and 100 mM, becoming increasingly elongated and/or lamellar as their size and monomer number steadily increase with mRL concentration. These fully formed micelles have a critical aggregation number of 26 monomers/micelle based on fluorescence quenching measurements.
The microenvironment of these micelles was probed using the polarity-sensitive pyrene and prodan fluorescent dyes. The results of the studies using pyrene confirm environments that are typical of premicelles at mRL concentrations <7.5 mM and micellar environments >7.5 mM. The spectral response of prodan confirms the dominance of micellar structures at all mRL concentrations at pH 8.0.
Molecular dynamics simulations on the most abundant congener of the mRL mixture, Rha-C10-C10, indicate the formation of stable mRL aggregates of varying sizes ranging from 7 to 95. Aggregates with N = 7 are taken to be the most stable premicellar structure. The most frequently observed micellar aggregate has an aggregation number of ~25 monomers/micelle, which is in agreement with the critical aggregation number determined with fluorescence measurements. The calculated radii of these aggregates support the experimental observations from DLS. The differentiation of the premicellar and micellar aggregates is further supported by the accessible surface area results. These simulations have also confirmed an average hydrophobic tail length for all aggregates and multiple conformations of the headgroup in more disordered aggregate structures than are generally observed. An analysis of hydrogen bonding confirms that intermolecular hydrogen bonding plays a significant role in stabilizing these aggregate structures.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge support of this research through a grant award from the National Science Foundation (CHE-1339597) jointly funded by the Environmental Protection Agency as part of the Networks for Sustainable Molecular Design and Synthesis Program. This work is adapted in part from the PhD Dissertation of R.J.E.69 J.E.P. and R.M.M. declare financial interest in an entity that produces materials related to those reported here. The details of this arrangement have been reviewed and approved by the University of Arizona.
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.7b00078.
Experimental details, surface tension data, fluorescence quenching experiments, and the molecular dynamics simulations (PDF)
ORCID
Elango Munusamy: 0000-0003-2389-7247
Steven D. Schwartz: 0000-0002-0308-1059
Jeanne E. Pemberton: 0000-0002-1710-2922
Notes
The authors declare the following competing financial interest(s): Two of the authors (JEP and RMM) declare financial interest in an entity that produces materials related to those reported here. The details of this arrangement have been reviewed and approved by the University of Arizona.
References
- 1.Kralova I, Sjoblom J. Surfactants Used in Food Industry: A Review. J Dispersion Sci Technol. 2009;30:1363–1383. [Google Scholar]
- 2.Rosen J. Surfactants and Interfacial Phenomena. 3rd ed. John Wiley & Sons, Inc; 2004. [Google Scholar]
- 3.Ruiz CC. Micellar Properties and Molecular Interactions in Binary Surfactant Systems Containing a Sugar-Based Surfactant. Sugar-Based Surfactants: Fundamentals and Applications. 2008;143:1–600. [Google Scholar]
- 4.Marchant R, Banat IM. Biosurfactants: A Sustainable Replacement for Chemical Surfactants? Biotechnol Lett. 2012;34:1597–1605. doi: 10.1007/s10529-012-0956-x. [DOI] [PubMed] [Google Scholar]
- 5.Lovaglio RB, Silva VL, Ferreira H, Hausmann R, Contiero J. Rhamnolipids Know-how: Looking for Strategies for its Industrial Dissemination. Biotechnol Adv. 2015;33:1715–1726. doi: 10.1016/j.biotechadv.2015.09.002. [DOI] [PubMed] [Google Scholar]
- 6.Jirku V, Cejkova A, Schreiberova O, Jezdik R, Masak J. Multicomponent Biosurfactants - A “Green Toolbox” Extension. Biotechnol Adv. 2015;33:1272–1276. doi: 10.1016/j.biotechadv.2015.03.005. [DOI] [PubMed] [Google Scholar]
- 7.Abdel-Mawgoud AM, Lépine F, Déziel E. Rhamnolipids: Diversity of Structures Microbial Origins Roles. Appl Microbiol Biotechnol. 2010;86:1323–1336. doi: 10.1007/s00253-010-2498-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhang YM, Miller RM. Effect of a Pseudomonas Rhamnolipid Biosurfactant on Cell Hydrophobicity Biodegradation of Octadecane. Appl Environ Microbiol. 1994;60:2101–2106. doi: 10.1128/aem.60.6.2101-2106.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen ML, Penfold J, Thomas RK, Smyth TJP, Perfumo A, Marchant R, Banat IM, Stevenson P, Parry A, Tucker I, Grillo I. Mixing Behavior of the Biosurfactant Rhamnolipid with a Conventional Anionic Surfactant Sodium Dodecyl Benzene Sulfonate. Langmuir. 2010;26:17958–17968. doi: 10.1021/la1031834. [DOI] [PubMed] [Google Scholar]
- 10.Chen ML, Penfold J, Thomas RK, Smyth TJP, Perfumo A, Marchant R, Banat IM, Stevenson P, Parry A, Tucker I, Grillo I. Solution Self-Assembly and Adsorption at the Air-Water Interface of the Monorhamnose and Dirhamnose Rhamnolipids and Their Mixtures. Langmuir. 2010;26:18281–18292. doi: 10.1021/la1031812. [DOI] [PubMed] [Google Scholar]
- 11.Penfold J, Thomas RK, Shen H. Adsorption and Self-Assembly of Biosurfactants Studied by Neutron Reflectivity and Small angle Neutron Scattering: Glycolipids, Lipopeptides and Proteins. Soft Matter. 2012;8:578–591. [Google Scholar]
- 12.Abbasi H, Noghabi KA, Hamedi MM, Zahiri HS, Moosavi-Movahedi AA, Amanlou M, Teruel JA, Ortiz A. Physicochemical Characterization of a Monorhamnolipid Secreted by Pseudomonas aeruginosa MA01 in Aqueous Media. An Experimental and Molecular Dynamics Study. Colloids Surf, B. 2013;101:256–265. doi: 10.1016/j.colsurfb.2012.06.035. [DOI] [PubMed] [Google Scholar]
- 13.Ozdemir G, Peker S, Helvaci SS. Effect of pH on the Surface and Interfacial Behavior of Rhamnolipids R1 and R2. Colloids Surf, A. 2004;234:135–143. doi: 10.1016/j.colsurfb.2004.01.001. [DOI] [PubMed] [Google Scholar]
- 14.Guo YP, Hu YY, Gu RR, Lin H. Characterization and Micellization of Rhamnolipidic Fractions and Crude Extracts Produced by Pseudomonas aeruginosa Mutant MIG-N146. J Colloid Interface Sci. 2009;331:356–363. doi: 10.1016/j.jcis.2008.11.039. [DOI] [PubMed] [Google Scholar]
- 15.Dahrazma B, Mulligan CN, Nieh MP. Effects of Additives on the Structure of Rhamnolipid (Biosurfactant): A Small-angle Neutron Scattering (SANS) Study. J Colloid Interface Sci. 2008;319:590–593. doi: 10.1016/j.jcis.2007.11.045. [DOI] [PubMed] [Google Scholar]
- 16.Manko D, Zdziennicka A, Janczuk B. Thermodynamic Properties of Rhamnolipid Micellization and Adsorption. Colloids Surf, B. 2014;119:22–29. doi: 10.1016/j.colsurfb.2014.04.020. [DOI] [PubMed] [Google Scholar]
- 17.Pornsunthorntawee O, Chavadej S, Rujiravanit R. Solution Properties and Vesicle Formation of Rhamnolipid Biosurfactants Produced by Pseudomonas aeruginosa SP4. Colloids Surf, B. 2009;72:6–15. doi: 10.1016/j.colsurfb.2009.03.006. [DOI] [PubMed] [Google Scholar]
- 18.Chen ML, Dong CC, Penfold J, Thomas RK, Smyth TJP, Perfumo A, Marchant R, Banat IM, Stevenson P, Parry A, Tucker I, Grillo I. Influence of Calcium Ions on Rhamnolipid and Rhamnolipid/Anionic Surfactant Adsorption and Self-Assembly. Langmuir. 2013;29:3912–3923. doi: 10.1021/la400432v. [DOI] [PubMed] [Google Scholar]
- 19.Guo Y, Mulligan CN, Nieh M. An Unusual Morphological Transformation of Rhamnolipid Aggregates Induced by Concentration and Addition of Styrene: A Small Angle Neutron Scattering (SANS) Study. Colloids Surf, A. 2011;373:42–50. [Google Scholar]
- 20.Champion JT, Gilkey JC, Lamparski H, Retterer J, Miller RM. Electron-Microscopy of Rhamnolipid (Biosurfactant) Morphology - Effects of pH, Cadmium, and Octadecane. J Colloid Interface Sci. 1995;170:569–574. [Google Scholar]
- 21.Parasassi T, Krasnowska EK, Bagatolli L, Gratton E. Laurdan and Prodan as Polarity-Sensitive Fluorescent Membrane Probes. J Fluoresc. 1998;8:365–373. [Google Scholar]
- 22.Karukstis KK, Duim CW, Van Hecke RG, Hara N. Biologically Relevant Lyotropic Liquid Crystalline Phases in Mixtures of n-Octylβ-D-Glucoside and Water. Determination of the Phase Diagram by Fluorescence Spectroscopy. J Phys Chem B. 2012;116:3816–3822. doi: 10.1021/jp208097c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Turro NJ, Aikawa M, Yekta A. Dynamics of Molecular-Oxygen in Micellar Solutions. Chem Phys Lett. 1979;64:473–478. [Google Scholar]
- 24.Turro NJ, Yekta A. Luminescent Probes for Detergent Solutions - Simple Procedure for Determination of Mean Aggregation Number of Micelles. J Am Chem Soc. 1978;100:5951–5952. [Google Scholar]
- 25.Mulligan CN, Mahmourides G, Gibbs BF. The Influence of Phosphate-Metabolism on Biosurfactant Production by Pseudomonas-Aeruginosa. J Biotechnol. 1989;12:199–210. [Google Scholar]
- 26.Koppel DE. Analysis of Macromolecular Polydispersity in Intensity Correlation Spectroscopy: The Method of Cumulants. J Chem Phys. 1972;57:4814–4820. [Google Scholar]
- 27.Berne BJ, Pecora R. Dynamic Light Scattering. Krieger: Malabar, FL; 1990. [Google Scholar]
- 28.Alsins J, Almgren M. Quenching Dynamics and Diffusion of Small Hydrophobic Molecules in Long Rodlike Micelles. J Phys Chem. 1990;94:3062–3069. [Google Scholar]
- 29.Gauthier T, Shane E, Guerin W, Seitz W, Grant C. Fluorescence Quenching Method for Determining Equilibrium-Constants for Polycyclic Aromatic-Hydrocarbons Binding to Dissolved Humic Materials. Environ Sci Technol. 1986;20:1162–1166. [Google Scholar]
- 30.Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, Darian E, Guvench O, Lopes PEM, Vorobyov I, MacKerell AD. CHARMM General Force Field: A Force Field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J Comput Chem. 2010;31:671–690. doi: 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Best RB, Zhu X, Shim J, Lopes PEM, Mittal J, Feig M, MacKerell AD. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ ψ and Side-Chain χ1 and χ2 Dihedral Angles. J Chem Theory Comput. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 33.Martinez L, Andrade R, Birgin EG, Martinez JM. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J Comput Chem. 2009;30:2157–2164. doi: 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- 34.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 35.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable Molecular Dynamics with NAMD. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Darden T, York D, Pedersen L. Particle Mesh Ewald - An N-log(N) Method For Ewald Sums in Large Systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 37.Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical-Integration of Cartesian Equations of Motion of a System with Constraints - Molecular-Dynamics of N-Alkanes. J Comput Phys. 1977;23:327–341. [Google Scholar]
- 38.Martyna GJ, Tobias DJ, Klein ML. Constant-Pressure Molecular-Dynamics Algorithms. J Chem Phys. 1994;101:4177–4189. [Google Scholar]
- 39.Feller SE, Zhang YH, Pastor RW, Brooks BR. Constant-Pressure Molecular-Dynamics Simulation - The Langevin Piston Method. J Chem Phys. 1995;103:4613–4621. [Google Scholar]
- 40.Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by Simulated Annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 41.Alargova RG, Kochijashky II, Sierra ML, Zana R. Micelle Aggregation Numbers of Surfactants in Aqueous Solutions: A Comparison Between the Results from Steady-state and Time-resolved Fluorescence Quenching. Langmuir. 1998;14:5412–5418. [Google Scholar]
- 42.Lebron-Paler A, Pemberton JE, Becker BA, Otto WH, Larive CK, Maier RM. Determination of the Acid Dissociation Constant of the Biosurfactant Monorhamnolipid in Aqueous Solution by Potentiometric and Spectroscopic Methods. Anal Chem. 2006;78:7649–7658. doi: 10.1021/ac0608826. [DOI] [PubMed] [Google Scholar]
- 43.Zhang YM, Miller RM. Enhanced Octadecane Dispersion and Biodegradation by a Pseudomonas Rhamnolipid Surfactant (Biosurfactant) Appl Environ Microb. 1992;58:3276–3282. doi: 10.1128/aem.58.10.3276-3282.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Peker S, Helvaci S, Ozdemir G. Interface-Subphase Interactions of Rhamnolipids in Aqueous Rhamnose Solutions. Langmuir. 2003;19:5838–5845. [Google Scholar]
- 45.Helvaci SS, Peker S, Ozdemir G. Effect of electrolytes on the surface behavior of rhamnolipids R1 and R2. Colloids Surf, B. 2004;35:225–233. doi: 10.1016/j.colsurfb.2004.01.001. [DOI] [PubMed] [Google Scholar]
- 46.Zhang YM, Miller RM. Enhanced Octadecane Dispersion and Biodegradation by a Pseudomonas Rhamnolipid Surfactant (Biosurfactant) Appl Environ Microbiol. 1992;58:3276–3282. doi: 10.1128/aem.58.10.3276-3282.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Israelachvili JN, Mitchell DJ, Ninham BW. Theory of Self-Assembly of Hydrocarbon Amphiphiles into Micelles and Bilayers. J Chem Soc, Faraday Trans 2. 1976;72:1525–1568. [Google Scholar]
- 48.Nagarajan R. Molecular Packing Parameter and Surfactant Self-Assembly: The Neglected Role of the Surfactant Tail. Langmuir. 2002;18:31–38. [Google Scholar]
- 49.Tanford C. Micelle Shape and Size. J Phys Chem. 1972;76:3020–3024. [Google Scholar]
- 50.Kegel LL, Szabo LZ, Polt R, Pemberton JE. Alkyl Melibioside and Alkyl Cellobioside Surfactants: Effect of Sugar Headgroup and Alkyl Chain Length on Performance. Green Chem. 2016;18:4446–4460. [Google Scholar]
- 51.Shag GQ, Yang ZZ, Wang M, Zhao QW, Nelles M, Cai JM, Wu K. Determination of Critical Micellar Aggregation Numbers of Surfactant by Steady-state Fluorescence Probe Method. Proc 2nd Internat Conf Asian-European Environ Technol Knowledge Transfer. 2008:420–423. [Google Scholar]
- 52.Krasnowska EK, Gratton E, Parasassi T. Prodan as a Membrane Surface Fluorescence Probe: Partitioning Between Water and Phospholipid Phase. Biophys J. 1998;74:1984–1993. doi: 10.1016/S0006-3495(98)77905-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ray GB, Chakraborty I, Moulik SP. Pyrene Absorption Can Be a Convenient Method for Probing Critical Micellar Concentration (cmc) and Indexing Micellar Polarity. J Colloid Interface Sci. 2006;294:248–254. doi: 10.1016/j.jcis.2005.07.006. [DOI] [PubMed] [Google Scholar]
- 54.Tachiya M. Application of Generating Function to Reaction-Kinetics in Micelles - Kinetics of Quenching of Luminescent Probes in Micelles. Chem Phys Lett. 1975;33:289–292. [Google Scholar]
- 55.Almgren M, Lofroth JE. Effects of Polydispersity on Fluorescence Quenching in Micelles. J Chem Phys. 1982;76:2734–2743. [Google Scholar]
- 56.Infelta PP. Fluorescence Quenching in Micellar Solutions and Its Application to the Determination of Aggregation Numbers. Chem Phys Lett. 1979;61:88–91. [Google Scholar]
- 57.Almgren M, Alsins J, Mukhtar E, Vanstam J. Fluorescence Quenching Dynamics in Rodlike Micelles. J Phys Chem. 1988;92:4479–4483. [Google Scholar]
- 58.Wu SY, Tachiya M, Yan ZN. An Improved Procedure for Determination of the Mean Aggregation Number of Micelles. Spectrochim Acta, Part A. 2015;138:807–810. doi: 10.1016/j.saa.2014.11.008. [DOI] [PubMed] [Google Scholar]
- 59.Lee Y-C, Liu H-S, Lin S-Y, Huang H-F, Wang Y-Y, Chou L-W. An Observation of the Coexistence of Multimers and Micelles in a Nonionic Surfactant C10E4 Solution by Dynamic Light Scattering. J Chin Inst Chem Eng. 2008;39:75–83. [Google Scholar]
- 60.Xu QY, Liu ZS, Nakajima M, Ichikawa S, Nakamura N, Roy P, Okadome H, Shiina T. Characterization of a Soybean Oil-based Biosurfactant and Evaluation of its Ability to Form Micro-bubbles. Bioresour Technol. 2010;101:3711–3717. doi: 10.1016/j.biortech.2009.12.093. [DOI] [PubMed] [Google Scholar]
- 61.Penfold J, Tucker I, Thomas RK, Staples E, Schuermann R. Structure of Mixed Anionic/Nonionic Surfactant Micelles: Experimental Observations Relating to the Role of Headgroup Electrostatic and Steric Effects and the Efects of Added Electrolyte. J Phys Chem B. 2005;109:10760–10770. doi: 10.1021/jp050727f. [DOI] [PubMed] [Google Scholar]
- 62.Mishic JR, Fisch MR. The Size and Flexibility of Grown Sodium Dodecyl-Sulfate Micelles in Aqueous Sodium-Chloride Solutions. J Chem Phys. 1990;92:3222–3229. [Google Scholar]
- 63.Infelta PP, Gratzel M, Thomas JK. Luminescence Decay of Hydrophobic Molecules Solubilized in Aqueous Micellar Systems -Kinetic Model. J Phys Chem. 1974;78:190–195. [Google Scholar]
- 64.Tachiya M. Kinetics of Quenching of Luminescent Probes in Micellar Systems. II. J Chem Phys. 1982;76:340–348. [Google Scholar]
- 65.Miller DD, Evans D. Fluorescence Quenching in Double-Chained Surfactants 0.1. Theory of Quenching in Micelles and Vesicles. J Phys Chem. 1989;93:323–333. [Google Scholar]
- 66.Miller DD, Magid LJ, Evans D. Fluorescence Quenching in Double-Chained Surfactants 0.2. Experimental Results. J Phys Chem. 1990;94:5921–5930. [Google Scholar]
- 67.vonBerlepsch H, Stahler K, Zana R. Micellar Properties of Sodium Sulfopropyl Alkyl Maleates in Aqueous Solution - A Time-Resolved Fluorescence Quenching Study. Langmuir. 1996;12:5033–5041. [Google Scholar]
- 68.Lee B, Richards FM. Interpretation of Protein Structures -Estimation of Static Accessibility. J Mol Biol. 1971;55:379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- 69.Eismin RJ. PhD Dissertation. University of Arizona; Tucson, AZ: 2016. Surface, Aggregation and Phase Characterization of Microbially-Produced and Chemically-Synthesized Monorhamnolipids. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


