Abstract
D3R 2016 Grand Challenge 2 focused on predictions of binding modes and affinities for 102 compounds against the Farnesoid X receptor (FXR). In this challenge, two distinct methods, a docking-based method and a template-based method, were employed by our team for the binding mode prediction. For the new template-based method, 3D ligand similarities were calculated for each query compound against the ligands in the co-crystal structures of FXR available in Protein Data Bank. The binding mode was predicted based on the co-crystal protein structure containing the ligand with the best ligand similarity score against the query compound. For the FXR dataset, the template-based method achieved a better performance than the docking-based method on the binding mode prediction. For the binding affinity prediction, an in-house knowledge-based scoring function ITScore2 and MM/PBSA approach were employed. Good performance was achieved for MM/PBSA, whereas the performance of ITScore2 was sensitive to ligand composition, e.g. the percentage of carbon atoms in the compounds. The sensitivity to ligand composition could be a clue for the further improvement of our knowledge-based scoring function.
Keywords: D3R, Drug Design Data Resource, molecular docking, scoring function, ligand similarity, template-based, binding mode prediction, binding affinity prediction, drug discovery
1 Introduction
Drug Design Data Resource (D3R, https://www.drugdesigndata.org) has become an excellent platform to test the existing methods of computer-aided drug discovery (CADD) and also to promote the development of new docking/scoring protocols [1]. The latest challenge, 2016 Grand Challenge 2, included one particular protein target, Farnesoid X receptor (FXR) [2–8], and 102 small-molecule compounds with molecular weights ranging from 363 to 634. Two stages were involved in this challenge. At Stage 1, participants were asked to predict the binding modes of the ligands with IDs ranging from FXR_1 to FXR_36, using the provided ligand SMILES strings and the FXR structures in all accessible resources. In the meantime, D3R organizers requested affinity predictions of all the 102 ligands. Then at Stage 2, co-crystal structures of FXR bound with the first 36 ligands were provided in PDB format, and the participants were asked to repeat the prediction of potencies for all the ligands by including those newly available FXR-ligand complexes structures.
For the binding mode prediction, in addition to using a docking-based strategy developed during Grand Challenge 2015 [9], we introduced a template-based method in this challenge. Specifically, all the available co-crystal structures of FXR were collected from the Protein Data Bank (PDB). For a query compound, its molecular similarities with respect to the ligands in the available co-crystal structures were calculated using a 3D molecular similarity calculation program SHAFTS (Shape Feature Similarity) [10, 11]. Then, the co-crystal structure containing the ligand with the highest molecular similarity to the query ligand was used as the template to predict the binding mode of the query ligand on the protein receptor. According to the binding mode predictions for the FXR dataset in the present study, the template-based method achieved better performance than the docking-based method. This finding is not surprising because ligands with high molecular similarity usually share similar activities and also similar binding modes, which is referred to as the molecular similarity principle [12, 13]. Yet, it is surprising that the template-based method has not yet been well studied for the binding mode prediction for protein-ligand complexes. The promising performance achieved by the template-based method for the FXR dataset suggests that this type of methods could be a good choice for the protein-ligand complex structure prediction when experimental structures with co-bound ligands are available.
For the binding affinity prediction, two distinct methods, ITScore2 and MM/PBSA (Molecular Mechanics/Poisson-Boltzmann Surface Area), were employed in this study. ITScore2 is a knowledge-based atomic pairwise scoring function that was derived based on the known protein-ligand complex structures (a refined set of PDBbind 2012 containing 2897 protein-ligand complexes [14, 15]) and the statistical mechanics-based iterative method [16–18]. MM/PBSA combines molecular mechanics energy and continuum solvent models to calculate protein-ligand binding free energies based on snapshots from molecular dynamics (MD) trajectories [19, 20]. For the binding affinity prediction of the FXR dataset, MM/PBSA yielded a better performance than ITScore2. However, the most obvious disadvantage of MM/PBSA comparing to the knowledge-based scoring function ITScore2 is the high demands of computing time. Interestingly, through analyzing the predicted results, we found that the binding affinity prediction of our atomic pairwise scoring function is sensitive to the ligand composition, e.g. the percentage of carbon atoms in the compounds. Significantly better performances were achieved when ITScore2 was applied to the subsets containing compounds with a high percentage of carbon (≥75%) or a low percentage of oxygen and nitrogen atoms (≤10%) than when the scoring function was applied to the remaining compounds in the dataset. This finding provides us a clue to further improve our knowledge-based scoring function for the binding affinity prediction.
2. Materials and Methods
2.1 Protein preparation
All the released crystal structures of human FXR protein-ligand molecule complexes were found in the Protein Data Bank (PDB) and were manually checked. A total of 26 FXR-ligand complex structures were retained and the PDB IDs are shown in the Supplementary Materials. All ions and solvent molecules in these structures were removed and the resulting structure files were used in following steps.
2.2 Ligand preparation and similarity calculation
3D conformational libraries with a maximum number of 500 were generated for a query ligand, using OMEGA (version 2.5.1.4, OpenEye Scientific Software, Santa Fe, NM. http://www.eyesopen.com) [21, 22] based on the SMILES strings from the D3R 2016 Grand Challenge 2 Dataset.
Molecular Similarities of a query ligand with the ligands in the 26 selected protein-ligand complex structures were calculated using the program SHAFTS [10, 11]. This program employs a hybrid approach for 3D similarity calculation by combining molecular shape overlay and pharmacophore feature matching between the two ligands. Therefore, this hybrid similarity consists a ShapeScore (shape-densities overlap) and a FeatureScore (pharmacophore feature fit values); both scores are normalized to a range of [0, 1]. The resulting HybridScore is the sum of ShapeScore and FeatureScore. HybridScore is scaled to [0, 2], with 0 representing no similarity and 2 corresponding to the same ligand.
2.3 Binding mode prediction
2.3.1 Docking approach
A docking approach that was developed during Grand Challenge 2015 [9] was employed for the binding mode prediction for the FXR dataset. Briefly, a receptor structure with a bound ligand sharing the best similarity (i.e., the highest HybridScore) with the query ligand was used for docking. If HybridScore was smaller than 1.2, all the 26 available FXR protein structures would be performed by ensemble docking. In ensemble docking, each query ligand was docked to the individual FXR structures, and the sampled binding modes were then merged for ranking/scoring.
In this study, a modified version of AutoDock Vina [18, 23] was employed for sampling. In this modified version, the maximum number of output modes is user-specified, and was set to 500 in the present study. The exhaustiveness value was increased to 30 to ensure exhaustive sampling. The protein was treated as a rigid body, and the single bonds of the ligands were considered to be rotatable. Thus, a maximum of 500 putative, flexible binding modes were generated, which were then re-ranked with ITScore2. The top five binding modes (i.e., with the lowest scores) for a query ligand were submitted as the binding mode prediction results.
2.3.2 Template-based approach
For a query ligand, the available FXR complex structures were ranked by ligand similarity scores (HybridScore) of their co-bound ligands with respect to the query ligand. If HybridScore was less than 1.2, only ShapeScore would be used. The top 5 PDB entries that had the best similarity scores with the query ligand were chosen as the templates. Then for each template, the query compound was superimposed onto the ligand using the program SHAFTS. Finally, the protein-query compound complex was used as the initial structure for minimization with AMBER11 [24] as described below (see the minimization step of the MD simulation subsection) so as to eliminate the possible atomic clashes upon superposition. The complex structure after the refinement would be used as the final submission. In summary, for each query ligand, with the top 5 templates, a total of 5 refined structures were submitted as the prediction for the template-based approach.
2.4 Binding affinity prediction
Two distinct methods, ITScore2 and MM/PBSA, were employed for the binding affinity prediction. ITScore2 [18] is a knowledge-based atomic pairwise scoring function that was derived based on a training set of 2897 protein-ligand crystal structures [14, 15] using an iterative approach [16, 17] to distinguish native binding modes from decoy binding modes. ITScore2 was also used for binding mode prediction in the docking-based approach as aforementioned. For each query ligand, the lowest score based on the docking approach was compared with the experimentally determined affinity. In addition, binding affinity predictions of ITScore2 were also analyzed when this scoring function was applied to the best binding mode that was predicted with the template-based approach for each query ligand.
On the other hand, MM/PBSA [19, 20] was applied to only the best mode that was predicted with the template-based approach for each query ligand. Unlike ITScore2, MM/PBSA was not applied to the binding modes generated from the docking approach for two reasons. First, the template-based approach achieved better performance than the docking approach on binding mode prediction. Second, MM/PBSA is a molecular dynamics (MD) simulation-based protocol, and running MD simulations for over a hundred protein-ligand complexes (a total of 102 compounds in the FXR dataset) is time-consuming. The details of the MD and MM/PBSA methods are described as follows.
2.4.1 MD Simulation
For each query ligand, the best binding mode predicted with the template-based approach was utilized as the initial structure for MD simulations. To create parameters of the ligand, the ligand 3D structure was optimized at the AM1 semi-empirical level [25] using Gaussian09 suit [26], and then the atomic charges were fitted using the AM1-bcc method [27] with the Antechamber program in the Amber11 package [24]. The AMBER03 [28] and Generalized Amber force field (GAFF) [29] were applied respectively to the protein and the ligand via the Leap module. Missing atoms and counter ions maintaining the neutrality were added to the complex, and this complex was solvated in a periodic box containing TIP3P water molecules [30] with a minimum distance of 10 Å between the complex and surface of the box. The Particle Mesh Ewald (PME) [31] approach was utilized to treat long-range electrostatic interactions, and a cutoff of 12 Å was applied to calculate the nonbonded interactions.
Thereafter, the solvated complexes were minimized by two steps. During the first step, the solvent molecules were minimized for 1000 steps via steepest descent method, followed by 3000 steps via conjugate gradient. A restraint of 500 kcal/mol/Å2 was imposed on all the protein and ligand atoms. During the second step, the protein-ligand complexes and the solvent were both minimized for 10,000 steps via steepest descent, followed by conjugate gradient minimization until the energy gradient of the system converged to 0.01 kcal/mol/Å. Next, the heating phase was conducted for the systems and the temperature climbed from 0 to 300 K in 100 ps, and then NPT simulation was performed for 3 ns at a time step of 2 fs. To regulate the system temperature in MD simulation, Langevin dynamics [32] was employed with a collision frequency of 4.0 ps−1. The SHAKE [33] algorithm was introduced to restrain the bonds involving hydrogen atoms.
2.4.2 MM/PBSA
MM/PBSA was used to calculate the binding free energy of a complex based on a combination of the molecular mechanics and a continuum solvent approach. The binding free energy is decomposed into three terms, molecular mechanics (MM), solvation contribution, and entropic contribution. In this study, 1500 snapshots taken from the last 1.5 ns simulations at 1 ps interval were used for calculating the MM term and the solvation contribution. The solvation energy was obtained via the PBSA module [34]. The grid spacing was set to 0.25 Å. The value of the exterior dielectric constant was set to 80. The solute interior dielectric constant was set to 1, because the binding interface on FXR is quite hydrophobic. A higher value (e.g., 2) of the interior dielectric constant did not improve the binding affinity prediction for this FXR dataset (data not shown). The nonpolar solvation energy was calculated with the solvent-accessible surface area (SASA) approach, following the equation Gnonpol = γΔSASA + β, where γ = 0.00542 kcal/(mol·Å2) and β = 0.92 kcal/mol [35]. The Nmode module [36] in AMBER11 was applied to derive the entropy loss during protein-ligand binding. 50 snapshots were obtained from the last 1.5 ns with 30 ps interval for each system to calculate the entropic contribution. Every snapshot was minimized under a distance-dependent dielectric function until the energy gradient’s root-mean-square fell below 10−5 kcal/mol/Å2.
3. Results and Discussion
3.1 Binding mode prediction
The criterion of root-mean-square deviations (RMSD) was used to assess the predicted binding modes of a query ligand on the protein FXR with the corresponding native binding mode in the released crystal structure. Briefly, the two protein structures were superimposed and the RMSD of the heavy atoms in the query ligand was calculated. For both the docking approach and the template-based approach, the top 5 predicted binding modes were submitted for each query ligand. The following analysis is based on the assessment data provided by the D3R evaluation team.
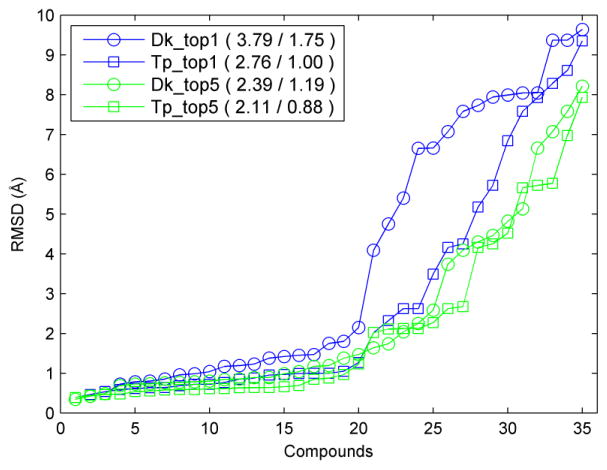
Fig. 1 shows the performances of these two approaches on the binding mode predictions of the 35 queried ligands. FXR_33 was removed from the list, because the FXR_33 ligand in the released co-crystal structure was inconsistent with the provided SMILES string. When only the best model (top 1) was considered for each query ligand, the template-based approach yielded significantly better performance than the docking approach. As shown in Fig. 1 for the template based approach, the mean and median RMSD values of the 35 ligands are 2.76 and 1.00 Å, respectively, which was ranked #2 by the median RMSD in all the 51 submissions. The result indicates that using the superimposition method based on a proper template selected by ligand similarity would raise the prediction accuracy of the binding mode. Interestingly, the docking-based approach achieved a comparable performance with the template-based method when top 5 models were considered. The corresponding mean and median RMSD values are 2.39 Å and 1.19 Å respectively for the docking-based approach. The results show that the sampling algorithm successfully generated near-native binding modes, but the scoring function (ITScore2) failed to rank them at the top for the same cases.
Fig. 1.
The results of binding mode prediction for the FXR dataset (i.e., FXR_1 to FXR_36) based on the top model (blue) or the best (i.e., the model with the lowest RMSD) among the top 5 models (green) using the docking approach (Dk) or the template-based approach (Tp) with the scoring function ITScore2. The mean value and the median value of RMSDs of the ligands are reported in the legend for each method.
It is noteworthy that the predicted binding modes generated by the template-based approach were minimized via MD to avoid possible atomic clashes, whereas the MD minimization was not applied to the binding modes predicted from the docking approach. We evaluated the effects of our minimization steps on the predicted binding modes so as to investigate whether minimization is the dominant reason for the better performance of the template-based approach. The ligand RMSDs between the structures before minimization and the released crystal structures were calculated. The mean/median RMSD values of the 35 query ligands were 2.77/1.11 Å and 2.16/1.00 Å for the top model and for the best one in top 5 models, respectively. The corresponding mean/median RMSD values of the models after minimization were 2.76/1.00 Å and 2.11/0.88 Å for the top model and for the best one in top 5 models, respectively. Thus, the minimization step only slightly improved the binding mode prediction results, and the template-based method without the minimization step still performed better than the docking approach. In other words, the good performance of the template-based method is mainly due to the assumption that ligands with similar structures share similar binding modes, instead of due to the minimization step.
To gain a better understanding on the importance of ligand similarity, Pearson’s correlation coefficient (R) between ligand similarity and the RMSD of the top predicted pose for each ligand was investigated. As described in Materials and Methods, the ligand similarity calculation was involved in both approaches to select a proper conformation of the binding pocket (for docking) or binding mode (for superimposing). It should be noticed that in the docking approach, ensemble docking was performed when no co-bound ligand was found sharing a HybridScore ≥ 1.2 with a query ligand. Therefore, here, our analysis is focused on the cases with HybridScore ≥ 1.2. Positive correlations were observed for both methods, with R values of 0.65 for the docking approach and 0.72 for the template-based method, respectively. The detailed data were also listed in Table S1 in the Supplementary Materials. The results suggest that ligands with high molecular similarities tend to share a similar binding mode and this tendency is in proportion to the similarity score. Therefore, known co-crystal structures could be an important resource to improve protein-ligand complex structure prediction.
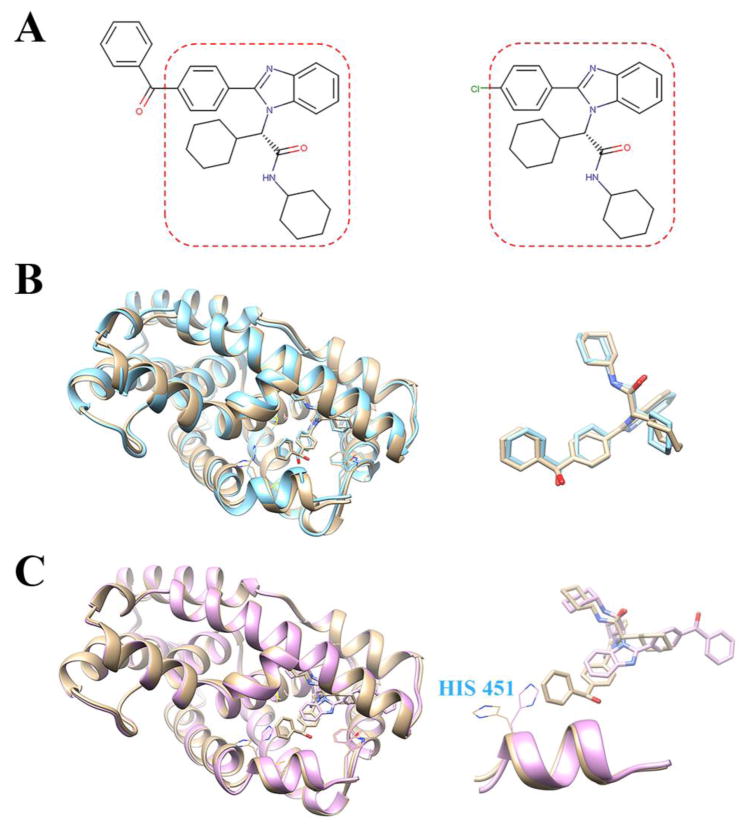
Furthermore, binding modes of all the cases with HybridScore ≥ 1.5 were successfully predicted (i.e., with RMSD ≤ 2.0 Å) for the template-based method, and only one case (i.e., FXR_13) failed for the docking approach. FXR_13 possessed a high molecular similarity (HybridScore = 1.626) with the ligand in PDB entry 3OKI, however, the binding modes predicted with the docking approach against chain A of 3OKI showed a large deviation from the co-crystal structure. The values of RMSD were 7.99 Å for the top model and 4.46 Å for the best in the top 5 models. As shown in Fig. 2A, FXR_13 shares the same chemical structure in the boxed part with ligand OKI of 3OKI; the only difference between these two compounds is the replacement of the chlorine atom in OKI by a benzaldehyde group. Also, direct superimposition of 3OKI onto the crystal structure of the protein-FXR_13 complex shows very similar binding modes, e.g., the RMSD between the best mode from the template-based approach and the native binding mode of FXR_13 is only 0.719 Å (Fig. 2B). However, in the docking approach, the compound in the best predicted model presented a 180-degree flip in comparison with the crystal structure. Examination of the structural details shows that the side chain of residue H451 in the released crystal structure is outside the binding pocket. However, in the protein structure that was used for docking (i.e., 3OKI), the side chain of H451 is rotated and is inside the binding pocket (Fig. 2C), which narrows the binding site and leads to the failure of docking the benzaldehyde group into the right location.
Fig. 2.
A. Chemical structures of compound FXR_13 (left) and ligand OKI in PDB entry 3OKI (right). B. The top model from the template-based approach (cyan) aligned with the crystal structure (tan) released by D3R. Left: the structure of FXR_13 bound to FXR; right: comparison of the predicted binding mode with the released binding mode. C. The top model from the docking approach using the ITScore2 scoring function (orchid) aligned with the released crystal structure (tan) by D3R (left: structure of FXR_13 bound to FXR; right: comparison between the predicted binding mode and the released binding mode, with residue H451 highlighted).
In summary, two distinct methods, a docking-based method and a template-based method, were employed for the binding mode prediction of 35 query ligands in the FXR dataset. The results show that the template-based method performed significantly better than the docking approach. However, it is worth mentioning that the performance/reliability of the template-based method is highly dependent on available templates, and a further systematic test is desirable for this method. Fortunately, with the increasing number of experimental structures solved for a specific target (e.g., an important druggable protein) co-bound with distinct ligands in the Protein Data Bank, the template-based method would become more and more useful. Also, the template-based allows for the selection of the appropriate protein conformation, an implicit way to account for protein flexibility, particularly protein sidechain flexibility.
3.2 Binding affinity prediction
To assess the performances of ITSore2 and MM/PBSA on binding affinity prediction, affinity rankings and energy predictions were analyzed in terms of Kendall’s tau and Pearson’s correlation coefficient (R), respectively. R was calculated based on the predicted binding energy scores and experimental affinities -pIC50 (i.e., log(IC50)). As aforementioned, FXR_33 was discarded, leaving a total of 101 compounds for the analysis. The results for the docking-based ITScore2 (Dk_ITS; D3R submission ID: pr2fp), template-based ITScore2 (Tp_ITS; D3R submission ID: bxn4v) and template-based MM/PBSA approach (Tp_MM/PBSA; D3R submission ID: erdfw) with the dataset of these 101 compounds (referred to as the Full dataset) are reported in the first row of Table 1. In addition, the results based on the all-atom molecular weights of the ligands were also presented for reference. Here, our analysis is focused on the results of Stage 2, in which more co-crystal FXR structures (FXR_1–36) were available than those in Stage 1, resulting in more confidence on the binding mode prediction in Stage 2 than in Stage 1.
Table 1.
The results on binding affinity prediction with the FXR dataset.
| Ranking (tau) | Binding affinity (R) | |||||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||
| Dataset | MWa | MM/PBSAb | Tp_ITSc | Dk_ITSd | MW | MM/PBSA | Tp_ITS | Dk_ITS |
| Full | 0.05 | 0.35 | 0.10 | 0.22 | 0.12 | 0.46 | 0.17 | 0.34 |
| CSet_1 (< 75%) | 0.23 | 0.32 | 0.18 | 0.13 | 0.31 | 0.43 | 0.27 | 0.22 |
| CSet_2 (≥ 75%) | 0.28 | 0.3 | 0.34 | 0.38 | 0.43 | 0.45 | 0.36 | 0.54 |
| ONSet_1 (≤10%) | 0.35 | 0.39 | 0.27 | 0.40 | 0.52 | 0.56 | 0.41 | 0.56 |
| ONSet_2 (>10%) | 0.29 | 0.21 | 0.16 | 0.10 | 0.40 | 0.29 | 0.26 | 0.17 |
| Set_size (<40) | 0.11 | 0.43 | 0.18 | 0.30 | 0.20 | 0.59 | 0.29 | 0.42 |
| Rot_bonds (<8) | 0.09 | 0.40 | 0.15 | 0.31 | 0.18 | 0.58 | 0.23 | 0.45 |
| Normal | 0.09 | 0.42 | 0.15 | 0.27 | 0.17 | 0.58 | 0.23 | 0.39 |
MW shorts for the all-atom molecular weight.
MM/PBSA shorts for the MM/PBSA approach based on the top model from the template-based approach.
Tp_ITS stands for the evaluation of the top model from the template-based approach using ITScore2.
Dk_ITS stands for the evaluation of the models from the docking approach using ITScore2.
In the affinity ranking assessment, the value of Kendall’s tau ranges from −1 to 1, in which −1 stands for perfectly reversed ranking and 1 represents perfect ranking. All the ranking results exhibited positive correlations with the experimental results, and presented better performances (i.e., larger values) than the molecular weight (tau = 0.05). Tp_mm/pbsa achieved significantly better performance (0.35) than the other two strategies with ITScore2. Encouragingly, Tp_mm/pbsa was ranked 9th in a total of 77 submissions. For ITScore2, the results were unsatisfactory for both docking-based and template-based approaches, with tau values of 0.22 and 0.10, respectively. Similar results were observed for the free energy predictions (R). Tp_mm/pbsa yielded the highest R value of 0.46, while the value for Dk_ITS and Tp_ITS were 0.34 and 0.17 respectively. Although the MM/PBSA approach achieved the best performance in our study, the result was still unsatisfactory with regard to its expensive computing cost. It is possible that the conducted simulations were not long enough to provide accurate predictions and that multiple-trajectory simulation might achieve better results than the present single-trajectory simulation.
As ITScore2 showed an unsatisfactory performance on the binding affinity prediction for the dataset of 101 FXR ligands, further analysis was made to reveal possible reasons in order to help future improvement of this scoring function. Because ITScore2 is based on atom types, the compounds in the FXR dataset were classified into two groups in terms of the percentage of certain types of heavy atoms in the query compounds. The results based on this classification are also listed in Table 1. By setting 75% as the cutline for the percentage of carbon atoms, the compounds were grouped into two sets, CSet_1 (< 75%, containing 53 entries) and CSet_2 (≥ 75%, containing 48 entries). The tau and R values of CSet_1 and CSet_2 showed minor deviations for MM/PBSA, however, tau and R increased significantly with the increase in the percentage of carbon atoms for ITScore2-involved approaches. Specifically, tau increased from 0.13 to 0.38 in Dk_ITS and from 0.18 to 0.34 in Tp_ITS, respectively. The corresponding Pearson’s correlation coefficient increased from 0.22 to 0.54 and from 0.27 to 0.36, respectively. Similarly, the total percentage of oxygen and nitrogen atoms was also introduced as another criterion. ONSet_1 (≤ 0.1) contained 44 entries and ONSet_2 (> 0.1) contained 57 entries. For all the strategies, the set possessing smaller percentage of oxygen and nitrogen atoms (i.e., ONSet_1) delivered a better performance. Particularly, for Dk_ITS, ITScore2 performed dramatically different with ONSet_1 and ONSet_2, in which the tau and R values increased from 0.1 to 0.4 and from 0.17 to 0.56, respectively, with the decrease in the percentage of oxygen and nitrogen atoms. These results implicate that ITScore2 acted better on the ligands possessing more carbon atoms and less oxygen and nitrogen atoms. It is possible that ITScore2 defines carbon-carbon interactions better than other types of atoms, as carbon is the most common atom type in the protein and ligand structures. Nevertheless, for oxygen and nitrogen atoms, ITScore2 lacks accuracy on defining the interactions involving these atom types, probably due to the fewer numbers of such interactions that were collected during the derivation of ITScore2.
Moreover, it is well known that the exiting binding affinity prediction methods are far from accurately on calculating contributions from entropic effects, and the entropic effects are related to the size and flexibility of a system. Therefore, the influences of the molecular size and flexibility on the performances of binding affinity predictions were also analyzed for both ITScore2 and MM/PBSA. Regarding the molecular size, ligands containing at least 40 heavy atoms were excluded (i.e., a total of eight ligands) from the full set of the FXR dataset, resulting in a subset (referred to as Set_size) consisting of 93 query ligands (each having fewer than 40 heavy atoms). The results for the subset Set_size are reported in Table 1. Interestingly, significantly improvements were found for all the strategies, MM/PBSA, Tp_ITS, and Dk_ITS on both ranking (tau) and the binding affinity (R) predictions. On the other hand, regarding the ligand flexibility, ligands with at least 8 rotatable bonds (a total of 18 ligands) were removed from the full set, resulting in a subset (named as Rot_bonds) consisting of 83 query ligands (each ligand containing fewer than 8 rotatable bonds). Similar to the findings with respect to the molecular size, significantly improvements were found for all the strategies for the subset Rot_bonds, as shown in Table 1. For example, for the strategy Dk_IST, the values of tau/R increased from 0.22/0.34 for the full set (first row) to 0.31/0.45 for the subset Rot_bonds (the second last row). Next, the compounds with both at least 40 heavy atoms and at least eight rotatable bonds (a total of five compounds: FXR_45, FXR_64, FXR_66, FXR_67, and FXR_68) were excluded from the full set, resulting a subset referred to as the “Normal” set. For this “Normal” subset, both tau and R increased significantly (see the last row of Table 1 cf. the first row), particularly for MM/PBSA. A correlation plot for the MM/PBSA results shows three of these five compounds are far deviated from the other compounds (data not shown). These findings suggest that too large or too flexible ligands pose a big challenge to current scoring functions, and are recommended to be separated or even removed from the list by the D3R organizers for future exercises.
Finally, the 35 ligands with co-bound crystal structures solved (i.e., FXR_1 to FXR_36, except that FXR_33 was discarded because its chemical structure in the co-crystal was different form the D3R-provided SMILES string) were further analyzed, using the corresponding co-crystal structures. For these 35 ligands, MM/PBSA achieved 0.23 for the Kendall’s tau and 0.39 for the Pearson’s correlation coefficient, respectively. Scoring directly with the co-crystal structures (including scoring minimization), ITScore2 yielded 0.28 for tau and 0.46 for R, respectively. The Tp_ITS approach, in which the initial structures were these co-crystals (as these structures yielded HybridScore of 2) followed by optimization with AMBER11, achieved 0.38 for tau and 0.56 for R, respectively. Finally, the molecular weight approach (for the reference purpose) yielded 0.32 for tau and 0.57 for R. Comparing these data, it is surprising that molecular weight achieved the best R value (0.57). ITScore2 with the template-based approach achieved a comparable result (R = 0.56). Also, ITScore2 with the template-based approach achieved the highest tau value. It is encouraging that the efficient ITScore2 showed a better performance than the computationally demanding MM/PBSA approach on both affinity ranking and binding affinity predictions with these 35 complexes using the co-crystal structures.
4. Conclusion
D3R provides a valuable platform to evaluate and to improve CADD methods. During 2016 Grand Challenge 2, we developed two distinct strategies, a docking method and a template-based method, for the binding mode prediction. We also employed two distinct methods, ITScore2 and MM/PBSA, for the binding affinity prediction. For the binding mode prediction, the template-based method achieved a significantly better performance than the docking method. For the binding affinity prediction, MM/PBSA performed significantly better than ITScore2 with the full dataset. Both ITScore2 and MM/PBSA were further applied to several subsets, which were constructed based on the atom type percentage (in terms of the number of atoms) in the compounds. The results show that the performance of ITScore2 was sensitive to the ligand composition. Namely, better performance was achieved when ITScore2 was applied to the subset containing ligands with a higher percentage of carbon atoms. Such bias was not found for MM/PBSA. This clue could be used to further improve the knowledge-based atomic pairwise scoring function (ITScore2). In future studies, it would be interesting to retrain the ITscore by introducing training structures with more polar functional groups.
Finally, our analysis shows that the big offset compounds usually contain too many heavy atoms (i.e., too large molecular weights) and too many rotatable bonds. It is recommended to the D3R organizers that these too large and too flexible ligands are better listed separately in the future exercises, because no existing scoring functions can well account for large ligand entropic contributions.
Supplementary Material
Acknowledgments
Support to XZ from OpenEye Scientific Software Inc. (Santa Fe, NM, http://www.eyesopen.com) is gratefully acknowledged. This work was supported by the NSF CAREER Award DBI-0953839, NIH R01GM109980, and American Heart Association (Midwest Affiliate) 13GRNT16990076 to XZ. The computations were performed on the high performance computing infrastructure supported by NSF CNS-1429294 (PI: Chi-Ren Shyu) and the HPC resources supported by the University of Missouri Bioinformatics Consortium (UMBC).
References
- 1.Gathiaka S, Liu S, Chiu M, Yang H, Stuckey JA, Kang YN, Delproposto J, Kubish G, Dunbar JB, Jr, Carlson HA, Burley SK, Walters WP, Amaro RE, Feher VA, Gilson MK. D3R grand challenge 2015: Evaluation of protein-ligand pose and affinity predictions. J Comput Aided Mol Des. 2016;30:651–668. doi: 10.1007/s10822-016-9946-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Forman BM, ode E, Chen J, Oro AE, Bradley DJ, Perlmann T, Noonan DJ, Burka LT, McMorris T, Lamph WW, Evans RM, Weinberger C. Identification of a nuclear receptor that is activated by farnesol metabolites. Cell. 1995;81:687–693. doi: 10.1016/0092-8674(95)90530-8. [DOI] [PubMed] [Google Scholar]
- 3.Parks DJ, Blanchard SG, Bledsoe RK, Chandra G, Consler TG, Kliewer SA, Stimmel JB, Willson TM, Zavacki AM, Moore DD, Lehmann JM. Bile acids: Natural ligands for an orphan nuclear receptor. Science. 1999;284:1365–1368. doi: 10.1126/science.284.5418.1365. [DOI] [PubMed] [Google Scholar]
- 4.Lambert G, Amar MJ, Guo G, Brewer HB, Jr, Gonzalez FJ, Sinal CJ. The farnesoid X-receptor is an essential regulator of cholesterol homeostasis. J Biol Chem. 2003;278:2563–2570. doi: 10.1074/jbc.M209525200. [DOI] [PubMed] [Google Scholar]
- 5.Ma K, Saha PK, Chan L, Moore DD. Farnesoid X receptor is essential for normal glucose homeostasis. J Clin Invest. 2006;116:1102–1109. doi: 10.1172/JCI25604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sinal CJ, Tohkin M, Miyata M, Ward JM, Lambert G, Gonzalez FJ. Targeted disruption of the nuclear receptor FXR/BAR impairs bile acid and lipid homeostasis. Cell. 2000;102:731–744. doi: 10.1016/s0092-8674(00)00062-3. [DOI] [PubMed] [Google Scholar]
- 7.Zhang Y, Ge X, Heemstra LA, Chen WD, Xu J, Smith JL, Ma H, Kasim N, Edwards PA, Novak CM. Loss of FXR protects against diet-induced obesity and accelerates liver carcinogenesis in ob/ob mice. Mol Endocrinol. 2012;26:272–280. doi: 10.1210/me.2011-1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cariou B, van Harmelen K, Duran-Sandoval D, van Dijk TH, Grefhorst A, Abdelkarim M, Caron S, Torpier G, Fruchart J, Gonzalez FJ, Kuipers F, Staels B. The farnesoid X receptor modulates adiposity and peripheral insulin sensitivity in mice. J Biol Chem. 2006;281:11039–11049. doi: 10.1074/jbc.M510258200. [DOI] [PubMed] [Google Scholar]
- 9.Xu X, Yan C, Zou X. Improving Binding Mode and Binding Affinity Predictions of Docking by Ligand-based Search of Protein Conformations: Evaluation in D3R Grand Challenge 2015. J Comput Aided Mol Des. 2017;31:689–699. doi: 10.1007/s10822-017-0038-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu X, Jiang H, Li H. SHAFTS: a Hybrid Approach for 3D Molecular Similarity Calculation. 1. Method and Assessment of Virtual Screening. J Chem Inf Model. 2011;51:2372–2385. doi: 10.1021/ci200060s. [DOI] [PubMed] [Google Scholar]
- 11.Lu W, Liu X, Cao X, Xue M, Liu K, Zhao Z, Shen X, Jiang H, Xu Y, Huang J, Li H. SHAFTS: a Hybrid Approach for 3D Molecular Similarity Calculation. 2. Prospective Case Study in the Discovery of Diverse P90 Ribosomal S6 Protein Kinase 2 Inhibitors to Suppress Cell Migration. J Med Chem. 2011;54:3564–3574. doi: 10.1021/jm200139j. [DOI] [PubMed] [Google Scholar]
- 12.Willett P, Barnard JM, Downs GM. Chemical similarity searching. J Chem Inf Model. 1998;38:983–996. [Google Scholar]
- 13.Bender A, Glen RC. Molecular similarity: a key technique in molecular informatics. Org Biomol Chem. 2004;2:3204–3218. doi: 10.1039/B409813G. [DOI] [PubMed] [Google Scholar]
- 14.Cheng T, Li X, Li Y, Liu Z, Wang R. Comparative Assessment of Scoring Functions on a Diverse Test Set. J Chem Inf Model. 2009;49:1079–1093. doi: 10.1021/ci9000053. [DOI] [PubMed] [Google Scholar]
- 15.Wang R, Fang X, Lu Y, Yang CY, Wang S. The PDBbind Database: Methodologies and Updates. J Med Chem. 2005;48:4111–4119. doi: 10.1021/jm048957q. [DOI] [PubMed] [Google Scholar]
- 16.Huang S, Zou X. An iterative knowledge-based scoring function to predict protein-ligand interactions: I. Derivation of interaction potentials. J Comput Chem. 2006;27:1866–1875. doi: 10.1002/jcc.20504. [DOI] [PubMed] [Google Scholar]
- 17.Huang S, Zou X. An Iterative Knowledge-based Scoring Function to Predict Protein–Ligand Interactions: II. Validation of the Scoring Function. J Comput Chem. 2006;27:1876–1882. doi: 10.1002/jcc.20505. [DOI] [PubMed] [Google Scholar]
- 18.Yan C, Grinter SZ, Merideth BR, Ma Z, Zou X. Iterative Knowledge-Based Scoring Functions Derived from Rigid and Flexible Decoy Structures: Evaluation with the 2013 and 2014 CSAR Benchmarks. J Chem Inf Model. 2016;56:1013–1021. doi: 10.1021/acs.jcim.5b00504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc Chem Res. 2000;33:889–97. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- 20.Srinivasan J, Cheatham TE, Cieplak P, Kollman PA, Case DA. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate–DNA helices. J Am Chem Soc. 1998;120:9401–9409. [Google Scholar]
- 21.Hawkins PC, Skillman AG, Warren GL, Ellingson BA, Stahl MT. Conformer Generation with Omega: Algorithm and Validation Using High Quality Structures from the Protein Databank and Cambridge Structural Database. J Chem Inf Model. 2010;50:572–584. doi: 10.1021/ci100031x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hawkins PC, Nicholls A. Conformer generation with OMEGA: learning from the data set and the analysis of failures. J Chem Inf Model. 2012;52:2919–2936. doi: 10.1021/ci300314k. [DOI] [PubMed] [Google Scholar]
- 23.Trott O, Olson AJ. AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J Comput Chem. 2010;31:455–461. doi: 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Walker RC, Zhang W, Merz KM, Roberts B, Wang B, Hayik S, Roitberg A, Seabra G, Kolossváry I, Wong KF, Paesani F, Vanicek J, Liu J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Cai Q, Ye X, Wang J, Hsieh MJ, Cui G, Roe DR, Mathews DH, Seetin MG, Sagui C, Babin V, Luchko T, Gusarov S, Kovalenko A, Kollman PA. AMBER 11. University of California; San Francisco: 2010. [Google Scholar]
- 25.Dewar MJS, Zoebisch EG, Healy EF, Stewart JJP. Development and use of quantum mechanical molecular models. 76. AM1: a new general purpose quantum mechanical molecular model. J Am Chem Soc. 1985;107:3902–3909. [Google Scholar]
- 26.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Jr, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas Ö, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ. Gaussian 09, Revision D.01. Gaussian, Inc.; Wallingford CT: 2009. [Google Scholar]
- 27.Jakalian A, Jack DB, Bayly CI. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J Comput Chem. 2002;23:1623–1641. doi: 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- 28.Duan Y, Wu C, Chowdhury S, Lee MC, Xiong G, Zhang W, Yang R, Cieplak P, Luo R, Lee T, Caldwell J, Wang J, Kollman P. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J Comput Chem. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 29.Wang J, Wolf RM, Caldwell JW, Kollman PA, Case DA. Development and testing of a general amber force field. J Comput Chem. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- 30.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 31.Darden T, York D, Pedersen L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 32.Pastor RW, Brooks BR, Szabo A. An analysis of the accuracy of Langevin and molecular dynamics algorithms. Mol Phys. 1988;65:1409–1419. [Google Scholar]
- 33.Ryckaert JP, Ciccotti G, Berendsen HJ. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J Comput Phys. 1977;23:327–341. [Google Scholar]
- 34.Luo R, David L, Gilson MK. Accelerated Poisson–Boltzmann calculations for static and dynamic systems. J Comput Chem. 2002;23:1244–1253. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 35.Sitkoff D, Sharp KA, Honig B. Accurate Calculation of Hydration Free Energies Using Macroscopic Solvent Models. J Phys Chem. 1994;98:1978–1988. [Google Scholar]
- 36.Nguyen DT, Case DA. On finding stationary states of large molecule potential energy surfaces. J Phys Chem. 1985;89:4020–4026. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.