Introduction of a prediction model to assigning periodontal prognosis based on survival time

Abstract

Aims

To develop a prediction model for tooth loss due to periodontal disease (TLPD) in patients following periodontal maintenance (PM), and assess its performance using a multicentre approach.

Material and methods

A multilevel analysis of eleven predictors of TLPD in 500 patients following PM was carried out to calculate the probability of TLPD. This algorithm was applied to three different TLPD samples (369 teeth) gathered retrospectively by nine periodontist, associating several intervals of probability with the corresponding survival time, based on significant differences in the mean survival time. The reproducibility of these associations was assessed in each sample (One‐way ANOVA and pairwise comparison with Bonferroni corrections).

Results

The model presented high specificity and moderate sensitivity, with optimal calibration and discrimination measurements. Seven intervals of probability were associated with seven survival time and these associations contained close to 80% of the cases: the probability predicted the survival time at this percentage. The model performed well in the three samples, as the mean survival time of each association were significantly different within each sample, while no significant differences between the samples were found in pairwise comparisons of means.

Conclusions

This model might be useful for predicting survival time in different TLPD samples.

Clinical relevance.

Scientific rationale for the study: There are no defined guidelines to predict tooth loss due to periodontal disease and assign a meaningful prognosis on which to base treatment decisions. The aim of this study was to develop and assess the performance of a prediction model to calculate the probability of tooth loss by associating it with the expected survival time.

Principal findings: This model is capable of associating intervals of probability with survival time, and fulfils this purpose in different tooth loss samples.

Practical implications: The usefulness of this model represents an alternative and promising approach to assigning periodontal prognosis.

1. INTRODUCTION

Conventional periodontal prognostic indices (Becker, Berg, & Becker, 1984; Checchi, Montevecchi, Gatto, & Trombelli, 2002; Fardal, Johannessen, & Linden, 2004; Kwok & Caton, 2007; McGuire & Nunn, 1996) developed to predict tooth loss due to periodontal disease (TLPD) are based on tooth‐related factors (TRFs) and present low accuracy (McGuire & Nunn, 1996). The categories used in each index are defined rather vaguely, and heterogeneous criteria are used (Faggion, Petersilka, Lange, Gerss, & Fleming, 2007). No single prognostic index has been unanimously accepted up to the time of writing, and this has been attributed to the paucity of knowledge of periodontal prognosis and predictors of TLPD in patients following periodontal maintenance (PM). A systematic review of the subject concluded that the only patient‐related factors (PRFs) that are clearly associated with TLPD were older age and smoking (Chambrone, Chambrone, Lima, & Chambrone, 2010).

However, this scenario contrasts with a newly emerging one as a result of research carried out in recent years. On the one hand, disease progression and tooth loss risk assessment (Fors & Sandberg, 2001; Lang & Tonetti, 2003; Lindskog et al., 2010; Page, Krall, Martin, Mancl, & Garcia, 2002; Teich, 2013) have improved knowledge of certain predictors, and some of these tools have been validated in different populations (Lang, Suvan, & Tonetti, 2015). On the other hand, more recent studies have reported an increase in the risk of TLPD according to each category of several TRFs in the presence or absence of certain PRFs (Dannewitz et al., 2016; Graetz et al., 2015; Martinez‐Canut, 2015; Miller, McEntire, Marlow, & Gellin, 2014).

Therefore, fairly broad knowledge of the subject is gained from gathering the most consistent findings. However, a method for applying it in a practical and useful manner has not been defined.

Insofar as research on periodontal prognosis enlarges the list of regression coefficients and relative risks of predictors, clinicians should interpret the data as far as possible in a practical way. However, there are no clearly defined guidelines for using this data and assigning a meaningful prognosis in terms of treatment decisions.

To date, periodontal prognosis has been interpreted through qualitative analysis with conventional logistic regression, by applying the inductive method to the interpretation of results; assigning a suspected weight or value based on how the statistical significance of each predictor is subjectively interpreted. This implies matching words with values.

In line with a clear tendency in many areas of medicine, periodontal prognosis might benefit from incorporating quantitative analysis to develop prediction models and make use of the data in a more practical, useful and perhaps more accurate way. The idea of a prediction model to assign periodontal prognosis was first introduced by Faggion et al. (2007), who questioned the actual meaning of certain prognostic categories (e.g. questionable).

Quantitative analysis uses the inference method to deduce properties, which are expressed in probabilistic terms: the probability of ascertaining (accuracy) the observed event (TLPD) in a statistical model. This probability is a p value from 0 to 1, supported by objective performance measurements.

A prediction model does not interpret but calculates an absolute and objective value, going beyond regression coefficients and relative risks (Cerrito, 2009; Pepe, Janes, Logton, Leisenring, & Newcomb, 2004; Steyerberg et al., 2010). This in itself is a prognosis or an absolute risk, with a unique and meaningful p value to make decisions, as long as this probability can be associated with a certain survival time.

The purpose of this study was to develop and evaluate the performance of a prediction model of TLPD in patients following PM. A multicentre approach enabled definition of survival time associated with the probability of TLPD and the performance of the model was assessed using different TLPD samples.

2. MATERIAL AND METHODS

This prediction model was developed by taking a systematic approach to model development (Steyerberg & Vergouwe, 2014) and is a web‐based algorithm (www.perioproject.es) that can be openly accessed by researchers and clinicians. The tool calculates the probability of TLPD according to the impact of 11 predictors, and this probability can be associated with a certain survival time. This makes it possible to define the prognosis of the whole dentition based on survival expectancy, but more importantly, to retrospectively assess the accuracy of the prediction with any tooth extracted for periodontal reasons.

The process consists of entering in the model the predictor of a certain tooth extracted after 20 years under PM, for instance, as it was at baseline, that is 20 years previously. This makes it possible to assess whether the calculated probability of TLPD and the associated survival time matched the actual survival rate of the extracted tooth.

2.1. Criteria for selecting the predictors

The database resulting from an analysis of TLPD predictors in a sample of 500 carefully documented patients (515 TLPD) following PM for a mean 20 years (Martinez‐Canut, 2015) was used to develop the prediction model. This analysis made it possible to select those variables more clearly associated with TLPD, which are also the ones that are most consistently found to be associated with TLPD in the literature, with fairly homogeneous relative risks. Thirty‐two studies of predictors of TLPD in patients following PM for more than 5 years were selected according to previously defined selection criteria (Chambrone et al., 2010; Faggion, Chambrone, & Tu, 2014). These are presented in Supporting Information (Table S1 and Appendix S1).

Finally, the number of variables to be analysed was adjusted to the sample size and the number of events per variable analysed (500 patients and 515 TLPD) so as to avoid overfitting the model (Peduzzi, Concato, Kemper, Holford, & Feistein, 1996; Steyerberg & Vergouwe, 2014; Wynants et al., 2015).

Based on the above criteria, the following variables were analysed. Five PRFs: age, severe periodontitis, heavy smoking, bruxism and baseline number of teeth; and six TRFs: type of tooth, furcation involvement, probing pocket depth, bone loss, mobility and C/R ratio.

2.2. Statistical analysis of the PRFs and TRFs selected to construct the model

These 11 predictors were analysed by independent statisticians (ERATEMA, I.A & L.D.), using the STATA software procedure xtmelogit (StataCorp. 2011. Stata Statistical Software: Release 12. College Station, TX: StataCorp LP).

Multilevel analysis was performed to assess the impact of these predictors. This generalized linear mixed regression uses a binomial distribution for the dichotomous dependent variable TLPD and the logit as link function. The base‐level tooth in all of the analysis was nested into the upper‐level patient. All patient effects were assumed to be random.

This analysis assesses the probability (p) of TLPD i in a patient j in terms of Odds ratio, as an exponential function of the variables analysed. Therefore, pij is the probability of TLPD i in a patient j and X k,ij (K = 1,2…,n) represent the independent variables for the tooth i in a patient j. Bk is the regression coefficients under analysis represent the estimated probability of TLPD. Error ui + eij is integrated by the inherent error of the model itself e ij or tooth effect (which independent variables do not explain) and the patient effect u j (error due to differences between patients). Beta regression coefficients represent the estimated probability of TLPD. Statistical significance was set at p < .05 (Wald′s test).

$$\frac{\mathit{pij}}{1-pij}={\mathrm{e}}^{{\mathrm{\beta }}_0+{\mathrm{\beta }}_1{X}_{1}ij+{\mathrm{\beta }}_2{X}_{2ij}+\cdots +\mathrm{\beta }nXnij+uj+eij}$$

Goodness of fit tests included Rᶻ Nagelkerke and variance partition coefficient (VPC) with discrimination measurements AUC, sensitivity, specificity, PV+ and PV−.

2.3. Criteria to adjust and utilize the prediction model

The model was adjusted in consideration of the following three main issues of model development:

2.3.1. The prevalence of the TLPD event

Due to the low prevalence of TLPD, the model performed better in discharging TLPD. Therefore, it is more appropriate for ascertaining that TLPD will not occur (TLPD−) (higher specificity) while it was less appropriate for ascertaining that TLPD will occur (TLPD+) (moderate sensitivity).

2.3.2. The usefulness or relevance of the prediction (TLPD+ and TLPD–)

A cut‐off point in the probability of TLPD making the prediction was defined, classifying the tooth as TLPD+ and TLPD−. The usefulness or relevance of this decision, according to the consequences, required a critical and discretional decision regarding what might have worse consequences: predicting TLPD that does not occur (False+) or not having predicted an actual TLPD (False−). It was assumed that the unexpected (unpredicted) loss of a tooth (False−) might have worse consequences than the retention of a tooth that was expected (predicted) to be lost (False+) and this decision was in line with the low prevalence of TLPD.

Therefore, the model was adjusted by giving more relevance to F− than F+, attaining high specificity and high PV−, moderate sensitivity and a lower PV+. The search for a model that is more able to ascertain TLPD would have the inconvenience of F− being too undesirable.

2.3.3. The prediction accuracy

The accuracy of the prediction could be interpreted from two perspectives.

The accuracy of the dichotomous event (TLPD+ or TLPD−)

The ideal approach to assessing the accuracy of the prediction is the prospective longitudinal approach. However, it does not seem to be practical, as TLPD usually takes place in the long term as half of the teeth are lost between 10 and 20 years of observation (Martinez‐Canut, 2015). The already described alternative retrospective approach enables an immediate assessment of the accuracy of the prediction.

The assignment of individual tooth prognosis using conventional periodontal indices should also be addressed. These are the routinely used tools to assign individual tooth prognosis, and their accuracy has been assessed by comparing it with the actual event TLPD. To complete this approach, the accuracy of the model′s prediction was compared with the conventional periodontal prognosis assigned by one of the authors (M‐C) to the whole dentition (12.839 teeth) in the sample (515 TLPD in 500 patients) used to construct the model. The results of this preliminary indicative assay are presented in Supporting Information (Table S2 and Appendix S2).

The accuracy of the TLPD+ prediction based on the survival time

Obviously, the accuracy of the TLPD+ prediction calculated by the model or estimated using conventional periodontal prognosis increases with the passage of time. The distribution of TLPD through the follow‐up period was quite even in the database of the present study: baseline to 5 years (31.6%), 5 to <10 years (20.2%), 10 to <15 years (26.5%) and >15 years (21.6%). Therefore, rather than the dichotomous alternative TLPD + or −, a more realistic and useful approach would be to attempt to predict when a certain tooth might be lost according to its probability.

To achieve this goal in this study, several intervals of LPD probability were associated with several survival time (mean and SD) as presented in the results (Table 2).

Table 2.

Number of teeth lost and mean survival time (SD) associated with each interval of probability of TLPD. Columns means of survival rates A to F were compared (pairwise comparisons with Bonferroni corrections)

	Intervals of probability
	<0.008	0.008–0.035	0.036–0.080	0.081–0.170	0.171–0.310	0.311–0.600	>0.600
n. of teeth lost	0	35	52	111	79	68	24
Mean survival		17	14.3	13.2	10.9	8.3	6
SD		4.4	4.7	5.7	5	4.4	3.4
Colum means		A	B	C	D	E	F
Pairwise
comparison		C D E F	D E F	D E F	E F
Survival time		12–22	9–20	6–20	5–18	4–13	2–7
% included		80%	83%	80%	80%	80%	83%

TLPD, tooth loss due to periodontal disease; n. teeth lost, number of teeth lost. According to differences between each pair of means (Pairwise comparison with Bonferroni corrections), for each significant pair, the key (A to F) of the smaller category appears under the category with larger mean.

2.4. Multicentre approach to evaluating model performance and define survival time

As the prediction model was developed using the database of 515 TLPD, it should perform well with these teeth but perhaps not with other TLPD samples. Therefore, three different TLPD samples with a total of 369 teeth were used to validate the model by associating the intervals of TLPD probability with the survival time and assessing possible differences between the samples.

These samples were a reference TLPD sample of 129 teeth (sample 1) that was used to construct the model, a TLPD sample also composed of 129 teeth that were consecutively extracted by the same clinician (M‐C) and which were not used to construct the model (sample 2), and a sample of 111 teeth (sample 3) gathered by the authors/clinicians from four dental practices with more than 25 years of experience in periodontics (A, J., A, J., Jr., A‐N, C., A‐N, P., M,T, A., N, B., N, F. & Z, I.).

The criteria to define TLPD were as follows: spontaneous exfoliation; and bone >75% with grade 3 mobility, which caused pain under function or spontaneously. For molars bone loss >50% associated with FI grade III and repeated abscesses. Teeth extracted for restorative purposes with BL >75 and grade 3 mobility were considered TLPD (Martinez‐Canut, 2015).

2.5. Statistical analysis

The correlation between the probability and survival rate was assessed (Pearson coefficient). To find the most appropriate distribution of the associations, one‐way ANOVA was used to assess differences between the mean survival time associated with each interval of probability. Pairwise comparison of means with post hoc (Tukey) test was used to assess differences between each pair of means. The Bonferroni corrections were applied to lower the threshold of significance and avoid the chance of finding rare events resulting from multiple comparisons. This more stringent approach reduced the chance of finding statistically significant differences. The same analysis was performed to assess differences within and between each of the three samples.

3. RESULTS

3.1. Multilevel analysis and performance measurements (Goodness of fit)

The results of the multilevel analysis using the 11 selected predictors are shown in Table 1. Calibration measurement was R² Nagelkerke 0.31 and 0.24 for molars and non‐molars, respectively, while the variation partition coefficient (VPC) demonstrated that 26% and 42% (molars and non‐molars, respectively) of the variability of the model was due to differences between patients, justifying the use of multilevel analysis. Discrimination measurements (for molars and non‐molars, respectively) were as follows: AUC 0.93 and 0.97; sensitivity 39% and 43%; specificity 98% and 99%, PV+ 72% and 60%, and PV− 94% and 98%.

Table 1.

Multilevel analysis with the selected patient‐ and tooth‐related factors for molars and non‐molars

	B	E.T.	Wald	gl	Sig.	Exp(B)	95% CI
Molars
Constant	−3,897	0.968	16,219	1	0.000	0.020
Baseline age	−0.019	0.009	4,965	1	0.026	0.981	0.964	0.998
Bruxism	0.476	0.146	10,678	1	0.000	1,609	1,210	2,140
Smoking	0.759	0.148	36,213	1	0.000	2,136	1,590	2,857
Type of molar A
Type of molar B	0.920	0.231	15,230	1	0.000	2,466	1,567	3,879
n. baseline teeth	−0.102	0.026	15,076	1	0.000	0.903	0.858	0.951
Mobility, reference			38,127	3	0.000
Mobility 1	0.527	0.161	10,051	1	0.002	1,665	1,215	2,281
Mobility 2	1,347	0.264	26,099	1	0.000	3,846	2,294	6,447
Mobility 3	1,872	0.544	11,859	1	0.001	6,502	2,240	18,870
PPD, reference			24,108	2	0.000
PPD 5–6 mm	0.799	0.313	6,534	1	0.011	2,224	1,205	4,105
PPD >6 mm	1,368	0.323	17,976	1	0.000	3,929	2,087	7,396
FI, reference			18,304	3	0.000
FI I	0.259	0.181	2,056	1	0.152	1,296	0.909	1,847
FI II	0.610	0.196	9,656	1	0.002	1,841	1,253	2,705
FI III	1,241	0.334	13,829	1	0.000	3,458	1,798	6,649
BL, reference			30,494	2	0.000
BL 30%–50%	0.545	0.202	7,287	1	0.007	1,724	1,161	2,561
BL >50%	1,196	0.222	28,931	1	0.000	3,307	2,139	5,113
Non‐Molars
Constant	−4.039	0.964	17,537	1	0.000	0.018
Severe periodontitis	0.669	0.223	8,964	1	0.003	1,952	1,260	3,025
Smoking*Bruxism	0.624	0.194	10,309	1	0.001	1,866	1,275	2,731
Type of non‐molar A			65,832	2	0.000
Type of non‐molar B	0.747	0.304	6,044	1	0.014	2,110	1,164	3,828
Type of non‐molar C	1,857	0.292	40,498	1	0.000	6,402	3,614	11,342
n. baseline teeth	−0.176	0.024	52,775	1	0.000	0.838	0.799	0.879
Mobility, reference			71,333	3	0.000			1.191
Mobility 1	0.598	0.216	7,629	1	0.006	1,818	1,190	2,779
Mobility 2	2,038	0.271	56,744	1	0.000	7,679	4,518	13,051
Mobility 3	2,468	0.541	20,845	1	0.000	11,798	4,090	34,034
PPD, reference			17,477	2	0.000
PPD 5–6 mm	0.354	0.219	2,622	1	0.105	1,425	0.928	2,187
PPD >6 mm	0.971	0.244	15,862	1	0.000	2,641	1,638	4,260
BL, reference			30,121	2	0.000			14.036
BL 30%–50%	0.286	0.243	1,838	1	0.240	1,331	0.826	2,145
BL >50%	1,217	0.263	21,501	1	0.000	3,379	2,020	5,652
Bruxism*C/R 1/2			11,111	2	0.004			2.256
Bruxism*C/R 1/1.5	0.110	0.191	0.330	1	0.566	1.11	0.767	1,623
Bruxism*C/R 1/1	1,195	0.359	11,104	1	0.001	3,304	1,636	6,672

Type of molar A, lower first molar; Type of molar B, upper first, upper second and lower second molars; Type of non‐molars A, lower canines and lower premolars; type of tooth B, upper canines, upper incisors and lower lateral incisors; Type of molar C, upper premolars and lower central incisors; n. baseline teeth, number of baseline teeth; PPD, probing pocket depth; FI, furcation involvement; BL, bone loss. Smoking*bruxism was an interaction effect; bruxism*C/R 1/1 was an interaction effect.

3.2. Survival time associated with the probability of TLPD

A moderate negative correlation was found between the probability of TLPD and the survival time in the whole sample (Pearson −0.502, p < .001), so that the survival time increased as the intervals of probability of TLPD decreased (Figure 1). The initial associations of survival time and intervals of probability were refined on the basis of the TLPD sample of each association as well as the statistical analysis.

Figure 1.

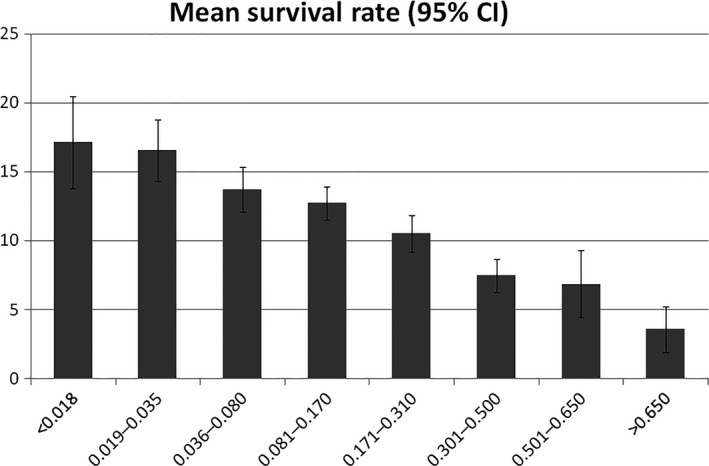
Mean survival rate (95% CI)

Significant differences were found between the mean survival time in the whole sample (ANOVA p < .0001). Pairwise comparison of means identified significant differences between the intervals, <0.036 (p = .014), 0.081–0.170 (p .011), 0.171–0.310 (p < .001) and >0.310 (p < .001), so that the means significantly decreased between each pair of increasing intervals (Table 2). TLPD did not occur in the interval <0.008; while the intervals 0.08–0.035 and 0.036–0.080 were associated with a survival time of 17 (4.4) and 14.3 (4.7) years, respectively, etc. At the opposite extreme, the interval 0.311–0.600 and >0.600 associated with a survival time of 8.3 (4.4) and 6 (3.4) years, respectively.

The percentage of cases included within each survival time was calculated according to the standard deviations and the percentiles of each mean. For instance, the interval 0.008–0.036 was associated with a survival rate of 12–22 years, containing 80% of the cases with this interval. This approach also made it possible to differentiate the lowest and the highest intervals which lacked on significant differences according to the Bonferroni corrections: <0.036 and 0.036–0.080, and 0.311–0.600 and >0.600 (Table 2).

The shorter the amplitude of the survival time was, the lower the percentage of cases fitting. Survival time between 5 and 10 years only included only 55% to 60% of the cases, while survival time between 10 and 15 years included the majority of cases. Therefore, the survival time were defined by balancing discrimination (the narrowest feasible survival time) and accuracy (the highest percentage of cases fitting within the defined survival time). The definitive associations included 80% to 83% of the cases fitting in rates of 5–11 years except for two wider rates of 13 and 14 years (Table 2).

3.3. Performance of the model using different TLPD samples

Table 3 and Figure 2 show the mean survival time (SD) associated with the intervals in samples 1, 2 and 3. Only the four intervals with significant differences (pairwise comparison with the Bonferroni corrections) were included in comparing these samples.

Table 3.

Number of teeth lost and mean survival rates (SD) associated with each interval of probability of TLPD in the three samples

	Sample 1				Sample 2				Sample 3
	<0.080	0.081–0.170	0.171–0.310	>0.310	<0.080	0.081–0.170	0.171–0.310	>0.310	<0.080	0.081–0.170	0.171–0.310	>0.310
n. of teeth lost	33	48	26	22	32	43	29	25	22	20	24	45
Mean survival	14.9	12.9	10.8	6.5	15	12.5	10.2	7.3	16.5	15.2	11.5	8.5
SD	5.5	5.6	5.2	3	4.4	5.8	4.5	3.7	3.8	5.5	5.3	4.9
Survival rates 1	11–20	6–20	6–18	4–13	11–20	6–20	6–18	4–13	11–20	6–20	6–18	4–13
% included	70%	77%	81%	86%	69%	74%	83%	84%	86%	85%	63%	73%
P.p. deviation	−4	−1	5	7	−5	−4	7	5	12	7	−13	−6
Survival rates 2	9–22	6–22	5–19	4–14	9–22	6–22	5–19	4–14	9–22	6–22	5–19	4–14
% included	85%	90%	81%	86%	94%	81%	83%	88%	91%	90%	92%	82%
P.p. deviation	−5	6	−4	1	4	−3	−2	3	1	6	7	−3

TLPD, tooth loss due to periodontal disease; n. teeth lost, number of teeth lost; P.p., deviation (in Percentage point) respect to the global estimation. Two different survival rates 1 and 2 were analysed. The latter, with longer survival rates, included between 81% to 92% of the cases. Percentage point deviation ranged from −5 to 7.

Figure 2.

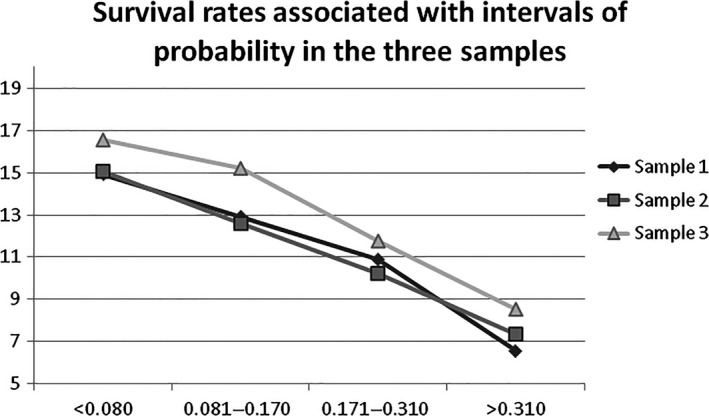
Survival rates associated with intervals of probability in the three samples

Significant differences were found between the mean survival rates in each one of the three samples (ANOVA p < .0001). In parallel, no significant differences were found between the means in each one of the intervals of the samples (p between .184 and .544), so the model performed well in the three samples. A similar tendency was found with pairwise comparison with Bonferroni corrections, despite six of the subsamples containing less than 30 teeth limited the opportunity for a more robust analysis. Two‐thirds of the comparisons had no significant differences while the remaining comparisons lacked any significance with a threshold of 0.10.

The magnitude of error based on the variation interval (absolute values) was calculated in order to estimate differences in the performance between the samples. It was +5.1%, −13.8%, and −13.3% between samples 1–2, 1–3, and 2–3, respectively.

Taken the above findings together, the model was useful in defining intervals of probability of TLPD associated with survival time in different TLPD samples.

3.4. The accuracy of the prediction model compared to the accuracy of a conventional subjective periodontal prognosis

Based on the relative differences, the prediction model was more accurate than the conventional periodontal prognosis, reducing the percentages of False+ between 25% and 75% and F− between 15% and 28% of the times. This is detailed in Supporting Information (Table S2 and Appendix S2).

4. DISCUSSION

This study has introduced a prediction model to assign periodontal prognosis based on survival time. The results of the multicentre approach also demonstrated that the model performed well in different TLPD samples gathered by different clinicians. According to the results, the probability of TLPD accurately predicted the survival time in close to 80% of the total TLPD sample analysed.

Besides calculating the probability of TLPD, this model has been adjusted to predict TLPD+ or TLPD–, being highly specific and moderately sensitive. Therefore, the model can accurately predict that TLPD will not occur while the capability of accurately predicting TLPD+ is only moderate. This is partially due to the low prevalence of TLPD. Despite this limitation, the comparisons between the accuracy of the model and the accuracy of the conventional prognosis assigned at baseline by one of the authors (M‐C) revealed that the model was more accurate, substantially reducing False+.

This might be partially due to the fact that the model does not feel, but calculates using the database. On the contrary, clinicians feel, among other things, fear of failing the prediction and producing a False−, which could be discouraging and even disappointing for the patient and the clinician. As a result, clinicians tend to assign more prognoses of TLPD+, as opposed to the model.

However, to our understanding, the accuracy of the TLPD+ or TLPD− prediction might not be the most relevant issue, as it may depend on the length of the study rather than the prognostic tool or index utilized. The longest the observation period, the higher the probability of TLPD might be. Therefore, the prediction of the TLPD event in time seems more useful than the accuracy of the TLPD+ prediction. From a clinical perspective, a TLPD+ prediction does not help to make any decision other than that regarding the extraction of a periodontally compromised tooth; the question would be when. Alternatively, the prediction of a certain survival time might help the clinician and patient to make a decision.

The estimation of survival time goes beyond the dichotomous alternative of predicting TLPD+ or TLPD–, and comes closer to the fact that TLPD occurs progressively in time. Thus, the concept of conventional prognostic categories (good, fair, poor, questionable and hopeless) is faced by a more realistic and useful one, that is the estimation of survival time.

This represents a different way of interpreting the data on predictors of TLPD. The finding that the survival time was accurately predicted in close to 80% of the total TLPD sample analysed, utilizing quantitative analysis, seems more useful than the data on the R² statistics of the regression coefficients reported with qualitative analysis, ranging from 0.12 to 0.31 (Tonetti, Muller‐Campanile, & Lang, 1998; Checchi et al., 2002; König et al. 2002, Faggion et al., 2007; Martinez‐Canut, 2015). These figures might represent the extent to which the variance in tooth loss could be explained: only from 12% to 31%, in comparison with the alternative of not considering any information provided by prognostic variables.

As this prediction model has been developed exclusively by analysing periodontal prognostic factors, it focuses exclusively on TLPD and therefore does not provide any prognostic information on other reasons for tooth loss.

It should be stressed that this model is the result of the analysis of a particular sample, whose results depend on a wide range of factors: the treatment philosophy, the criteria to indicate extraction, the level of compliance with PM, etc. Consequently, these results cannot be automatically extrapolated to other patient samples. On the contrary, the rather low variation interval between the samples gathered by different clinicians in the present study may partially depend on the inclusion criteria of the study; implying strict compliance with PM. Further research with different patient samples and different clinicians is needed for a comprehensive validation of the model. However, prospective long‐term follow‐ups to 22 years, as have performed retrospectively in the present study, do not seem feasible. Prospective medium‐term studies at around 10 years could easily be performed, despite lacking information on longer survival time of 10–22 years.

There are three main limitations. First, the moderate capability of ascertaining TLPD (moderate PV+), so that 28% to 40% of teeth predicted to be lost were still retained (False+) during the observational period of this study. However, some of these teeth were non‐functional and/or presented extreme mobility. We still lack information to elucidate whether the TLPD prediction might be more accurate in certain patients as compared to others. This might be to do with the proclivity of patients to experience higher rates of TLPD (Martinez‐Canut, Llobel, & Romero, 2017). Second, in 20% of the cases, the probability of TLPD did not fit within the associated survival time defined in the present study. Finally, the long span of certain survival time, of 13 and 14 years. These limitations might be partially attributed to the paucity of knowledge to categorize PRFs and the TLPD sample size.

TRFs present well‐defined categories (e.g. furcation involvement I, II, III), while PRFs are interpreted as a dichotomous alternative (e.g. smoking + or −). However, smoking and bruxism might have quite different impacts depending on the intensity and the length of the habits (Martinez‐Canut, 2015). The simultaneous impact of smoking and bruxism might be much more relevant than previously suspected (Martinez‐Canut et al., 2017).

Despite the sample total of 369 TLPD being relatively large, it is still too small for a more detailed analysis. The prevalence of teeth presenting the worst category of TRFs is usually low. In parallel, differences depending on the type of tooth, which is a variable implemented in the model, seems to be relevant. Upper and lower second molars accumulated 54% of the total TLPD in our study, enabling a more precise distribution of the associations. However, this was not possible in teeth with lower TLPR rates. This data is presented in the Supporting Information (Appendix S3).

As this prediction model is available online to researchers and clinicians, it can be used as a guideline and reference for further research. As other authors have suggested for risk assessment (Lang et al., 2015), this prediction model could be used as a complementary tool to improve our knowledge of the multifactorial nature of periodontal disease and periodontal prognosis.

To our understanding, the actual usefulness of this prediction model, in daily practice, is twofold. It helps to assign a more accurate prognosis and behaves as a master model. The estimation of a certain survival rate, which has been accurate in 80% of cases in the present study, represents an additional datum to incorporate in the routine process to assign periodontal prognosis. Second, and perhaps more importantly, this model can be utilized as a master model, as it contains relevant and reliable information on predictors of TLPD that can be interpreted and applied by using the tool.

Utilising the retrospective approach with any tooth extracted for periodontal reasons, as described in this paper, the accuracy of the model is assessed. Each extracted tooth contains valuable information on periodontal prognosis, explaining the event TLPD according to the peculiarities of the tooth and the patient. This might help when assigning prognosis at baseline to a comparable tooth in a similar patient.

The probability of TLPD can be manipulated by including or excluding certain predictors, as well as modifying their categories. This enables definition of practical rules to understand and apply periodontal prognosis. For instance, it is possible to estimate the survival rate of teeth presenting the intermediate category of TRFs (bone loss 30%–50%, mobility 2, etc.) depending on the participation of one, two or more PRFs. The progressive incorporation of predictors helps to understand what is actually observed in daily practice. For instance, a long root (C/R 1/2) with bone loss >50% in the absence of any TRF; in the presence of smoking; in the presence of bruxism; a short root (C/R 1/1) instead of a large root; the latter situation plus fewer baseline teeth, etc.

The lowest threshold of probability of TLPD was 0.008. No tooth with lower values was lost. This threshold corresponded to the presence of only one of the following TRFs in the absence of bruxism and smoking: furcation involvement grade III, bone loss >50%, mobility 2 and probing pocket depth >6 mm. This threshold also corresponded to the presence of smoking and bruxism in the absence of any TRF. The interval 0.09–0.036 resulted from the above described TRFs scenario but in the presence of smoking. This interval predicted TLPD in the long term in 80% of cases, that is, between 12 and 22 years.

The assessment of molar survival time depending on the extent of furcation involvement represents relevant additional information. The increase in the risk of furcation involvement II and III has been defined (Dannewitz et al., 2016; Graetz et al., 2015; Martinez‐Canut, 2015), and also associated with smoking (Graetz et al., 2015). This tool itself can corroborate this finding and extend the information to the impact of other PRFs. Moreover, the tool enables the definition of a practical rule on the survival rates of these molars, with a mean 20 years in the absence of PRFs and a mean 10 years in the presence of the main PRFs. In the presence of mobility grades 2 and 3 plus more than two TRFs, the survival time decreases dramatically.

This prediction model has been conceived as a dynamic tool that is capable of progressively incorporating additional and reliable data to overcome its current limitations. Better knowledge to categorize PRFs and additional TLPD samples could be incorporated in the model for more precise estimation of survival time according to the probability of TLPD. Certain parameters that characterize patients experiencing higher TLPD rates during PM (Martinez‐Canut et al., 2017) could also be implemented in order to assess whether the survival time are related with the proclivity of the patient to lose more teeth. Thus, the model could also represent a framework in which additional suspected prognostic factors could be incorporated in the analysis to assess their impact using well‐defined statistical means (Fardal, Grytten, Martin, Houliban, & Heasman, 2016; Pencina, D'Agostino, D'Agostino, & Vasan, 2008; Steyerberg et al., 2012).

5. CONCLUSIONS

A highly specific but moderately sensitive prediction model of TLPD in patients following PM was developed using 11 PRFs and TRFs.

This model enabled the definition of intervals of probability of TLPD associated with survival time, so that based on the probability of TLPD, the survival time was accurately predicted in close to 80% of the total TLPD sample analysed.

The multicentre approach demonstrated that the model might be useful in different TLPD samples.

CONFLICT OF INTEREST

Pedro Martinez‐Canut has developed and owns Perioproject (patent pending), a web based with an open access and free of charge tool to assigning periodontal prognosis. No external funding apart from the self‐support of this author was available for this study. The other authors have stated explicitly that there is no conflict of interest in connection with this article.

Supporting information

 

 

 

 

 

Martinez‐Canut P, Alcaraz J, Alcaraz Jr. J , et al. Introduction of a prediction model to assigning periodontal prognosis based on survival time. J Clin Periodontol. 2018;45:46–55. https://doi.org/10.1111/jcpe.12810