Abstract
Background:
Fuzzy logistic regression model can be used for determining influential factors of disease. This study explores the important factors of actual predictive survival factors of breast cancer's patients.
Materials and Methods:
We used breast cancer data which collected by cancer registry of Kerman University of Medical Sciences during the period of 2000–2007. The variables such as morphology, grade, age, and treatments (surgery, radiotherapy, and chemotherapy) were applied in the fuzzy logistic regression model. Performance of model was determined in terms of mean degree of membership (MDM).
Results:
The study results showed that almost 41% of patients were in neoplasm and malignant group and more than two-third of them were still alive after 5-year follow-up. Based on the fuzzy logistic model, the most important factors influencing survival were chemotherapy, morphology, and radiotherapy, respectively. Furthermore, the MDM criteria show that the fuzzy logistic regression have a good fit on the data (MDM = 0.86).
Conclusion:
Fuzzy logistic regression model showed that chemotherapy is more important than radiotherapy in survival of patients with breast cancer. In addition, another ability of this model is calculating possibilistic odds of survival in cancer patients. The results of this study can be applied in clinical research. Furthermore, there are few studies which applied the fuzzy logistic models. Furthermore, we recommend using this model in various research areas.
Keywords: Breast cancer, fuzzy logistic regression, mean degree of membership, survival
INTRODUCTION
Epidemiology of breast cancer
Cancer is a leading cause of death in the world.[1] The burden of cancer is rising gradually throughout the world. Among all types of cancer, lung cancer is the most prevalent cancer (worldwide) in men. When compared to men, in women, breast cancer is the first leading cause of cancer death in developed and developing countries.[2,3] Regarding the global cancer statistics report in 2011, breast cancer included around 23% of total cancer. Besides, the incidence rate of breast cancer had the maximum rate (89.9%) in western European countries based on standardized age (2011).[4]
Nearly 7% of woman diagnosed with breast cancer are at an age younger than 40 years.[5] Expected number of deaths for breast cancer, US, 2015, is estimated near 40,290 women.[6] Southern Africa had the highest rate of breast cancer incidence mortality (19.3%). In addition, western Asia countries had the highest incidence rate and mortality rate of breast cancer 31.8% and 18.9%, respectively.[4] When compared to other countries, breast cancer is the second common cancer in Iranian females (21.4%).[7,8]
Etiology and predictive factors of breast cancer
The main predictive risk factors of breast cancer are “age, geographic area of residence, age at first birth, certain indicators of ovarian activity, history of benign breast disease, and familiar history of breast cancer.”[9] Breast cancer treatment usually involves a combination of surgery, radiation therapy, chemotherapy, and hormone therapy. In addition, prognosis and selection of therapy can determine by age, menopausal status, stage of disease, histologic, and nuclear grade of the primary tumor.[10,11] Some studies indicated that survival of breast cancer's patients depends on tumor size and biological factors.[12] In some patients who received the radiotherapy before chemotherapy, the actual 5-year breast failure rate was 4% in 99 of them. In other patients (54 people) who received chemotherapy sequentially then radiotherapy without concurrent chemotherapy, this rate was 8%. Furthermore, the failure rate was 6% in 116 patients with receiving concurrent chemotherapy and radiotherapy.[13]
For determining actual predictive survival factors in breast cancer, the fuzzy logistic regression model can be used. In addition, one of the abilities of this model is predicting the status of the new patients by possibilistic odds (fuzzy logistic regression was based on the possibilistic odds approach). A few studies applied this model for survival of cancer patients. In this study, we conducted the fuzzy logistic regression model (new statistical regression model) for determining important factors influencing survival of breast cancer patients and predicting the status of the new patient. The main purpose of this study is to introduce a new statistical model and applying the results in the clinical research.
MATERIALS AND METHODS
Patients
This study used data of breast cancer registered by cancer registry of Kerman (the largest province of Iran) during the period of 2000–2007. The aim of the study was to determine important factors in survival of breast cancer patients. There were 1311 patients with breast cancer (both gender). Males and some patients with incomplete information excluded from the study. Finally, 924 patients remained but we studied just 71 patients of them (we used Lingo software for solving inequalities of fuzzy logistic regression model, but the Lingo software can solve inequalities in a sample of 71). Fuzzy logistic regression was performed with a binary dependent variable (survival status which had two states: alive or dead) and some independent variables such as age, morphology, grade, and treatments (radiotherapy, chemotherapy, and surgery).
The data of death results from breast cancer were available. Therefore, we determined 5-year survival from incidence (diagnosed with a disease during a given period of time) to death.
Types of morphology were neoplasm malignant, carcinoma, and infiltrating duct carcinoma. Radiotherapy, chemotherapy, and surgery were treatments approaches. Some cancer patients received treatments while some others did not. In other words, in some cases, radiotherapy, chemotherapy, and surgery used to cure or control the disease. Tumor grade had three levels (I = well-differentiated, II = moderate-differentiated, III = poor-differentiated). Furthermore, the status of patients who died from 2000 to 2007 was zero.
Statistical analysis
The fuzzy logistic regression is an important tools for evaluating the relationship between independent variable (crisp or fuzzy) and fuzzy binary outcome (The status of some patients was one, and some were zero with a probability of μ and 1-μ, respectively).
At first step, we fitted a logistic regression model to the data. After that, we used predicted probabilities as μi for modeling fuzzy logistic regression. Note that, possibilistic was used instead of probability in fuzzy logistic regression. In the mentioned model μi = Poss(Yi = 1) is the possibility of having the related property and 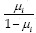 shows possibilistic odds. Then, we applied the Fuzzy logistic regression on data. To estimate fuzzy coefficients, R and Lingo software were used but Lingo software could not support data with large sample sizes.
shows possibilistic odds. Then, we applied the Fuzzy logistic regression on data. To estimate fuzzy coefficients, R and Lingo software were used but Lingo software could not support data with large sample sizes.
Suppose that X =(x1, x1,....,xn) denoted a vector of explanatory variables, then the formulation of Fuzzy logistic regression with fuzzy coefficients is defined as:
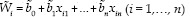 Eq(1)
Eq(1)
That, 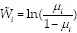 and
and 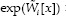 is possibilistic odds of survival of breast cancer for each patient. Also
is possibilistic odds of survival of breast cancer for each patient. Also 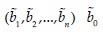 are the slops of explanatory variables and intercept respectively [more details exist in Appendix 1].
are the slops of explanatory variables and intercept respectively [more details exist in Appendix 1].
Moreover ultimately, mean degree of membership (MDM) used for checking goodness of fit in fuzzy logistic regression which is a value between 0 and 1. As MDM is closer to one, the model has a good fit to the data.
RESULTS
Based on the results of Table 1, Mean (SD) of age was 47.9 (12.5) in patients with breast cancer. Nearly 41% of patients were in neoplasm and malignant group. Furthermore, 2.8% and 56.3% of patients were in carcinoma and infiltrating duct carcinoma, respectively. More than two-third of patients were still alive after 5-year survival. Most of the patients had a moderate grade (90.1%). Patients based on their conditions received surgery (54.9%), radiotherapy (46.9%), and chemotherapy (19.7%).
Table 1.
The basic and clinical characteristics of study participants

We obtained the fuzzy logistic regression model as follows:

The coefficient of some variables such as age and radiotherapy were fuzzy and were not interpretable. Therefore, we used defuzzification approach for fuzzy coefficients (more information about defuzzification exists in Appendix 1).
After defuzzification, coefficients of variables were compared for detecting the importance of variables. According to obtained model, the most important factors influencing survival were chemotherapy, morphology, and radiotherapy, in order (Eq [3]) [Table 2].
Table 2.
Coefficients defuzzification

In addition, the value of possibilistic odds of all cases determined. The possibilistic odds of five patients are reported in Table 3.
Table 3.
The observed and the estimated fuzzy outputs of breast cancer

For example, a possibilistic odds of survival of breast cancer for the first patient is 0.84. We can also interpret possibilistic odds for other patients in similar way. Furthermore, possibilistic odds for a new case can be obtained by Eq.[3]
For instance, suppose we have a new case with following variables:
Age = 45 years old, Grade II, morphology = Infiltrating duct carcinoma, gave all treatments (surgery, radiotherapy, and chemotherapy). The possibilistic odds of this patient can be calculated as follows:
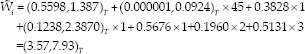
Therefore, possibilistic odds of survival of breast cancer for this case were 0.73 after difuzzification.
Finally, model performance was assessed by MDM. The value of MDM was 0.86 which it showed fuzzy logistic regression had a good fit on the data.
DISCUSSION
In this study, we determined the importance of factors may affect survival of breast cancer, namely, fuzzy logistic regression model. The study results demonstrated the important factors were chemotherapy, morphology, and radiotherapy. Furthermore, the fuzzy logistic regression had a good fit on the data (MDM = 0.86). Such findings were consistent with similar study that pointed out in pre- and post-menopausal patients with high risk of breast cancer. The short-term surgical with combination of chemotherapy was effective.[16] In another study, the factor which influenced the results of 5-year survival was number of axillary lymph nodes involved (not by menopausal status). Furthermore, the combination chemotherapy at full dose is vital for achieving clinical benefit.[17] In similar study, the combination of radiotherapy with chemotherapy declined rates of loco regional after modified radical mastectomy.[18]
Regarding the morphological factors, we found that through fuzzy logistic regression model-these factors had an important role at survival status in cancer patients. Similarly, morphological assessments studies showed that specific morphological characteristics strongly associated with “basal-like breast carcinoma” and can provide helpful information of prognosis of breast cancer.[19] Morphological assessment of the difference has been shown in numerous studies to provide useful information in breast cancer [20] that shows the power of fuzzy logistic regression for exploring the influential factors.
This method is applied in other areas such as diabetic's patients, lupus, and tuberculosis. In one of them, the fuzzy logistic regression model introduced as a new possibilistic model for determining the diabetic status.[14] Another study measured the association between tuberculosis and smoking through this model.[21] Furthermore, Pourahmad applied fuzzy logistic regression in the suspected cases to systematic lupus erythematosus disease.[22]
In this research, we introduced fuzzy logistic regression, a new statistical method, for determining breast cancer's survival factors. By this model which extracts possibilistic odds of survival and predicts status it is possible to calculate the odds for survival of the new patient which can be introduced. Furthermore, the results of this study can be applied in clinical research.
CONCLUSION
According to our findings, we recommended fuzzy logistic regression model: first, this model is useful for determining the survival of the breast cancer's patients regarding to real data. Another advantage of Fuzzy logistic regression model is that possibilistic odds of survival status can be calculated for a new case.
Financial support and sponsorship
Nil.
Conflicts of interest
The authors have no conflicts of interest.
APPENDIX 1
Fuzzy number definitions - A fuzzy number is a quantity whose value is imprecise, as is the case with “ordinary” numbers. Let X be a nonempty set of elements x, each fuzzy subset of x is defined by membership function as Ã: X →[0,1]. The grade of membership of X in fuzzy subset for each x ∈ X identifies by Ã(x).
We define one of the basic types of fuzzy numbers used in practice. A triangular fuzzy number is defined by three numbers and there are two types of triangular fuzzy number: symmetric and nonsymmetric.
Triangular Fuzzy Number - Let be a triangular à fuzzy number on X that can be written as (sL, m , sR)T where m identifies the mode of triangular fuzzy number and sL, sR are left and right bound of triangular fuzzy number respectively. Ã(x) is the membership function as Ã: X →[0,1] that identifies the grade of membership of X in fuzzy subset for each x∈X.[15]
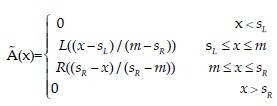 Eq(4)
Eq(4)
If the left and right bound are equal, then Ã(x) is called a symmetrical fuzzy number. On the other hand the support of A is the set of elements {x∈X| sL<x<sR}. When, sL = sR = m it is a nonfuzzy number.[16]
In this paper, fuzzy form of W and b introduced as 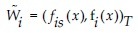 and
and 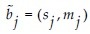
Possibilistic odds - If à is a fuzzy number and 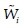 is its membership function and f(x)=exp(x), then f(Ã)=exp(Ã) is a fuzzy number with following membership function:
is its membership function and f(x)=exp(x), then f(Ã)=exp(Ã) is a fuzzy number with following membership function:
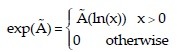 Eq(5)
Eq(5)
The following formula is used for calculating exp (W(x))(possibilistic odds).
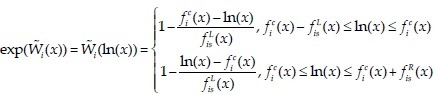 Eq(6)
Eq(6)
The membership function of fuzzy estimated output is as follow:
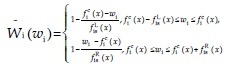 Eq(7)
Eq(7)
We supposed two assumptions for estimating
1. For each observation, h is membership degree. so:
Wi(wi)≥h and wi=ln(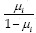 ),h∈(0,1) Eq(8)
),h∈(0,1) Eq(8)
2. Minimization is as bellow equations:
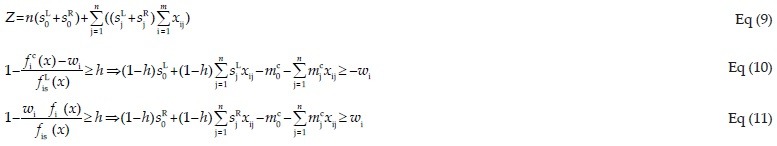
The following formula is used for calculating exp (W(x)) (possibilistic odds).
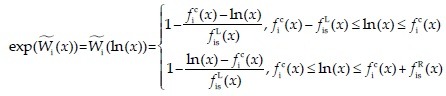 Eq(12)
Eq(12)
Defuzzification - Changing fuzzy number to real number is called defuzzification. Defuzzification formula for 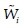 is defined:
is defined:
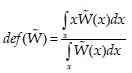 Eq(13)
Eq(13)
REFERENCES
- 1.Parkin DM, Pisani P, Ferlay J. Global cancer statistics. CA Cancer J Clin. 1999;49:33–64. doi: 10.3322/canjclin.49.1.33. 1. [DOI] [PubMed] [Google Scholar]
- 2.Travis WD, Lubin J, Ries L, Devesa S. United States lung carcinoma incidence trends: Declining for most histologic types among males, increasing among females. Cancer. 1996;77:2464–70. doi: 10.1002/(SICI)1097-0142(19960615)77:12<2464::AID-CNCR8>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 3.Fentiman IS, Fourquet A, Hortobagyi GN. Male breast cancer. Lancet. 2006;367:595–604. doi: 10.1016/S0140-6736(06)68226-3. [DOI] [PubMed] [Google Scholar]
- 4.Jemal A, Bray F, Center MM, Ferlay J, Ward E, Forman D, et al. Global cancer statistics. CA Cancer J Clin. 2011;61:69–90. doi: 10.3322/caac.20107. [DOI] [PubMed] [Google Scholar]
- 5.Anders CK, Johnson R, Litton J, Phillips M, Bleyer A. Breast cancer before age 40 years. Seminars in oncology. 2009;36:237–249. doi: 10.1053/j.seminoncol.2009.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.DeSantis , Carol E, Fedewa , Stacey A, Goding Sauer, Ann Kramer, et al. Vol. 66. CA: a cancer journal for clinicians; 2016. Breast cancer statistics, 2015: Convergence of incidence rates between black and white women; pp. 31–42. [DOI] [PubMed] [Google Scholar]
- 7.Sadjadi A, Nouraie M, Mohagheghi MA, Mousavi-Jarrahi A, Malekezadeh R, Parkin DM, et al. Cancer occurrence in Iran in 2002, an international perspective. Asian Pac J Cancer Prev. 2005;6:359–63. [PubMed] [Google Scholar]
- 8.Babu GR, Samari G, Cohen SP, Mahapatra T, Wahbe RM, Mermash S, et al. Breast cancer screening among females in Iran and recommendations for improved practice: A review. Asian Pac J Cancer Prev. 2011;12:1647–55. [PubMed] [Google Scholar]
- 9.MacMahon B, Cole P, Brown J. Etiology of human breast cancer: A review. J Natl Cancer Inst. 1973;50:21–42. doi: 10.1093/jnci/50.1.21. [DOI] [PubMed] [Google Scholar]
- 10.Simpson JF, Gray R, Dressler LG, Cobau CD, Falkson CI, Gilchrist KW, et al. Prognostic value of histologic grade and proliferative activity in axillary node-positive breast cancer: Results from the eastern cooperative oncology group companion study, EST 4189. J Clin Oncol. 2000;18:2059–69. doi: 10.1200/JCO.2000.18.10.2059. [DOI] [PubMed] [Google Scholar]
- 11.Frkovic-Grazio S, Bracko M. Long term prognostic value of Nottingham histological grade and its components in early (pT1N0M0) breast carcinoma. Journal of clinical pathology. 2002;55:88–92. doi: 10.1136/jcp.55.2.88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bundred NJ. Prognostic and predictive factors in breast cancer. Cancer Treat Rev. 2001;27:137–42. doi: 10.1053/ctrv.2000.0207. [DOI] [PubMed] [Google Scholar]
- 13.Recht A, Come SE, Gelman RS, Goldstein M, Tishler S, Gore SM, et al. Integration of conservative surgery, radiotherapy, and chemotherapy for the treatment of early-stage, node-positive breast cancer: Sequencing, timing, and outcome. J Clin Oncol. 1991;9:1662–7. doi: 10.1200/JCO.1991.9.9.1662. [DOI] [PubMed] [Google Scholar]
- 14.Pourahmad S, Ayatollahi S, Taheri S. Fuzzy logistic regression: A new possibilistic model and its application in clinical vague status. Iran J Fuzzy Syst. 2011;8:1. [Google Scholar]
- 15.Pourahmad S. Shiraz: University of Medical Sciences, LAP LAMBERT Academic Publishing; 2013. Fuzzy Logistic Regression Models with their Application in Medical. [Google Scholar]
- 16.Cooper RG, Holland JF, Glidewell O. Adjuvant chemotherapy of breast cancer. Cancer. 1979;44:793–8. doi: 10.1002/1097-0142(197909)44:3<793::aid-cncr2820440302>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- 17.Bonadonna G, Valagussa P. Dose-response effect of adjuvant chemotherapy in breast cancer. N Engl J Med. 1981;304:10–5. doi: 10.1056/NEJM198101013040103. [DOI] [PubMed] [Google Scholar]
- 18.Cuzick J, Stewart H, Peto R, Baum M, Fisher B, Host H, et al. Overview of randomized trials of postoperative adjuvant radiotherapy in breast cancer. Cancer Clin Trials. 1988;111:108–29. doi: 10.1007/978-3-642-83419-6_15. [DOI] [PubMed] [Google Scholar]
- 19.Fulford LG, Easton DF, Reis-Filho JS, Sofronis A, Gillett CE, Lakhani SR, et al. Specific morphological features predictive for the basal phenotype in grade 3 invasive ductal carcinoma of breast. Histopathology. 2006;49:22–34. doi: 10.1111/j.1365-2559.2006.02453.x. [DOI] [PubMed] [Google Scholar]
- 20.Elston CW, Ellis IO. Pathological prognostic factors in breast cancer. I. The value of histological grade in breast cancer: Experience from a large study with long-term follow-up. Histopathology. 1991;19:403–10. doi: 10.1111/j.1365-2559.1991.tb00229.x. [DOI] [PubMed] [Google Scholar]
- 21.Zainuddin NH, Safiih LM. A Relationship between Tuberculosis and Smoking: Fuzzy Logistic Regression Approach. Empowering Science, Technology and Innovation Towards a Better Tomorrow. 2011 [Google Scholar]
- 22.Pourahmad S, Ayatollahi SM, Taheri SM, Agahi ZH. Fuzzy logistic regression based on the least squares approach with application in clinical studies. Comput Math Appl. 2011;62:3353–65. [Google Scholar]



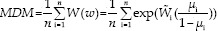 Eq(2)[
Eq(2)[