Kinetics of H₂O₂-driven degradation of chitin by a bacterial lytic polysaccharide monooxygenase

Abstract

Lytic polysaccharide monooxygenases (LPMOs) catalyze the oxidative cleavage of glycosidic bonds in recalcitrant polysaccharides, such as cellulose and chitin, and are of interest in biotechnological utilization of these abundant biomaterials. It has recently been shown that LPMOs can use H₂O₂, instead of O₂, as a cosubstrate. This peroxygenase-like reaction by a monocopper enzyme is unprecedented in nature and opens new avenues in chemistry and enzymology. Here, we provide the first detailed kinetic characterization of chitin degradation by the bacterial LPMO chitin-binding protein CBP21 using H₂O₂ as cosubstrate. The use of ¹⁴C-labeled chitin provided convenient and sensitive detection of the released soluble products, which enabled detailed kinetic measurements. The k_cat for chitin oxidation found here (5.6 s⁻¹) is more than an order of magnitude higher than previously reported (apparent) rate constants for reactions containing O₂ but no added H₂O₂. The k_cat/K_m for H₂O₂-driven degradation of chitin was on the order of 10⁶ m⁻¹ s⁻¹, indicating that LPMOs have catalytic efficiencies similar to those of peroxygenases. Of note, H₂O₂ also inactivated CBP21, but the second-order rate constant for inactivation was about 3 orders of magnitude lower than that for catalysis. In light of the observed CBP21 inactivation at higher H₂O₂ levels, we conclude that controlled generation of H₂O₂ in situ seems most optimal for fueling LPMO-catalyzed oxidation of polysaccharides.

Introduction

It has very recently been shown that monocopper enzymes may use H₂O₂ as cosubstrate (1). Importantly, this finding concerns lytic polysaccharide monooxygenases (LPMOs),² which are abundant key players in enzymatic biomass conversion (2). LPMOs catalyze the oxidative cleavage of glycosidic bonds in poly- and, in a few cases, oligosaccharides (3, 4), including abundant recalcitrant polysaccharides, such as chitin (5) and cellulose (6–8). Unlike glycoside hydrolases, LPMOs can act on glycan chains that are embedded in a crystalline lattice, cleaving glycosidic bonds by hydroxylation of the C1 or C4 carbon. This ability is conferred by their unusual active-site architecture, a single copper atom coordinated by two conserved histidines, displayed on a solvent-exposed, flat substrate-binding surface (9, 10). It has been widely acknowledged that LPMOs are monooxygenases (8). The recent finding that H₂O₂ is the preferred cosubstrate (1) calls for further studies on the H₂O₂-based mechanism. Kinetic studies on LPMOs are scarce, mostly showing very low rates (11). Such kinetic studies are challenging because of the multisubstrate nature of the reaction, the insolubility of one of the substrates, and oxidative enzyme inactivation (1). Here, we set out to provide the first detailed kinetic insights into H₂O₂ utilization by LPMOs using the bacterial C1-oxidizing, chitin-active CBP21 (5) as a model enzyme and ¹⁴C-labeled chitin nanowhiskers (CNWs) (12) as substrate.

Results

Kinetics of the H₂O₂-driven degradation of chitin by CBP21

The use of ¹⁴C-labeled CNWs made it possible to perform detailed kinetic measurements by providing convenient and sensitive detection of the released ¹⁴C-labeled soluble products, the amount of which is expressed in N-acetylglucosamine equivalents (NAG_eq) as explained under “Experimental procedures.” Because the release of soluble products from chitin by CBP21 is the result of oxidative action only, the formation of NAG_eq is directly proportional to the CBP21 activity, and the quantitative relationship between the two follows from the work described below. To activate the enzyme, which is otherwise in its inactive Cu(II) resting state, the reactions must be supplemented with a priming amount of reductant, like ascorbic acid (AscA) as outlined in Bissaro et al. (1). From Fig. 1A (see also Table S1), it follows that variation of the concentration of AscA over 2 orders of magnitude had no major effects on the kinetics of degradation of CNWs. Based on these results, we chose an AscA concentration of 100 μm for all further experiments. Control reactions also showed that the outcome of the experiment was not affected by the order of the addition of AscA and H₂O₂ (Fig. 1B) and that the addition of non-labeled CNWs, used to improve the sedimentation of CNWs during separation of soluble ¹⁴C-labeled products from residual ¹⁴C-labeled CNWs by centrifugation (12), did not affect the outcome of the experiment (Fig. 1B).

Figure 1.

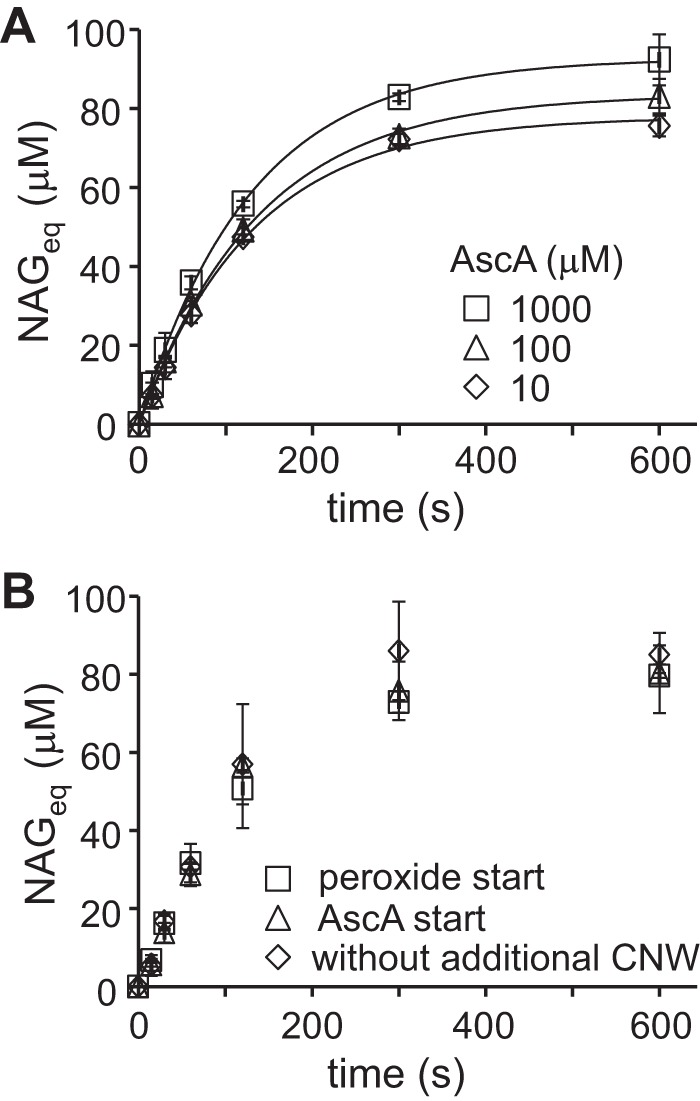
Control experiments for setting reaction conditions. A, screening for the concentration of AscA. The reactions contained CNWs (1.0 mg ml⁻¹), H₂O₂ (20 μm), CBP21 (50 nm), and AscA (10, 100, or 1,000 μm). Solid lines represent the best fit of non-linear regression analysis according to Equation 1. The best fit parameter values are listed in Table S1. B, assessing the importance of the sequence of adding the various chemicals. The reaction mixtures contained CNWs (1.0 mg ml⁻¹), H₂O₂ (20 μm), CBP21 (50 nm), and AscA (100 μm). The reactions were initiated either by the addition of H₂O₂ or AscA and were all carried out in NaAc buffer at 25 °C. In one of the series, the reaction was initiated by the addition of H₂O₂, and the addition of non-labeled CNWs before centrifugation (to separate soluble and insoluble ¹⁴C-labeled products) was omitted. For more details, see “Experimental procedures.” Error bars represent S.D. and are from at least two independent measurements.

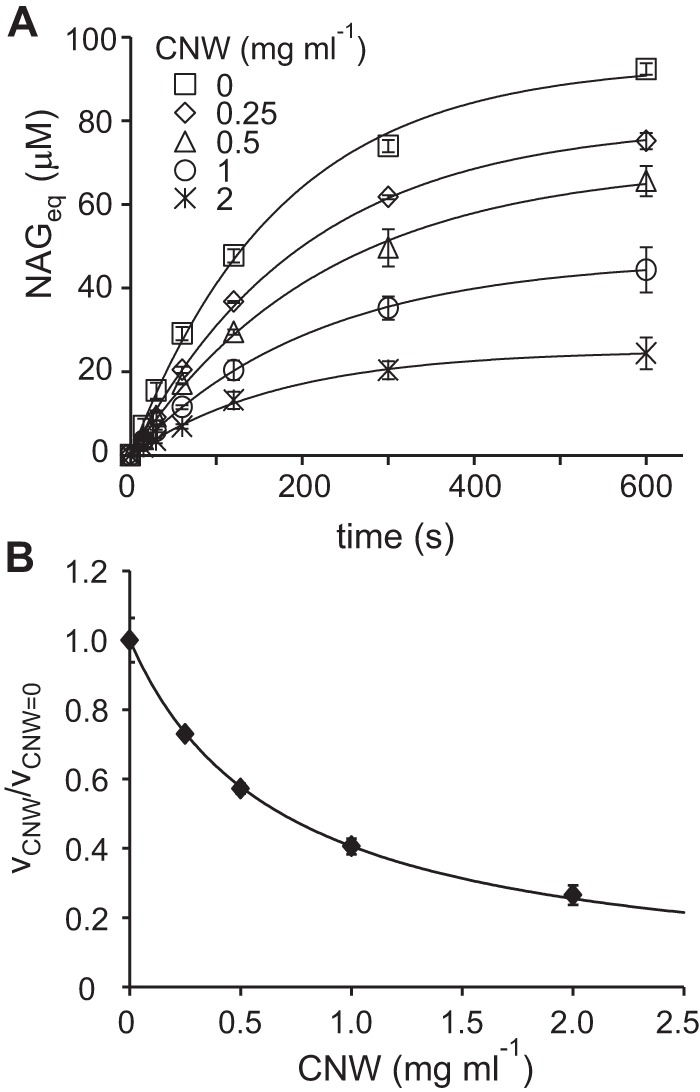
Time curves of the formation of NAG_eq at different [CNW] and [H₂O₂] are shown in Fig. 2. The time curves were fitted to empirical Equation 1, which was used as a first approximation in the treatment of data.

$$\left[{\text{NAG}}_{\text{eq}}\right]={\left[{\text{NAG}}_{\text{eq}}\right]}_{\max }\hspace{0.17em}\left(1-e^{-k_{\text{obs}}t}\right)$$ (Eq. 1)

Figure 2.

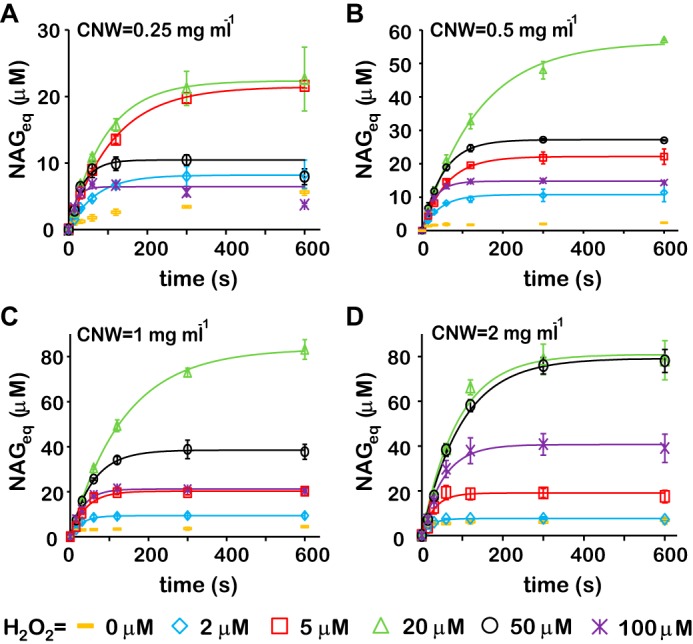
Time curves of the formation of soluble products (in NAG equivalents) during degradation of chitin (CNWs) by CBP21 using H₂O₂ as cosubstrate. Reactions were done in NaAc buffer at 25 °C and contained CNWs, H₂O₂, CBP21 (50 nm), and AscA (0.1 mm). CNW concentrations were 0.25 (A), 0.5 (B), 1.0 (C), and 2.0 mg ml⁻¹ (D). The readings of the experiments without added H₂O₂ (H₂O₂ = 0 μm) were subtracted from the readings of the experiments with H₂O₂. The color coding for [H₂O₂] is indicated in the figure. Solid lines are derived from Equation 1. Error bars represent S.D. and are from at least two independent measurements.

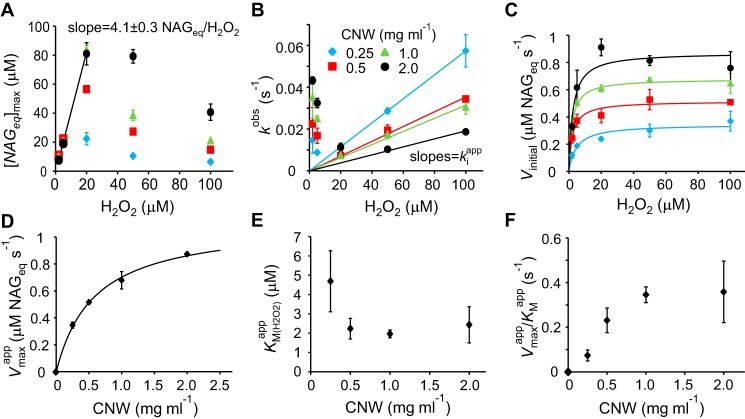
In Equation 1, [NAG_eq]_max is the plateau value of released NAG_eq, and k_obs is an observed first-order rate constant, which notably may have quite different meanings depending on the reaction conditions as outlined below. The time courses show that CBP21 activity increases with initial [H₂O₂] (2–20 μm) but with apparent inhibition at [H₂O₂] >20 μm (Fig. 2). The biphasic profiles of the dependence of [NAG_eq]_max (Fig. 3A) and k_obs (Fig. 3B) on [H₂O₂] suggest that H₂O₂ serves as both substrate and inhibitor for CBP21. At low H₂O₂ concentrations, the kinetics (the values of [NAG_eq]_max and k_obs) is governed by the depletion of H₂O₂, whereas at high H₂O₂ concentrations, the kinetics is governed by the inactivation of CBP21. Rapid rate retardation did not permit measuring the initial rates by monitoring the reaction in the linear region of the time curves. Therefore, the initial rates were calculated as [NAG_eq]_maxk_obs, which is the time derivative of Equation 1 in the limiting condition of t close to zero. The dependence of initial rates on [H₂O₂] was in accordance with Michaelis-Menten saturation kinetics (Fig. 3C and Equation 2).

$$v_{\text{initial}}=\frac{V_{\max }^{\text{app}}\left[{\text{H}}_2{\text{O}}_2\right]}{K_{m\left({\text{H}}_2{\text{O}}_2\right)}^{\text{app}}+\left[{\text{H}}_2{\text{O}}_2\right]}$$ (Eq. 2)

Figure 3.

Kinetics of degradation of chitin (CNWs) by CBP21 using H₂O₂ as cosubstrate. Reactions were done in NaAc buffer at 25 °C and contained CNWs, H₂O₂, CBP21 (50 nm), and AscA (0.1 mm). Error bars represent S.D. and are from at least two independent measurements. A, [NAG_eq]_max as a function of [H₂O₂]. The solid line shows linear regression of the data obtained using low [H₂O₂] (5.0, 10, and 20 μm) and high [CNW] (1.0 and 2.0 mg ml⁻¹). B, k_obs as a function of [H₂O₂]. Solid lines show linear regression of the data obtained using high [H₂O₂] (50 and 100 μm) with fixed intercept = 0. C, dependence of initial rates on [H₂O₂]. Solid lines are according to the Michaelis-Menten equation (Equation 2). The legend code for [CNW] (shown in B) also applies for A and C. D–F, apparent V_max (D), apparent K_m for H₂O₂ (E), and apparent V_max/K_m for H₂O₂ (F) as a function of [CNW]. The solid line in D is derived from Equation 3.

V_max^app and K_m(H2O2)^app are the apparent V_max and K_m for H₂O₂ at a particular concentration of CNWs. It must be noted that the applicability of the Michaelis-Menten equation in describing heterogeneous interfacial catalysis assumes that binding sites on the polymer are in excess compared with the total enzyme concentration (13). The half-saturating concentration of free CBP21 for binding to β-chitin is in the μm range (14). It is well known that the binding affinity of CBP21 to α-chitin is much lower than that to β-chitin (15–17). Thus, under our experimental conditions (50 nm CBP21), there is a clear excess of binding sites, and the Michaelis-Menten equation is applicable.

The dependence of apparent V_max (V_max^app) on [CNW] (Fig. 3D) was consistent with the hyperbolas described by Equation 3.

$$V_{\max }^{\text{app}}=\frac{V_{\max }\left[\text{CNW}\right]}{K_{m\left(\text{CNW}\right)}+\left[\text{CNW}\right]}$$ (Eq. 3)

In Equation 3, V_max is the true maximum velocity (i.e. enzyme is saturated with both H₂O₂ and CNWs), and K_m(CNW) is the Michaelis constant for CNWs. The best estimates for V_max and K_m(CNW) were 1.11 ± 0.04 μm NAG_eq s⁻¹ and 0.58 ± 0.05 mg ml⁻¹, respectively. The apparent K_m values for H₂O₂ (K_m(H2O2)^app) measured at different [CNW] are shown in Fig. 3E. Because of the low values of K_m(H2O2)^app, their estimates come with high uncertainty. To avoid overinterpretation, we do not discuss the possible dependence of K_m(H2O2)^app on the concentration of CNWs. Instead K_m(H2O2) is given as an average value of K_m(H2O2)^app from experiments with different concentrations of CNWs. Using this approach, we estimate that K_m(H2O2) = 2.8 ± 1.3 μm. Consistency with Equation 3 is expected for enzymatic reactions involving two substrates regardless of whether the substituted-enzyme (ping–pong) or ternary-complex mechanism is in use (18). However, a characteristic feature of the ping–pong mechanism is that (V_max/K_m)^app is independent of the concentration of either the donor or the acceptor of the group to be transferred (18). Here, the apparent V_max/K_m(H2O2) clearly appeared dependent on the concentration of CNWs (Fig. 3F), suggesting the use of a ternary-complex mechanism.

To establish conditions with low and stable H₂O₂ levels, we used an experimental setup with in situ generation of H₂O₂ by the glucose/glucose oxidase (GO) reaction at different rates (Fig. S1). The use of GO-generated H₂O₂ yielded progress curves with steady-state regions where the release of NAG_eq in time was linear (Fig. 4A). For conditions where the H₂O₂ feeding rate was below the V_max^app of its consumption by CBP21, there was a linear correlation between the steady-state rate of the CBP21 reaction and the rate of H₂O₂ generation by GO with a slope equal to 3.8 ± 0.3 NAG_eq/H₂O₂ (Fig. 4B). Consistently, a similar stoichiometry (4.1 ± 0.3 NAG_eq/H₂O₂) was obtained by plotting the [NAG_eq]_max measured at high concentrations of CNWs against [H₂O₂] (Fig. 3A). Thus, one can approximate that an average of 4 NAG_eq are released in solution for each molecule of H₂O₂ consumed by CBP21. Based on these results, the k_cat based on detected NAG_eq can be converted into a k_cat based on molecules of H₂O₂ consumed as follows: k_cat = V_max/n[CBP21]_tot = 5.6 ± 0.2 s⁻¹ with [CBP21]_tot = 50 nm, V_max = 1.11 ± 0.04 μm NAG_eq s⁻¹ as derived from Fig. 3D, and n = 4 NAG_eq/H₂O₂. Importantly, the H₂O₂-based value represents a total activity, independent of whether the generated oxidized product is solubilized (and thus detected) or remains in the insoluble fraction (see text below).

Figure 4.

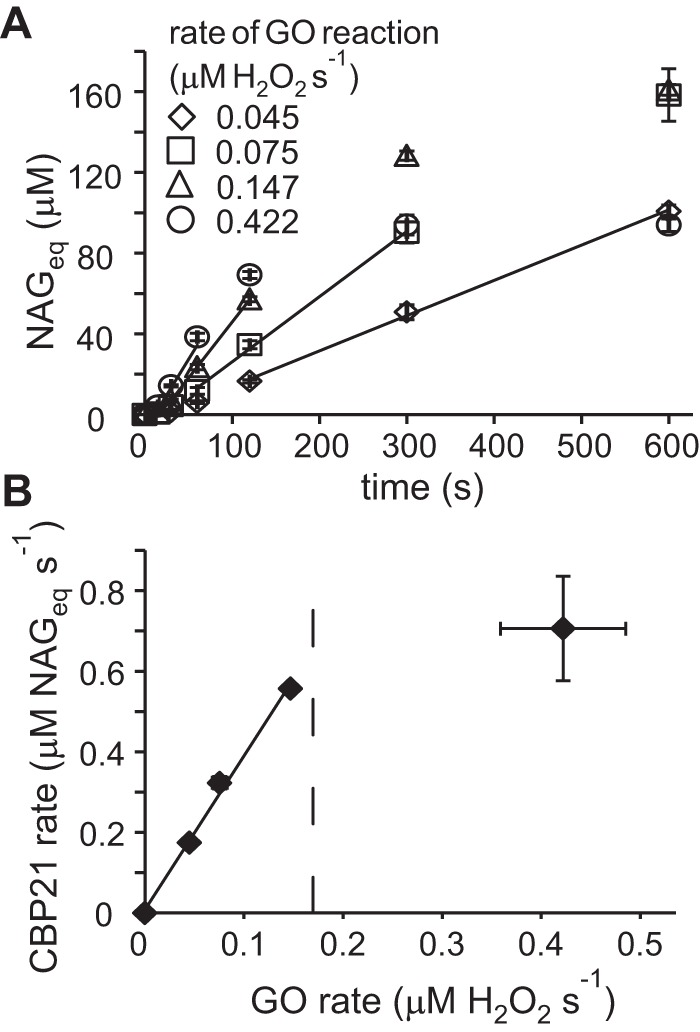
Degradation of CNWs by CBP21 with feeding of H₂O₂ by glucose/GO. Reactions were performed in NaAc buffer at 25 °C and contained CNWs (1.0 mg ml⁻¹), CBP21 (50 nm), AscA (0.1 mm), glucose (10 mm), and GO. Error bars represent S.D. and are from at least two independent measurements. A, release of NAG_eq at different rates of production of H₂O₂ by GO. The slopes of the solid lines are equal to the steady-state rates of the CBP21 reaction. B, steady-state rates of the CBP21 reaction at different rates of the GO reaction. The slope of the line equals 3.8 ± 0.3 NAG_eq/H₂O₂. The vertical dashed line indicates V_max^app of the CBP21 reaction on the basis of H₂O₂ consumption at [CNWs] = 1.0 mg ml⁻¹ (i.e. 0.68 NAG_eq s⁻¹ (see Fig. 3D) divided by 4 NAG_eq/H₂O₂).

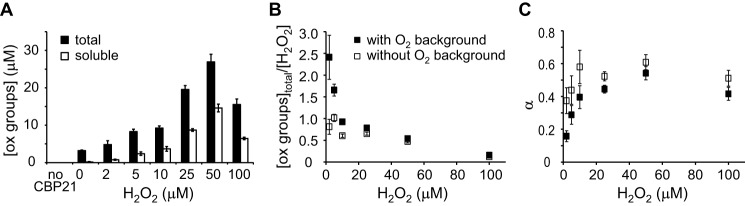
To find the total number of CBP21-generated oxidized groups per molecule of H₂O₂ consumed, we conducted direct measurements of the formation of both soluble and total oxidized groups generated by CBP21 to non-labeled CNWs at different concentrations of H₂O₂ (Fig. 5A). The concentration of insoluble oxidized groups was found as [Oxidized groups]_insoluble = [Oxidized groups]_total − [Oxidized groups]_soluble. The probability of oxidized group being in the soluble fraction (α) is defined as α = [Oxidized groups]_soluble/[Oxidized groups]_total. We note that both [Oxidized groups]_total/[H₂O₂] (Fig. 5B) and α (Fig. 5C) depend on whether the formation of oxidized groups in the experiment without added H₂O₂ ([H₂O₂] = 0 μm background) was subtracted or not. The experiment without added H₂O₂ represents O₂-driven CBP21 activity for which various catalytic scenarios have been proposed (11), including one in which the LPMO itself first converts O₂ to H₂O₂ (1). Therefore, it seems plausible that subtraction of the O₂-driven background reaction is justified and needed in the case of experiments with low (2.0 and 5.0 μm), but not with high, initial H₂O₂ loads. Taken together, the direct measurements of oxidized groups suggest that (i) at low [H₂O₂] about one oxidized group is generated per one H₂O₂ molecule supplied in accordance with previous observations (1) and (ii) about 50% of the oxidized groups are in the soluble fraction (the average value of α in the series with subtracted O₂ background is 0.5 ± 0.1; Fig. 5C). We note that the value of α has no influence on the measured k_cat value because the value of the coefficient n (4 ± 0.3 NAG_eq/H₂O₂), used for calculating the k_cat value from the amount of released NAG_eq, was determined from the consumption of H₂O₂, which represents the formation of total oxidized groups.

Figure 5.

Generation of oxidized (ox) groups by CBP21. The reactions contained non-labeled CNWs (1.0 mg ml⁻¹), CBP21 (50 nm), AscA (0.1 mm), and H₂O₂ (as indicated in the plots). Reactions were conducted in NaAc buffer at 25 °C for 10 min. Error bars represent S.D. and are from three independent measurements. A, formation of soluble and total oxidized (soluble + insoluble) groups upon incubation of CNWs with CBP21 at different initial H₂O₂ loads. Formation of oxidized groups was not observed in a control experiment without CBP21. B, the concentration of total oxidized groups (from A) divided by the initial concentration of H₂O₂ ([oxidized groups]_total/[H₂O₂]) at different initial H₂O₂ loads. In one series (labeled as without O₂ background), the number of total oxidized groups measured in the experiment without added H₂O₂ ([H₂O₂] = 0 μm) was subtracted from the total oxidized groups measured in the experiments with added H₂O₂. C, distribution of oxidized groups between the soluble and insoluble fractions (α = [Oxidized groups]_soluble/[Oxidized groups]_total) at different initial H₂O₂ loads. In one series, the number of oxidized groups measured in the experiment without added H₂O₂ ([H₂O₂] = 0 μm) was subtracted from the number oxidized groups measured in the experiments with added H₂O₂. For labeling of the series, see B.

Importantly, CBP21 produces ∼4 NAG_eq per consumed H₂O₂, which may give the impression that the average degree of polymerization of the solubilized oxidized products is in the order of 4. However, the actual average degree of polymerization of soluble oxidized chito-oligosaccharides (defined as n/α) is dependent on the value of α. With α being 0.5 and n being 4, the true estimated average degree of polymerization of solubilized products is 8, which is a reasonable value in light of actual product profiles that have been published for CBP21 (5).

Inactivation of CBP21 by H₂O₂

Besides being a cosubstrate, H₂O₂ can also cause enzyme inactivation especially in the absence of substrate, which is due to oxidative damage inflicted on residues in and near the catalytic center (1). Indeed, the activity of CBP21 was completely and irreversibly lost upon 10-min incubation with 20 μm H₂O₂ and ascorbic acid (Fig. S2). The k_obs in Equation 1 represents the rate constant of the decay of the reaction (the formation of NAG_eq in time). At low [H₂O₂] (up to 20 μm), the k_obs decreases with increasing [H₂O₂] (Fig. 3B) indicating that the decay of the reaction is governed by the depletion of H₂O₂ (the decay is slower with more H₂O₂ present). However, at high H₂O₂ concentrations (>20 μm), the k_obs starts to increase with increasing [H₂O₂] (Fig. 3B), indicating that a factor other than H₂O₂ depletion is responsible for the decay of the formation of NAG_eq in time. We suggest that in these conditions the decay of the reaction is governed by the H₂O₂-induced inactivation of CBP21. The faster inactivation at higher H₂O₂ concentrations is revealed in faster decay (higher k_obs values) at higher [H₂O₂] (see also Equation S2). Provided that the decay of the reaction is governed by the inactivation of CBP21, the observed decrease of k_obs values with increasing [CNW] in experiments with [H₂O₂] >20 μm (Fig. 3B) thus suggests that the inactivation of CBP21 is relieved by CNWs. As a control, the presence of cellulose had no effect on CBP21 kinetics (Fig. S3), indicating that the stabilizing effect of [CNW] is not just the effect of a higher concentration of solids. At [H₂O₂] >20 μm, there was a near-linear correlation between k_obs and [H₂O₂] (Fig. 3B). The slope of this linear correlation provides an estimate of the value of the apparent second-order rate constant for inactivation of CBP21 by H₂O₂ (k_i^app) at a particular concentration of CNWs.

$$k_i^{\text{app}}=\frac{k_i{K}_{m\left(\text{CNW}\right)}}{K_{m\left(\text{CNW}\right)}+\left[\text{CNW}\right]}$$ (Eq. 4)

Plotting k_i^app as a function of [CNW] (Fig. 6) and non-linear regression using Equation 4 (with K_m(CNW) fixed to 0.58 mg ml⁻¹) provides a second-order inactivation constant in the absence of chitin (k_i) of 778 ± 46 m⁻¹ s⁻¹. Although different approaches (see supporting discussion) lead to somewhat different k_i values, they all fall in the order of 10³ m⁻¹ s⁻¹. This translates into a half-life of CBP21 of less than 10 s in the presence of reductant and 100 μm H₂O₂ and in the absence of chitin.

Figure 6.

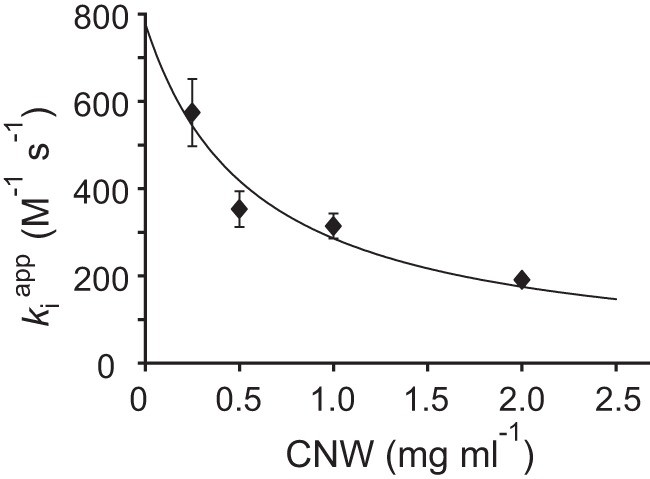
Inactivation of CBP21 is relieved by chitin. Dependence of the apparent second-order rate constant of inactivation of CBP21 (k_i^app) on the concentration of CNWs is shown. k_i^app was derived from the data presented in Fig. 3B by linear regression (i.e. from the slope of the lines in Fig. 3B). The solid line represents the best fit of non-linear regression analysis according to Equation 4 with the value of K_m(CNW) fixed to 0.58 mg ml⁻¹ (found from the analysis of the data in Fig. 3D according to the Equation 3). Error bars represent S.D. and are from at least two independent measurements.

Possible mechanism of H₂O₂-driven degradation of chitin

The simplest mechanism that can account for the data presented here is the compulsory-order ternary-complex mechanism with irreversible inactivation of free enzyme by H₂O₂. The dependence of the (apparent) parameters in the Michaelis-Menten equation on the concentration of substrates (as in Equation 3) does not provide information about the order of the binding of the substrates (18). Therefore, we also measured the binding of CBP21 to CNWs without adding H₂O₂ (Fig. 7A). The estimated half-saturating concentration of CNWs for the binding of CBP21 was 0.68 ± 0.01 mg ml⁻¹ (Fig. 7B). This figure is close to the value of K_m(CNW) in the presence of H₂O₂ (see above), indicating that H₂O₂ has little influence on the binding of CBP21 to CNWs. The rate of inactivation of CBP21 showed no saturation with H₂O₂ in the concentration range studied (Fig. 3B), suggesting that binding of H₂O₂ to free CBP21 is weak (here we assume that only the CBP21 free from CNWs is subject to inactivation). The possible reaction mechanism is depicted in Fig. 8. The mechanism can be described quantitatively by combining the rate equation for the compulsory-order ternary-complex mechanism (18) and the exponential term that accounts for irreversible inactivation of free enzyme, which results in Equation 5.

$$\frac{\text{d}\left[{\text{NAG}}_{\text{eq}}\right]}{\text{d}t}=\frac{\left[\text{CNW}\right]{\left[{\text{H}}_2{\text{O}}_2\right]}_{t}n{k}_{cat}{\left[\text{CBP}21\right]}_{\text{tot}}{e}^{-k_i^{\text{app}}{\left[{\text{H}}_2{\text{O}}_2\right]}_{t}t}}{K_{i\left(\text{CNW}\right)}{K}_{m\left({\text{H}}_2{\text{O}}_2\right)}+K_{m\left({\text{H}}_2{\text{O}}_2\right)}\left[\text{CNW}\right]+K_{m\left(\text{CNW}\right)}{\left[{\text{H}}_2{\text{O}}_2\right]}_t+\left[\text{CNW}\right]{\left[{\text{H}}_2{\text{O}}_2\right]}_t}$$ (Eq. 5)

Figure 7.

Binding of CBP21 to CNWs in the absence of added H₂O₂. Binding of CBP21 to unlabeled CNWs was assessed by measuring CBP21 activity in supernatants using ¹⁴C-labeled CNWs as described under “Experimental procedures.” A, time curves for the formation of soluble products (in NAG_eq) upon degradation of ¹⁴C-labeled CNWs by unbound CBP21 in the supernatants of the binding reactions. Solid lines are the best fit lines from non-linear regression analysis according to Equation 1. Error bars show S.D. and are from two independent experiments. B, the ratio of initial rates of CBP21 activity in the supernatants from binding experiments made in the presence (v_CNW) and absence (v_{CNW = 0}) of CNWs. The concentration of CNWs in the binding experiment is shown on the x axis. The initial rates of CBP21 were measured as initial slopes ([NAG_eq]_maxk_obs) according to Equation 1 using the time curves shown in A. The solid line in B is the best fit line according to Equation 7.

Figure 8.

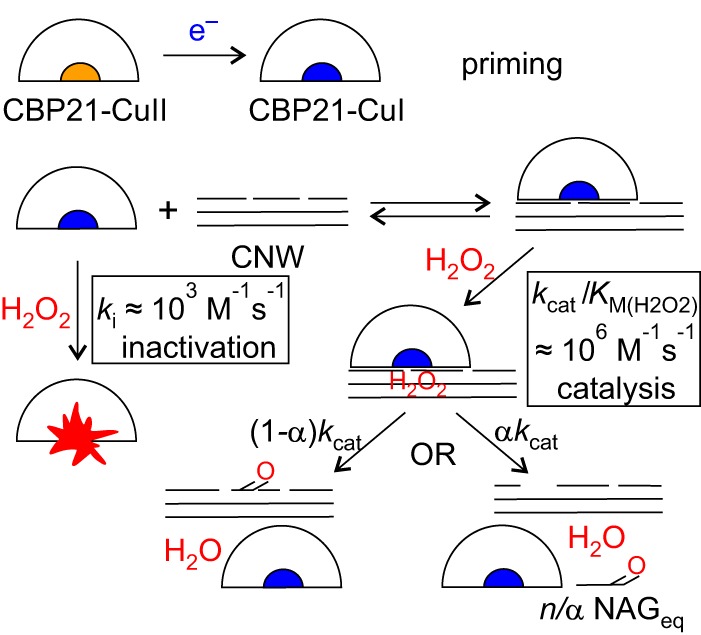
Possible mechanism of H₂O₂-driven degradation of chitin by CBP21. The enzyme in its resting state (CBP21-CuII) is activated by an external electron donor, leading to its Cu(I) state (priming) (CBP21-CuI). The primed enzyme will bind to chitin (K_i(CNW)) followed by binding of H₂O₂ (K_m(H2O2)) and oxidative cleavage of a glycosidic bond (k_cat) that may lead to the formation of a soluble (with a probability of α; α = 0.5 ± 0.1; Fig. 5C) or insoluble (with probability of 1 − α) oxidized group. Here, it is assumed that NAG_eq are not released upon generation of an insoluble oxidized group. The n is an average number of NAG_eq released per one oxidative cleavage. The average length of soluble products equals n/α, i.e. ∼8. The primed enzyme can also combine with H₂O₂ in a way that leads to enzyme inactivation (shown as an enzyme with a red splash). The reaction scheme can be captured by the combined Equation 4 and 5. The best estimates of the values of parameters of Equation 4 and 5 are as follows: k_cat = 5.6 ± 0.2 s⁻¹, n = 4 ± 0.3 NAG_eq/H₂O₂, K_i(CNW) = 0.68 ± 0.01 mg ml⁻¹, K_m(CNW) = 0.58 ± 0.05 mg ml⁻¹, and K_m(H2O2) =2.8 ± 1.3 μm. The estimates of the values of the second-order rate constants for inactivation (k_i) and catalysis (k_cat/K_m(H2O2)) are given in the figure.

Using designation of constants as defined in Cornish-Bowden (18), K_i(CNW) is the equilibrium dissociation constant for CNWs, K_m(H2O2) and K_m(CNW) are Michaelis constants for H₂O₂ and CNWs, respectively, k_cat is the catalytic constant for oxidative cleavage, and n is the average number of soluble NAG_eq released per one oxidative cleavage. The time-dependent [H₂O₂]_t is related to the concentration of products according to [H₂O₂]_t = [H₂O₂]_{t = 0} − [NAG_eq]/n. [CBP21]_tot is the total concentration of CBP21, and k_i^app is as defined in Equation 4. Note that in Equation 5 [CNW] is time-invariant. This simplification was judged to be plausible under our experimental conditions (Fig. S4). Equation 5 has no analytical solution in terms of elementary functions unless further simplifying assumptions are made. At both extremes (low and high [H₂O₂]), Equation 5 can be approximated by the single exponential function in the form of Equation 1. However, the meaning of [NAG_eq]_max and k_obs depends on whether the kinetics is governed by H₂O₂ depletion (low [H₂O₂]; see Equations S3–S5) or enzyme inactivation (high [H₂O₂]; see Equations S1 and S2) (see supporting discussion). Numerical solutions according to Equation 5 were in general accordance with the data (Fig. S5). We note that Equation 5 assumes that H₂O₂ is consumed only in the enzymatic reaction that leads to the oxidative cleavage of a glycosidic bond. The non-enzymatic consumption of H₂O₂ in the reaction with AscA was judged to be not significant in our experimental conditions (Fig. 1A and Table S1). (If the non-enzymatic consumption of H₂O₂ was significant, one would expect to see lower [NAG_eq]_max values at higher AscA concentrations, which was not the case as shown in Fig. 1A.) Notably, the consumption of H₂O₂ in enzymatic reactions that do not lead to the oxidative cleavage of a glycosidic bond cannot be excluded (i.e. a free enzyme could perhaps turn over a number of H₂O₂ molecules before inactivation occurs). Although not likely at low [H₂O₂], the latter scenario is plausible at high H₂O₂ concentrations. Different approaches to estimating the parameter values of Equation 5 yielded similar values and are summarized in Fig. 8.

Discussion

Since their recognition as oxidative enzymes (5, 6), LPMOs have been extensively studied. Over the past years, LPMOs have been implemented in commercial enzymatic mixtures and have become instrumental for the development of sustainable biorefinery processes (19). The recently discovered H₂O₂-driven mechanism of LPMOs opens new avenues for utilization of these abundant, phylogenetically widespread, but still enigmatic enzymes. Here, we present the first thorough kinetic characterization of H₂O₂-driven degradation of recalcitrant polysaccharide using one of the best studied LPMOs, chitin-active CBP21.

Notably, the k_cat found here (5.6 s⁻¹) is much higher than the apparent rate constants reported for the oxidation of chitin by CBP21 without adding H₂O₂ (0.02 s⁻¹) (5). On that note, the highest reported turnover number for a cellulose-active LPMO is 0.25 s⁻¹ (at 25 °C) (20). It remains to be clarified whether the rates of LPMO-catalyzed oxidation of polysaccharides measured without the addition of H₂O₂ reflect the direct reaction with O₂ (11, 21) or possibly the reaction of LPMO with H₂O₂ generated in situ by either the LPMO itself (22–24) or the reaction of the reductant with O₂ (25). In support of the second hypothesis, Bissaro et al. (1) have shown that a cellulose-active LPMO is totally inhibited when a peroxidase is added in a standard reaction mixture (i.e. no added H₂O₂) despite the presence of O₂ and reductant. Importantly, CBP21 was highly efficient in H₂O₂ utilization with a k_cat/K_m(H2O2) value in the order of 10⁶ m⁻¹ s⁻¹. This places CBP21 alongside peroxygenases in terms of catalytic efficiency (26, 27). Although CBP21 is inactivated by H₂O₂, chitin degradation is favored over enzyme inactivation by a factor of 10³ (k_cat/K_m(H2O2) ≈ 10⁶ m⁻¹ s⁻¹ versus k_i ≈ 10³ m⁻¹ s⁻¹; Fig. 8).

Enzyme inactivation is a well known issue in industrial applications of H₂O₂-utilizing enzymes in general (28). More generally, in the presence of redox species, such as transition metals, H₂O₂ can be transformed to highly reactive oxygen species that may damage biomolecules. For example, Scott et al. (29), who were not aware of the interplay between LPMOs and H₂O₂, showed that addition of catalase to an LPMO-containing commercial cellulolytic mixture led to improved saccharification efficiency and explained this as the catalase reducing H₂O₂-mediated oxidative inactivation of cellulases. As shown here and in Bissaro et al. (1), LPMO activity and stability are critically dependent on controlling [H₂O₂] and on the presence of saturating concentrations of the LPMO substrate. Importantly, optimal H₂O₂ concentrations are in the low micromolar range, i.e. much lower than the concentrations usually considered harmful. Because reduced LPMOs become inactivated in the presence of H₂O₂, the presence of saturating amounts of binding sites is important for LPMO stability. In nature, LPMO action on the substrate surface would be followed by regeneration of LPMO-binding sites by hydrolases that peel off the oxidized (and broken) chains on the substrate surface, thus making new surface available to the LPMO. It is thus conceivable that the discovery and potential industrial implementation of H₂O₂-driven LPMO reactions calls for a re-evaluation of the ratio of hydrolytic and oxidative enzymes in current enzyme mixtures.

Because the K_m(H2O2) value for CBP21 is in the low micromolar range, it is impossible to supplement the reactions with initial H₂O₂ loads that would be sufficient for extended degradation of the substrate but would not harm the LPMO. Therefore, similarly to peroxygenases (30), gradual addition of H₂O₂ using pumps and in situ generation of H₂O₂ seem to be the most favorable options for fueling LPMO reactions. Existing data for cellulose-active LPMOs also indicate a low K_m for H₂O₂ (1), and such a low K_m is thus expected to be a common feature of all members of the LPMO superfamily. Importantly, studies on the degradation of Avicel with Cellic CTec2, an LPMO-containing commercial cellulase mixture, using bioreactors with controlled gradual addition of H₂O₂ have already shown good results: a gradual supply of H₂O₂, at low concentrations, gave stable LPMO activity over time, revealed a clear correlation between the amount of H₂O₂ supplied and the amount of LPMO products in the reaction mixtures, and led to high saccharification yields (1).

The apparently low K_m(H2O2) values of LPMOs are of high relevance from a biological standpoint because low H₂O₂ levels are likely to be found in the natural environments of LPMOs. Housekeeping enzymes for H₂O₂, such as catalases, usually display low affinity for H₂O₂ (in the mm range) (31, 32), which is compatible with an H₂O₂-driven LPMO activity because the LPMO has a much higher affinity for H₂O₂. It has been shown that LPMOs can be fueled by a wide variety of reductants, including several redox enzymes that are commonly produced by biomass-degrading fungi, the most well known of which is cellobiose dehydrogenase (23, 33–36). Reductant effects are usually ascribed to the ability to reduce the LPMO to its Cu(I) state, but it is now clear that reductant effects on the H₂O₂ levels in reaction mixtures play a major role. Considering the present findings, it is tempting to speculate that H₂O₂ produced by strict oxidases, whose genes co-occur with lpmo genes in fungal genomes lacking cellobiose dehydrogenase (33), could play a role in fueling LPMO-catalyzed polysaccharide oxidation despite the fact that such oxidases are not capable of reducing the LPMO. Future kinetic studies dedicated to the interplay among various redox enzymes potentially involved in biomass conversion are of major interest.

Experimental procedures

Substrates and enzymes

CNWs were prepared essentially as described in Kuusk et al. (12): α-chitin from crab shells (Sigma C7170) was purified by sequential treatments with HCl (0.55 m), NaOH (0.3 m), ethanol, and acetone. The purified α-chitin was incubated at 100 °C in 3 m HCl for 90 min. The HCl-treated chitin was washed with water and sodium acetate (NaAc) buffer (50 mm, pH 6.1) followed by dialysis against methanol. 5 mCi of [1-¹⁴C]acetic anhydride (50 mCi mmol⁻¹; Hartmann Analytic GmbH, Braunschweig, Germany) was added to the chitin (2 g) in methanol (85 ml) and incubated for 24 h with stirring at room temperature. To ensure complete N-acetylation, 1.86 ml of nonradioactive acetic anhydride was added (final concentration of 230 mm), and the overnight incubation was repeated. Next, O-deacetylation was carried out by adding KOH (to 100 mm) in methanol and incubating for 3 h at room temperature with stirring. The resulting CNWs were washed repeatedly with 47.86 mm NaOH via repeated centrifugation (5 min at 2,900 × g) and resuspension. Finally, 20% glacial acetic acid was added to adjust the pH to 6.1 after which 0.01% NaN₃ was added, and the CNWs were stored at 4 °C. The total concentration of CNWs was expressed on the basis of dry weight, and the specific radioactivity of the CNW preparation was 4.18 × 10⁶ dpm mg⁻¹. Non-labeled CNWs were prepared exactly as described above, but the treatment with [1-¹⁴C]acetic anhydride was omitted. The possible influence of NaN₃ (used to avoid microbial contamination of the CNW stock solution) was tested in comparative experiments where CNWs were used as prepared above or thoroughly washed with buffer before use. No effect of NaN₃ on the activity of CBP21 was observed (data not shown).

Ascorbic acid (Sigma A7506) stock solution (10 mm in water) was prepared less than 10 min before use. Dilutions of a commercial H₂O₂ stock solution (Honeywell lot number SZBG2070) with known concentration (30 weight %; 9.8 m) were prepared in water less than 10 min before use. The water was Milli-Q ultrapure water (>18.2 megaohms cm⁻¹).

CBP21 was produced and purified as described previously (14). Purified CBP21 was saturated with copper. For that, CBP21 (144 μm) was incubated with CuSO₄ (500 μm) in NaAc buffer at 25 °C for 22 h. The unbound copper was removed by extensive washing with NaAc buffer using an Amicon ultracentrifugation device equipped with a 5-kDa-cutoff membrane. The estimated concentration of free copper after washing (calculated from the total dilution factor) was 5 pm. The concentration of CBP21 was determined by measuring absorbance at 280 nm using a theoretical molar extinction coefficient of 29,450 m⁻¹ cm⁻¹.

CBP21 kinetics

Here, we describe the standard experimental setup for the degradation of CNWs by CBP21. All reactions were done in 1.5-ml polypropylene microcentrifuge tubes in NaAc buffer at 25 °C without stirring. Although there was no significant sedimentation of CNW suspension during the experiment (10 min), the suspension was mixed by pipetting before withdrawing samples at each sampling time point. All reagents were used as purchased. The water was Milli-Q ultrapure water (>18.2 megaohms cm⁻¹).

Degradation of CNWs by CBP21

If not stated otherwise, the reaction mixture contained ¹⁴C-labeled CNW, CBP21 (50 nm), H₂O₂, and AscA (0.1 mm). The total volume of the reactions was 0.8 ml. CBP21 was added to CNWs, and after 5–10 min of incubation AscA was added. 30 s after the addition of AscA, the reactions were initiated (zero time point) by the addition of H₂O₂ to a desired concentration. The volume of the added H₂O₂ was less than 1% of the total volume so that the concentrations of the CBP21, CNWs, and AscA before the addition of H₂O₂ are essentially the same as their final concentrations. At selected time points, 0.1-ml aliquots were withdrawn and mixed with 25 μl of 1.0 m NaOH to stop the reaction. Non-labeled CNWs (to 3 mg ml⁻¹) in 0.2 m NaOH were added to improve the sedimentation of the CNWs during centrifugation (12). After centrifugation (5 min at 10⁴ × g), 50 μl of supernatant was withdrawn, and the radioactivity in the supernatant was measured using a scintillation counter (PerkinElmer Life Sciences). The sample for the zero time point was withdrawn before the addition of H₂O₂ and was treated as the other samples. The reading of the zero time point was subtracted from the readings of all time points. The reactions without the addition of H₂O₂ were performed exactly as described above with the addition of an equal amount of NaAc buffer instead of H₂O₂. If not stated otherwise, the readings of the experiments without the addition of H₂O₂ were subtracted from the readings of the experiments with H₂O₂. At least two independent replicates were carried out for each experiment (standard deviations (S.D.) are derived from at least two experiments).

Control reaction for the order of the addition of AscA and H₂O₂

The experiment was performed with CBP21 (50 nm), CNWs (1.0 mg ml⁻¹), H₂O₂ (20 μm), and AscA (0.1 mm) as described above with an opposite order of addition of AscA and H₂O₂.

Calculation of the concentration of NAG_eq from the radioactivity readings

Calculation of released NAG equivalents was done essentially as described in Kuusk et al. (12). Because the acetylation step needed to generate CNWs takes place under heterogeneous conditions, the ¹⁴C label is not expected to be distributed equally within the CNW microcrystals, and the relationship between released label and enzyme activity is not linear. Extensive analyses of chitinase activity on these CNWs (12) have shown that the release of reducing groups (a common indicator for the determination of the activity of hydrolytic enzymes) relates to the release of ¹⁴C label according to Equation 6.

$${\text{NAG}}_{2\%}=a\left(e^{-b14C_{\%}}-1\right)$$ (Eq. 6)

NAG_2% represents the degree of solubilization of ¹⁴C-labeled CNWs on the basis of released NAG dimers (NAG₂; chitobiose). ¹⁴C_% represent the degree of solubilization of ¹⁴C-labeled CNWs on the basis of released radioactivity, and a and b are calibration constants. The values of the calibration constants were determined previously using calibration curves (12) that were made using parallel measurements of released radioactivity (¹⁴C) and reducing groups during hydrolysis of ¹⁴C-labeled CNWs with Serratia marcescens ChiA, an enzyme producing predominantly chitobiose (37). To find the concentration of NAG_eq released by CBP21, the ¹⁴C_% measured in the supernatants was first converted to NAG_2% using Equation 6. Then the concentration of [NAG₂] was found from NAG_2% and the total amount of NAG₂ in CNWs (2.46 μmol mg⁻¹ CNWs). Finally, the [NAG_eq] was calculated as [NAG_eq] = 2[NAG₂]. It is worth noting that although we used non-linear calibration the deviation of the calibration curve from linearity is not very prominent below a degree of solubilization of 4% (12), which is a higher degree of solubilization than the degree of solubilization reached in the experiments presented in this study.

Soluble versus insoluble oxidized products

To assess the total degree of substrate oxidation, reactions were set up as described above. In short, the reaction mixture contained non-labeled CNWs (1.0 mg ml⁻¹) in NaAc buffer and CBP21 (50 nm), and reactions were initiated by the addition of AscA (100 μm) and, 30 s later, H₂O₂ (0–100 μm). A control reaction was carried out in the absence of CBP21 to assess the quantity of background products present in CNWs. After 10 min of reaction (25 °C; no stirring), all the reactions were incubated for 15 min at 98 °C to heat-inactivate CBP21, half of the mixture was filtrated to recover the soluble fraction, and the other half constituted the total fraction (containing insoluble and soluble products). 5 μl of a mixture of chitinases (ChiA and ChiC; 3 μm final concentration) and a chitobiase (4 μm final concentration) from S. marcescens prepared in 20 mm Tris-HCl, pH 8.0, was added to 50 μl of the samples to hydrolyze the mixture of products down to N-acetylglucosamine and chitobionic acid as final and only products (23). The soluble fractions were hydrolyzed by the chitobiase only (4 μm final concentration); ChiA and ChiC were replaced by equivalent volumes of Tris-HCl buffer (20 mm, pH 8.0). Hydrolysis reactions were incubated at 40 °C overnight. ChiA, ChiC, and the chitobiase were produced in-house as described previously (14, 38). Reaction products were analyzed by high-performance anion-exchange chromatography and monitored by pulsed amperometric detection using a Dionex Bio-LC equipped with a CarboPac PA1 column as described previously for cello-oligosaccharides (39). Chitobionic acid was quantified using a standard obtained by oxidation of chitobiose by a chito-oligosaccharide oxidase as described previously (38).

Binding of CBP21 to CNWs in the absence of added H₂O₂

In the binding experiment, CBP21 (100 nm) was incubated with non-labeled CNWs (at different concentrations) in the presence of AscA (0.1 mm). After 5 min, the CNWs were pelleted by centrifugation (1 min at 10⁴ × g). The concentration of unbound CBP21 was estimated by measuring CBP21 activity in the supernatant using ¹⁴C-labeled CNWs as substrate. To do this, the labeled CNWs and a fresh portion of AscA were added to the supernatant. 30 s after the addition of fresh AscA, the reaction was initiated by the addition of H₂O₂, and the release of ¹⁴C-labeled products (in NAG_eq) was measured. The final concentrations of ¹⁴C-labeled CNWs, fresh AscA, and H₂O₂ were 1.0 mg ml⁻¹, 0.05 mm, and 20 μm, respectively. In this procedure, the supernatant of the binding reaction was diluted 2-fold, meaning that the maximal (i.e. no binding of CBP21 to non-labeled CNWs) total concentration of CBP21 in the activity measurement was 50 nm. The control experiment ([CNW] = 0 mg ml⁻¹) was undertaken exactly as described above without the non-labeled CNWs in the binding experiment. The results of the binding experiments were analyzed according to Equation 7.

$$\frac{v_{\text{CNW}}}{v_{\text{CNW}=0}}=\frac{1}{1+\frac{\left[\text{CNW}\right]}{K_{i\left(\text{CNW}\right)}}}$$ (Eq. 7)

In Equation 7, [CNW] is the concentration of CNWs in the binding experiment, and K_i(CNW) is the concentration of CNWs at which 50% of the CBP21 molecules are bound to CNWs and 50% are free in the solution.

Author contributions

P. V., M. S., and V. G. H. E. conceived and coordinated the study. S. K., B. B., and P. V. designed, performed, and analyzed the experiments. Z. F. performed experiments. P. K. derived the rate equations. S. K., P. V., B. B., M. S., and V. G. H. E. wrote the paper. All authors reviewed the results and approved the final version of the manuscript.