Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Dec 14;122(1):98–105. doi: 10.1021/acs.jpcb.7b10002

SOMO–HOMO Level Inversion in Biologically Important Radicals

Anil Kumar 1, Michael D Sevilla 1,*
PMCID: PMC5767877  PMID: 29240424

Abstract

graphic file with name jp-2017-100026_0004.jpg

Conventionally, the singly occupied molecular orbital (SOMO) of a radical species is considered to be the highest occupied molecular orbital (HOMO), but this is not the case always. In this study, we considered a number of radicals from smallest diatomic anion radicals such as superoxide anion radical to one-electron oxidized DNA related base radicals that show the SOMO is energetically lower than one or more doubly occupied molecular orbitals (MOs) (SOMO–HOMO level inversion). The electronic configurations are calculated employing the B3LYP/6-31++G** method, with the inclusion of aqueous phase via the integral equation formalism of the polarized continuum model solvation model. From the extensive study of the electronic configurations of radicals produced by one-electron oxidation or reduction of natural-DNA bases, bromine-, sulfur-, selenium-, and aza-substituted DNA bases, as well as 20 diatomic molecules, we highlight the following important findings: (i) SOMO–HOMO level inversion is a common phenomenon in radical species. (ii) The more localized spin density in σ-orbital on a single atom (carbon, nitrogen, oxygen, sulfur, or selenium), the greater the gap between HOMO and SOMO. (iii) In species with SOMO–HOMO level inversion, one-electron oxidation takes place from HOMO not from the SOMO, which produces a molecule in its triplet ground state. Oxidation of aqueous superoxide anion producing triplet molecular oxygen is one example of many. (iv) These results are for conventional radicals and in contrast with those reported for distonic radical anions in which SOMO–HOMO gaps are smaller for more localized radicals and the orbital inversions vanish in water. Our findings yield new insights into the properties of free radical systems.

Introduction

Normally, the electronic configuration of an atom or molecule conforms to the aufbau principle, which states that “a maximum of two electrons are put into orbitals in the order of increasing orbital energy: the lowest-energy orbitals are filled before electrons are placed in higher-energy orbitals”. Accordingly, in the case of free radicals (odd electron systems), the singly occupied molecular orbital (SOMO) should be the highest occupied molecular orbital (HOMO).1 In recent years, several studies pointed out the violation of the aufbau principle for distonic radicals in which SOMO is found to be energetically lower in energy than the doubly occupied HOMO.2−13 Recently, Coote and co-workers11−13 extensively used ab initio multiconfigurational self-consistent field (MCSCF) and density functional theory (DFT) methods to show the pH-induced SOMO–HOMO level switching in several distonic radical anions and they, also, proposed the SOMO–HOMO energy level inversion in deprotonated DNA/RNA base radicals, although these orbital inversions were found to largely vanish in water.11,12 In our work, SOMO–HOMO energy level switching induced by inter base proton transfer in canonical DNA base pairs was found to be predicted by ab initio approaches including various DFT methods, ab initio complete active space self-consistent field (CASSCF), and MP2.14 Earlier studies have thus focused on SOMO–HOMO level inversion in distonic radicals or radicals with multiple ring systems. In this work, we show that single-ring DNA base radicals formed by one-electron oxidation and even small diatomic anion radicals formed by one-electron reduction often show SOMO–HOMO inversion, which is not significantly affected by solvation.

One-electron oxidized DNA base radicals have been studied in many electron paramagnetic resonance (EPR) and pulse radiolysis experiments often  aided by theory which were mainly limited to the identification of the radical and its nature (σ- or π-type).11,14−19 The nature of the electronic configurations of these radical species was not reported. Because it is well known that molecular orbitals (MOs) of one-electron oxidized molecule may rearrange from that of the parent, we have investigated the electronic configurations of a variety of one-electron oxidized DNA base analogues and their deprotonated neutral radicals, as well as bromine-, sulfur-, selenium, and aza-substituted DNA bases and found many that show SOMO–HOMO level inversion on radical formation. For any neutral molecule, removal of an electron (one-electron oxidation) from the HOMO splits the HOMO of the neutral molecule into β-lowest unoccupied molecular orbital (LUMO) and α-SOMO in the one-electron oxidized species with the α-SOMO normally the highest occupied MO. However, in this work, we show that in many small one-electron oxidized radical systems, the α-SOMO lies buried in the filled orbitals by one to three levels, see Scheme 1. This inversion and burial beneath doubly filled orbitals has important implications for the redox chemistry of these radicals; for example, one-electron oxidation of these radicals leads to species in their triplet states. This study also serves as a warning about the blind use of molecular modeling software that plot the highest occupied molecular orbital of a radical as the SOMO.

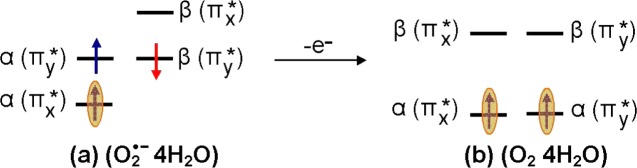
Scheme 1. Schematic Diagram Showing the Electronic Configuration (α- and β-MOs) of a Neutral Parent Molecule and Its One-Electron Oxidized Radical.

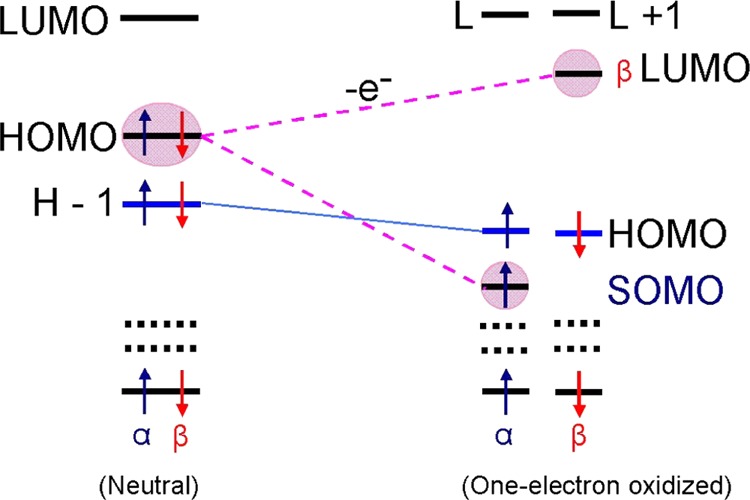
Scheme 1

Open in a new tab

In the neutral molecule, each MO is doubly occupied; however, on one-electron oxidation (removal of an electron), α- and β-MOs rearranged independently. For all of the molecules described in this work, removal of an electron from HOMO of a neutral molecule splits HOMO of neutral molecule into β-LUMO and α-SOMO, with the SOMO buried in the filled orbitals by one to three levels. Note, as expected, the SOMO and the β-LUMO have near identical wave functions. HOMO = highest occupied molecular orbital; LUMO = lowest unoccupied molecular orbital; and SOMO = singly occupied molecular orbital. Blue and red arrows represent α and β spin of an electron, respectively.

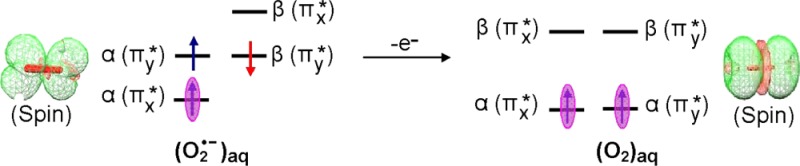
We further note that one-electron reduction of small molecules such as diatomics in their triplet ground states is found to lead to SOMO–HOMO inversion in the resultant anion radical. For example, the aqueous superoxide anion radical, which results from one-electron reduction of triplet molecular oxygen, is found to have the SOMO below the HOMO. In this work, we elucidate conditions that favor such inversions of SOMO and HOMO.

Methods of Calculation

The ground-state geometries of all one-electron oxidized/reduced molecules and their deprotonated radicals considered in this study were fully optimized using the B3LYP density functional method and 6-31++G** basis set. Further, the full account of the aqueous phase was considered via the integral equation formalism of the polarized continuum model (PCM) of Tomasi et al.20 The complete methodology herein is designated as B3LYP-PCM/6-31++G**. The molecular orbitals and spin density of radicals were plotted using the IQmol molecular modeling software.21 In earlier studies,11−14 several different DFT (B3LYP, wb97x, and M06-2x) methods were used to study the SOMO–HOMO level inversion in distonic radicals and in A–T and G–C base pairs and compared with those calculated using the ab initio MP2, MCSCF, and CASSCF methods. From the comparison between DFT and ab initio calculations, it was found that the electronic configurations calculated by DFT were well supported by the ab initio calculations. Thus, to save substantial computational time, we used the B3LYP method in this present study. In addition, we also used ωb97xd and M06-2x functionals and the ab initio Hartree–Fock (HF) method for cytosine radicals to check the reliability of the B3LYP method. The spin contamination calculated by the B3LYP method for all radicals lies in the range 0.7524–0.7767. Figures S1–S5 and Tables S1–S5 are presented in the Supporting Information. Open-shell singlets (OSSs) were calculated using the guess = (mix, always) option in Gaussian 09. All of the calculations were carried out using the Gaussian 09 suite of programs.22

Results and Discussion

Superoxide (O2•–)

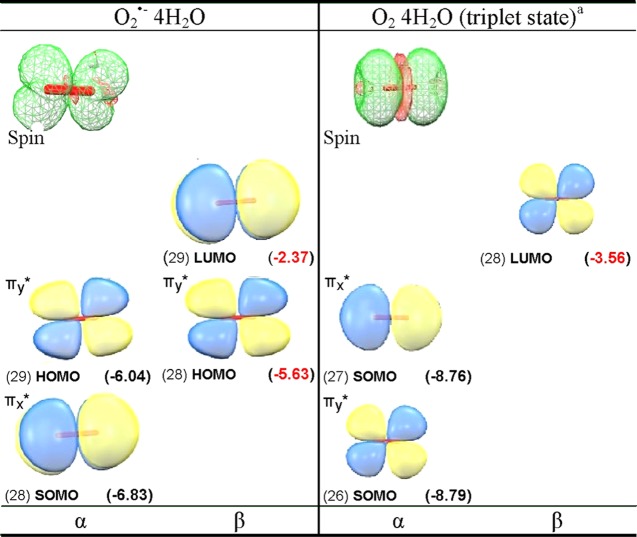
One-electron reduction of molecular oxygen (O2) produces doublet superoxide anion radical (O2•–), which is perhaps the most important and ubiquitous reactive oxygen species in the cell.23 The ground state of O2 is a triplet state having two unpaired electron, with each spin residing in a separate degenerate π*-antibonding molecular orbital with MO configuration πx*1πy*1. On one-electron reduction, O2 becomes O2•–, which is a doublet paramagnetic species with degenerate configurations πx*2πy*1 or πx*1πy*2. These degenerate configurations are lifted by hydrogen-bonding interactions. Because both O2 and O2•– are paramagnetic, they have been studied in aqueous systems using electron paramagnetic resonance (EPR).24,25 Using infrared spectroscopy and ab initio theory, Weber et al. proposed that four water molecules form the first hydration layer around O2•–.26,27 In this present study, we fully optimized the structure of O2•– in the presence of four water molecules using the B3LYP-PCM/6-31++G** method. The optimized structure shown in the Supporting Information (Figure S1) has the water hydrogen bonding along the y axis, thus stabilizing the πx*1πy*2 configuration. The electronic configuration of O2•– in the presence of four waters is shown in Figures 1a and S1 in the Supporting Information. The electronic configuration of O2•– 4H2O shows that SOMO lies below the doubly occupied HOMO (Figure 2). The SOMO–HOMO inversion in O2•– was previously indicated in other theoretical works but not discussed.28,29 The spin density distribution plot of O2•– 4H2O shows that spin is equal on each oxygen with the MO π* in nature, see Figure 2. Using EPR, Sevilla et al.25 measured the O-17 hyperfine coupling constants (HFCCs) of O2•–. The experimental isotropic couplings in Gauss (G) for O2•– were found to be −21 G for each oxygen, and the total of isotropic and anisotropic coupling on each oxygen of O2•– was reported to be: Axx = −77.3 G, Ayy = 0 G, and Azz = 15 G.25 The B3LYP-PCM/6-31++G**-calculated isotropic HFCCs on each oxygen of O2•– is −18.8 G, and the total couplings (isotropic + anisotropic) on each oxygen of O2•– is Axx = −74.2 G, Ayy = 8.3 G, and Azz = 9.5 G. Earlier, Raiti and Sevilla used B3LYP and small basis set (6-31G) to calculate the HFCCs of O2•–, which are found to be in closer agreement with the experimental values and maximum deviation of only 2.2% from the experiment.30 These couplings fully confirm a πx*1 type radical with the spin density equally distributed between the oxygens with an anisotropic structure expected for the πx*1 πy*2 configuration.

Figure 1.

Figure 1

Open in a new tab

B3LYP-PCM/6-31++G**-based electronic configuration of (a) O2•– and (b) O2 in the presence of four water molecules (see Figure 2).

Figure 2.

Figure 2

Open in a new tab

B3LYP-PCM/6-31++G**-calculated spin density distribution and electronic configuration (α and β MOs) of O2•– 4H2O and O2 4H2O (triplet state). MO energies in parentheses are given in electronvolt (eV). For clarity, waters are not shown, complete plots including waters are shown in the Supporting Information. aOnly MOs on O2 are shown, see the Supporting Information for details.

From the electronic configuration of O2•– 4H2O shown in Figure 1a, it is clear that one-electron oxidation of O2•– 4H2O should occur from the HOMO, which then results in the triplet ground state found for O2. In this context, we consider the optimized structure of O2•– 4H2O as the starting structure for molecular oxygen in water [O2 4H2O] and fully optimize the structure of O2 4H2O in both triplet and singlet “ground” states. As expected, we found that triplet of O2 4H2O is more stable than the closed-shell singlet by ca. 1.56 eV, as calculated by B3LYP-PCM/6-31++G**. Experimentally, the triplet state of O2 in the gas phase is found to be 1.64 eV more stable than the 1∑g+ singlet state.31 The electronic configuration of O2 4H2O in its triplet state is shown in Figure 1b, and its spin density and MO plots are shown in Figure 2. In addition, we, also, considered 19 other diatomics (B2, Al2, Si2, S2, NH, PH, CH–, OH+, SiH–, SH+, BN, NF, PCl, NO–, NCl, AlN, PF, SO, and PO–), all of which have triplet ground states,32,33 and calculated the electronic configurations of their corresponding anions using the B3LYP/6-31++G** method. The B3LYP/6-31++G**-calculated electronic configurations of these anions show SOMO–HOMO level switching, see Table S4 in the Supporting Information. Experimentally, the natural degeneracy in MO configurations of these species is also lifted by solvent or matrix interactions. However, DFT inherently provides only one of the degenerate states. Thus, both O2•– (gas) and O2•– (PCM) give nondegenerate electronic configurations showing SOMO–HOMO inversion identical to that found for O2•– 4H2O PCM (compare Figure S1a,b). We note that the SOMO–HOMO gap for hydrated O2•– is 0.8 versus 1.1 eV for O2•– in the gas phase or in a continuous dielectric (PCM). For O2•– 4H2O PCM, hydrogen bonding to the lone pairs of the HOMO apparently stabilizes the HOMO relative to the SOMO. Another important species to radiation chemistry in this group is the hydroxyl radical, OH•, for which our calculations using the B3LYP-PCM/6-31++G** confirm the SOMO–HOMO inversion (see Table S4).

1-Methylcytosine

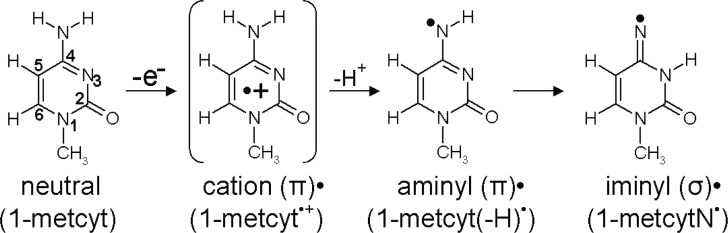
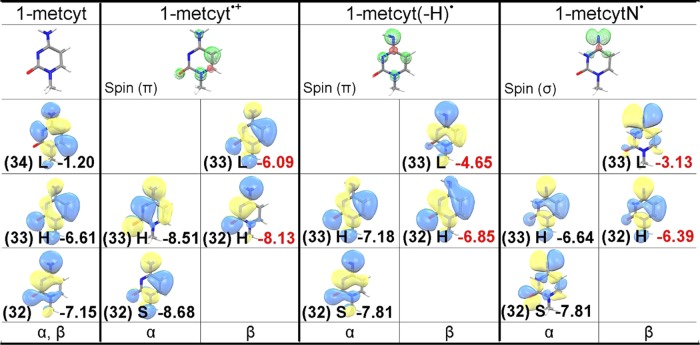
The one-electron oxidation reaction of 1-methylcytosine (1-metcyt) is shown in Figure 3. The EPR and pulse radiolysis experiments show that one-electron oxidation of 1-metcyt initially produces π-type cation radical (1-metcyt•+), which has pKa ca. 4 and has been found to deprotonate from its NH2 group to produce aminyl radical (1-metcyt(-H)•), which is also a π-type radical.15,17,34−37 The aminyl radical subsequently tautomerizes to σ-type iminyl radical (1-metcytN•).34,35 Reduction of 5-bromocytosine has been proposed to lead to the formation of 1-metcytN• in a theoretical study.38 The 1-metcytN• (iminyl radical) has been found to be quite reactive and is able to oxidize guanine in double-stranded DNA.34,35,38,39 The B3LYP-PCM/6-31++G**-calculated electronic configurations of the parent 1-metcyt (neutral) and one-electron oxidized species, 1-metcyt•+, 1-metcyt(-H)• (aminyl radical), and 1-metcytN• (iminyl radical), are shown in Figure 4 (see Figure S2 in the Supporting Information). From the electronic configurations of 1-metcyt and 1-metcyt•+, it is evident that the HOMO of neutral 1-metcyt on one-electron oxidation splits into β-LUMO and α-SOMO, as these three MOs (HOMO, β-LUMO, and α-SOMO) have similar shape (see Figure 4), but the α-SOMO is buried one level below the HOMO of 1-metcyt•+, resulting in SOMO–HOMO level inversion as proposed in Scheme 1. From the electronic configuration of 1-metcyt(-H)•, we see that α-SOMO lies below the HOMO, and in 1-metcytN•, the nitrogen-centered σ-type α-SOMO also lies below the HOMO of 1-metcytN•, see Figure 4. We also note that the shapes of β-LUMO of 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• match with the α-SOMO and the corresponding spin density plots shown in Figure 4. The electronic configurations of 1-metcytosine and its one-electron oxidized radicals calculated using the HF-PCM/6-31++G** also show the SOMO–HOMO level inversion (see Figure S3a in the Supporting Information), as predicted by the B3LYP-PCM/6-31++G** method. The LUMOs in HF-PCM/6-31++G** are very diffused owing to mixing with the continuum; to avoid this problem, we employed the HF-PCM/6-31G** method and plotted these electronic configurations in Figure S3b in the Supporting Information.

Figure 3.

Figure 3

Open in a new tab

Radicals formed after one-electron oxidation of 1-methylcytosine. Each radical has been experimentally observed by ESR (ref (34)).

Figure 4.

Figure 4

Open in a new tab

B3LYP-PCM/6-31++G**-calculated spin density distribution and electronic configuration (α and β MOs) of 1-metcyt (neutral), 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN•. MO energies are given in eV. H = HOMO, L = LUMO, and S = SOMO.

We also calculate the electronic configuration of 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• using ωb97xd-PCM/6-31++G** and M06-2x-PCM/6-31++G** methods. These results are presented in Table S1 in the Supporting Information. Further, we also calculate the electronic configuration of 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• in the SMD solvation model as well as in the gas phase employing the B3LYP, ωb97xd, and M06-2x methods. The results are presented in Tables S2 and S3 in the Supporting Information. From Tables S1 to S3, we find that all of the levels of theory predict the SOMO–HOMO inversion in 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• and environment (whether aqueous or gas phase) has no effect on the orbital ordering and the magnitude of the HOMO–SOMO gap is nearly the same. This clearly indicates that the SOMO–HOMO inversion is a property of the molecules themselves and not of their environment or method of calculation.

The electronic configuration of 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• shown in Figure 4, on further one-electron oxidation (ionization), leads to electron removal from the HOMO not from the SOMO. Thus, the ground state triplets rather than singlet states are formed, see Scheme 2. To test this hypothesis, we calculate the adiabatic ionization potentials (IPadia) of 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• forming the ionized products in their triplet or singlet states. We find that the ionization potential of each radical to form the triplet state is lower than the ionization potential value to form the closed shell singlet state. The calculated adiabatic ionization potential of doublet state 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• to triplet states is 7.95, 6.68, and 6.10 eV, respectively, whereas the corresponding adiabatic ionization potential to close shell singlet states is 8.55, 7.32, and 7.74 eV, respectively. These results are presented in Figure 5.

Scheme 2. One-Electron Oxidation of a HOMO–SOMO Inverted Radical in Doublet State Produces a Stable Triplet Diradical That Is Lower in Energy Than the Singlet State.

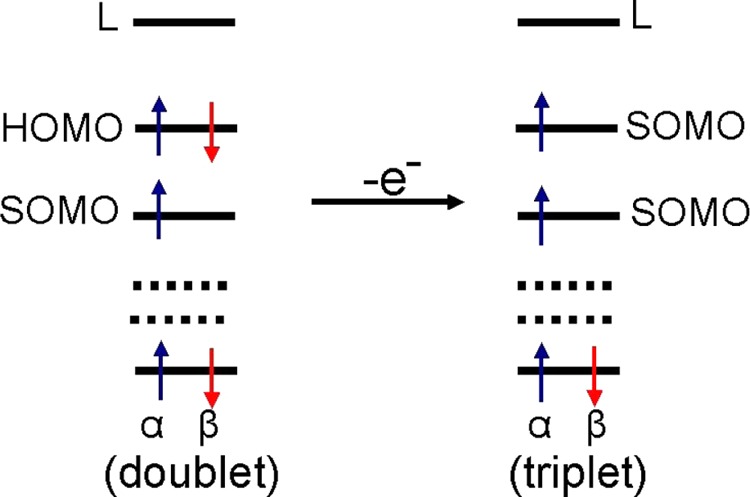
Scheme 2

Open in a new tab

See Figure 5.

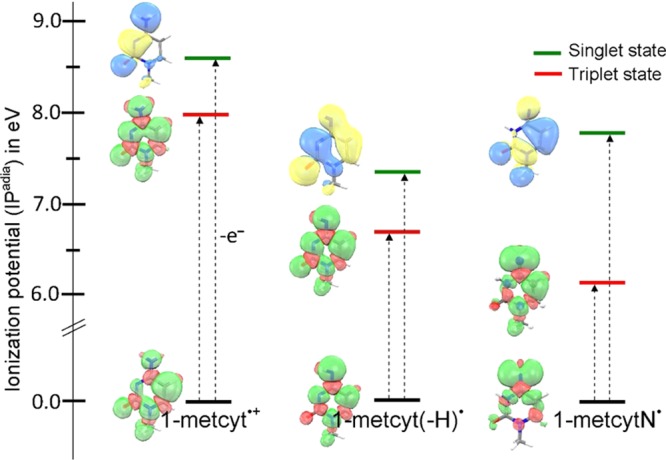
Figure 5.

Figure 5

Open in a new tab

B3LYP-PCM/6-31++G**-calculated adiabatic ionization potentials (IPadia) of 1-metcyt•+, aminyl radical (1-metcyt(-H)•), and iminyl radical (1-metcytN•) in their closed-shell singlet and open-shell triplet states in eV. Triplets lie lower than singlet in every case because electron loss is from the HOMO not the SOMO, see Scheme 2.

The ωb97xd-PCM/6-31++G** and (M06-2x-PCM/6-31++G**) calculated adiabatic ionization potentials of 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• to triplet states are 7.96 eV (8.12 eV), 6.68 eV (6.79 eV), and 6.14 eV (6.21 eV), respectively, and the corresponding adiabatic ionization potential to singlet states are 8.75 eV (8.81 eV), 7.53 eV (7.56 eV), and 7.79 eV (NA), respectively. We note that all of the methods give similar values for ionization potentials, all showing the triplets are favored over the singlets. The geometry optimization of one-electron ionized 1-metcytN• in the singlet state using M06-2x is not available, as it forms a seven-ring system in which N is bonded to the C5 atom of the cytosine.

We have also optimized the geometries of one-electron oxidized 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• using the B3LYP, ωb97xd, and M06-2x methods in their open-shell singlet (OSS) states to check whether OSS states remain higher in energy than their corresponding triplet states. Our calculations show that OSS diradicals of one-electron oxidized 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• are still higher in energy than their corresponding triplet states; however, S2 for OSS diradicals are near 1 not 0 as expected for a singlet state (see Table S5 in the Supporting Information). For these OSS states, we find the IPs are 8.24, 6.90, and 6.71 eV (B3LYP), which are all still above the triplet IPs, which were 7.95, 6.68, and 6.10 eV, respectively.

In Figure 6, we plot the SOMO and HOMO energies calculated by the B3LYP-PCM/6-31++G** method versus the degree of localization of the spin. The HOMO is taken as the average energy of α and β HOMOs. Our calculations show that the SOMO–HOMO level energy gaps in 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• are 0.36, 0.8, and 1.3 eV, respectively. The inspection of the spin density in each of 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• shows that in 1-metcyt•+, the largest spin density (0.7) is localized on the C5 atom, in 1-metcyt(-H)•, the largest spin density (0.75) is localized on the N4 atom, and in 1-metcytN•, the N4 atom has the largest spin density (1.0), which is in p-type orbital in the σ system, whereas in 1-metcyt•+ and 1-metcyt(-H)•, the spin is distributed in the π-systems mainly in a single atomic p-orbital, see Figures 4 and 6. The extent of the spin localization in the SOMO and delocalization in the HOMO we believe controls the SOMO–HOMO gap.

Figure 6.

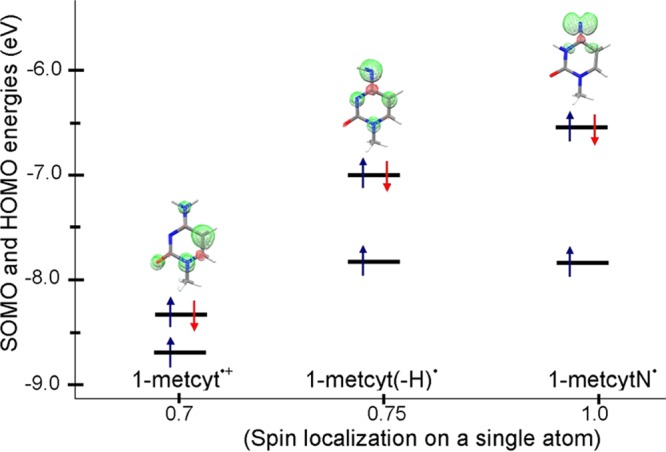
Figure 6

Open in a new tab

B3LYP-PCM/6-31++G**-calculated SOMO and HOMO energies in 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• in eV. The highest spin density localized on a single atom in 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN• are 0.7 on C5, 0.75 on N4, and 1.0 on N4, respectively. The energy gap between the SOMO and HOMO increases with increasing the spin localization.

2-Thiothymine and 2-Thiocytosine

Sulfur-substituted pyrimidines are known photosensitive probes, for example, 2-thiothymine is used for targeting selected sites in nucleic acids.40 The γ-irradiated single crystal of 2-thiothymine is studied by EPR at 77 K, which shows a sulfur-centered σ-radical deprotonated from N3.41,42 The electronic configurations of 2-thiocytosine and 2-thiothymine radicals are shown in Figure S2 in the Supporting Information. These radicals show localized spins and have SOMO–HOMO inversion in which the SOMOs are buried 2–3 levels below the HOMOs, with a substantial SOMO–HOMO gap. For example, following radicals have significant SOMO–HOMO gaps as indicated: 2-thiocyt•+ (1.2 eV), 2-thiocyt(N–H)• (1.83 eV), 2-thiocyt• (1.5 eV), 2-thiothy•+ (2.42 eV), and 2-aminopyridineN• (1.6 eV), respectively. The spin densities in these radicals are largely localized on a single sulfur or nitrogen atom, and they are σ-type in nature, see Figure S2 in the Supporting Information.

2-Selenothymine and Phenylselenyl

Selenium-substituted compounds are found to play a key role in biology as antioxidants and antiviral agents. Using the B3LYP-PCM/6-31++G** method, we also calculate the MOs energy of phenylselenyl radical and 2-selenothymine cation radical (2-selenothymine•+) and plot their spin densities and MOs as shown in Figure S4(a) in the Supporting Information. Like 2-thiothymine radicals, the spin densities of phenylselenyl radical and 2-selenothymine•+ are also completely localized on the Se atom and it is σ-type in nature. The σ-type SOMOs of phenylselenyl radical and 2-selenothymine•+ are located two and three levels below the doubly occupied HOMOs, which are π in nature, and these radicals have similar SOMO–HOMO gaps of ca. 1.85 eV. As a check, we also employ the effective core potential (ECP LANL2DZ) for Se in phenylselenyl radical as well as the relativistic correction via Douglas–Kroll–Hess using 6-31++G** basis set for all other atoms. No significant difference in orbital energies are found between the three methods. All of the methods predict a SOMO–HOMO gap of ca. 1.7 eV, and have the SOMO buried two levels below the HOMO (see Figures S4a,b in the Supporting Information).

8-Bromopurine

The Br-substituted DNA bases such as 8-bromoguanine, 8-bromoadenine, 5-bromocytosine, and 5-bromouracil are important radiosensitizing agents. The radiosensitizing activity of these molecules is due to their reactivity with the radiation-produced electron, which dissociates the C–Br bond and produces a highly reactive σ-type carbon-centered radical. The B3LYP-PCM/6-31++G**-calculated electronic configurations of guanine-C8-yl•, adenine-C8-yl•, cytosine-C5-yl•, and uracil-C5-yl• are shown in Figures S2 and S5 in the Supporting Information. The MO ordering of these localized radicals all show SOMO–HOMO level inversion.

6-Azapyrimidine

The radicals of 6-azacytosine, 6-azauracil, and 6-azathymine are produced by Cl2– attack in basic 12 M LiCl glasses and investigated by ESR spectroscopy at low temperatures by Sevilla and Swarts.43 One-electron oxidation of these 6-aza compounds produces N1 deprotonated neutral radicals. The spin density plots and electronic configurations of these radicals are also presented in the Supporting Information, and these molecules also show the SOMO–HOMO inversion.

Thus, it is clear that many classes of radical systems show the inversion of SOMO and HOMO. This is especially so for radicals with localized spin densities. We find, for example, more delocalized systems such as one-electron oxidation of uracil and thymine that do not show SOMO–HOMO inversion, and in these molecules SOMO is the highest MO.

Conclusions

This study and others show that SOMO–HOMO level inversion is a general phenomenon that occurs in radical systems from diatomics such as superoxide (O2•–), to small molecular systems (DNA radicals), to large distonic anion radicals3−13 and DNA base-pair radicals.14 Our calculations show that among all of the natural DNA bases (adenine, guanine, thymine, and cytosine), only one-electron oxidized cytosine showed SOMO–HOMO level switching, see Figure S2 in the Supporting Information. Our predicted SOMO–HOMO level switching in O2•– gets a strong support from the fact that one-electron oxidation of O2•– produces O2 in triplet ground state. Our investigations show that radical intermediates produced from bromine-, sulfur-, selenium-, and aza-substituted DNA bases all form localized radicals that show the SOMO–HOMO inversion. From the electronic configuration of 1-metcyt•+, 1-metcyt(-H)•, and 1-metcytN•, it is evident that further oxidation will take place from the HOMO not from the SOMO and produce stabilized triplet ground states, see Figures 4 and 5. We find the extent of spin density localization controls the SOMO–HOMO energy gap, for example, the gap increases from 0.36 to 1.3 eV, as the spin localization on a single atom increases from 0.7 to 1.0 in one-electron oxidized 1-methylcytosine (Figure 6). For strongly localized σ-type radicals such as 2-thiothy•+, the gap is 2.42 eV, where the spin density is mainly localized on the sulfur atom, see Figures S2 in the Supporting Information. Finally, from our extensive spin density and α- and β-MO plots of different radicals, we observe somewhat paradoxically that the β-LUMO is often a better fit to the spin density than the α-SOMO, although they are all similar in shape. Apparently, for deeply buried SOMOs, the wave function tends to mix with nearby MOs.

The depth of the SOMO–HOMO inversion in newly formed SOMO from that of the original doubly filled MO, see Scheme 1, increases with localization of the radical. These results are fully in keeping with our previous work that has shown that one electron addition to a radical’s SOMO raises the resultant MO energy significantly more for a localized radical than for a delocalized radical.44

In summary, our results lead to the following general findings: (i) SOMO–HOMO inversion is most common in radicals with localized spin densities on carbon, nitrogen, oxygen, sulfur, selenium, and likely other atoms. Further, the more localized the spin, the greater the gap between HOMO and SOMO. (ii) For those molecules considered in this work, molecules in ground triplet states, such as molecular oxygen, on one electron reduction all produce radicals with SOMO–HOMO level inversion. (iii) As a complementary property, one-electron oxidation of radicals with SOMO–HOMO inversion is found to lead to a molecule in its triplet state. (iv) The present results for conventional radical species are in contrast with those previously reported for distonic radical anions11,12 in which SOMO–HOMO gaps are smaller for more localized radicals and the orbital inversions vanish in water.

Acknowledgments

We thank Maria Bryant for many helpful discussions. The National Cancer Institute of the National Institutes of Health (Grant R01CA045424) for support. We are also thankful to Research Excellence Fund (REF) and Center for Biomedical Research (CBR) at Oakland University for support.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.7b10002.

  • Electronic configurations of O2•– 4H2O and O2 4H2O; electronic configurations of different DNA radicals considered in this study; complete Gaussian reference (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp7b10002_si_001.pdf (5.5MB, pdf)

References

  1. IUPAC. Compendium of Chemical Terminology (the “Gold Book”), 2nd ed.; McNaught A. D., Wilkinson A., Eds.; Blackwell Scientific Publications: Oxford, 2017. http://goldbook.iupac.org/AT06996.html (accessed Aug 22, 2017). [Google Scholar]
  2. Scerri E. R. The Trouble with the Aufbau Principle. Educ. Chem. 2013, 50, 24–26. [Google Scholar]
  3. Sugawara T.; Komatsu H.; Suzuki K. Interplay Between Magnetism and Conductivity Derived from Spin-polarized Donor Radicals. Chem. Soc. Rev. 2011, 40, 3105–3118. 10.1039/c0cs00157k. [DOI] [PubMed] [Google Scholar]
  4. Kusamoto T.; Kume S.; Nishihara H. Realization of SOMO–HOMO Level Conversion for a TEMPO-Dithiolate Ligand by Coordination to Platinum(II). J. Am. Chem. Soc. 2008, 130, 13844–13845. 10.1021/ja805751h. [DOI] [PubMed] [Google Scholar]
  5. Wang Y.; Zhang H.; Pink M.; Olankitwanit A.; Rajca S.; Rajca A. Radical Cation and Neutral Radical of Aza-thia[7]helicene with SOMO–HOMO Energy Level Inversion. J. Am. Chem. Soc. 2016, 138, 7298–7304. 10.1021/jacs.6b01498. [DOI] [PubMed] [Google Scholar]
  6. Westcott B. L.; Gruhn N. E.; Michelson L. J.; Lichtenberger D. L. Experimental Observation of Non-Aufbau Behavior: Photoelectron Spectra of Vanadyloctaethyl-porphyrinate and Vanadylphthalocyanine. J. Am. Chem. Soc. 2000, 122, 8083–8084. 10.1021/ja994018p. [DOI] [Google Scholar]
  7. Gary J. B.; Buda C.; Johnson M. J. A.; Dunietz B. D. Accessing Metal-Carbide Chemistry. A Computational Analysis of Thermodynamic Considerations. Organometallics 2008, 27, 814–826. 10.1021/om0702072. [DOI] [Google Scholar]
  8. Zuo T.; Xu L.; Beavers C. M.; Olmstead M. M.; Fu W.; Crawford T. D.; Balch A. L.; Dorn H. C. M2@C79N (M = Y, Tb): Isolation and Characterization of Stable Endohedral Metallofullerenes Exhibiting M-M Bonding Interactions inside Aza[80]fullerene Cages. J. Am. Chem. Soc. 2008, 130, 12992–12997. 10.1021/ja802417d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bester G.; Reuter D.; He L.; Zunger A.; Kailuweit P.; Wieck A. D.; Zeitler U.; Maan J. C.; Wibbelhoff O.; Lorke A. Experimental Imaging and Atomistic Modeling of Electron and Hole Quasiparticle Wave Functions in InAs/GaAs Quantum Dots. Phys. Rev. B 2007, 76, 075338 10.1103/PhysRevB.76.075338. [DOI] [Google Scholar]
  10. Slipchenko L. V.; Munsch T. E.; Wenthold P. G.; Krylov A. I. 5-Dehydro-1,3-quinodimethane: A Hydrocarbon with an Open-shell Doublet Ground State. Angew. Chem., Int. Ed. 2004, 43, 742–745. 10.1002/anie.200352990. [DOI] [PubMed] [Google Scholar]
  11. Gryn’ova G.; Marshall D. L.; Blanksby S. J.; Coote M. L. Switching Radical Stability by pH-induced Orbital Conversion. Nat. Chem. 2013, 5, 474–481. 10.1038/nchem.1625. [DOI] [PubMed] [Google Scholar]
  12. Gryn’ova G.; Coote M. L. Origin and Scope of Long-Range Stabilizing Interactions and Associated SOMO–HOMO Conversion in Distonic Radical Anions. J. Am. Chem. Soc. 2013, 135, 15392–15403. 10.1021/ja404279f. [DOI] [PubMed] [Google Scholar]
  13. Gryn’ova G.; Coote M. L.; Corminboeuf C. Theory and Practice of Uncommon Molecular Electronic Configurations: Uncommon Molecular Electronic Configurations. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2015, 5, 440–459. 10.1002/wcms.1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kumar A.; Sevilla M. D. Proton Transfer Induced SOMO-to-HOMO Level Switching in One-Electron Oxidized A-T and G-C Base Pairs: A Density Functional Theory Study. J. Phys. Chem. B 2014, 118, 5453–5458. 10.1021/jp5028004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. von Sonntag C.Free-Radical-Induced DNA Damage and Its Repair: A Chemical Perspective; Springer: Berlin, 2006. [Google Scholar]
  16. Kumar A.; Sevilla M. D. Proton-Coupled Electron Transfer in DNA on Formation of Radiation-Produced Ion Radicals. Chem. Rev. 2010, 110, 7002–7023. 10.1021/cr100023g. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Steenken S. Purine Bases, Nucleosides, and Nucleotides: Aqueous Solution Redox Chemistry and Transformation Reactions of Their Radical Cations and e- and OH Adducts. Chem. Rev. 1989, 89, 503–520. 10.1021/cr00093a003. [DOI] [Google Scholar]
  18. Sevilla M. D.; Becker D.; Kumar A.; Adhikary A. Gamma and Ion-Beam Irradiation of DNA: Free Radical Mechanisms, Electron Effects, and Radiation Chemical Track Structure. Radiat. Phys. Chem. 2016, 128, 60–74. 10.1016/j.radphyschem.2016.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kumar A.; Sevilla M. D.. Theoretical Modeling of Radiation-Induced DNA Damage. In Radical and Radical Ion Reactivity in Nucleic Acid Chemistry; Greenberg M. M., Ed.; John Wiley & Sons, Inc., 2009; pp 1–40. [Google Scholar]
  20. Tomasi J.; Mennucci B.; Cammi R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
  21. IQmol Is a Free Open-Source Molecular Editor and Visualization Package. http://iqmol.org/features.html.
  22. Frisch M. J.; Trucks G. W.; Cheeseman J. R.; Scalmani G.; Caricato M.; Hratchian H. P.; Li X.; Barone V.; Bloino J.; Zheng G.. et al. Gaussian 09; Gaussian Inc.: Wallingford, CT, 2009. [Google Scholar]
  23. Byczkowski J. Z.; Gessner T. Biological Role of Superoxide Ion-Radical. Int. J. Biochem. 1988, 20, 569–580. 10.1016/0020-711X(88)90095-X. [DOI] [PubMed] [Google Scholar]
  24. Kon H. Parmagnetic Resonance of Molecular Oxygen in Condensed Phases. J. Am. Chem. Soc. 1973, 95, 1045–1049. 10.1021/ja00785a009. [DOI] [Google Scholar]
  25. Sevilla M. D.; Becker D.; Yan M. Structure and Reactivity of Peroxyl and Sulphoxyl Radicals from Measurement of Oxygen-17 Hyperfine Couplings: Relationship with Taft Substituent Parameters. J. Chem. Soc., Faraday Trans. 1990, 86, 3279. 10.1039/ft9908603279. [DOI] [Google Scholar]
  26. Weber J. M.; Kelley J. A.; Nielsen S. B.; Ayotte P.; Johnson M. A. Isolating the Spectroscopic Signature of a Hydration Shell with the Use of Clusters: Superoxide Tetrahydrate. Science 2000, 287, 2461–2463. 10.1126/science.287.5462.2461. [DOI] [PubMed] [Google Scholar]
  27. Weber J. M.; Kelley J. A.; Robertson W. H.; Johnson M. A. Hydration of a Structured Excess Charge Distribution: Infrared Spectroscopy of the O2–·(H2O)n, (1 ≤ n ≤ 5) Clusters. J. Chem. Phys. 2001, 114, 2698–2706. 10.1063/1.1338529. [DOI] [Google Scholar]
  28. Lespade L. On the Importance of Water Molecules in the Theoretical Study of Polyphenols Reactivity Toward Superoxide Anion. J. Theor. Chem. 2014, 2014, 1–9. 10.1155/2014/740205. [DOI] [Google Scholar]
  29. Workman A. S. Real-Time TD-DFT Study on the Dioxygen/Superoxide Radical Charge Transfer Reaction. Comput. Theor. Chem. 2017, 1117, 207–214. 10.1016/j.comptc.2017.08.020. [DOI] [Google Scholar]
  30. Raiti M. J.; Sevilla M. D. Density Functional Theory Investigation of the Electronic Structure and Spin Density Distribution in Peroxyl Radicals. J. Phys. Chem. A 1999, 103, 1619–1626. 10.1021/jp983514h. [DOI] [Google Scholar]
  31. Pauling L. The Nature of the Chemical Bond. II. The One-Electron Bond and the Three-Electron Bond. J. Am. Chem. Soc. 1931, 53, 3225–3237. 10.1021/ja01360a004. [DOI] [Google Scholar]
  32. Ekesan S.; Lin D. Y.; Herzfeld J. Magnetism and Bond Order in Diatomic Molecules Described by Semiclassical Electrons. J. Phys. Chem. B 2016, 120, 6264–6269. 10.1021/acs.jpcb.6b02576. [DOI] [PubMed] [Google Scholar]
  33. Johnson R. D.NIST Computational Chemistry Comparison and Benchmark Database. NIST Standard Reference Database Number 101, Release 15b, August 2011. http://cccbdb.nist.gov.
  34. Adhikary A.; Kumar A.; Bishop C. T.; Wiegand T. J.; Hindi R. M.; Adhikary A.; Sevilla M. D. π-Radical to σ-Radical Tautomerization in One-Electron-Oxidized 1-Methylcytosine and Its Analogs. J. Phys. Chem. B 2015, 119, 11496–11505. 10.1021/acs.jpcb.5b05162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Naumov S.; Hildenbrand K.; von Sonntag C. Tautomers of the N-Centered Radical Generated by Reaction of SO4·– with N1-Substituted Cytosines in Aqueous Solution. Calculation of Isotropic Hyperfine Coupling Constants by a Density Functional Method. J. Chem. Soc., Perkin Trans. 2 2001, 1648–1653. 10.1039/b101680f. [DOI] [Google Scholar]
  36. Close D. M. One-Electron Oxidation of Individual DNA Bases and DNA Base Stacks. J. Phys. Chem. A 2010, 114, 1860–1867. 10.1021/jp906963f. [DOI] [PubMed] [Google Scholar]
  37. Close D. M.; Hole E. O.; Sagstuen E.; Nelson W. H. EPR and ENDOR Studies of X-Irradiated Single Crystals of Deoxycytidine 5′-Phosphate Monohydrate at 10 and 77 K. J. Phys. Chem. A 1998, 102, 6737–6744. 10.1021/jp981610c. [DOI] [Google Scholar]
  38. Kumar A.; Sevilla M. D. Cytosine Iminyl Radical (cytN•) Formation via Electron Induced Debromination of 5-Bromocytosine: A DFT and Gaussian 4 Study. J. Phys. Chem. A 2017, 121, 4825–4829. 10.1021/acs.jpca.7b04034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Anderson R. F.; Shinde S. S.; Maroz A. Cytosine-Gated Hole Creation and Transfer in DNA in Aqueous Solution. J. Am. Chem. Soc. 2006, 128, 15966–15967. 10.1021/ja0658416. [DOI] [PubMed] [Google Scholar]
  40. Kutyavin I. V.; Rhinehart R. L.; Lukhtanov E. A.; Gorn V. V.; Meyer R. B.; Gamper H. B. Oligonucleotides Containing 2-Aminoadenine and 2-Thiothymine Act as Selectively Binding Complementary Agents. Biochemistry 1996, 35, 11170–11176. 10.1021/bi960626v. [DOI] [PubMed] [Google Scholar]
  41. Bešić E.; Sanković K.; Gomzi V.; Herak J. N. Sigma Radicals in Gamma-Irradiated Single Crystals of 2-Thiothymine. Phys. Chem. Chem. Phys. 2001, 3, 2723–2725. 10.1039/b103210k. [DOI] [Google Scholar]
  42. Kumar A.; Sevilla M. D. π- vs σ-Radical States of One-Electron-Oxidized DNA/RNA Bases: A Density Functional Theory Study. J. Phys. Chem. B 2013, 117, 11623–11632. 10.1021/jp407897n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sevilla M. D.; Swarts S. Electron Spin Resonance Study of Radicals Produced by One-Electron Loss from 6-Azauracil, 6-Azathymine, and 6-Azacytosine. Evidence for both σ and π Radicals. J. Phys. Chem. 1982, 86, 1751–1755. 10.1021/j100207a002. [DOI] [Google Scholar]
  44. Colson A.-O.; Sevilla M. D. Ab Initio Molecular Orbital Calculations of Radicals Formed by H• and OH• Addition to the DNA Bases: Electron Affinities and Ionization Potentials. J. Phys. Chem. 1995, 99, 13033–13037. 10.1021/j100034a051. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp7b10002_si_001.pdf (5.5MB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES