Adsorption and Desulfurization Mechanism of Thiophene on Layered FeS(001), (011), and (111) Surfaces: A Dispersion-Corrected Density Functional Theory Study

Abstract

Layered transition-metal chalcogenides have emerged as a fascinating new class of materials for catalysis. Here, we present periodic density functional theory (DFT) calculations of the adsorption of thiophene and the direct desulfurization reaction pathways on the (001), (011), and (111) surfaces of layered FeS. The fundamental aspects of the thiophene adsorption, including the initial adsorption geometries, adsorption energies, structural parameters, and electronic properties, are presented. From the calculated adsorption energies, we show that the flat adsorption geometries, wherein the thiophene molecule forms multiple π-bonds with the FeS surfaces, are energetically more favorable than the upright adsorption geometries, with the strength of adsorption decreasing in the order FeS(111) > FeS(011) > FeS(001). The adsorption of the thiophene onto the reactive (011) and (111) surfaces is shown to be characterized by charge transfer from the interacting Fe d-band to the π-system of the thiophene molecule, which causes changes of the intramolecular structure including loss of aromaticity and elongation of the C–S bonds. The thermodynamic and kinetic analysis of the elementary steps involved in the direct desulfurization of thiophene on the reactive FeS surfaces is also presented. Direct desulfurization of thiophene occurs preferentially on the (111) surface, as reflected by the overall exothermic reaction energy calculated for the process (E_R = −0.15 eV), with an activation energy of 1.58 eV.

1. Introduction

Direct desulfurisation (DDS) or catalytic hydrodesulfurization (HDS) of sulfur-containing organic molecules from petroleum is of considerable technological and fundamental interest because of increasingly stringent global environmental regulations on the maximum sulfur level in fuel.¹⁻⁴ Natural petroleum contains different organosulfur compounds, where aromatic species like thiophene (C₄H₄S) are the least reactive, which makes them common impurities in transportation fuels.⁵ The HDS process consists of the reaction of the sulfur-containing compound with hydrogen to form hydrocarbons and H₂S.⁶⁻⁸ The key step of the desulfurization process is the C–S bond cleavage, but it is not well-understood.⁹ Gaining an improved understanding of the catalytic desulfurization process relies heavily on knowledge about the initial adsorption geometry, the nature of the active sites, and a model mechanism for the C–S bond dissociation process.^9,10 As a reaction model of desulfurization, the adsorption and reaction of thiophene on various transition-metal surfaces has been studied to help understand the catalytic desulfurization mechanism and for testing the reactivity of aromatic compounds.¹⁰⁻¹⁵

The most widely used catalysts for HDS are based on the layered transition-metal chalcogenides, usually a combination of Mo and W sulfides with Co and Ni.¹⁶⁻²⁰ Layered transition-metal sulfides have attracted particular attention because they possess high specific reactive surface areas, which is ideal for catalysis.^21,22 Molybdenum disulfide (MoS₂) and tungsten disulfide (WS₂), for instance, operate in almost every refinery in the world today to upgrade fuels by removing contaminants, as well as increase the hydrogen content of the feedstock through hydrogenation of aromatic molecules.²³ The adsorption of thiophene on the catalytically active surfaces of MoS₂ has been studied using ab initio DFT calculations,^5,17 whereas the hydrogenation and direct desulfurization reaction pathways in thiophene hydrodesulfurization over an MoS₂ catalyst at realistic conditions have also been reported.¹⁶ These studies have shown that the adsorption of thiophene at the Mo edge site leads to strong chemisorption of the thiophene molecule and a disruption of the aromatic ring. Recently, the reaction mechanism of thiophene hydrodesulfurization over the ReS₂(001) surface under typical HDS reaction conditions was investigated using density functional theory calculations.²⁴ The adsorption kinetics of thiophene on WS₂ nanoparticles with fullerene-like (onion-like) structures has been studied under ultrahigh vacuum conditions by sample temperature ramping techniques.²⁵ It was shown that at low temperatures, the thiophene adsorbs molecularly, whereas the formation of H₂S and alkanes was observed at higher temperatures on the reduced and oxidized WS₂ nanoparticles.²⁵ The reactivity of thiophene has also been characterized on clean multiwall WS₂ nanotubes (INT-WS₂), as well as on Ni- and Co-coated INT-WS₂ using an ambient pressure flow reactor and ultrahigh vacuum kinetics techniques.²⁶

Despite the efficiency of MoS₂, WS₂, ReS₂, CoMoS, and NiMoS catalysts, the use of these materials is reported to generally result in a reduction of the octane rating due to the saturation of olefins, and to lower-quality fuels and high consumption of hydrogen,^27,28 which motivates the development of cost-efficient and more active catalysts. Recently, layered iron(II) sulfide (mackinawite) has begun to attract significant attention for environmental remediation applications because of its ubiquity in nature, low price, interesting electronic properties, and prominent catalytic features.²⁹⁻³² FeS crystallizes in the tetragonal structure with space group P4/nmm (Figure 1a), with lattice parameters a = b = 3.674 Å and c = 5.033 Å and c/a ratio = 1.370 Å.³³⁻³⁵ Like MoS₂ and WS₂, the FeS structure is formed by vertically stacked two-dimensional layers with strong covalent bonding between the Fe and S atoms within a given layer and very weak van der Waals bonding between the adjacent layers.³³ Each iron atom is arranged in square-planar coordination with neighboring irons, and the sulfur atoms are in an asymmetric one-sided 4-fold coordination with iron.³⁴

Figure 1.

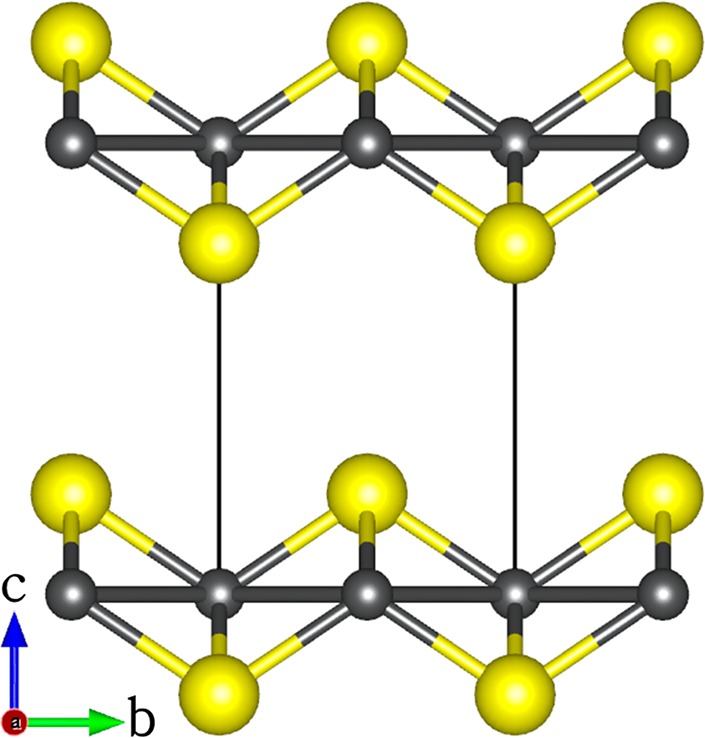
Layered structure of mackinawite, with the tetragonal unit cell highlighted by continuous lines. (Color scheme: Fe, gray; S, yellow.)

FeS nanoparticles can be synthesized relatively easily,³⁶⁻³⁹ which makes the material a promising candidate for environmental catalytic applications. Owing to its unique structure and surface chemical properties, FeS particles have been applied extensively in the treatment of groundwater and soil contaminated by arsenic⁴⁰⁻⁴² and heavy metals such as mercury^43,44 and chromium.^45,46 FeS along with greigite (Fe₃S₄), which has an inverse spinel crystal structure, are also increasingly considered to be the early catalysts for a series of biochemical reactions leading to the emergence of life.^30,47−49 The low-index surfaces of FeS exhibit strong reactivity toward greenhouse gases such as carbon dioxide (CO₂)³¹ and nitrogen oxides (NO_x).³² Interestingly, the chemical reactivity of FeS toward the adsorption and desulfurization mechanisms of organosulfur compounds has not been investigated until now. In the present study, we have used dispersion-corrected density functional theory (DFT-D2) calculations to carry out a detailed computational investigation of the structural and electronic properties of thiophene adsorption complexes on the low-index (001), (011), and (111) surfaces of FeS, followed by the investigation of the catalytic properties of the reactive (011) and (111) surfaces toward the direct desulfurization of the adsorbed thiophene. The adsorption of thiophene represents the first step in the catalytic cycle of desulfurization, which in many cases involves weakening of the C–S bond. Insight into the bonding mechanisms of thiophene at the FeS surfaces is provided through analysis of projected density of states and differential charge density iso-surface contours.

2. Computational Details

The optimized structures were determined using plane-wave density functional theory (PW-DFT) calculations within the Vienna Ab-initio Simulation Package (VASP code).^50,51 The interactions between the valence electrons and the ionic core were described with the projected augmented wave (PAW) method,^52,53 and the electronic exchange-correlation was treated using the generalized gradient approximation (GGA) with the Perdew–Wang (PW91) functional.⁵⁴ The PW91 functional was used in this study to remain consistent with previous work and to ensure that direct comparison could be made with our earlier studies. However, we have carried out a number of test calculations using the PBE functional, as mentioned in the text where relevant, but found that PW91 leads to only marginal overbinding of the thiophene molecule to the FeS surfaces compared to PBE, and by an almost constant energy difference. Dispersion interactions, which are essential for the accurate description of the interlayer interactions in FeS³² and the thiophene–FeS interactions, were accounted for through the Grimme DFT-D2 functional.⁵⁵ An energy cutoff of 400 eV was used for the expansion of the plane-wave basis set, which ensured convergence of the total energy of the FeS and the adsorbate–substrate systems to within 10^–6 eV. Geometry optimizations were performed using the conjugate gradient minimization algorithm until the magnitude of the residual Hellman–Feynman force on each relaxed atom was ≤0.03 eV/Å. A Monkhorst–Pack⁵⁶ K-point grid of 11 × 11 × 11 and 5 × 5 × 1 was used to sample the Brillouin-zone of bulk FeS and the thiophene–surface system, respectively. By performing full geometry optimizations, we obtained FeS unit cell parameters a = 3.587 Å, c = 4.908 Å, and c/a = 1.368 Å, which all compare closely with earlier theoretical results⁵⁷⁻⁶⁰ and those measured experimentally.³³⁻³⁵

The thiophene–FeS interactions were investigated on the low-index (001), (011), and (111) surfaces by employing the periodic slab model. The slabs were constructed with identical surfaces in order to avoid artificial electric fields in the vacuum for studies of polar surfaces. The (3 × 3), (4 × 2), and (4 × 2) supercells of the elementary FeS units were used to model to the (001), (011), and (111) surfaces, respectively. In each simulation cell, a vacuum region of 15 Å was added to avoid interactions between periodic slabs. An analysis of the surface energies for each FeS surface with varying stoichiometry versus the sulfur chemical potential, μ_S, is presented and discussed in section 3.1., where μ_S characterizes the surface stabilities under different environmental conditions (S-rich or Fe-rich conditions).

The structural optimizations of the thiophene–FeS systems were carried out without any symmetry constraints, and in particular, the thiophene molecule was free to move away laterally and vertically from the initial binding site or reorient itself to find the minimum energy adsorption structure. Surface relaxation was taken into account, and the three topmost atomic layers together with the thiophene molecule were allowed to fully relax in the surface supercell until residual forces on all atoms were ≤0.03 eV/Å, while the bottom layers were kept fixed in their bulk positions so as to represent a semi-infinite bulk crystal. Bader charge analysis was carried out for all the adsorbate–substrate systems, using the code implemented by Henkelman and co-workers⁶¹ to quantify charge transfer between the surfaces and adsorbates. The climbing-image nudged elastic band (CI-NEB) method,⁶² a robust and efficient approach for reaction path searches, was used to locate energy barriers and transition states (TS) through the minimum energy pathway (MEP) by connecting two minima, the initial (IS) and final (FS) states. Typically, six images were produced between the states of reactant and product in each elementary process as the initial guesses for the reaction coordinates. Identified transition states were further confirmed through vibrational frequency calculations, in which only one imaginary frequency is obtained corresponding to the reaction coordinate. The activation energy (E_A) barriers were estimated to be the energy difference between TS and IS, whereas the reaction energies (E_R) were calculated as the energy difference between the FS and IS.

3. Results and Discussion

3.1. Surface Characterization

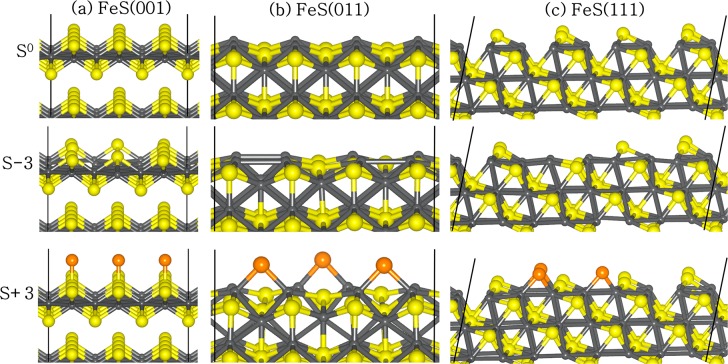
The surfaces were created from the relaxed structure of bulk FeS in order to eliminate the presence of fictitious forces during surface relaxation. In order to characterize the surface stabilities under different environmental conditions (S-rich or Fe-rich conditions), we have performed an analysis of the surface energies of the different FeS surfaces with varying stoichiometries versus the sulfur chemical potential, μ_S. When the chemical potential of sulfur is high, there is an excess of sulfur in the reservoir, and the conditions are described as S-rich. When the chemical potential of sulfur is low, there is a deficiency of sulfur in the reservoir, and the conditions are described as Fe-rich. Different stoichiometries of the low index (001), (011), and (111) surfaces of FeS were modeled in order to establish a trend between surface composition and relative stability. For convenience we denote the sulfur-deficient and sulfur-rich surfaces by S–n and S+n, respectively, where n is the number of S atoms removed (−) from or added (+) to the stoichiometric surface, which itself is denoted as S⁰. Figure 2 shows the relaxed structures of S⁰, S–3, and S+3 compositions for each surface. To quantify the structural stabilities of the different stoichiometric surfaces, we have calculated the surface energies at temperature T and pressure p defined as

1

Here, G^surf denotes the Gibbs free energy of a periodically repeated slab, which exposes a surface with area A. For the determination of A, the bottom and the top side of the slab are taken into account resulting in a factor of 2. The terms N_i and μ_i are the number and the chemical potential of species i, respectively, present in the system. For the FeS surface, i = Fe and S. Because the surface is in equilibrium with the underlying bulk sulfide, the two chemical potentials, μFe and μS, are related via the Gibbs free energy of the bulk, i.e., μFe + μS = g_FeS^bulk, where g_FeS denotes the Gibbs free energy per formula unit. Inserting this constraint in eq 1 leads to a surface energy as a function of the chemical potential of sulfur:

2

Under ambient conditions, G can be approximated by the total energies from DFT calculations, without contributions from configurational or vibrational entropies.⁶³ Values of γ(T, p) are shown in Figure 3 for μ_S ranging from the energy of a sulfur atom in SO₂ (−6.32 eV) to that of an isolated sulfur atom (0 eV) to simulate environments from oxidizing conditions to S-rich conditions. Other annealing environments, employing H₂S (μ_S = −3.77 eV) and S₂ (μ_S = −2.63 eV) as the sulfur reservoirs, were also considered to simulate sulfur-poor (iron-rich) to sulfur-rich conditions.

Figure 2.

Geometry-optimized surface structures of the (a) FeS(001), (b) FeS(011), and (c) FeS(111) surfaces with S⁰, S–3, and S+3 composition. (Color scheme: Fe, gray; S_surface, yellow; and S_added, orange.)

Figure 3.

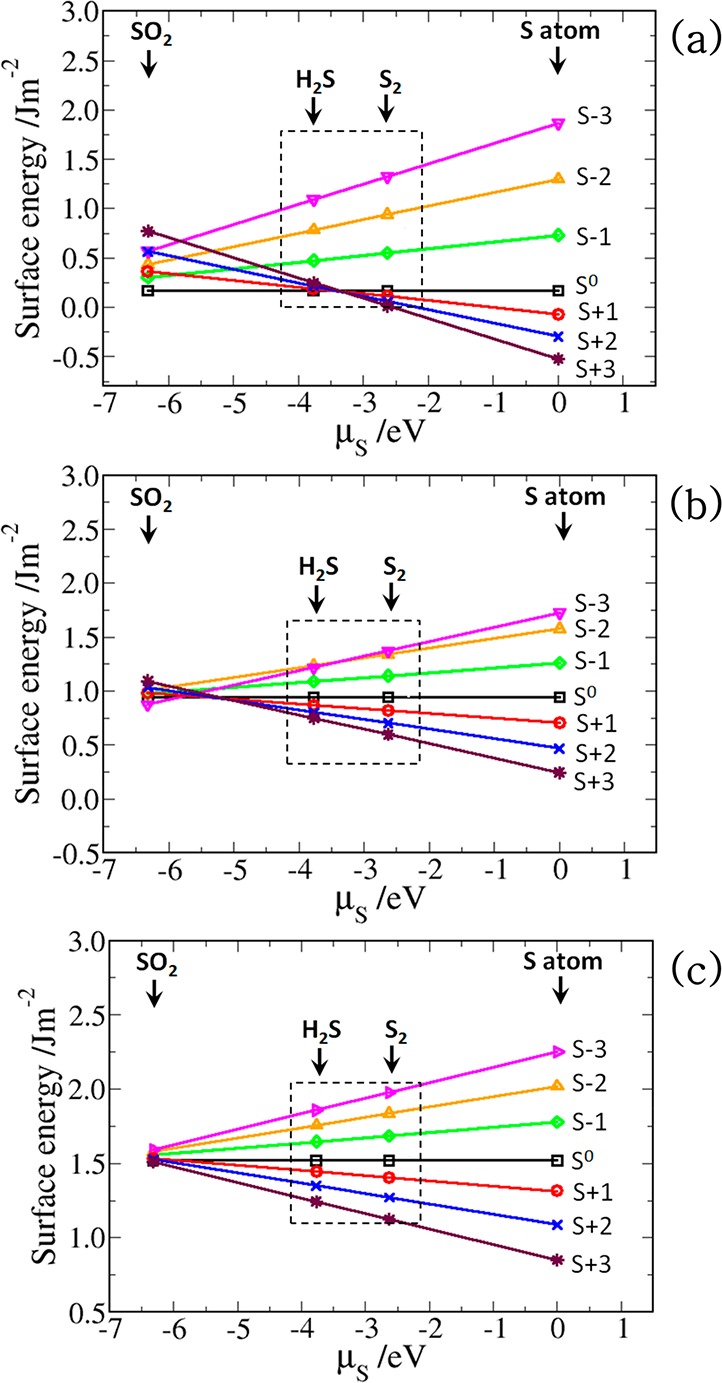
Calculated surface energies of the (a) (001), (b) (011), and (c) (111) surfaces of FeS as functions of the change in sulfur chemical potential μ_S.

The surface energies of the fully relaxed stoichiometric surfaces (S⁰) of the (001), (011), and (111) surfaces were calculated at 0.17, 0.95, and 1.52 J m^–2, respectively, in agreement with our previous calculations.^32,64 The significant stability of the (001) surface compared to the other surfaces can be attributed to the fact that its creation involves only breaking the weak van der Waals interactions between the sulfide layers. It can be seen from Figure 3 that the equilibrium surface stoichiometries of the FeS surfaces can be tuned by changing μ_S through the use of different FeS growth and annealing environments. For all values of μ_S, the stoichiometric surfaces are found to be more stable than the sulfur-deficient surfaces (S–1, S–2, and S–3). Under sulfur-rich annealing conditions (S atom and S₂), the surfaces with excess sulfur atoms (S+1, S+2, and S+3) become more stable than the stoichiometric surfaces, S⁰, which is consistent with the results obtained at other iron sulfide surfaces, including pyrite.^65,66 Our results show that under sulfur-rich growth and annealing conditions, the FeS surfaces will preferentially exist fully covered with sulfur atoms. The increased stability of the sulfur-covered surfaces (nonstoichiometric (S+n)) compared to the stoichiometric S⁰ surfaces can be explained by considering the fact that the additional sulfur atoms adsorb at the low-coordinated surface Fe sites, thereby terminating dangling bonds and stabilizing the surface.

3.2. The Free Thiophene Molecule

Thiophene is a heterocyclic compound that resembles benzene, and it is especially common in petroleum. Owing to its relatively simple structure, thiophene is often used as a model molecule for studying the catalytic C–S bond scission and HDS mechanism. Figure 4a shows the schematic molecular structure, and the projected density of states (PDOS) is depicted in Figure 4b. The thiophene molecule has two pairs of electrons on the S atom, with one pair in the six-electron π-system and the other in the plane of the ring. Consequently, thiophene can act as either an n-type donor by donating the lone pair of electrons of the sulfur atom to a surface cation (direct S–M bond) or as a π-type donor by utilizing the delocalized electrons of the aromatic ring to form a π-complex with the cation. The PDOS shows the 1a₂ and 2b₁ orbitals composed mainly of the C and S p-states, respectively, around the Fermi level (Figure 4b), and these orbitals are expected to play an important role in the linkage of the thiophene molecule to the FeS substrate.

Figure 4.

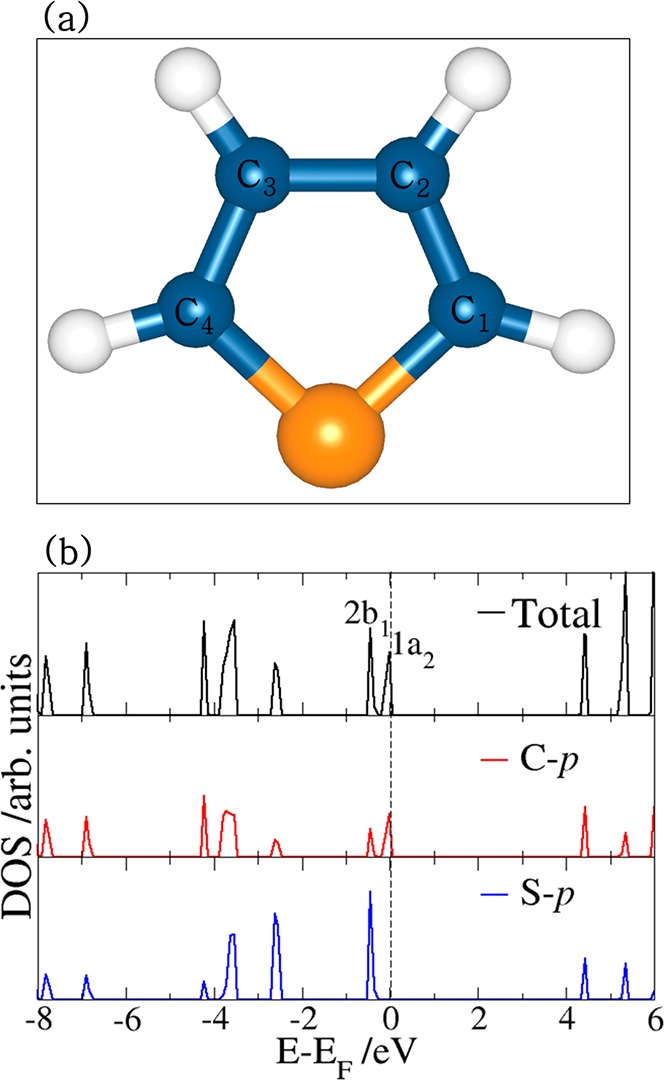
(a) Optimized structure of the thiophene molecule. The number x in C_x represents the position of the C atom in the thiophene ring. (b) The partial density of states showing the total and p-states projection on the C and S atoms.

To validate the accuracy of the calculation, we have calculated and compared the geometrical parameters of the free thiophene (C₄H₄S) molecule with available experimental data^67,68 and previous theoretical^9,69 results. The optimized geometrical parameters of the thiophene molecule are summarized in Table 1. The experimental and other calculated data are also provided for comparison. It is clear that all bond lengths calculated by the DFT method with BLYP and B3LYP basis sets are overestimated when compared with the experimental geometries. The present calculations using the PW91-GGA functional with dispersion-correction yield better agreement with the experimental geometries, thus making our calculation method reliable. The C–S bond length for free thiophene is calculated at 1.718 Å, in good agreement with the experimental value of 1.714 Å.^67,68

Table 1. Relaxed Geometry Bond Lengths of C₄H₄S^a.

bond length	this work PW91-D2	BLYP69	B3LYP69	PW919	exptl67,68
d(C1–S) (Å)	1.718	1.754	1.736	1.729	1.714
d(C1–C2) (Å)	1.375	1.378	1.367	1.374	1.369
d(C2–C3) (Å)	1.423	1.437	1.429	1.422	1.423
d(C3–C4) (Å)	1.374	1.378	1.369	1.374	1.369
d(C4–S) (Å)	1.718	1.758	1.737	1.729	1.714

^aThe experimental and other theoretical results are given for comparison.

3.3. Thiophene Adsorption

The adsorption of the thiophene molecule on the catalyst surface is an important starting step in its desulfurization process. If the interaction of the thiophene molecule with the catalyst is too weak, it is impossible to activate it for further reaction.⁷⁰ The first interest of this study is therefore to determine the lowest-energy adsorption configurations of thiophene on the stoichiometric and nonstoichiometric (S+n) surfaces with additional adsorbed sulfur and to characterize the strength of their interaction and the extent of C–S bond activation. The nonstoichiometric (S–n) surfaces were not considered for the thiophene adsorption as they are unstable relative to the stoichiometric S⁰ surface. Different initial adsorption possibilities, including flat and upright configurations, have been subjected to geometry optimization until the residual forces on all atoms were ≤0.03 eV/Å. The adsorption energy (E_ads), which is a measure of the strength of the thiophene–FeS interactions, is defined as follows:

3

where E_{surface+thiophene} is the total energy of the adsorbate–substrate system in the equilibrium state, E_surface the total energy of the substrate alone, and E_thiophene the total energy of the isolated adsorbate. By this definition, a negative value of E_ads indicates an exothermic and stable adsorption, whereas a positive value indicates unstable. In this work, all of the reported adsorption and activation energies were corrected by the zero-point energy (ΔZPE), calculated as the difference between the ZPE correction of the thiophene molecule on the surface and in the gas phase, according to eq 4:

4

where h is the Planck constant and ν_i are the vibrational frequencies.

3.3.1. Thiophene Adsorption on Nonstoichiometric (S+n) Surfaces

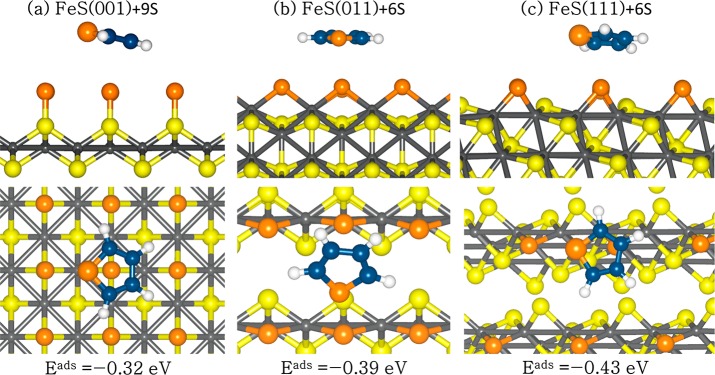
As the FeS surfaces with excess sulfur atoms (S+n) become more stable than the stoichiometric surfaces, S⁰, under sulfur-rich annealing conditions (S atom and S₂), we have first investigated the adsorption of the thiophene molecule on the nonstoichiometric (S+n) (001), (011), and (111) surfaces, where the surfaces are fully covered with additional sulfur. The optimized structures of thiophene adsorption are shown in Figure 5, and the calculated adsorption energies and optimized geometry parameters are summarized in Table 2. The thiophene molecule was physisorbed on all three sulfur-covered FeS surfaces, releasing adsorption energies of 0.32, 0.39, and 0.43 eV on the (001)+9S, (011)+6S, and (111)+6S surfaces, respectively. In each adsorption structure, the thiophene molecule remains planar without any significant changes to the internal conformations, which is consistent with the physisorbed character of thiophene. The average C–S_surf, S–S_surf, and H–S_surf interatomic bond distances were calculated to be larger than 3 Å in each adsorption structure, and no charge transfer occurred between the surfaces and the adsorbed thiophene molecule, as shown in Table 2. The weak adsorption of the thiophene molecule on the nonstoichiometric (S+n) FeS surfaces can be explained by considering the fact that the layer of negatively charged S atoms shields the inner Fe atoms, giving rise to repulsive interactions between the S atom in the thiophene molecule and the surface S atoms. These weakly bound structures suggest that the nonstoichiometric (S+n) surfaces with coordinatively saturated sulfur sites are not suitable for activating the thiophene molecule for further surface reactions.

Figure 5.

Optimized adsorption structures of a thiophene on the nonstoichiometric (S+n) FeS surfaces fully covered with additional sulfur, in side (top) and top (bottom) views. (Color scheme: Fe, gray; S_slab, yellow; C, blue; S_{molecule/added}, orange.)

Table 2. Adsorption Energies and Structural Parameters of Thiophene Adsorbed on Nonstoichiometric (S+n) FeS (001), (011), and (111)^a.

surface	(001)+9S	(011)+6S	(111)+6S
configuration	physisorbed	physisorbed	physisorbed
Eads (eV)	–0.32 (−0.21)	–0.39 (−0.27)	–0.43 (−0.32)
∑q (e–)	0.00	0.00	0.00
d(C1–C2) (Å)	1.376	1.375	1.377
d(C2–C3) (Å)	1.425	1.424	1.421
d(C3–C4) (Å)	1.375	1.375	1.380
d(C1–S) (Å)	1.719	1.719	1.720
d(C4–S) (Å)	1.719	1.719	1.717
d(SThio–Ssurf) (Å)	3.619	3.576	3.362
d(C–Ssurf) (Å)	3.157	3.291	3.075
d(H–Ssurf) (Å)	3.281	3.279	3.461

^aThe PBE E_ads are shown in parentheses.

3.3.2. Thiophene Adsorption on Stoichiometric (S⁰) Surfaces

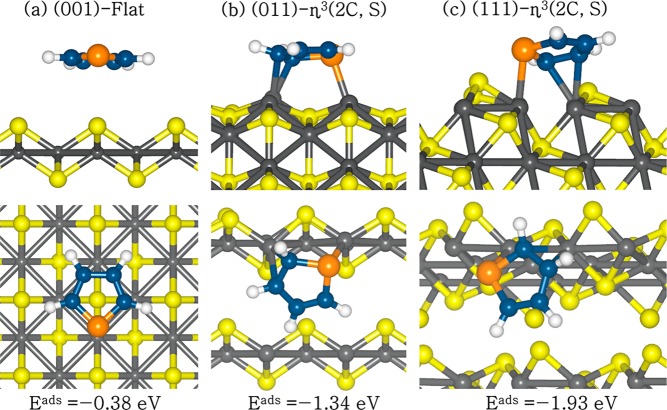
Following the trend generally observed for surface reactivity, where the thermodynamically less stable surfaces are more reactive toward adsorbing species,^64,71,72 we have also investigated the adsorption and surface-bound reactions of thiophene on the stoichiometric (S⁰) surfaces as they are the next most stable surfaces under sulfur-rich annealing conditions and the most stable under oxidizing conditions. Several possible configurations and binding sites were studied for thiophene adsorption on the stoichiometric surfaces, but only the lowest-energy structures are shown in Figure 6 and Table 3 (the remaining adsorption geometries and calculated adsorption energies are given in the Supporting Information (Figures S1–S3 and Table S1, respectively).

Figure 6.

Optimized adsorption structures of a thiophene on stoichiometric (S⁰) FeS surfaces, in side (top row) and top (bottom row) views. (Color scheme: Fe, gray; S_slab, yellow; C, blue; S_molecule, orange.)

Table 3. Adsorption Energies and Structural Parameters of Thiophene Adsorbed on Stoichiometric (S⁰) FeS (001), (011), and (111) Surfaces^a.

surface	FeS(001)	FeS(011)	FeS(111)
configuration	flat	η3(2C, S)	η3(2C, S)
Eads (eV)	–0.38 (−0.26)	–1.34 (−1.21)	–1.93 (−1.80)
∑q (e–)	0.00	0.45	0.57
d(C1–C2) (Å)	1.376	1.422	1.367
d(C2–C3) (Å)	1.423	1.443	1.427
d(C3–C4) (Å)	1.375	1.359	1.433
d(C1–S) (Å)	1.718	1.807	1.810
d(C4–S) (Å)	1.718	1.422	1.782
d(S–Fe) (Å)	–	2.331	2.448
d(C–Fe) (Å)	–	2.133	2.282
d(SThio–Ssurf) (Å)	3.487	3.237	3.255
d(C–Ssurf) (Å)	3.290	2.995	3.158
d(H–Ssurf) (Å)	3.359	3.095	2.731

^aThe PBE E_ads are shown in parentheses.

3.3.2.1. Thiophene Adsorption on Stoichiometric FeS(001) Surface

At the stoichiometric FeS(001) surface terminated by sulfur in the topmost layer, the flat adsorption configuration, wherein the thiophene molecular ring lies symmetrically flat around the interacting surface S atom (top view of Figure 6a), released an adsorption energy of 0.38 eV. The symmetric nature of the flat adsorption geometry around the surface S atom can be attributed to the delocalization of electrons within the aromatic ring. The average C–S interatomic bond distance was calculated at 3.325 Å, whereas the S–S distance converged at 3.487 Å. The large interatomic bond distances are characteristic of physisorption. Compared to the flat configuration, the upright adsorption geometries with the S atom of the molecule pointing either away from the surface (upright–H) or toward the surface (upright–S) as shown in Figure S1 have adsorption energies of only −0.19 and −0.13 eV, respectively. Consistent with the physisorbed character observed at the nonstoichiometric (S+n) surfaces, we found that in each adsorption structure on the stoichiometric FeS(001) surface, the thiophene molecule remains planar without any significant changes in the internal conformations.

3.3.2.2. Thiophene Adsorption on Stoichiometric FeS(011) Surface

Compared to the stoichiometric FeS(001) surface, stronger chemisorption of the thiophene molecule is obtained on the stoichiometric FeS(011) surface, because it favors direct cation−π interactions between the thiophene molecule and the Fe-terminating sites. The coordination of the thiophene molecule onto the surface is denoted as η^x(m, n), where the superscript x represents the number of interacting atoms of the molecule and (m, n) denotes the specific atoms of the adsorbate that interacts with the surface species. As on the other surfaces, the adsorption configurations, wherein the thiophene molecule lies almost flat on the FeS(011) surface, were found to be energetically more favorable than the upright ones. Similar results were previously reported for thiophene adsorption on other layered materials including MoS₂^5,16,17 and ReS₂.²⁴ The lowest-energy stable adsorption configuration of thiophene on the stoichiometric FeS(011) surface is a tridentate structure (denoted as η³(2C, S) as shown in Figure 6b). In this structure, the thiophene molecule is adsorbed on the surface via two short C–Fe bonds of average length 2.133 Å and one S–Fe bond of length 2.331 Å. The adsorption energy of the tridentate structure η³(2C, S) is −1.34 eV. This can be compared to the adsorption energy of another tridentate structure (η³(3C), Figure S2b), in which the thiophene molecule interacts with surface cations via three C–Fe bonds of average length 2.201 Å, with an adsorption energy of −1.21 eV. The upright adsorption configuration in which the thiophene interacts via one S–Fe bond of length 2.255 Å (denoted by η¹(S) as in Figure S2c) released the least energy of 0.59 eV. The interaction via a single S–Fe bond is not sufficient to produce a substantial adsorption energy, which explains why the flat adsorption configurations are energetically more stable than the upright configuration. The thiophene molecule is slightly distorted out-of-plane in the flat adsorption configurations and it is characterized by weakening of the C–S bonds as they are elongated from 1.718 Å in the gas phase to the range of 1.765–1.807 Å after adsorption (Table 3). We have also observed elongations in the C–C bond distances after adsorption, which suggest that the adsorption has a clear effect in the loss of aromaticity of the thiophene ring. The flat adsorption configurations therefore represent preferential precursors for direct desulfurization or hydrodesulfurization reactions of thiophene on the stoichiometric FeS(011) surface.

3.3.2.3. Thiophene Adsorption on Stoichiometric FeS(111) Surface

The strongest adsorption of the thiophene molecule was obtained on the stoichiometric FeS(111) surface, which is in agreement with it being the least stable stoichiometric surface and therefore the most reactive.²⁶ As on the stoichiometric FeS(011) surface, the flat configurations wherein the thiophene lies almost flat on the surface and interacts via multiple carbon–iron and sulfur–iron bonds are found to be energetically more favorable than the upright configuration in which the thiophene interacts with the iron sites via only the sulfur atom. The lowest-energy adsorption configuration of thiophene on the stoichiometric FeS(111) surface is calculated to be a tridentate structure (η³(2C, S), Figure 6c), in which the thiophene molecule forms two short C–Fe and one S–Fe bonds with the surface cations, releasing an adsorption energy of 1.93 eV, i.e., 0.59 eV more than the lowest-energy structure obtained on the thiophene FeS(011) surface. The average C–Fe bond length was calculated to be 2.284 Å, whereas the S–Fe bond was calculated to be 2.448 Å. The other flat configuration in which the thiophene forms two C–Fe bonds at an average length of 2.124 Å (denoted as η²(2C), Figure S3b), released an adsorption energy of 1.58 eV. In both flat adsorption configurations, the C–S bonds are weakened as they are elongated (Table 3) compared to the gas-phase bond distance (Table 1), which indicates that the C–S bonds are activated. The upright thiophene adsorption configuration on the stoichiometric FeS(111) surface was found to be favorable at a bridge-Fe site (E_ads = 1.43 eV), with the S atom bridging two Fe atoms (η²(S), Figure S3c) at an average S–Fe bond of 2.194 Å. The superior reactivity of the FeS(111) surface toward thiophene coupled with the significant activation of the C–S bonds compared to the other surfaces suggests that further surface reactions of direct desulfurization or hydrodesulfurization may take place preferentially on FeS nanoparticles expressing the (111) surface.

3.4. Electronic Structures

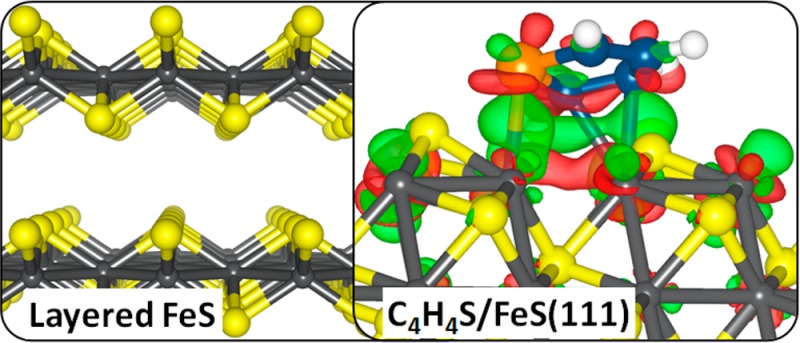
We now discuss the electronic structure and bonding mechanism of the thiophene molecule on the different FeS surfaces. For the (001) surface, where the thiophene molecule is only weakly physisorbed, we have plotted contours of the electron localization function (ELF) as displayed in Figure 7a for the lowest-energy flat adsorption structure. As evident from the ELF plot, the weak interaction can be attributed to the steric repulsion between the electron density of the molecule’s sulfur atom and the surface-terminating S atoms. Consistent with the physisorbed character of thiophene on the FeS(001) surface, we observe negligible changes in the partial density of states projected on the C and S p-states of the adsorbed thiophene (Figure 7b) compared to that of the gas-phase molecule (Figure 4b). On the stoichiometric (011) and (111) surfaces where the thiophene molecule is chemisorbed, differential charge density (Δρ) was employed to gain insight into the electron density redistribution within the adsorbate–substrate systems due to the formation of new bonds. Δρ is obtained by subtracting from the electron density of the total FeS–thiophene systems both the electron density of the clean FeS surface and that of an isolated thiophene.

5

The atomic positions of the clean FeS surface and of the thiophene array (i.e., including the molecule’s images in neighboring cells) are taken to be the same as those of the relaxed FeS–thiophene system. In this way, the presentation highlights the change in electronic structure and bond formation as a result of the adsorption. Shown in panels a1 and b1 of Figure 8 are the iso-surface contour plots of the differential charge density for the lowest-energy adsorption configurations of thiophene on the FeS(011) and FeS(111) surfaces, respectively. On both surfaces, we find that the chemisorptive character of the thiophene leads to significant charge density increase (green isosurfaces) around the centers of the newly formed bonds and further in the iron t_2g-like states and antibonding states of the thiophene molecule. The main charge density decrease (red isosurfaces) is found in the d-states of the interacting Fe atoms and the HOMO-π-states of the aromatic ring. Further information on the electronic structures of thiophene adsorption on the FeS surfaces was obtained from analyses of the electronic density of states projected (PDOS) on the C and S p-orbitals of the molecule and on the interacting surface iron atoms, as presented in panels a2 and b2 of Figure 8 for thiophene adsorbed on the FeS(011) and FeS(111) surfaces, respectively. The PDOS clearly shows the chemisorptive character of thiophene on the (011) and (111) surfaces, as reflected in the disappearance of the 2b₁ and 1a₂ orbitals of the adsorbed thiophene in the vicinity of the Fermi level, which confirms that the thiophene molecule is linked to the FeS surfaces through its π-system. The newly formed bonds arise from the hybridization of surface Fe 3d and the C-2p and S-3p states of the thiophene molecule, showing the Fe–C and Fe–S bonds to be of covalent character. Our Bader population analyses reveal that the adsorption is characterized by charge transfer from the interacting surface species to the thiophene molecule at the (011) and (111) surfaces (Table 3). In the lowest-energy adsorptions, the thiophene molecule gained a net charge of 0.45e^– and 0.57e^– from the (011) and (111) FeS surfaces, respectively. The larger charge transfers from the (111) surface is consistent with the larger adsorption energy released upon thiophene adsorption on the (111) surface. We believe that the effective hybridization between surface Fe 3d states and the thiophene C-2p and S-3p states, characterized by charge transfer from the surface to the thiophene molecule, is responsible for the weakening of the C–S bonds.

Figure 7.

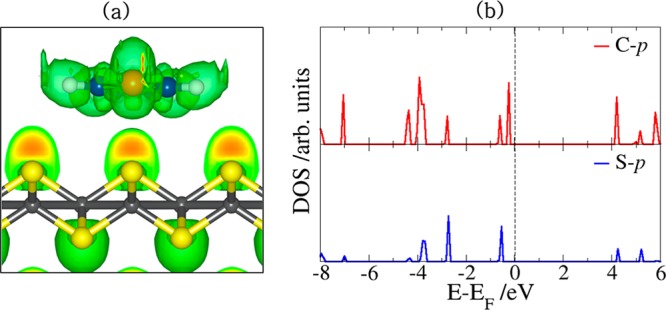
(a) Isosurface contours of the electron localization function of the thiophene–FeS(001) system and (b) the partial DOS projected on the C and S p-states of the adsorbed thiophene.

Figure 8.

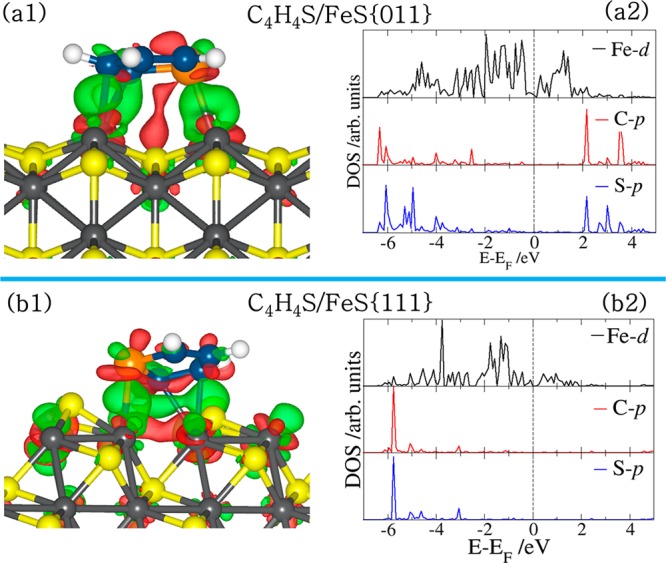
(Left) Electron density difference isosurface contours upon thiophene adsorption on the stoichiometric (011) and (111) FeS surfaces, showing regions of electron density accumulation (green) and depletion (red) by 0.02 e/ų, respectively. (Right) Partial DOS projected on the interacting surface Fe d-states and on the C and S p-states of the adsorbed thiophene.

3.5. Vibrational Frequencies

In order to propose an assignment for the observed features of the adsorbed thiophene, we have computed the wavenumbers of the normal modes for the lowest-energy adsorption geometries on the (001), (011), and (111) surfaces (Table 4). Our computed wavenumbers for the free thiophene molecule compare closely with experimental data⁷³ and earlier theoretical results,¹⁷ which ensures the reliability and accuracy of our approximate assignments. For example, the asymmetric and symmetric υ(C=C) stretching modes for the free thiophene were computed at 1494 and 1408 cm^–1, which compare closely with the experimental values of 1507 and 1409 cm^–1, respectively. For the adsorbed thiophene molecule on the stoichiometric FeS surfaces, we have restricted our analysis to wavenumbers above 600 cm^–1, because below this value an important mixing of the various normal modes occurs when thiophene is adsorbed, making comparison of the free and adsorbed molecules difficult and unreliable.

Table 4. Vibrational Frequencies (cm^–1) of the Lowest-Energy Thiophene Adsorption Configurations on the Stoichiometric FeS (001), (011), and (111) surfaces^a.

	free C4H4S		FeS(001)	FeS(011)	FeS(111)
vib. mode	experiment73	calculated	flat	η3(2C, S)	η4(2C, S)
υ(C–H)	3126	3133	3135	3120	3121
υ(C–H)	3125	3128	3133	3139	3127
υ(C–H)	3098	3103	3109	3110	3107
υ(C–H)	3098	3105	3106	3111	3102
υ(C=C)asym	1504	1494	1489	1481	1469
υ(C=C)sym	1409	1407	1406	1348	1370
υ(ring)	1360	1349	1349	1292	1287
δ(C–H)	1256	1233	1228	1188	1191
δ(C–H)	1085	1066	1063	1068	1070
δ(C–H)	1083	1061	1059	1039	1062
δ(C–H)	1036	1034	1035	983	880
υ(C–S)asym	751	740	736	620	667

^aThe stretching and bending modes are denoted by υ and δ, respectively.

Generally, we observe no significant differences between the vibrational frequencies of the thiophene adsorbed on the stoichiometric FeS(001) surface compared to the free thiophene molecule, in good agreement with the physisorbed characteristics observed. However, we do observe notable differences between adsorbed thiophene on the stoichiometric FeS(011) and FeS(111) surfaces, where it was chemisorbed, compared to the free thiophene molecule. For instance, the C=C asymmetric and symmetric stretching frequencies of the adsorbed thiophene molecule were assigned at 1478 and 1370 cm^–1 on the (011) surface and at 1459 and 1348 cm^–1 on the (111) surface, which represents softening compared to the gas-phase C=C asymmetric and symmetric stretching frequencies of 1494 and 1407 cm^–1. We also observe softening of the C–S asymmetric stretching modes, calculated at 667 and 620 cm^–1 on the stoichiometric FeS(011) and FeS(111) surfaces, respectively, compared to the gas-phase value of 740 cm^–1, which is consistent with the elongated C–S calculated for the adsorbed thiophene on these surfaces. The frequency of the υ(ring) mode also becomes lower for the adsorbed thiophene compared to the gas-phase molecule. They are assigned at 1292 and 1287 cm^–1 at the stoichiometric FeS(011) and FeS(111) surfaces, respectively, compared to the gas-phase value of 1349 cm^–1. The wavenumbers exhibited by the adsorbed thiophene molecule around 3000 cm^–1 can all be assigned to the C–H stretching modes, which are shifted only slightly with respect to the gas-phase frequencies.

3.6. Thiophene Dissociation

The results presented above show that thiophene adsorbs strongly onto the stoichiometric (011) and (111) surfaces, where the adsorption process results in weakening of the C–S bonds. We now seek to determine how the differences in the structure and electronic properties may dictate the reactivity and direct desulfurization of the thiophene molecule (i.e., C₄H₄S → C₄H₄ + S) on the stoichiometric (011) and (111) surfaces. Beginning with the molecularly adsorbed complexes in the lowest-energy configurations, the direct desulfurization process involves the successive scission of the two C–S bonds. In the first step of the reaction, a single C–S bond is broken, giving a monodissociated intermediate molecule, and the second step of the reaction involves the scission of the second C–S bond. The relative energies were calculated with respect to the lowest-energy adsorption complexes on each surface, and the zero of energy was set at the initial molecularly adsorbed thiophene state. Shown in Figures 9 and 10 are the reaction profiles for the direct desulfurization of C₄H₄S into C₄H₄ and S fragments on the (011) and (111) surfaces, respectively, with the insets showing schematic representation of the steady states along the reaction coordinates. On the FeS(011) surface, the scission of the first S–C bond was found to have an endothermic reaction energy of 0.63 eV with an activation barrier of 1.28 eV (Figure 9). The dissociated C–S bond of this intermediate structure was calculated at 3.092 Å, with the S–Fe distance at 2.331 Å. The length of the dissociating C–S bond in the transition state (E_A¹) was calculated at 2.288 Å compared to 1.807 Å in the initial molecular adsorption state. The next step of the dissociation, which involves the scission of the second C–S bond, shows the dissociated sulfur atom at a top Fe site (S–Fe = 2.019 Å) and the C₄H₄ fragment linked to the surface Fe ions through the terminal carbon atoms (average Fe–C = 1.867 Å). The terminal carbons are bonded to Fe atoms in an sp³-like configuration, whereas the two middle carbon atoms are pushed away from the surface, in an sp²-like configuration. In the final state, the process is endothermic with overall reaction energy of 1.04 eV along with a second reaction barrier of 1.62 eV. Similar high activation energy barriers and endothermicity have been reported for the direct desulfurisation pathway of thiophene on the ReS₂(001) surface²⁴ and on transition-metal carbides and nitride.^8,75 On the ReS₂(001) surface,²⁴ the breaking of the first and second C–S bonds needs to surmount activation energy barriers of 1.76 and 1.85 eV, respectively, whereas on the NbC(001) surface,⁷⁴ activation energy barriers of 1.74 and 1.82 eV have to be overcome. Similarly, on the VC(001) surface,⁸ the scission of the first and second C–S bonds needs to overcome activation energy barriers of 1.49 and 1.88 eV, respectively.

Figure 9.

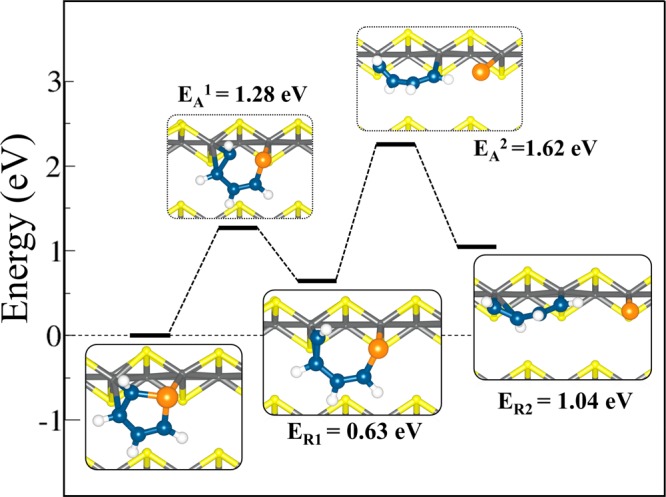
Reaction profile for the direct desulfurization of C₄H₄S on stoichiometric FeS(011). The desulfurization reaction proceeds in two steps with successive scission of the two C–S bonds.

Figure 10.

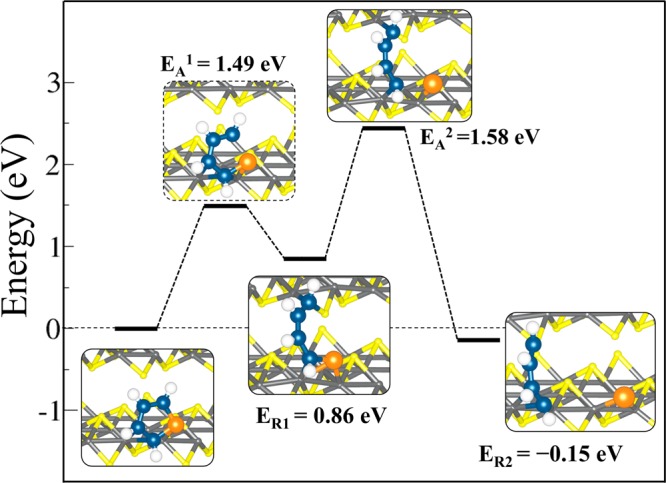
Reaction profile for the direct desulfurization of C₄H₄S on stoichiometric FeS(111). The desulfurization reaction proceeds in two steps with successive scission of the two C–S bonds.

On the FeS(111) surface, the scission of the first S–C bond was found to be an endothermic reaction requiring an overall energy of 0.86 eV with an activation barrier of 1.49 eV (Figure 10). The dissociated CH-end of this intermediate structure is bound across the FeS layer at a bridge site between S and Fe (C–Fe = 2.084 Å and C–S = 1.762 Å). The length of the dissociated C–S bond in this intermediate structure was calculated at 3.714 Å compared to 2.277 Å in the transition state and 1.810 Å in the initial molecular adsorption state. Relative to the first C–S bond dissociated state, the scission of the second C–S bond is found to be exothermic (E_R = −1.01 eV), with an activation of 1.58 eV. The overall reaction energy of the entire process is slightly exothermic with E_R2 = −0.15 eV. The completely dissociated sulfur atom binds at a bridge site between adjacent surface Fe sites at an average S–Fe distance of 2.075 Å. One of the terminal carbon atoms of the C₄H₄ fragment was bound at a bridge Fe site (average C–Fe = 1.937 Å), whereas the other end was bound to a S site (C–S = 1.742 Å) across the FeS layer. On both reactive (011) and (111) surfaces, the activation barriers were always found to be smaller than the desorption energies, suggesting that, when adsorbed, the thiophene will more readily undergo further surface chemical reactions, including direct desulfurization and hydrodesulfurization, than desorb from the surface. It should be noted that the butadiene fragment may react further by hydrogenation or intramolecular rotation. These cases were not explored here because they would occur only after S removal and are not the key feature of desulfurization.

4. Summary and Conclusions

In the present periodic DFT-D2 study, we have studied the adsorption structures and bonding mechanism of thiophene on the stoichiometric (S⁰) and nonstoichiometric (S+n) (001), (011), and (111) surfaces of layered FeS, as well as the catalytic properties of the reactive stoichiometric (011) and (111) surfaces toward the direct desulfurization of the adsorbed thiophene. We found that the strength of adsorption of thiophene onto the FeS surfaces is related to the stability of the different surfaces, where it adsorbs most strongly onto the least stable FeS(111) surface and most weakly onto the most stable FeS(001) surface. In general, we have shown that the flat adsorption structures in which the thiophene molecule forms multiple π-bonds with the surface Fe ions were energetically more favorable than the upright adsorption geometries. The adsorption of the thiophene onto the stoichiometric (011) and (111) surfaces was shown to be characterized by charge transfer from the interacting Fe d-states into the π-system of the thiophene molecule, which induced changes in the intramolecular structure including loss of aromaticity and elongation of its C–S bonds. On the basis of the thermodynamic and kinetic analysis of the elementary steps involved in the direct desulfurization of thiophene on the FeS surfaces, we have shown that direct desulfurization of thiophene is most likely to occur on the (111) surface, as reflected by the overall exothermic reaction energy (E_R2 = −0.15 eV), calculated for the process, although a very high activation energy of 1.58 eV has to be overcome. The high activation barriers suggest that the direct desulfurization of thiophene on the FeS surfaces may occur only at elevated pressure and temperature conditions, which is typical of industrial HDS units, such as in a refinery over a catalyst consisting of an alumina base impregnated with cobalt and molybdenum (usually called a CoMo catalyst).^75,76 This work provides a molecular-level insight into the surface structures and electronic factors governing the adsorption and direct desulfurization of thiophene on layered FeS. Future investigations will extend the present study to systematically investigate the hydrogenation pathways (HYD) for thiophene desulfurisation in order to draw comparison between the HYD and the DDS mechanism reported in this work. The thermodynamic and kinetic data presented in this study may also be used to develop relevant microkinetic models for the desorption processes, including temperature-programmed desorption (TPD) of butadiene and H₂S and in the presence of H₂.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.7b08711.

• Detailed information on all other conformations of thiophene adsorption configurations and structural parameters on stoichiometric (S0) FeS (001), (011), and (111) (PDF)

The authors declare no competing financial interest.