Membrane Tension Inhibits Rapid and Slow Endocytosis in Secretory Cells

Abstract

Endocytosis generates spherical or ellipsoid-like vesicles from the plasma membrane, which recycles vesicles that fuse with the plasma member during exocytosis in neurons and endocrine secretory cells. Although tension in the plasma membrane is generally considered to be an important factor in regulating endocytosis, whether membrane tension inhibits or facilitates endocytosis remains debated in the endocytosis field, and has been rarely studied for vesicular endocytosis in secretory cells. Here we report that increasing membrane tension by adjusting osmolarity inhibited both the rapid (a few seconds) and slow (tens of seconds) endocytosis in calyx-type nerve terminals containing conventional active zones and in neuroendocrine chromaffin cells. We address the mechanism of this phenomenon by computational modeling of the energy barrier that the system must overcome at the stage of membrane budding by an assembling protein coat. We show that this barrier grows with increasing tension, which may slow down or prevent membrane budding. These results suggest that in live secretory cells, membrane tension exerts inhibitory action on endocytosis.

Introduction

Endocytosis generates intracellular vesicles from the plasma membrane, which results in internalization of extracellular fluids as well as the plasma membrane proteins and lipids (1). One of the essential functions of endocytosis is to recycle exocytic vesicles and thus maintain exocytosis in secretory cells, such as neurons that mediate synaptic transmission by releasing transmitters and endocrine cells that mediate important physiological response by releasing hormones and transmitters (2, 3).

Generation of an endocytic vesicle out of a nearly flat plasma membrane can be divided into two sequential steps: generation of a strongly curved membrane bud, whose radius of curvature in the case of clathrin-mediated endocytosis is ∼20–30 nm (see, for example, (4)); and fission of the membrane neck connecting the bud to the plasma membrane, which leads to formation of a separate vesicle. Obviously, the two steps include substantial changes of the membrane curvature and connectivity. The budding stage effectively consumes the area of the plasma membrane. Therefore, the efficiency of endocytosis must depend, essentially, on the membrane elastic properties (5), and can be controlled by application to the membrane of external forces, which generate membrane curvature and lateral tension (6).

The impact of the membrane lateral tension on the endocytic vesicle generation became controversial over the last decade. Early studies in nonsecretory cells proposed that membrane tension generates an energy barrier for endocytic machinery to overcome during the course of vesicle formation (6). Consistent with this idea, it was proposed that actin cytoskeleton generates forces counteracting the membrane tension during clathrin-mediated endocytosis in nonsecretory cells, for which the plasma membrane tension is high, whereas actin is not required for endocytosis in cells with low plasma membrane tension (7). Actin polymerization has recently been shown to be involved in various forms of endocytosis at synapses (8, 9, 10). In contrast, in vitro liposome assays showed that dynamin-mediated membrane fission, the process completing generation of an endocytic vesicle, occurs within minutes if membrane tension is low (11, 12), whereas it takes only a few seconds when membrane tension is high (13, 14). This suggests that membrane tension facilitates the endocytic reaction through promoting the membrane fission step. The reason for this apparent discrepancy is unclear, although it is worth noting that these different conclusions were made from different preparations of nonsecretory cells versus in vitro liposome fission assays, and from endocytosis reaction versus fission reaction.

In secretory cells, endocytosis is usually 1–2 orders-of-magnitude faster than that in nonsecretory cells, which is crucial for maintaining a functional recycling pool of exocytic vesicles (15). Whether and how membrane tension affects endocytosis have rarely been studied in secretory cells. To our knowledge, only one pioneer study in goldfish retinal bipolar nerve terminals showed that increase of membrane tension reduces the rate of slow endocytosis with a time course of tens of seconds (16), which is, presumably, mediated by a clathrin-dependent mechanism (2, 3). However, this study showed that increase of membrane tension does not affect fast endocytosis with a time course of a few seconds, leading to the suggestion that membrane tension may inhibit slow, but not fast endocytosis (16). It is unclear whether this conclusion is applicable to other types of nerve terminals and cells. Indeed, a specific feature of goldfish retinal bipolar nerve terminals is that the release occurs at ribbons as triggered by graded depolarization. On the other hand, in most other nerve terminals the release occurs at active zones as triggered by action potentials, whereas in endocrine secretory cells the release occurs with no apparent active zones or ribbons.

The goal of this work was to address the mode by which the plasma membrane tension affects endocytosis in nerve terminals containing active zones and in endocrine secretory cells. We found that membrane tension inhibits both rapid and slow endocytosis in both preparations. We performed computational modeling of the membrane budding process to determine the tension dependence of the energy barrier the system has to overcome by generating an endocytic vesicle. Our results suggest that the rate-limiting step of both rapid and slow endocytosis in neurons and endocrine secretory cells is related to overcoming an energy barrier created by the lateral tension.

Materials and Methods

Animals

Animal care and use were carried out in accordance with National Institutes of Health (NIH) guidelines and was approved by the NIH Animal Care and Use Committee.

Calyx preparation and recordings

Parasagittal brainstem slices (200-μm thick) containing the medial nucleus of the trapezoid body were prepared from 7- to 10-days-old male or female mice using a vibratome. Whole-cell capacitance measurements were made with the EPC-9 amplifier (17, 18). We pharmacologically isolated Ca²⁺ currents with a bath solution (∼22–24°C) containing 105 mM NaCl, 20 mM TEA-Cl, 2.5 mM KCl, 1 mM MgCl₂, 2 mM CaCl₂, 25 mM NaHCO₃, 1.25 mM NaH₂PO₄, 25 mM glucose, 0.4 mM ascorbic acid, 3 mM myo-inositol, 2 mM sodium pyruvate, 0.001 mM tetrodotoxin, and 0.1 mM 3,4-diaminopyridine, pH 7.4 when bubbled with 95% O₂ and 5% CO₂. The presynaptic pipette contained 125 mM Cs-gluconate, 20 mM CsCl, 4 mM MgATP, 10 mM Na₂-phosphocreatine, 0.3 mM GTP, 10 mM HEPES, and 0.05 mM BAPTA, pH 7.2, adjusted with CsOH.

Primary chromaffin cell culture and electrophysiology

We prepared primary chromaffin cell culture as described previously (19, 20, 21). Two-month-old bovine adrenal glands were immersed in a dissociation solution containing 80 mM Na-glutamate, 55 mM NaCl, 6 mM KCl, 1 mM MgCl₂, and 10 mM HEPES, pH 7.0 adjusted with NaOH. Medulla was dissected and digested in the dissociation solution with papain (30 U/mL), BSA (0.5 mg/mL), and DTT (0.1 mM, 37°C, 10 min), and further digested with collagenase F (3 U/mL), BSA (0.5 mg/mL), and CaCl₂ (0.1 mM, 37°C, 10 min). The digested medulla was minced in DMEM medium (Invitrogen, Carlsbad, CA) containing 10% fetal bovine serum and then centrifuged (2000 RPM, 2 min). Final cell pellet was resuspended in prewarmed DMEM medium and plated onto poly-L-lysine (0.005% w/v) and laminin (4 μg/mL)-coated glass coverslips. Cells were incubated at 37°C with 8% CO₂ and used within 4 days.

At room temperature (22–24°C), whole-cell voltage-clamp and capacitance recordings were performed with an EPC-10 amplifier (holding potential: −80 mV; sinusoidal frequency: 1000–1500 Hz; peak-to-peak voltage ≤50 mV). The bath solution contained 125 mM NaCl, 10 mM glucose, 10 mM HEPES, 5 mM CaCl₂, 1 mM MgCl₂, 4.5 mM KCl, 0.001 mM tetrodotoxin, and 20 mM TEA, pH 7.3 adjusted with NaOH. The pipette (3–5 MΩ) solution contained 130 mM Cs-glutamate, 0.5 mM Cs-EGTA, 12 mM NaCl, 30 mM HEPES, 1 mM MgCl₂, 2 mM ATP, and 0.5 mM GTP, pH 7.2 adjusted with CsOH. These solutions pharmacologically isolated calcium currents.

Data collection and analysis

To avoid rundown, calyces were measured within 10 min after break-in (22), and chromaffin cells were measured within 2 min after break-in (first stimulus only). Rate_decay at calyces was measured within 1.5 s after depol_20ms×10 that induced rapid endocytosis, and within 4 s after depol_20ms that induced slow endocytosis. We used depol_20ms×10 to induce rapid endocytosis, because the Rate_decay after depol_20ms×10 reflected mostly (∼85%) the rapid component of endocytosis, as described previously (23). For chromaffin cells, Rate_decay was measured within 0.5–4 s after depolarization or from peak to 4 s later. The statistical test was t-test. Means were presented as mean ± SE.

Results

Rapid endocytosis in control calyx nerve terminal

We determined whether membrane tension affects endocytosis at the mouse calyx of Held nerve terminal, where release at the active zone is induced by action potentials (24). Before determining the effects of membrane tension on endocytosis, we first measured endocytosis under control conditions.

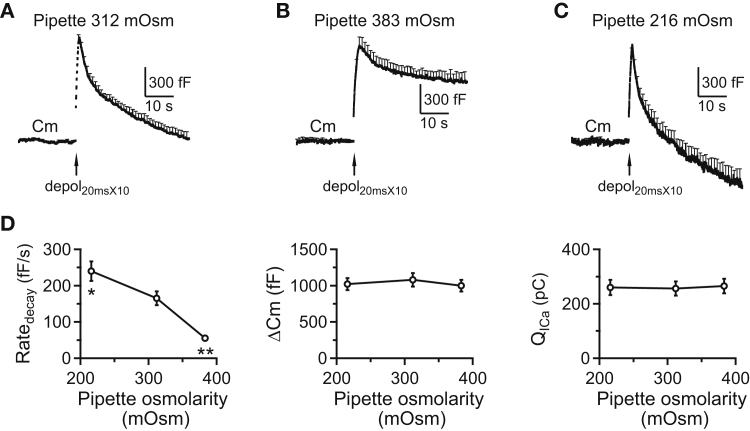
Under control conditions at the whole-cell configuration, we performed voltage-clamp recordings at the calyx of Held in 7–10 days old mice. The osmolarity of the bath solution was 310 mOsm, and the osmolarity of the pipette solution was 312 ± 2 mOsm (n = 6). At the calyx, calcium influx has been found to trigger endocytosis and speed up the endocytosis rate ((23); for detail, see (3)). Accordingly, rapid endocytosis with a time constant of a few seconds can be induced by 10 pulses of 20-ms depolarization from −80 to +10 mV at 10 Hz (depol_20ms×10) via the pipette at the whole-cell configuration, whereas slow endocytosis with a time constant of ∼10–30 s can be reduced by a 20-ms depolarization (−80 to +10 mV, depol_20ms) (8, 17, 23). We studied these two forms of endocytosis, which cover most time courses of endocytosis observed at synapses (3).

Depol_20ms×10 was analogous to a 1 s train of action potentials at 100–300 Hz in inducing exocytosis and rapid endocytosis, but was easier to operate and its resulting calcium currents were more convenient to measure (17, 23, 25). Depol_20ms×10 induced a membrane capacitance jump (ΔC_m) of 1080 ± 84 fF, followed by a biexponential decay with time constants (τ) of 1.9 ± 0.3 s (amplitude: 28 ± 5%) and 28.0 ± 3.4 s (n = 10, Fig. 1 A). The rate of the initial capacitance decay after the capacitance jump (Rate_decay), measured from the trace between 0.5 and 1.5 s after stimulation, was 165 ± 19 fF/s (n = 10, Fig. 1, A and D). We did not measure the first 0.5 s after stimulation, because it may contain capacitance artifacts with a τ of ∼200 ms (23, 25, 26).

Figure 1.

Changing the pipette solution osmolarity changes the rate of rapid endocytosis at calyces. (A) Given here is the averaged capacitance (C_m, mean + SE) induced by depol_20msX10 (arrow) from P7 to 10 mice (10 calyces, 10 mice) with a control whole-cell pipette solution (mean: 312 mOsm). Mean + SE is plotted every 1 s. (B) Shown here is the averaged C_m (mean + SE) induced by depol_20ms×10 (arrow) from calyces (10 calyces, 10 mice) with a whole-cell pipette solution at higher osmolarity (mean: 383 mOsm). (C) Shown here is the averaged C_m (mean + SE) induced by depol_20ms×10 (arrow) from calyces (seven calyces, seven mice) with a whole-cell pipette solution at lower osmolarity (mean: 216 mOsm). (D) Given here is Rate_decay, ΔC_m, and calcium current charge (QI_Ca) induced by depol_20ms×10 in mouse calyces with a mean pipette osmolarity of 312 mOsm (control, 10 calyces for Rate_decay measurements), 383 mOsm (10 calyces for Rate_decay measurements), or 216 mOsm (seven calyces for Rate_decay measurements) in the whole-cell pipette solution. ^∗p < 0.05; ^∗∗p < 0.01 (t-test in comparison with control group).

The Rate_decay reflected mostly the rapid component of endocytosis (23, 25, 27), as confirmed below. Based on the averaged capacitance trace in control (Fig. 1 A), the Rate_decay of the rapid component of endocytosis, which can be theoretically calculated as the ratio between the amplitude and the τ, was 159 fF/s (= 1080 fF ^∗ 0.28/1.9 s), whereas the Rate_decay of the slow component of endocytosis was only ∼27.8 fF/s (= 1080 fF^∗0.72/28 s). Thus, the rapid component represented ∼85% (= 159/(159 + 27.8)) of the overall Rate_decay. In this study, Rate_decay was measured directly from the trace, but not from theoretical calculation, because the block of endocytosis at higher membrane tension, as described later, made it difficult for exponential fitting (8, 23, 27) (see also Figs. 1, 2, and 3). Likewise, we did not use endocytosis τ for statistics.

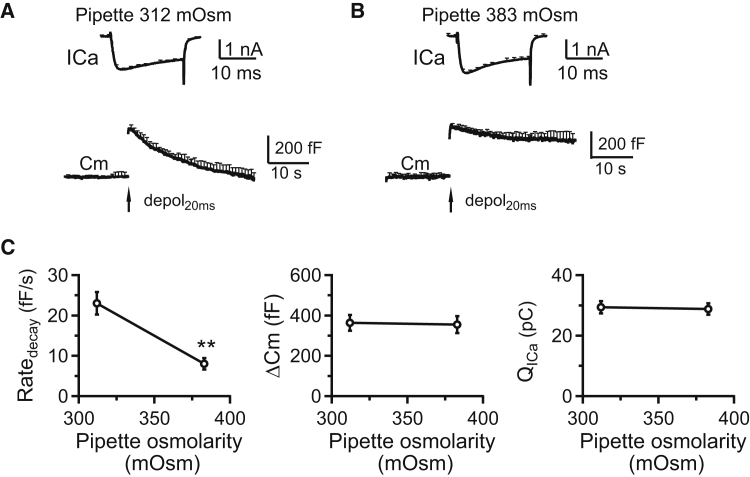
Figure 2.

Increasing the osmolarity of pipette solution inhibits slow endocytosis at calyces. (A) Shown here is the averaged I_Ca and capacitance (C_m, mean + SE) induced by depol_20ms (arrow) from calyces (10 calyces, 10 mice) with a control whole-cell pipette solution (mean: 312 mOsm). Note that I_Ca and C_m are plotted in different timescales. Mean + SE is plotted every 2 ms in the I_Ca trace, but every 1 s in the C_m trace. (B) Given here is the averaged I_Ca and C_m (mean + SE) induced by depol_20ms (arrow) from calyces (10 calyces, 10 mice) with a whole-cell pipette solution at higher osmolarity (mean: 383 mOsm). (C) Given here is Rate_decay, ΔC_m, and QI_Ca induced by depol_20ms in mouse calyces with a mean pipette osmolarity of 312 mOsm (control, 10 calyces for Rate_decay measurements) or 383 mOsm (10 calyces for Rate_decay measurements) in the whole-cell pipette solution. ^∗∗p < 0.01 (t-test in comparison with control group).

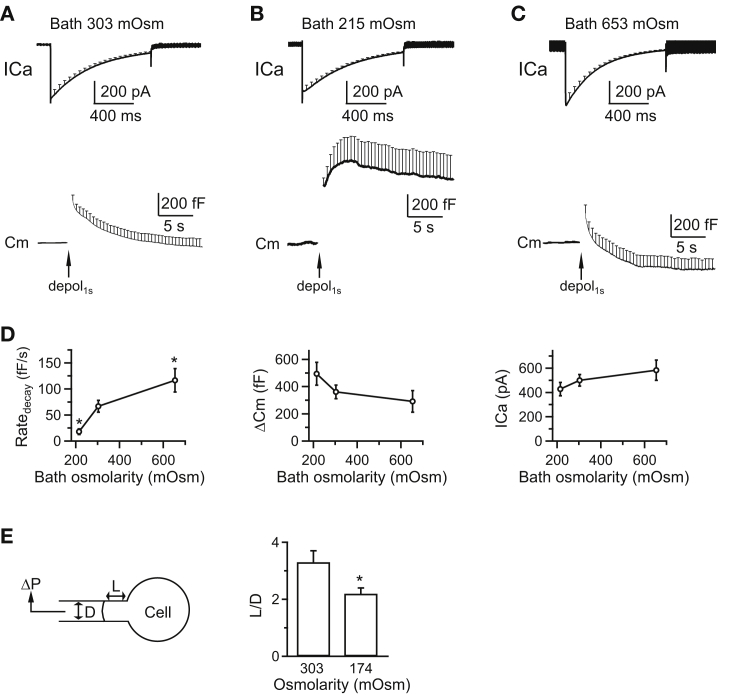
Figure 3.

Varying the bath solution osmolarity changes the rate of rapid endocytosis and the membrane tension at chromaffin cells. (A) Shown here is the averaged I_Ca and capacitance (C_m, mean + SE) induced by depol_1s (arrow) from bovine chromaffin cells (20 cells, three bovines) with a control bath solution (mean: 303 mOsm). Mean + SE is plotted every 50 ms in the I_Ca trace, but every 0.5 s in the C_m trace. (B) Shown here is the averaged I_Ca and C_m (mean + SE) induced by depol_1s (arrow) from chromaffin cells (nine cells, three bovines) with a bath solution at lower osmolarity (mean: 215 mOsm). (C) Given here is the averaged I_Ca and C_m (mean + SE) induced by depol_1s (arrow) from chromaffin cells (14 cells, three bovines) with a bath solution at higher osmolarity (mean: 653 mOsm). (D) Shown here is the Rate_decay, ΔC_m, and calcium current charge (QI_Ca) induced by depol_1s in bovine chromaffin cells with a mean bath osmolarity of 303 mOsm (control, 20 cells for Rate_decay measurements), 215 mOsm (nine cells for Rate_decay measurements), or 653 mOsm (14 cells for Rate_decay measurements). ^∗p < 0.05 (t-test in comparison with control group). (E) Decreasing the bath solution osmolarity increased membrane tension. (Left) Given here are drawings of micropipette aspiration technique. A negative pressure (ΔP) on the pipette (with a diameter D) draws the cell membrane into the pipette by a length L. (Right) Given here is a normalized projection length (L/D, mean + SE) for aspirated cells in a bath solution with a mean osmolarity of 303 mOsm (control, n = 10 cells for L/D measurements) or 174 mOsm (n = 9 cells for L/D measurements; ^∗p < 0.05; unpaired two-tailed student’s t-test). ΔP = 1500 Pa.

Osmolarity changes regulate rapid endocytosis at the calyx

To determine how membrane tension affects endocytosis, we changed the membrane tension using a commonly used method, the change of the osmolarity either inside or outside the cell (7, 28, 29). Here, we increased membrane tension by adding ∼70 mM Cs-gluconate in the pipette solution, which increased the osmolarity of the pipette solution from 312 ± 2 mOsm in control to 383 ± 2 mOsm (n = 6). With an increased osmolarity in the pipette solution, both rapid and slow components of endocytosis induced by depol_20ms×10 were largely blocked. The Rate_decay decreased from 165 ± 19 fF/s (n = 10) in control to 55 ± 7 fF/s (n = 10, p < 0.01, t-test, Fig. 1, B and D), whereas the ΔC_m and the calcium current charge induced by depol_20ms×10 were not different from the control (Fig. 1 D).

In contrast, reducing the pipette solution osmolarity to 216 ± 1 mOsm (n = 6) by reducing Cs-gluconate in the pipette significantly increased the Rate_decay after depol_20ms×10 (Fig. 1 C), but did not affect ΔC_m or calcium current charge (Fig. 1 D). We also observed endocytosis overshoot, that is, the capacitance trace returned to a value below the baseline (Fig. 1 C), which did not occur in control conditions (Fig. 1 A). Taken together, increasing osmolarity inside the cell, which should increase membrane tension, inhibited rapid endocytosis, whereas decreasing osmolarity inside the cell, which should decrease membrane tension, facilitated rapid endocytosis and promoted endocytosis overshoot.

Increasing intracellular osmolarity inhibits slow endocytosis at the calyx

We induced slow endocytosis by a depol_20ms (8, 17, 23). In control, depol_20ms induced a ΔC_m of 364 ± 39 fF, followed by a decay with a τ of 19 ± 1.5 s and a Rate_decay of 23 ± 2.8 fF/s (n = 10, Fig. 2, A and C), as measured within the first 4 s after stimulation. Increasing the osmolarity to 383 ± 2 mOsm (n = 6) in the pipette solution blocked endocytosis, reduced Rate_decay, but did not affect ΔC_m or calcium current charge (Fig. 2, B and C), suggesting that increased membrane tension inhibits slow endocytosis.

Changes in the extracellular osmolarity regulate endocytosis in chromaffin cells

In control with a bath solution osmolarity of 303 ± 2 mOsm (n = 6), a 1 s depolarization (depol_1s, from 80 to +10 mV, if not mentioned otherwise) in the whole-cell configuration induced a calcium current (I_Ca) of 499 ± 47 pA (mean ± SE, n = 20 cells) and a ΔC_m of 361 ± 50 fF in primary cultured bovine adrenal chromaffin cells (Fig. 3, A and D). The capacitance jump induced by depol_1s decayed to about the baseline level in ∼10–30 s (Fig. 3 A). The initial rate of decay (Rate_decay), measured between 0.5 and 4 s after depol_1s, was 66 ± 11 fF/s (n = 20 cells, Fig. 3, A and D), which reflects the initial rate of endocytosis (20, 23, 25, 30).

To determine how membrane tension affects endocytosis, we changed the membrane tension by changing the osmolarity of the bath solution (7, 28, 29). By decreasing the extracellular NaCl concentration from 125 mM in control to 75 mM, we decreased the bath solution osmolarity from 303 ± 2 mOsm in control to 215 ± 1 mOsm (n = 6). This manipulation increased membrane tension by swelling the cells as we recently imaged (29). The decrease of the osmolarity significantly reduced the capacitance decay and reduced Rate_decay (18 ± 5 fF/s, n = 9 cells, measured from peak to 4 s later), but did not affect I_Ca (427 ± 54 pA) or ΔC_m (494 ± 83 fF) induced by depol_1s (Fig. 3, B and D). In contrast, increasing the bath osmolarity to 653 ± 6 mOsm (n = 6) by adding 295 mM sucrose into the bath led to significant shrinking of chromaffin cells, as we showed recently (29), which increased Rate_decay significantly (116 ± 2 fF/s, n = 14 cells, measured within 0.5–4 s after depolarization), but did not affect I_Ca (582 ± 83 pA) or ΔC_m (291 ± 79 fF) induced by depol_1s (Fig. 3, C and D). The bath osmolarity increase also promoted an endocytosis overshoot after depol_1s (Fig. 3 C).

By adding sucrose to the bath to increase the bath solution osmolarity, we observed an increased Rate_decay and the appearance of an endocytosis overshoot in chromaffin cells (Fig. 3 C). Similar increases of the Rate_decay and endocytosis overshoot were observed in calyces where the pipette solution osmolarity was decreased via a reduction of Cs-gluconate (Fig. 1 C). These results suggest that the observed endocytosis changes are due to the osmolarity changes, but not the ion concentration changes. Our experiments relied on changing the osmolarity to change the membrane tension (7, 28, 29). To confirm this method, we estimated the membrane tension, the force needed to pull the surface by certain length (force per unit length), using the micropipette aspiration technique in chromaffin cells. A negative pressure applied to a micropipette in contact with the plasma membrane drew the plasma membrane into the pipette to a length L ((31), and see (29) for detail). The normalized length, calculated as L divided by the pipette diameter D (L/D), is inversely correlated with Young’s module, a membrane elasticity measurement that is correlated with Tension_pm (31). With a negative pressure of 1500 Pa, the L/D value was 3.3 ± 0.4 (n = 10 chromaffin cells) in the control bath solution with an osmolarity of 303 ± 2 mOsm (n = 6), but decreased significantly to 2.2 ± 0.2 (n = 9 chromaffin cells, p < 0.05, t-test; Fig. 3 E) in a bath solution with an osmolarity of 174 ± 1 mOsm (n = 6). Similarly, we observed significant differences with a negative pressure of 2000 Pa (data not shown). These results suggest that decreasing the bath solution osmolarity increased membrane tension, further supporting the method of using the osmolarity change to manipulate membrane tension (7, 28, 29).

We used a bath solution with an osmolarity of 174 ± 1 mOsm for the measurement of the L/D value (Fig. 3 E), but 215 ± 1 mOsm for the measurement of endocytosis (Fig. 3, A–D). This was because the L/D value varied in our hands and was less sensitive to smaller changes. However, we did also observe a similar block of endocytosis at 174 ± 1 mOsm (data not shown).

Taken together, in bovine chromaffin cells, increasing membrane tension by decreasing bath osmolarity blocked endocytosis, whereas decreasing membrane tension by increasing bath osmolarity facilitates endocytosis and endocytosis overshoot.

Membrane tension creates an energy barrier for endocytic vesicle formation

Model

In this section we present a computational model of plasma membrane budding upon polymerization on the membrane surface of a spherical protein coat taking the clathrin coat with associated proteins (1) as a prototype. The aim of the model is to estimate, quantitatively, the energy barrier the system has to overcome on the way to the endocytic vesicle formation and to evaluate the dependence of this barrier on the membrane tension.

We consider an element of the plasma membrane subject to the protein coat polymerization, and refer to it as the “budding” site. In its initial state preceding the coat formation, this membrane element has a flat shape of area A₀. The budding site can freely exchange its area with the surrounding plasma membrane through membrane flow. The surrounding membrane plays a role of a membrane reservoir for the budding site. The membrane reservoir is characterized by a constant lateral tension, γ₀, the energy needed to pull a unit area of the membrane out of the reservoir. The process of budding requires energy input related to generation of the curvature of the bud membrane and to pulling additional membrane area from the reservoir to the budding site.

To compute the bending energy cost, we use a Helfrich model of membrane bending (32), according to which the bending energy related to the membrane unit area, f_B, depends on the local mean, J, and Gaussian, K, curvatures of the membrane surface (33). The bending energy scale is determined by three elastic parameters of the membrane: the membrane bending modulus, κ_B; modulus of Gaussian curvature, $\overline{\kappa }$; and the spontaneous curvature, J_s (32). Here we assume the membrane to be symmetric and have, therefore, a vanishing spontaneous curvature, J_s = 0, and we consider only the budding step, which does not include any changes of the membrane connectivity so that the energy of the Gaussian curvature does not change according to the Gauss-Bonnet theorem (32). Under these assumptions, the bending energy per unit area is given by

$$f_B=\frac{1}{2}\cdot {\kappa }_B\cdot J^2,$$

whereas the total bending energy, F_B, is given by integration of f_B over the area of the budding site,

$$F_B=\frac{1}{2}\cdot {\kappa }_B\cdot \oint J^{2}dA.$$ (1)

The energy cost related to the area change of the budding site, F_A, is given by

$$F_A={\gamma }_0\left(A-A_0\right).$$ (2)

The energy necessary for the membrane budding, F_M = F_B + F_A, is provided by polymerization of the protein coat on the membrane surface. Two possible scenarios have been suggested in the literature for the clathrin coat assembly: the constant area regime, where the coat first polymerizes up to a certain area and then acquires its curvature (34); and the constant curvature mode, where the elements of the coat are, ab initio, intrinsically bent so that the polymerizing coat is curved at all stages of polymerization (35). According to our analysis, the two coat models give similar predictions concerning the energy of the budding process (data not shown). Here we present the results for the constant curvature model (35). We assume the protein coat to be much more rigid than the membrane so that the coat does not undergo any deformation upon the forces applied to it by the membrane underneath and retains its intrinsic curvature, J_p, throughout the whole assembly process. The energy released by the polymerizing coat will be taken as

$$F_C=-\mathit{ϵ}\cdot A_p,$$ (3)

where A_p is the coat area, ϵ is the coat polymerization energy per unit area, and the minus sign accounts for the energy release.

Computational results

We computed the total energy of the system, F_tot, which includes the bending, F_B (Eq. 1), and area, F_A (Eq. 2), energies of the membrane, and the coat polymerization energy F_C (Eq. 3),

$$F_{\text{tot}}=F_B+F_A+F_C,$$ (4)

for different degrees of the coat assembly. This is characterized by the ratio between the coat area and the area of a complete sphere of the same radius, A_p/4π R_p², where R_p = 2/J_p (Fig. 4 A). The membrane element directly underneath the coat is required to adopt the spherical shape of the coat with the radius R_p, whereas the rest of the membrane of the budding site adopts the equilibrium shape of the minimal elastic energy, FM = FB + FA. For each value of the ratio A_p/4π R_p², the energy minimization and determination of the equilibrium shape were performed numerically using the Brakke’s “Surface Evolver” program. The results are presented in Fig. 4, B and C. Fig. 4 B illustrates the change of the system energy with increasing degree of polymerization, A_p/4π R_p², for different values of the coat polymerization energy per unit area, ϵ.

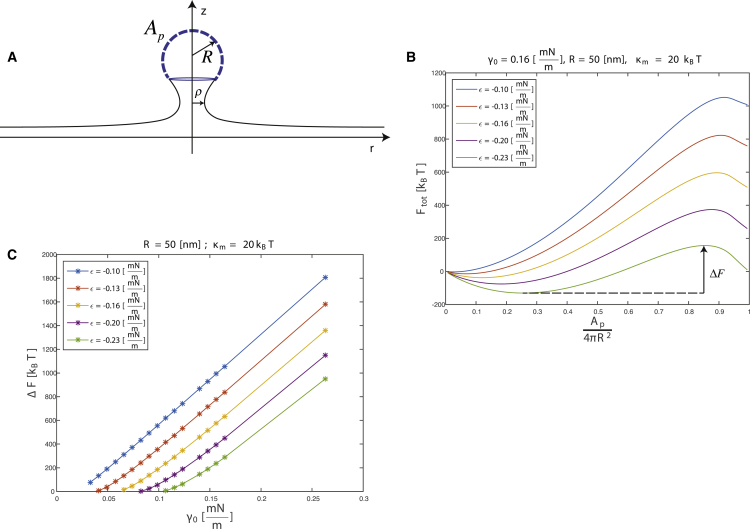
Figure 4.

Computational model for the effect of tension on the energy of membrane budding by a protein coat. (A) Given here is a model illustration and definitions. Coat area, A_p; coat radius of curvature, R (same as R_p in the main text); radius of the membrane neck, ρ. (B) Given here is the energy of the budding membrane, F_tot, as a function of the extent of the protein coat assembly, A_p/4π R_p², for different values of the coat polymerization energy, ϵ. The value of the lateral tension is taken to be γ₀ = 0.16 mN/m, the curvature radius of the protein coat R = 50 nm. ΔF is the energy barrier. (C) Shown here is the energy barrier of budding, ΔF, as a function of membrane tension, γ₀, for different values of the coat polymerization energy, ϵ.

In accordance with previous works analyzing similar systems by different computational approaches (36, 37), in the experimentally relevant range of membrane tensions close to 0.1 mN/m, the system energy exhibits a minimum corresponding to an equilibrium configuration and a maximum at the values of the ratio A_p/4π R_p² close to 1, which corresponds to advanced stages of the coat polymerization (Fig. 4 B). For the values of A_p/4π R_p² beyond the energy maximum, the energy decreases, which means that closure of the coat and the related tightening of the membrane neck completing the budding process must proceed spontaneously. Fission of the narrowing membrane neck would lead to the vesicle formation. Complete budding necessary for formation of a narrow membrane neck, whose fission would lead to the vesicle formation, requires overcoming by the system of the state with the maximal energy. To this end, the system has to cross the energy barrier, ΔF, equal to the energy differences between the states of the maximal and minimal energies. This event needs, obviously, an additional energy source such as a dynamin ring or short spiral constricting around the forming neck (34). However, whatever is the specific protein machinery helping the membrane to complete the bud assembly and undergo fission, it needs to take the system over the computed energy barrier, ΔF. Fig. 4 C presents the value of ΔF as a function of the membrane tension for different values of the coat polymerization energy. The barrier vanishes for zero tensions but strongly increases with growing tension. Moreover, for a given tension, the energy barrier decreases with increasing absolute value of the coat polymerization energy per unit area, ϵ.

This result (Fig. 4 B and C) suggests that membrane tension may slow down membrane budding and, hence, membrane fission. The role of proteins driving membrane fission, such as dynamin, may be to overcome the inhibitory effect of tension.

Discussion

In this work, we varied plasma membrane tension by changing either the intracellular or extracellular solution osmolarity in mouse calyx of Held nerve terminals and bovine chromaffin cells. We found that increasing membrane tension inhibits both rapid and slow endocytosis, whereas decreasing membrane tension facilitates endocytosis and endocytosis overshoot. Our simulation showed that endocytic pit generation needs to overcome energy barrier generated by membrane tension, which provides a theoretical framework explaining how the membrane tension regulates endocytosis in secretory cells.

This work is a significant extension over an early pioneering work regarding the effects of membrane tension on endocytosis at synapses (16). The early work found that increasing membrane tension inhibits slow endocytosis, but does not affect a rapid form of endocytosis at the goldfish retinal bipolar synapse, a ribbon-type synapse where release is triggered by graded potentials (16). This work showed that increasing membrane tension inhibits not only slow endocytosis, but also rapid endocytosis with a time constant of a few seconds in two different secretory cells: 1) calyx-type nerve terminals where release occurs at active zones as in the majority of synapses in the nervous system; and 2) chromaffin cells, the endocrine cells containing no apparent active zones. Furthermore, we found that decreasing membrane tension facilitates rapid endocytosis and promotes endocytosis overshoot in both calyces and chromaffin cells. We also provided a theoretical framework for understanding the mechanism by which membrane tension regulates endocytosis.

The lack of blocking rapid endocytosis by increasing membrane tension at retinal bipolar synapses (16) might be due to insufficient increase of membrane tension. Consistent with this possibility, we observed a partial, but not a complete block of rapid endocytosis when the intracellular pipette solution osmolarity was increased to ∼383 mOsm (Fig. 1, A and B).

The results of this work are different from those of in vitro liposome fission assays, which suggest that membrane tension is needed to facilitate fission (11, 12, 13, 14). This apparent discrepancy might be due to differences in preparations and methods. We used live cells, whereas liposome fission assay used artificial membrane tubes. Our assay did not distinguish between pit formation and membrane fission, whereas liposome fission assay measured only the fission reaction. It remains possible that membrane tension facilitates fission, but prevents pit formation in live cells, which may reconcile the apparent discrepancy between this work and the fission assay. However, our model computation suggests that fission machinery would need to counteract the resistance of membrane tension to mediate fission. It is also possible that the major role of the fission machinery, such as a dynamin ring, is to overcome the energy barrier produced by the tension by constricting the membrane neck beyond the radius corresponding to the maximal energy (Fig. 4 C).

Our finding that membrane tension regulates rapid and slow endocytosis raises the possibility that this mechanism may be employed in various physiological and pathological conditions to regulate endocytosis and many biological processes downstream of endocytosis. Examples of the processes regulated by endocytosis include exocytosis, which is maintained via endocytosis-mediated vesicle recycling; vesicle mobilization to the readily releasable pool, which may be facilitated by an endocytic process that clears the active zone (23, 38, 39); and the maintenance of a constant membrane area in secretory cells, which depends on the balance between exo- and endocytosis (3). Atomic force microscopy reveals that an action potential generates a transient volume increase in nerve terminals of the mouse neurohypophysis (40), which may transiently change membrane tension and thus regulate endocytosis. Increase of the cell spreading area enhances the short-lived clathrin-coated pits possibly by increasing the membrane tension (41). Dehydration may regulate endocytosis and exocytosis by regulating cell volume and membrane tension. The often-reported endocytosis overshoot (23, 42, 43, 44, 45), which is facilitated by a reduced membrane tension (Figs. 1 and 3), may be a physiological mechanism to control the membrane area of nerve terminals and endocrine cells, which in turn may regulate membrane tension and thus provide a feedback loop for the regulation of membrane tension. Testing these possibilities would be of great interest in the future.

Author Contributions

X.-S.W. performed and analyzed calyx experiments. S.E. performed model computation. H.L. performed and analyzed chromaffin-cell experiments. J.H., P.J.W., and A.P.L. performed pipette aspiration experiments. M.M.K. and L.-G.W. designed and wrote the article.

Editor: Edward Stuenkel.