Low-Resolution Structure of Detergent-Solubilized Membrane Proteins from Small-Angle Scattering Data

Abstract

Despite the ever-increasing usage of small-angle scattering as a valuable complementary method in the field of structural biology, applications concerning membrane proteins remain elusive mainly due to experimental challenges and the relative lack of theoretical tools for the treatment of scattering data. This fact adds up to general difficulties encountered also by other established methods (crystallography, NMR) for the study of membrane proteins. Following the general paradigm of ab initio methods for low-resolution restoration of soluble protein structure from small-angle scattering data, we construct a general multiphase model with a set of physical constraints, which, together with an appropriate minimization procedure, gives direct structural information concerning the different components (protein, detergent molecules) of detergent-solubilized membrane protein complexes. Assessment of the method’s precision and robustness is evaluated by performing shape restorations from simulated data of a tetrameric α-helical membrane channel (Aquaporin-0) solubilized by n-Dodecyl β-D-Maltoside and from previously published small-angle neutron scattering experimental data of the filamentous hemagglutinin adhesin β-barrel protein transporter solubilized by n-Octyl β-D-glucopyranoside. It is shown that the acquisition of small-angle neutron scattering data at two different solvent contrasts, together with an estimation of detergent aggregation number around the protein, permits the reliable reconstruction of the shape of membrane proteins without the need for any prior structural information.

Introduction

Membrane proteins perform their biological role that includes signaling, molecular transport, cell-cell recognition, and energy production, by being partially embedded in the cellular membrane. Even though knowledge of their structure is of paramount importance for better understanding a multitude of biological processes, they are heavily underrepresented in the Protein Data Bank (PDB) in comparison to soluble globular proteins, with <700 unique membrane structures resolved (http://blanco.biomol.uci.edu/mpstruc/). The severe difficulties in their study by high resolution structural techniques such as crystallography and NMR is, on the one hand, related to the laborious biochemical expression and purification steps needed for the preparation of appropriate samples, and on the other hand, to the need of special strategies for their extraction and solubilization.

In the endeavor to keep membrane proteins folded and active outside their natural membrane environment, different approaches have been developed including the use of detergent micelles (1), amphipols (2), nanodics (3, 4), and bicelles (5). In all cases these molecular assemblies attempt to shield the hydrophobic transmembrane surface of the protein, which would otherwise lead to the aggregation and denaturation of the proteins in a solution. The use of detergents (small amphiphilic molecules) above their critical micelle concentration represents the easiest and more widespread method, having the relative drawback of its tendency to destabilize certain proteins, something that can be partially remedied by the development of new milder detergents or by using mixed lipid/detergent micelles (bicelles) that provide a more native environment to the proteins. In turn, short amphiphilic polymers named “amphipols”, despite their strong stabilizing properties, tend to be much larger than the protein that they encompass. This disadvantage, together with difficulties in sample preparation and protein reconstitution complexity, is shared by the nanodisc system. Nanodiscs are noncovalent assemblies of a phospholipid bilayer that is surrounded by a genetically engineered lipoprotein dimer and probably represent the best mimic of the membrane environment that can, at the same time, solubilize membrane proteins.

Success in keeping membrane proteins stable and active in solution gives the ability to implement various experimental techniques for the study of membrane protein structure as NMR (6), circular dichroism (7), and small-angle scattering (SAS) (8), whereas for flash-frozen proteins, cryo-electron microscopy represents a quite promising technique with many recent breakthroughs (9). However, in all cases, special attention should be paid for the usually nontrivial subtraction of the contribution of detergents, amphipols, etc., which coexist with the protein in solution. This is especially true in the case of small-angle neutron (SANS) and x-ray (SAXS) scattering, which offer the ability to acquire direct information concerning the low-resolution (>1 nm) structure of biological molecules (10, 11) for a wide range of solution conditions and molecular sizes.

In a small-angle scattering experiment of detergent-solubilized membrane proteins, the measurable signal may contain contributions from both free detergent micelles and the protein detergent complex (PDC) (12). Even when the scattering intensity belonging only to the PDC can be extracted, calculations regarding scattering invariants or application of structure recovery tools (13, 14) that have been developed for soluble proteins do not apply in a direct manner, thus hindering the widespread use of the technique for this class of systems. From the experimental point of view, isolation of the scattering curve corresponding only to the PDC involves the careful subtraction of buffer solution having the same free-micelle concentration as the PDC solution. This can be accomplished either by collecting reference buffer that is eluted before the PDC during a size exclusion chromatography (SEC) step right before the scattering experiment (15), or by performing extensive dialysis of the PDC solution against detergent containing buffer (16). Another proposed method based on singular value decomposition involves the acquisition of scattering data for many different protein-detergent stoichiometries (17). Alternatively, the use of on-line SEC-SAXS has proven as a very efficient way for the proper subtraction of micelle contributions (18, 19).

The determination of the scattering curve corresponding to the PDC provides information about the overall size and shape of the system. In previous SAXS and SANS investigations where a high-resolution structure of the protein molecule or a candidate model was available, modeling and molecular simulations (18, 20, 21, 22) provided a better understanding of detergent organization around the protein molecule. The ability to model adequately the detergent belt around a known protein structure (23) opens the road for experimental investigations, where conformational transitions or interaction of membrane proteins with other molecules need to be resolved (24, 25).

A more ambitious approach to the whole problem aims to exploit the big advantage of the SANS technique, i.e., contrast variation, to remove contributions to the scattering from detergent molecules (26, 27, 28, 29, 30). In principle, using appropriate D₂O/H₂O ratios as solvent and the full or partial deuteration of detergent molecules, one may obtain the same scattering length density (sld) for the solvent and the detergents, thus rendering the detergent belt around the protein and free micelles invisible to neutrons (31). However, due to the chemically heterogeneous nature of the hydrophilic and hydrophobic part of detergents, the elimination of their scattering contribution over the entire q-range is difficult to achieve, and has been demonstrated only for special cases of detergent molecules (32). Such combinations of detergent and solvent with homogeneous matching, provided that they are able to solubilize the protein under study, permit easy sample preparation and the acquisition of scattering curves that correspond only to the protein. This same approach has been shown to be feasible also for the nanodisc system (33).

Because the requirement for simultaneous membrane protein solubilization and detergent contrast matching in a SANS experiment is quite strict and is expected to apply in limited cases, it would be interesting to explore different approaches for the determination of membrane protein structure from small-angle scattering data. Recently, Kynde et al. (34) developed a sophisticated hybrid ab initio approach with the aim to recover the low-resolution structure of a protein embedded in a nanodisc system from a combination of SANS and SAXS data. It was reported that for the case of bacteriorhodopsin embedded in a nanodisc, the amount of experimental information was not enough for this approach to be successful. The same method was shown to give better results for human cytochrome P450 anchored in a nanodisc environment (35).

The goal of this work is to explore the potential of an ab initio strategy for the general case of detergent-solubilized membrane proteins. In this context, we develop a multiphase coarse-grained bead model with a set of appropriate constraints and a minimization algorithm where, with no prior knowledge of the shape of the protein, we attempt to recover the low-resolution structure of the entire PDC. The required input to the algorithm consists of a set of scattering curves, the molecular characteristics of the detergent, and its aggregation number around the protein, which can be independently estimated by other experimental techniques (e.g., analytical ultracentrifugation or refractometry). We explicitly show that a single scattering curve contains insufficient amount of information for obtaining a unique and physically meaningful solution. On the contrary, for a set of at least two SANS curves at different solvent contrasts, the concurrent fit of the data leads to stable solutions where the obtained molecular envelopes are representative of the structure of each PDC component. The efficiency of the presented methodology is evaluated using two different sets of data: 1) scattering curves of a tetrameric α-helical membrane channel (Aquaporin-0) solubilized by n-Dodecyl β-D-Maltoside (dDM), calculated from all-atom molecular dynamics trajectories of the system; and 2) SANS experimental curves of the filamentous hemagglutinin adhesin (Fhac) β-barrel protein transporter solubilized by n-Octyl β-D-glucopyranoside (OG_D), taken from the work of Gabel et al. (22).

Methods

Model and minimization procedure

Following the methodology that was initially proposed by Chacón et al. (13), further improved and popularized by Svergun and co-worker (14, 36) for the low-resolution restoration of biomolecule shape from small-angle scattering data, and also based on previous work (20, 23, 37, 38), we have developed an algorithm where a set of different types of beads participate in a simulated annealing procedure that aims to arrange the beads in a way that is compatible with the experimentally measured scattering curves and also with the general anticipated organization of detergent molecules around a membrane protein.

Small-angle scattering curves of membrane protein/detergent complexes contain three different contrast contributions from the protein, detergent heads, and tails. In this respect, the constructed model consists of three types of beads (dummy atoms) corresponding to the membrane protein, detergent hydrocarbon tails, and detergent hydrophilic heads, with different contrasts δρ_M, δρ_T, and δρ_H relative to the solvent. These beads of packing radius r are placed on a close-packed face-centered cubic (fcc) lattice, having a maximum of 12 nearest neighbors. The fcc lattice constant L is equal to $4r/\sqrt{2}$. The search space available for the placement of beads is not bounded.

The scattering curve I(q) versus q (scattered intensity versus wavevector transfer) of each bead configuration at each solvent contrast is calculated using the Debye equation (39):

$$I\left(q\right)=\sum _{i=1}^N\sum _{j=1}^N{f}_i\left(q\right)f_j\left(q\right)\frac{\sin q{r}_{ij}}{q{r}_{ij}},$$ (1)

where N is the total number of beads, f_i(q) is the form factor of each bead given by V_iδρ_i with V_i = L³/4 being the effective bead volume, and r_ij is the distance between the ith and jth bead.

The target of the simulated annealing procedure is to obtain a compact configuration that reproduces the (M) experimentally measured scattering curves for a given number of detergent molecules (N_det) around the protein. The algorithm proceeds by selecting random positions of the fcc lattice and by performing trial additions, removals, and changes of the type of beads in an effort to obtain an overall bead configuration (X) that minimizes the score function:

$$f\left(X\right)=\sum _{l=1}^M{R}_l{\left(I_{\text{exp,l}},X\right)}^2+\sum _{k=1}^4{\alpha }_k{P}_k\left(X\right).$$ (2)

The main contribution in f(X) comes from the sum for each different contrast (l) of the q²-weighted discrepancies R(I_l,X)² between the scaled intensity I_l(X) (scaling factor is calculated according to Eq. 16 in (40)) corresponding to the configuration X and the experimental scattering intensity I_exp,J, given by

$$R_l{\left(I_l,X\right)}^2=\frac{{\sum }_q{\left[I_l\left(X,q\right)q^2-I_{\text{exp},l}\left(q\right)q^2\right]}^2}{{\sum }_q{\left[I_{\text{exp},l}\left(q\right)q^2\right]}^2}.$$ (3)

Because small-angle scattering curves are decaying rapidly as a function of q, the choice of q²-weighting ensures that experimental points at intermediate-q (where most of the shape information is contained) will contribute substantially to the score function (41). Note that especially in the case of SANS curves where resolution effects have to be considered, I_exp,J represents the desmeared curve calculated according to the iterative method proposed by Lake (42), taking into account the beam divergence Δθ and wavelength spread Δλ/λ.

Additional terms in the score function are related to various penalty weights α_k and penalties P_k having to do with protein’s compactness P₁, detergent belt compactness P₂, detergent aggregation number P₃, and overall radius of gyration (R_g,i) penalty P₄. Penalties P₁ and P₂ are calculated as described by Svergun (14) for the ensemble of protein and tail beads, respectively. Penalty P₃(X) ensures that the number of head and tail beads corresponds to the given detergent aggregation number N_det, and is defined as

$$P_3\left(X\right)=\frac{{\left(N_{\text{det}}-N_t{L}^3/4V_t\right)}^2}{N_{\text{det}}^2}+\frac{{\left(N_{\text{det}}-N_h{L}^3/4V_h\right)}^2}{N_{\text{det}}^2},$$ (4)

where N_h and N_t represent the number of head and tail beads in the configuration X, and V_h,V_t is the known molecular volume of detergent heads and tails, respectively.

Penalty P₄(X) is given by

$$P_4\left(X\right)=\sum _{l=1}^M\frac{{\left(R_{g,l}-R_{gIFT,l}\right)}^2}{R_{gIFT,l}^2},$$ (5)

where R_g,l is the radius of gyration of the configuration X for the contrast l, and R_gIFT,l is the corresponding radius of gyration that is estimated from the indirect Fourier transform of the experimental curve (see also next subsection). Because the search space is not bounded, this penalty prohibits large deviations of the size of the complex from the expected values, especially in the beginning of the minimization procedure.

To guide the algorithm toward physically meaningful arrangements, it is essential to impose an additional set of constraints related to the anticipated general properties of detergent organization around the hydrophobic transmembrane surface of the proteins. These are as follows: 1) prohibition of any hydrophobic bead contacts with empty lattice positions that represent the solvent; 2) hydrophobic detergent tail beads must be separated from the solvent by a single layer of hydrophilic head beads; 3) thickness of the hydrophobic tail bead core along the z axis is bounded and cannot exceed the limit 2L_hb-max; 4) tail beads should always stay connected and also encircle the z axis; and 5) protein beads cannot be disconnected.

The first two constraints reflect the requirement that hydrophobic tails should avoid contact with water. The third and fourth constraint is implemented to promote doughnut-like detergent belt structures around the protein transmembrane hydrophobic surface. Note that the z axis is assumed to coincide with the approximate axis of the protein’s transmembrane part. Bounding the thickness of the detergent structure (along the z axis) is related to the properties of both detergent and proteins. For compact lipid packings, we expect that there is a maximum detergent hydrocarbon tail extension (L_hb-max) given by the Tanford formula (43) L_hb-max = 1.5 + 1.265 n_c Å, where n_c is the number of carbons of the detergent tail. However, for more disordered detergent arrangements, a more relaxed limit can be used by arguing that the maximum thickness of the tail structure (2L_hb-max) should be roughly equal to the typical hydrocarbon core thickness of cell membranes (≈40 Å) where the transmembrane part of proteins is embedded and performs its function. Finally, the last constraint is simply implemented for keeping the protein beads interconnected, as it is expected for a protein molecule.

From the definition of the model, it can be seen that the thickness of the hydrophilic detergent head layer depends on the selected size of the beads, and is equal to two times the packing radius, 2r. However, the real thickness of this layer t, as can be determined by fitting small-angle scattering data of detergent micelles in solution (44), might be different than 2r. Because the contribution of this thin layer to the scattering depends primarily on the product of layer thickness and layer contrast (45), the effective contrast of the head beads ρ_H^′ is adjusted so that 2rδρ_H^′ = tδρ_H. Additionally, a modified molecular volume V_h^′ is used in the second term of Eq. 4, following the relation V_h^′ = (2r/t)V_h.

A spherical configuration of tail beads, covered with a single layer of head beads, together with an embedded string of protein beads, along the z axis, is constructed. This configuration respects all the constraints described above and serves as the initial state for the minimization of the score function f(X). The simulated annealing minimization involves the definition of an effective annealing temperature T and proceeds as proposed in (14, 36). We begin at a high temperature where the majority of trials is accepted. Then random trials producing modified bead configurations X′ (that always respect the defined constraints) are attempted and accepted if the score function is reduced or if f(X′) > f(X) with a probability e^{[f(X) – f(X′)]/T}. For the results presented in this work, an annealing schedule of T′ = 0.90T was used, and 100N trials at each temperature are attempted. Note that because only one bead is modified in each trial, the recalculation of only N cross terms of Eq. 1 are needed, thus avoiding the computationally intensive recalculation of the whole double sum (37). The annealing procedure is stopped when no further reduction of the score function is observed. The following values of the penalty weights were used: a₁ = 0.1, a₂ = 0.1, a₃ = 1, and a₄ = 1, which are expected to provide in the general case a balance between compactness and flexibility in the obtained PDC shapes. The used bead packing radius during the runs was in the range 2.5–3.0 Å. In all reconstructions, scattering data up to q = 0.2 Å⁻¹ are considered, because in this q-range the scattering contribution from the shape of the PDC dominates (14). For smaller protein molecules where a higher q-range needs to be considered and internal inhomogeneities from each phase might contribute to the scattered intensity, an appropriate constant has to be subtracted from the scattering data, so that shape scattering curves are used with a q⁻⁴ behavior at high q.

Scattering data and initial treatment

Two different sets of scattering data were considered for validating the efficiency and robustness of the presented algorithm. The first set concerns theoretically calculated SAXS and SANS curves from all-atom molecular dynamics (MD) trajectories of n-Dodecyl β-D-Maltoside/Aquaporin-0 (dDM/AQ0) complexes, whereas the second set consists of experimental SANS curves of OG_D-solubilized Fhac protein transporter in 90% D₂O and 42% D₂O, taken from the elegant work of Gabel et al. (22).

The AQ0 dataset was calculated as follows. In previous computational works (19, 20), it was shown that all-atom MD simulations of dDM/AQ0 complexes can reliably reproduce the SEC-SAXS experimental data (18) of this system. Following the exact same methodology as in Koutsioubas et al. (20) and by placing 270 dDM molecules around the backbone-restrained structure of AQ0 (PDB: 2B6P (46)), we have sampled, after the proper equilibration of the system, the MD trajectory over a time frame of 5 ns. Using the programs CRYSOL v.2.8.2 (40) and CRYSON v.2.7 (45) (applying default parameters including a 3 Å, 20% contrast hydration layer), we calculated the corresponding SAXS and SANS curves at various solvent contrasts (100% D₂O, 42% D₂O, and 0% D₂O). Averaging of scattering curves corresponding to the various time frames (over a simulation time of 5 ns) yielded the final scattering curves that were further smeared (in the neutron case), by assuming a beam divergence of Δθ = 0.002 rad and Δλ/λ = 0.1, which are typical for a neutron instrument.

All simulated and experimental scattering curves were treated using the program GNOM v.4.6 (47), which performs an indirect transform of the data and among other parameters, provides as output a regularized scattering curve I_exp and an estimation of the protein/detergent complex radius of gyration R_gIFT that are, in turn, used as input for our simulated annealing algorithm.

Postprocessing of molecular envelopes

For each shape reconstruction, 10 independent runs were executed. Using the programs DAMAVER (48), we aligned the obtained protein molecular envelopes, compared all models with each other, and found the most probable one. Additionally, the mean normalized spatial discrepancy (NSD) is calculated, which represents a measure of the similarity between the obtained envelopes. For ideally superimposed objects, NSD tends to 0, although it exceeds 1 if the objects are systematically different. Additionally, the SD of the NSD is indicative of the overall stability of the solution. The most probable envelope is in turn aligned with the crystallographic structure of the protein using the program SUPCOMB (49). The structural similarity between the ab initio shape and the crystallographic structure is quantified as follows: using the program PDB2SAX (SITUS package) (50), the all-atom structure of the protein is mapped to a close-packed sphere model on a hexagonal lattice, with the same lattice parameter as the ab initio bead model. Subsequently, the NSD_cryst between the ab initio shape and the mapped crystallographic structure is calculated using SUPCOMB. Visualization of the PDC envelopes was performed with the program PyMOL (51).

Results

First example: dDM-solubilized Aquaporin-0 channel

The generation of simulated scattering data concerning a well-characterized system such as AQ0, gave us the ability to explore different combinations of data input to our algorithm and also understand the required amount of experimental information that is needed for obtaining stable and realistic shape reconstructions. In this respect, ab initio runs from a single SAXS curve and from two or three SANS curves at different solvent contrasts were executed for the 270 dDM/AQ0 system. Additionally, for each of these input data combinations, two sets of runs are performed—one with no assumed symmetry and another one with imposed fourfold axial symmetry around the z axis. The used sld or electron densities ρ for each component of the system and detergent molecular volumes V are given in Table 1. Furthermore, the thickness of the detergent hydrophilic heads t is taken to be equal to 6 Å, as found by core-shell model fits of experimental free-micelle scattering curves (44).

Table 1.

Slds at Different Contrasts, Electron Densities, and Molecular Volumes of Protein, Detergent Parts, and Solvent Used during the Ab Initio Runs for the AQ0/dDM System

Bead Phase	ρ(e−/Å3)	$sl{d}_{100{\text{\%D}}_2\text{O}}$ (10−6 A−2)	$sl{d}_{42{\text{\%D}}_2\text{O}}$ (10−6 A−2)	$sl{d}_{0{\text{\%D}}_2\text{O}}$ (10−6 A−2)	V (Å3)
dDM detergent heads	0.52	3.93	2.72	1.85	350
dDM detergent tails	0.28	−0.41	−0.41	−0.41	340
AQ0 protein	0.44	2.90	2.26	1.80	—
Solvent	0.33	6.40	2.36	−0.56	—

Molecular volume (V) and sld values for the detergents were taken from the work of Breyton et al. (31). Electron densities (ρ) were taken from the work of Oliver et al. (44). Note that owing to the H/D exchange occurring in solvents containing a certain ratio of D₂O (55), the sld of a protein is adjusted accordingly for each solvent contrast. The related calculations are performed using the contrast calculator of the program SASSIE (56).

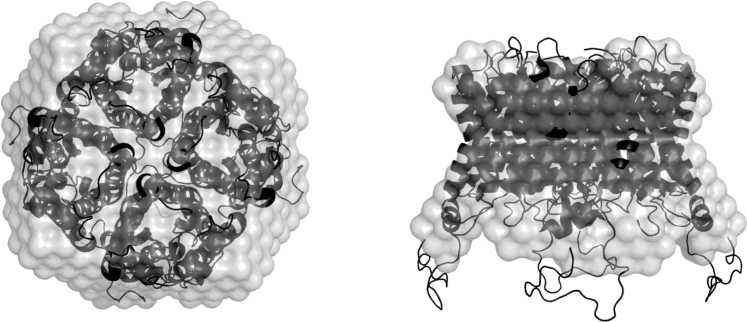
In all ab initio runs, the algorithm was able to fit the MD generated input curves. In Fig. 1, PDC shapes for the SAXS and two curve SANS (100% D₂O and 0% D₂O) reconstructions are depicted, whereas in Table 2 we give a summary of the mean NSD values and their corresponding SD for each set of shape reconstructions. Also, the calculated NSD_cryst between the most probable shape and the AQ0 tetramer crystallographic structure is presented. It is found that for a single SAXS curve as input without symmetry, the obtained NSD values are quite high, indicating shape variability in the final solution. By comparing the most probable shape with the crystallographic structure, we observe systematic deviations. Only when we impose a fourfold symmetry, NSD_cryst tends close to 1, but still the obtained shape possesses clear differences from the AQ0 tetramer structure. We also note that the detergent belt around the protein is not quite compact as it is expected from the MD trajectories. The same conclusions are reached in the case where a single SANS curve is used as input.

Figure 1.

Ab initio shape reconstructions of the 270 dDM/AQ0 tetramer. (First row) Given here is the MD structure. (Second row) Given here is a single SAXS curve with no imposed symmetry. (Third row) Given here is a single SAXS curve with imposed fourfold axial symmetry. (Fourth row) Given here are two SANS curves with no imposed symmetry. (Fifth row) Given here are two SANS curves with imposed fourfold axial symmetry. The first three columns show the top view of the different PDC components (entire PDC, detergent belt, and protein, respectively), whereas the last three columns show the side view. (The bead colors correspond to green, protein; cyan, detergent hydrophilic heads; and magenta, detergent hydrophobic tails.) To see this figure in color, go online.

Table 2.

Summary of Mean NSD, its SD, and the NSD_cryst Values for Ab Initio Runs of the 270 dDM/AQ0 System with Different Numbers of Curve Inputs and Imposed Symmetries

Ab Initio Run	NSD	σNSD	NSDcryst
Single SAXS, no symmetry	1.082	0.056	1.64
Single SAXS, fourfold symmetry	1.035	0.161	1.10
Two SANS, no symmetry	0.668	0.077	0.73
Two SANS, fourfold symmetry	0.457	0.048	0.70
Three SANS, no symmetry	0.715	0.041	0.75
Three SANS, fourfold symmetry	0.454	0.018	0.73

In contrast, when two or three SANS curves at different solvent contrast are used as input, then the ab initio run is much more constrained and the algorithm is guided toward stable solutions (NSD < 1) whereas, as can be seen in Fig. 2, the resemblance of ab initio shapes with the crystallographic structure is evident (NSD_cryst ≈ 0.7) and all major structural features of the tetramer are well reproduced. The application of symmetry restrictions improves solution stability, and leads to marginally better agreement with the crystallographic structure. We also note that the inclusion of a third solvent contrast (42% D₂O) or of the SAXS curve as input does not lead to lowered NSD and NSD_cryst values compared to the two-curve SANS runs, while identical final shapes are obtained. Additionally, from a visual inspection of Fig. 1 we may notice that, especially for the two SANS curves run with fourfold symmetry, the detergent belt is highly compact and its size and shape identical to the one of the MD trajectories.

Figure 2.

Comparison of most probable ab initio envelope (shaded) with the crystallographic structure of the AQ0 tetramer PDB: 2B6P (46) (solid). The reconstruction belongs to the ab initio run performed with two SANS curves as input and with imposed fourfold symmetry.

All above results were obtained by assuming a fixed detergent aggregation number N_det = 270. But because in real cases this quantity has to be estimated experimentally and might be prone to error, we have tested the stability of the ab initio reconstructions against small variations of the parameter N_det. We have found that a 10% variation of N_det leads to small degradation of the obtained NSD_cryst values, whereas visual inspection of the protein envelopes shows only minor differences compared to the runs with N_det = 270. In more detail: for N_det = 240, NSD_cryst = 0.83; and for N_det = 300, NSD_cryst = 0.72.

Second example: OG_D-solubilized Fhac protein transporter

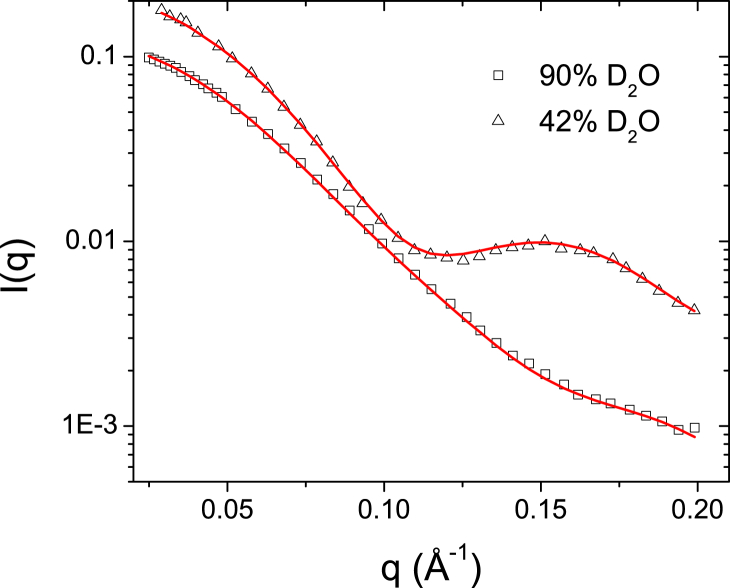
The second application of the algorithm concerned an actual set of SANS experimental data (Fig. 3) from the OG_D-solubilized outer-membrane β-barrel transporter of the Bordetella pertussis Fhac (22), which consists of a 16-stranded β-barrel that is occluded by an N-terminal α-helix and an extracellular loop and a periplasmic module composed of two aligned polypeptide-transport-associated (POTRA) domains (52). The used detergent had its hydrophobic tail part fully deuterated, thus presenting high contrast in relation to the protein. The two SANS measurements were performed at 90% D₂O and 42% D₂O solvent contrast, which represents the matching point for the overall detergent molecule and protein, respectively. As reported, by the use of a dialysis step against solvents with the same detergent concentrations, the free-micelle contribution was subtracted and the SANS curves belonging only to the PDC were obtained. Additionally, for this particular system, the detergent aggregation number around the protein N_det was determined by analytical ultracentrifugation and was found to be equal to 142 ± 10 OG_D molecules.

Figure 3.

Fit of the two Fhac/OG_D SANS experimental curves by the ab initio algorithm. To see this figure in color, go online.

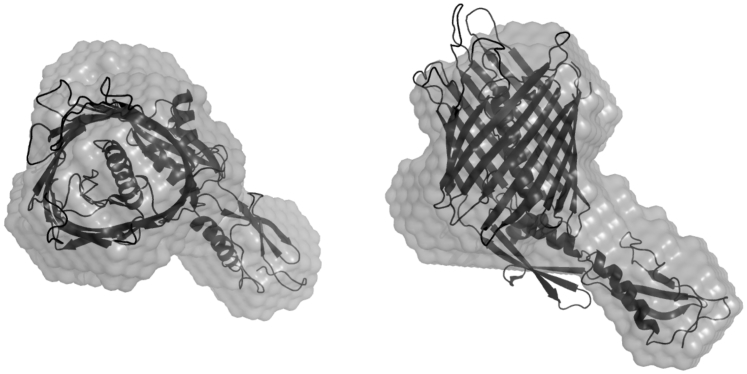
For the ab initio runs using both SANS contrasts, the applied sld for each component of the system and OG_D molecular volumes V are given in Table 3. N_det is fixed at the value 140 and the thickness of the detergent hydrophilic heads t is taken to be equal to 3.2 Å (44). The resulting fit of the experimental results is presented in Fig. 3 and the corresponding PDC shapes are presented in Fig. 4. The obtained NSD values of the ab initio runs are equal to 0.657 ± 0.046, suggesting a stable set of solutions, whereas from the comparison with the crystallographic structure we get NSD_cryst = 0.75. Inspection of the crystallographic structure aligned with the most probable shape (Fig. 5) reveals that the ab initio envelope is representative of the overall molecular shape and that the β-barrel, extramembrane periplasmic POTRA domains, and their relative orientation, are nicely reproduced. It is interesting to note that although the detergent belt encompasses the transmembrane part of the protein, its shape is somewhat disordered and not highly compact, which exposes a small part of the protein β-barrel surface to the solvent. This result will be further discussed below in relation to previous MD modeling investigations (22).

Table 3.

Slds at Different Contrasts and Molecular Volumes of Protein, Detergent Parts, and Solvent Used during the Ab Initio Runs for the Fhac/OG_D System

Bead Phase	$sl{d}_{90{\text{\%D}}_2\text{O}}$ (10−6 A−2)	$sl{d}_{42{\text{\%D}}_2\text{O}}$ (10−6 A−2)	V (Å3)
OGD heads	3.79	2.72	190
OGD tails	7.28	7.28	230
Fhac protein	3.07	2.43	—
Solvent	5.70	2.36	—

Molecular volume (V) and sld values for the detergents were taken from the work of Breyton et al. (31). Protein sld is adjusted for each solvent contrast (56).

Figure 4.

Most probable ab initio shape reconstruction of the 140 OG_D/Fhac PDC. (First row) Given here is the top view. (Second row) Given here is the side view. In each column, different PDC components (entire PDC, detergent belt, and protein, respectively) are depicted. (The bead colors correspond to green, protein; cyan, detergent hydrophilic heads; and magenta, detergent hydrophobic tails.) To see this figure in color, go online.

Figure 5.

Comparison of most probable ab initio envelope (light shading) with the crystallographic structure of the Fhac transporter PDB: 2QDZ (52) (solid). (Left) Given here is the top view. (Right) Given here is the side view.

As in the case of the AQ0 tetramer, we have checked the effect of detergent aggregation variation on the final solution, where we again find that for N_det in the range 125–155, the determined envelopes are very similar and NSD_cryst values remain almost constant (for N_det = 125, we find N_cryst = 0.77 and for N_det = 155, N_cryst = 0.75).

Discussion

In general, the different chemical nature of detergent heads and tails makes it difficult to contrast-match their contribution over the entire q-range in a small-angle scattering experiment. That means that to directly access protein structural information from SAXS or SANS measurements where detergents bound to the protein contribute to the scattering, we need to rely on modeling. We note that since their introduction almost two decades ago, ab initio structure recovery algorithms for soluble globular proteins have become increasingly popular in the literature, assuming a complementary role in integrative structural studies of proteins and nucleic acids. What makes ab initio approaches quite attractive, despite their low resolution, is that no prior structural information is required concerning the biomolecule under study.

The main goal of this work is to develop an ab initio shape recovery method for detergent-solubilized membrane proteins without the need for special contrast-matched detergents, so that sample preparation can be more flexible and focused on the proper solubilization of the protein in a folded and active state. Following the paradigm of ab initio methods, we constructed a four-phase bead model (protein, detergent heads, detergent tails, and solvent) together with a set of geometric constraints that reflect the anticipated structure of the detergent belt around the protein, which should resemble a core-shell doughnut-like structure. The importance of applying constraints may be also illustrated by performing ab initio reconstructions using the multiphase program MONSA (14), where no detergent belt related constraints are implemented and only bead connectivity and compactness is considered. Related results for the Fhac/OG_D system correspond to nonphysical final shapes, whereas reconstructions for the dDM/AQ0 system using three SANS curves as input (Fig. S1) reveal that in the final models, phases of similar contrast (protein, detergent heads) cannot be easily differentiated and the obtained protein shape possesses systematic differences from the crystallographic structure.

Ideally, an additional bead phase corresponding to the hydration layer that surrounds the entire PDC has to be included in our model (53), but because only a marginal improvement of the obtained shapes is expected (38) and due to the increased complexity of such an approach, we opted not to implement it in this algorithm. We stress that no particular geometry (for example, a torus) is assumed for the detergent belt. Two extra restraints that are imposed are related 1) to the maximum thickness of the belt that cannot exceed the typical cellular membrane thickness, and 2) to the total number of detergent molecules that are bound to the protein (aggregation number, N_det). By fixing N_det and considering the molecular volume of detergent heads and tails, we essentially fix the corresponding number of beads in the final solution.

All the geometric constraints together with the requirement for model compactness and the discrepancy between the calculated and input scattering curves contribute to the defined score function f(X). Successful minimization of the score function by simulated annealing leads to a bead arrangement that respects all the described constraints and also fits the small-angle scattering curves. The final bead arrangement represents the molecular envelope for each of the PDC components. The major finding of the minimizations of the MD-generated dDM/AQ0 scattering data is that a single curve, even with appropriate axial symmetry applied, cannot lead to a stable solution; and for obtaining molecular envelopes that are representative of the PDC shape, we need to provide at least two SANS curves at different solvent contrasts as input (Fig. 1). Addition of a third contrast does not improve the shape reconstructions. Enforcement of fourfold axial symmetry, as it is expected for the AQ0 tetramer, improves the agreement with the known crystallographic structure.

In an effort to better understand these results, we can think of the PDC system as having two principal contributions to the scattering—one coming from the protein and a second from the hydrophobic part of the detergent belt. The hydrophilic head layer that covers the belt is indeed contributing to the scattering, but by design, this structural feature is inherently considered in our model, because hydrophobic beads are separated from the solvent by a layer of hydrophilic beads that reproduce the scattering contribution of detergent head layers as determined in measurements of detergent micelles (31, 44). Consequently, it is not surprising that two scattering curves at different contrast can lead to stable solution and to an objective shape for both the protein and the detergent belt. Here we note that the term “two different contrasts” refers to well-separated contrasts (>30% D₂O content). Additional tests have revealed that shape reconstruction quality is improved when one of the two contrasts is close to the matching point of the hydrophobic part of detergent micelles. During experimental planning and in the case of two SANS measurements, one should consider acquiring scattering data either close to the overall matching points of detergent tails and protein or at the most distant possible contrasts (0% and 100% D₂O). In the latter case, one of the two measurements will always be close to the matching point of detergent tails for both deuterated and hydrogenated hydrocarbon chains.

Having established that two contrast-separated SANS curves provide enough information for the ab initio reconstruction, we tested the algorithm using previously published SANS data of the Fhac transporter in two different solvent contrasts. The final obtained molecular shape of the protein is highly similar to the crystallographic structure (Fig. 5), with the β-barrel and POTRA domains easily distinguishable. It is interesting that the resulting detergent belt seems somewhat disordered and does not cover the entire β-barrel surface (Fig. 4). Inspection of PDC shapes belonging to different ab initio runs (Fig. S2) reveals detergent belt shapes with gaps and, in some cases, protrusions. The same topological variability was present in the all-atom MD models that gave the best fits to the scattering data in the work of Gabel et al. (22), which indicates, on the one hand, the relative ambiguity of small-angle data-derived models and, on the other hand, the dynamic nature of the PDC. In this respect, we note that a compact detergent belt is not a universal characteristic of solubilized membrane proteins, something that has to be carefully considered in modeling approaches.

Given that the number of protein-bound detergents N_det is an important input parameter in our method and because its estimation by experimental methods like analytical ultracentrifugation (22), refractometry, or absolute scale small-angle scattering (18) may contain systematic or statistical errors, it was relevant to investigate the stability of the shape reconstructions to small variations of N_det. Our findings suggest that an error of the order of ±10% is not appreciably affecting the shape reconstructions. This observation gives confidence that the typical uncertainty that characterizes the aforementioned experimental techniques should not affect the accuracy of our method.

The design of the PDC bead model was performed by having mainly in-focus systems of integral membrane proteins solubilized by detergents. However, our effort to not heavily constrain the detergent belt shape gives the ability to straightforwardly extend the applicability of this method to bicelle/protein systems (5). Provided that the contrast and structural parameters of empty bicelles are known from previous investigations, the bicelle belt can be modeled in the same manner as in the case of detergents. Furthermore, the method in its current formulation also seems appropriate for the study of peripheral membrane proteins that have only a small fraction of their amino-acid sequence anchored inside the detergent micelle.

From the experimental and sample preparation point of view, it is absolutely essential to properly subtract free-micelle contributions from the scattering data to obtain curves corresponding solely to the PDC. Extensive dialysis against detergent-containing solutions is a viable method, but the in-situ combination of SEC and SAXS has proved to be a very efficient technique for this task (18). In this context and because our methodology relies on multicontrast SANS, the recent development of an in situ SEC-SANS platform at the Institute Laue-Langevin (54) presents special interest in relation to the acquisition of high-quality scattering data from detergent-solubilized membrane proteins. Such setups coupled with upcoming high flux diffractometers at future neutron sources like the European Spallation Source, may bring down the requirements for protein sample amounts, thus rendering the method as a medium-throughput option for membrane protein structure determination.

The executable code of the presented ab initio algorithm (program DANVILLE) for all major software platforms is freely available for academic use from the author upon request. A typical shape reconstruction with no imposed symmetry takes 5–20 h on the single core of modern processors.

Conclusions

In summary, we have presented a method for the determination of the low-resolution structure of detergent-solubilized membrane proteins from SANS datasets. Measurements at two different solvent contrasts together with an independent estimation of the detergent aggregation number around the protein appear to provide reliable shape reconstructions. The generality of the model permits the treatment of data from detergent- or bicelle-solubilized integral or peripheral membrane proteins where their membrane-embedded part is surrounded by a detergent belt of arbitrary shape. Given the extreme difficulties in the study of membrane protein structure, this work offers a powerful tool that allows the general use of small-angle scattering for detailed studies of membrane proteins in solution without the need for any prior structural information. Related ab initio approaches for soluble globular proteins have proved increasingly popular in the literature in recent years. In this respect, we expect that the proposed methodology coupled with the preparation of high-quality samples and the implementation of adapted experimental protocols will allow the investigation of challenging systems and will also complement current advances in other fronts like cryo-electron microscopy.

Author Contributions

A.K. designed and performed research, wrote scientific software, analyzed data, and wrote the manuscript.

Editor: Jill Trewhella.