Assessing Exhaustiveness of Stochastic Sampling for Integrative Modeling of Macromolecular Structures

Abstract

Modeling of macromolecular structures involves structural sampling guided by a scoring function, resulting in an ensemble of good-scoring models. By necessity, the sampling is often stochastic, and must be exhaustive at a precision sufficient for accurate modeling and assessment of model uncertainty. Therefore, the very first step in analyzing the ensemble is an estimation of the highest precision at which the sampling is exhaustive. Here, we present an objective and automated method for this task. As a proxy for sampling exhaustiveness, we evaluate whether two independently and stochastically generated sets of models are sufficiently similar. The protocol includes testing 1) convergence of the model score, 2) whether model scores for the two samples were drawn from the same parent distribution, 3) whether each structural cluster includes models from each sample proportionally to its size, and 4) whether there is sufficient structural similarity between the two model samples in each cluster. The evaluation also provides the sampling precision, defined as the smallest clustering threshold that satisfies the third, most stringent test. We validate the protocol with the aid of enumerated good-scoring models for five illustrative cases of binary protein complexes. Passing the proposed four tests is necessary, but not sufficient for thorough sampling. The protocol is general in nature and can be applied to the stochastic sampling of any set of models, not just structural models. In addition, the tests can be used to stop stochastic sampling as soon as exhaustiveness at desired precision is reached, thereby improving sampling efficiency; they may also help in selecting a model representation that is sufficiently detailed to be informative, yet also sufficiently coarse for sampling to be exhaustive.

Introduction

Integrative structure determination is an approach for characterizing the structures of large macromolecular assemblies that relies on multiple types of input information, including from varied experiments, physical theories, and statistical analysis (1, 2, 3, 4). Therefore, it maximizes the accuracy, precision, completeness, and efficiency of structure determination. Moreover, it can often produce a structure for systems that are refractive to traditional structure determination methods (5, 6, 7, 8, 9, 10, 11), such as x-ray crystallography, electron microscopy, and NMR spectroscopy. Integrative structure determination proceeds in four stages. First, all information that describes the system of interest, including data from wet lab experiments, statistical tendencies such as atomic statistical potentials (12, 13, 14), and physical laws such as molecular mechanics force fields (15, 16), is collected. Second, a suitable representation for the system is chosen depending on the quantity and resolution of the available information. The available information is then translated into a set of spatial restraints on the components of the system. The spatial restraints are combined into a single scoring function that ranks alternative models based on their agreement with input information. Third, the alternative models are sampled using a variety of techniques, such as conjugate gradients, molecular dynamics, Monte Carlo (17), and divide-and-conquer message passing methods (18). The sampling generates an ensemble of models that are as consistent with the input information as possible. Finally, input information and output structures need to be analyzed to estimate structure precision and accuracy, detect inconsistent and missing information, and suggest more informative future experiments. Assessment begins with structural clustering of the modeled structures produced by sampling, followed by assessment of the thoroughness of structural sampling, estimating structure precision based on variability in the ensemble of good-scoring structures, quantification of the structure fit to the input information, structure assessment by cross-validation, and structure assessment by data not used to compute it. Integrative modeling can iterate through these four stages until a satisfactory model is built.

A key challenge in integrative modeling of biomolecular structures is to map the complete ensemble of models consistent with the input information (good-scoring models) (1, 2, 19, 20). The variation among the models in this ensemble quantifies the uncertainty of modeling (model precision). Because sampling large macromolecular systems is often necessarily stochastic, we can only aim to find representative good-scoring models. These representative models sample all good-scoring models at some precision, which we define as the sampling precision. Clearly, the sampling precision imposes a lower limit on the model precision. Therefore, exhaustive sampling of good-scoring models is a prerequisite for accurate modeling and assessment of model precision. Sampling is exhaustive at a certain precision when it generates all sufficiently good-scoring models at this precision. Importantly, sampling exhaustiveness and sampling precision are invariably intertwined. There is always a precision at which any sampling is exhaustive; for example, even a single structure provides an exhaustive sample at a precision worse than the scale of the system.

Accurate estimation of model precision is key in assessing an integrative structure. It is perhaps more important to assess the precision of a model than to compute a model in the first place. The reason is that the utility of a model is determined significantly by its precision. First, model precision provides an estimate of the aggregate uncertainty in the input information; second, it likely provides the lower bound on model accuracy; finally, applications of models strongly depend on their accuracy, with different applications having varied requirements for accuracy and precision (20, 21, 22). Further, only when model precision is estimated accurately, can the model be used to inform future choices, such as whether to gather more data, change the system representation, scoring functions, or sampling algorithms. Commonly used structural features for estimating model precision include the particle positions, distances, and contacts (5, 6, 23, 24), although specific systems may benefit from the use of derived features, such as the distance to a membrane in a transmembrane assembly. Of particular interest are the features that have a single maximum in their probability distribution. The spread around the maximum describes how precisely the feature was determined by the input information.

Sampling convergence in Monte Carlo simulations for protein and RNA structure prediction has been assessed by checking for abundance of structures close to the lowest energy structure(s) (25, 26, 27, 28, 29, 30, 31, 32). Convergence in molecular dynamics (MD) simulations has been measured by counting the number of structural clusters (33, 34, 35) and their relative populations (36, 37, 38, 39, 40), cosine of the principal components (41), distance between the free energy surfaces of different parts of the simulation (42), and drift in the free energies (43). Some methods assess convergence in MD simulations by comparing different trajectories via a difference in populations for each cluster (36, 37, 38, 39, 40). For example, models from a “reference” simulation are first clustered based on a predetermined cutoff (38), followed by assigning models from additional simulation to the nearest cluster in the reference simulation; thus, each simulation produces a histogram of populations of clusters that enables comparison of any two simulations.

As mentioned above, testing for sampling exhaustiveness is the first step of the analysis and validation stage of our four-stage integrative modeling process, immediately following the sampling stage (2, 4, 7, 8, 9, 44). Here, we present an objective and automated protocol that aims to estimate the precision at which sampling is exhaustive, thereby assessing sampling exhaustiveness for integrative structural modeling. As a proxy for assessing sampling exhaustiveness, we evaluate whether or not two independently and stochastically generated sets of models (model samples) are sufficiently similar. Model samples for assessment can be obtained, for example, from two independent simulations using random starting models or different random number generator seeds. The protocol for evaluating exhaustiveness includes two tests that consider the model scores, followed by two tests that consider the model structures.

There are at least two major limitations of our approach. First, sampling convergence is at best an approximation of sampling exhaustiveness. Although similarity between independent model samples does indicate sampling convergence, we can only hypothesize that the convergence of stochastic sampling at some precision also indicates sampling exhaustiveness at that precision, for scoring function landscapes like those used in integrative structure modeling (many dimensions, rugged, few major minima). This hypothesis is supported by all five examined cases of binary docking solutions enumerated at a specified precision. Accordingly, passing the proposed tests is a necessary, but not sufficient condition for exhaustive sampling; a positive outcome of the test may be misleading if, for example, the landscape contains only a narrow, and thus difficult to find, pathway to the pronounced minimum corresponding to the native state. Second, our tests are also not applicable to methods whose sampling is not stochastic (e.g., a conjugate gradients minimization from a fixed unique starting point) or so expensive that they cannot generate a large enough sample of independent models.

The rest of the article is organized as follows. In Methods, we describe the four-part protocol for estimating sampling precision and assessing sampling exhaustiveness, including its application to five illustrative cases of binary protein complexes. In Results, we demonstrate the protocol on the illustrative cases and validate it by comparing stochastic model samples with models from exhaustive enumeration using rigid docking (45, 46). Parameters of the protocol, its applicability and uses, its shortcomings, the relationship between various kinds of precision in integrative modeling, relation to prior work, and future work are addressed in Discussion.

Methods

The protocol for estimating sampling precision and assessing sampling exhaustiveness (Fig. 1) consists of four tests that are increasingly stringent; each test needs to be passed before it makes sense to proceed to the next test. Given two model samples and their scores as input, the tests check 1) convergence of the model score, 2) whether model scores for the two model samples were drawn from the same parent distribution, 3) whether each structural cluster includes models from each sample proportionally to its size, and 4) whether there is sufficient structural similarity between the two model samples in each cluster. Next, each step in the flowchart (Fig. 1) is described in turn.

Figure 1.

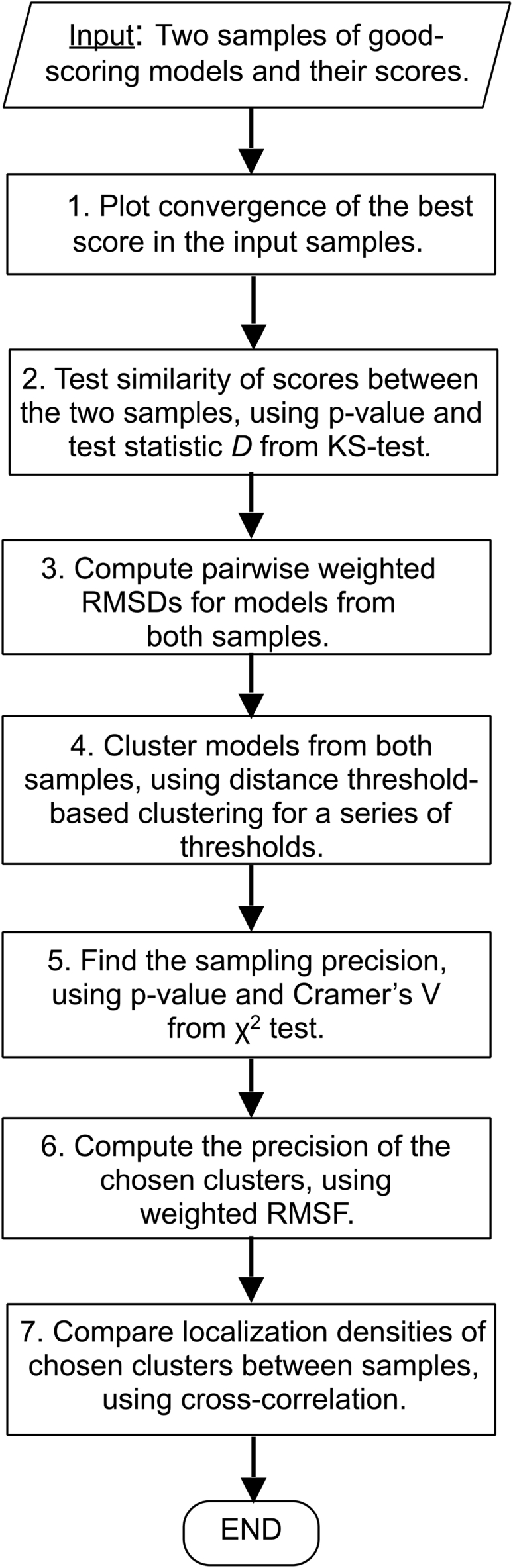
Flowchart of the protocol for estimating sampling precision and assessing sampling exhaustiveness.

Generating inputs for the protocol

The necessary input for the protocol is two model samples of approximately equal size and their scores. Each model sample consists of random, independently generated models. Both model samples must be generated using the same sampling method. In integrative structure modeling, we are generally not interested in all sampled models, but only in models that are good-scoring (i.e., those that are sufficiently consistent with input information) (2, 4, 7, 8, 9, 44).

The precise definition of good-scoring models is left to the user and can be application-dependent. Example choices include all models scoring better than a threshold on the total score (2, 4, 7, 8, 9, 44), or all models satisfying all types of input information within acceptable thresholds. For example, if a protein complex is modeled by fitting its components into an electron microscopy density map subject to cross-linking, excluded volume, and sequence connectivity, the corresponding scoring function can be a sum of the correlation coefficient between the EM map and a model as well as harmonic (Gaussian) restraints for chemical cross-links, pairs of overlapping atoms, and sequence connectivity; a good-scoring model can then be defined as a model that fits the EM density with a cross-correlation >0.80 and violates (e.g., a restraint value > 2 SD from the mean) a smaller number of harmonic restraints than expected for the corresponding Gaussian distributions (e.g., 5%).

The samples are usually generated by a stochastic sampling algorithm. One such algorithm is the Metropolis Monte Carlo scheme (47) that starts from a different configuration and/or random number seed for each run. For our purposes, a larger number of shorter runs is preferable over a smaller number of longer runs for two reasons. First, a larger number of runs benefits more easily from parallel execution than a smaller number of runs. Second, independent runs are guaranteed to result in uncorrelated models, whereas, additional care is needed to ensure the lack of correlation for models from a single run.

Convergence of the best score

The first test assesses whether the best model score continues to improve as more models are sampled. This test operates on random subsets of the model scores of the two samples combined. Model score subsets of several sizes (e.g., 20, 40, 60, 80%, and the complete set) are each created several times (replicates). The best score in each subset is averaged across the replicates. Plotting the average best score for each model subset size shows whether the best score converges as the number of models is increased.

Similarity of scores

The second test confirms that good-scoring models in the two model samples have similar score distributions (i.e., satisfy the data equally well). Specifically, the nonparametric Kolmogorov-Smirnov two-sample test (48, 49) tests the null hypothesis that the distributions of model scores in the two model samples were drawn from the same parent distribution. The p value from the Kolmogorov-Smirnov two-sample test is a measure of the statistical significance of the difference between the two distributions. A p value lower than the cutoff of significance (usually 0.05) indicates that the difference in the two score distributions is statistically significant.

Even a tiny difference between two distributions can be significant if the samples are large (50, 51). Therefore, we additionally use an effect size measure for the Kolmogorov-Smirnov two-sample test. Conveniently, the Kolmogorov-Smirnov two-sample test statistic, D, is itself a proportion (48, 49). The proportion ranges from 0 to 1, where 0 represents no difference between the two samples and 1 no overlap between the two samples. A value of 0.30 (medium effect size) or higher suggests that the two score distributions are different (48, 49).

Finally, we conclude that the score distributions are similar if the difference is not statistically significant (p value > 0.05) or if the difference is significant (p value < 0.05) but its magnitude is small (D < 0.30).

Computing pairwise root-mean-square deviations

The third test assesses whether models from each sample are present in each structural cluster proportionally to the sample size; when the sample sizes are equal, each cluster should contain approximately the same number of models from each sample. The test requires clustering models from both samples combined. It may be necessary to select sufficiently small random subsets of the two model samples, to make clustering computationally feasible.

The first step of clustering is to compute root-mean-square deviation (RMSD) values between all pairs of models from both samples combined (8):

$$RMS{D}_{i,j}={\left({\sum }_{k=1}^b{n}_k{\left({\overrightarrow{\mathit{x}}}_{\mathit{i,k}}-{\overrightarrow{x}}_{j,k}\right)}^2/{\sum }_{k=1}^b{n}_k\right)}^{1/2}$$

where ${\overrightarrow{x}}_{i,k}$ is the Cartesian coordinate of the kth of b beads in model i, $n_k$ is the number of residues in bead k, and n is the total number of models; other structural dissimilarity or similarity measures may be used.

Finding the sampling precision

A stochastic sampling method does not enumerate all good-scoring models, but generates only a sample of them. Here, the sampling precision is defined as the radius of the clusters in the finest clustering for which each sample contributes models proportionally to its size (considering both significance and magnitude of the difference) and for which a sufficient proportion of all models occur in sufficiently large clusters (Fig. 2).

Figure 2.

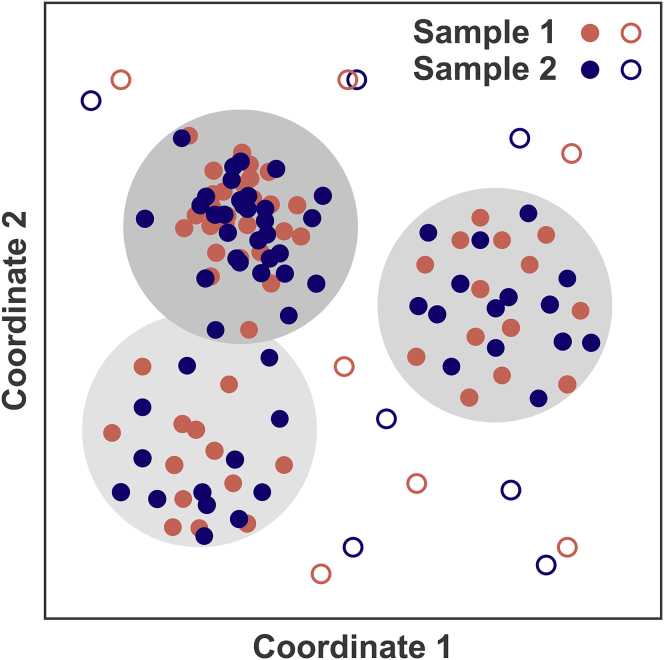
Conceptual representation of the χ² test for sampling exhaustiveness, showing models in a 2D coordinate space. Two independent equal-sized random samples of good-scoring models are shown in red and blue. Models in the two samples are clustered together. The gray circles indicate cluster boundaries and the gray-scale indicates the density of models in the cluster. The size of the circles indicates the clustering threshold. The test assesses whether the proportion of models from the two samples (red and blue) is similar in each significant cluster. Note that some models are shown as open circles, indicating that these models belong to insignificant clusters (i.e., small clusters containing few models).

Clustering models using several thresholds

To find the sampling precision, we evaluate increasingly coarser clusterings, obtained using the following threshold-based clustering method (33). For each model, we first find all neighboring models, defined as models whose RMSD distance (above) from the model is less than the input threshold. Initially all models are unclustered. The unclustered model with the maximum number of neighbors and its neighbors are added to form a new cluster, and the list of unclustered models is updated. The last step is repeated until no unclustered models remain. This clustering is performed for all thresholds sampling the interval between the minimum and maximum RMSDs in steps of 2.5 Å. The next three paragraphs describe the three criteria evaluated for each clustering.

Significance. To assess the significance of the difference between the proportions of each sample in the clusters, we use the χ² test for homogeneity of proportions (52). This test evaluates the null hypothesis that the two model samples are distributed nearly equally (for equal-sized samples) or approximately in proportion to their sizes (for unequal sized samples) in all major clusters. The p value from the test is a measure of the statistical significance of proportionate contributions to clusters from both samples. A p value lower than the cutoff of significance (usually 0.05) indicates that the difference in the two distributions is statistically significant.

Magnitude. To assess the magnitude of the difference between the proportions of each sample in the clusters, we use an effect size measure for the χ² test, Cramer’s V (53). This test measures the magnitude of the difference between the distributions of the two samples across clusters. Cramer’s V is defined as $\sqrt{{\mathit{\chi }}^2/n}$, where χ² is the χ² test metric and n is the total number of models in both samples. A value of V of at least 0.1 suggests that the difference between the two distributions is large; it corresponds approximately to a p value of 0.05 for the case of two clusters and 500 models per sample.

Population. The calculation of the p value and Cramer’s V requires that each sample has at least 10 expected models per cluster (54). Therefore, we remove all clusters containing <10 models from either sample. To allow us to proceed with the assessment, we also require that at least 80% of the models remain after this removal.

Computing precision of clusters

For defining clusters and visualization, any threshold equal to or worse than the sampling precision can be chosen. The sampling precision is the smallest clustering threshold at which sampling is exhaustive; choosing a larger threshold will result in fewer, larger clusters, and may be preferable for analysis and/or visualization.

Although the sampling precision limits the maximum radius of a cluster (Fig. 2), models could be more tightly distributed inside a cluster. To quantify the actual spread of models in clusters, we define the cluster precision as the weighted root-mean-square fluctuation (RMSF) of all models in the cluster. Weighted RMSF accounts for differing sizes of beads often used to represent integrative structures (8, 55). It is computed using

$${\langle RMS{F}^2\rangle }^{1/2}={\left[\left(\sum _{n=1}^b{n}_k\sum _{i=1}^n{\left({\overrightarrow{x}}_{i,k}-\langle x_k\rangle \right)}^2\right)/n\left(\sum _{k=1}^b{n}_k\right)\right)}^{1/2}.$$

The cluster precision is ∼1.4 times the sampling precision, reflecting the general relationship between RMSD and RMSF (8, 55).

Computing localization densities and their cross correlation

The final test involves computing the cross correlation between the model densities from each sample, for each cluster. The density maps are created at a resolution equal to the threshold used for defining clusters (above). The cross-correlation coefficients between the maps are calculated using the software UCSF Chimera (56).

Validation of the protocol

We illustrate our protocol by relying on five binary protein complexes of known structure from the ZDOCK Benchmark 4.0 (57), spanning a range of docking difficulty, and 5–7 simulated distance restraints per complex. We modeled the structure of each complex by stochastic sampling as implemented in an integrative modeling platform (IMP; Supporting Material). We assessed the sampling exhaustiveness protocol based on a comparison of stochastic sampling with exhaustive enumeration, as follows.

The quality of the sampling exhaustiveness protocol is quantified by the fraction of good-scoring models from exhaustive enumeration (below) that are located within any sufficiently large cluster of the good-scoring models from the tested sampling, for the clustering threshold equal to the tested sampling precision; an enumerated model is located in a cluster, if its distance to the cluster center is within the tested sampling precision.

Fast-Fourier transform-based protein docking algorithms (45, 58, 59, 60) efficiently construct models of binary protein complexes by enumerating all possible rigid rotations and translations on a uniform 3D grid. The set of all models (57) produced by ∼1.2 Å and 6° uniform sampling on an FFT grid was used. Good-scoring models from enumeration were identified as in stochastic sampling (models for which at least 90% of cross-links span a Cα-Cα distance of <12 Å). For each good-scoring ZDOCK model, its distance to the nearest major cluster center from IMP was calculated.

The distribution of models from stochastic sampling in IMP cannot be compared directly to enumerated models computed by ZDOCK. The ZDOCK models are enumerated on a uniform grid, whereas IMP samples the posterior probability of models and therefore produces a nonuniform model distribution. In addition, ZDOCK and IMP use different representations (atomic and coarse-grained, respectively).

Results

We demonstrate the sampling exhaustiveness protocol on an example from the Protein Data Bank (PDB), 1AVX. The remaining four examples are described in Figs. S1–S5.

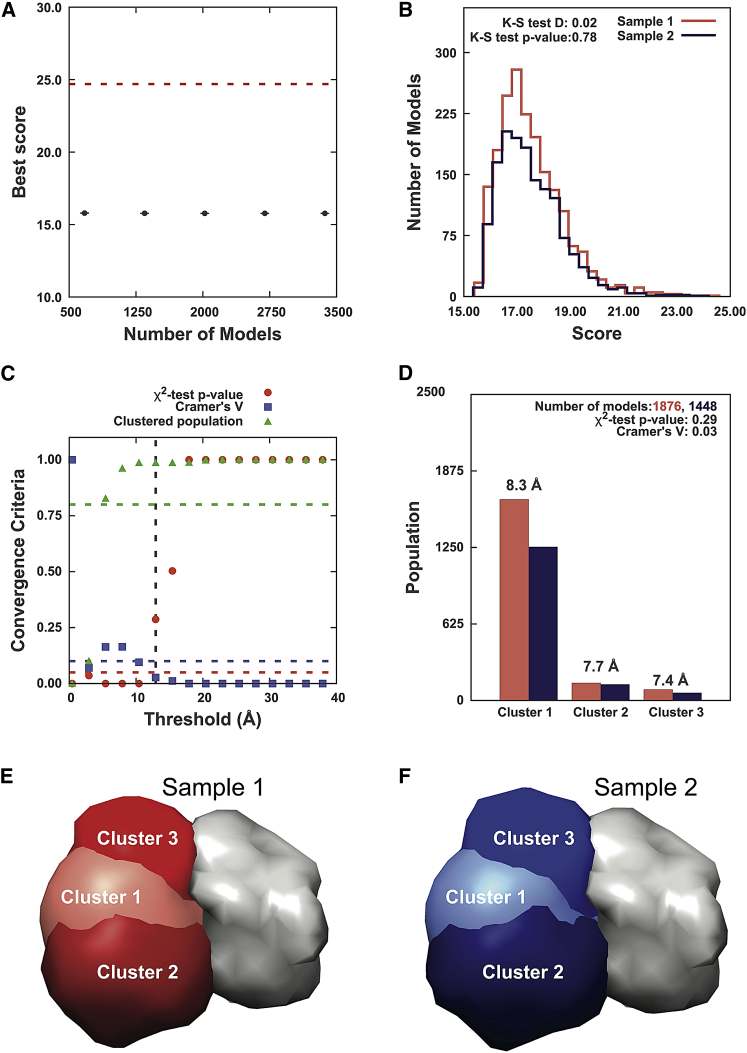
There are 3369 good-scoring models for PDB: 1AVX (1896 in sample 1 and 1473 in sample 2). The score convergence test shows that the best score does not continue to improve significantly with an increase in the number of models sampled (Fig. 3 A; to visualize the relatively rapid convergence in model scores, see Fig. S6). The two score distributions are similar to each other, as shown by the overlap in the score histograms and the insignificant p value and small D value from the Kolmogorov-Smirnov two-sample test (Fig. 3 B).

Figure 3.

Results for sampling exhaustiveness protocol for PDB: 1AVX. (A) Shown here are results of test 1, convergence of the model score, for the 3369 good-scoring models; the scores do not continue to improve as more models are computed essentially independently. The error bar represents the SD of the best scores, estimated by repeating sampling of models 10 times. The red dotted line indicates a lower bound on the total score. (B) Shown here are results of test 2, testing similarity of model score distributions between samples 1 (red) and 2 (blue); the difference in distribution of scores is not significant (Kolmogorov-Smirnov two-sample test p value > 0.05) and the magnitude of the difference is small (the Kolmogorov-Smirnov two-sample test statistic D is 0.02); thus, the two score distributions are effectively equal. (C) Shown here are results of test 3, containing three criteria for determining the sampling precision (y axis), evaluated as a function of the RMSD clustering threshold (33) (x axis). First, the p value is computed using the χ² test for homogeneity of proportions (52) (red dots). Second, an effect size for the χ² test is quantified by the Cramer’s V value (blue squares). Third, the population of models in sufficiently large clusters (containing at least 10 models from each sample) is shown as green triangles. The vertical dotted gray line indicates the RMSD clustering threshold at which three conditions are satisfied (p value > 0.05 (dotted red line), Cramer’s V < 0.10 (dotted blue line), and the population of clustered models > 0.80 (dotted green line)), thus defining the sampling precision of 12.93 Å. (D) Populations of sample 1 and 2 models in the clusters are obtained by threshold-based clustering using the RMSD threshold of 12.93 Å. Cluster precision is shown for each cluster. (E and F) Shown here are results of test 4: comparison of localization probability densities of models from sample 1 (red) and sample 2 (blue) in each cluster. The density map of the receptor, which is kept fixed through the simulation, is shown in gray. All densities were visualized at a threshold equal to one-third the maximum. The cross-correlation of the density maps of the two samples is 0.99 for each of the three clusters.

Next, exhaustiveness is examined at varying thresholds between the minimum and maximum RMSDs of 0.43 and 42.93 Å (Fig. 3 C; Table 1). Based on the p value, Cramer’s V, and the population of models in the contingency table, the χ² test is satisfied from the threshold of 12.93 Å onwards (Table 1). Hence, the sampling precision is 12.93 Å. In general, stricter (smaller) clustering thresholds result in many small clusters, which are ignored (Table 1, last column; Fig. 3 C). In contrast, more lenient (larger) clustering thresholds result in fewer, larger clusters that are more likely to be retained in the analysis. For example, for the lowest clustering threshold of 0.43 Å, each model is in its own cluster and hence all clusters are small and eliminated from the contingency table. In contrast, for thresholds >25.43 Å (Fig. 3 C), only one cluster containing all models remains.

Table 1.

Three Criteria for Determining the Sampling Precision for PDB: 1AVX, Evaluated as a Function of the Clustering Threshold

Threshold in Ångstroms	p Value	Cramer’s V	Population of Models in Contingency Table [%]
0.4	0.0	1.0	0.0
2.9	0.0	0.1	10.1
5.4	0.0	0.2	82.7
7.9	0.0	0.2	96.2
10.4	0.0	0.1	98.7
12.9	0.3	0.0	98.7
15.4	0.5	0.0	98.7
17.9	1.0	0.0	98.8
20.4	1.0	0.0	99.8
22.9	1.0	0.0	100.0
25.4	1.0	0.0	100.0
27.9	1.0	0.0	100.0
30.4	1.0	0.0	100.0
32.9	1.0	0.0	100.0
35.4	1.0	0.0	100.0
37.9	1.0	0.0	100.0
40.4	1.0	0.0	100.0
42.9	1.0	0.0	100.0

The three criteria are 1) p values and 2) Cramer’s V, both from the χ² test; and 3) the population of models in the contingency table after eliminating small clusters.

Finally, we chose the sampling precision as the clustering threshold for visualizing clusters. Inspection of the cluster populations (Fig. 3 D) shows that they are similar for the two samples. The sampling precision is ∼1.4 times the cluster precision, as expected from the general relationship between RMSD and RMSF (Methods; (55)). The agreement between the localization densities for samples 1 and 2 (Fig. 3, E and F) is demonstrated by the high cross-correlation coefficient of 0.99 for each cluster.

Validation by comparison to exhaustive enumeration

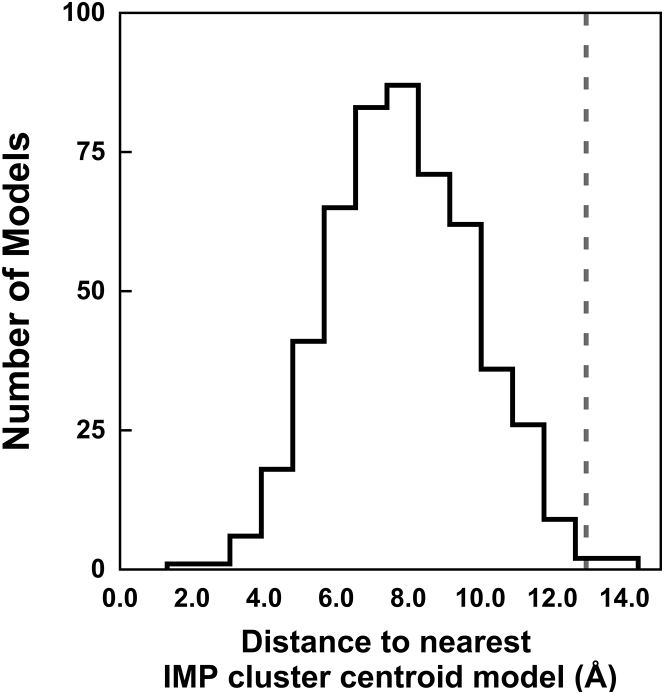
The sampling exhaustiveness protocol was validated by showing that 99.2% of the good-scoring ZDOCK models were within an IMP cluster for PDB: 1AVX (Fig. 4); the corresponding fraction was 100% for the other four examples (Fig. S5). For PDB: 1AVX, out of 510 good-scoring ZDOCK models, 506 were within the sampling precision of the center of a significant cluster and the distances for the other four models were less than one grid spacing further away (Fig. 4). Similarly, the largest distances between good-scoring ZDOCK and IMP models were 1.52, 3.96, 1.56, and 0.96 Å short of their sampling precisions for PDB: 1I2M, 1SYX, 2IDO, and 7CEI, respectively (Fig. S5). In conclusion, the sampling exhaustiveness protocol neither overestimates nor underestimates the sampling precision, for the five examined cases.

Figure 4.

Histogram showing the distribution of distance (measured by weighted ligand RMSD) of a good-scoring PDB: 1AVX model from enumeration (ZDOCK) to the nearest cluster centroid model from stochastic sampling (IMP). The dotted line indicates the sampling precision for the IMP model sample determined by the sampling exhaustiveness protocol.

Discussion

Summary of the protocol

Accurate assessment of model uncertainty in integrative modeling necessitates that sampling is exhaustive at a precision sufficient for assessing model uncertainty. In this article, we introduce a protocol for determining the sampling precision of integrative structural models computed by a stochastic sampling algorithm. The protocol requires two samples of independently and stochastically generated sets of models and their scores. It includes two tests for convergence of the score and two tests for convergence of the structures. The tests for score convergence assess whether the scores in the two samples are from similar distributions. The tests for structural convergence rely on structural clustering of the models, followed by assessing whether the models in the two samples are distributed similarly across the clusters. The five illustrative cases demonstrate the relative accuracy of the sampling exhaustiveness protocol (Figs. 3 and 4; Figs. S1–S5). Below, we discuss the parameters used in the protocol, and its applicability, shortcomings, and relationship among various kinds of precision in integrative modeling; we then address overfitting in integrative modeling, relation to prior work, and future work.

Parameters

All parameters used in the protocol are listed next; their values are chosen based on rules-of-thumb in statistics literature. First, the significance cutoff for the KS test is 0.05 and the magnitude cutoff for the KS statistic, D, is 0.3, the latter corresponding to medium effect size (49). Second, due to the inability of the χ² test to handle small expected cell counts, we eliminate clusters with <10 models for either sample from the contingency table for the test, as recommended (54). Third, because we are eliminating these small clusters, we additionally check if the population of models remaining in the contingency table from both samples is >80%. Finally, the significance cutoff for the χ² test is 0.05 and the magnitude cutoff on Cramer’s V is 0.1, the latter corresponding approximately to a p value of 0.05 for the case of two clusters and 500 models per sample.

Applicability and uses

The sampling exhaustiveness protocol is broadly applicable to a range of sampling methods, a range of clustering or binning methods, features of models other than model scores, and models other than macromolecular structures, and it can be used dynamically during sampling to stop as soon as desired sampling precision is reached, as follows.

First, any stochastic sampling method that generates a large number of independent model samples is appropriate. Metropolis Monte Carlo sampling can satisfy this requirement of independence by 1) sampling models from multiple independent trajectories (e.g., starting from different random initial configurations) and 2) sampling models at sufficiently distant intervals on a single trajectory, such that samples are effectively uncorrelated with each other. The sampling exhaustiveness protocol can only compare model samples produced by the same sampling algorithm (e.g., samples from uniform sampling and importance sampling are clearly not directly comparable).

Second, any one of the variety of clustering or binning methods for grouping models based on their similarity could be used instead of the distance threshold-based clustering. In principle, even a uniform grid could be applied to bin the models. This clustering is used as a relatively rapid method to assign most models to a relatively small number of groups of similar precision. As a result, we can easily quantify the sampling precision across the entire space of models and convey the results in terms of a small number of model clusters. In contrast, for example, k-means clustering generally results in clusters of varying precision, thus obfuscating the relationship between the cluster precision and sampling precision.

Third, any quantity of interest, such as radius of gyration and distance to a membrane, can be tested in the same manner as the model scores here.

Fourth, the protocol is applicable to stochastic sampling of any kind of a model, not just a structural model.

Fifth, and finally, the protocol can be applied to estimate sampling precision dynamically during a simulation, so that sampling is stopped as soon as desired sampling precision is reached, maximizing sampling efficiency. Assessment of exhaustiveness is particularly important for modeling large systems with many degrees of freedom, where exhaustive sampling of representative good-scoring solutions is particularly difficult.

Critique

In the absence of enumeration, exhaustiveness of stochastic sampling cannot be proved with complete certainty. Therefore, we suggest that even a statistical test such as the one proposed here is better than no test. As a proxy for assessing exhaustiveness, our protocol evaluates whether two independent random model samples are similar to each other (Introduction). Our tests are not applicable to methods that do not generate independent random samples (e.g., a conjugate gradients minimization from a fixed unique starting point), or are so expensive that they cannot generate a large enough sample of independent models. Further, passing the proposed tests is a necessary, but not sufficient, condition for exhaustive sampling; a positive outcome of the test may be misleading if, for example, the landscape contains only a narrow, and thus difficult to find, pathway to the pronounced minimum corresponding to the native state. Nevertheless, based on the five examples, we argue that convergence of stochastic sampling at some precision often also indicates sampling exhaustiveness at that precision.

Precision in integrative modeling

In this article, we used the model (ensemble) precision, sampling precision, and cluster precision. In addition, the data precision (uncertainty) reflects the experimental noise (systematic and random error) (4); and the representation precision can be defined, for example, by the diameter of the largest primitive (Gaussian, bead) used to represent the system. We now discuss these five precisions in the context of each other.

First, the sampling precision imposes a lower limit on the model precision. The shape of the scoring function landscape at precisions better than the sampling precision is not sampled accurately by definition; thus, any features of the model landscape more precise than the sampling precision are unlikely to be estimated accurately.

Second, because the model ensemble is divided into one or more clusters, the model precision is always equal to or worse than any cluster precision.

Third, for the final description of the model ensemble, it only makes sense to cluster the models using a clustering threshold that is equal to or larger than the sampling precision (due to the first point above; see Fig. 4).

Fourth, and lastly, the sampling precision is in turn limited by the representation precision and data precisions. Although the model, sampling, and cluster precisions, as defined here, are directly comparable to each other, the representation and data precisions are defined on different scales. Nevertheless, qualitatively speaking, the sampling precision cannot be significantly higher than the representation and data precisions; moreover, it is likely not beneficial to use a representation with a precision that is significantly higher than the data precision.

Addressing overfitting in integrative structure modeling

Overinterpretation of the data (overfitting) is a frequent concern in any modeling. For example, a single high-resolution atomic model may fit an EM density map at intermediate resolution well; proposing such a model as the solution is often a case of overfitting because there are likely many other atomic models that also fit the data equally well. Our sampling exhaustiveness test provides a potential insurance against overfitting. When a test is passed, overfitting is not a problem (at the sampling precision) because all models (at this precision) that are consistent with the data are provided in the output model ensemble.

Relation to prior work

The methods most related to that in this article, applied in the context of MD simulations, are those in (36, 37, 38, 39) (also used in (40)). In (36, 37), models from multiple MD simulations are combined and compared in terms of their relative populations. In (38), a new simulation is compared against a reference simulation, by clustering models from the reference simulation based on a predetermined cutoff. The models of the new simulation are then assigned to the nearest cluster from the reference simulation. Thus, each simulation produces a histogram of populations across clusters and any two simulations can be compared by the difference in their populations for each cluster. In (39), this method is expanded by computing the number of independent samples in an MD trajectory as a way of assessing the sampling quality. The number of independent samples in an MD simulation is determined by comparing the observed variance in the population of a cluster to the expected analytical variance from an independent and identically distributed sample, for various subsample sizes.

Our protocol additionally determines the significance and magnitude of the difference in population distributions across clusters, using the χ² test. More importantly, our protocol also determines the sampling precision objectively, by applying the χ² test for a range of clustering thresholds (Figs. 3 and 4). Moreover, we test both score convergence and convergence of structural coordinates (Fig. 1). A few minor differences exist in our respective clustering methods as well: 1) similarly to (36, 37), we cluster models from all simulations, potentially producing a more comprehensive set of clusters, in contrast to clustering only models from the reference simulation (38, 39); and 2) our cluster centers are chosen based on the density of models close to the cluster center, in contrast to choosing cluster centers randomly (38), choosing clusters of uniform probability (39), or choosing cluster centers based on average linkage with a similarity cutoff (36, 37). Finally, our statistical test applies to independent samples from a stochastic algorithm such as Monte Carlo sampling, whereas some other methods do not require the samples to be independent (36, 37, 38, 39, 40). Preliminary versions of our sampling exhaustiveness protocol have been already used in several integrative modeling applications (9, 10, 11, 61, 62, 63). Earlier, sampling exhaustiveness for integrative modeling was estimated, at best, by manual visual inspection of localization densities of clusters (7, 8, 44).

Future directions

Future directions include expanding this protocol to establish more detailed tests for exhaustiveness. For instance, it will be useful to determine not just the sampling precision for the entire macromolecular system, but also the sampling precision for different components of the system (e.g., proteins, domains) separately. Such more detailed information would be useful in the analysis stage of the iterative four-stage integrative modeling process (2, 4) to determine, for instance, what representations to change and what input data to reexamine to improve the sampling precision for the entire system.

Structures of macromolecular systems are increasingly computed by integrative modeling that relies on various types of experimental data and theoretical information (20). However, validation of integrative models and data is a major open research challenge. It is particularly timely because of the Worldwide Protein Data Bank effort to expand the scope of its archive to integrative structures (20). We suggest that a sampling exhaustiveness protocol, such as the one described here, is the first assessment applied to all integrative models.

Availability

Benchmark data and code used in this article are freely available at http://salilab.org/sampcon. The code relies on our open source IMP package (http://integrativemodeling.org).

Author Contributions

S.V., I.E.C., and A.S. designed research. S.V. and I.E.C. performed research. P.C. contributed computational tools. S.V., I.E.C., and A.S. analyzed data. S.V., I.E.C., and A.S. wrote the manuscript.

Editor: Amedeo Caflisch.