An engineered CARS substrate with giant field enhancement in crisscross dimer nanostructure

Abstract

We theoretically investigate the optical properties of a nanostructure consisting of the two identical and symmetrically arranged crisscrosses. A plasmonic Fano resonance is induced by a strong interplay between bright mode and dark modes, where the bright mode is due to electric dipole resonance while dark modes originate from the magnetic dipole induced by LC resonances. In this article, we find that the electric field “hotspots” corresponding to three different wavelengths can be positioned at the same spatial position, and its spectral tunability is achieved by changing geometric parameters. The crisscrosses system can be designed as a plasmonic substrate for enhancing Coherent Anti-Stokes Raman Scattering (CARS) signal. This discovery provides a new method to achieve single molecule detection. At the same time, it also has many important applications for multi-photon imaging and other nonlinear optical processes, such as four-wave mixing and stimulated Raman scattering.

Introduction

A common coupling characteristic for metallic plasmonic nanostructures is the Fano-type resonance with a distinct asymmetric line shape. The plasmonic Fano resonance arises from the coherent interference between the narrowband dark plasmonic mode and the broadband bright plasmonic mode¹, which has attracted broad research interests due to its significant applications such as electromagnetically induced transparency (EIT)^2,3, optical switching^4,5, surface enhanced Raman scattering (SERS)^6,7, biological sensors^8,9, nonlinear^10–12 and slow-light optical device¹³. In the complex metal nanostructures, plasmonic interferences and hybridizations provide a strong strategy to intensify local field enhancements and tailor the spectral response at nanometer scale.

So far, many studies have been focused on plasmonic nanostructures that exhibit Fano resonance depending on various excitation ways. In coupled metamaterial structures, structurally configurations take astonishing roles for modifying the electromagnetic property. The most common way is introducing asymmetric geometry structure. It is the planar ring-disk or three-dimensional sphere-shell metallic nanostructures that can exhibit a sharp Fano resonance by introducing a coupling between dipolar modes (bright) and the quadrupolar modes (dark) through shifting the center particle with respect to the center of the surrounding ring or shell^14,15. In nanoparticle pairs, the coupling will be introduced to produce Fano resonances, when we change the size or composition of the one of nanoparticles. For instance, the asymmetric nanorod pairs structure¹⁶ with a length offset l can exhibit a Fano resonance due to the strong interference between the electric dipole resonance and the magnetic dipole resonance. Another type of symmetry breaking is the introduction of asymmetric dielectric environment or substrate^17,18. The Fano resonance has been experimentally observed in gold nanorods structure supported on a substrate with very high dielectric constant¹⁹. Furthermore, the Fano resonance in metal nanostructures can also be obtained in a variety of arrays^20–22 or grating structures²³. This is mainly due to the interaction between narrow diffraction resonance and wide plasmonic excitation modes. Metal nanostructure is one of the most important elements to construct the plasmonic compounds, and plays an important role in promoting the rapid growth of the plasmonic metamaterials.

Recently, metallic plasmonic nanostructures are of particular interest for the detection and identification of single molecules using Fano resonance. Halas research group²⁴ had proposed that the coherent anti-Stokes Raman spectroscopy (CARS) can be applied to acquire single molecule detection sensitivity based on a Fano substrate. This model explains in detail how it observes the four-wave mixing, which provides a new strategy for implementing the third-order process in nanostructures. Subsequently, He²⁵ present a design consisted of three asymmetric gold disks with large local field enhancement. It is interesting to achieve a high enhancement factor about ~10¹³ as a CARS substrate.

Recently, we have theoretically investigated the plasmonic film-crisscross dimer array system²⁶, which can be acted as a multi-resonance plasmonic substrate. In this structure, the three plasmonic resonance modes excited in the visible or near infrared spectral range can be matched with the pump light, Stokes and anti-Stokes lights, respectively, to achieve a significant amplification of the CARS signal. The mainly factors to achieve this purpose are that this film-crisscross dimer substrate can excite multiple plasmonic resonances with strong local characteristics, all of them have same hotspot positions, and the spectral will overlap between plasmonic resonances and input beams or output beams. It is the multi-resonance plasmonic substrate that will be more conducive to the realization of enhanced nonlinear spectroscopy and imaging.

In this paper, we continue to investigate in-depth this crisscross-dimer structure consisted of two identical and symmetrically arranged crisscrosses in a scattering system. Here, we mainly research the scattering performance of crisscross dimer by changing the structural parameters to flexibly adjust the resonance spectra, and using circuit model theory to analyze and predict the resonance characteristics. Scattering spectra with Fano-type profile is excited in the crisscrosses structure. Furthermore, another resonance peak will appear, when the arm length of l₂ and l₃ is unequal. This find provides a new tactic for the design of multi-resonances plasmonic CARS substrate, and the surface enhanced CARS signal can reach about ~10¹³. Although the CARS enhancement in the scattering system is less than that our study of film-crisscross dimer array structure, it can still reach the level of previous research by other scholars, which still has an important guiding significance for single molecule detection.

Structures Description

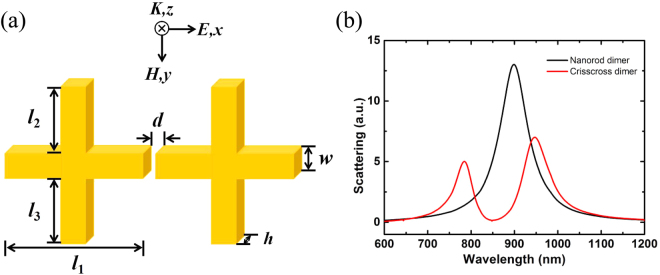
In this study, we use crisscross dimer as a metamaterial design platform to study scattering effects, coupling strength and symmetry breaking. The schematic drawing of the crisscross dimer is shown in Fig. 1(a), consisting of two identical crisscrosses arranged symmetrically about the y-axis, with the subunit length of l₁, l₂ and l₃, where l₁ = 120 nm, the width w = 30 nm, the thickness h = 20 nm, the spacing gap between two crisscrosses d = 10 nm is kept constant, and the length of l₂ and l₃ can be changed. In the simulation process, we select the parameter m = l₂ − l₃ as a variable to describe the asymmetric system. A plane electromagnetic wave is incident along the z-direction with the electric field polarized along the x-direction. The scattering property and field distribution in proposed structure are realized by finite element analysis method with the physical simulation function of COMSOL multiphysics software. The solution domain is composed of perfect match layers (PMLs) as boundary condition for all six boundaries. Silver is chosen as crisscross dimer nanostructure, surrounded by vacuum.

Figure 1.

(a) Sketch of the designed two identical crisscrosses structure with a incident plane wave at the z axis direction and the electric fields polarized along the x direction; (b) Scattering spectra for nanorod dimer (black) and crisscross dimer (red).

Results and Discussions

Crisscrosses structure

For the crisscross dimer structure in scattering system, we mainly study its scattering properties by adjusting the length of l₂ and l₃. When l₂ = l₃ = 0, there exist only a nanorod pair with a gap d and arm length l₁, which is also known as the end-end nanorod dimer²⁷, which is effectively excited by the incident light to provide a bonding dipole resonance. Its scattering spectra exhibits a standard Lorenz lineshape, as shown in Fig. 1(b) for the black curve. However, when adjusting l₂ = l₃ ≠ 0, an asymmetric Fano resonance occurs due to the destructive interference between bonding dipole resonance and the magnetic resonance, which is shown in Fig. 1(b) for the red curve.

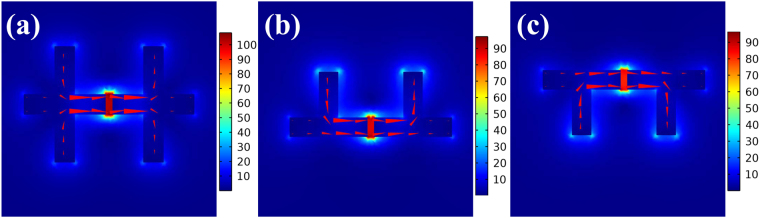
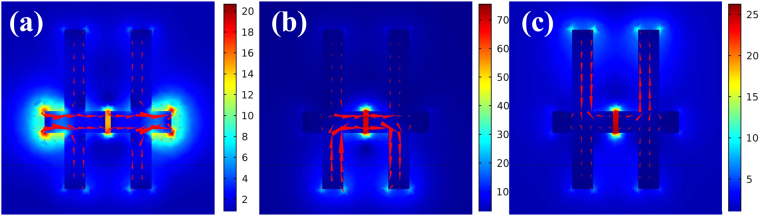
In order to well analyze the optical response for the crisscross dimer structure, we first research the crisscross dimer with l₂ = l₃ = 70 nm, while the other parameters are the same as the initial settings. The black curve in Fig. 2 shows measured normal incidence, horizontal polarization scattering spectra. The short wavelength peak marked with mode 1 is derived from the bonding dipole resonant depending on the antenna pairs of arm length l₁. The other peak marked with mode 2 is typically produced to a LC resonant behavior, due to an antibonding magnetic dipole resonance. In this article, we will mainly analyze this magnetic dipole resonance mode 2. As shown in Fig. 3(a), the electric field is concentrated in the gap between two crisscrosses. There are two current loops are located at the bottom and the top of the crisscrosses, depending on the anti-parallel current distribution in the crisscrosses. This resonance is therefore attributed to the out-of-phase magnetic dipole oscillations. It is analogous to LC resonance in SRR or U structure^28,29. Nanorods serve as inductance L and the gap d between the crisscross dimer provide a capacitance C.

Figure 2.

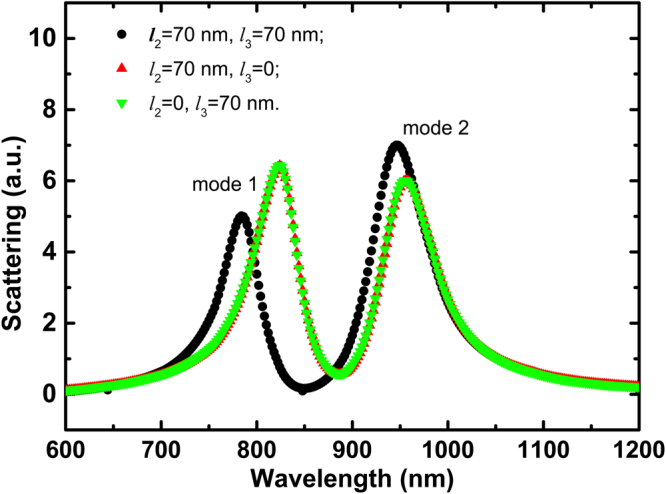
Scattering spectra for the structures of l₂ = l₃ = 70 nm (black); l₂ = 70 nm, l₃ = 0 (red); and l₂ = 0, l₃ = 70 nm (green).

Figure 3.

Simulated electric field and current flow distribution of the crisscrosses at mode 2 with different values of l₂ and l₃: (a) l₂ = l₃ = 70 nm; (b) l₂ = 70 nm, l₃ = 0; (c) l₂ = 0, l₃ = 70 nm. The red arrows represent the induced current flow direction and the color bars represent the electric field density.

Equivalent circuit analysis of crisscrosses structure

In our designed nanostructures, the two crisscrosses are identical and symmetrically placed with respect to y-axis. In LC resonant mode 2, the structural elements in parallel with the y-axis play an important role. For the crisscross dimer, as shown in Fig. 3(a), the current direction in the subunit of the length l₂ is opposite to that of the subunit with the length l₃. Moreover, the current directions of the same part between the two crisscrosses are also reversed. Thus, two current loops are formed in the bottom and the top parts of the crisscross dimer. Based on the above analysis, we assume that the resonance mode 2 can be determined by the bottom and top parts, respectively.

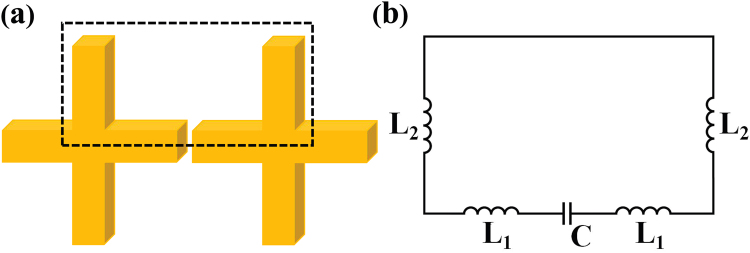
To verify our assumption, we also consider the other two cases: (a) l₂ = 70 nm, l₃ = 0 and (b) l₂ = 0, l₃ = 70 nm, while maintaining other parameters unchanged. Their corresponding scattering spectra are shown by the red curve and the green curve in Fig. 2, respectively. In contrast to the crisscross dimer, the resonant mode 1 has a significant redshift in each of the upper or lower structures, which is primarily affected by the subunit length in the y direction³⁰. For the resonant mode 2, the resonant position does not change substantially, except that the scattering intensity becomes smaller. The Fig. 3(b),(c) illustrate the electric field and current flow distribution in the upper or lower parts of the crisscrosses. They have same resonance frequency and electric field distribution, and correspond to the dimer structure. So we can only consider the part of the dashed box in Fig. 4(a). A simple equivalent circuit model is established as shown in Fig. 4(b).

Figure 4.

(a) The equivalent structure of the crisscrosses can be transformed into the part of the dashed box for LC resonance mode 2; (b) Simplified LC equivalent circuit model of the crisscross dimer.

So far, the inductor-capacitor (LC) circuit model has been applied to predict the plasmonic resonance frequency³¹. It is useful to understand physical mechanisms and the geometric effects in nanostructure metamaterial. The electric field intensity distribution shows a large number of charge accumulations in the gap in mode 2. By adding successive image charges method proposed by Corrigan³², the coupling capacitance C can be approximated as:

$$C\cong 4\pi \epsilon a\left(1+\frac{a^2}{{\mathrm{g}}^2-a^2}+\frac{a^4}{g^4-3g^2{a}^2+a^4}\right)$$ 1

where, the capacitor is formed at the gap, ε is the permittivity of free space, a is the equivalent radius of the sphere and g is the center spacing of the isolated spheres. The equivalent sphere essentially originates from the same volume of the cylinder with a cross-sectional radius r and a height 2r.

The inductance of the current carrying can be calculated by the Bueno theory³³:

$$\mathrm{\Lambda }(l)=\frac{{\mu }_{0}l}{4\pi }[2{\sinh }^{-1}(\frac{l}{w})+(1+k)\left(\frac{l}{w}\right){\sinh }^{-1}\left(\frac{w}{l}\right)-\frac{(3-k)}{3}\frac{{(w^2+l^2)}^{3/2}}{l{w}^2}+(\mathrm{1}-k)\frac{l}{w^2}{(w{}^2+l^2)}^{1/2}+\frac{2k}{3}{\left(\frac{l}{w}\right)}^2+\frac{(3-k)}{3}\left(\frac{w}{l}\right)]$$ 2

where l is the length of nanostructure, µ₀ is the permeability of free space, and k is an integer number, according to the Neumann model, k = 1 is selected during the calculation. Thus, the self-inductance in our proposed structure can be simply expressed as: $L_{\mathrm{1}}=\mathrm{\Lambda }(l_1/2)$, $L_2=\mathrm{\Lambda }(l_2/\mathrm{2})$. In addition, the mutual inductance between the nanorods is expressed as:

$$M(l,g)=-\frac{{\mu }_0}{4\pi }[2l{\sinh }^{-1}\left(\frac{l}{g}\right)+(3-k)(g-{(g^2+l^2)}^{1/2})]$$ 3

The negative sign indicates that the direction of the current is reversed, and g is the distance between nanorods. To simplify the circuit model based on equivalent structure in Fig. 4, the inductance of the entire loop can be expressed as: $L=2L_1+2L_2-2M$. So the resonant wavelength λ_r in a single closed loop can be extracted through the relation:

$${\lambda }_r=2c\pi \sqrt{LC}$$ 4

Fano resonance in symmetric crisscrosses structure

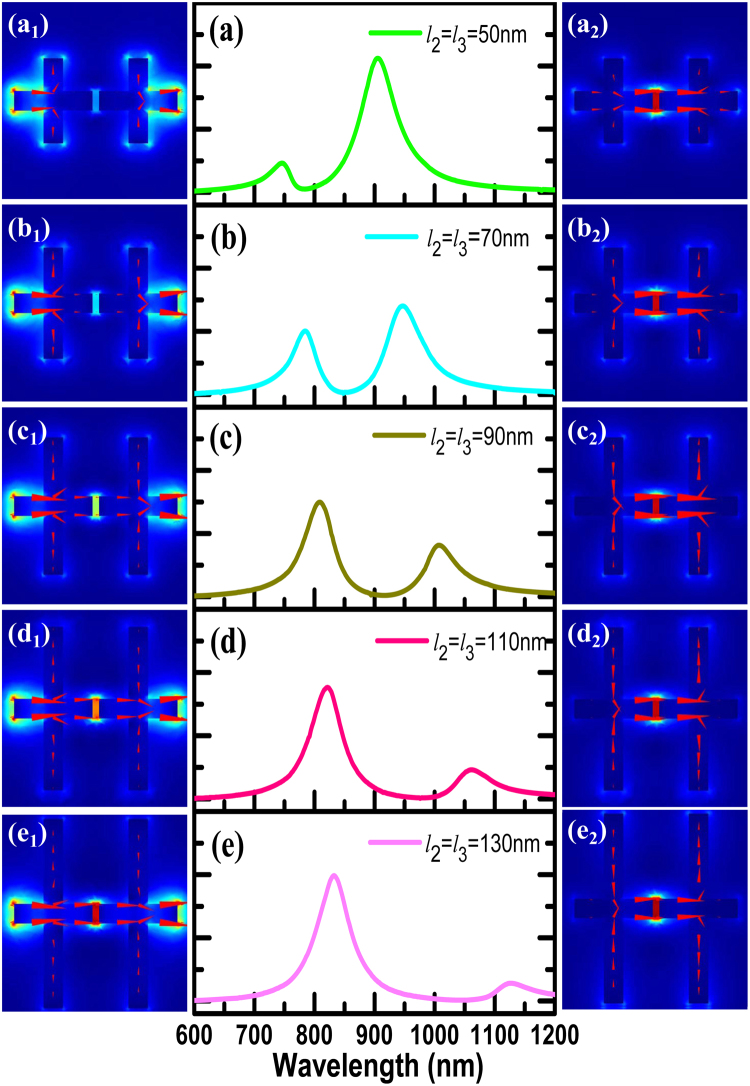
The LC circuit model would be useful to predict how the resonances shift as the varied shape and position of the elements. In order to verify its effectiveness, we have rigorous simulation calculations. We flexibly change the length of l₂ and l₃, so that their values are l₂ = l₃ = 50, 70, 90, 110, 130 (nm), and other parameters remain unchanged. In the symmetrical crisscross dimer, we simply express structural adjustment by describing the changes in l₂ value instead of the description of l₂ and l₃. When the length of l₂ is gradually increased, the resonance scattering spectra is shown in Fig. 5(a–e). The interaction between the electric dipole resonance and the magnetic dipole resonance leads to a significant Fano resonance. Simultaneously, the spectral line shape can be flexibly controlled with the increase of l₂. The resonance wavelength dependence on l₂ is shown in Fig. 6. The red dots indicate the simulated resonant mode, and the black rectangles represent the calculated LC resonance mode. With the length of l₂ gradually increasing, when the magnetic dipole resonant mode induced by the subunits l₂ matches with electric dipole the resonance provided by the nanorod dimmer of length l₁, the two modes will produce strong coupling phenomenon and linewidth of the coupled states appears obvious intersect splitting phenomenon, as shown in the anti-crossing region. The spectral line shape can be flexibly controlled with the adjustment of l₂. However, when the length of l₂ continues to increase, the two modes will be independent of each other, keeping their own characteristics due to their mismatch. According to formula (4), the LC resonant mode we calculated is in good agreement with the simulation, as shown in the black rectangles in Fig. 6. So this method can be well used to predict the resonance mode 2 by adjusting the length of l₂.

Figure 5.

(a–e) Simulated scattering resonance properties for the l₂ = l₃ = 50, 70, 90, 110, 130 (nm); (a₁–e₁) and (a₂–e₂) The electric field intensity and current distribution for resonance mode 1 and mode 2, respectively.

Figure 6.

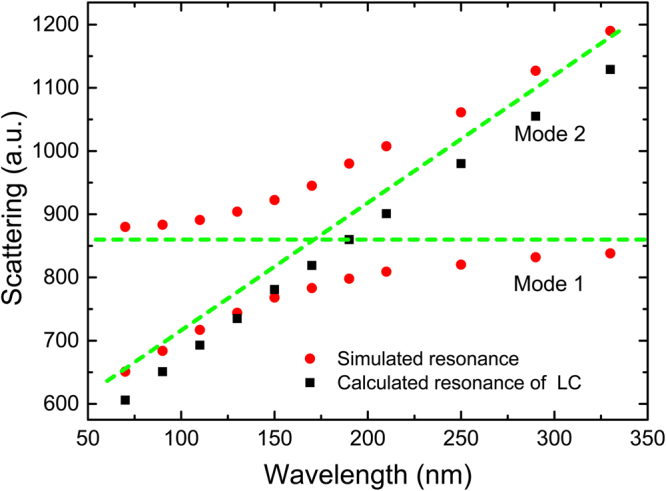
Dependence of resonance wavelength on the length l₂ and l₃. The red dots indicate the simulated resonant mode 1 and mode 2, the black rectangles represent the calculated resonance.

Figure 5 (a₁–e₁) and (a₂–e₂) depict the electric field intensity and current density distributions of modes 1 and mode 2, respectively. It can be seen from the modes 1 in Fig. 5(a₁–e₁), bonding dipoles are formed in the bottom and top parts in the crisscross dimer. When the l₂ length is relatively short, the electric field “hotspot” is mainly concentrated at the end of the end-end nanorod dimer due to the influence of the subunit l₂, and the current density distribution is mainly around the outer corners (from l₁ to l₂ or vice versa). With the increase of l₂, the electric field “hotspot” moves from the end to the middle gap, obviously. It is important for us to realize the same “hotspot” distribution. Furthermore, for the mode 2 in Fig. 5(a₂–e₂), it originates from the opposite charge flow between two subunits of the length l₂, which builds up intense magnetic fields. It is clear that the electric field “hotspot” is always localized at the gap position.

Multi-plasmon resonance in asymmetric crisscross dimer

Obviously, structural symmetry has not been destroyed in our designed crisscross dimer. It has been proved that the symmetric structure can produce a Fano-like resonance. However, another striking spectral characteristic is found in Fig. 7. In the crisscross dimer, when the sum of l₂ and l₃ is a fixed value of 150 nm (shown in Fig. 7(a)), the resonant spectra exhibits a clear asymmetric Fano line shape due to the interaction between the magnetic dipole and the electric dipole, as described above. However, we do not change the sum of l₂ and l₃, only adjust the length of l₂ and l₃ to make the difference m = l₂ − l₃. The scattering performance is shown in Fig. 7(b–e). When m is not equal to 0, the magnetic dipole moments at the bottom and the top parts of the crisscross dimer are unequal, so that the resonance mode 2 splits to appear an additional resonance peak³⁰. This result indicates that the spectral linetype can be adjusted by changing the m value, and it provides a new method for achieving multiple plasmonic resonance.

Figure 7.

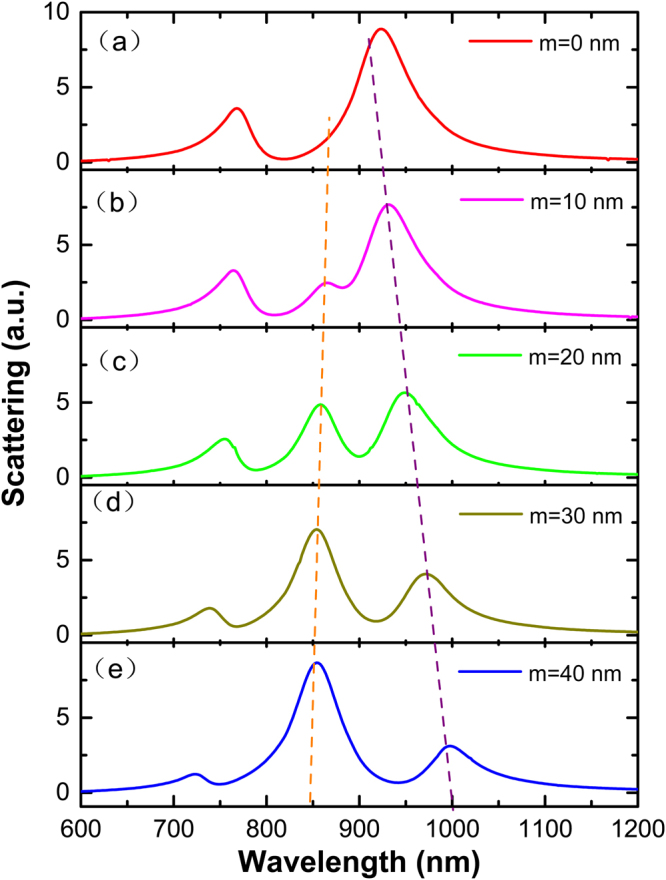
Simulated scattering resonance properties in asymmetry crisscross dimer with different values between l₂ and l₃. The sum of l₂ and l₃ is a fixed value of 150 nm, m represents the difference between l₂ and l₃ (m = l₂ − l₃).

The SECARS based on crisscross dimer

Recently, the development of substrate has provided tremendous impetus for surface-enhanced spectroscopy studies. CARS has also been widely studied to enable the detection of single molecules³⁵ and the design of surface enhanced spectroscopic substrate³⁶. We are known that it is a third-order nonlinear optical process. When the pump beam with frequency ω_p and the Stokes beam with frequency ω_s interact with the medium and the frequency difference ω_p−ω_s satisfies the Raman dipole-forbidden band distribution condition of the molecule, it will lead to the generation of an anti-Stokes signal with frequency ω_as. The CARS signal will result in resonance enhancement at the position of the resonance peak. The enhanced CARS signal may be realized using a metal plasmonic substrate, which can be regarded as surface enhanced CARS (SECARS). The electromagnetic field enhancement factor (EF) at the anti-Stokes frequency is expressed as:

$$G_{SECARS}={|E({\omega }_p)/E_0({\omega }_p)|}^4\times {\left|E({\omega }_s)/E_0({\omega }_s)\right|}^2\times {\left|E({\omega }_{as})/E_0({\omega }_{as})\right|}^2={g_p}^4\times {g_s}^2\times {g_{as}}^2$$ 5

Which implies that the CARS signal enhancement of local electromagnetic field is determined by three characteristic frequencies. The g_p, g_s and g_as are the enhancements of the localized electric fields at the pump($|E({\omega }_p)/E_0({\omega }_p)|$), Stokes($\left|E({\omega }_s)/E_0({\omega }_s)\right|$) and anti-Stokes ($\left|E({\omega }_{as})/E_0({\omega }_{as})\right|$) resonance, respectively. Thus a suitable plasmonic substrate that achieves the CARS signal will provide strong electromagnetic field depending on three characteristic frequencies. If the three resonant modes that form the “mixed frequency coherent mode” have same spatial positions. It will be useful as a CARS substrate to achieve a strong field enhancement. Simultaneously, the surface plasmonic resonance plays a crucial role in exciting extremely large intensities near the metal surface and field localization is always induced by constructive coherences in nanostructures³⁷.

In our designed the crisscross dimer structure, when the length of l₂ and l₃ is adjusted so that they are not equal, three different plasmonic resonances can be achieved. In order to achieve large CARS signal enhancement, it is necessary to localize the “hotspot” positions of the three resonant frequencies at the same spatial location. Only in this way can the maximum resonance enhancement be realized. Based on CARS performance studies of crisscross dimer nanostructures, we matched and achieved CARS signal enhancement for the different configuration parameters by adjusting the length of nanorods l₁, l₂ and l₃, keeping other parameters constant, as shown in Table 1. The large SECARS EF with the order of ~10¹² can be achieved based on multi-plasmon resonance.

Table 1.

Evaluation of the SECARS EF with the different configuration parameters.

Structure	l1(nm)	l2(nm)	l3(nm)	Anti-Stokes		Pump		Stokes		GSECARS
				λ(nm)	gas	λ(nm)	gp	λ(nm)	gs
1	125	270	200	718	11.2	800	29.3	885	60.7	3.4*1011
2	100	240	200	730	21.5	821	37	1010	56.8	2.8*1012
3	114	294	200	714	16.6	800	52.9	912	59.7	7.9*1012

Also, we have calculated magnitude of the SECARS EF for a Raman mode of molecules at 2278 cm⁻¹. We tune the geometric parameters of nanostructure so that middle resonance peak corresponds to the frequency of the pump laser, then the dipole resonance mode 1 and another resonance peak correspond to the anti-Stokes and Stokes regions in the spectra, respectively. When l₁ = 83 nm, l₂ = 212 nm, d = 8 nm and m = 34 nm, we can choose 848 nm pump laser, and the anti-Stokes and Stokes wavelengths are 654 nm and 1048 nm, respectively. The electric field distribution at three different wavelengths is shown in the Fig. 8.

Figure 8.

The simulated distributions of the electric field intensity and current distribution at the three different resonance wavelengths: (a) λ₁ = 654 nm, (b) λ₂ = 846 nm, (c) λ₃ = 1048 nm, corresponds to anti-Stokes, pump and Stokes wavelength, respectively.

It clearly shows that the electric field can be localized at the same gaps at three different resonance wavelengths. Based on formula (5), we can calculate the corresponding CARS signal EF about ~10¹³ ($G_{SECARS}={75.1}^4\times$${21.2}^2\times {26.5}^2\approx 1.0\times {10}^{13}$). This result suggests that crisscross dimer nanostructure have great promise to achieve huge electromagnetic field enhancement for single-molecule detection.

Conclusions

In this paper, we have studied and analyzed the crisscross dimer in the scattering system. The crisscross dimer exhibit Fano resonances via the destructive interference between an electric dipole mode and magnetic dipole modes supported by different subelements. Its scattering character is strongly depending on the length of the l₂ and l₃. Also, it has been proved that the LC circuit model can be used to predict the magnetic dipole resonances in this structure, which plays an important role for the design and adjustment of structure, and provides a new method for structural design in the future scientific research process. We have shown that the multi-resonance electric “field hotpots” can be localized at the same space position, which can be use to achieve a huge CARS signal field enhancement, up to 10¹³. Thence, the crisscross dimer have an important guiding significance for detectors or other optical devices.

Author Contributions

Junqiao Wang and Jia Zhang conceived the idea. Jia Zhang completed the numerical simulation and wrote the manuscript. Jia Zhang, Shu Chen, Junqiao Wang, Kaijun Mu, Chunzhen Fan, Erjun Liang, and Pei Ding discussed the results and contributed to the manuscript.

Competing Interests

The authors declare that they have no competing interests.