Abstract
Modern medicine is overwhelmed by a plethora of both established risk factors and novel biomarkers for diseases. The majority of this information is expressed by probabilistic measures of association such as the odds ratio (OR) obtained by calculating differences in average “risk” between exposed and unexposed groups. However, recent research demonstrates that even ORs of considerable magnitude are insufficient for assessing the ability of risk factors or biomarkers to distinguish the individuals who will develop the disease from those who will not. In regards to coronary heart disease (CHD), we already know that novel biomarkers add very little to the discriminatory accuracy (DA) of traditional risk factors. However, the value added by traditional risk factors alongside simple demographic variables such as age and sex has been the subject of less discussion. Moreover, in public health, we use the OR to calculate the population attributable fraction (PAF), although this measure fails to consider the DA of the risk factor it represents. Therefore, focusing on CHD and applying measures of DA, we re-examine the role of individual demographic characteristics, risk factors, novel biomarkers and PAFs in public health and epidemiology. In so doing, we also raise a more general criticism of the traditional risk factors’ epidemiology. We investigated a cohort of 6103 men and women who participated in the baseline (1991–1996) of the Malmö Diet and Cancer study and were followed for 18 years. We found that neither traditional risk factors nor biomarkers substantially improved the DA obtained by models considering only age and sex. We concluded that the PAF measure provided insufficient information for the planning of preventive strategies in the population. We need a better understanding of the individual heterogeneity around the averages and, thereby, a fundamental change in the way we interpret risk factors in public health and epidemiology.
Abbreviations: AUC, Area under the ROC curve; ACE, Average causal effect; CABG, Coronary artery bypass graft; CHD, Coronary heart disease; CRP, C-reactive protein; DA, Discriminatory accuracy; FPF, False positive fraction; HR, Hazard ratios; HDL, High-density lipoprotein cholesterol; ICE, Individual causal effect; Lp-PLA2, Lipoprotein-associated phospholipase A2; LDL, Low-density lipoprotein cholesterol; NTBNP, N-terminal pro–brain natriuretic peptide; OR, Odds ratio; PCI, Percutaneous coronary intervention; PAH, Phenylalanine hydroxylase; PKU, Phenylketonuria; PAF, Population attributable fraction; RCT, Randomized clinical trial; ROC, Receiver operating characteristic; RR, Relative risk; MDC study, The Malmö Diet and Cancer; TPF, True positive fraction
Keywords: Risk factors, Coronary heart disease, Discriminatory accuracy, Population attributable fraction, Over-diagnosis, Overtreatment, Individual heterogeneity, Multilevel analysis
Highlights
-
•
There is a plethora of differences in “average” risk between exposed and unexposed groups of individuals.
-
•
Individual heterogeneity around average values is seldom considered in Public Health.
-
•
Measures of discriminatory accuracy (DA) informs on the underlying individual heterogeneity.
-
•
Most know risk factors and other categorizations associated with diseases have low DA.
-
•
We need a fundamental change in the way we investigate risk factors and other categorizations in Public Health.
1. Introduction
Modern medicine is overwhelmed by a plethora of both traditional risk factors and novel biomarkers for diseases. All over the world, large amounts of economic and intellectual resources are allocated to the identification of new biomarkers and risk factors for diseases. For this purpose, we normally use simple measures of average association such as the relative risk (RR) or the odds ratio (OR). When using those measures, the implicit expectation is that of our capacity to accurately distinguish the individuals who will develop the disease from those who will not, improves (Pepe, Janes, Longton, Leisenring, & Newcomb, 2004) in order for the provision of targeted preventive intervention. From a population-level perspective, we also use the RR or the OR of those risk factors to calculate the population attributable fraction (PAF). The PAF aims to distinguish the share of the disease burden in a population that is attributable to a certain risk factor and, therefore, is potentially preventable (Merlo and Wagner, 2013, Rockhill et al., 1998).
A classic example of the prevailing risk factors approach concerns preventive strategies for coronary heart disease (CHD) in which traditional risk factors such as, for example, smoking habits and blood pressure are systematically evaluated in healthcare, frequently within a risk score equation such as the Framingham, SCORE, QRISK, etc. (Cooney et al., 2009, Greenland et al., 2003). Thereafter, individuals receive treatment according to their predicted level of disease risk. Namely, screening and preventive interventions are closely linked since the measurement of risk factors is aimed at discriminating which individuals are, and which are not, candidate for different degrees of preventive treatment (Rockhill, 2005).
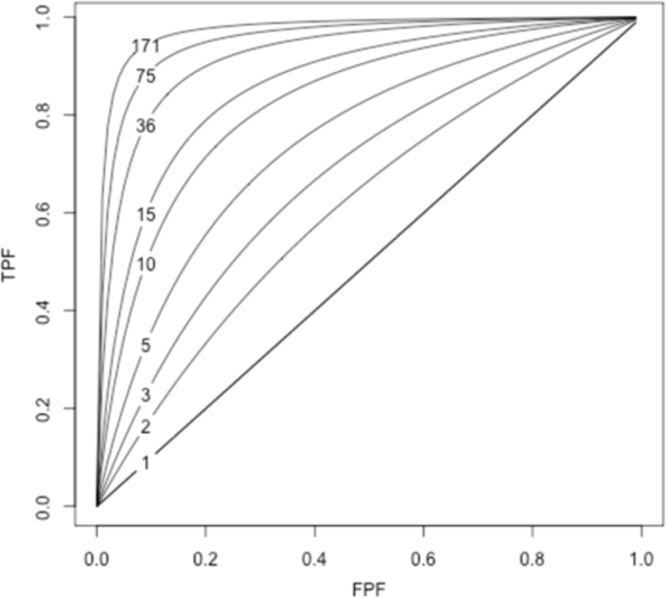
Nevertheless, during the last few decades, a number of relevant publications (Boyko and Alderman, 1990, Khoury et al., 1985, Pepe et al., 2004, Royston and Altman, 2010, Wald et al., 1999, Ware, 2006) have pointed out that measures of association alone are unsuitable for this discriminatory purpose. In fact, what we normally consider as a strong association between a risk factor and a disease (e.g., an OR for a disease of 10), is related to a somewhat low capacity of the risk factor to discriminate cases and non-cases of disease in the population (Pepe et al., 2004, Wald et al., 1999). Pepe et al. (2004), illustrated that, in order to obtain a suitable discriminatory accuracy (DA) of, for example, a true positive fraction (TPF) = 90% and a false positive fraction (FPF) = 5%, we would need an OR = 176. See Fig. 1 and elsewhere (Pepe et al., 2004) for an extended explanation.
Fig. 1.
Correspondence between the true-positive fraction (TPF) and the false-positive fraction (FPF) of a binary risk factor and the odds ratio (OR). Values of TPF and FPF that yield the same OR are connected (The figure has been created following the model described elsewhere by Pepe et al. (2004).
Therefore, from a clinical and even from a public health perspective, it is not enough to know the magnitude of the association between the exposure and the disease, what matters most is its DA, i.e., the capacity of the exposure to discriminate between individuals who will subsequently suffer a disease from those who will not. It does not matter whether the exposure is a novel biomarker, a traditional risk factor (Juarez, Wagner, and Merlo, 2013; Rodriguez-Lopez, Wagner, Perez-Vicente, Crispi, and Merlo, 2017), or any other exposure categorization shaped by socioeconomic (Axelsson-Fisk & Merlo, 2017), ethnic (Wemrell, Mulinari, & Merlo, 2015), geographic (Merlo, Wagner, Ghith, and Leckie, 2016), or other criteria (Merlo and Mulinari, 2015, Wemrell et al., 2017b). Therefore, and from a public health perspective, it seems necessary to not only revisit the value added of both traditional risk factors and novel biomarkers over and above simple demographic characteristics such as age and sex, but also even the interpretation of the PAF, since this measure does not consider the DA of the risk factors it represents (Merlo and Wagner, 2013).
This critical approach is of fundamental relevance since —in analogy with diagnostic tests— promotion of screening and treatment of risk factors/biomarkers with a low DA may lead to unnecessary side effects and costs. The approach also raises ethical and political issues related to risk communication (Li et al., 2009) and the perils of both unwarranted medicalization (Conrad, 2007) and stigmatization of individuals with the risk factor/biomarker. There is also a growing apprehension that financial interests might lead to a market-driven approach to introducing and expanding screening (Andermann and Blancquaert, 2010) and treatment. In the end, an indiscriminate use of risk factors and biomarkers with low DA may shadow the identification of relevant health determinants and harm the scientific credibility of modern epidemiology.
The ideas discussed above are relevant in many areas of clinical and public health research. For instance, the incremental value of assessing levels of biomarkers (e.g., C-reactive protein, Cystatin C, LpPLA2, NTBNP) in combination with traditional risk factors (e.g., cholesterol, blood pressure, smoking, diabetes) for the prediction of cardiovascular diseases has been debated (Cooney et al., 2009; Melander et al., 2009; Wald & Law, 2004; Zethelius et al., 2008). Moreover, some authors have even questioned the value of adding information on various traditional risk factors to risk predictions based exclusively on age (Wald, Simmonds, and Morris, 2011). In fact, the historical identification of risk factors was not based on an exhaustive scrutiny of all candidate factors supported by measures of DA. Indeed, the identification and use of traditional risk factors was promoted by insurance companies on the basis of simple physiopathological mechanisms (e.g., hypertension) and the availability of measurement instruments (e.g., the sphygmomanometer) (Kannel, Gordon, & National Heart Institute (U.S.), 1968; Keys, 1980; Rothstein, 2003).
In the present study, focusing on CHD, we investigate two concrete questions. Firstly, we aim to quantify the extent to which the DA of the simple demographic variables age and sex is improved by adding traditional cardiovascular risk factors and novel biomarkers. Although seemingly straightforward, this question has nevertheless been scarcely discussed in the literature (Wald et al., 2011). Secondly, we aim to analyze the relation between measures of PAF and the DA of the risk factors used for the computation of the PAF. This issue is of central relevance to planning strategies of prevention based on specific risk factors or a combination of them. For the purpose of our study, we reanalyze data from the cardiovascular cohort of the Malmö Diet and Cancer (MDC) study (Melander et al., 2009).
2. Population and methods
2.1. Subjects
The MDC study is a population-based, prospective epidemiologic cohort of 28 449 individuals enrolled between 1991 and 1996. From this cohort, 6103 individuals were randomly selected to participate in the MDC cardiovascular cohort, which was primarily designed to investigate the epidemiology of carotid artery disease (Persson, Hedblad, Nelson, and Berglund, 2007). From this sample, we excluded participants with prior coronary artery bypass graft (CABG), percutaneous coronary intervention (PCI), ischemic heart disease, or myocardial infarction or stroke at baseline (n = 176).
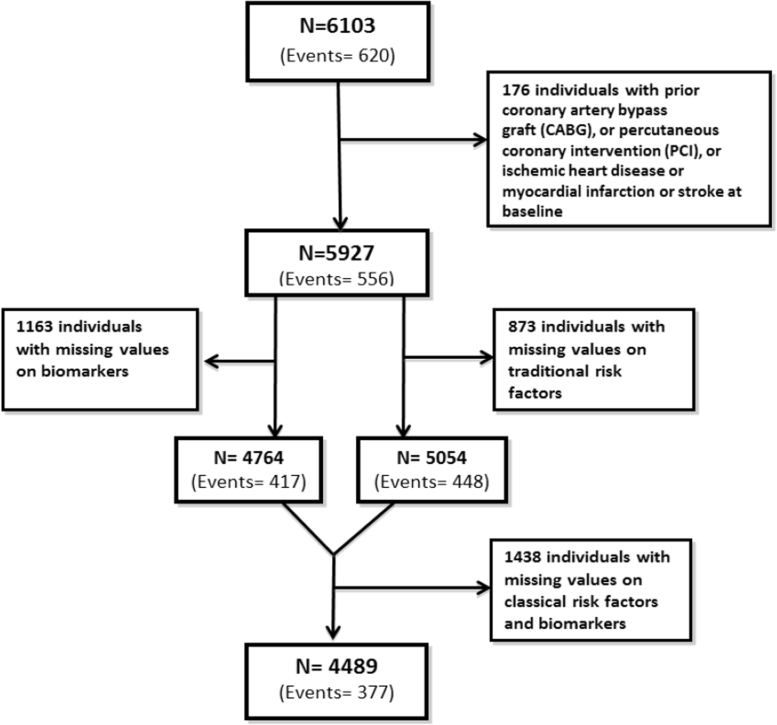
Of the remaining 5927 participants, 5054 had complete information on traditional risk factors, 4764 on biomarkers, and 4489 on both traditional risk factors and biomarkers. See Fig. 2 for more detailed information. The analyzed sample did not differ from eligible participants in the original MDC cardiovascular cohort with regards to mean age, sex, mean systolic and diastolic blood pressure, mean body mass index, and smoking prevalence (Melander et al., 2009).
Fig. 2.
Flow diagram indicating the number of individuals remaining in the study sample after the application of the exclusion criteria.
The database is available on request from the MDC study project (http://www.med.lu.se/klinvetmalmo/befolkningsstudier/malmoe_kost_cancer_och_malmoe_foerebyggande_medicin/uttagsansoekningar).
2.2. Coronary end points
The end point in our analyses was the first ever CHD event defined as fatal or nonfatal myocardial infarction, CABG, PCI or death due to ischemic heart disease according the International Classification of Diseases 9th (ICD-9) and 10th (ICD10) revisions. We operationalized myocardial infarction using the diagnosis codes 410 (ICD-9) or I21 (ICD-10), and ischemic heart disease as codes 412 and 414 (ICD-9) or codes I22-I23 and I25 (ICD10). We identified CABG and PCI according the International Classification of Procedures 9th version codes 36.1, 36.2 and 10th version codes 0210–0213.
Case finding was performed by record linkage between the study cohort and the Swedish Hospital Discharge Register and the Swedish Cause of Death Register. For the linkage, we used a 10-digit personal identification number that is unique for every individual residing in Sweden. Follow-up for events extended from the baseline date when the participants entered the study in 1991–1996 to January 1, 2009. The total and median number of follow-up years were, respectively, 88 789 and 16 years. The number of CHD events is depicted in Fig. 3. The identification of outcomes using these Swedish registers has been previously validated and judged to be adequate (Engstrom et al., 2001, Hammar et al., 2001, Merlo et al., 2000, National Board of Health and Welfare, 2000, 2010a, 2010b). To facilitate the discussion, we used the terminology of a case-control study design and denominated individuals that suffer from a CHD event as “cases” and those that remain free from CHD event as “controls”.
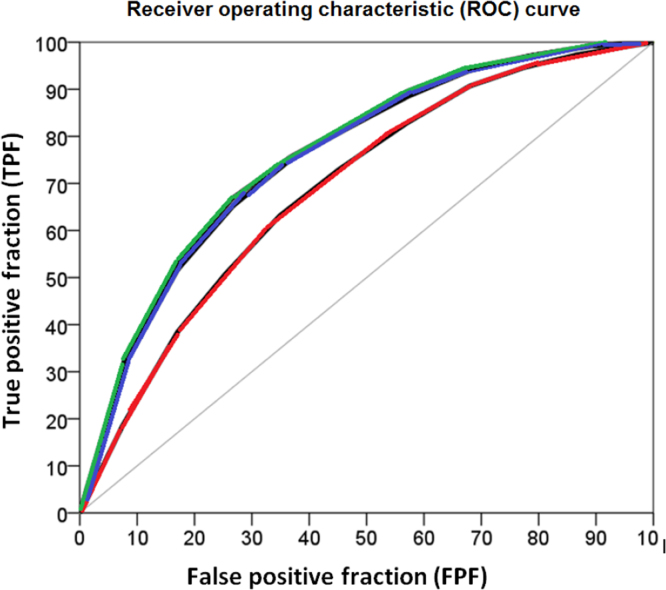
Fig. 3.
Receiver operating characteristic (ROC) curves for the model including age and sex (red color) and the models including age, sex and traditional risk factors (blue color) and age, sex, traditional risk factors and biomarkers (green color), respectively.
2.3. Assessment of cardiovascular risk factors and biomarkers
We obtained information from the medical history, physical examination, and laboratory assessments that all the participants underwent at the baseline period of the cardiovascular arm of the MDC study.
2.3.1. Classical cardiovascular risk factors
Blood pressure in mmHg was measured using a mercury-column sphygmomanometer after 10 minutes of rest in the supine position. Only two individuals had missing values on blood pressure level. Using weight and height, we calculated Body Mass Index (BMI) in kg/m2. Eight individuals had missing values on BMI. Diabetes mellitus was defined as a fasting whole blood glucose level greater than 109 mg/dL (6.0 mmol/ L), a self-reported physician diagnosis of diabetes, or use of antidiabetic medication. Information on medication use was based on a personal diary (Merlo, Berglund, Wirfalt, Gullberg, Hedblad et al., 2000). We measured (mmol/l) fasting triglycerides, total cholesterol, high-density lipoprotein (HDL) cholesterol and low-density lipoprotein (LDL) cholesterol (Friedewald’s formula) according to standard procedures at the Department of Clinical Chemistry, Skåne University Hospital in Malmö. We computed the LDL/HDL ratio. A total of 703 individuals had missing information on the LDL/HDL ratio. Information on cigarette smoking was obtained by a self-administered questionnaire, with current cigarette smoking defined as any use within the past year. In total, 873 individuals had missing information on one or more of the classical risk factors indicated above.
2.3.2. Cardiovascular biomarkers
Cardiovascular biomarkers were analyzed in fasting EDTA plasma specimens that had been frozen at -80°C immediately after collection. Levels of C-reactive protein (CRP) in mg/L were measured using a high-sensitivity assay (Roche Diagnostics, Basel, Switzerland). Information on CRP was missing in 769 individuals. Levels of cystatin C in mg/L were measured using a particle-enhanced immunonephelometric assay (N Latex Cystatin C; Dade Behring, Deerfield, Illinois) (Shlipak et al., 2005). Information on cystatin C was missing in 911 individuals. Lipoprotein-associated phospholipase A2(Lp-PLA2) activity in nmol/min/mL was measured in duplicate using [3 H]-platelet activating factor as substrate (Persson et al., 2007). Information on Lp-PLA2 activity was missing in 672 individuals. Levels of N-terminal pro–brain natriuretic peptide (NTBNP) in pg/mL were determined using the Dimension RxL automated NTBNP method (Siemens Diagnostics, Nürnberg, Germany) (Di Serio et al., 2005). We dichotomized this variable and considered the NTBNP to be elevated when the values were higher than 309 pg/mL (Zethelius et al., 2008). Information on NTBNP activity was missing in 904 individuals. In total, 1163 individuals had missing information in one or more of the biomarkers indicated above.
2.4. Statistical analyses
2.4.1. Measures of association
We performed Cox proportional hazards regression models to examine the association (i.e., hazard ratios (HR) and 95% confidence intervals (CI)) between, on the one hand, age, sex, traditional risk factors and biomarkers and, on the other, CHD events. We also used logistic regression, since the follow-up was complete and the length of the follow-up was not related to the measurement of exposure. The logistic regression allows for the easy calculation of both odds ratio (OR) and 95% CI, predicted probabilities and measures of DA (see also the next Section, 2.4.2).
We performed a series of simple regression analyses modeling one variable at a time (i.e., age, sex, each risk factor and each biomarker alone). Thereafter, we created combined models including age and sex, traditional risk factors, biomarkers, biomarkers and/or traditional risk factors and the correspondent age and sex adjusted models. In the full model, we performed a stepwise logistic regression (see Table 3). The use of stepwise regression has been criticized (Harrell, 2001, Babyak, 2004). It is recommended to have a priori knowledge of the variables selected in the models and, preferably, that this selection should be performed within the framework of a carefully designed causal diagram. However, our empirical study did not aim at identifying novel risk factors and biomarkers, but was instead focused on prediction. Furthermore, variables such as systolic blood pressure, diastolic blood pressure and hypertension arterial, glucose and diabetes or the cholesterol variables bear similar predictive information. In addition, we performed sensitivity analyses and tried different variable definitions and different models, achieving similar results in terms of prediction. Therefore, in order to achieve a parsimonious model, we let the stepwise regression choose the variables in the combination models.
Table 3.
Discriminatory accuracy of traditional risk factors and of biomarkers for identifying individuals with and without coronary heart disease. Values are area under the receiver operating characteristic (AUC) curve and 95% confidence intervals (CI) as well as the True Positive Fraction (TPF) for a False Positive Fraction (FNF) of 5% (TPFFPF 5%).
| AUC (95% CI) |
TPFFPF5% | ||
|---|---|---|---|
| Difference | |||
| Age | 0.63 (0.60–0.65) | -0.05 | 0.08 (0.06–0.10) |
| Sex | 0.61 (0.59–0.64) | -0.07 | –a |
| Age and sex | 0.68 (0.66–0.70) | Reference | 0.09 (0.07–0.13) |
| Traditional risk factors | |||
| – Systolic blood pressurea | 0.65 (0.62–0.67) | -0.03 | 0.10 (0.08–0.14) |
| – Diastolic blood pressure | 0.60 (0.58–0.62) | -0.08 | 0.08 (0.05–0.10) |
| – Hypertension arterial | 0.58 (0.56–0.61) | -0.10 | – |
| – Glucose | 0.61 (0.59–0.64) | -0.07 | 0.14 (0.10–0.17) |
| – Diabetes | 0.57 (0.54–0.59) | -0.11 | – |
| – Total cholesterol | 0.57 (0.54–0.59) | -0.11 | 0.06 (0.04–0.08) |
| – HDL cholesterol | 0.64 (0.61–0.66) | -0.04 | 0.02 (0.01–0.04) |
| – LDL cholesterol | 0.58 (0.55–0.61) | -0.10 | 0.07 (0.04–0.09) |
| – LDL/HDL ratio | 0.65 (0.63–0.68) | -0.03 | 0.11 (0.09–0.17) |
| – Triglycerides | 0.61 (0.58–0.63) | -0.07 | 0.09 (0.07–0.12) |
| – Body Mass Index (BMI) | 0.59 (0.56–0.61) | -0.09 | 0.07 (0.05–0.10) |
| – Cigarette smoking | 0.58 (0.55–0.60) | -0.14 | – |
| Biomarkers | |||
| – CRP | 0.61 (0.58–0.63) | -0.07 | 0.09 (0.06–0.11) |
| – Cystatin C | 0.62 (0.59–0.65) | -0.06 | 0.11 (0.08–0.14) |
| – Lp-PLA2 activity | 0.61 (0.58–0.64) | -0.07 | 0.11 (0.07–0.14) |
| – N-BNP | 0.54 (0.51–0.57) | -0.14 | 0.10 (0.07–0.12) |
| – N-BNP (309 pg/mL) | 0.52 (0.49–0.55) | -0.16 | – |
| Combinations | |||
| – Traditional risk factors (RF) | 0.71 (0.69–0.74) | 0.03 | 0.19 (0.16–0.23) |
| – Biomarkers (BM) | 0.67 (0.64–0.69) | -0.01 | 0.13 (0.10–0.17) |
| – RF and BM | 0.74 (0.71–0.76) | 0.06 | 0.21 (0.17–0.26) |
| – Age, sex and RF | 0.75 (0.73–0.77) | 0.07 | 0.22 (0.18–0.27) |
| – Age, sex and BM | 0.72 (0.69–0.74) | 0.04 | 0.16 (0.11–0.20) |
| – Age, sex, RF and BM | 0.77 (0.74–0.79) | 0.08 | 0.23 (0.17–0.28) |
CRP: C-Reactive Protein. LpPLA2: Lipoprotein-associated phospholipase A2. NTBNP: N-terminal B-type natriuretic peptide.
Value not calculated as the variable is dichotomous.
All variables except sex, diabetes and smoking habits were continuous. To facilitate the interpretation of the measures of association, we categorized the continuous variables into groups defined by cut-offs based on quartile values or on SDs.
2.4.2. Measures of discriminatory accuracy
In everyday practice, measures of association are frequently used to gauge the ability of a factor to predict future cases of disease. For example, when we say that people with diabetes have a threefold higher risk for CHD (i.e., OR = 3), we are implicitly using diabetes as a predictive test to classify who will, and will not, suffer from a coronary event in the population. However, contrary to popular belief, measures of association alone are inappropriate for this discriminatory purpose. The reader can find an extended explanation of this concept elsewhere (Choi, 1997, Law et al., 2004, Pepe et al., 2008, Pepe et al., 2004, Royston and Altman, 2010, Wald and Morris, 2011, Wald et al., 2005). Therefore, we applied the following measures of DA.
2.4.2.1. The true positive fraction (TPF) and the false positive fraction (FPF)
The DA of a risk factor is better appraised by measuring the TPF and the FPF for the specific thresholds of the risk factor variable. The TPF expresses the probability of having been exposed to the risk factor if the disease occurs (i.e., cases that are exposed to the risk factor).
| (1) |
The FPF indicates the probability of having been exposed to the risk factor when the disease does not occur (i.e., controls exposed to the risk factor).
| (2) |
2.4.2.2. TPF for a specific FPF of 5% (TPFFPF 5%)
We evaluated the DA of an exposure threshold by identifying the TPF for a specific FPF of 5% (Wald, Hackshaw, and Frost, 1999) and calculated 95% CIs. The choice of the FPF level is arbitrary, but 5% seems reasonable in public health medicine. Maintaining the FPF at a low level is crucial in primary screening (Pepe et al., 2008) and, analogously, in many public health interventions. For instance, if the pharmacological preventive treatment of a risk factor was launched on false positive individuals it would constitute an act of unnecessary medicalization (Kawachi and Conrad, 1996) with potentially unwanted adverse effects and costs.
2.4.2.3. The receiver operating characteristic (ROC) curve and the area under the ROC curve (AUC)
In the context of DA, the ROC curve is constructed by plotting the TPF against the FPF. The ROC curve informs in regard to the tradeoff between TPF and FPF when the threshold value of the predicted absolute risk for what we consider as a relevant definition of the existence or absence of a “risk factor” is moved. Because the ROC curve is a function of the TPF and FPF it provides information of crucial importance for quantifying DA (Pepe et al., 2004, Pepe, 2003, Zweig et al., 1992). A traditional measure of DA is the AUC or C statistic (Gerds, Cai, & Schumacher, 2008; Pepe et al., 2004; Pepe, 2003; Pepe, Janes, and Gu, 2007; Royston & Altman, 2010). The AUC measures discrimination; that is, the ability of the risk factor (i.e., the “test”) to correctly classify those with and without the disease. The accuracy of a test depends on how well the categorization (e.g., by a risk factor or biomarker) correctly classifies the individuals into those with and without the disease in question. The AUC extends from 0.5 to 1.0. An AUC = 0.5 means that the DA of the candidate risk factor or biomarker is similar to that obtained by flipping a coin. That is to say, a risk factor with an AUC = 0.5 is useless for predictive purposes. An AUC = 1.0 means complete accuracy. Arbitrarily, we could categorize the AUC as excellent (0.90–1.00), good (0.80–0.90), fair (0.70–0.80), poor (0.60–0.70) and fail (0.50–0.60).
2.4.2.4. The risk assessment plot
The risk assessment plot described by Pepe and colleagues (Pepe et al., 2008) and later applied by Pickering and Endre (Pickering and Endre, 2012) represents the TPF and FPF against the predicted risk. The greater the separation between TPF and FPF curves, the better the model is at discriminating between individuals with or without the event (i.e. cases and controls, respectively).
While the ROC curve plots the TPF versus the corresponding FPF for all possible threshold criteria, the risk assessment plot incorporates the predicted risk (i.e., risk score) and also informs in regard to the specific threshold risk related to each TPF-FPF pair, which is relevant information for deciding when to start a treatment or not (Pepe et al., 2008).
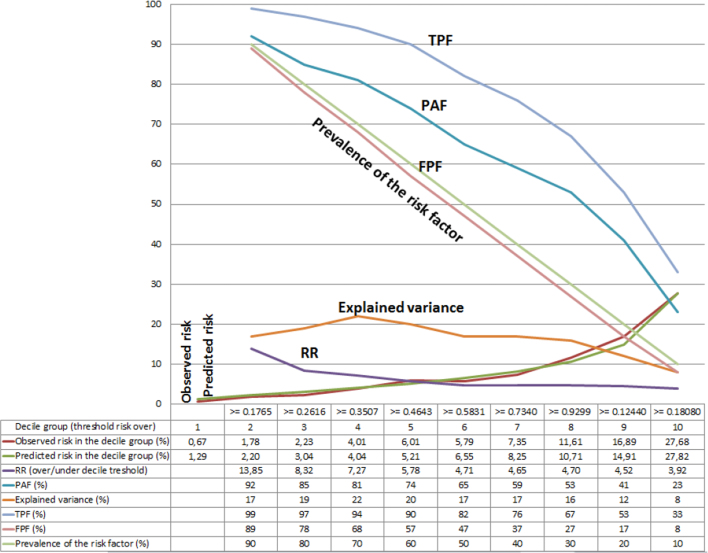
For obtaining the risk assessment plot, we created 10 groups by deciles of predicted CHD risk (i.e., risk score) according to the model under consideration. Thereafter, we defined binary risk factor variables by dichotomizing the continuous risk score according to specific decile values. That is, in the first definition of the risk factor variable, the unexposed individuals were those included in the first decile group, and the exposed were all other individuals. Analogously, in the last risk factor variable, the unexposed individuals were those included within the decile groups one to nine, and the exposed were the individuals in the tenth decile group. Finally, using the number of cases and controls in the exposed and unexposed categories, we calculated the TPF and FPFs for each risk threshold (see Fig. 4, Fig. 5).
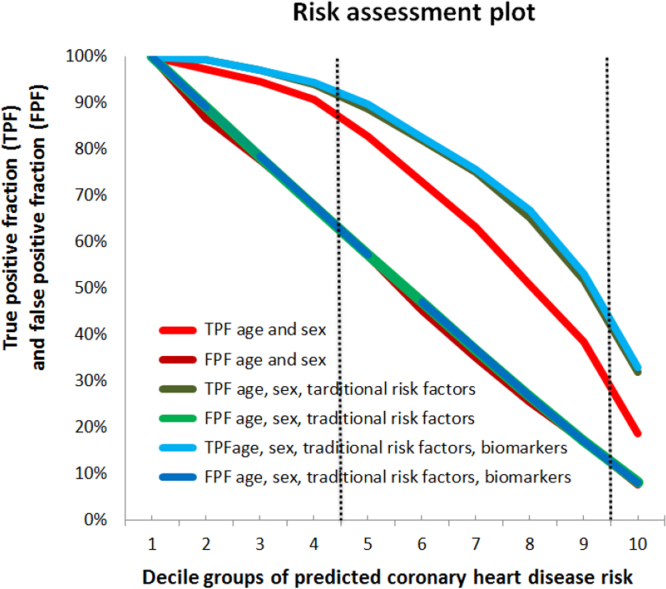
Fig. 4.
Risk assessment plots. Risk assessment plots for the model including age and sex (red color) and the models including age, sex and traditional risk factors (blue color) and age, sex, traditional risk factors and biomarkers (green color). To obtain the risk assessment plot we created 10 groups by deciles of predicted coronary heart disease risk (i.e., risk score) according to the model under consideration. Thereafter, we defined binary risk factor variables by dichotomizing the continuous risk score according to specific decile values. That is, in the first definition of risk factor variable, the unexposed individuals were those included in the first decile group, and the exposed were all the other individuals. Analogously, in the last risk factor variable, the unexposed individuals were those included within the decile groups one to nine, and the exposed were the individual in the tenth decile group. Finally, using the risk factor variables and the number of cases and controls in the exposed and unexposed categories, we calculated the TPF and FPFs for each risk threshold. IN COLOR.
Fig. 5.
Expanded risk assessment plot for the model including age, sex, traditional risk factors and biomarkers. The graph includes the true positive fraction (TPF), the false positive fraction (FPF), the population attributable fraction (PAF), the explained variance, the relative risk (RR), the observed and the predicted risk as well as the prevalence of the risk factor. For obtaining the risk assessment plot, we created 10 groups by deciles of predicted coronary heart disease risk (i.e., risk score) according the model under consideration. Thereafter, we defined binary risk factor variables by dichotomizing the continuous risk score according to specific decile values. That is, in the first definition of risk factor variable, the unexposed individuals were those included in the first decile group, and the exposed were all the other individuals. Analogously, in the last risk factor variable, the unexposed individuals were those included within the decile groups one to nine, and the exposed were the individuals in the tenth decile group. Finally, using the risk factor variables and the number of cases and controls in the exposed and unexposed categories, we calculated the TPF and FPFs for each risk threshold.
In Fig. 5, we obtained the risk score from the most elaborated model including age, sex, traditional risk factors and biomarkers. Thereafter, we constructed a risk assessment plot including, in addition to the TPF and FPF, the mean of the predicted and observed CHD risk of every decile group. We also added the prevalence of the risk factor (defined by the specific threshold), the RR, the values of the PAF (see Section 2.4.4. below) and the value of the variance explained (see Section 2.4.3 below).
2.4.2.5. Measuring improvement of the discriminatory accuracy
A main goal of our study was to quantify the improvement of the DA when reclassifying individuals according their predicted risk by adding traditional risk factors and biomarkers to a reference model including only age and sex. For this purpose, we quantified the difference between the AUCs and risk assessment plots of the models with traditional risk factors/biomarkers and the reference model including only age and sex.
2.4.3. Explained variance
DeMaris (DeMaris, 2002) stressed that measures of explained variance inform in regard to the discriminatory power of a model for distinguishing those who have experienced an event from those who have not. The author compared different measures of explained variance and concluded that the McKelvey and Zavoina Pseudo R2 ( ) (McKelvey and Zavoina, 1975) is an optimal estimator of discriminatory power in binary logistic regression.
| (3) |
where are the regression coefficients of the variables in the model and is the individual level variance of the underlying latent variable for the dichotomous outcome. We included the in the risk assessment plot.
2.4.4. Population attributable fraction (PAF)
The PAF can be interpreted as the proportion of disease cases over a specified time that would be prevented following elimination of the exposure, assuming that the exposure is causal (Rockhill et al., 1998).
In a simplified form, we can formulate the PAF as
| (4) |
where is the prevalence of the outcome in the population and is the prevalence of the outcome in the non-exposed individuals.
We can also express the PAF as
| (5) |
where is the relative is risk of the outcome in the exposed as compared with the unexposed individuals, and is the prevalence of the risk factor in the population. More information on this formula and on the relation between DA and PAF is available on request (Wagner P, & Merlo J. (2017). Measures of Discriminatory Accuracy (DA) and Population Attributable Fraction (PAF) in Epidemiology (manuscript under elaboration)).
To clarify the relation between the different measures indicated above, we constructed an expanded risk assessment plot (Pepe et al., 2008) (Fig. 5).
2.4.5. Model fitting
To assess global fitting of the risk models, we calculated modified Hosmer-Lemeshow statistics for models with increasing complexity (D’Agostino and Nam, 2004). We also plotted the observed and the predicted incidence of CHD events by decile groups of the predicted incidence (Hlatky et al., 2009) (Fig. 5). The correlation between observed and predicted values was very high in all models, but marginally higher in the one that included age, sex, traditional risk factors and biomarkers.
It is well known that model performance can be overestimated if it is estimated on the same dataset as the one used to fit the risk model, especially when the model includes many predictor variables (Moons et al., 2014). However, in our analyses, the model that included traditional risk factors and biomarkers together with age and sex showed only a minor improvement over the model including age and sex. Therefore, if our results are overestimations, the true DA of both traditional risk factors and biomarkers should be even lower than those obtained here, so our conclusion would be conservative.
For all analyses, we used Stata version 12 (StatCorp LP. 2011. College Station, TX), SPSS version 20, and “R” version 2.15.1.
3. Results
3.1. Characteristics of the population and measures of association
In this population of men and women without previous CHD events, around 9% developed such an event during the 18-year follow-up. As expected, compared with individuals who remained free from events (Table 1), those suffering from CHD were somewhat older, more frequently men, and had more traditional risk factors as well as elevated biomarkers. Our analyses also replicated the established associations between, on the one hand age, sex, traditional risk factors and biomarkers and, on the other, CHD (Table 2a, Table 2b).
Table 1.
Characteristics of individuals by presence of coronary heart disease during follow-up time.
| Coronary heart disease |
||||
|---|---|---|---|---|
| No | Yes | |||
| Mean | SD | Mean | SD | |
| Age (years) | 57 | 6 | 60 | 6 |
| Men (%) | 39% | 49% | 62% | 49% |
| Systolic blood pressure (mmHg) | 140 | 19 | 150 | 19 |
| Diastolic blood pressure (mmHg) | 87 | 9 | 90 | 9 |
| Body Mass Index (Kg/m2) | 26 | 4 | 27 | 4 |
| Cholesterol (mmol/l) | 6.1 | 1.1 | 6.4 | 1.1 |
| Triglycerides (mmol/l) | 1.3 | 0.8 | 1.6 | 1.0 |
| HDL (mmol/l) | 1.4 | 0.4 | 1.2 | 0.3 |
| LDL (mmol/l) | 4.1 | 1.0 | 4.4 | 1.0 |
| LDL/HDL ratio | 3.2 | 1.2 | 3.8 | 1.3 |
| Glucose (mmol/l) | 5.1 | 1.2 | 5.7 | 2.2 |
| Diabetes. | 7% | 25% | 18% | 39% |
| CRP (mg/L) | 2.5 | 4.3 | 3.4 | 4.8 |
| NTBNP (pg/mL) | 93.2 | 141.6 | 141.5 | 455.1 |
| Cystatin C (mg/L) | 0.8 | 0.1 | 0.8 | 0.2 |
| LpPLA2 activity (nmol/min/mL) | 44.9 | 12.8 | 49.9 | 13.7 |
| Smoking habits | ||||
|
41% | 49% | 28% | 45% |
|
32% | 47% | 36% | 48% |
|
5% | 21% | 6% | 23% |
|
23% | 42% | 31% | 46% |
CRP: C-Reactive Protein.
LpPLA2: Lipoprotein-associated phospholipase A2.
NTBNP: N-terminal B-type natriuretic peptide.
Table 2a.
Association between traditional risk factors and risk for coronary heart disease. Values are hazard ratios and 95% confidence intervals (CI).
| HR | 95% CI | |||
|---|---|---|---|---|
| Sex (men vs. women) | 2.48 | 2.09–2.94 | ||
| Age (years) | ||||
| 46–50 | 1.00 | |||
| 51–55 | 1.31 | 0.93–1.86 | ||
| 56–59 | 1.95 | 1.39–2.74 | ||
| 60–63 | 2.53 | 1.83–3.49 | ||
| 64–68 | 3.67 | 2.68–5.02 | ||
| Systolic blood pressure (mmHg) | ||||
| < 139 | 1.00 | |||
| 140‒159 | 2.19 | 1.78–2.69 | ||
| 160‒179 | 3.02 | 2.38–3.82 | ||
| > 180 | 4.3 | 3.12–5.92 | ||
| Diastolic blood pressure (mmHg) | ||||
| < 89 | 1.00 | |||
| 90‒99 | 1.63 | 1.36–1.96 | ||
| 100‒109 | 1.98 | 1.54–2.55 | ||
| > 110 | 2.34 | 1.41–3.89 | ||
| Total cholesterol (mmol/L) | ||||
| < 5.07 | 1.00 | |||
| 5.08 ‒ 6.17 | 1.4 | 1.02–1.92 | ||
| 6.18 ‒ 7.26 | 1.72 | 1.26–2.35 | ||
| > 7.27 | 1.97 | 1.4–2.77 | ||
| HDL (mmol/L) | ||||
| < 1.01 | 1.00 | |||
| 1.02 ‒ 1.38 | 0.58 | 0.47–0.72 | ||
| 1.39 ‒ 1.75 | 0.32 | 0.25–0.42 | ||
| > 1.76 | 0.24 | 0.17–0.35 | ||
| LDL (mmol/L) | ||||
| < 3.18 | ||||
| 3.19 ‒ 4.16 | 1.22 | 0.88–1.7 | ||
| 4.17 ‒ 5.15 | 1.77 | 1.28–2.44 | ||
| > 5.16 | 2.14 | 1.51–3.02 | ||
| HDL/LDL ratio | ||||
| < 2.06 | 1.00 | |||
| 2.07 ‒ 3.24 | 1.23 | 0.86–1.77 | ||
| 3.25 ‒ 4.42 | 2.29 | 1.62–3.25 | ||
| > 4.43 | 4.29 | 3.01–6.11 | ||
| (Log.)Triglycerides (mmol/L) | ||||
| < -0.27 | 1.00 | |||
| -0.26–0.20 | 2.48 | 1.69–3.63 | ||
| 0.21–0.67 | 2.98 | 2.03–4.37 | ||
| > 0.68 | 4.41 | 2.97–6.55 | ||
HDL: High-density lipoprotein cholesterol
LDL: Low-density lipoprotein cholesterol.
Table 2b.
Association between traditional risk factors and biomarkers and risk of coronary heart disease Values are hazard ratios and 95% confidence intervals (CI).
| HR | 95% CI | |||
|---|---|---|---|---|
| Diabetes (yes vs. no) | 3.11 | 2.51–3.86 | ||
| BMI (Kg/m2) | ||||
| < 23.15 | 1.00 | |||
| 23.16 - 25.38 | 1.50 | 1.14–1.96 | ||
| 25.39 - 28.06 | 1.86 | 1.43–2.42 | ||
| > 28.07 | 2.24 | 1.74–2.89 | ||
| Smoking habits | ||||
| Never | 1.00 | |||
| Past | 1.63 | 1.31–2.03 | ||
| Intermittent | 1.86 | 1.25–2.76 | ||
| Current | 2.09 | 1.66–2.62 | ||
| CRP (mg/L) | ||||
| < 0.70 | 1.00 | |||
| 0.71 - 1.40 | 1.25 | 0.92–1.71 | ||
| 1.41 - 2.80 | 1.82 | 1.38–2.39 | ||
| > 2.81 | 2.54 | 1.96–3.31 | ||
| Cystatin C (mg/L) | ||||
| < 0.69 | 1.00 | |||
| 0.70 -0.76 | 1.51 | 1.11–2.05 | ||
| 0.77 -0.85 | 1.92 | 1.43–2.57 | ||
| > 0.86 | 3.20 | 2.44–4.21 | ||
| LpPLA2 activity (nmol/min/mL) | ||||
| < 36.31 | 1.00 | |||
| 36.32 - 44.14 | 1.24 | 0.91–1.67 | ||
| 44.15 - 52.90 | 1.65 | 1.24–2.19 | ||
| > 52.91 | 2.47 | 1.89–3.23 | ||
| NTBNP (pg/mL) | ||||
| < 34 | 1.00 | |||
| 35–61 | 0.81 | 0.61–1.06 | ||
| 62–112 | 0.87 | 0.67–1.14 | ||
| > 113 | 1.41 | 1.10–1.80 | ||
| NTBNP (309 pg/mL) | Yes vs. No | 2.43 | 1.70–3.49 | |
CRP: C-Reactive Protein. LpPLA2: Lipoprotein-associated phospholipase A2. NTBNP: N-terminal B-type natriuretic peptide.
3.2. Measures of discriminatory accuracy
3.2.1. The ROC curve, AUC, TFPFNP 5%
Fig. 3 represents the ROC curves for model (A) including age and sex (red color), and models (B) and (C) including age, sex and traditional risk factors (blue color) and age, sex, traditional risk factors and biomarkers (green color), respectively.
Table 3 indicates that the AUC was slightly higher than 0.60 for both age and sex separately. However, the combination of both demographic variables increased the AUC to a value of 0.68. Analyzed individually, neither the traditional risk factors nor any of the novel biomarkers reached the value of the age and sex combination.
The AUC for the joint effect of all traditional risk factors was only 0.03 units higher than that of the AUC for age and sex. The AUC for the combination of all the biomarkers studied did not surpass the AUC for age and sex (i.e., the difference between AUCs was -0.01 units). The AUC for the model combining traditional risk factors and biomarkers but not age and sex was 0.74 which is just only 0.06 units higher than the AUC for the model including only age and sex. We also observed a minor improvement when adding traditional risk factors or biomarkers to the model with age and sex. We detected the highest AUC (i.e., 0.76) for the combined effect of age, sex, traditional risk factors and biomarkers, but compared to the model including only age and sex, the difference was somewhat small (i.e., 0.08). We do not provide 95% CIs for the differences between AUCs but only for the AUC values. However, this information allows for the evaluation of the uncertainty of the AUC differences.
Table 3 also informs in regard to the values of the TPFFPF 5% for all the models studied. Overall, the values of the TPFFPF 5% were very low. For instance, in the model with the highest AUC (i.e., age, sex, traditional risk factors and biomarkers) the TPFFPF 5% was 23%, which is certainly very low. Compared with the TPFFPF 5% of the model including age and sex, it represents an increase of 13%.
3.2.2. The risk assessment plot
To investigate DA, we performed logistic regression models including (A) age and sex, (B) traditional risk factors (blood pressure, cholesterol, diabetes, smoking), and (C) biomarkers (CRP, NTBNP, Cystatin C, LpPLA2 activity) and combinations of A, B, C.
The risk assessment plots presented in Fig. 4 inform that defining high risk individuals as those with a predicted risk equal or higher than the fourth decile value renders a FPF of 57% for all models (i.e., models A; A+B; A+B+C). However, the TPF increases from of 83% to around 90% when traditional risk factors are added alone or together with biomarkers (i.e., model A vs. A+B and A+B+C). When the ninth decile is used as a cutoff for defining high risk, the FPF equals 18% for all models and the TPF increases from 39% to 53% by adding traditional risk factors alone or together with biomarkers.
In other words, the model including only age and sex is only slightly improved by the inclusion of traditional risk factors. In Fig. 4, we can also observe that the addition of biomarkers did not further expand the area between TPF and FPF curves compared to the model including age, sex and traditional risk factors.
In Fig. 5, we provide a risk assessment plot for the full model (i.e., including age, sex, traditional risk factors and biomarkers) that, in addition to the TPF and FPF also contains the values of the observed and predicted risk, the prevalence of the risk factor (i.e., having a predicted risk equal or over a specific decile), the RR, the explained variance, and the PAF. If we, for instance, define high risk individuals as those in the second to the tenth decile groups, we see that the prevalence of the risk factor is 90%. These people have a risk almost 14 times higher than that of the individuals in the first decile group. Moreover, the TPF is very high (i.e., 99%) which offers a PAF of 99%. However, in this case, the explained variance is low (i.e. 17%) and the FPF is very high (i.e., 89%). To obtain a low FPF (which is pertinent when planning an effective strategy of prevention) we would need to define high-risk individuals as those belonging to the tenth decile group (i.e., FPF = 8%). However, in this situation, the TPF is also low (i.e., 33%).
4. Discussion
We found that, besides age, sex and classical risk factors, novel biomarkers did not add any substantial accuracy for discriminating between individuals who will subsequently suffer a coronary event from those who will not. These findings were certainly expected, as similar results have been described in several previous studies (De Backer et al., 2012, Kaptoge et al., 2012, Wang et al., 2006, Zethelius et al., 2008) including an early investigation performed on the Malmö Diet and Cancer cohort using the same dataset (Melander et al., 2009). We want to clarify that the aim of our study was not to question this previous publication, and so we did not strive to repeat precisely the same models. Therefore, our results were very similar, yet not a repetition of the previous study. Rather, we aimed to illustrate and discuss some key concepts in risk factors epidemiology.
From this perspective, our study contributes in two significant ways: First, we confirmed a straightforward but scarcely discussed observation (Wald et al., 2011) indicating that classical risk factors only provide a minor improvement to the DA of a model including simple demographic characteristics, i.e., age and sex. Second, we provide innovative evidence indicating that the PAF measure gives incomplete —if not misleading— information on the relevance of risk factors for planning strategies of prevention against CHD in the population. A key weakness of the PAF measure is that it does not take into account the FPF of the risk factor used for its calculation and, therefore, disregards its DA.
4.1. The discriminatory paradox: Measures of association vs. Measures of discrimination
There is a tacit —but misguided— belief that the predictive accuracy of an exposure (e.g., risk factor) is very high when it is supported by a conclusive average association of considerable magnitude (e.g., OR = 10). Nonetheless, a risk factor ‘strongly’ associated with a disease is not necessarily an accurate instrument for classifying individuals according to their disease status. As shown in Fig. 1, for an association to be an accurate instrument for discrimination, the association must be of a size seldom observed in epidemiologic studies (Boyko and Alderman, 1990, Khoury et al., 1985, Pepe et al., 2004, Wald et al., 1999). Our study illustrates this important point.
Our conclusions are based on standard measures of DA such as the AUC. This measure has, however, been criticized because it is insensitive to small changes in predicted individual risk (Cook, 2007). However, more specific measures of reclassification such as the net reclassification improvement (NRI), and the integrated discrimination improvement (IDI) (Pencina, D’Agostino, Pencina, Janssens and Greenland, 2012; Pencina et al., 2008, Pencina et al., 2011) do not add any decisive information to that obtained by the analyses of AUC curves. Thus, our conclusions would not be affected by using NRI or IDI. Furthermore, the new NRI and IDI measures have also been criticized (Pepe, 2011), and some authors (Hidden and Gerds, 2012) explicitly advise against their use in common epidemiological practice. According to these authors, unlike IDI and NRI, traditional measures of discrimination such as the AUC, have the characteristic that prognostic performance cannot be manipulated and high performance necessarily represents clinical gain expressed on a well-defined, interpretable scale. Therefore, we preferred to quantify DA by analyzing ROC curves, AUC and risk assessment plots.
In the course of our analyses, we observed that risk assessment plots (Pepe et al., 2008, Pickering and Endre, 2012) constructed by drawing the predicted risk for CHD against the TPF and FPF alone or in combination with other measures (e.g., RR, explained variance, the prevalence of the risk factor) are a more appropriate tool for evaluating the relevance of a risk factor in public health than simple measures such as the AUC, since the risk assessment plot allows for the evaluation of the TPF and FPF for different risk score thresholds (i.e., definitions of high risk). As a second choice, the TPFFPF5% appears as a simple but informative measure.
4.2. Strategies of prevention and DA
All over the world, there is a very strong conviction regarding the advantages of strategies of prevention against CHD based on the reduction of traditional modifiable risk factors such as high blood pressure (hypertension), high cholesterol, smoking, obesity, physical inactivity, diabetes, and unhealthy diets. However, we need to honestly confront the fact that, because of their low DA, none of those risk factors, alone or in any combination, provide an ideal ground for planning strategies of prevention in the general population. This conclusion should not be surprising. In fact, an analogous argument is today being applied in other medical fields. For instance, the use of the Prostate-Specific Antigen (PSA) test in the screening of prostate cancer in the general population is not recommended since the DA of PSA is low, meaning that an unselective PSA screening will identify many men who will never develop prostate cancer as positive, leading to unnecessary biopsies of their prostates (Djulbegovic et al., 2010, Ilic et al., 2013).
The fact that traditional cardiovascular risk factors have a low DA conveys consequences in regard to planning strategies of prevention in the general population. Non-pharmacological strategies of prevention directed towards life-style modification (for example, quitting smoking, increasing physical activity, eating healthy food, etc.) are normally safe and could be recommended to most people in the population even if the FPF is high. On the other hand, treatment of cardiovascular risk factors by pharmacological strategies of prevention (e.g., blood pressure lowering drugs, statins) does not appear to be suitable since treating false positive individuals may imply obvious problems of medicalization (Conrad, 2007) and, eventually, stigmatization of healthy individuals with the ‘risk factor’ who receive a pharmacological treatment. Furthermore, alongside the unnecessary pharmacological effects there is a risk of unwanted adverse effects. This situation translates itself into avoidable costs for both the individual and the community.
Interestingly, in our study we actually arrived at the same conclusion as Wald et al., 1999, Wald and Law, 2003, Wald et al., 2011 concerning the minor incremental value added by traditional risk factors over and above age alone for discriminating future cases of cardiovascular disease. However, paradoxically, rather than questioning pharmacological preventive strategies against cardiovascular risk factors Wald and Law (2003), promote the “Polypill approach” (Charan et al., 2013, Wald and Wald, 2012). Wald et al.’s approach is a form of anti-ageing strategy consisting of a combination of medications that may simultaneously reduce several cardiovascular risk factors in all individuals above a specified age (e.g., 55 years) but without previous selection based on screening for risk factors. Our study shows, however, that this approach is flawed since it does not consider the DA of the risk factors. It does not matter that those risk factor are ‘causal’ on average. The Polypill approach is an extreme example, but it reflects how modern medicine in its most naïve form is falling towards a simplistic interpretation of human health based on pharmacological interventions targeting a few risk factors with low DA. Indeed, a somewhat satirical but arguably more attractive alternative strategy (in light of the problems associated with unselective use of drugs) could be the non-pharmacological ‘Polymeal approach’ described by Franco and colleagues in 2004 (Franco et al., 2004) in response to the Polypill initiative.
4.3. ‘Representative’ samples of heterogeneous populations?
The existence of inter-individual heterogeneity of effects; that is, the fact that some individuals may respond intensively to the exposure while others are resilient (see also later in this discussion) may explain some of the apparently conflicting findings concerning the DA of biomarkers for cardiovascular diseases previously identified in the literature (Melander et al., 2009). Thus, studies analyzing ‘representative’ samples of the general population may find that novel biomarkers have low DA while others examining homogeneous or highly selected samples may find a higher DA. This discordance should not be interpreted as an under- or overestimation of the true DA value. Rather, it may reflect the existence of an inter-individual heterogeneity of responses and the fact that ‘representative’ samples of the general population produce average values that, paradoxically, are not necessarily representative (Rothman, Gallacher, and Hatch, 2013). Therefore, rather than ‘representative’ samples of the general population, we need to analyze many homogenous samples that are heterogeneous in relation to each other. In the ideal scenario, we need to identify the individuals that benefit from pharmacological treatment and distinguish them from those that do not benefit at all or even suffer harm from the treatment (see later in this discussion).
4.4. Is there an ‘etiological’ and a ‘screening’ perspectives when Interpreting the effect of a risk factor with low discriminatory accuracy?
Several authors justify the low DA of a risk factor by distinguishing between ‘etiological’ and ‘screening’ perspectives (Wald et al., 1999) or between ‘association’ versus ‘classification’ (Pepe et al., 2004). For example, Wald et al. (Wald et al., 1999) stated that a high cholesterol concentration is a ‘strong risk factor’ for ischemic heart disease in ‘etiological terms’, even if the association is not sufficiently strong to be used as a basis for screening tests, since, in practice, its screening performance is poor. Pepe et al. (Pepe et al., 2004) state that “a binary marker with a relative risk of, for instance, three, can be used to identify a population with a risk factor that has three times the risk as the population without the risk factor. This method may be used to target prevention or screening strategies”. Pepe and colleagues comment that although measures of association such as the OR do not characterize a marker’s accuracy for classifying risk for individual subjects, these measures are valuable for characterizing population differences in risk.
We do not agree. The distinction between ‘etiological’ and ‘screening’ or ‘association’ and ‘classification’ purposes bears an underlying contradiction. Those authors (Pepe et al., 2004, Wald et al., 1999) implicitly adopt a probabilistic approach when assessing the etiological value of risk factors at the population level but, contradictorily, they apply a deterministic or mechanistic approach when assessing their screening value. However, a low DA of a risk factor not only expresses itself in a poor screening performance but also in the fact that the estimated average effect of a risk factor is not generalizable to most individuals in the population. Our statements need a more extended argumentation, which we now present in the next sections of this discussion.
4.5. Is there individual heterogeneity? the mechanistic vs. The stochastic (i.e., “chance”) approaches to individual risk
It is possible to imagine a situation where a homogeneous exposure in a group causes a homogenous effect in all the individuals of the group. In this case, the exposure will have a DA of 100%. For instance, a blood pressure lowering drug may reduce diastolic blood pressure by 5 mmHg in each and every one of the individuals treated. However, this is not the case on most occasions. A possible reason for the low DA of many average associations is that average effects are a mixture of heterogeneous individual level effects (i.e., some individuals respond intensively to the exposure while others are resilient or might even respond in the opposite direction) (Kravitz, Duan, and Braslow, 2004). The approach based on DA understands average effects as an idealized mean value that does not necessarily represent the heterogeneity of individual effects. To be precise, reducing exposure to a risk factor would only be effective when the intervention targets the susceptible but not the resilient individuals. Consequently, a possible criticism of the analysis of DA is that it adopts a mechanistic perspective. For instance, we assume that certain individuals will respond to the risk factor exposure (i.e., true positives) while others will not (i.e., false positives). An alternative would be to assert that the risk factor homogenously affects the exposed group as a whole and that any individual could, in principle, express the effect (e.g., disease). From this perspective, since we do not know who will develop the disease, we could conceive the individual risk as the expression of a stochastic phenomenon that is best estimated by the average risk using a probabilistic approach (Cook, 2007). In line with this idea, Davey-Smith (Smith, 2011, p. 556) states that:
“Chance leads to averages being the only tractable variables in many situations, and this is why epidemiology makes sense as a science. We should embrace the effects of chance, rather than pretend to be able to discipline them”.
However, the main question is whether the individual risk is a stochastic or ‘chance’ phenomenon that can only be estimated by a probabilistic model or if it, instead, reflects the inter-individual heterogeneity of responses that can be determined. A logical contradiction of the stochastic viewpoint is the fact that we are interested in identifying causal mechanisms, but a stochastic phenomenon is, by definition, not causal (Zernicka-Goetz and Huang, 2010). It is more reasonable to think that the mechanism underlying an individual response might be very complex and difficult to determine so it might look like a stochastic phenomenon. However, rather than vindicating the ‘chance’ approach and an indiscriminate use of probabilistic estimations, we should recognize our current epistemological uncertainty (i.e., ignorance) and acknowledge that our lack of knowledge could be amended by a better understanding of individual responses (Zernicka-Goetz and Huang, 2010). See elsewhere for further discussion on these ideas (Merlo, 2014). A didactical example may also clarify those concepts.
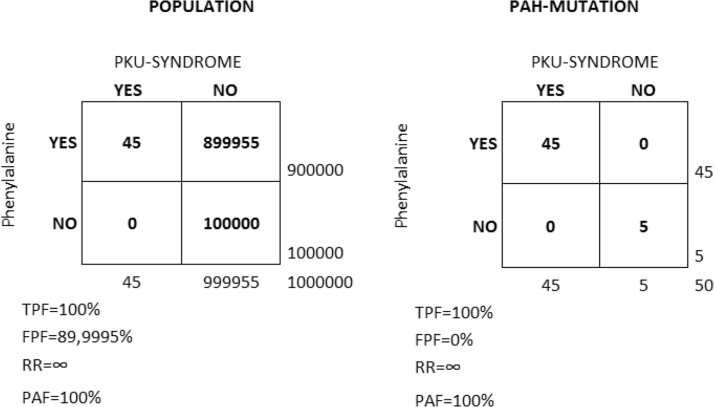
4.6. The classical phenylketonuria (PKU) example
If a risk factor affects the susceptible individuals, we should expect both the RR and the DA of the risk factor to be very high. We illustrate this situation using the classical PKU example (Fig. 6) where exposure to phenylalanine in the diet only gives clinical symptoms (a syndrome characterized by mental retardation, seizures, and other serious medical problems) in people with a mutation in the gene coding for the hepatic enzyme phenylalanine hydroxylase (PAH). This enzyme is necessary to metabolize phenylalanine to the amino acid tyrosine. When enzyme activity is reduced, phenylalanine accumulates and is converted into phenylpyruvate, which can be identified in the urine as phenylketone.
Fig. 6.
Classical Phenylketonuria (PKU) example. In the classical PKU example, exposure to phenylalanine in the diet only gives clinical symptoms (PKU-SYNDROME) in people with a mutation in the gene coding for the hepatic enzyme phenylalanine hydroxylase (PAH-MUTATION). We assume a population (N = 1,000,000) with 90% of the people exposed and 10% non-exposed to phenylalanine in the diet. In this population, 50 individuals present the PAH-MUTATION. Among the people with the mutation, 90% are exposed and 10% are non-exposed to phenylalanine in the diet. The figure shows the values of the true positive fraction (TPF), false positive fraction (FPF), relative risk (RR) and population attributable fraction (PAF) in both the general population (left) and in the strata of people with the PAH-MUTATION (right).
Let us assume a population (N = 1,000,000) with 90% of the people exposed and 10% non-exposed to phenylalanine in the diet. In this population, 50 individuals (5/100,000) present a mutation in the gene that codifies the PAH enzyme. Among those with the mutation, 90% (n = 45) are exposed and 10% (n = 5) are non-exposed to phenylalanine in the diet.
In a first scenario (A), we assume that we do not know of the existence of the mutation and perform a study in the whole population. We investigate the risk of PKU in people exposed to phenylalanine compared to those not exposed to phenylalanine. We will observe a RR of a very high (in fact, infinite) magnitude, indicating that only those exposed to phenylalanine develop PKU. Obviously, the TPF is 100%, as all the cases need to be exposed to phenylalanine. The PAF is also 100%, indicating that if we remove phenylalanine from the whole population we will prevent all the PKU cases.
In the second scenario (B), we assume that we are aware of the existence of the mutation and perform the study on those with the mutation rather than on the whole population. The conclusion of our analysis will be very similar. The RR is infinite, the TPF is 100% and the PAF is 100%, indicating that if we remove phenylalanine from the people with the mutation we will prevent all the PKU cases.
The difference between the scenarios (A) and (B) resides only in the FPF. That is, in scenario (A), almost 90% of the exposed do not develop PKU while in scenario (B) the FPF is 0%. This means that eliminating phenylalanine from the diet in scenario (A) will produce unnecessary discomfort in the vast majority of people, while in scenario (B) the discomfort will be limited and worthwhile, as it targets only those who would otherwise develop PKU. Admittedly, the PKU example is very simple and the identification of the individuals that react to cardiovascular risk factors may be much more complicated. However, this does not alter the fact that the distribution of individual risk is not a chance phenomenon and that knowledge of inter-individual heterogeneity of effects is crucial for planning efficient public health interventions to prevent cardiovascular disease.
4.7. The “Tyranny of the means”
We reiterate that a major problem is that measures of association disregard the heterogeneity of individual-level effects but are often presumed as the best estimation of what is assumed to be stochastics and undeterminable individual risk. This imposition of an average value on the individual is very common in Epidemiology and it has been denominated the “Tyranny of the means” (Tabery, 2011) or the “Mean centric approach” (Downs and Roche, 1979). Alongside the medical field, this problem has been discussed in other scientific disciplines such as political science (Braumoeller, 2006, Downs and Roche, 1979) and evolutionary biology (Gould, 1996). Similar ideas have also been developed in social epidemiology in the investigation of contextual effects (Merlo, 2003, Merlo et al., 2005, Merlo et al., 2009b; Merlo, Viciana-Fernandez, Ramiro-Farinas, & Research Group of Longitudinal Database of Andalusian, 2012). The key concept here is that common measures of association correspond to abstractions that do not represent the heterogeneity of individual effects. This idea points to the study of inter-individual heterogeneity around group averages as being fundamental for the understanding of the effect of an exposure (e.g., a risk factor) in the population. Analogous ideas had already been described in the 19th century by Claude Bernard (1813–1878†) (Bernard, 1949) who stated that:
“Averages must therefore be rejected, because they confuse, while aimed to unify, and distort while aiming to simplify.”
Later, Bernard’s ideas were shared by Hogben (1895–1975†) (Hogben and Sim, 1953, Hogben and Sim, 2011) as well as by clinical epidemiologists (Guyatt et al., 1986, Larson, 2010) promoting “n-of-1” design. The same notion is also behind the current movement towards personalized (or stratified) medicine (Lillie et al., 2011).
4.8. Discriminatory accuracy and the estimation of average causal effects in experimental and observational epidemiology
We distinguish between observational effects (i.e., associations) and causal effects, even if the term “effect” assumes causality by itself (Hernan and Robins, 2006). According to the counterfactual theory of causation in Epidemiology, a fundamental task lies in the identification of individual causal effects (ICE) (Kaufman and Kaufman, 2002). The ICE is the potential outcome that an individual would experience under a counterfactual exposure. That is, to quantify an ICE, we would need to observe the very same individual living in a parallel world that exactly replicates the actual world with the exception of the exposure. This ideal but unobservable counterfactual situation would isolate the influence of the exposure and would inform us whether —ceteris paribus— the exposure causes the outcome. Since the ICE is unobservable, we need some strategy of analysis to estimate it. A common one is to estimate the average causal effect (ACE) in a population. Theoretically, to calculate the ACE, we would need to observe the effect of an exposure in the very same population but in a parallel world that exactly replicates the actual world with the exception of the exposure. This situation is however also unobservable. Nevertheless, statistically, two random samples drawn from the same population each estimate the same parameters (i.e., the mean and the variance) of that population and are —with some statistical uncertainty—exchangeable. Being random, the selection of the samples is not related to the outcome and we can experimentally allocate the exposure to one random sample and leave the other random sample as control. In this case, the difference between the average risks of the exposed and the control groups is the ACE. This is the reason why randomized clinical trials (RCT) inform in regard to the ACE of a treatment.
However, the critique we directed in the previous section concerning the “tyranny of the means” also applies to the information provided by many RCT investigating the ACE of a treatment. This is a serious allegation, since RCTs are currently the cornerstone of evidence-based medicine. The problem is that the estimation of the individual effect from the ACE obtained in a RCT necessarily follows a probabilistic approach and considers the ACE to be the best estimation of the ICE. That is, group randomization facilitates exchangeability of the exposed and unexposed groups but the measure of ACE hides inter-individual heterogeneity of responses behind the group average. The RCT design implicitly assumes homogeneity of the individual responses or that the distribution of effect modifiers is the same in the exposed and unexposed group (i.e., that the within group heterogeneity is exchangeable). Those assumptions, however, make no sense within the deterministic framework of DA. Indeed, in a RCT, the variance (σ2) is not a measure of statistical uncertainty (as sometimes interpreted) but instead expresses a natural phenomenon that corresponds to the underlying inter-individual heterogeneity of responses. Statistical uncertainty is quantified by both the standard error (SE) of the mean and by the SE of the σ2 that, unlike the σ2, will typically decrease as the number of individuals sampled increases. In short, the variance σ2 may be large but estimated with high precision (i.e., a low SE of the σ2).
To clarify the relation between causality and DA, we can mentally imagine the otherwise unobservable ICE situation and construct a counterfactual cross-tabulation between a counterfactual risk factor exposure and a potential disease occurrence within one imaginary individual (Fig. 7). In this situation, the individual potentially develops the disease when she is exposed to the risk factor in an unobservable counterfactual scenario, and she does not develop the disease when she is not exposed in the factual scenario. Therefore, the RR = 1/0 so RR = ∞, the TPF and the TNF are = 1/1 so the TPF and the TNF = 1 and, logically, the FPF = 0 and the FNF = 0.
Fig. 7.
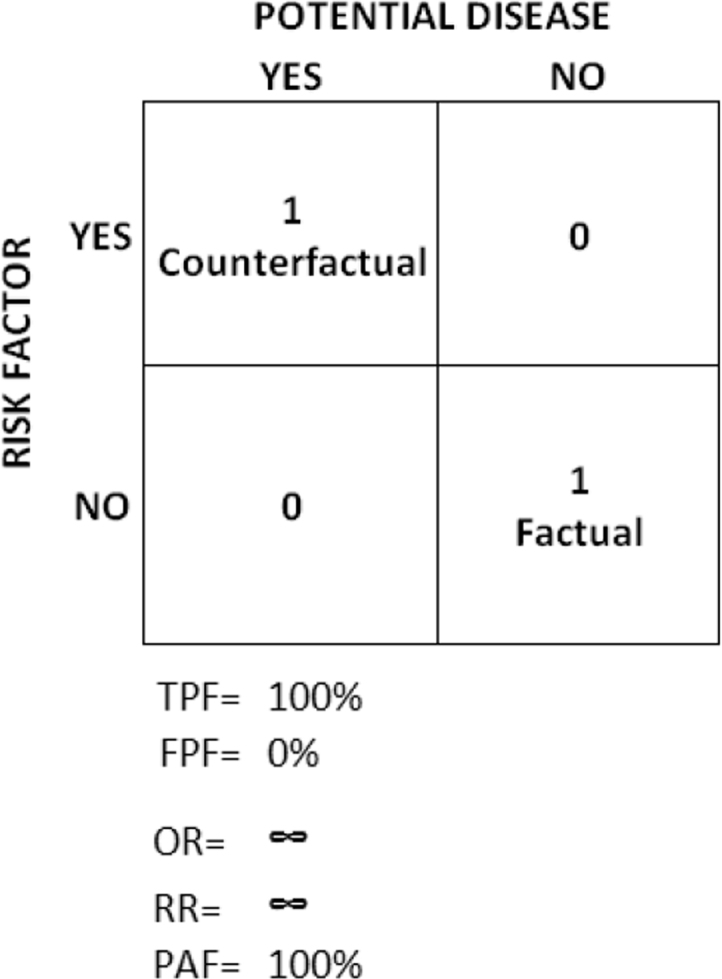
Cross-table illustrating the discriminatory accuracy of an unobservable individual causal effect (ICE) where the potential outcome only occurs in a counterfactual situation of exposure.
In other words, in the ICE situation, the counterfactual exposure is infinitely associated with the potential outcome, and it is also completely sensitive and specific because the potential outcome always occurs when the counterfactual exposure is present, and it never occurs otherwise.
The ideal ICE scenario contrasts with the much lower ORs and DA values observed for most risk factors and treatment of risk factors estimated by the ACE idealization. The same is true for most other exposures in epidemiology. In contrast to the ICE scenario described above, in the ACE situation, the possible values of the RR extend from 0 to ∞, and the possible values of the TPF and FPF, extend from 0 to 1. This spectrum of values reflects that the ACE is a mixture of heterogeneous individual effects, because the ACE is based on the comparison of two samples from a population that is intrinsically heterogeneous. Obviously, the average value provided by the ACE might provide misleading information, even if there is neither confounding nor bias and the distribution of heterogeneous individual effects is the same in the exposure and control samples. In fact, the important information is the heterogeneity hidden behind the average. Consequently, the ACE approach also leads to unusual ICE interpretations in regards to unalterable individual heterogeneity (Kaufman and Cooper, 1999) such as, for instance, the association between individual country of birth and health that lack modifiable counterfactual states.
It is a common clinical experience that the ACE obtained from a clinical trial does not seem to be reflected in the individual patient response to treatment (Guyatt et al., 1986). Nonetheless, this apparent conflict only reflects the fact that ACEs are just average measures. The normal assumption that the ACE is the best estimation across all individuals in the trial and, even outside the trial, is unsustainable, since the underlying individual heterogeneity in the population is normally large. Hogben (Hogben and Sim, 1953) had a clear understanding of this phenomenon when he wrote:
“The now current recipe for a clinical trial based on group comparison sets out a balance sheet in which individual variability … does not appear as an explicit item in the final statement of the account; but such variability of response to treatment may be of paramount interest in practice.”
Namely, the results of a RCT provide very limited information for launching a treatment in the general population. This is the fundamental argument underlying the need for personalized (or stratified) medicine that considers the heterogeneity of individual effects. Kravitz, Duan and Braslow concluded in 2004 (Kravitz, Duan, and Braslow, 2004).
“Clinical trials provide good estimates of average effects. But averages do not apply to everyone. By attending to risk without treatment, responsiveness to treatment, vulnerability to adverse effects, and utility for different outcomes, researchers can design studies that better characterize who will—and who will not—benefit from medical interventions. Clinicians and policymakers can, in turn, make better use of the results.”
Finally, the criticism and reflection presented above concerning experimental epidemiology (i.e., RCT) is also relevant for observational epidemiology, adding to the already recognized difficulties confronted by observational epidemiology when trying to estimate ACE (Hernan and Robins, 2006, Kaufman and Cooper, 1999).
4.9. A serious critique to the PAF measure
Our study demonstrates that the PAF is an inappropriate measure for evaluating the public health relevance of a risk factor because it does not consider the portion of people that are exposed to the risk factor but who never develop the disease (i.e., the FPF). When the ratio between the prevalence of the risk factor and the prevalence of the disease is high, both the TPF and the FPF tend to be high. Therefore, a highly prevalent risk factor for an uncommon disease necessarily gives a high PAF but simultaneously has low DA. This situation expresses itself in a low explained variance value. This apparently counterintuitive situation of a risk factor having a high PAF but a low explained variance has been interpreted as a weakness of the explained variance measure (Pearce, 2011). However, we rather think the interpretation should be the opposite: a weakness of the PAF measure is that it does not consider the explained variance. The explained variance measure is actually an indicator of DA (DeMaris, 2002) and our study illustrates the relevance of this measure in public health. In Fig. 5, for instance, we see that when the prevalence of the risk factor and the magnitude of the RR are large (i.e., prevalence = 90%, and RR = 14) the PAF is as high as 99%. However, in this case, the explained variance is somewhat low (i.e., 17%) and the FPF very high (i.e., 89%), which underscores the unsuitability of planning strategies of prevention exclusively based on the PAF measure alone. It should be observed that the explained variance measure (as with any other measure of DA) is not an explicit measure of ‘causal effects’ but only indicates the amount of inter-individual heterogeneity that has been identified by the identification of candidate causal associations. See, for instance, the PKU example explained earlier in this discussion.
4.10. A clinical and public health perspective
In our study, it is argued that the key criteria of clinical usefulness of a new risk factor should be its added capacity to discriminate between individuals who experience an adverse outcome from those who do not. We think, moreover, that this capacity to discriminate is not only of clinical relevance but also has major and general relevance in public health, as this concept can be applied to any exposure categorization in epidemiology (Merlo, 2014, Merlo and Mulinari, 2015). Nonetheless, most of the current strategies used to analyze individual disease risk are based on measures of average association of rather low, and even tiny, magnitude (Siontis and Ioannidis, 2011) which, in turn, suggests that those findings have a low DA (Pepe et al., 2004). Our study, therefore, reveals a general problem that affects many epidemiological fields.
The question is how to deal with the growing plethora of published average associations with low DA. To improve individual and community health as well as to improve the credibility of epidemiological findings among laypeople, we urgently need to identify which exposure categorizations (e.g., risk factors) are more relevant than others for specific individuals or homogenous groups of individuals. That is, we need to distinguish which individuals are susceptible and which are resilient to specific risk factors. We need to develop instruments that recognize the existence of an inter-individual heterogeneity of responses. We need to understand that ‘representative’ samples of the general population produce average values that paradoxically are not necessarily representative. Therefore, rather than ‘representative’ samples of the general population, we need to analyze many homogenous samples that are heterogeneous in relation to each other. In the ideal scenario, we should be able to identify and appropriately map individual responses. On occasion, the whole population may behave as a homogeneous group for a particular exposure (for instance, exposure to 1.5 mg/kg body weight of potassium cyanide is lethal for every one). In contrast, other exposures only cause a response in specific individuals (for instance, exposition to phenylalanine is only dangerous in people with the PHA mutation). Our ideas might help to clarify the current confusion concerning the ‘representativeness’ of epidemiological findings (Ebrahim and Smith, 2013, Elwood, 2013, Nohr and Olsen, 2013, Richiardi et al., 2013, Rothman et al., 2013).
We need a new epidemiological approach that systematically provides information on inter-individual heterogeneity of effects, rather than relies on averages (Grove, 2011). For this purpose, we ideally need large databases and biobanks with multiple measurements within individuals. We need an extended use of stratified and interaction analyses and longitudinal analyses of multiple measurements within individuals, multilevel variance modeling. (Merlo et al., 2004, Merlo et al., 2006; Evans, C. R., 2015) and multilevel regression analyses of case-crossover and n-of-1 designs (Zucker et al., 1997, Zucker et al., 2010).
Future (Social) Epidemiology will not become a prisoner of the proximate (McMichael, 1999) if we adopt a multilevel approach that decomposes individual heterogeneity at different levels of analysis. This multilevel analysis of individual heterogeneity (MAIH) (Merlo, 2014, Wemrell et al., 2017a) enables the study of both between- and within-group components of individual heterogeneity. In this way, group effects (in the present study the groups are defined by categories of risk factors) are thereby appraised not through mere study of differences between group averages (as it is the norm in current public health and Epidemiology), but rather through quantification of the share of the individual heterogeneity (i.e., variance) that exists at the group level, This idea corresponds with the concept of clustering in multilevel analyses (Merlo et al., 2005) which is analogous to the concept of DA applied in the present study (Wagner and Merlo, 2014). The higher this share (i.e., the higher the DA) the more relevant the exposure category (e.g., risk factor level, neighborhood, ethnic group) is for public health (Merlo, 2003, Merlo et al., 2004, Merlo and Mulinari, 2015, Merlo et al., 2009a).
The idea of MAIH converges with the current movement of precision (i.e., individualized, personalized, stratified) medicine in public health (Khoury, Iademarco, & Riley, 2016) and its efforts toward understanding individual heterogeneity. However, a radical conceptual difference exists: rather than only considering individual biomedical susceptibilities or dislocating individual from “population” health, MAIH tries to identify the components of individual heterogeneity in health that are at the contextual level and across the life-course (Merlo, 2014, Wemrell et al., 2017a).
4.11. Conclusions
The ideas developed in our study are still not widely recognized, and many areas of public health and epidemiology are still suffering from the ‘tyranny of the averages’. However, an increasing awareness of the low DA of most exposure categories considered today in public health and epidemiology will necessarily have profound consequences. We need a fundamental change in the way in which we currently interpret exposure categorizations in public health epidemiology for, if their DA is very low, what happens with the vast majority of recommendations given so far in epidemiology and public health? Are we misleading the community by creating alarm over risks that may be harmless for most individuals? Are we stigmatizing groups of people (e.g., people with mild hypertension) by blaming them for a bad ‘average’ health when, in fact, mild arterial hypertension cannot discriminate sick from healthy individuals? What are the ethical repercussions of using exposure categorizations with low DA? Are there problems of inefficiency, medicalization and stigmatization? Against this background, we not only need to urgently review new risk factors and biomarkers, but also classical and well-established risk factors as well as most other categorization being used in public health and (social) epidemiology (Ivert, Mulinari, van Leeuwen, Wagner, and Merlo, 2016; Juarez, Wagner, and Merlo, 2013; Merlo, Wagner, Ghith, and Leckie, 2016; Mulinari, Bredstrom, and Merlo, 2015; Wagner and Merlo, 2013; Wemrell, Mulinari, and Merlo, 2017b; Rodriguez-Lopez, Wagner, Perez-Vicente, Crispi, and Merlo, 2017). We believe that the questions we raise have strong relevance for both the individual and community and need to be confronted in future public health research.
Competing interests
None.
Ethics statement
The study was approved by, the Ethical committee in South Sweden and by the Malmö Diet and Cancer database committee at Lund University.
Acknowledgements
This work was supported by the Swedish Research Council (VR) (Dnr 2013–2484 PI JM). We want to express our gratitude to Sol Juarez for commenting an earlier version of the manuscript and to Philippe Wagner for provided the formulas and revising the analyses of the empirical example.
Contributor Information
Juan Merlo, Email: juan.merlo@med.lu.se.
Shai Mulinari, Email: shai.mulinari@soc.lu.se.
Maria Wemrell, Email: maria.wemrell@med.lu.se.
SV Subramanian, Email: svsubram@hsph.harvard.edu.
Bo Hedblad, Email: bo.hedblad@med.lu.se.
References
- Andermann A., Blancquaert I. Genetic screening: A primer for primary care. Canadian Family Physician. 2010;56(4):333–339. [PMC free article] [PubMed] [Google Scholar]
- Axelsson-Fisk S., Merlo J. Absolute rather than relative income is a better socioeconomic predictor of chronic obstructive pulmonary disease in Swedish adults. International Journal for Equity in Health. 2017;16(1):70. doi: 10.1186/s12939-017-0566-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babyak M.A. What you see may not be what you get: A brief, nontechnical introduction to overfitting in regression-type models. Psychosomatic Medicine. 2004;66(3):411–421. doi: 10.1097/01.psy.0000127692.23278.a9. [DOI] [PubMed] [Google Scholar]
- Bernard C. Schuman; New York: 1949. An introduction to the study of experimental medicine. [Google Scholar]
- Boyko E.J., Alderman B.W. The use of risk factors in medical diagnosis: Opportunities and cautions. Journal of Clinical Epidemiology. 1990;43(9):851–858. doi: 10.1016/0895-4356(90)90068-z. [DOI] [PubMed] [Google Scholar]
- Braumoeller B. Explaining variance; or, stuck in a moment we can’t Get Out Of. Political Analysis. 2006;14(3):268–290. [Google Scholar]
- Charan J., Goyal J.P., Saxena D. Effect of Pollypill on cardiovascular parameters: Systematic review and meta-analysis. Journal of Cardiovascular Disease. 2013;4(2):92–97. doi: 10.1016/j.jcdr.2012.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi B.C. Causal modeling to estimate sensitivity and specificity of a test when prevalence changes. Epidemiology. 1997;8(1):80–86. doi: 10.1097/00001648-199701000-00013. [DOI] [PubMed] [Google Scholar]
- Conrad P. Johns Hopkins University Press; Baltimore: 2007. The medicalization of society: On the transformation of human conditions into treatable disorders. [Google Scholar]
- Cook N.R. Use and misuse of the receiver operating characteristic curve in risk prediction. Circulation. 2007;115(7):928–935. doi: 10.1161/CIRCULATIONAHA.106.672402. [DOI] [PubMed] [Google Scholar]
- Cooney M.T., Dudina A.L., Graham I.M. Value and limitations of existing scores for the assessment of cardiovascular risk: A review for clinicians. Journal of the American College of Cardiology. 2009;54(14):1209–1227. doi: 10.1016/j.jacc.2009.07.020. [DOI] [PubMed] [Google Scholar]
- De Backer G., Graham I., Cooney M.T. Do novel biomarkers add to existing scores of total cardiovascular risk? European Journal of Preventive Cardiology. 2012;19(2 Suppl):14–17. doi: 10.1177/2047487312448988. [DOI] [PubMed] [Google Scholar]
- DeMaris A. Explained variance in logistic regression: A Monte Carlo study of proposed measures. Sociological Methods & Research. 2002;31(1):27–74. [Google Scholar]
- Di Serio F., Ruggieri V., Varraso L., De Sario R., Mastrorilli A., Pansini N. Analytical evaluation of the Dade Behring Dimension RxL automated N-Terminal proBNP (NT-proBNP) method and comparison with the Roche Elecsys 2010. Clinical Chemistry and Laboratory Medicine. 2005;43(11):1263–1273. doi: 10.1515/CCLM.2005.217. [DOI] [PubMed] [Google Scholar]
- Djulbegovic M., Beyth R.J., Neuberger M.M., Stoffs T.L., Vieweg J., Djulbegovic B., Dahm P. Screening for prostate cancer: Systematic review and meta-analysis of randomised controlled trials. BMJ. 2010;341:c4543. doi: 10.1136/bmj.c4543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downs G.W., Roche D.M. Interpreting Heteroscedasticity. American Journal of Political Science. 1979;23(4):816–828. [Google Scholar]
- D’Agostino R.B., Nam B.H. Evaluation of the performance of survival analysis models: discrimination and calibration measures. In: Balakrishnan N., Rao C.R., editors. Handbook of statistics, volume 23: advances in survival analysis. Elsevier; Amsterdam: 2004. pp. 1–25.https://www.elsevier.com/books/advances-in-survival-analysis/balakrishnan/978-0-444-50079-3 [Google Scholar]
- Ebrahim S., Smith G.D. Commentary: Should we always deliberately be non-representative? International Journal of Epidemiology. 2013;42(4):1022–1026. doi: 10.1093/ije/dyt105. (doi:1010.1093/ije/dyt1105) [DOI] [PubMed] [Google Scholar]
- Elwood J.M. Commentary: On representativeness. International Journal of Epidemiology. 2013;42(4):1014–1015. doi: 10.1093/ije/dyt101. (doi:1010.1093/ije/dyt1101) [DOI] [PubMed] [Google Scholar]
- Engstrom G., Jerntorp I., Pessah-Rasmussen H., Hedblad B., Berglund G., Janzon L. Geographic distribution of stroke incidence within an urban population: Relations to socioeconomic circumstances and prevalence of cardiovascular risk factors. Stroke. 2001;32(5):1098–1103. doi: 10.1161/01.str.32.5.1098. [DOI] [PubMed] [Google Scholar]
- Evans C.R. Harvard University; Boston, Massachusetts: 2015. Innovative approaches to investigating social determinants of health - social networks, environmental effects and intersectionality (PhD)http://nrs.harvard.edu/urn-3:HUL.InstRepos:23205168 [Google Scholar]
- Franco O.H., Bonneux L., de Laet C., Peeters A., Steyerberg E.W., Mackenbach J.P. The Polymeal: A more natural, safer, and probably tastier (than the Polypill) strategy to reduce cardiovascular disease by more than 75% British Medical Journal. 2004;329(7480):1447–1450. doi: 10.1136/bmj.329.7480.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerds T.A., Cai T., Schumacher M. The performance of risk prediction models. Biometrical Journal. 2008;50(4):457–479. doi: 10.1002/bimj.200810443. [DOI] [PubMed] [Google Scholar]
- Gould S.J. Three Rivers Press; New York: 1996. Full house: The spread of excellence from plato to Darwin. [Google Scholar]
- Greenland P., Knoll M.D., Stamler J., Neaton J.D., Dyer A.R., Garside D.B., Wilson P.W. Major risk factors as antecedents of fatal and nonfatal coronary heart disease events. Journal of the American Medical Association. 2003;290(7):891–897. doi: 10.1001/jama.290.7.891. [DOI] [PubMed] [Google Scholar]
- Grove A. Rethinking clinical trials. Science. 2011;333(6050):1679. doi: 10.1126/science.1212118. [DOI] [PubMed] [Google Scholar]
- Guyatt G., Sackett D., Taylor D.W., Chong J., Roberts R., Pugsley S. Determining optimal therapy--randomized trials in individual patients. New England Journal of Medicine. 1986;314(14):889–892. doi: 10.1056/NEJM198604033141406. [DOI] [PubMed] [Google Scholar]
- Hammar N., Alfredsson L., Rosen M., Spetz C.L., Kahan T., Ysberg A.S. A national record linkage to study acute myocardial infarction incidence and case fatality in Sweden. International Journal of Epidemiology. 2001;30(Suppl 1):S30–S34. doi: 10.1093/ije/30.suppl_1.s30. [DOI] [PubMed] [Google Scholar]
- Harrell F.E. Springer; New York: 2001. Regression modeling strategies: With applications to linear models, logistic regression, and survival analysis. [Google Scholar]
- Hernan M.A., Robins J.M. Estimating causal effects from epidemiological data. J Epidemiol Community Health. 2006;60(7):578–586. doi: 10.1136/jech.2004.029496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hidden J., Gerds T. Evaluating the impact of novel biomarkers: Do not rely on IDI and NRI. Department of Biostatistics, University of Copenhagen; Denmark: 2012. Research Report 12/08. [Google Scholar]
- Hlatky M.A., Greenland P., Arnett D.K., Ballantyne C.M., Criqui M.H., Elkind M.S.…Wilson P.W. Criteria for evaluation of novel markers of cardiovascular risk: A scientific statement from the American Heart Association. Circulation. 2009;119(17):2408–2416. doi: 10.1161/CIRCULATIONAHA.109.192278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogben L., Sim M. The self-controlled and self-recorded clinical trial for low-grade morbidity. British Journal of Preventive & Social Medicine. 1953;7(4):163–179. doi: 10.1136/jech.7.4.163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogben L., Sim M. The self-controlled and self-recorded clinical trial for low-grade morbidity. International Journal of Epidemiology. 2011;40(6):1438–1454. doi: 10.1093/ije/dyr026. [DOI] [PubMed] [Google Scholar]
- Ilic D., Neuberger M.M., Djulbegovic M., Dahm P. Screening for prostate cancer. Cochrane Database of Systematic Reviews. 2013;1:CD004720. doi: 10.1002/14651858.CD004720.pub3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivert A.K., Mulinari S., van Leeuwen W., Wagner P., Merlo J. Appropriate assessment of ethnic differences in adolescent use of psychotropic medication: Multilevel analysis of discriminatory accuracy. Ethnicity & Health. 2016;21(6):578–595. doi: 10.1080/13557858.2016.1143090. [DOI] [PubMed] [Google Scholar]
- Juarez S., Wagner P., Merlo J. Applying discriminative measures to revisit the determinants of small-for-gestational-age. European Journal of Epidemiology. 2013;28:S146–S147. [Google Scholar]
- Kannel W.B., Gordon T., National Heart Institute (U.S.) The Framingham study; an epidemiological investigation of cardiovascular disease. U.S. Dept. of Health, Education, and Welfare, National Institutes of Health; Bethesda, Md: 1968. for sale by the Supt. of Docs., U.S. Govt. Print. Off., Washington. [Google Scholar]
- Kaptoge S., Di Angelantonio E., Pennells L., Wood A.M., White I.R., Gao P.…Danesh J. C-reactive protein, fibrinogen, and cardiovascular disease prediction. New England Journal of Medicine. 2012;367(14):1310–1320. doi: 10.1056/NEJMoa1107477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman J.S., Cooper R.S. Seeking causal explanations in social epidemiology. American Journal of Epidemiology. 1999;150(2):113–120. doi: 10.1093/oxfordjournals.aje.a009969. [DOI] [PubMed] [Google Scholar]
- Kaufman J.S., Kaufman S. Commentary: Estimating causal effects. International Journal of Epidemiology. 2002;31(2):431–432. (discussion 435-438.) [PubMed] [Google Scholar]
- Kawachi I., Conrad P. Medicalization and the pharmacological treatment of blood pressure. In: Davis P., editor. Contested ground. Public purpose and private interests in the regulation of prescription drugs. Oxford University Press; New. York: 1996. p. 1996. [Google Scholar]
- Keys A.B. Harvard University Press; Cambridge, MA: 1980. Seven countries: A multivariate analysis of death and coronary heart disease. [Google Scholar]
- Khoury M.J., Iademarco M.F., Riley W.T. Precision public health for the era of precision medicine. American Journal of Preventive Medicine. 2016;50(3):398–401. doi: 10.1016/j.amepre.2015.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khoury M.J., Newill C.A., Chase G.A. Epidemiologic evaluation of screening for risk factors: Application to genetic screening. American Journal of Public Health. 1985;75(10):1204–1208. doi: 10.2105/ajph.75.10.1204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kravitz R.L., Duan N., Braslow J. Evidence-based medicine, heterogeneity of treatment effects, and the trouble with averages. Milbank Quarterly. 2004;82(4):661–687. doi: 10.1111/j.0887-378X.2004.00327.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson E.B. N-of-1 trials: A new future? Journal of General Internal Medicine. 2010;25(9):891–892. doi: 10.1007/s11606-010-1440-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Law M.R., Wald N.J., Morris J.K. The performance of blood pressure and other cardiovascular risk factors as screening tests for ischaemic heart disease and stroke. Journal of Medical Screening. 2004;11(1):3–7. doi: 10.1177/096914130301100102. [DOI] [PubMed] [Google Scholar]
- Li C., Aronsson C.A., Hedblad B., Gullberg B., Wirfalt E., Berglund G. Ability of physical activity measurements to assess health-related risks. European Journal of Clinical Nutrition. 2009;63(12):1448–1451. doi: 10.1038/ejcn.2009.69. [DOI] [PubMed] [Google Scholar]
- Lillie E.O., Patay B., Diamant J., Issell B., Topol E.J., Schork N.J. The n-of-1 clinical trial: The ultimate strategy for individualizing medicine? Per Med. Personalized Medicine. 2011;8(2):161–173. doi: 10.2217/pme.11.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKelvey R.D., Zavoina W. A statistical model for the analysis of ordinal level dependent variables. Journal of the Mathematical Society. 1975;4:103–120. [Google Scholar]
- McMichael A.J. Prisoners of the proximate: Loosening the constraints on epidemiology in an age of change. American Journal of Epidemiology. 1999;149(10):887–897. doi: 10.1093/oxfordjournals.aje.a009732. [DOI] [PubMed] [Google Scholar]
- Melander O., Newton-Cheh C., Almgren P., Hedblad B., Berglund G., Engstrom G.…Wang T.J. Novel and conventional biomarkers for prediction of incident cardiovascular events in the community. Journal of the American Medical Association. 2009;302(1):49–57. doi: 10.1001/jama.2009.943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merlo J. Multilevel analytical approaches in social epidemiology: Measures of health variation compared with traditional measures of association. Journal of Epidemiology & Community Health. 2003;57(8):550–552. doi: 10.1136/jech.57.8.550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merlo J. Invited commentary: Multilevel analysis of individual heterogeneity-a fundamental critique of the current probabilistic risk factor epidemiology. American Journal of Epidemiology. 2014 doi: 10.1093/aje/kwu108. [DOI] [PubMed] [Google Scholar]
- Merlo J., Wagner P. Discriminatory accuracy and population attributable fractions: The case of traditional risk factors and novel biomarkers for coronary heart disease. European Journal of Epidemiology. 2013;28:S147–S148. [Google Scholar]
- Merlo J., Asplund K., Lynch J., Rastam L., Dobson A. Population effects on individual systolic blood pressure: A multilevel analysis of the World Health Organization MONICA Project. American Journal of Epidemiology. 2004;159(12):1168–1179. doi: 10.1093/aje/kwh160. [DOI] [PubMed] [Google Scholar]
- Merlo J., Bengtsson-Bostrom K., Lindblad U., Rastam L., Melander O. Multilevel analysis of systolic blood pressure and ACE gene I/D polymorphism in 438 Swedish families--a public health perspective. BMC Medical Genetics. 2006;7:14. doi: 10.1186/1471-2350-7-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merlo J., Berglund G., Wirfalt E., Gullberg B., Hedblad B., Manjer J.…Ostergren P.O. Self-administered questionnaire compared with a personal diary for assessment of current use of hormone therapy: An analysis of 16,060 women. American Journal of Epidemiology. 2000;152(8):788–792. doi: 10.1093/aje/152.8.788. [DOI] [PubMed] [Google Scholar]
- Merlo J., Chaix B., Yang M., Lynch J., Rastam L. A brief conceptual tutorial of multilevel analysis in social epidemiology: Linking the statistical concept of clustering to the idea of contextual phenomenon. Journal of Epidemiology & Community Health. 2005;59(6):443–449. doi: 10.1136/jech.2004.023473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merlo J., Lindblad U., Pessah-Rasmussen H., Hedblad B., Rastam J., Isacsson S.O.…Rastam L. Comparison of different procedures to identify probable cases of myocardial infarction and stroke in two Swedish prospective cohort studies using local and national routine registers. European Journal of Epidemiology. 2000;16(3):235–243. doi: 10.1023/a:1007634722658. [DOI] [PubMed] [Google Scholar]
- Merlo J., Mulinari S. Measures of discriminatory accuracy and categorizations in public health: A response to Allan Krasnik’s editorial. European Journal of Public Health. 2015;25(6):910. doi: 10.1093/eurpub/ckv209. [DOI] [PubMed] [Google Scholar]
- Merlo J., Ohlsson H., Lynch K.F., Chaix B., Subramanian S.V. Individual and collective bodies: Using measures of variance and association in contextual epidemiology. Journal of Epidemiology & Community Health. 2009;63(12):1043–1048. doi: 10.1136/jech.2009.088310. [DOI] [PubMed] [Google Scholar]
- Merlo J., Ohlsson H., Lynch K.F., Chaix B., Subramanian S.V. Individual and collective bodies: Using measures of variance and association in contextual epidemiology. Journal of Epidemiology & Community Health. 2009;63(12):1043–1048. doi: 10.1136/jech.2009.088310. [DOI] [PubMed] [Google Scholar]
- Merlo J., Viciana-Fernandez F.J., Ramiro-Farinas D., Research Group of Longitudinal Database of Andalusian Bringing the individual back to small-area variation studies: A multilevel analysis of all-cause mortality in Andalusia, Spain. Social Science & Medicine. 2012;75(8):1477–1487. doi: 10.1016/j.socscimed.2012.06.004. [DOI] [PubMed] [Google Scholar]
- Merlo J., Wagner P., Ghith N., Leckie G. An original stepwise multilevel logistic regression analysis of discriminatory accuracy: The case of neighbourhoods and health. PLoS One. 2016;11(4):e0153778. doi: 10.1371/journal.pone.0153778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moons K.G., de Groot J.A., Bouwmeester W., Vergouwe Y., Mallett S., Altman D.G.…Collins G.S. Critical appraisal and data extraction for systematic reviews of prediction modelling studies: The CHARMS checklist. PLoS Med. 2014;11(10):e1001744. doi: 10.1371/journal.pmed.1001744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulinari S., Bredstrom A., Merlo J. Questioning the discriminatory accuracy of broad migrant categories in public health: Self-rated health in Sweden. European Journal of Public Health. 2015;25(6):911–917. doi: 10.1093/eurpub/ckv099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Board of Health and Welfare . National Board of Health and Welfare; Stockholm, Sweden: 2000. Evaluation of quality of diagnosis of acute myocardial infarction, inpatient register 1997 and 1995. [Google Scholar]
- Nohr E.A., Olsen J. Commentary: Epidemiologists have debated representativeness for more than 40 years—has the time come to move on? International Journal of Epidemiology. 2013;42(4):1016–1017. doi: 10.1093/ije/dyt102. (1010.1093/ije/dyt1102) [DOI] [PubMed] [Google Scholar]
- Pearce N. Epidemiology in a changing world: Variation, causation and ubiquitous risk factors. International Journal of Epidemiology. 2011;40(2):503–512. doi: 10.1093/ije/dyq257. [DOI] [PubMed] [Google Scholar]
- Pencina M.J., D’Agostino R.B., Pencina K.M., Janssens A.C., Greenland P. Interpreting incremental value of markers added to risk prediction models. American Journal of Epidemiology. 2012;176(6):473–481. doi: 10.1093/aje/kws207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pencina M.J., D’Agostino R.B., Sr, D’Agostino R.B., Jr, Vasan R.S. Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond. Statistics in Medicine. 2008;27(2):157–172. doi: 10.1002/sim.2929. [DOI] [PubMed] [Google Scholar]
- Pencina M.J., D’Agostino R.B., Sr, Steyerberg E.W. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Statistics in Medicine. 2011;30(1):11–21. doi: 10.1002/sim.4085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe M.S., Feng Z., Huang Y., Longton G., Prentice R., Thompson I.M., Zheng Y. Integrating the predictiveness of a marker with its performance as a classifier. American Journal of Epidemiology. 2008;167(3):362–368. doi: 10.1093/aje/kwm305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe M.S., Janes H., Longton G., Leisenring W., Newcomb P. Limitations of the odds ratio in gauging the performance of a diagnostic, prognostic, or screening marker. American Journal of Epidemiology. 2004;159(9):882–890. doi: 10.1093/aje/kwh101. [DOI] [PubMed] [Google Scholar]
- Pepe M.S. Oxford University Press; Oxford; New York: 2003. The statistical evaluation of medical tests for classification and prediction. [Google Scholar]
- Pepe M.S. Problems with risk reclassification methods for evaluating prediction models. American Journal of Epidemiology. 2011;173(11):1327–1335. doi: 10.1093/aje/kwr013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe M.S., Janes H., Gu J.W. Letter by Pepe et al. regarding article, “Use and misuse of the receiver operating characteristic curve in risk prediction”. Circulation. 2007;116(6) doi: 10.1161/CIRCULATIONAHA.107.709253. (e132; author reply e134) [DOI] [PubMed] [Google Scholar]
- Persson M., Hedblad B., Nelson J.J., Berglund G. Elevated Lp-PLA2 levels add prognostic information to the metabolic syndrome on incidence of cardiovascular events among middle-aged nondiabetic subjects. Arteriosclerosis Thrombosis, and Vascular Biology. 2007;27(6):1411–1416. doi: 10.1161/ATVBAHA.107.142679. [DOI] [PubMed] [Google Scholar]
- Pickering J.W., Endre Z.H. New metrics for assessing diagnostic potential of candidate biomarkers. Clinical Journal of the American Society of Nephrology. 2012;7(8):1355–1364. doi: 10.2215/CJN.09590911. [DOI] [PubMed] [Google Scholar]
- Richiardi L., Pizzi C., Pearce N. Commentary: Representativeness is usually not necessary and often should be avoided. International Journal of Epidemiology. 2013;42(4):1018–1022. doi: 10.1093/ije/dyt103. (1010.1093/ije/dyt1103) [DOI] [PubMed] [Google Scholar]
- Rockhill B. Discriminatory accuracy of a risk prediction model. Biostatistics. 2005;6(3):500–502. doi: 10.1093/biostatistics/kxi034. (author reply 503-504) [DOI] [PubMed] [Google Scholar]
- Rodriguez-Lopez M., Wagner P., Perez-Vicente R., Crispi F., Merlo J. Revisiting the discriminatory accuracy of traditional risk factors in preeclampsia screening. PLoS One. 2017;12(5):e0178528. doi: 10.1371/journal.pone.0178528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockhill B., Newman B., Weinberg C. Use and misuse of population attributable fractions. American Journal of Public Health. 1998;88(1):15–19. doi: 10.2105/ajph.88.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothman K.J., Gallacher J.E., Hatch E.E. Why representativeness should be avoided. International Journal of Epidemiology. 2013;42(4):1012–1014. doi: 10.1093/ije/dys223. (1010.1093/ije/dys1223) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothstein W.G. University of Rochester Press; Rochester, NY: 2003. Public health and the risk factor: A history of an uneven medical revolution. [Google Scholar]
- Royston P., Altman D.G. Visualizing and assessing discrimination in the logistic regression model. Statistics in Medicine. 2010;29(24):2508–2520. doi: 10.1002/sim.3994. [DOI] [PubMed] [Google Scholar]
- Shlipak M.G., Fried L.F., Cushman M., Manolio T.A., Peterson D., Stehman-Breen C.…Psaty B. Cardiovascular mortality risk in chronic kidney disease - Comparison of traditional and novel risk factors. Journal of the American Medical Association. 2005;293(14):1737–1745. doi: 10.1001/jama.293.14.1737. [DOI] [PubMed] [Google Scholar]
- Siontis G.C., Ioannidis J.P. Risk factors and interventions with statistically significant tiny effects. International Journal of Epidemiology. 2011;40(5):1292–1307. doi: 10.1093/ije/dyr099. [DOI] [PubMed] [Google Scholar]
- Smith G.D. Epidemiology, epigenetics and the ‘Gloomy Prospect’: Embracing randomness in population health research and practice. International Journal of Epidemiology. 2011;40(3):537–562. doi: 10.1093/ije/dyr117. [DOI] [PubMed] [Google Scholar]
- Tabery J. Commentary: Hogben vs the Tyranny of averages. International Journal of Epidemiology. 2011;40(6):1454–1458. doi: 10.1093/ije/dyr027. [DOI] [PubMed] [Google Scholar]
- The National Board of Health and Welfare(2010a). Cause of Death Registry (Dödsorsaksregistret). 〈http://www.socialstyrelsen.se/register/dodsorsaksregistret〉.
- The National Board of Health and Welfare (2010b). The National Patient Register 〈http://www.socialstyrelsen.se/register/halsodataregister/patientregistret/inenglish〉.
- Wagner P., Merlo J. Measures of discriminatory accuracy in multilevel analysis. European Journal of Epidemiology. 2013;28(1, Supplement):135. [Google Scholar]
- Wagner P., Merlo J. Discriminatory accuracy of a random effect in multilevel logistic regression. International Journal of Epidemiology. 2014;44:i49–i50. [Google Scholar]
- Wald D.S., Wald N.J. Implementation of a simple age-based strategy in the prevention of cardiovascular disease: The Polypill approach. Journal of Evaluation in Clinical Practice. 2012;18(3):612–615. doi: 10.1111/j.1365-2753.2011.01637.x. [DOI] [PubMed] [Google Scholar]
- Wald N.J., Hackshaw A.K., Frost C.D. When can a risk factor be used as a worthwhile screening test? British Medical Journal. 1999;319(7224):1562–1565. doi: 10.1136/bmj.319.7224.1562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wald N.J., Law M.R. A strategy to reduce cardiovascular disease by more than 80% BMJ. 2003;326(7404):1419. doi: 10.1136/bmj.326.7404.1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wald N.J., Morris J.K. Assessing risk factors as potential screening tests: A simple assessment tool. Archives of Internal Medicine. 2011;171(4):286–291. doi: 10.1001/archinternmed.2010.378. [DOI] [PubMed] [Google Scholar]
- Wald N.J., Morris J.K., Rish S. The efficacy of combining several risk factors as a screening test. Journal of Medical Screening. 2005;12(4):197–201. doi: 10.1258/096914105775220642. [DOI] [PubMed] [Google Scholar]
- Wald N.J., Simmonds M., Morris J.K. Screening for future cardiovascular disease using age alone compared with multiple risk factors and age. PLoS One. 2011;6(5):e18742. doi: 10.1371/journal.pone.0018742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T.J., Gona P., Larson M.G., Tofler G.H., Levy D., Newton-Cheh C.…Vasan R.S. Multiple biomarkers for the prediction of first major cardiovascular events and death. New England Journal of Medicine. 2006;355(25):2631–2639. doi: 10.1056/NEJMoa055373. [DOI] [PubMed] [Google Scholar]
- Ware J.H. Statistics and medicine - The limitations of risk factors as prognostic tools. New England Journal of Medicine. 2006;355(25):2615–2617. doi: 10.1056/NEJMp068249. [DOI] [PubMed] [Google Scholar]
- Wemrell M., Mulinari S., Merlo J. An intersectional approach to multilevel analysis of individual heterogeneity (MAIH) and discriminatory accuracy. Social Science & Medicine. 2017 doi: 10.1016/j.socscimed.2017.02.040. [DOI] [PubMed] [Google Scholar]
- Wemrell M., Mulinari S., Merlo J. Intersectionality and risk for ischemic heart disease in Sweden: Categorical and anti-categorical approaches. Social Science & Medicine. 2017;177:213–222. doi: 10.1016/j.socscimed.2017.01.050. [DOI] [PubMed] [Google Scholar]
- Zernicka-Goetz M., Huang S. Stochasticity versus determinism in development: A false dichotomy? Nature Reviews Genetics. 2010;11(11):743–744. doi: 10.1038/nrg2886. [DOI] [PubMed] [Google Scholar]
- Zethelius B., Berglund L., Sundstrom J., Ingelsson E., Basu S., Larsson A.…Arnlov J. Use of multiple biomarkers to improve the prediction of death from cardiovascular causes. New England Journal of Medicine. 2008;358(20):2107–2116. doi: 10.1056/NEJMoa0707064. [DOI] [PubMed] [Google Scholar]
- Zucker D.R., Ruthazer R., Schmid C.H. Individual (N-of-1) trials can be combined to give population comparative treatment effect estimates: Methodologic considerations. Journal of Clinical Epidemiology. 2010;63(12):1312–1323. doi: 10.1016/j.jclinepi.2010.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucker D.R., Schmid C.H., McIntosh M.W., D’Agostino R., Selker H.P., Lau J. Combining single patient (N-of-1) trials to estimate population treatment effects and to evaluate individual patient responses to treatment. Journal of Clinical Epidemiology. 1997;50(4):401–410. doi: 10.1016/s0895-4356(96)00429-5. [DOI] [PubMed] [Google Scholar]
- Zweig M.H., Broste S.K., Reinhart R.A. ROC curve analysis: An example showing the relationships among serum lipid and apolipoprotein concentrations in identifying patients with coronary artery disease. Clinical Chemistry. 1992;38(8 Pt 1):1425–1428. [PubMed] [Google Scholar]