Skip to main content
PMC home page
SSM - Population Health logoLink to SSM - Population Health
. 2017 Nov 21;4:95–99. doi: 10.1016/j.ssmph.2017.11.008

Machine learning approaches to the social determinants of health in the health and retirement study

Benjamin Seligman a,⁎, Shripad Tuljapurkar b, David Rehkopf c
PMCID: PMC5769116  PMID: 29349278

Abstract

Background

Social and economic factors are important predictors of health and of recognized importance for health systems. However, machine learning, used elsewhere in the biomedical literature, has not been extensively applied to study relationships between society and health. We investigate how machine learning may add to our understanding of social determinants of health using data from the Health and Retirement Study.

Methods

A linear regression of age and gender, and a parsimonious theory-based regression additionally incorporating income, wealth, and education, were used to predict systolic blood pressure, body mass index, waist circumference, and telomere length. Prediction, fit, and interpretability were compared across four machine learning methods: linear regression, penalized regressions, random forests, and neural networks.

Results

All models had poor out-of-sample prediction. Most machine learning models performed similarly to the simpler models. However, neural networks greatly outperformed the three other methods. Neural networks also had good fit to the data (R2 between 0.4–0.6, versus <0.3 for all others). Across machine learning models, nine variables were frequently selected or highly weighted as predictors: dental visits, current smoking, self-rated health, serial-seven subtractions, probability of receiving an inheritance, probability of leaving an inheritance of at least $10,000, number of children ever born, African-American race, and gender.

Discussion

Some of the machine learning methods do not improve prediction or fit beyond simpler models, however, neural networks performed well. The predictors identified across models suggest underlying social factors that are important predictors of biological indicators of chronic disease, and that the non-linear and interactive relationships between variables fundamental to the neural network approach may be important to consider.

Keywords: Social determinants of health, Machine learning, Neural network, Biomarkers, Health and retirement study

Highlights

  • •

    “Big data” methods may aid understanding of social determinants of health.

  • •

    Neural networks outperform other methods in prediction and variance explained.

  • •

    No individual machine learning method was readily interpretable.

  • •

    Variables in common among machine learning methods suggest core social determinants.

1. Introduction

Biomedical practice and research often generate large quantities of data, from administrative records to molecular information. While how to “learn from data” is not a new challenge, the scale of data has prompted interest in algorithm driven approaches to analysis and interpretation. Due to the large number of loci studied and relative lack of a priori knowledge relevant to a particular disease, genomic research has been both a major user and source of innovation in these methods (Risch and Merikangas, 1996). These approaches have also been used in environmental health and nutrition, identifying environmental contaminants that have strong associations with diabetes (Patel, Bhattacharya, & Butte, 2010), adverse lipid profiles (Patel et al., 2012) as well as micronutrient associations with hypertension (Tzoulaki et al., 2012). They have been used to study pediatric obesity and mortality as well (Rehkopf and Laraia, 2011, Patel et al., 2013). Similarly, there is a proliferation of “-omics” approaches to studying disease, such as metabolomics (Trygg et al., 2007, Wang et al., 2011, Wishart, 2016, Fearnley and Inouye, 2016) and epigenomics (Emes and Farrell, 2012, Lee et al., 2012, Horvath, 2013), which seek to understand biochemical pathway and genetic regulatory bases of disease respectively.

By contrast, research on the social determinants of health has usually focused on hypothesis-driven models to understand how factors such as poverty and education contribute to health. This has aided in understanding causal mechanisms underlying social determinants’ effects on health. This focus on causation has perhaps in some ways been one reason why there has been a limited use of machine learning, although efforts to bring causal inference to machine learning are making great strides (van der Laan and Rose, 2011, Varian, 2014, Athey and Imbens, 2015) with compelling results (Ahern, Balzer, & Galea, 2015).

Like genomic studies, many social science studies also generate large quantities of data. There is a role for machine learning to explore these data as hypothesis generation and validation of theory (Raftery, 1995, Sala-I-Martin, 1997, Hendry and Krolzig, 2004, Glymour et al., 2013). In addition to traditional survey data, information such as credit scores and social networks have predictive power for health and add to our understanding of how social determinants may operate; (Christakis and Fowler, 2007, Israel et al., 2014) integrating multiple sources of data will increase the scale of potentially useful datasets. It is important to understand how methods commonly used to analyze and interpret “big data” may be applied to the social determinants of health. Two questions about machine learning methods are particularly relevant: first, do they lead to substantially better predictions than models based on established theory about the social determinants of health, and second, do they enhance our understanding of how social determinants may result in differences in health outcomes?

We compare four major regression based methods in machine learning with both a minimal and a theory-driven model. We assess the performance of each in predicting four health-related biomarkers using data from a large social science survey. Secondarily, we also consider the interpretability of the models. The answers to our study question are relevant both to professionals managing social, educational, or health service data systems as well as scientists exploring high-dimensional social data.

2. Methods

2.1. Data

Data were from the Health and Retirement Study (HRS), a rolling cohort of men and women 50 years old and above and their spouses begun in 1992, with biennial follow-up and periodic recruitment of eligible new participants; this analysis incorporates only primary participants, not spouses (Health and Retirement Study, RAND public use dataset, 2014). 15,784 participants had medical examinations with anthropometry and blood biomarker measurement in either 2006 or 2008 (Crimmins, Guyer, & Langa, 2008). We investigate four outcomes that are biological markers of chronic disease risk: systolic blood pressure (SBP, N = 13,784), body mass index (BMI, N = 13,568), waist circumference (N = 13,995), and telomere length (N = 5808). Telomere length was measured from buccal cells collected from a smaller subsample of HRS respondents than the other measurements. Biologically implausible values were removed as described in Supplementary Table 1; the logarithm of values for telomere length was taken following removal of biologically implausible values to eliminate skew. Distributions of each biomarker are given in Supplementary Figure 1. The first three are associated with a variety of health risks, including cardiovascular disease, stroke, and diabetes. Further, BMI and waist circumference are related measures, both intended to assess adiposity. We consider telomere length as a novel biomarker that may have associations with health, in particular with cardiovascular disease (Haycock et al., 2014), but for which connections to health are less established.

Social and economic data on participants were taken from the RAND HRS data file version N for the wave prior to the measurement of the biomarkers (RAND, 2014). The RAND HRS Data file is an easy to use longitudinal data set based on the HRS data. It was developed at RAND with funding from the National Institute on Aging and the Social Security Administration. Among the variables included are information on individual, spousal, and household income and wealth, education, family structure, receipt of Social Security and other benefits, and health behaviors.

Variables from all sections of the survey were initially included. These are predominantly social and economic data, including health and health insurance, family structure, income, pensions, Social Security, and employment. Based on a priori criteria there were categories of variables that we did not include in our analysis: 1) variables with more than 10% missing values; 2) subject, household, and wave identifiers; 3) death variables; and 4) biometric or certain health variables from the RAND dataset that were duplicates of data from the biomarker file or were closely associated with them (i.e. BMI, cholesterol, height, weight, hypertension, diabetes, stroke, heart disease, lung disease, and number of conditions). Binary and categorical variables were then mode-imputed for missing data and categorical variables converted into dummy variables. Variables with a variance less than 0.0475 (equivalent to a binary variable with at least 95% of values in one category) were then removed. The resulting 458 variables were then standardized and missing values of continuous variables were mean-imputed.

2.2. Analytic methods

To assess different machine learning methods’ ability to predict the biomarkers of interest, we first considered two OLS regression models. The first was minimal and included gender, age, and age squared. The second was based on current understanding of social determinants of health, particularly that education and economic position have demonstrated associations with health. This theory-based model was parsimonious and included, as linear variables, household income, household wealth, and two binary variables indicating a high school-level education and less than a high school-level education, in addition to the parameters in the minimal model.

We next consider four machine learning algorithms: repeated linear regressions - akin to genome-wide association studies (GWAS), penalized linear regressions (Hastie, 2009), random forests (Breiman, 2001), and neural networks (Kriesel, 2007). These cover parametric and nonparametic approaches, with varying abilities to account for nonlinearity. While it is not possible to consider all machine learning algorithms, in addition to the broad coverage offered by these algorithms, all have been used in the medical literature (Patel et al., 2010, Rehkopf and Laraia, 2011, Horvath, 2013, Kapetanovic et al., 2004, Sato et al., 2005, Goldstein et al., 2010) and penalized regressions and random forests are particularly commonly-taught methods (Hastie et al., 2009, Bishop, 2006). These four also offer some prospect for interpretation rather than being completely “black box” approaches.

Approaches similar to GWAS have been previously used in studies surveying many potential disease predictors (Patel et al., 2013, Patel et al., 2015) however this is the first attempt to systematically analyze the associations between a broad range of social measures and biomarkers of health. For brevity we refer to this as SWAS, for society-wide association study. Similar to GWAS, for each biomarker Y we screen for adjusted associations with the candidate predictor X using the following model:

Yi=α+βGenderGenderi+βAgeAgei+βAge^2Agei2+βkXi+εi

where subscript i denotes one of the subjects in the dataset, βs are regression coefficients, α is the y-intercept, and ε is an independent, normally-distributed error term with a mean of 0. P-values for βk were deemed significant if they were below a Bonferroni-corrected α = 0.05. Those variables with statistically significant βk were then included in a final linear regression model of the biomarker Y.

LASSO is a penalized regression, adding the sum of the absolute values of the coefficients in the model to the residual sum of squares, as in this formula for a linear regression (Hastie, 2009):

RSSLASSO=12∑i=1N(Yi−α−∑k=1PβkXi,k)2+λ∑k=1P|βk|

Where i, Y, X, α, and β are as defined above, k denotes the different variables included in the model, P is the total number of variables in the model, N is the total number of subjects in the model, and λ is a weight assigned to the sum of the coefficients. The sum of the absolute values of the coefficients penalizes the inclusion of additional variables and forces those that do not substantially enhance prediction to have a coefficient of 0, and this penalty is weighted by λ. λ can be identified by a number of methods, including Akaike and Bayes Information Criteria and cross-validation. We use cross-validation to find the optimal penalty.

Random forests are an extension of classification and regression trees, which use recursive partitioning among the independent variables to approximate values of the dependent variable. Random forests add to this by repeatedly taking random subsets of the data to produce a large number of trees, then choosing among a random subset of the variables for each split within each tree (Breiman, 2001). We did a random search for the optimal number of trees per forest with 20 random draws from a range of 1 to 500 trees, with 5 terminal nodes per tree. This model neither does variable selection nor produces effect sizes in the manner of SWAS or LASSO. Instead, interpretation comes from variable importance values that show which among correlated variables is the strongest predictor. Here, importance is the mean decrease in mean squared error across all of the nodes where the variable appears in the random forest.

Neural networks take weighted sums of nonlinear transformations of the independent variables through a series of hidden layers, which then similarly produce the estimate for the dependent variable (Kriesel, 2007). If these used linear transformations of the independent variables, this would simplify to a linear regression. Outside of this scenario, which is not typical of neural networks including the ones used here, the variable weights that are produced are not akin to effect sizes in the manner of an ordinary linear regression due to the many nonlinearities and interactions that are built into the model. While there are many possible network structures and feedbacks, we use a feed-forward neural network, which does not involve feedback loops, with a random search for optimal hidden layer size with 10 random draws in a range of 1 to 229 (one half the number of input variables).

Predictive performance of each of the approaches was assessed by five-fold cross-validation. For each outcome of interest, we generated a random sequence of numbers from one to the number of subjects with non-missing data for, then divided the sequence into five equal groups. This generated folds for the cross validation, with each fold comparable across algorithms for a given outcome, but not necessarily across outcomes for the same algorithm. Values from the start of the sequence were repeated so as to be evenly divisible by five. For each fold, the algorithms were fit to four-fifths of the data and tested on the remaining one-fifth. For each cross-validation run, we calculated the root mean squared error (RMSE), which is the square root of the average squared residual between the model estimate and the true value. For assessing performance this can be interpreted as the average magnitude of the difference between the estimate and the true value. As our focus is not on the standard errors of regression coefficient estimates, we do not explicitly consider issues of multicollinearity.

Each algorithm for each outcome was run on the full dataset to estimate R2 and consider model interpretation. Analysis was conducted in R version 3.2.2 (R Core Team, 2012). LASSO regressions were done using cv.glmnet from the package glmnet and random forests were done using randomForest from the package randomForest (Friedman et al., 2010, Liaw and Wiener, 2002). Neural networks were constructed using Python version 2.7.5 and PyBrain (Python Software Foundation. Python, 2013, Schaul et al., 2010).

3. Results

3.1. Prediction and fit

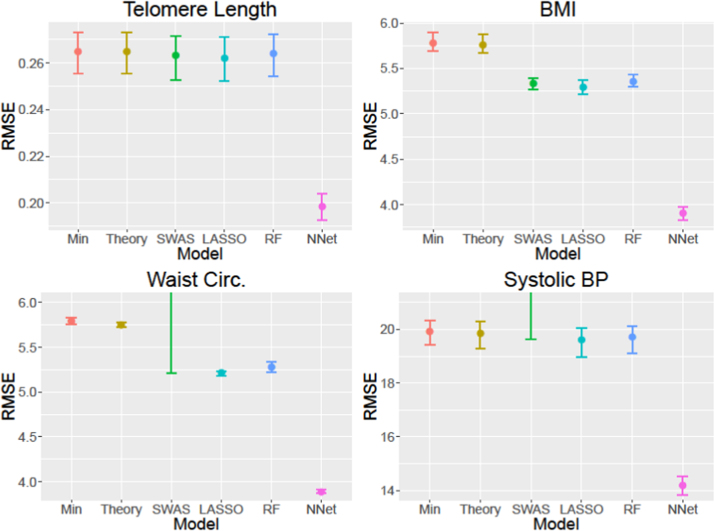
Fig. 1 and Supplementary Table 2 present, for each model or machine learning algorithm, the mean and range of the RMSE across the cross-validation folds.

Fig. 1.

Fig. 1

Open in a new tab

Mean and range, cross-validation root mean squared errors for each model of each biomarker considered.

The minimal and theory-based models perform very similarly and only differ past the third significant digit. While LASSO and, sometimes, SWAS outperformed the theory-based model, their advantages in RMSE are small. Notably, SWAS has very high mean and maximum RMSE for blood pressure and waist circumference. These are due to one outlier cross-validation fold of the five with exceptionally high RMSE, which all other approaches are able to effectively handle, rather than higher RMSE in every fold. Random forests was more consistently superior to the minimal and theory-based models, though again the advantage is often small. However, neural networks substantially outperformed all other approaches in terms of RMSE, reaching the lowest mean cross-validation RMSE in each case and with the maximum lower than the best performance of any other model for all biomarkers considered. Nonetheless, no model or algorithm was particularly accurate. For example, the RMSEs for models of BMI and SBP span categories within each (normal weight, overweight, and obese for BMI and normotensive, pre-hypertension, and stages I and II hypertension for SBP).

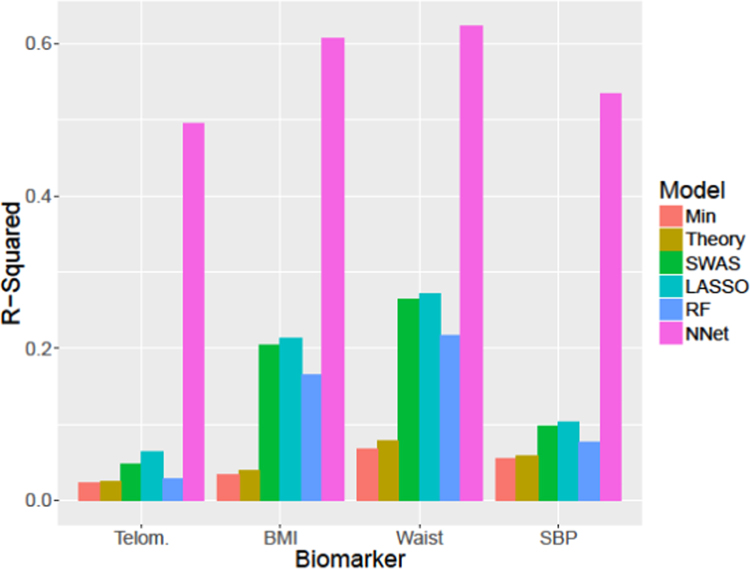
Estimates for R2 are given in Fig. 2 and Supplementary Table 3. Although the theory-based models incorporate known social predictors of health, R2 is only marginally greater than the minimal model, and both explained only a few percent of total variation. SWAS and LASSO have somewhat larger R2 values, while random forests and neural networks see considerable jumps in R2. Random forests typically explain 80% of the variance, however this in the context of the minimal improvements to cross-validation RMSE and using dozens or hundreds of variables. By contrast, neural networks explain roughly one-third to one-half of the variance which, with their substantially lower RMSE, suggests that these models are well-fitted.

Fig. 2.

Fig. 2

Open in a new tab

R2 for each model of each biomarker considered on full dataset.

3.2. Model interpretation

The details of the resulting models are given in the supplement. For SWAS and LASSO models, which explicitly select variables, the resulting models were typically not sparse, containing anywhere from 55 to 235 variables. One exception was the SWAS model for telomere length which incorporated only 6 variables.

For random forests and neural networks, which do not explicitly conduct variable selection, we analyzed variable importance (for random forests) and weights (neural networks) (Supplementary Figures 6 and 7). In both cases, the majority of variables had relatively low importance or weight, with a much smaller proportion of variables having substantial influence over predictions.

To find commonalities among machine learning models we determined which variables they share. As random forests and neural networks do not select variables, we averaged the number of variables selected by SWAS and LASSO for each biomarker. We then selected that many variables from the random forest and neural network by descending importance or absolute value of weight. No variables were shared in common across all models for all biomarkers, as there were no variables in common across models of telomere length. Excluding telomere length, five variables were shared among models, given in Table 1.

Table 1.

Variables selected by all machine learning models for BMI, waist circumference, and systolic blood pressure.

Meaning Survey section
Current self-rated health is good Health
Self-rated probability of leaving an inheritance of at least $10,000 Retirement plans
Black/African-American Race Demographics
Gender Demographics
No. of children ever born Family Structure
Open in a new tab

4. Discussion

In this comparison of four machine learning approaches to studying social determinants of health, we find that, with one exception, these methods do not typically perform better than simpler models for prediction of four health related biomarkers. Further, the machine learning approaches used do not lend themselves to ready interpretation, often incorporating dozens or hundreds of variables in the cases of SWAS and LASSO. The exception to this, for prediction though not interpretability, were neural networks. This suggests a promising new direction for models incorporating a more detailed range of variables measuring the social and physical environment with respect to predicting disease risk biomarkers.

Simple regression models, though much sparser than the machine learning methods considered, often had similar prediction error. This performance, in fact, yields concerns. The theory-based model only considered income, wealth, and education, while SWAS and LASSO, which incorporated such features as tobacco use, physician visits, and other measures closely related to health, did have substantially better prediction or fit. This may speak to the power of fundamental social factors, except that the theory-based model performs only marginally better than the minimal model of just age and gender. One interpretation is that biological factors, partially captured by age and gender, are more important predictors. However, given these models’ high cross-validation RMSE and the low R2, the real lesson may be that the social causation of health is more complex than linear models capture. This is at least partly substantiated by the superior cross-validation RMSE of the neural networks, which do not rely on variables behaving linearly, although random forests have R2 similar to SWAS and LASSO.

Across models, the five variables selected by all machine learning models as predictors of SBP, BMI, and waist circumference cover several domains: health, captured by self-rated health; wealth, captured by probability of bequeathing an inheritance; social support, reflected by number of children born; and sex and race, which capture a number of social factors as well as some biological ones. However, these are not the only interpretations possible and the extent to which sex and race reflect biological factors as well as social ones is unclear and, in the case of race, controversial. Interpretation is further limited as random forests do not offer a direction of association.

Neural networks may have much promise as an approach to understanding how social determinants of health interact to shape morbidity and mortality, as they have had in other domains. While we used a feed-forward neural network with a single hidden layer, deep learning, which uses multiple hidden layers, may predict with less variability. Alternative network structures could also result in simpler networks with equal accuracy. Further, the ability of neural networks to learn in real-time as new data arise make them attractive in making predictions from electronic medical record data. However, as with standard regression techniques, they may be affected by multicollinarity. Further, interpretation of these models, particularly identifying the interactions and nonlinearity that they can accommodate, remains challenging.

Further limitations to our findings include limitations to the data and machine learning algorithms we could consider. We consider four biomarkers, all of which are measured as continuous variables; binary health outcomes, such as the presence of a disease, might require larger sample sizes to attain similar values of RMSE. We focus our analysis on the Health and Retirement Study, a standard-setting survey of aging in the United States, but which has few domestic comparators for validation. As we note earlier, there are more algorithms than we could investigate, and other machine learning approaches should be explored as tools for studying social determinants of health. In particular, while we consider parametric and nonparametric models, we do not consider semiparametric models which may offer flexibility beyond parametric models like LASSO or SWAS without the challenges of interpretation faced by random forests and neural networks. We also do not consider ensemble methods, which combine the results of multiple different machine learning algorithms and have many advantages in prediction. With the exception of random forests, which break correlations among independent variables by randomly selecting subsets of them at each node, the methods we consider may also have issues with interpretability related to multicollinearity. Finally, we were limited in our ability to tune parameters for random forests, and it is possible that further refinement of tree depth may lead to further improvements in prediction or fit.

In conclusion, our current understanding of the social determinants of health, modeled quantitatively by regression, performs well compared with several “big data” approaches. However, neural networks, which readily allow for interaction and nonlinearity among input variables, may help us expand our knowledge of how social determinants operate. Further work, investigating other approaches to machine learning, other data sets, as well as exploring the models considered here, should be pursued to find new ways of analyzing and understanding social determinants of health.

Acknowledgments

This study was supported by NIA grant R24AG039345. BS was additionally supported by the Stanford Interdisciplinary Graduate Fellowship and the Stanford Medical Scientist Training Program.

Footnotes

Appendix A

Supplementary data associated with this article can be found in the online version at doi:10.1016/j.ssmph.2017.11.008.

Appendix A. Supplementary material

supplementary table 1

Supplementary material

mmc1.docx (472.8KB, docx)

.

References

  1. Ahern J., Balzer L., Galea S. The roles of outlet density and norms in alcohol use disorder( ) Drug and Alcohol Dependence. 2015;151:144–150. doi: 10.1016/j.drugalcdep.2015.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Athey S., Imbens G. (2015). Recursive Partitioning for Heterogeneous Causal Effects. ArXiv Published Online First: 5 April. 〈http://arxiv.org/abs/1504.01132〉 (Accessed 10 May 2016). [DOI] [PMC free article] [PubMed]
  3. Bishop C. Springer; New York, NY: 2006. Pattern Recognition and Machine Learning. [Google Scholar]
  4. Breiman L. Random forests. Machine Learning. 2001;45:5–32. [Google Scholar]
  5. Christakis N.A., Fowler J.H. The spread of obesity in a large social network over 32 years. The New England Journal of Medicine. 2007;357:370–379. doi: 10.1056/NEJMsa066082. [DOI] [PubMed] [Google Scholar]
  6. Crimmins E., Guyer H., Langa K. (2008)., et al. Documentation of Biomarkers in the Health and Retirement Study. Ann Arbor, Michigan.
  7. Emes R.D., Farrell W.E. Make way for the ‘next generation’: Application and prospects for genome-wide, epigenome-specific technologies in endocrine research. Journal of Molecular Endocrinology. 2012;49(R19):27. doi: 10.1530/JME-12-0045. [DOI] [PubMed] [Google Scholar]
  8. Fearnley L.G., Inouye M. Metabolomics in epidemiology: From metabolite concentrations to integrative reaction networks. International Journal of Epidemiology. 2016 doi: 10.1093/ije/dyw046. (dyw046) [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Friedman Jerome, Hastie Trevor, Tibshirani Robert. Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software. 2010;33:1–22. 〈http://www.jstatsoft.org/v33/i01/〉 [PMC free article] [PubMed] [Google Scholar]
  10. Glymour M. Maria, Osypuk Theresa L., Rehkopf David H. Off-roading with social epidemiology — Exploration, causation, translation. American Journal of Epidemiology. 2013;178:858–863. doi: 10.1093/aje/kwt145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Goldstein B.A., Hubbard A.E., Cutler A. An application of Random Forests to a genome-wide association dataset: Methodological considerations {&} new findings. BMC Genetics. 2010;11:49. doi: 10.1186/1471-2156-11-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hastie Trevor, Tibshirani Robert, Friedman Jerome. 2nd ed. Springer; 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. [Google Scholar]
  13. Haycock P.C., Heydon E.E., Kaptoge S. Leucocyte telomere length and risk of cardiovascular disease: Systematic review and meta-analysis. BMJ. 2014;349:g4227. doi: 10.1136/bmj.g4227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Health and Retirement Study, RAND public use dataset (2014).
  15. Hendry D.F., Krolzig H.-M. We ran one regression*. Oxford Bulletin of Economics and Statistics. 2004;66:799–810. [Google Scholar]
  16. Horvath S. DNA methylation age of human tissues and cell types. Genome Biology. 2013;14:R115. doi: 10.1186/gb-2013-14-10-r115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Israel S., Caspi A., Belsky D.W. Credit scores, cardiovascular disease risk, and human capital. Proceedings of the National Academy of Sciences. 2014;111:17087–17092. doi: 10.1073/pnas.1409794111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kapetanovic I.M., Rosenfeld S., Izmirlian G. Overview of commonly used bioinformatics methods and their applications. Annals of the New York Academy of Sciences. 2004;1020:10–21. doi: 10.1196/annals.1310.003. [DOI] [PubMed] [Google Scholar]
  19. Kriesel D. (2007). A Brief Introduction to Neural Networks. available.
  20. Lee H., Jaffe A.E., Feinberg J.I. DNA methylation shows genome-wide association of NFIX, RAPGEF2 and MSRB3 with gestational age at birth. International Journal of Epidemiology. 2012;41:188–199. doi: 10.1093/ije/dyr237. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Liaw Andy, Wiener Matthew. Classification and Regression by randomForest. R News. 2002;2:18–22. 〈http://cran.r-project.org/doc/Rnews/〉 [Google Scholar]
  22. Patel C.J., Bhattacharya J., Butte A.J. An Environment-Wide Association Study (EWAS) on type 2 diabetes mellitus. PLoS One. 2010;5:e10746. doi: 10.1371/journal.pone.0010746. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Patel C.J., Cullen M.R., Ioannidis J.P.A. Systematic evaluation of environmental factors: Persistent pollutants and nutrients correlated with serum lipid levels. International Journal of Epidemiology. 2012;41:828–843. doi: 10.1093/ije/dys003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Patel C.J., Ioannidis J.P.A., Cullen M.R. Systematic assessment of the correlations of household income with infectious, biochemical, physiological, and environmental factors in the United States, 1999–2006. American Journal of Epidemiology. 2015;181:171–179. doi: 10.1093/aje/kwu277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Patel C.J., Rehkopf D.H., Leppert J.T. Systematic evaluation of environmental and behavioural factors associated with all-cause mortality in the United States National Health and Nutrition Examination Survey. International Journal of Epidemiology. 2013;42:1795–1810. doi: 10.1093/ije/dyt208. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Python Software Foundation. Python (2013). v. 2.7.5.
  27. R Core Team (2012). R: A Language and Environment for Statistical Computing. 〈http://www.r-project.org/〉.
  28. Raftery A.E. Bayesian model selection in social research. Sociological Methodology. 1995;25:111–164. [Google Scholar]
  29. RAND (2014). Center for the Study of Aging with funding from the National Institute on Aging and the Social Security Administration. RAND HRS Data, Version N.
  30. Rehkopf David H., Laraia Barbara A. and Segal, Mark and Braithwaite, Dejana and Epel, Elissa. The relative importance of predictors of body mass index change, overweight and obesity in adolescent girls. International Journal of Pediatric Obesity. 2011;6(e233):e242. doi: 10.3109/17477166.2010.545410. [DOI] [PubMed] [Google Scholar]
  31. Risch N., Merikangas K. The future of genetic studies of complex human diseases. Science (80-) 1996;273:1516–1517. doi: 10.1126/science.273.5281.1516. [DOI] [PubMed] [Google Scholar]
  32. Sala-I-Martin X.X.I. Just ran two million regressions. The American Economic Review. 1997;87:178–183. 〈http://www.jstor.org/stable/2950909〉 [Google Scholar]
  33. Sato F., Shimada Y., Selaru F.M. Prediction of survival in patients with esophageal carcinoma using artificial neural networks. Cancer. 2005;103:1596–1605. doi: 10.1002/cncr.20938. [DOI] [PubMed] [Google Scholar]
  34. Schaul T., Bayer J., Wierstra D. PyBrain. Journal of Machine Learning Research. 2010 [Google Scholar]
  35. Trygg J., Holmes E., Lundstedt T. Chemometrics in metabonomics. Journal of Proteome Research. 2007;6:469–479. doi: 10.1021/pr060594q. [DOI] [PubMed] [Google Scholar]
  36. Tzoulaki I., Patel C.J., Okamura T. A nutrient-wide association study on blood pressure. Circulation. 2012;126:2456–2464. doi: 10.1161/CIRCULATIONAHA.112.114058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. van der Laan M.J., Rose S. Springer; New York, NY: 2011. Targeted Learning. [Google Scholar]
  38. Varian H.R. Big data: new tricks for econometrics. Journal of Economic Perspectives. 2014;28:3–28. 〈http://www.jstor.org/stable/23723482?seq=1#page_scan_tab_contents〉 (Accessed 10 May 2016) [Google Scholar]
  39. Wang T.J., Larson M.G., Vasan R.S. Metabolite profiles and the risk of developing diabetes. Nature Medicine. 2011;17:448–453. doi: 10.1038/nm.2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Wishart D.S. Emerging applications of metabolomics in drug discovery and precision medicine. Nature Reviews Drug Discovery. 2016 doi: 10.1038/nrd.2016.32. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

supplementary table 1

Supplementary material

mmc1.docx (472.8KB, docx)

Articles from SSM - Population Health are provided here courtesy of Elsevier

RESOURCES