Electric Fields and Fast Protein Dynamics in Enzymes

Abstract

In recent years, there has been much discussion regarding the origin of enzymatic catalysis and whether including protein dynamics is necessary for understanding catalytic enhancement. An important contribution in this debate was made with the application of the vibrational Stark effect spectroscopy to measure electric fields in the active site. This provided a window on electric fields at the transition state in enzymatic reactions. We performed computational studies on two enzymes where we have shown that fast dynamics is part of the reaction mechanism and calculated the electric field near the bond-breaking event. We found that the fast motions that we had identified lead to an increase of the electric field, thus preparing an enzymatic configuration that is electrostatically favorable for the catalytic chemical step. We also studied the enzyme that has been the subject of Stark spectroscopy, ketosteroid isomerase, and found electric fields of a similar magnitude to the two previous examples.

Graphical abstract

Explanation, in atomistic detail, of how enzymes catalyze a reaction remains elusive. Recently, experiments based on the vibrational Stark effect have provided significant insights (a recent review is ref 1). The focus of this Letter is on enzymes whose substrate configuration can be approximated as an electric dipole. Then, the effect of the active site on the substrate can be represented as an electric field that acts on this dipole. This electric field description includes all noncovalent interactions, including long-range and H-bond interactions, which are known to be crucial for catalysis. This “electric field on a dipole” approximation is not always valid; for example, it would not be appropriate when the transition state (TS) is formed by a rotational rearrangement of the substrate. However, interactions in the active sites of many enzymes can be described within such a framework.

The work reviewed in ref 1 focuses on ketosteroid isomerase (KSI), which is a paradigmatic proton transfer enzyme reaction. The vibrational Stark effect probe is on a carbonyl group in the active site. This carbonyl group reorients very little during the reaction, which makes the dipole approximation suitable for this system. Experimental work showed that in the TS of KSI the combined electrostatic field on this dipole takes what was assumed to be large values, which makes the catalytic enhancement possible. Identifying particular details of how this large field arises (interactions with local residues near the active site; possible distal binding interactions and specific H-bonds) provides an atomistic description of the electrostatic preorganization of the active site.

In KSI, the same protein conformation is used for binding the substrate, isomerizing it, and allowing subsequent product release. This may not be true in other enzymes, and that would require conformational transitions to find structures that are efficient for each step of a catalytic cycle. For example, it is well-known that in dihydrofolate reductase slow conformation dynamics is necessary.² We have proposed that in some enzymes another mechanism is possible: fast subps motions that bring the reactive species close together. In this work, we will examine computationally if and how these fast motions affect the electrostatics of the active site. The computational work will employ transition path sampling (TPS),³ which is a rare event method that performs a Monte Carlo search in the reactive pathway space.

The structure of this Letter will be as follows. First we will perform a TPS study of KSI. This will allow us to validate the scheme that we use for describing fields in the quantum subregion of the active site. Then we will turn our attention to two enzymes that we have studied in the past, in which we believe that fast dynamics plays a role in catalysis. We will find that these fast motions modulate the electric field to produce an enzyme pose that is ready to react, rather than one preorganized for reaction.

Transition Path Sampling and Electric Fields in KSI

Ketosteroid isomerase plays a critical role in converting cholesterol to testosterone.⁴ It is one of the fastest enzymes known and is a paradigm of enzymatic proton transfer. It catalyzes the isomerization of 3-oxo-D5-steroids into their D4-conjugated isomers, such as isomerization of 5-androstene-3,17-dione to 4-androstene-3, 17-dione.⁵ KSI has been extensively studied both experimentally and computationally.^6–8 As mentioned in the introduction, it has provided insights into the atomistic details of electrostatic preorganization.^9–13 The active site provides an environment, called the oxyanion hole, that stabilizes the TS via H-bonds. Boxer and co-workers have suggested that the oxyanion hole, along with charges and dipoles of distal residues,¹⁴ produces an electric field that stabilizes the dipole on the C=O bond. The experimentally measured electric field on the C=O dipole was stated to be unusually large (around 150 MV/cm), likely due to the proximity of the carbonyl to the H-bond network.

We used TPS to generate and analyze the ensemble of reactive trajectories. Details about the preparation and simulations are described in the Supporting Information. Trajectories and the structure for PNP and hLDH enzymes were obtained from our previous studies.

There are two steps in the chemical reaction of KSI (Figures S1 and S2). The first is proton transfer (H1) from carbon C2 of the substrate to oxygen OD2 of the catalytic base, Asp40, and the second is proton transfer (H1) from the same oxygen OD2 to carbon C10 of the substrate. It takes approximately 25 fs from bond breaking of the first step to bond forming of the second step. In Figure 1, we show a representative reactive trajectory.

Figure 1.

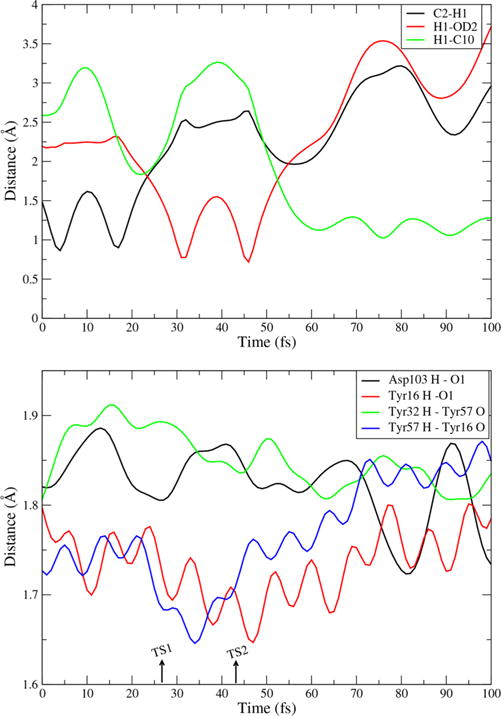
(Top) Distances in a representative trajectory of the KSI reaction: C2–H1 is bond breaking and H1–OD2 is bond forming in the first step; H1–C10 is proton transfer in the second step. (Bottom) Important hydrogen bonds in the KSI reaction, plotted along the same reactive trajectory. The dashed lines at the bottom indicate the location of the TS for each step.

Previous studies¹⁵ have emphasized the importance of a hydrogen bond network. The important H-bonds are shown in Figure 1 for the same representative trajectory shown above. Asp103 and Tyr16 donate hydrogen bonds directly to the carbonyl oxygen of the substrate, and the Tyr32 side-chain oxygen is hydrogen-bonded to Tyr57, while Tyr57 shares a hydrogen bond with the Tyr16 side-chain oxygen. All H-bond distances become smaller from the first bond breaking until the second TS, indicating the important role of the hydrogen bond network in stabilizing the deprotonated residue.

From the harvested reactive trajectories, we identified a transition state ensemble (TSE) of 15 uncorrelated TS structures for each step of the reaction. In the TPS framework, the TS is defined as the structure along a trajectory that has an “iso-committal” property: new trajectories initiated from that structure have a probability of 0.5 to reach reactants or products. Analyzing the TS ensemble, we found that the average TS structure distances for the first step of the reaction are 1.90 Å for C2–H1 and 1.42 Å for H1–OD2; for the second step, the OD2–H1 distance is 2.05 Å and the H1–C10 distance is 1.30 Å.

Next, we identified the reaction coordinate for both steps of the reaction. Unlike other methods (e.g., umbrella sampling), TPS does not require any prior assumptions about the reaction coordinate. It uses the definition of the TS as the structure with the iso-committal property. One selects some degrees of freedom, constrains them while evolving the rest of the system, and checks if the iso-committal property has been preserved during the constrained dynamics. If not, another set of degrees of freedom is selected and the process is repeated. For each step, we used five uncorrelated TSs as starting points for finding the reaction coordinate. In the initial attempt, we constrained only the QM region (we included all of the tyrosines that participate in the H-bond network as part of the QM region) and found that the iso-committal property was preserved, showing that indeed in KSI there is no protein motion involvement in the reaction coordinate (Figure 2). However, as we will see later, this does not mean that the electric field is not affected.

Figure 2.

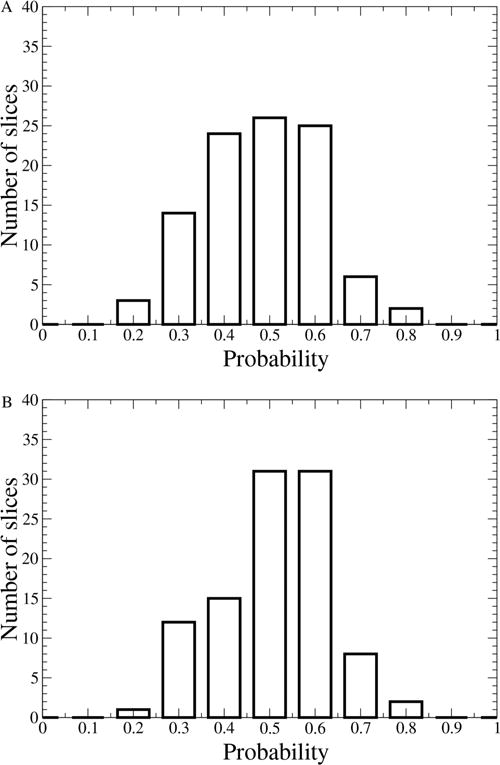
Committor distribution histograms constraining only the QM atoms for (a) the first step, proton transfer from C2 to Asp40 (OD2 proton abstraction) and (b) the second step, proton transfer from Asp40 OD2 to C10 (protonation).

From the reactive trajectory, we calculated the Mulliken charges. The field on point j is a sum over contributions from all neighboring charges i

$${\overrightarrow{E}}_j={\displaystyle \sum _i{\text{charge}}_i\cdot \frac{{\overrightarrow{R}}_i-{\overrightarrow{R}}_j}{{\left|{\overrightarrow{R}}_i-{\overrightarrow{R}}_j\right|}^3}}$$ (1)

We calculated the field on the C and O atoms and took their projections along the C=O axis, and the dipole field is 1/2 the sum of the two projections.

From these trajectories, we calculated the field on the C=O dipole for KSI. In Figure 3, we show three representative trajectories that all share the same trend for this electric field. We calculated the electric field at five time slices: at a random slice well before the TS, at the first bond-breaking point, at the TS of the first step, at the second bond-breaking point, and at the TS of the final step. In all trajectories, the electric field increases before the first bond breaks (when the OD2 oxygen of the base abstracts the proton from C2 of the steroid) and then decreases as we reach the TS and the reaction proceeds to the second step. The initial rise of the field is due to compression of the H-bonds (see Figure 1). When the bond between the OD2 of the catalytic base and the H breaks (donating the proton back to the C10 of the steroid), we notice a significant increase in the field, reaching a maximum of 225 MV/cm at the second TS. The electric field of the carbonyl dipole when the first bond breaks is approximately 225 MV/cm, at the first TS it ranges between 175 and 200 MV/cm, and at the second bond breaking it ranges ranges between 160 and 180 MV/cm. Breaking the bond separates the charge in the bonding pair, and that obviously contributes to the background dipole. The values of the electric field calculated from the MD simulations are comparable to the experimentally measured values, which shows that the framework that we have used for the QM/MM interactions (see the Supporting Information) does not produce spurious results. As reference, we calculated the field on the other C=O dipole of the steroid and the C= O dipole of Asp103. The el. field does not change along the reaction coordinate for these two. Finally, to determine the magnitude of the effect of active site electrostatics, we isolated the steroid in solution and calculated the field as a function of different equilibration times. We show the results in Table S1

Figure 3.

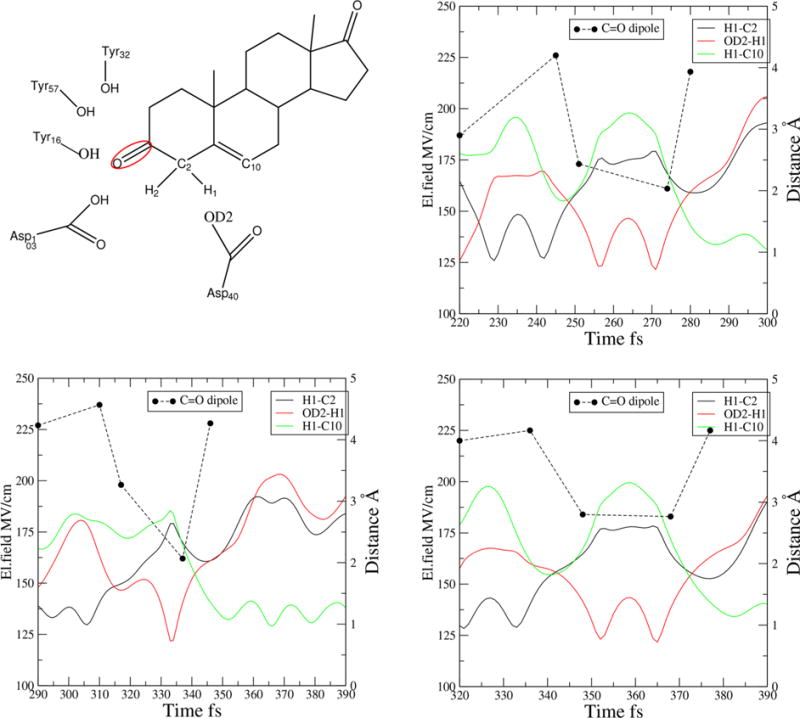
Electric field calculation in KSI for three representative trajectories. The five points are in a reactant configuration, bond breaking of the first step, the TS of the first step, bond breaking of the second step, and the TS of the second step.

Electric Fields in LDH

Lactate dehydrogenase catalyzes the interconversion of pyruvate and lactate through proton transfer between an active site histidine and a substrate oxygen and hydride transfer between the NAD cofactor and the substrate (the active site is shown in Figure 4). The rate-limiting step is hydride transfer, which we and others have studied computationally.^16–19 We have argued that fast subps motions that bring the hydride donor and acceptor close together are crucial for the reaction mechanism. In particular, the residue Ile252 that lies behind the nicotinamide ring of NAD pushes it toward the substrate, reducing the transfer distance.²⁰

Figure 4.

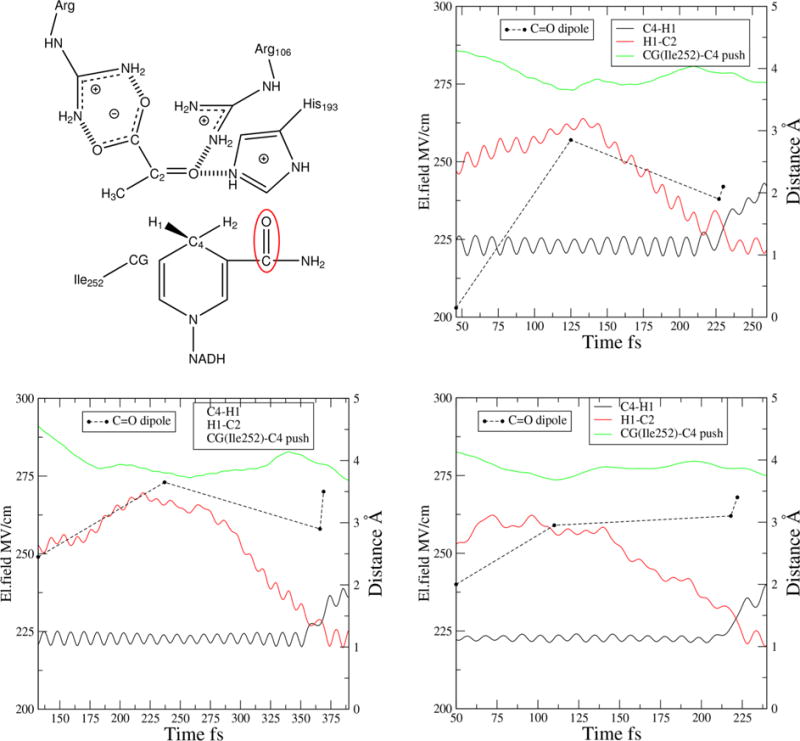
Active site and field calculation in LDH: when the compression on the NAD ring starts, when it reaches its minimum, when the hydride transfer starts, and at the TS.

We calculated the electric field on a carbonyl dipole that is part of the NAD ring (Figure 4) and lies very close to the atoms that participate in the hydrogen transfer. In Figure 4, we plot the bond-breaking and bond-forming distances, and the distance between CG of ILe252 and the donor C4 on NAD. In Figure 4, we also plot the calculated electric field on the C=O dipole at four time points for three representative reactive trajectories: when the compression on the NAD ring starts, when it reaches its minimum (ca. 100 fs before the bond-breaking event), when the hydride transfer starts, and at the TS. The electric field has values very similar to the ones that we found in KSI, meaning that LDH is also an enzyme with extreme values of the electric field. Whereas in KSI the electric field increases as we approach the TS, in LDH the field rises during the compression on the NAD ring, and then it increases very slightly from the bond breaking to the TS. A plausible explanation is that the compression on the NAD ring brings the enzyme to a very favorable pose to reaction, which can then proceed to the TS without further geometrical restructurings. This concept is similar to near-attack conformations,²¹ but while in NAC the system searches stochastically for the favorable pose, in LDH it finds it through a directed motion.

Electric Fields in PNP

Finally, we examine electric fields on human purine nucleoside phosphorylase (PNP). PNP catalyzes the phosphorolysis of the N-ribosidic bond of 6-oxypurine nucleosides and deoxynucleosides to form phosphorylated α-D-ribose products in the presence of phosphate. The cleavage of the C1′—N9 ribosidic bond occurs in a dissociative mechanism that forms a TS with a substantial oxycarbenium ion character. The phosphate provides electrostatic stabilization of this oxycarbenium ion, encouraging TS formation. Combined experimental and computational studies^22–25 showed that protein motions in hPNP and its substrates cause the O5′, O4′, and O_p oxygens to squeeze together and push electrons toward the purine ring, stabilizing the oxycarbenium character of the TS. Note that, unlike LDH, maximum compression happens after bond breaking; its significance is for stabilizing the TS and leaving group.

We calculated the electric field on the C=O dipole of the leaving group (the active site is shown in Figure 5). This choice makes our calculation comparable to that of the other two enzymes. In Figure 5, we show for three representative trajectories the bond-breaking and bond-forming distances and the compression between O5′ and O4′. We use the O5 – O4′ distance as reference for choosing four time slices for calculating electric field values: the time when the O5′— O4′ distance is at its maximum, the point where the C₁′–N₉ bond starts to break, the time when the oxygen distance is at its minimum (i.e., maximum compression), and the TS. We find that the electric field rises as we approach the maximum compression (minimum of the O5′–O4′ distance). The electric field values at the TS are approximately 225 MV/cm. In both LDH and PNP, the field increases during the compression motions that we have argued that are necessary for the reaction.

Figure 5.

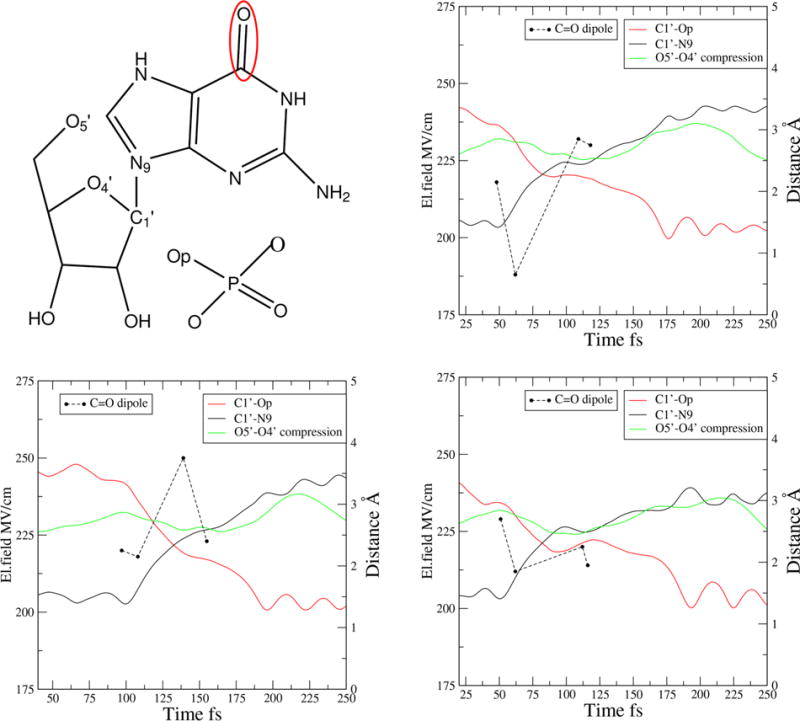
Active site and electric field calculation in PNP: at a maximum O5′–O4′ distance, when the C′1-N₉ bond starts to break, at a minimum O5′–O4′ distance, and at the TS.

Progress has recently been made in identifying the atomistic details that lead to electrostatic preorganization of the active site in enzymes. A useful experimental probe proved to be the vibrational Stark effect, which allows measurement of the dipole of a bond close to the atoms that participate in the chemical step. The experimental work has focused on KSI, which has the simplification that the same enzyme configuration is optimized for all of the stages of turnover. We calculated the electric field for two enzymes in which we showed that fast dynamics is important, which means that several enzymatic configurations are visited during the catalytic process. We found that during the compression that we had proved is crucial in LDH and PNP, the electric field in the active site increases, allowing the enzyme to find an optimal configuration for the chemical step. The electric field calculations showed that in LDH the field rises well before the bond breaks; in PNP, it occurs as the TS is formed and stabilized, and in KSI, it is before the bond breaking of the first step. The magnitude of the increase of the electric field in KSI is actually similar to that of LDH and PNP. We see that this magnitude is moderate on the order of 20% of the entire electric field. This is not surprising as changes in the active site as the TS is traversed are also modest. These changes, we have shown, can cause adiabatic barriers to chemical reaction to disappear,¹⁹ but it is also clear from this work that they modulate the environmental electric field in a nontrivial way. The data shown in the Supporting Information demonstrate that rather than simply increasing the electric field the protein environment (as compared to solution) modulates the field. The seemingly different views on enzymes, electrostatic preorganization, and fast protein dynamics are reconciled in LDH and PNP; the fast dynamics provides a particular atomistic description of the electrostatic preorganization, and the sum of effects of electrostatic and quantum mechanical combine to facilitate reaction and so cause catalysis.