First-Principles Prediction of Enthalpies of Formation for Polycyclic Aromatic Hydrocarbons and Derivatives

Abstract

In this article, the first-principles prediction of enthalpies of formation is demonstrated for 669 polycyclic aromatic hydrocarbon (PAH) compounds and a number of related functionalized molecules. It is shown that by extrapolating density functional theory calculations to a large basis set limit and then applying a group based correction scheme that good results may be obtained. Specifically, a mean unsigned deviation and root mean squared deviation from the experimental enthalpies of formation data of 5.0 and 6.4 kJ/mol, respectively, are obtained using this scheme. This computational scheme is economical to compute and straightforward to apply, while yielding results of reasonable reliability. The results are also compared for a smaller set of molecules to the predictions given by the G3B3 and G3MP2B3 variants of the Gaussian-3 model chemistry with a mean unsigned deviation and root mean squared deviation from the experimental enthalpies of formation of 4.5 and 4.8 kJ/mol, respectively.

Graphical abstract

INTRODUCTION

Background

Polycyclic aromatic hydrocarbons (PAHs) are a class of substances that have been associated with a number of acute and chronic health effects. Additionally, PAHs are suspected carcinogens, mutagens, and teratogens. PAHs occur in the environment due to a number of natural sources including forest fires, volcanoes, and as a component of crude oil. However, their primary source is overwhelmingly anthropogenic. PAHs are created through a number of processes including incomplete combustion of fossil fuels, high-temperature cooking of foods, and burning of municipal refuse and in petroleum based products such as coal tar and asphalt. PAHs in the atmosphere frequently occur as particles attached to dust or as components of soot (soots generally contain a mixture of PAHs). Due to their low solubility in water, PAHs tend to accumulate in soils and on lake and river beds, rather than as a significant water contaminant. Unfortunately, this type of accumulation makes PAH pollutants rather long-lived and difficult to remove from the environment. A number of aquatic species are known to concentrate PAHs in their tissues.

Due to the environmental and health risks associated with PAHs, and because the largest source of PAH molecules is combustion from human activities, it is important to develop a thorough understanding of their chemistry. Thermodynamics quantities are important for understanding the formation and growth of PAHs and are of particular value in modeling studies. These large molecules are important precursors for the formation of soot particles during the combustion of hydrocarbons fuels under fuel-rich conditions. Many detailed chemical kinetic models have been developed to describe the growth of PAHs to predict their concentrations and to aid in predicting sooting behavior. The relative stabilities of these molecules and their derivatives influence the rate of formation and consumption of PAHs, and ultimately affect the rate of soot formation. Many of the important reactions in the formation of initial PAH species, and the subsequent growth of larger PAHs, involve chemically activated steps, such as additions/eliminations, isomerizations (e.g., H atom migrations), cyclizations (ring growth), and β bond scissions (bond breaking reactions in radicals) that are often strongly temperature and pressure dependent. Among the various thermodynamic quantities that may be computed, the enthalpy of formation is of particular importance in characterizing their thermal stability and is thus the subject of the present study.

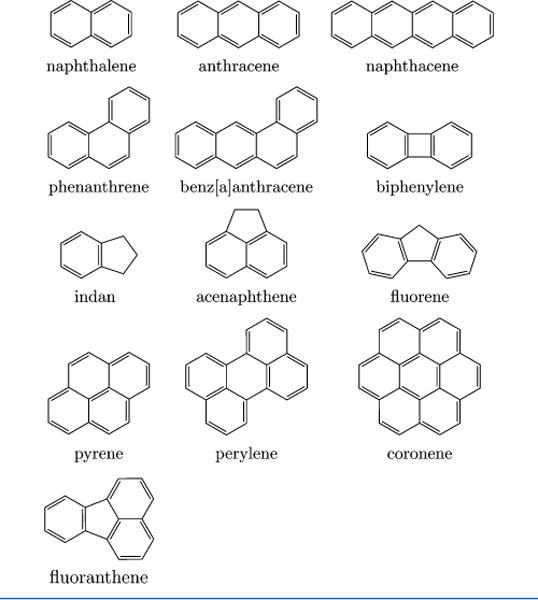
PAHs are characterized by possessing more than two fused aromatic benzene rings and by having no non-hydrogen substituents.¹ Several examples of small PAHs are given in Table 1 showing aromatic and other rings fused in different manners. This figure gives a hint at the diversity of possible PAH structures.

Table 1.

Structures of Representative Polycyclic Aromatic Hydrocarbon Compounds (PAHs)

The purpose of the present article is to survey the current state of thermochemical data on PAHs from experiment, group additivity, and computational chemistry, and to provide a comprehensive and consistent set of predicted values for the heat of formation of PAHs. Prediction of PAH values will rely on computational chemistry methods with reasonable cost and on group additivity correction schemes to account for systematic errors in those methods.

The remainder of this article is organized as follows. A survey of relevant literature is given in the remainder of this section. The details of the ab initio calculations performed for this work and the procedures and equations necessary for producing enthalpies of formation are presented in the following section. The results of these calculations are compared to experimental data, and to computational and empirical estimates, in the next section. Finally, the value of the present approach in light of previous work is discussed.

Survey of Related Prior Work

Although there has been much work over many years investigating the stability of PAHs using computational methods (as well as experimental measurements), many of these studies have been limited in scope to a few species, have employed quantum chemical methods at lower levels of theory, have not performed a full review of experimental and computational values in the literature, and/or have not made adequate comparisons between the computed and experimental values. The current work significantly expands on the set of PAHs previously studied computationally and uses a range of quantum chemical methods to provide a measure of uncertainties in the computational methods and to facilitate better comparison with experimental data. The thermochemical data (enthalpies of formation) for PAHs are also compiled and briefly evaluated. (For a more detailed evaluation on a more limited set of PAHs, the reader is referred to a recent work by Chickos and coworkers.²) In the present work, quantum chemical calculations are used as a screening tool to identify species where there are significant differences between experimentally derived enthalpies of formation and the corresponding computed values. In these cases, a further examination of both the experimental data and computational values (and methods) is warranted.

A general overview of related prior work is now provided. There are many excellent references (cited below) that provide a better overview of many important background subjects than this article can realistically achieve, on the topics of aromaticity, thermochemical data, group additivity, quantum chemical methods, and detailed chemical kinetic models. These areas will be briefly surveyed before reiterating the objectives of the present work and fully discussing the present methodology and results.

PAH Structures

Polycyclic aromatic hydrocarbons (PAHs) are defined as having more than two fused benzene rings and no non-hydrogen substitutions. However, on a practical level PAHs are formed and grow via many reactions involving smaller PAHs that have unsaturated substituents.^3–8 The inclusion of hydrocarbon-substituted PAHs in this study is in recognition of this consideration.

There are several types of fusion that occur in PAHs, and we now briefly discuss these and the related common terminology.¹ Several examples of different types of PAH structures are provided in Table 1, showing different types of ring fusion. PAHs that have adjacent rings with two adjacent atoms in common are termed “ortho-fused”, whereas those that have rings with two adjacent atoms in common with two or more rings are termed “ortho- and peri-fused”.

The simplest example of an ortho-fused compound is naphthalene, resulting from the fusion of two benzene rings at two common atoms (fused on one face; see Table 1). Naphthalene has eight peripheral aromatic carbon sites (CbH) terminated by hydrogen atoms, and two fused aromatic carbon sites (Cf), each having two rings in common. The simplest example of a compound with ortho- and peri-fused carbon atoms is pyrene, resulting from the ortho- and peri-fusion of four benzene rings where two or more adjacent bonds are involved (fused on two faces). Pyrene has ten peripheral (CbH) sites, four fused (Cf) sites, and two interior ortho- and peri-fused (Cp) sites.

There are different types of PAH structures (see Table 1 for a number of examples). Polyacenes such as anthracene and naphthacene have ortho-fused benzene rings in a linear arrangement where the next benzene ring is fused on the opposite or “b” face from the previous ring. For example, anthracene could be named as benzo[b]naphthalene. Poly-aphenes are ortho-fused PAHs, such as phenanthrene, and have the next benzene ring fused on an adjacent face that is at 120° (the “a” face) from the previous ring. For example, phenanthrene could be named as benzo[a]naphthalene. As discussed above, ortho- and peri-fused PAHs occur when the aromatic rings are fused on two or more faces; pyrene, perylene, and coronene are representative structures.

PAHs can also involve fused structures where the fused ring involves rings other than six-membered benzene rings. Indan (Table 1), for example, can alternately be named benzocyclopentane or cyclopentabenzene, indicative of a cyclopentene ring fused on a single face (ortho-fused) to a benzene ring. These are sometimes termed as cycloalkane or cycloalkene rings that are fused by being attached or joined to the aromatic rings. Such rings can also be ortho- and peri-fused, as in acenaphthene, where a five-membered ring is created by a –CH₂CH₂– bridge between the 1 and 8 positions on naphthalene. Compounds with this type of bridge fusion are termed ace-ylenes. Larger representative examples of multifused PAHs with cycloalkane or cycloalkene fused rings are biphenylene, fluorene, and fluoranthene (Table 1), which might be systematically named as benzocyclobuttabenzene, benzocyclopentabenzene, and benzocyclopenta[de]-naphthalene.

As there are a large number of PAH structures that have been optimized in this study, a Web site⁹ has been created to disseminate this information. The Web site contains data such as names, molecular formulas, 2-D structures, and 3-D structures (that may be viewed on the Web site as well as downloaded as Cartesian coordinates).

Aromaticity

The stability and resonance stabilization energies of polycyclic aromatic hydrocarbons (PAHs) have been the subject of considerable theoretical interest for many years. The earliest work using molecular orbital calculations dates over half a century to work in the 1950s to 1960s by Pariser and Parr,¹⁰ by Pople,¹¹ and by Dewar and co-workers.¹² These early calculations implemented and further developed the concepts of electron delocalization energies and molecular orbital theory that were formulated by Hückel¹³ in the 1930s that are, in turn, built on the foundational concepts of chemical valence (Frankland, 1852),¹⁴ of structural connectivity (Kekulé, 1858),¹⁵ and of aromaticity (Kekulé, 1865).¹⁶

There are a number of excellent recent review articles and books on aromaticity, electron delocalization, and resonance stabilization energies, including those by Schleyer,¹⁷ Poater et al.,¹⁸ Curaski,¹⁹ Merino et al.,²⁰ and Aihara.²¹ The reviews by Schleyer and co-workers^22,23 and by Matta and Hernandez-Trujillo²⁴ are very informative and helpful. In a recent work, Cappel et al.²⁵ studied conjugative and hyperconjungative stabilization effects in various conjugated species.

A significant number of current methodologies and discussions in the area of aromaticity derive from work published in 1967 by Polansky and Derflinger,²⁶ who pioneered useful characterizations for quantifying aromaticity in molecules. For data derived from experiment, much of the quantitative knowledge regarding the stability of PAHs is influenced in a number of ways by the work of Kistiakowsky and co-workers in the 1930s who examined the enthalpies of hydrogenation of a variety of unsaturated compounds.^27–29 Turner and co-workers^30–32 in an extensive series about three decades ago measured the enthalpies of hydrogenation for different classes of compounds. These systematic studies have been continued in more recent times through the extensive work of Roth and co-workers^33,34 and by Rogers and coworkers.^35–38 A summary of enthalpies of hydrogenation is given by Jensen.³⁹

Sources of Thermochemical Data

A variety of sources of thermochemical data were used in tabulating the experimental enthalpies of formation of the PAHs and reference hydrocarbons studied in this work. These sources included: Pedley et al.,⁴⁰ Cox and Pilcher,⁴¹ the NIST Chemistry Webbook,⁴² the reports of the IUPAC Commission on Chemical Kinetics,^43,44 and the thermochemical tables produced by Gurvich et al.,⁴⁵ by the JANAF Working Group,⁴⁶ by the Thermodynamics Research Center,⁴⁷ and by Burcat.^48,49

Additionally, Slayden and Liebman⁵⁰ have reviewed thermochemical data for PAH species. Thermochemical functions for cyclic hydrocarbons and cyclopentadiene derivatives have been provided by Dorofeeva et al.^51,52 and Karni et al.,⁵³ respectively. Of extreme value is the extensive compilation of enthalpies of hydrogenation for unsaturated molecules including PAHs that is given in the widely cited work by Roth et al.³³

Chickos et al. have provided an extensive compilation of experimental enthalpies of vaporization and sublimation^54,55 for a wide range of compounds and have developed group additivity based methods for estimating enthalpies of vaporization and sublimation.^56,57 Sabbah et al.⁵⁸ have reviewed experimental data and methods for determining enthalpies of vaporization and sublimation. A text book review of enthalpies of vaporization has been provided by Majer and Svoboda.⁵⁹

The most reliable and self-consistent set of thermochemical data for species relevant to combustion employs the Active Thermochemical Tables (ATcT) approach pioneered about 10 years ago by Ruscic and co-workers.⁴³ The ATcT approach simultaneously considers all species in a thermochemical network through a set of enthalpies of reactions for all reactions involving the species, providing a self-consistent set of constraints that can be minimized. The concept of free energy minimization in chemical systems was first discussed in depth 90 years ago in the seminal work by Lewis and Randall.⁶⁰ This work was revised 50 years ago by Pitzer and Brewer.⁶¹ Computer optimization of thermochemical data was first extensively used in the 1970s and 1980s by Pedley and coworkers in the CATCH tables^62,63 at the National Bureau of Standards in producing the NBS Tables,^64–68 and by the CODATA Thermodynamics Task Group.⁶⁹ Optimization of thermochemical free energy relationships has also been used to produce evaluated thermochemistry in biochemical reaction systems.^70–72 Although this thermodynamic network methodology has not been applied yet to large molecules such as PAHs, the data produced in this effort are important in determining enthalpies of formation of smaller fundamental hydrocarbon reference species, which are needed for benchmarking ab initio calculations on PAHs, where empirical corrections are needed to generate accurate values.

Empirical Approaches and Quantum Chemistry

Group additivity is an empirical method for predicting thermochemical properties of compounds as sums of the properties of their component parts that has been very successful in predicting data for aliphatic hydrocarbons and other species. This method was initially developed and utilized by Benson and co-workers.^73–77

Stein et al. used group additivity techniques to predict thermochemical properties of PAHs.^78,79 Alberty and Reif⁸⁰ estimated the enthalpies of formation (and other standard thermodynamic quantities) of a number of PAH molecules using Benson group additivity⁷³ with various group values.^75,78,79 Several articles expanded on this method to correct for deficiencies in the model. Armitage and Bird⁸¹ and Moiseeva and co-workers gave updated values for a few critical groups, leading to small improvements in accuracy for PAHs⁸² and for compounds with five-membered rings.⁸³ Herndon et al.⁸⁴ compared the performance of group additivity with molecular mechanics and semiempirical quantum chemistry methods on a set of 11 polycyclic benzenoid aromatic hydrocarbons to experimental values, finding that the results were generally in good agreement. Armitage and Bird⁸¹ extended the use of group additivity to predict the stability of very large PAH species such as fullerenes (cage-like fused rings). Benzenoid molecules, including radicals of these species, were studied by Wang and Frenklach using the semiempirical AM1 Hamiltonian.⁸⁵ Heats of formation and heats of sublimation were estimated using a quantitative structure–property relationship (QSPR) model that was derived from a 3-dimensional quantitative structure–activity relationship (QSAR) known as comparative molecular field analysis (CoMFA) by Welsh et al.⁸⁶ Their results were in very good agreement with experimental results for a small set molecules on which the model was tested. Welsh et al. also used group additivity to estimate enthalpies of sublimation of PAHs.

Yu et al.⁸⁷ developed a method for estimating thermochemical properties, including heats of formation, of PAHs based on density functional theory (DFT) calculations. Their model, called bond-centered group additivity (BCGA) used 20 structural parameters and yielded average errors (note that this is not the uncertainty) of less than 3 kcal/mol (≈12.5 kJ/mol) over a set of 107 molecules.

Other methods have also been used to examine PAH properties and reaction pathways. Using molecular mechanics methods, Allinger et al.⁸⁸ studied the stability of five-membered rings, which are important precursors and intermediates in PAH formation.

Both ab initio and DFT methods have been used to calculate physical and chemical properties for PAHs. Given its low computational cost and ability to replicate geometric parameters and vibrational frequencies with reasonable accuracy, B3LYP is widely employed for computing molecular structures, vibrational frequencies, and enthalpies of formation in large molecules with many heavy atoms (non-hydrogen) such as PAHs. To produce more accurate results, the selected method generally requires a large basis set and a good treatment of electron correlation. The B3LYP method includes LYP correlation, giving it an advantage over approaches such as Hartree–Fock, which are uncorrelated methods. Composite methods such as the complete basis set (CBS) method and the Gaussian-n model chemistries use a balanced set of calculations to converge the one-particle (basis set) and n-particle (correlation) expansions, producing high-quality results at an additional computational expense.

Several studies have used advanced group additivity approaches in conjunction with quantum chemical methods, in studying PAHs. Sivaramakrishnan et al.⁸⁹ used the hybrid DFT method B3LYP^90,91 to calculate enthalpies of formation of a significant number of PAHs and substituted-aromatic species and developed a detailed group additivity method for reproducing enthalpies of formation to within about 8 kJ/mol. This work built on earlier B3LYP and the group additivity formalism by Yu et al.⁸⁷ mentioned above. These studies extended the development of group additivity values for large unsaturated hydrocarbons by Sumathi and Green⁹² using G2⁹³ and CBS-Q⁹⁴ methods. Sabbe et al.⁹⁵ used the CBS-QB3 method⁹⁶ in conjunction with group additivity values applied to a large set of aliphatic hydrocarbons, including cyclic species, and a number of substituted-benzene derivatives. Their group additivity scheme was able to reproduce the enthalpies of formation for the substituted aromatics reportedly within 0.7 kJ/mol. These deviations are comparable to the uncertainties of the experimental values that are on the order of 2 kJ/mol. Herndon¹⁰⁰ and co-workers have extensively used group additivity approaches in conjunction with quantum chemical methods. They used the semiempirical AM1 method,⁹⁷ the DFT method B3LYP,^90,91 and the ab initio MP2 theory⁹⁸ to determine enthalpies of formation for many common PAHs.^84,99,100 Marsh and Wornat¹⁰¹ used the semiempirical AM1 method to compute thermochemical functions for a number of PAHs (indene, fluoranthene, pyrene, coronone, fluorene) and their cyclopenta-fused derivatives. Pope and Howard¹⁰² employed group additivity in conjunction with the molecular mechanics method MM3¹⁰³ and the semiempirical MOPAC methods MNDO,¹⁰⁴ AM1,⁹⁷ and PM3¹⁰⁵ to study the stability of common PAHs, as well as the fullerenes.

Kassaee et al. used B3LYP to compute thermochemical functions for substituted benzene¹⁰⁶ and naphthalenes;¹⁰⁷ comparable systematic studies of PAHs have been completed by Wiberg¹⁰⁸ and Pogodin and Agranat.^109,110 Van Speybroeck et al.¹¹¹ computed bond dissociation energies (BDE) for aromatic species including PAHs. Papas et al.¹¹² studied the radicals of linear PAHs (naphthalene through pentacene) and found computed electron affinities to be in good agreement with experimental values. Reaction pathways and important intermediates in the pyrolysis of cyclopentadiene were studied by Wang et al. using various DFT methods.¹¹³ In a more recent work, Hemelsoet et al.¹¹⁴ have used B3P86 and other DFT methods to predict C–H and C–C bond dissociation energies in PAHs. They also employed the G3(MP2)-RAD method¹¹⁵ to computed BDEs for the smaller (benzene through anthracene) molecules.

In an extensive series of studies, Schulman and co-workers used ab initio (HF, MP2) and density functional methods (B3LYP) to compute enthalpies of formation for PAH species^116,117 including benz[e]pyrene, coronene, benz[ghi]-perylene (HF),¹¹⁸ pyracyclene and biphenylene (MP2),¹¹⁹ coronene and benz[ghi]perylene (MP2, B3LYP),¹²⁰ and helicenes and phenacenes (B3LYP).¹²¹

Work by Li et al.¹²² using the G2 method found a correlation between computed and experimental values for enthalpies of formation and the number of double bonds in the molecules. Notario et al. employed the G2 and G2(MP2) methods⁹³ for predicting enthalpies of formation of hydrocarbons including aromatic species¹²³ and in the case of linear polyacenes.¹²⁴ Cheung et al.¹²⁵ used the G2 and CBS-Q methods to predict the relative stabilities of the various isomers of benzene. A recent systematic study using high level ab initio composite model chemistries is found in the work of Bond,¹²⁶ where enthalpies of formation for hydrocarbons, substituted-hydrocarbons, and derivatives, including for a number of PAH species, were computed using a number of different methods (variations of G2, G3, and CBS-Q).

The G3B3 and G3MP2B3 methods have been used with success by Burcat⁴⁸ and Janoschek and Rossi¹²⁷ to generate data for species of interest to combustion. Rogers and McLafferty have conducted a series of studies using the G3MP2 method¹²⁸ to explore the stability of a number of substituted benzenes,¹²⁹ strained conjugated molecules,¹³⁰ and triquinacene.¹³¹ Melius and co-workers developed and utilized the BAC (bond additivity correction) method^132,133 with ab initio calculations to predict enthalpies of formation of important hydrocarbon species, and have recently extended this method to utilize G3B3 energies.¹³⁴ Fishtik et al.¹³⁵ employed the G3 method¹²⁷ and found it to be accurate, not requiring any empirical corrections for the molecules studied. A database of thermochemical properties for PAHs has been created by Blanquart and Pitsch, consisting of 46 molecules with sizes ranging from benzene to coronene (C₂₄H₁₂).¹³⁶. The values were derived from G3MP2B3 calculations and employed corrections for hindered rotors as well as group based corrections. Their group-corrected G3MP2B3 showed a deviation from experiment of 2.3 kJ/mol for 8 PAH molecules based on 10 groups (the uncorrected deviation was 22.1 kJ/mol).

Rayne and Forest have reported a set of G4(MP2) calculations on PAHs and substituted PAHs.¹³⁷ The present results are compared to these to the greatest extent possible. Dorofeeva has questioned the methodology used in this work because the computed values are systematically different than other published values.¹³⁸ In a recent study, Zauer¹³⁹ computed enthalpies of formation for 139 PAH compounds using the MINDO, MNDO, AM1, and PM3 semiempirical quantum chemistry methods. The study showed deviations from experiment of at least 13 kJ/mol, and employed a correction scheme using a linear expression in the enthalpy of formation.

Review of Literature

An evaluation of the experimental thermochemical data found in the literature was performed for the PAH species and reference molecules, drawing upon the body of work cited above. The present work significantly expands on the set of PAHs and level of theory employed (in most cases) in earlier works (cited above) on PAHs using other quantum chemical methods and group additivity approaches.

A critical evaluation of experimental data for 63 PAH molecules covering enthalpies of combustion, enthalpies of formation in the condensed state, enthalpies of sublimation, enthalpies of vaporization, and enthalpies of fusion has been carried out by Roux et al.² Importantly, this work provides gas-phase enthalpies of formation for PAHs at 298.15 K. The values in this reference may be considered to be the best currently available, and each of the molecules included in that study has been computed in the present study, with the recommendation of Roux et al.² being used to evaluate the quality of the results of the present study. Roux et al.² have provided critically evaluated thermochemical data for PAHs. In particular, species where substantial disagreement exists between experimentally determined and theoretically calculated enthalpies of formation were identified. In this paper, the possibility that either the experimental value or the computed value must be in error is discussed. It is noted that it is important to consider the thermochemical quantities, both experimental and calculated, for each species relative to data for similar molecules with more well-established values; for example, considering the enthalpies of formation of methylbenzene (toluene) and the methylnaph-thalenes relative to that for benzene and naphthalene, and considering the enthalpies of hydrogenation of ethenylbenzene (styrene) and ethynylbenzene (phenylacetylene) relative to that for propene and propyne.

When gas-phase enthalpies of formation were unavailable, but condensed-phase enthalpies of formation and vaporization or sublimation enthalpies could be found, gas-phase values were computed from these data, as indicated in the tables below. In a few cases, estimated enthalpies of vaporization were employed, derived from the empirical relationship ${\mathrm{\Delta }}_v{H}_{298.15\mathrm{K}}^{\text{∞}}=\left(4.8\text{nC}+4.6\right)\text{kJ/mol}$, where nC is the number of carbon atoms in the molecule. This relationship was determined by fitting experimental enthalpies of vaporization for a representative series of about 20 C₆–C₁₃ aromatic species. An uncertainty (2σ) of 3 kJ/mol was estimated from the fit.

CALCULATIONS

Selection of Molecules

A set of 983 molecules was created for the present work. This set included 660 PAH compounds (including benzene) taken from NIST Special Publication 922: Polycyclic Aromatic Hydrocarbon Structure Index (SP922).¹⁴⁰ Although the focus of NIST SP922 is a model for computing retention indices for gas and liquid chromatography, it serves as a very nice source of PAH molecules for the present work. An additional 5 PAH parent compounds that did not appear in SP922 were added (the others were already included) as well as 4 other PAHs. The compound 5-methylchrysene was added from the 15 + 1 EU PAH list (Commission Regulation (EC) No 1881/2006), and 11 fluorinated PAHs from a commercial catalog were included.¹⁴¹,^a The list also contains 98 substituted benzenes, 36 benzene radicals (including substituted benzenes), 14 PAH radicals, and 56 substituted PAHs (including radical substituted). Finally, the list contains 109 aliphatic hydrocarbons used to enhance the fitting of the group correction (described below), including n-alkanes, branched alkanes, alkenes, and alkynes.

Density Functional Theory and ab Initio Calculations

Calculations on the full set of 983 molecules were carried out at the B3LYP/cc-pVDZ level of theory. Each molecular structure was fully optimized at this level of theory and calculations of the vibrational frequencies were used to ensure that each structure was a minimum-energy structure on the potential energy surface and to provide (within the ideal gas, rigid rotor, harmonic oscillator approximations) the values of the zero-point energy, enthalpy increment, and enthalpy for each molecule. Additional energy calculations were carried out at the B3LYP/cc-pVTZ//cc-pVDZ level of theory for use in an energy extrapolation scheme described below. Finally, energy calculations at the B3LYP/cc-pV6Z//cc-pVDZ level of theory were carried out for a set of 16 PAH compounds for calibrating the extrapolation scheme (described below). The choice of computational method (B3LYP) was motivated by the reliability of this functional and its common use by many practitioners, as well as its reasonable computational expense, particularly when applied to larger molecules. All B3LYP calculations were carried out using the GAMESS computational chemistry package.^142,143

It is noted that the largest PAH considered in this study has a molecular formula of C₃₈H₂₂, and that it is desirable that the extrapolation model accommodate even larger molecules without a prohibitive computational requirement. These considerations have informed the choice of method and basis set described above.

Ab initio calculations using the G3//B3LYP (hereafter G3B3) and G3(MP2)//B3LYP (hereafter G3MP2B3)¹⁴⁴ variants of the Gaussian-3¹⁴⁵ model chemistry were carried out on a subset of the compounds described above. Carrying out G3B3 or G3MP2B3 calculations on the full set of 983 molecules was not practical due to limitations in computational time and scratch storage space, making such calculations difficult or impossible on the larger molecules in the set. The largest molecule computed with the G3MP2B3 methods was coronene (C₂₄H₁₂). All G3B3 and G3MP2B3 calculations were carried out using the Gaussian 09 computational chemistry package.¹⁴⁶ The G3B3 and G3MP2B3 quantum chemical methods¹⁴⁷ were used to compute molecular structures, vibrational frequencies, and molecular energies. (Note that optimized geometries and vibrational frequencies are computed at the B3LYP/6-31g(d) level of theory in the G3B3 and G3MP2B3 methods.) These composite methods are model chemistries that compute total molecular energies from the sums and differences of a set of ab initio calculations using different levels of electron correlation and different basis sets. The G3B3 and G3MP2B3 methods include empirical corrections to the computed ab initio total energies of about 3.4 and 4.2 kJ/mol per electron in each valence bond, respectively. The “B3” in the methods denotes that the hybrid density functional theory (DFT) method B3LYP using 6-31G(d) basis sets to compute molecular geometries and frequencies rather than employing HF and MP2 optimizations as done in the standard G3 and G3MP2 methods; the B3LYP geometries have been shown to be generally more reliable (especially in the case of spin-contaminated radicals) and correlate well with higher level QCISD or CCSD optimizations.¹⁴⁷

The G3MP2B3 method was used to compute enthalpies of formation for about 120 PAHs and other substituted aromatics, and the more computationally expensive G3B3 method was also applied to about 40–50 of the smaller molecules. The newer G4 method was not used as the present authors already had an extensive computational database of G3 based calculations. Later in this paper, a comparison is made to results from G3, G4, and other methods by other workers. In short, the different model chemistry methods, after applying (different) systematic corrections, produce the same enthalpies of formation for the PAHs (and aliphatic hydrocarbons) within several kJ/mol and are not statistically significant. The computed enthalpies of formation are compared to experimental values for about 80 molecules. Enthalpies of formation were also computed using the G3MP2B3 and G3B3 model chemistries for about 60 aliphatic hydrocarbons, including saturated and unsaturated species, both acyclic and cyclic, for use as reference values. It was found that the average deviation between experimental enthalpies of formation and computed values was about 3–6 kJ/mol for the G3B3 and 4–8 kJ/mol for the G3MP2B3 method depending on the test set (class of molecules).

In this work, enthalpies of formation for the molecules were computed using atomization energies taken from the CODATA recommendations¹⁴⁸ as presented in Table 2. Note that the more recent values due to Ruscic and co-workers¹⁴⁹ have a significantly lower uncertainty. These values are 217.9979 ± 0.0001 kJ/mol for H, 716.880 ± 0.054 kJ/mol for C, and 79.393 ± 0.053 kJ/mol for F. The older CODATA values were used in this publication for a variety of reasons, but the use of the more recent values is recommended for future work. Zero point vibrational energies (ZPEs) were computed using scaled B3LYP/6-31G(d) (scaling factor = 0.96)¹⁵⁰ and B3LYP/cc-pVDZ (scaling factor = 0.97)¹⁵¹ frequencies. Thermal corrections to the enthalpy were computed using harmonic oscillator partition functions and treating torsional modes as rigid rotors (not as hindered rotors).

Table 2.

Values of the Atomic Enthalpy of Formation (Δ_fH°(298 K), kJ/mol) and Atomic Enthalpy Increment (H_inc = H°(298K) − H°(0K), kJ/mol) Taken from the CODATA Recommendation^148,171,^a

	H	C	F
ΔfH°	217.998(±0.006)	716.68(±0.45)	79.38(±0.30)
Hinc = H°(298K) − H°(0K)	6.197(±0.001)	6.536(±0.001)	6.518(±0.001)

^aUncertainties are given in parentheses. These values were used to compute the enthalpies of formation as described in the text.

Chemical Group Based Corrections

The concept of using group based values to compute thermodynamic quantities goes back to the pioneering work of Benson and Buss.⁷³ They showed that various thermodynamic quantities could be computed with good accuracy by considering a molecule as a collection of atoms, chemical bonds, or chemical groups. Briefly, the idea of group additivity is to identify chemical groups within a molecule and sum their corresponding contributions to the property of interest. For example, normal alkanes CH₃–(CH₂)_n–CH₃ can be considered to be composed of two types of groups: methyl groups –CH₃ and methylene groups –CH₂–. The enthalpy of formation of these molecules, or other physical or chemical properties, could be estimated using group additivity as the sum of values for each of the groups. A slightly more complicated molecule, 1-pentene (CH₃CH₂CH₂CH=CH₂), can be considered to be composed of five groups: two sp²-hybridized double-bonded groups –CH= and =CH₂ and three sp³-hybridized single-bonded groups –CH₃, –CH₂–, and –CH₂—C=. The latter group is a modified –CH₂– group because it is adjacent to an unsaturated site (C_d). In group additivity, there are other types of modified groups that are typically employed such as a correction for alkyl groups on the same side of a double bond, e.g., (Z)-2-butene; corrections for ortho-, meta-, and para-substitution; corrections for steric interactions in branched molecules (repulsion between gauche alkyl groups); and corrections for ring strain (e.g., cyclobutane and cyclopentane have ring strain corrections of 110 and 26 kJ/mol, respectively). This approach has been used by many authors for a variety of purposes. Naturally, some authors have used a group additivity approach as the basis for the correction of values to minimize the error versus experimental data. An early example of this approach has been given by Wiberg for various hydrocarbon compounds.¹⁵² Another example is seen in a paper by Wang and Frenklach⁸⁵ in which they used group based methods to correct a series of AM1 calculations of the enthalpies of formation for substituted benzenes and benzene radicals.

The present article uses group based empirical corrections, and the particular scheme used is now described for the B3LYP set of calculations. The carbon atoms in each molecular structure were classified into one of 14 groups on the basis of their chemical environment. The full list of groups and their descriptions are given in Table 3. These groups are illustrated in Figure 1. The identification of groups within a molecule was aided by the chemical informatics algorithms implemented in the OpenBabel package,^153,154 which provides a number of useful algorithms including those to detect chemical bonds and bond orders, perceive ring structures, and determine aromaticity. Optimization of the group error correction values was performed using a linear least-squares approach. It was found that subtracting 6 from the number of benzylic carbon atoms (CbH) reduced the mean unsigned error by about 2 kJ/mol, and this modification was retained in the final algorithm. The full expression for the group based error correction (ε_corr) for the B3LYP set of calculations is

$${\mathrm{\epsilon }}_{\text{corr}}=n_{\text{CH}3}f\left(\text{CH}3\right)+n_{\text{CH}2}f\left(\text{CH}2\right)+n_{\text{CH}2\mathrm{d}}f\left(\text{CH}2\mathrm{d}\right)+n_{\text{CCH}}f\left(\text{CCH}\right)+n_{\text{CCC}}f\left(\text{CCC}\right)+n_{\text{CdH}2}f\left(\text{CdH}2\right)+n_{\text{CdH}}f\left(\text{CdH}\right)+n_{\text{CdC}}f\left(\text{CdC}\right)+n_{\text{CtH}}f\left(\text{CtH}\right)+n_{\text{Ct}}f\left(\text{Ct}\right)+\left(n_{\text{CbH}}-6\right)f\left(\text{CbH}\right)+n_{\text{Cb}}f\left(\text{Cb}\right)+n_{\text{Cf}}f\left(\text{Cf}\right)+n_{\text{Cp}}f\left(\text{Cp}\right)$$ (1)

where n_x represents the number of groups of type x present in the molecule and f(x) represents the group correction value for group x. Optimized group correction values are presented in Table 3.

Table 3.

Base Group Names, Optimized Values (kJ/mol) of Parameters, and Descriptions Used in the Group based Error Correction Scheme Used in the B3LYP based Scheme

base group	optimized value	description
CH3	−1.0506	terminal methyl group (primary), –CH3
CH2	5.5183	sp3 methylene group (secondary), –CH2–
CH2d	6.3631	sp3 methylene group adjacent to sp2 group, –CH2–C=
CCH	20.1479	sp3 methylidyne group (tertiary), –CH<
CCC	36.2218	methanetetrayl group (quaternary), >C<
CdH2	−1.0962	terminal methylene group, =CH2
CdH	3.2000	sp2 alkene group bonded to a single sp3 group, –CH=
CdC	12.1747	sp2 isoalkene group bonded to two sp3 groups, >C=
CtH	0.0574	terminal triple-bonded terminal carbon, ≡CH
Ct	1.5573	triple-bonded carbon, ≡C–
CbH	3.2202	aromatic carbon terminated by hydrogen
Cb	9.6256	aromatic carbon terminated by carbon
Cf	7.9813	fused aromatic carbon connected to one Cf or Cp group
Cp	9.8124	pericondensed aromatic carbon (interior) connected to two Cf or Cp groups

Figure 1.

Atom-centered groups needed for describing PAH molecules included in this special publication. 1-Methylpyrene and 2-methyl-1-vinyl-1,2,3,4-tetrahydronaphthalene are depicted with group identifiers indicated.

The correction term ε_corr is added to the calculated enthalpy of formation to obtain the corrected enthalpy of formation

$${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{corr}}^{°}={\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{calc}}^{°}+{\mathrm{\epsilon }}_{\text{corr}}$$ (2)

Extrapolation of the Energy

One of the primary sources of error when enthalpies of formation are calculated comes from the molecular energy due to the use of a small basis set. Indeed, initial predictions of enthalpies of formation based solely on the results at the B3LYP/cc-pVDZ level of theory showed poor agreement with the available experimental data, as seen in Table 4. Calculations with sufficiently large basis sets are too computationally resource intensive to be practical. To overcome these limitations, schemes whereby the energy computed using two or more smaller basis sets is extrapolated to the result of a larger basis set calculations were examined. A number of such schemes exist such as those due to Feller,¹⁵⁵ Halkier et al.,¹⁵⁶ and Truhlar.¹⁵⁷ Among these, the method due to Truhlar was found to be the most appropriate for the present work.

Table 4.

Statistical Descriptors of the Errors (kJ/mol) in the Uncorrected (uncorr) and Corrected (corr) Enthalpies of Formation at 298 K Derived from the B3LYP Results^a

	cc-pVDZ		cc-pVTZ		extrapolated
	uncorr	corr	uncorr	corr	uncorr	corr
MSD	138.2	4.8	34.0	0.2	16.1	−0.7
MUD	138.2	14.5	36.0	3.7	23.4	4.8
δmin	25.2	0.3	0.7	0.0	0.0	0.0
δmax	338.8	71.7	152.2	15.6	123.2	17.7
RMSD	151.4	19.0	47.2	5.1	32.3	6.1

^aStatistics include the mean unsigned deviation (MUD), the mean signed deviation (MSD), the minimum (δmin) and maximum (δmax) absolute deviations, and the root mean square deviation (RMSD). Results are presented for the cc-pVDZ and cc-pVTZ basis sets, and for the large basis set extrapolated from them.

The basis set extrapolation method of Truhlar¹⁵⁷ builds on an observation made by Halkier et al.¹⁵⁶ that the optimal extrapolation coefficient be obtained by minimization of the mean unsigned error versus the best estimate of the basis set limit, rather than fitting calculations made with three or more basis sets. Truhlar’s method used the root-mean-square deviation (RMSD), as is also used in the present work. The basis of the method is to write the total energy as the sum of a Hartree–Fock (i.e., uncorrelated) energy and a correlation energy,

$$E^{\text{tot}}=E^{\text{HF}}+E^{\text{corr}}$$ (3)

and assume that each of the contributions to the total energy reaches its basis set limiting value via a power law functional dependence

$$E_X^{\lambda }=E_{\text{∞}}^{\lambda }+A^{\lambda }{X}^{-\alpha }$$ (4)

where λ represents either the Hartree–Fock or the correlation energy in the previous equation and X is an integer related to the basis set. The exponent α may be selected in such a way as to produce an optimal fit to the data. When the cc-pVDZ (X = 2) and cc-pVTZ (X = 3) basis sets are used for extrapolation, the formula for the extrapolated energy may be written¹⁵⁷

$$E_{\text{∞}}^{\text{tot}}=\frac{3^{\alpha }{E}_3^{\text{HF}}-2^{\alpha }{E}_2^{\text{HF}}}{3^{\alpha }-2^{\alpha }}+\frac{3^{\beta }{E}_3^{\text{corr}}-2^{\beta }{E}_2^{\text{corr}}}{3^{\beta }-2^{\beta }}$$ (5)

where the exponents α and β are optimized separately. Truhlar found that extrapolating results based on the cc-pVDZ and cc-pVTZ basis sets produced a lower RMSD from the complete basis set limit than the corresponding calculation made with the cc-pV6Z basis set at a significantly reduced computational cost. Truhlar states that the motivation for the scheme was economical, which aligns well with the needs of the present work.

It has been noted¹⁵⁶ that including extrapolated results computed with the cc-pVDZ basis set (as opposed to only using larger basis sets from the same family) increases the mean error. The paper by Truhlar deliberately used the cc-pVDZ and cc-pVTZ basis sets, obtaining good results but did not address whether this scheme used with the cc-pVTZ and cc-pVQZ basis sets (for example) would produce markedly better results. Due to the number of C atoms in many of the molecules considered in this work, the scheme using the cc-pVDZ and cc-pVTZ basis sets was retained to keep the computational time reasonable. However, this does not preclude the possibility that better results would be obtained if the cc-pVDZ results were omitted and larger basis sets were included.

Thus, the scheme due to Truhlar¹⁵⁷ has been implemented in the present work as described in the following. The contributions to the energy from the exchange and correlation parts of the B3LYP functional are separated as follows

$$E_{\text{tot}}^{\text{B3LYP}}=E^{\text{B3}}+E^{\text{LYP}}$$ (6)

where E^B3 is the energy from the Becke three-parameter exchange term,⁹⁰ and E^LYP is the energy from the Lee–Yang–Parr correlation term.⁹¹ These energetic contributions were used in the following formula for the extrapolation of the B3LYP energy to a large basis set limit (in the present case, the cc-pV6Z basis set)

$$E_{\text{extrap}}^{\text{B3LYP}}=\frac{3^{\alpha }{E}_3^{\mathrm{B}3}-2^{\alpha }{E}_2^{\mathrm{B}3}}{3^{\alpha }-2^{\alpha }}+\frac{3^{\beta }{E}_3^{\text{LYP}}-2^{\beta }{E}_2^{\text{LYP}}}{3^{\beta }-2^{\beta }}$$ (7)

Fitting was accomplished by subtracting the cc-pV6Z energy values from the cc-pVDZ and cc-pVTZ energy values and minimizing the fitting error using a Levenberg–Marquardt algorithm.^158,159 The optimized coefficients (α, β) produced using this scheme are presented in Table 5.

Table 5.

Optimized Values of α and β Used in the Energy Extrapolation, Eq 7, of the B3LYP based Scheme

α	3.9807
β	0.5542

Enthalpies of Formation

Computation of enthalpies of formation from ab initio results has been addressed by a number of authors.^160,161 The fundamental steps in this computation are given here. The enthalpy of formation for a molecule may be expressed as the difference between a thermodynamic term and the atomization energy

$${\mathrm{\Delta }}_{\mathrm{f}}H°=H_0-E_{\text{atom}}$$ (8)

The thermodynamic term (H₀) is computed as the sum of the atomic enthalpies of formation, the molecular zero-point energy, and the molecular enthalpy increment, minus the sum of atomic enthalpy increments

$$H_0={\displaystyle \sum _{i=1}^n{\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{atom},i}^{°}}+\text{ZPE}+H_{\text{inc,molecule}}-{\displaystyle \sum _{i=1}^n{H}_{\text{inc},\text{atom},i}}$$ (9)

Values for the atomic enthalpies of formation, ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{atom},i}^{°}$, for atom i at 0 K and enthalpy increment, H_inc, are given in Table 2. The atomization energy of a molecule may be computed by summing the energies of each atom in the molecule and subtracting the molecular energy obtained from the ab initio calculation (E_tot)

$$E_{\text{atom}}={\displaystyle \sum _{i=1}^N{E}_i-E_{\text{tot}}}$$ (10)

where i is an index that runs over all N atoms in the molecule, and E_i is the energy of atom i. Values for the atomic energies are given in Table 6. The values of the cc-pV6Z atomic energies were used in the calculations of the enthalpies of formation.

Table 6.

Values of the Atomic Energies (Given in E_h) Computed Using the B3LYP Functional and the Stated Basis Set^a

atom	cc-pVDZ	cc-pVTZ	cc-pV6Z
H	−0.497859	−0.498765	−0.499053
C	−37.829103	−37.835471	−37.838510
F	−99.691370	−99.727135	−99.740409

^aThese values were used to compute the enthalpies of formation as described in the text.

Computation of enthalpies of formation in the Gaussian-x model chemistries proceeds along very similar lines. The interested reader is directed to the work of Curtiss et al. for additional details.¹⁶¹

Corrections for Gaussian-3 Values

When the underlying ab initio data are of higher quality, and in particular when the error of the method is more regular, a significantly simpler error correction scheme may be employed. The G3B3 and G3MP2B3 values of the enthalpy of formation reported in this work employ a simpler correction scheme. Thus, the expression for the corrected enthalpy of formation becomes

$${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{corr}}^{°,\lambda }={\mathrm{\Delta }}_{\mathrm{f}}H°+{\mathrm{\epsilon }}_{\text{corr}}$$ (11)

where λ represents either the G3B3 or the G3MP2B3 enthalpy of formation, but the correction factor is now written as

$${\mathrm{\epsilon }}_{\text{corr}}=n_{\text{Cb}}f\left(\text{Cb}\right)+n_{\text{Cf}}f\left(\text{Cf}\right)+n_{\text{Cd}}f\left(\text{Cd}\right)+n_{\text{Ct}}f\left(\text{Ct}\right)$$ (12)

where n_Cb is the number of benzene-like (unfused) aromatic carbon atoms, n_Cf is the number of fused aromatic carbon atoms, n_Cd is the number of sp²-hybridized carbon atoms, n_Ct is the number of sp-hybridized carbon atoms, and f (Cb), f (Cf), f (Cd), and f (Ct) are the corresponding correction factors. Optimal values for the correction factors for the G3MP2B3 and G3B3 methods are presented in Table 7.

Table 7.

Values of Correction Factors (kJ/mol) Used To Correct G3MP2B3 Results

method	Cb	Cf	Cd	Ct
G3MP2B3	1.25	0.93	1.00	1.20

Statistical Descriptors

To facilitate assessment of the results, several statistical measures of data quality (compared to experiment) are used. The deviation δ is defined as the difference between the experimental value and the computed value

$$\delta ={\mathrm{\Delta }}_{\mathrm{f}}H°\left(\text{expt}\right)-{\mathrm{\Delta }}_{\mathrm{f}}H°\left(\text{calc}\right)$$ (13)

The minimum and maximum (absolute) deviations are defined as

$${\delta }_{\text{min}}=\underset{i}{\text{min}}|{\delta }_i|$$ (14)

$${\delta }_{\text{max}}=\underset{i}{\text{max}}|{\delta }_i|$$ (15)

The mean signed deviation (MSD) and mean unsigned deviation (MUD) are computed as

$$\text{MSD}=\frac{1}{n}{\displaystyle \sum _i^n{\delta }_i}$$ (16)

$$\text{MUD}=\frac{1}{n}{\displaystyle \sum _i^n|{\delta }_i|}$$ (17)

It should be noted that, although the MUD is a commonly used metric for comparing calculated results to experimental ones, the MUD is not the same as the uncertainty. The work of Ruscic covers this topic in some detail.¹⁶² In particular, the uncertainty in thermodynamic values such as the enthalpies of formation reported here is the 95% confidence interval (u_95%), which is twice the standard deviation (|sigma). The MUD is approximately 2.5 times smaller than u_95%. Thus, care should be used when the values from this publication are combined with other values with conventional uncertainties. Finally, the root-mean-square deviation (RMSD) is defined

$$\mathrm{RMSD}=\sqrt{\frac{1}{n}{\displaystyle \sum _i^n{\delta }_i^2}}$$ (18)

Values of these statistical descriptors are given in Table 4.

RESULTS

Having described the various calculations in the preceding section, the results of these calculations are now considered. Several different comparisons will be made. The first set of comparisons involves intercomparison between the present results and previous results from estimation (e.g., group additivity) and computational techniques. As the amount of experimental data on enthalpies of formation for PAHs is somewhat limited, it is reasonable to examine how the present results fare against other predictions. Also, as the expense of group additivity calculations and some of the quantum chemistry calculations used in the preset work is rather modest, a great deal of thermochemistry of PAHs can be obtained where experiments have not been performed. This comparison will also permit examination of the advantages and shortcomings of the various predictive methods.

The second set of comparisons, and perhaps the most meaningful, involves comparison to experimental data. Though agreement with experimental data may be regarded at the “gold standard” by which the present results should be judged, the reality is a bit more complicated. It will be seen that some of the experimental data are likely to be incorrect for some reason. In this way, the computational predictions for the enthalpies of formation serve as a screening tool by which some erroneous values may be identified. Nevertheless, the agreement between the present results and the available experimental data will firmly establish the reliability of the present results, implying a similar performance for the predicted results.

Comparison to Predicted Values

In the Introduction, a number of previous studies of enthalpy of formation in PAHs were referenced. These studies used a group additivity based method,^79–84,86 semiempirical methods,^85,139 and quantum chemistry.^87,136,137 Summary statistics for the results from these calculations compared to the present extrapolated and corrected B3LYP results are given in Table 8, and the individual values are given in Tables 9, 10, and 11. It may be noted that the present results are in generally good agreement with root-mean-square deviations (RMSD) less than about 6 kJ/mol for all but two studies. The mean unsigned deviations (MUD) are larger, with only three studies having a MUD less than 10 kJ/mol, and all but two having a MUD less than 21 kJ/mol. Given the diversity of the methods employed, this agreement is very reasonable.

Table 8.

Statistical Measures (kJ/mol) of the Deviations of Various Predictions of the Enthalpy of Formation at 298 K versus the Present Results for the B3LYP based Scheme^a

reference	n	MUD	RMSD	citation
Stein	26	20.70	5.78	78, 79
Alberty	19	13.10	3.97	80
Moiseeva	24	17.36	4.51	82, 83
Herndon	105	15.03	2.14	84
Armitage	25	15.16	3.84	81
Wang	32	5.15	1.09	85
Welsh	21	27.80	11.96	86
Yu	23	8.32	2.19	87
Blanquart	9	8.12	3.07	136
Rayne	25	15.20	3.40	137
Zauer	50	33.05	9.63	139

^aThe table gives the number of data, n, used in computing the mean unsigned deviation, MUD, and the root mean square deviation, RMSD.

Table 9.

Comparison of Enthalpies of Formation ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$ (kJ/mol) Predicted in Previous Studies to B3LYP Results and to Experiment Where Available (Further Discussion in Text)

molecule	CAS registry no.	Alberty80	Blanquart136	Welsh86	Rayne137	present	experiment
1-methylnaphthalene	90-12-0				103.8	113.5	116.9(±2.7)
1H-benz[e]indene	232-54-2				209.8	224.7
1H-benz[f]indene	268-40-6				209.6	220.4
1H-cyclopent[b]anthracene	259-06-3				282.0	300.5
1H-cyclopenta[l]phenanthrene	235-92-7				261.3	290.1
1H-phenalene	203-80-5				192.2	205.5
1,2-dihydrobenz[j]aceanthrylene	479-23-2				260.0	289.4
1,4-diethenylbenzene	935-14-8				546.9	552.6
2,3-benzofluorene	243-17-4				230.0	244.8
2-methylnaphthalene	91-57-6				102.9	108.7	116.1(±2.6)
3,4-dihydrocyclopenta[cd]pyrene	25732-74-5				213.3	343.4
17H-cyclopenta[a]phenanthrene	219-08-9				261.5	287.5
aceanthrylene	202-03-9				316.3	339.8
acenaphthene	83-32-9			154.0	143.3	150.7	156.8(±3.1)
acenaphthylene	208-96-8		244.2	176.9	245.9	259.8	263.2(±3.7)
anthracene	120-12-7	218.3	230.1	226.4	210.8	222.6	230.9(±3.7)
benz[a]anthracene	56-55-3	276.9			254.7	277.1	290.3(±6)
benzene	71-43-2	82.8	83.0			75.2	83.2(±0.3)
benzo[a]fluorene	238-84-6			258.5	228.3	246.5
benzo[a]naphthacene	226-88-0	344.7				362.9
benzo[a]pyrene	50-32-8			314.9		296.0
benzo[b]chrysene	214-17-5	335.5				347.0
benzo[b]fluoranthene	205-99-2			305.8		332.2
benzo[b]triphenylene	215-58-7	326.3				348.0
benzo[c]chrysene	194-69-4	339.0				362.2
benzo[c]phenanthrene	195-19-7	280.5		292.4		295.3
benzo[e]pyrene	192-97-2			335.3		289.9
benzo[ghi] fluoranthene	203-12-3				335.5	364.8
biphenyl	92-52-4				165.7	174.2	180.3(±3.3)
biphenylene	259-79-0			191.9	403.1	410.9	417.2(±1.9)
chrysene	218-01-9	267.7	259.9	275.6		271.1	268.5(±2.8)
coronene	191-07-1		292.4	352.8		296.7	300.9(±9.9)
dibenz[a,c]anthracene	215-58-7			357.2		348.0
dibenz[a,h]anthracene	53-70-3	335.5				335.0
dibenz[a,j]anthracene	224-41-9	335.5				336.3
dibenzo[b,g]phenanthrene	195-06-2	348.3				371.5
fluoranthene	206-44-0			284.7	262.6	277.9	282.4(±2.8)
fluorene	86-73-7			167.0	172.2	179.6	179.4(±3)
naphthacene	92-24-0	286.1		297.0		310.5	340.7(±3.9)
naphthalene	91-20-3	150.6	148.8	158.4	137.1	141.0	150.6(±1.6)
pentacene	135-48-8	353.9				401.3
pentaphene	222-93-5	344.7				349.3
perylene	198-55-0		306.1	330.0		319.2	317.4(±3.5)
phenanthrene	85-01-8	209.1	201.8	207.0	187.8	202.7	201.4(±3.5)
picene	213-46-7	326.3				336.9
pyrene	129-00-0		226.1	225.8	203.4	221.3	225.5(±4.3)
triphenylene	217-59-4	258.5		276.1		275.1	270.1(±3.1)

Table 10.

Comparison of Enthalpies of Formation ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$ (kJ/mol) Predicted in Previous Studies to B3LYP Results and to Experiment Where Available (Further Discussion in Text)

molecule	CAS registry no.	Stein78,79	Moiseeva82,83	Armitage81	Yu87	present	experiment
acenaphthalene	208-96-8	254.8	242.7			259.8
acenaphthylene	208-96-8	218.4				259.8	263.2(±3.7)
anthanthrene	191-26-4	310.5	335.1	310.5	341.0	323.0
anthracene	120-12-7	218.4	231.0	218.4	230.5	222.6	230.9(±3.7)
benz[a]aceanthrylene	203-33-8		356.5	352.3	364.4	363.5
benz[a]acephenanthrylene	192-28-9		344.8	381.6	386.6	394.0
benz[a]anthracene	56-55-3	277.0	288.3	277.0	275.7	277.1	290.3(±6)
benzene	71-43-2	82.8	69.5	82.8	82.4	75.2	83.2(±0.3)
benzo[a]coronene	190-70-5		329.7	372.0	374.9	371.8
benzo[a]pyrene	50-32-8	289.1				296.0
benzo[c]chrysene	194-69-4			331.0	344.8	362.2
benzo[c]phenanthrene	195-19-7	273.6	276.6	272.4	279.7	295.3
benzo[e]pyrene	192-97-2	280.3	293.7	279.9	291.6	289.9
benzo[ghi] fluoranthene	203-12-3		356.9	360.2	365.7	364.8
benzo[k] fluoranthene	207-08-9	254.4	369.9	356.9		339.0
chrysene	218-01-9	267.8	262.3	267.8	266.9	271.1	268.5(±2.8)
corannulene	5821-51-2	428.4		459.4		498.1
coronene	191-07-1	322.6	295.8	322.6	318.0	296.7	300.9(±9.9)
cyclopenta[cd]perylene	189-01-5		420.1	389.1	423.4	429.5
dibenz[a,c]anthracene	215-58-7	326.4				348.0
dibenz[a,j]anthracene	224-41-9	335.6				336.3
dibenzo[a,h]pyrene	189-64-0	348.1				375.6
dibenzo[a,i]pyrene	189-55-9	348.1				366.0
dibenzo[a,1]pyrene	191-30-0	356.5				393.3
fluoranthene	206-44-0		289.1	289.1	270.3	277.9	282.4(±2.8)
indeno[5,6,7,1-pqra]perylene	96915-18-3		388.3	410.5	425.9	419.8
naphthacene	92-24-0		311.7	286.2	314.6	310.5	340.7(±3.9)
naphthalene	91-20-3	150.6	150.2	150.6	151.5	141.0	150.6(±1.6)
ovalene	190-26-1	414.6	376.7	414.6	418.4	404.5
pentacene	135-48-8	354.0				401.3
perylene	198-55-0	280.3	293.7	279.9	306.7	319.2	317.4(±3.5)
phenanthrene	85-01-8	211.3	207.5	209.2	200.8	202.7	201.4(±3.5)
pyrene	129-00-0	231.0	259.8	230.5	241.0	221.3	225.5(±4.3)
triphenylene	217-59-4	258.6	241.4	258.6	273.2	275.1	270.1(±3.1)

Table 11.

Comparison of Enthalpies of Formation ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$ (kJ/mol) Predicted in Previous Studies to B3LYP Results and to Experiment Where Available (Further Discussion in Text)

molecule	CAS registry no.	Zauer139	Wang3	Herndon99	present	experiment
1-ethyl-2-methylbenzene	611-14-3		1.3		0.3	1.2(±1.2)
1-ethyl-3-methylbenzene	620-14-4		−2.9		−1.6	−1.9(±1.2)
1-ethyl-4-methylbenzene	622-96-8		−2.9		−5.8	−3.3(±1.4)
1-methylnaphthalene	90-12-0		120.5		113.5	116.9(±2.7)
1H-benz[e]indene	232-54-2			371.25	224.7
1H-phenalene	203-80-5	179.1			205.5
1,2-dimethylbenzene	95-47-6		20.1		15.0	19(±1.1)
1,2,3-trimethylbenzene	526-73-8		−7.5		−6.9	−9.6(±1.3)
1,2,4-trimethylbenzene	95-63-6		−13		−15.5	−13.9(±1.1)
1,3-dimethylbenzene	108-38-3		17.6		13.3	17.2(±0.8)
1,3,5-trimethylbenzene	108-67-8		−15.5		−17.5	−15.9(±1.3)
1,4-dimethylbenzene	106-42-3		17.6		13.6	17.9(±1.0)
1,4-diphenylbenzene	92-94-4	258.3			272.4	284.4(±3.8)
1,8-dimethylnaphthalene	569-41-5		111.3		114.0	108.8(±3.0)
2-methylnaphthalene	91-57-6		116.3		108.7	116.1(±2.6)
[6]helicene	187-83-7	693.4			471.7
acenaphthene	83-32-9	162.5			150.7	156.8(±3.1)
acenaphthylene	208-96-8	286.2	259.8		259.8	263.2(±3.7)
anthanthrene	191-26-4	354.4			323.0
anthra[1,2-a]anthracene	195-00-6			451.24	448.2
anthra[2,1,9-qra]naphthacene	189-52-6			484.67	458.8
anthracene	120-12-7	221.1	231.4	229.7	222.6	230.9(±3.7)
azulene	275-51-4	299.6			271.2
benz[a]anthracene	56-55-3	277.1	282.8	285.98	277.1	290.3(±6.0)
benz[mno]indeno[1,7,6,5-cdef]chrysene	96915-21-8	453.8			443.9
benz[mno]indeno[5,6,7,1-defg]chrysene	96915-20-7	506.7			444.6
benzene	71-43-2		83.7	79.04	75.2	83.2(±0.3)
benzo[a]naphth[2,1-j]anthracene	58029-41-7			429.19	428.8
benzo[a]naphthacene	226-88-0	362.0		373.59	362.9
benzo[a]naphtho[2,1,8-hij]naphthacene	190-05-6			457.48	431.1
benzo[a]pentacene	239-98-5			467.69	451.2
benzo[a]pentaphene	7689-57-8			419.99	408.2
benzo[a]perylene	191-85-5			433.09	428.0
benzo[a]picene	58029-45-1			424.68	428.5
benzo[a]pyrene	50-32-8	310.9			296.0
benzo[b]chrysene	214-17-5	348.1		356.1	347.0
benzo[b]fluoranthene	205-99-2	386.2			332.2
benzo[b]naphthacene	135-48-8	402.8			401.3
benzo[b]perylene	197-70-6			394.47	384.3
benzo[b]picene	217-42-5			421.04	413.9
benzo[b]triphenylene	215-58-7			358.65	348.0
benzo[c]chrysene	194-69-4	353.7		358.11	362.2
benzo[c]naphtho[2,1-p ]chrysene	27798-46-5	586.8			559.1
benzo[c]pentaphene	222-54-8			419.99	407.7
benzo[c]phenanthrene	195-19-7	326.2	295.0	292.29	295.3
benzo[c]picene	217-37-8			409.53	403.8
benzo[def]chrysene	50-32-8			318.32	296.0
benzo[e]pyrene	192-97-2	298.1	282.4	306.06	289.9
benzo[f]picene	58029-47-3			426.56	434.3
benzo[ghi]cyclopenta[cd]perylene	190-88-5	474.4			417.2
benzo[ghi]perylene	191-24-2		289.5	326.1	301.2
benzo[g]chrysene	196-78-1	354.8		362.17	368.8
benzo[h]pentaphene	214-91-5			429.74	419.0
benzo[j]fluoranthene	205-82-3	389.7			352.0
benzo[k]fluoranthene	207-08-9	376.6			339.0
benzo[mno]naphtho[1,2-c]chrysene	120835-49-6			466.26	453.0
benzo[pqr]naphtho[8,1,2-bcd]perylene	190-71-6	419.9			382.8
benzo[pqr]picene	189-96-8			380.87	359.4
benzo[rsf]pentaphene	189-55-9			389.74	366.0
benzo[s]picene	31540-94-0			442.21	474.5
benzo[vwx]hexaphene	2828-72-0			470.37	443.8
biphenyl	92-52-4	165.1	179.9		174.2	180.3(±3.3)
biphenylene	259-79-0	430.9			410.9	417.2(±1.9)
cholanthrene	479-23-2	286.8			289.4
chrysene	218-01-9	269.7	274.1	275.73	271.1	268.5(±2.8)
coronene	191-07-1	414.4	286.6	336.48	296.7	300.9(±9.9)
dibenz[a,j]anthracene	224-41-9			344.89	336.3
dibenzo[a,c]naphthacene	216-00-2			444.05	431.7
dibenzo[a,f]perylene	191-29-7			547.81	555.4
dibenzo[a,j]naphthacene	227-04-3			427.81	415.1
dibenzo[a,j]perylene	191-87-7			539.53	553.0
dibenzo[a,l]naphthacene	226-86-8			427.81	416.2
dibenzo[a,l]pentacene	227-09-8	525.4			503.1
dibenzo[a,n]perylene	191-81-1			495.64	489.9
dibenzo[a,o]perylene	190-36-3			526.85	532.9
dibenzo[a,pqr]picene	120835-40-7			463.8	452.2
dibenzo[a,rst]pentaphene	120835-51-0			469.28	455.0
dibenzo[b,ghi]perylene	5869-30-7			396.22	373.1
dibenzo[b,g]chrysene	53156-67-5			442.79	446.0
dibenzo[b,g]phenanthrene	195-06-2	365.6			371.5
dibenzo[b,k]chrysene	217-54-9			436.14	425.4
dibenzo[b,l]chrysene	58029-38-2			436.14	438.0
dibenzo[b,pqr]perylene	190-95-4			393.38	373.7
dibenzo[b,p]chrysene	58029-42-8	430.9		436.18	441.0
dibenzo[c,g]chrysene	53156-66-4			429.03	455.0
dibenzo[c,g]phenanthrene	188-52-3			360.58	385.5
dibenzo[c,l]chrysene	42850-69-1			439.82	461.7
dibenzo[c,mno]chrysene	196-28-1			395.97	383.9
dibenzo[c,pqr]picene	120835-44-1			448.65	427.6
dibenzo[c,p]chrysene	196-52-1			442.21	464.3
dibenzo[def,mno]chrysene	191-26-4			361.04	323.0
dibenzo[def,p]chrysene	191-30-0			396.06	393.3
dibenzo[de,ij]pentaphene	120835-46-3			509.19	487.8
dibenzo[de,kl]pentaphene	83786-06-5			574.97	536.1
dibenzo[de,mn]naphthacene	214-63-1			446.64	421.4
dibenzo[de,qr]naphthacene	193-09-9			377.77	362.6
dibenzo[de,qr]pentacene	120835-53-2			509.19	483.4
dibenzo[de,st]pentacene	14147-38-7			471.08	458.5
dibenzo[de,wv]pentaphene	120835-48-5			462.71	462.3
dibenzo[fg,ij]pentaphene	197-69-3			457.02	449.8
dibenzo[fg,op]naphthacene	192-51-8			371.	363.0
dibenzo[fg,qr]pentacene	197-74-0			457.02	448.2
dibenzo[g,p]chrysene	191-68-4			439.36	479.7
dibenzo[h,rst]pentaphene	192-47-2			447.1	435.0
dibenzo[pq,wv]pentaphene	137593-97-6			592.54	569.1
ethylbenzene	100-41-4		30.1		24.8	29.8(±0.8)
ethynylbenzene	536-74-3		308.8		314.1	306.6(±1.7)
fluoranthene	206-44-0	312.4			277.9	282.4(±2.8)
fluorene	86-73-7	189.8			179.6	179.4(±3.0)
heptacene	258-38-8	691.5			586.9
hexacene	258-31-1	492.6		517.52	493.7
hexaphene	222-78-6			448.94	432.6
indene	95-13-6	158.4			156.4
indeno[5,6,7,1-pqra]perylene	96915-18-3	497.3			419.8
naphthacene	92-24-0	308.8		320.91	310.5	340.7(±3.9)
naphthalene	91-20-3	139.5	149.8	146.77	141.0	150.6(±1.6)
naphtho[1,2,3,4-ghi]perylene	190-84-1			404.09	382.0
naphtho[1,2,3,4-rst]pentaphene	191-20-8			487.31	505.1
naphtho[1,2-a]naphthacene	58029-39-3			460.16	456.9
naphtho[1,2-b]chrysene	220-77-9			414.05	404.3
naphtho[1,2-b]triphenylene	215-26-9			419.24	405.8
naphtho[1,2-c]chrysene	58029-46-2			424.68	429.7
naphtho[1,2-g]chrysene	191-67-3			434.76	460.3
naphtho[2,1,8-def]picene	120835-39-4			452.33	450.9
naphtho[2,1,8-fgh]pentaphene	19301-88-3			448.65	435.6
naphtho[2,1-a]naphthacene	220-82-6			445.01	434.0
naphtho[2,1-b]chrysene	58029-43-9			414.05	404.9
naphtho[2,1-b]perylene	120835-43-0			477.39	474.0
naphtho[2,1-c]chrysene	58029-44-0			427.14	450.9
naphtho[2,3-c]chrysene	58029-37-1			436.14	437.1
naphtho[2,3-g]chrysene	196-64-5			436.18	441.3
ovalene	190-26-1	759.1			404.5
pentacene	135-48-8			417.4	401.3
pentaphene	222-93-5	350.5		359.99	349.3
perylene	198-55-0	317.5	304.6	331.92	319.2	317.4(±3.5)
phenanthrene	85-01-8	201.1	207.5	209.37	202.7	201.4(±3.5)
phenanthro[1,10,9,8-opqra]perylene	190-39-6	507.6			467.0
phenanthro[1,2,3,4-def]chrysene	137570-58-2			461.87	458.5
phenanthro[3,4-c]chrysene	31124-69-3			501.75	537.6
phenanthro[4,3-a]anthracene	58029-40-6			438.61	461.2
phenyl	2396-01-2		328.9		326.6	337.3(±0.6)
picene	213-46-7	341.6		342.96	336.9
pyranthrene	191-13-9	495.3			458.1
pyrene	129-00-0	237.2	225.5	242.17	221.3	225.5(±4.3)
styrene	100-42-5		148.1		142.1	146.9(±1.0)
toluene	108-88-3		50.6		44.1	50.1(±1.1)
tribenzo[a,hi,mn]naphthacene	54961-30-7			438.73	421.2
tribenzo[b,defp]chrysene	66032-75-9			472.16	470.6
tribenzo[c,g,mno]chrysene	108650-10-8			459.45	477.2
triphenylene	217-59-4	267.2	270.3	286.06	275.1	270.1(±3.1)

Table S1 compares the enthalpies of formation computed using the G3MP2B3 and G3B3 methods for 51 aromatic compounds. It may be observed that the G3MP2B3 values are consistently lower than the G3B3 values and can be adjusted to agree with the G3B3 values within about 0.6 kJ/mol (1 standard deviation) by applying corrections of 1.35 kJ/mol per CbH site, 0.85 kJ/mol per other aromatic carbon sites, 1.24 kJ/mol per Cd (double-bonded carbon), and 0.87 per Ct (triple-bonded carbon).

Table 12 compares the enthalpies of formation computed using the G3MP2B3 and G3B3 methods for 80 unsaturated aliphatic compounds. It was observed that the G3MP2B3 values for this set of molecules could be adjusted to agree with the G3B3 values within about 0.3 kJ/mol (1 standard deviation) by applying corrections of 1.06 kJ/mol per Cd (double-bonded carbon), and 1.09 kJ/mol per Ct (triple-bonded carbon). We note that for the allenes (e.g., propadiene, 1,2-butadiene) we computed the correction per double bond (not per atom). Thus, for example, the same correction is applied to 1,3-butadiene and 1,2-butadiene.

Table 12.

Values of the Enthalpy of Formation ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$ (kJ/mol) Computed Using the G3MP2B3 and G3B3 Model Chemistries for Non-PAH Molecules

			${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$
name	formula	CAS registry no.	G3MP2B3	G3B3
Alk-1-enes
ethene	C2H4	74-85-1	49.4	51.5
propene	C3H6	115-07-1	17.8	20.0
but-1-ene	C4H8	106-98-9	−1.8	0.5
pent-1-ene	C5H10	109-67-1	−23.3	−20.9
hex-1-ene	C6H12	592-41-6	−44.7	−42.1
Branched Alk-1-enes
3-methylbut-1-ene	C5H10	563-45-1	−30.3	−28.1
3-methylpent-1-ene	C6H12	760-20-3	−52.4	−50.0
3-methylhex-1-ene	C7H14	3404-61-3	−73.7	−71.2
4-methylpent-1-ene	C6H12	691-37-2	−50.8	−48.1
3-ethylpent-1-ene	C7H14	4038-04-4	−74.0	−71.6
3,3-dimethylpent-1-ene	C7H14	3404-73-7	−82.4	−79.8
Alk-2-enes
(E)-but-2-ene	C4H8	624-64-6	−12.2	−10.3
(E)-pent-2-ene	C5H10	646-04-8	−32.2	−30.3
(E)-hex-2-ene	C6H12	4050-45-7	−53.9	−51.8
(E)-hex-3-ene	C6H12	13269-52-8	−52.3	−50.3
(E)-4-methylpent-2-ene	C6H12	674-76-0	−61.0	−59.2
(Z)-but-2-ene	C4H8	590-18-1	−7.3	−5.0
(Z)-pent-2-ene	C5H10	627-20-3	−26.9	−24.5
(Z)-hex-2-ene	C6H12	7688-21-3	−48.8	−46.2
(Z)-hex-3-ene	C6H12	7642-09-3	−46.6	−44.2
Branched Alk-2-enes
(Z)-4-methylpent-2-ene	C6H12	691-38-3	−55.8	−53.5
Isoalkenes
2-methylprop-1-ene	C4H8	115-11-7	−18.1	−16.1
2-methylbut-1-ene	C5H10	563-46-2	−36.0	−33.9
2-methylpent-1-ene	C6H12	763-29-1	−57.6	−55.4
2-ethylbut-1-ene	C6H12	760-21-4	−54.2	−52.1
Isoalk-2-enes
2-methylbut-2-ene	C5H10	513-35-9	−41.7	−39.7
2-methylpent-2-ene	C6H12	625-27-4	−61.9	−59.9
(Z)-3-methylpent-2-ene	C6H12	922-62-3	−60.3	−58.3
(E)-3-methylpent-2-ene	C6H12	616-12-6	−60.0	−58.0
Alk-1-ynes
ethyne	C2H2	74-86-2	225.0	227.4
propyne	C3H4	74-99-7	182.4	184.5
but-1-yne	C4H6	107-00-6	163.8	165.9
pent-1-yne	C5H8	627-19-0	142.1	144.4
Alk-2-ynes
but-2-yne	C4H6	503-17-3	145.3	147.0
pent-2-yne	C5H8	627-21-4	126.2	128.1
isohexyne	C6H10	7154-75-8	113.9	116.4
Branched Alk-1-ynes
isopentyne	C5H8	598-23-2	136.6	138.8
tert-hexyne	C6H10	917-92-0	103.5	105.5
Unconjugated Alkadienes
penta-1,4-diene	C5H8	591-93-5	100.5	105.5
hexa-1,5-diene	C6H10	592-42-7	78.8	84.1
1,3 Conjugated Alkadienes
(E)-buta-1,3-diene	C4H6	106-99-0	105.9	110.9
(E)-penta-1,3-diene	C5H8	2004-70-8	73.9	78.6
(Z)-buta-1,3-diene	C4H6	106-99-0	118.3	123.5
(Z)-penta-1,3-diene	C5H8	1574-41-0	91.4	96.6
Branched 1,3 Conjugated Alkadienes
2-methylbuta-1,3-diene	C5H8	78-79-5	83.2	87.9
2,3-dimethylbuta-1,3-diene	C6H10	513-81-5	40.4	45.5
2,4 Conjugated Alkadienes
(E,Z)-hexa-2,4-diene	C6H10	5194-50-3	47.5	52.2
Conjugated Alkenynes
butenyne	C4H4	689-97-4	283.4	288.0
(E)-pent-3-en-1-yne	C5H6	2004-69-5	248.1	252.8
(Z)-pent-3-en-1-yne	C5H6	1574-40-9	249.8	254.0
pent-1-en-3-yne	C5H6	646-05-9	242.9	247.1
3-methylbut-1-en-3-yne	C5H6		248.5	252.7
Unconjugated Alkenynes
pent-1-en-4-yne	C5H6	871-28-3	270.2	275.3
Unconjugated Alkadiynes
penta-1,4-diyne	C5H4	24442-69-1	447.0	452.1
hexa-1,5-diyne	C6H6	628-16-0	412.3	417.5
Conjugated Alkadiynes
butadiyne	C4H2	460-12-8	454.5	458.4
penta-1,3-diyne	C5H4	1033-27-7	408.4	411.9
Alkatrienes
(E)-hexa-1,3,5-triene	C6H8	821-07-8	158.9	166.6
(Z)-hexa-1,3,5-triene	C6H8	2612-46-6	165.1	173.0
Diallenes
propadiene	C3H4	463-49-0	183.8	188.1
buta-1,2-diene	C4H6	590-19-2	157.3	161.3
penta-1,2-diene	C5H8	591-95-7	135.5	139.8
penta-2,3-diene	C5H8	591-96-8	130.3	134.0
hexa-2,3-diene	C6H10	592-49-4	109.4	113.2
3-methylpenta-1,2-diene	C6H10	7417-48-3	105.2	108.9
4-methylpenta-1,2-diene	C6H10	13643-05-5	107.0	111.3
Cum-Allenes
penta-1,2,3-triene	C5H6	62018-46-6	282.7	288.4
penta-1,2,4-triene	C5H6	10563-01-6	246.0	252.7
butatriene	C4H4	2873-50-9	313.9	319.9
(E)-hexa-2,3,4-triene	C6H8	59660-65-0	252.6	258.0
(E)-hexa-1,2,4,5-tetraene	C6H6	29776-96-3	387.9	396.3
pentatetraene	C5H4	21986-03-8	437.4	444.6
hexapentaene	C6H4	13703-38-3	560.0	568.4
Allenynes
penta-1,2-dien-4-yne	C5H4	33555-85-0	427.1	433.5
hexa-1,2-dien-4-yne	C6H6	34783-10-3	384.3	390.3
hexa-1,2-dien-5-yne	C6H6	33142-15-3	413.5	420.6
hexa-1,2,3-trien-5-yne	C6H4	895126-88-2	551.8	559.8
Alkendiynes
(E)-hex-3-en-1,5-diyne	C6H4	16668-68-1	516.3	523.2
(Z)-hex-3-en-1,5-diyne	C6H4	16668-67-0	517.1	524.3
Alkatriynes
hexatriyne	C6H2	3161-99-7	679.0	684.3

The G3MP2B3 method is a significantly less expensive calculation than the G3B3 method. It uses a single MP2 calculation to approximate the composite total energies in the G3B3 method that are determined from a set of MP2, MP4, and QCISD(T) energies using different basis sets. The good agreement here (after systematic corrections) suggests that not only does the G3MP2B3 method perform adequately well relative to the G3B3 method but also both methods can likely produce accurate values because little difference is observed (after correction) between two different methods—one approximate and the other more exact. Thus, in the following tables, we present only (corrected) enthalpies of formation from the G3MP2B3 method, because our analysis here shows that it is unnecessary to use the much more computationally expensive G3B3 method.

Comparison to Experimental Data

B3LYP

Experimental data are available for 49 PAHs and substituted PAHs, and for 52 benzene and substituted benzene compounds. Experimental data for an additional 81 alkanes, alkenes, and alkynes were used to make the fitting procedure more reliable and to assess the quality of the computational scheme. In total, up to 171 data were used for fitting and evaluation purposes. These values may be found in Table 13. This table also serves as a summary of the available experimental and review data available for the compounds used in the present study, and thus in some cases more than one value is given for a compound.

Table 13.

Experimental and Review Values of Enthalpy of Formation ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$ (Including Uncertainties in Parentheses Where Available) at 298 K^a

molecule	formula	CAS registry no.	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$	method	reference
methane	C1H4	74-82-8	−74.5(±0.6)	review	48
			−74.520(±0.054)	network	172
ethane	C2H6	74-84-0	−84.4(±0.4)	review	173
			−83.8(±0.2)	review	48
			−83.91(±0.14)	network	172
propane	C3H8	74-98-6	−104.7(±0.6)	review	48
butane	C4H10	106-97-8	−125.9(±0.4)	review	48
pentane	C5H12	109-66-0	−146.8(±0.6)	calorim	174
hexane	C6H14	110-54-3	−167.2(±0.8)	calorim	175
heptane	C7H16	142-82-5	−187.8(±0.8)	calorim	175
isobutane	C4H10	75-28-5	−134.4(±0.4)	review	48
isopentane	C5H12	78-78-4	−153.7(±0.6)	calorim	174
2-methylpentane	C6H14	107-83-5	−174.3(±1)	calorim	175
2-methylhexane	C7H16	591-76-4	−195(±1.3)	calorim	175
3-methylpentane	C6H14	96-14-0	−171.6(±1)	calorim	175
2,4-dimethylpentane	C7H16	108-08-7	−202.1(±1)	calorim	175
3,3-dimethylpentane	C7H16	562-49-2	−201.5	calorim	175
neopentane	C5H12	463-82-1	−167.9(±0.6)	calorim	174
2,2-dimethylbutane	C6H14	75-83-2	−185.6(±1)	calorim	175
2,2-dimethylpentane	C7H16	590-35-2	−206.2(±1.3)	calorim	175
ethene	C2H4	74-85-1	52.6(±0.2)	review	48
			52.45(±0.13)	network	172
propene	C3H6	115-07-1	20.2(±0.4)	review	48
but-1-ene	C4H8	106-98-9	0(±0.5)	review	48
			−0.6(±0.8)	calorim	176
pent-1-ene	C5H10	109-67-1	−21.3	heat hydrog	177
			−17.1(±0.4)	equil	178
hex-1-ene	C6H12	592-41-6	−42.1(±1.2)	heat hydrog	177
			−42.1	heat hydrog	179
			−41.5(±1.2)	heat hydrog	35
hept-1-ene	C7H14	592-76-7	−62.3	calorim	181
3-methylbut-1-ene	C5H10	563-45-1	−27.7(±1.2)	calorim	180
3-methylpent-1-ene	C6H12	760-20-3	−47(±1.1)	heat hydrog	182
3-ethylpent-1-ene	C7H14	4038-04-4	−69.5(±2)	heat hydrog	183
4-methylpent-1-ene	C6H12	691-37-2	−49.4(±0.7)	calorim	184
3-methylhex-1-ene	C7H14	3404-61-3	−68.2(±1.5)	heat hydrog	183
2-methylhex-2-ene	C7H14	2738-19-4	−87.8(±1.4)	review	185
3,3-dimethylbut-1-ene	C6H12	558-37-2	−59.7(±2)	heat hydrog	182
3,3-dimethylpent-1-ene	C7H14	3404-73-7	−78.5(±1.7)	heat hydrog	183
2,4-dimethylhex-2-ene	C8H16	14255-2-3−3	−104.9(±2.1)	review	185
(E)-but-2-ene	C4H8	624-64-6	−11.2(±0.5)	review	48
			−10.8(±1)	calorim	176
(Z)-but-2-ene	C4H8	590-18-1	−7.3(±0.5)	review	48
			−7.7(±1.3)	calorim	176
(E)-pent-2-ene	C5H10	646-04-8	−33.1(±1.3)	heat hydrog	186
(Z)-pent-2-ene	C5H10	627-20-3	−28(±0.8)	heat hydrog	186
(E)-4-methyl-pent-2-ene	C6H12	674-76-0	−60.1(±1.5)	heat hydrog	182
(Z)-4-methyl-pent-2-ene	C6H12	691-38-3	−57.9(±1.4)	heat hydrog	182
(E)-hex-2-ene	C6H12	4050-45-7	−51.7(±2)	equil	187
(Z)-hex-2-ene	C6H12	7688-21-3	−47.9(±2)	equil	187
(E)-hex-3-ene	C6H12	13269-52-8	−49.3(±1.1)	equil	187
(Z)-hex-3-ene	C6H12	7642-09-3	−46.9(±2)	equil	187
2-methylprop-1-ene	C4H8	115-11-7	−17.5(±0.5)	review	48
			−16.9(±0.9)	review	185
2-methylbut-2-ene	C5H10	513-35-9	−41.5(±0.88)	equil	188
			−41.8(±1.1)	review	185
2-methylbut-1-ene	C5H10	563-46-2	−35.1(±0.8)	equil	188
			−35.3(±1)	review	185
2-ethylbut-1-ene	C6H12	760-21-4	−56.1(±0.9)	calorim	188
2-methylpent-1-ene	C6H12	763-29-1	−58(±1.1)	heat hydrog	182
			−59.4(±1.3)	review	185
(E)-3-methyl-pent-2-ene	C6H12	616-12-6	−63.5(±0.9)	calorim	188
2-methylpent-2-ene	C6H12	625-27-4	−62.7(±1.2)	heat hydrog	182
			−63.2(±1.5)	review	185
(Z)-3-methylpent-2-ene	C6H12	922-62-3	−61.9(±0.9)	calorim	188
2,3-dimethylbut-1-ene	C6H12	563-78-0	−62.6(±1.3)	review	185
2,3-dimethyl-ent-1-ene	C7H14	3404-72-6	−90.2(±1.4)	review	185
ethyne	C2H2	74-86-2	226.7(±0.8)	calorim	189
			228.27(±0.13)	network	172
propyne	C3H4	74-99-7	185.4(±0.9)	calorim	189
but-1-yne	C4H6	107-00-6	166.1(±2.1)	calorim	189
			165.2(±0.9)	calorim	176
pent-1-yne	C5H8	627-19-0	144.3(±2.1)	calorim	189
hex-1-yne	C6H10	693-02-7	122.3(±1.2)	heat hydrog	190
hept-1-yne	C7H12	628-71-7	103.8(±2.6)	heat hydrog	190
isopentyne	C5H8	598-23-2	136.4(±2.1)	calorim	189
tert-hexyne	C6H10	917-92-0	106.1	calorim	191
but-2-yne	C4H6	503-17-3	148(±1.5)	calorim	189
			145.1(±1)	calorim	176
pent-2-yne	C5H8	627-21-4	128.9(±2.1)	calorim	189
hex-2-yne	C6H10	764-35-2	107.7(±2.4)	heat hydrog	190
hept-2-yne	C7H12	1119-65-9	84.8(±2.2)	heat hydrog	190
hept-3-yne	C7H12	2586-89-2	82.8(±2.4)	heat hydrog	190
penta-1,4-diene	C5H8	591-93-5	106.3(±1.3)	calorim	192
hexa-1,5-diene	C6H10	592-42-7	85(±2)	heat hydrog	193
(E)-buta-1,3-diene	C4H6	106-99-0	108.8(±0.8)	calorim	176
(E)-penta-1,3-diene	C5H8	2004-70-8	75.77(±0.7)	calorim	192
(Z)-penta-1,3-diene	C5H8	1574-41-0	82.72(±0.9)	calorim	192
(E)-hexa-1,3-diene	C6H10	20237-34-7	54.(±2)	heat hydrog	193
(Z)-hexa-1,3-diene	C6H10	14596-92-0	59(±2)	heat hydrog	193
(Z)-hexa-1,4-diene	C6H10	7318-67-4	77(±2)	heat hydrog	193
2-methylbuta-1,3-diene	C5H8	78-79-5	75.7(±1)	calorim	192
2,3-dimethylbuta-1,3-diene	C6H10	513-81-5	56.4(±1.2)	heat hydrog	177
2-ethylbuta-1,3-diene	C6H10	3404-63-5	63.6	heat hydrog	194
(E,E)-hexa-2,4-diene	C6H10	5194-51-4	44(±2)	heat hydrog	193
(E,Z)-hexa-2,4-diene	C6H10	5194-50-3	48(±2)	heat hydrog	193
(E)-hexa-1,3,5-triene	C6H8	821-07-8	168(±3)	heat hydrog	193
(Z)-hexa-1,3,5-triene	C6H8	2612-46-6	172(±3)	heat hydrog	193
1-buten-3-yne	C4H4	689-97-4	295(±3)	heat hydrog	194
2-methylbut-1-en-3-yne	C5H6	78-80-8	259(±1.3)	calorim	195
(E)-pent-3-en-1-yne	C5H6	2004-69-5	259(±3)	heat hydrog	194
(Z)-pent-3-en-1-yne	C5H6	1574-40-9	258.(±3)	heat hydrog	194
(E)-hex-3-en-1,5-diyne	C6H4	16668-68-1	538(±3)	heat hydrog	194
(Z)-hex-3-en-1,5-diyne	C6H4	16668-67-0	541.8(±3)	heat hydrog	194
ethenylbenzene	C8H8	100-42-5	146.9(±1)	calorim	196
(E)-propen-1-ylbenzene	C9H10	873-66-5	117.2	calorim	197
(Z)-propen-1-ylbenzene	C9H10	766-90-5	121.4	calorim	197
propen-2-ylbenzene	C9H10	98-83-9	118.3(±1.4)	equil	198
propen-3-ylbenzene	C9H10	300-57-2	133.8(±1.1)	heat hydr	199
isopropenylbenzene	C9H10	98-83-9	113.8(±2.1)	review	185
2-methylpropen-1-ylbenzene	C10H12	768-49-0	86.1(±2.1)	review	185
benzene	C6H6	71-43-2	82.9(±0.9)	review	2
			82.9(±0.5)	calorim	196
			82.9(±0.9)	calorim	200
			82.8(±0.9)	calorim	201
			83.2(±0.3)	network	202
toluene	C7H8	108-88-3	50.1(±1.1)	review	2
			50(±0.6)	calorim	200
			49.9(±1.1)	calorim	201
ethylbenzene	C8H10	100-41-4	29.8(±0.8)	calorim	200
prop-1-ylbenzene	C9H12	103-65-1	7.8(±0.8)	calorim	200
prop-2-ylbenzene	C9H12	98-82-8	3.9(±1.1)	calorim	200
but-1-ylbenzene	C10H14	104-51-8	−13.8(±1.3)	calorim	200
but-2-ylbenzene	C10H14	135-98-8	−17.4(±1.4)	calorim	200
isobutylbenzene	C10H14	538-93-2	−21.5(±1.4)	calorim	200
tert-butylbenzene	C10H14	98-06-6	−22.7(±1.4)	calorim	200
1,2-dimethylbenzene	C8H10	95-47-6	19.(±1.1)	calorim	200
			17.7	calorim	203
1,3-dimethylbenzene	C8H10	108-38-3	17.2(±0.8)	calorim	200
			14.9	calorim	203
1,4-dimethylbenzene	C8H10	106-42-3	17.9(±1)	calorim	200
			16.5	calorim	203
1-ethyl-2-methylbenzene	C9H12	611-14-3	1.2(±1.2)	calorim	196
1-ethyl-3-methylbenzene	C9H12	620-14-4	−1.9(±1.2)	calorim	204
1-ethyl-4-methylbenzene	C9H12	622-96-8	−3.3(±1.5)	calorim	204
1,2-diethylbenzene	C10H14	135-01-3	−19.5(±2.2)	calorim	200
1,3-diethylbenzene	C10H14	141-93-5	−21.6(±2.2)	calorim	200
1,4-diethylbenzene	C10H14	105-05-5	−22.1(±2.2)	calorim	200
1,2,3-trimethylbenzene	C9H12	526-73-8	−9.6(±1.3)	calorim	200
1,2,4-trimethylbenzene	C9H12	95-63-6	−13.9(±1.1)	calorim	200
1,3,5-trimethylbenzene	C9H12	108-67-8	−15.9(±1.3)	calorim	204
ethynylbenzene	C8H6	536-74-3	306.6(±1.7)	heat hydrog	169
propyn-1-ylbenzene	C9H8	673-32-5	268.2(±2.2)	heat hydrog	169
butyn-1-ylbenzene	C10H10	622-76-4	248.6(±1)	heat hydrog	169
benzyne	C6H4	462-80-6	446(±13)	ion	205
m-benzyne	C6H4	1828-89-3	490(±10)	ion	[206
			511(±13)	ion	[205
p-benzyne	C6H4	3355-34-8	540(±10)	ion	206
			575(±14)	ion	205
cyclopropylbenzene	C9H10	873-49-4	150.7(±1)	calorim	207
1-cyclopropyl-2-methylbenzene	C10H12	27546-46-9	125.5(±2.2)	calorim	208
cyclohexylbenzene	C12H16	827-52-1	−16.7(±1.5)	calorim	209
phenylbenzene	C12H10	92-52-4	180.3(±3.3)	review	2
			182(±0.7)	calorim	210
benzylbenzene	C13H12	101-81-5	162.3(±2.3)	review	2
			164.8(±1.6)	calorim	211
2-phenyltoluene	C13H12	643-58-3	152.8(±1.5)	calorim	211
3-phenyltoluene	C13H12	643-93-6	152.5(±8)	calorim	212
4-phenyltoluene	C13H12	644-08-6	138.2(±2.9)	calorim	213
phenylethylbenzene	C14H14	103-29-7	135.6(±1.3)	review	2
(E)-1,2-diphenylethene	C14H12	103-30-0	233.7(±2)	calorim	214
(Z)-1,2-diphenylethene	C14H12	645-49-8	245.9(±1.3)	calorim	215
diphenylethyne	C14H10	501-65-5	385(±2.7)	heat hydrog	169
			407.5(±1.6)	calorim	216
1,2-diphenylbenzene	C18H14	84-15-1	282.8(±3.2)	review	2
1,3-diphenylbenzene	C18H14	92-06-8	280(±3.9)	review	2
1,4-diphenylbenzene	C18H14	92-94-4	284.4(±3.8)	review	2
			279(±5)	calorim	217
triphenylmethane	C19H16	519-73-3	276.1(±4.1)	review	2
			268(±4)	calorim	218
phenyl	C6H5	2396-01-2	330.1(±3.3)	review	219
			337(±2.5)	equil	220
			338(±3)	review	221
			339(±8)	review	222
			339.7(±2.5)	ion	223
			337.3(±0.6)	network	202
1,2-dihydronaphthalene	C10H10	447-53-0	124.8(±3.3)	heat hydrog	224
1,4-dihydronaphthalene	C10H10	612-17-9	137.5(±3.2)	heat hydrog	224
1,2,3,4-tetrahydronaphthalene	C10H10	119-64-2	24(±3.2)	calorim	225
trans-decalin	C10H18	493-02-7	−182.2(±2.3)	calorim	226
cis-decalin	C10H18	493-01-6	−169.2(±2.3)	calorim	226
benzocyclobutene	C8H6	4026-23-7	406.(±17)	ion	227
benzocyclobutane	C8H8	694-87-1	199.4(±0.9)	calorim	228
naphthalene	C10H8	91-20-3	150.6(±1.6)	review	2
			150.6(±1.1)	calorim	229
1-methylnaphthalene	C11H10	90-12-0	116.9(±2.7)	calorim	226
2-methylnaphthalene	C11H10	91-57-6	116.1(±2.6)	calorim	226
1,8-dimethylnaphthalene	C12H12	569-41-5	108.8(±3)	calorim	230
2,3-dimethylnaphthalene	C12H12	581-40-8	79.9(±2)	calorim	231
			76.1(±2)	calorim	232
2,6-dimethylnaphthalene	C12H12	581-42-0	78.7(±2.5)	calorim	231
2,7-dimethylnaphthalene	C12H12	582-16-1	79.5(±0.6)	calorim	233
1-ethyl-8-methylnaphthalene	C13H14	61886-71-3	98.1(±1.5)	calorim	234
1,4,5,8-tetramethylnaphthalene	C14H16	2717-39-7	81.6(±3.6)	calorim	230
indan	C9H10	496-11-7	60.7(±1.5)	calorim	235
			60.9(±2.1)	review	2
1,1-dimethyl-2,3-dihydro-1H-indene	C11H14	4912-92-9	−1.6(±2)	calorim	235
4,6-dimethylindan	C11H14	1685-82-1	−5.8(±1.7)	calorim	235
4,7-dimethylindan	C11H14	6682-71-9	−7.4(±1.7)	calorim	235
indene	C9H8	95-13-6	161.2(±2.3)	review	2
			163.3(±1.6)	calorim	236
			156.7	equil	237
anthracene	C14H10	120-12-7	230.9(±3.7)	review	2
			230.8(±4.6)	calorim	229
phenanthrene	C14H10	85-01-8	201.4(±3.5)	review	2
			201.7(±2.9)	calorim	238
			201.2(±4.7)	calorim	239
			206.9(±4.6)	calorim	229
biphenylene	C12H8	259-79-0	417.2(±1.9)	review	2
			420.4(±1.9)	calorim	240
acenaphthylene	C12H8	208-96-8	263.2(±3.7)	review	2
			263.8(±3.4)	heat hydrog	241
			258.2(±5.9)	calorim	242
acenaphthene	C12H10	83-32-9	156.8(±3.1)	review	2
			156.5(±3.8)	calorim	242
			155.9(±2.5)	calorim	241
fluorene	C13H10	86-73-7	176.7(±3.1)	review	2
			175(±1.5)	calorim	243
			179.4(±3)	calorim	244
9-methylfluorene	C14H12	2523-37-7	148(±1.1)	calorim	243
cyclopropa[b]naphthalene	C11H8	286-85-1	435(±5)	calorim	245
naphthacene	C18H12	92-24-0	340.7(±3.9)	review	2
			331.6(±4.4)	calorim	238
			238.1	calorim	166
benz[a]anthracene	C18H12	56-55-3	290.3(±6)	review	2
			294(±5)	calorim	246
chrysene	C18H12	218-01-9	268.5(±2.8)	review	2
			263(±5)	calorim	246
benzo[c]phenanthrene	C18H12	195-19-7	295.3(±9.1)	review	2
			291(±5)	calorim	246
pyracyclene	C14H8	187-78-0	408.6(±5)	review	2
			411.5(±6.2)	calorim	241
			419.2(±6.2)	heat hydrog	241
			409.3(±6.2)	calorim	247
pyracene	C14H12	567-79-3	174.1(±5.1)	review	2
			174.3(±5.3)	calorim	241
pyrene	C16H10	129-00-0	225.5(±4.3)	review	2
			225.7(±1.3)	calorim	248
fluoranthene	C16H10	206-44-0	291.4(±4)	review	2
			292(±2.2)	calorim	242
			282.4(±2.8)	calorim	168
triphenylene	C18H12	217-59-4	270.1(±3.1)	review	2
			272(±4)	calorim	246
5,12-dihydrotetracene	C18H14	959-02-4	224.9	review	2
			227(±4)	calorim	246
perylene	C20H12	198-55-0	317.4(±3.5)	review	2
			309(±5)	calorim	249
			319.4(±2.2)	calorim	250
benzo[a]pyrene	C20H12	50-32-8	296.9(±5.5)	review	2
benzo[e]pyrene	C20H12	192-97-2	330.7(±9.2)	review	2
benzo[k]fluoranthene	C20H12	207-08-9	306.2(±6.2)	review	2
benzo[b]triphenylene	C22H14	215-58-7	331(±11)	review	2
dibenz[a,h]anthracene	C22H14	53-70-3	328(±11)	review	2
corannulene	C20H10	5821-51-2	458.7(±9.1)	review	2
			460.6(±6.5)	calorim	250
coronene	C24H12	191-07-1	300.9(±9.9)	review	2
			307.5(±9.8)	calorim	250
			285.5(±7.3)	calorim	251
			294.9(±11.1)	calorim	251
			286.1(±11.4)	calorim	252
			279.4(±5.3)	calorim	253
			296.2(±8.8)	review	present work
triquinacene	C10H10	6053-74-3	224(±4.2)	heat hydrog	254
azulene	C10H8	275-51-4	308	heat hydrog	255
			280	calorim	256
6,6-diphenylfulvene	C18H14	2175-90-8	402(±15)	calorim	257

^aUnits are kJ/mol. Experimental types are denoted “review” (consensus value), “calorim” (calorimetry), “heat hydrog” (heat of hydrogenation), “ion” (ion cycles), “equil” (equilibrium), and “network” (thermochemical network).

The previous studies mentioned above,^{79–87,136,137,139} are compared to the experimental values individually in Tables 9, 10, and 11, and in summary form in Table 14. One can see slightly better agreement with experiment that with the present extrapolated corrected B3LYP results for most of the studies, though the results of Welsh et al.⁸⁶ show larger deviations, and the results of Rayne and Forest¹³⁷ and Zauer¹³⁹ still show larger deviations as above.

Table 14.

Statistical Measures (kJ/mol) of the Accuracy of Various Predictions of the Enthalpy of Formation at 298 K versus Experiment^a

reference	n	MUD	RMSD	citation
Stein	11	14.28	6.06	78, 79
Alberty	8	12.60	7.41	80
Moiseeva	12	12.61	5.06	82, 83
Herndon	11	11.90	4.61	84
Armitage	12	13.91	6.13	81
Wang	29	2.71	0.86	85
Welsh	14	33.68	17.97	86
Yu	12	9.35	3.73	87
Blanquart	9	5.67	2.81	136
Rayne	13	17.32	5.25	137
Zauer	17	17.73	7.50	139
B3LYP	21	5.1	6.7

^aThe table gives the number of data, n, used in computing the mean unsigned deviation, MUD, and the root mean square deviation, RMSD.

In the case of the extrapolated and corrected B3LYP-derived enthalpies of formation, a set of 171 data were used to adjust the parameters of the group additivity based error correction scheme. The optimized group parameters are given in Table 3. A histogram plot of the deviations in the corrected B3LYP enthalpy of formation values with respect to the experimental data used in the fitting process is shown in Figure 2. From this figure, the reliability of the B3LYP scheme is clearly seen, with most errors less than 5 kJ/mol and all errors less than 20 kJ/mol. The corrections to the enthalpies of formation for the extrapolated B3LYP calculations were examined in more detail by the class of compound.

Figure 2.

Histogram plot of deviations of corrected enthalpies of formation derived from B3LYP calculations versus experiment.

Predictions of enthalpies of formation are made for 810 compounds using the extrapolated and corrected B3LYP scheme. The presentation of the results is split into four tables. In Table 15, the B3LYP results for PAHs are compared to experimental values, and in Table 16 the same results for non-PAH molecules are presented. In these tables, the uncorrected and corrected values of the enthalpy of formation are given so that the magnitude of the correction is evident, and the error in the corrected value with respect to the experimental value is given. As a measure of the overall quality of the B3LYP scheme, a mean unsigned deviation of 5.1 kJ/mol and a root-mean-square deviation of 6.7 kJ/mol may be seen for the PAH compounds presented in Table 15. In Table S2, predictions (i.e., no experimental data are available) of the enthalpy are made for PAH compounds, and in Table S3 the same results are presented for non-PAH molecules.

Table 15.

Predicted (B3LYP, Uncorrected, and Corrected) and Experimental Enthalpies of Formation ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$ (kJ/mol) for PAH Molecules and Error $\left({\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{corr}\right)-{\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{expt}\right)\right)$

molecule	formula	CAS registry no.	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{uncorr}\right)$	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{corr}\right)$	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{expt}\right)$	error
acenaphthene	C12H10	83-32-9	196.5	150.7	156.8(±3.1)	−6.1
acenaphthylene	C12H8	208-96-8	300.8	259.8	263.2(±3.7)	−3.2
anthracene	C14H10	120-12-7	265.1	222.6	230.9(±3.7)	−8.3
benz[a]anthracene	C18H12	56-55-3	340.8	277.1	290.3(±6.0)	−13.2
benzene	C6H6	71-43-2	75.2	75.2	83.2(±0.3)	−8.0
benzo[a]pyrene	C20H12	50-32-8	379.0	296.0	296.9(±5.5)	−0.9
benzo[b]triphenylene	C22H14	215-58-7	432.9	348.0	331.0(±11)	17.0
benzo[c]phenanthrene	C18H12	195-19-7	359.1	295.3	295.3(±9.1)	0.0
benzocyclobutene	C8H6	4026-23-7	427.9	409.8	406.0(±17)	3.8
biphenylene	C12H8	259-79-0	447.3	410.9	417.2(±1.9)	−6.3
chrysene	C18H12	218−01−9	334.9	271.1	268.5(±2.8)	2.6
coronene	C24H12	191−07−1	418.1	296.7	300.9(±9.9)	3.3
corannulene	C20H10	5821−51−2	594.2	498.5	458.7	39.8
dibenz[a,h]anthracene	C22H14	53−70−3	420.0	335.0	328.0	7.0
fluoranthene	C16H10	206−44−0	343.8	277.9	282.4	−4.5
fluorene	C13H10	86-73-7	227.8	179.6	179.4	0.2
indene	C9H8	95-13-6	180.6	156.4	161.2	−4.8
naphthacene	C18H12	92-24-0	374.0	310.5	340.7	−30.2
naphthalene	C10H8	91-20-3	162.3	141.0	150.6	−9.6
perylene	C20H12	198-55-0	402.2	319.2	317.4	1.8
phenanthrene	C14H10	85-01-8	245.2	202.7	201.4	1.3
pyracene	C14H12	567-79-3	261.6	191.4	174.1	17.3
pyracyclene	C14H8	187-78-0	498.9	438.2	408.6	29.6
pyrene	C16H10	129-00-0	283.0	221.3	225.5	−4.2
triphenylene	C18H12	217-59-4	338.8	275.1	270.1	5.0

Table 16.

Predicted (B3LYP, Uncorrected and Corrected) and Experimental Enthalpies of Formation ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$ (kJ/mol) for Non-PAH Molecules and Error $\left({\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{corr}\right)-{\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{expt}\right)\right)$

molecule	formula	CAS registry no.	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{uncorr}\right)$	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{corr}\right)$	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{expt}\right)$	error
1-buten-3-yne	C4H4	689-97-4	274.2	290.6	295.0(±3)	−4.4
1-cyclopropyl-2-methylbenzene	C10H12	27546-46-9	152.3	111.1	125.5(±2.2)	−14.4
1-ethyl-2-methylbenzene	C9H12	611-14-3	14.9	0.3	1.2(±1.2)	−0.9
1-ethyl-3-methylbenzene	C9H12	620-14-4	13.0	−1.6	−1.9(±1.2)	0.3
1-ethyl-4-methylbenzene	C9H12	622-96-8	8.8	−5.8	−3.3(±1.5)	−2.5
1-ethyl-8-methylnaphthalene	C13H14	61886-71-3	141.2	105.4	98.1(±1.5)	7.3
1-methylnaphthalene	C11H10	90-12-0	139.4	113.5	116.9(±2.7)	−3.4
1,1-dimethyl-2,3-dihydro-1H-indene	C11H14	4912-92-9	48.8	−7.2	−1.6(±2)	−5.6
1,2-diethylbenzene	C10H14	135-01-3	3.7	−16.1	−19.5(±2.2)	3.4
1,2-dihydronaphthalene	C10H10	447-53-0	154.0	124.7	124.8(±3.3)	−0.1
1,2-dimethylbenzene	C8H10	95-47-6	24.4	15.0	19.0(±1.1)	−4.0
1,2-diphenylbenzene	C18H14	84-15-1	345.0	290.5	282.8(±3.2)	7.7
(E)-1,2-diphenylethene	C14H12	103-30-0	264.7	228.6	233.7(±2)	−5.1
(Z)-1,2-diphenylethene	C14H12	645-49-8	285.8	249.7	245.9(±1.3)	3.8
1,2,3-trimethylbenzene	C9H12	526-73-8	7.2	−6.9	−9.6(±1.3)	2.7
1,2,3,4-tetrahydronaphthalene	C10H12	119-64-2	59.0	25.8	24.0(±3.2)	1.8
1,2,4-trimethylbenzene	C9H12	95-63-6	−1.3	−15.5	−13.9(±1.1)	−1.6
1,3-diethylbenzene	C10H14	141-93-5	−5.4	−25.2	−21.6(±2.2)	−3.6
1,3-dimethylbenzene	C8H10	108-38-3	22.8	13.3	17.2(±0.8)	−3.9
1,3-diphenylbenzene	C18H14	92-06-8	328.1	273.6	280.0(±3.9)	−6.4
1,3,5-trimethylbenzene	C9H12	108-67-8	−3.4	−17.5	−15.9(±1.3)	−1.6
1,4-diethylbenzene	C10H14	105-05-5	−5.4	−25.2	−22.1(±2.2)	−3.1
1,4-dihydronaphthalene	C10H10	612-17-9	166.1	136.0	137.5(±3.2)	−1.5
1,4-dimethylbenzene	C8H10	106-42-3	23.0	13.6	17.9(±1)	−4.3
1,4-diphenylbenzene	C18H14	92-94-4	326.9	272.4	284.4(±3.8)	−12.0
1,4,5,8-tetramethylnaphthalene	C14H16	2717-39-7	139.4	99.3	81.6(±3.6)	17.7
1,8-dimethylnaphthalene	C12H12	569-41-5	144.7	114.0	108.8(±3)	5.2
2-ethylbut-1-ene	C6H12	760-21-4	−52.1	−53.2	−56.1(±0.9)	2.9
2-ethylbuta-1,3-diene	C6H10	3404-63-5	56.1	58.2	63.6	−5.4
2-methylbut-1-en-3-yne	C5H6	78-80-8	244.7	253.5	259.0(±1.3)	−5.5
2-methylbut-1-ene	C5H10	563-46-2	−41.7	−36.9	−35.3(±0.8)	−1.6
2-methylbut-2-ene	C5H10	513-35-9	−51.3	−43.5	−41.5(±0.88)	−2.0
2-methylbuta-1,3-diene	C5H8	78-79-5	77.6	85.7	75.7(±1)	10.0
2-methylhexane	C7H16	591-76-4	−186.6	−199.4	−195.0(±1.3)	−4.4
2-methylnaphthalene	C11H10	91-57-6	134.7	108.7	116.1(±2.6)	−7.4
2-methylpent-1-ene	C6H12	763-29-1	−45.7	−46.0	−58.0(±1.1)	12.0
2-methylpent-2-ene	C6H12	625-27-4	−53.8	−51.9	−63.2(±1.2)	11.3
2-methylpentane	C6H14	107-83-5	−170.3	−177.8	−174.3(±1)	−3.5
2-methylprop-1-ene	C4H8	115-11-7	−31.0	−20.2	−16.9(±0.5)	−3.3
2-phenyltoluene	C13H12	643-58-3	186.3	154.3	152.8(±1.5)	1.5
2,2-dimethylbutane	C6H14	75-83-2	−170.4	−187.6	−185.6(±1)	−2.0
2,2-dimethylpentane	C7H16	590-35-2	−184.7	−207.1	−206.2(±1.3)	−0.9
2,3-dimethylbuta-1,3-diene	C6H10	513-81-5	44.3	44.8	56.4(±1.2)	−11.6
2,3-dimethylnaphthalene	C12H12	581-40-8	110.1	79.5	79.9(±2)	−0.4
2,4-dimethylpentane	C7H16	108-08-7	−185.3	−206.0	−202.1(±1)	−3.9
2,6-dimethylnaphthalene	C12H12	581-42-0	106.6	76.0	78.7(±2.5)	−2.7
2,7-dimethylnaphthalene	C12H12	582-16-1	106.7	76.0	79.5(±0.6)	−3.5
3-ethylpent-1-ene	C7H14	4038-04-4	−46.9	−57.1	−69.5(±2)	12.4
3-methylbut-1-ene	C5H10	563-45-1	−22.9	−22.8	−27.7(±1.2)	4.9
3-methylhex-1-ene	C7H14	3404-61-3	−48.9	−59.2	−68.2(±1.5)	9.0
3-methylpent-1-ene	C6H12	760-20-3	−35.0	−40.0	−47.0(±1.1)	7.0
(E)-3-methylpent-2-ene	C6H12	616-12-6	−72.7	−70.8	−63.5(±0.9)	−7.3
(Z)-3-methylpent-2-ene	C6H12	922-62-3	−61.5	−59.6	−61.9(±0.9)	2.3
3-methylpentane	C6H14	96-14-0	−166.4	−173.9	−171.6(±1)	−2.3
3-phenyltoluene	C13H12	643-93-6	175.3	143.3	152.5(±8)	−9.2
3,3-dimethylbut-1-ene	C6H12	558-37-2	−36.1	−50.7	−59.7(±2)	9.0
3,3-dimethylpent-1-ene	C7H14	3404-73-7	−43.6	−63.5	−78.5(±1.7)	15.0
3,3-dimethylpentane	C7H16	562-49-2	−184.3	−206.6	−201.5	−5.1
4-methylpent-1-ene	C6H12	691-37-2	−46.8	−52.7	−49.4(±0.7)	−3.3
(E)-4-methylpent-2-ene	C6H12	674-76-0	−50.0	−52.8	−60.1(±1.5)	7.3
(Z)-4-methylpent-2-ene	C6H12	691-38-3	−42.9	−45.7	−57.9(±1.4)	12.2
4-phenyltoluene	C13H12	644-08-6	174.8	142.9	138.2(±2.9)	4.7
4,6-dimethylindan	C11H14	1685-82-1	33.3	−4.2	−5.8(±1.7)	1.6
4,7-dimethylindan	C11H14	6682-71-9	32.4	−5.1	−7.4(±1.7)	2.3
5,12-dihydrotetracene	C18H14	959-02-4	302.0	227.4	224.9	2.5
6,6-diphenylfulvene	C18H14	2175-90-8	474.9	409.2	402.0(±15)	7.2
9-methylfluorene	C14H12	2523-37-7	212.3	150.9	148.0(±1.1)	2.9
benzocyclobutane	C8H8	694-87-1	212.9	190.0	199.4(±0.9)	−9.4
benzylbenzene	C13H12	101-81-5	195.7	160.0	162.3(±2.3)	−2.3
but-1-ene	C4H8	106-98-9	−14.7	−2.2	0.0(±0.5)	−2.2
but-1-ylbenzene	C10H14	104-51-8	2.6	−17.7	−13.8(±1.3)	−3.9
but-1-yne	C4H6	107-00-6	156.2	170.1	166.1(±2.1)	4.0
(E)-but-2-ene	C4H8	624-64-6	−20.3	−4.8	−11.2(±0.5)	6.4
(Z)-but-2-ene	C4H8	590-18-1	−22.8	−7.3	−7.3(±0.5)	−0.0
but-2-ylbenzene	C10H14	135-98-8	8.6	−19.6	−17.4(±1.4)	−2.2
but-2-yne	C4H6	503-17-3	129.1	147.9	148.0(±1.5)	−0.1
(E)-buta-1,3-diene	C4H6	106-99-0	91.8	107.5	108.8(±0.8)	−1.3
buta-1,3-diyne	C4H2	460-12-8	450.4	467.5	464.0(±5)	3.5
butane	C4H10	106-97-8	−140.1	−129.4	−125.9(±0.4)	−3.5
butyn-1-ylbenzene	C10H10	622-76-4	261.8	249.6	248.6(±1)	1.0
cyclohexylbenzene	C12H16	827-52-1	36.8	−15.2	−16.7(±1.5)	1.5
cyclopropa[b]naphthalene	C11H8	286-85-1	459.9	421.0	435.0(±5)	−14.0
diphenylethyne	C14H10	501-65-5	421.8	389.0	385.0(±2.7)	4.0
ethane	C2H6	74-84-0	−107.0	−85.9	−83.91(±0.14)	−1.99
ethene	C2H4	74-85-1	31.9	53.3	52.45(±0.13)	0.85
ethenylbenzene	C8H8	100-42-5	149.5	142.1	146.9(±1)	−4.8
ethylbenzene	C8H10	100-41-4	34.7	24.8	29.8(±0.8)	−5.0
ethyne	C2H2	74-86-2	215.9	235.2	226.7(±0.8)	8.5
ethynylbenzene	C8H6	536-74-3	320.8	314.1	306.6(±1.7)	7.5
hept-1-ene	C7H14	592-76-7	−62.6	−65.8	−62.3(±1.5)	−3.5
hept-1-yne	C7H12	628-71-7	107.3	105.6	103.8(±2.6)	1.8
hept-2-yne	C7H12	1119-65-9	82.3	85.5	84.8(±2.2)	0.7
hept-3-yne	C7H12	2586-89-2	82.8	86.0	82.8(±2.4)	3.2
heptane	C7H16	142-82-5	−187.8	−192.6	−187.8(±0.8)	−4.8
hex-1-ene	C6H12	592-41-6	−46.8	−44.8	−42.1(±1.2)	−2.7
hex-1-yne	C6H10	693-02-7	123.4	127.0	122.3(±1.2)	4.7
(E)-hex-2-ene	C6H12	4050-45-7	−60.6	−56.3	−51.7(±2.0)	−4.6
(Z)-hex-2-ene	C6H12	7688-21-3	−53.3	−49.0	−47.9(±2.0)	−1.1
hex-2-yne	C6H10	764-35-2	98.6	107.0	107.7(±2.4)	−0.7
(E)-hex-3-en-1,5-diyne	C6H4	16668-68-1	524.1	535.5	538.0(±3.0)	−2.5
(Z)-hex-3-en-1,5-diyne	C6H4	16668-67-0	516.1	527.5	541.8(±3.0)	−14.3
(E)-hex-3-ene	C6H12	13269-52-8	−46.2	−42.7	−49.3(±1.1)	6.6
(Z)-hex-3-ene	C6H12	7642-09-3	−51.3	−47.9	−46.9(±2.4)	−1.0
(E)-hexa-1,3-diene	C6H10	20237-34-7	60.9	67.7	54.0(±2.0)	13.7
(Z)-hexa-1,3-diene	C6H10	14596-92-0	53.0	59.8	59.0(±2.0)	0.8
(E)-hexa-1,3,5-triene	C6H8	821-07-8	146.9	157.0	168.0(±3.0)	−11.0
(Z)-hexa-1,3,5-triene	C6H8	2612-46-6	156.2	166.3	172.0(±3.0)	−5.7
(Z)-hexa-1,4-diene	C6H10	7318-67-4	73.8	80.6	77.0(±2.0)	3.6
hexa-1,5-diene	C6H10	592-42-7	78.3	82.0	85.0(±2.0)	−3.0
(E,E)-hexa-2,4-diene	C6H10	5194-51-4	29.6	39.5	44.0(±2.0)	−4.5
(E,Z)-hexa-2,4-diene	C6H10	5194-50-3	36.9	46.7	48.0(±2.0)	−1.3
hexane	C6H14	110-54-3	−171.7	−171.3	−167.2(±0.8)	−4.1
indan	C9H10	496-11-7	84.3	56.3	60.9(±2.1)	−4.6
isobutane	C4H10	75-28-5	−143.7	−140.9	−134.4(±0.4)	−6.5
isobutylbenzene	C10H14	538-93-2	1.0	−27.2	−21.5(±1.4)	−5.7
isopentane	C5H12	78-78-4	−155.4	−157.7	−153.7(±0.6)	−4.0
isopentyne	C5H8	598-23-2	138.0	138.8	136.4(±2.1)	2.4
m-benzyne	C6H4	1828-89-3	521.3	482.8	490.0(±10)	−7.2
neopentane	C5H12	463-82-1	−163.6	−175.6	−167.9(±0.6)	−7.7
pent-1-ene	C5H10	109-67-1	−30.9	−23.7	−21.3(±2.7)	−2.4
pent-1-yne	C5H8	627-19-0	139.5	148.2	144.3(±2.1)	3.9
(E)-pent-2-ene	C5H10	646-04-8	−44.1	−34.6	−33.1(±1.3)	−1.5
(Z)-pent-2-ene	C5H10	627-20-3	−37.3	−27.8	−28.0(±0.8)	0.2
pent-2-yne	C5H8	627-21-4	114.4	128.0	128.9(±2.1)	−0.9
(E)-pent-3-en-1-yne	C5H6	2004-69-5	240.8	254.2	259.0(±3.0)	−4.8
(Z)-pent-3-en-1-yne	C5H6	1574-40-9	240.6	254.0	258.0(±3.0)	−4.0
(E)-penta-1,3-diene	C5H8	2004-70-8	60.3	73.1	75.8(±0.7)	−2.7
(Z)-penta-1,3-diene	C5H8	1574-41-0	82.9	95.7	82.7(±0.9)	13.0
penta-1,4-diene	C5H8	591-93-5	95.0	104.7	106.3(±1.3)	−1.6
pentane	C5H12	109-66-0	−156.0	−150.4	−146.8(±0.6)	−3.6
phenyl	C6H5	2396-01-2	326.6	326.6	337.0(±2.5)	−10.4
phenylbenzene	C12H10	92-52-4	201.5	174.2	180.3(±3.3)	−6.1
phenylethylbenzene	C14H14	103-29-7	176.0	135.1	135.6(±1.3)	−0.5
prop-1-ylbenzene	C9H12	103-65-1	20.7	5.6	7.8(±0.8)	−2.2
prop-2-ylbenzene	C9H12	98-82-8	20.6	−2.4	3.9(±1.1)	−6.3
propane	C3H8	74-98-6	−124.0	−108.0	−104.7(±0.6)	−3.3
(E)-propen-1-ylbenzene	C9H10	873-66-5	130.7	120.4	117.2(±10)	3.2
(Z)-propen-1-ylbenzene	C9H10	766-90-5	119.0	108.7	121.4(±10)	−12.7
propen-2-ylbenzene	C9H10	98-83-9	128.7	113.7	118.3(±1.4)	−4.6
propen-3-ylbenzene	C9H10	300-57-2	144.4	131.0	133.8(±1.1)	−2.8
propene	C3H6	115-07-1	0.2	18.6	20.2(±0.4)	−1.6
propyn-1-ylbenzene	C9H8	673-32-5	276.4	269.4	268.2(±2.2)	1.2
propyne	C3H4	74-99-7	170.6	189.7	185.4(±0.9)	4.3
tert-butylbenzene	C10H14	98-06-6	12.7	−25.0	−22.7(±1.4)	−2.3
tert-hexyne	C6H10	917-92-0	119.7	105.7	106.1(±1.5)	−0.4
toluene	C7H8	108-88-3	48.9	44.1	50.1(±1.1)	−6.0
trans-decalin	C10H18	493-02-7	−112.6	−175.7	−182.2(±2.3)	6.5
triphenylmethane	C19H16	519-73-3	353.0	278.4	276.1(±4.1)	2.3

G3MP2B3

In Figure 3, the corrections for the aliphatic species are examined. For each molecule, a value of 7.35 kJ/mol per methylene group (–CH₂–) was subtracted from the difference between ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$ for the calculated extrapolated G3MP2B3 value and the literature experimental value. The residuals are plotted in Figure 3 as a function of the number of –CH₂– groups in the molecule and correspond to a sum of the corrections for the remaining groups in the molecule. For example, the residuals for the n-alkanes (bottom curve at about −19 kJ/mol) correspond to the sum of the corrections for two CH₃– groups, the residuals for the 1-alkenes (second to bottom curve at about −14 kJ/mol) correspond to the sum of the corrections for a CH₃–, a ≡CH, and a =CH₂ group, and the residuals for the tert-alkanes (top curve at about +22 kJ/mol) correspond to the sum of the corrections for four terminal CH₃– groups plus one tertiary group –C(C)(C)–. The standard deviation for all of these groups (difference between the individual points and the corresponding line) was about 0.8 kJ/mol, which is comparable to the average uncertainty (about 1.1 kJ/mol) in the experimental values for this group of molecules.

Figure 3.

Plot of group corrections by chemical class for aliphatic compounds for G3MP2B3 results.

In Figure 4, corrections for the PAH species for each type of aromatic carbon are studied. We found a correction of −1.28 kJ/mol for each CbH group (benzene has six). Using the ortho-fused PAHs (e.g., naphthalene, anthracene), the residuals show that each Cf ortho-fused group (naphthalene has two) has a correction of about 16.4 kJ/mol. Using the ortho- and peri-fused PAHs (e.g., pyrene, coronene), the residuals show a correction of about 13.2 kJ/mol for each Cp group (pyrene has two). Using PAHs where one aromatic ring is “joined” or “linked” to another (e.g., biphenylene, fluoranthene in Table 1), we find a correction of about 10.8 kJ/mol for each “Cj” group (biphenylene has four). The resultant standard deviation for all these classes of PAHs is about 3 kJ/mol, which is comparable to the average uncertainties in the experimental values.

Figure 4.

Plot of group corrections by chemical class for PAHs for G3MP2B3 results.

Alkyl-substituted benzene compounds (e.g., 1,3-dimethyl-benzene, prop-1-ylbenzene) and benzocycloalkanes (e.g., indan, 1,4-dihydronaphthalene) were considered and group values (shown in Figure 4) of about 14.9 kJ/mol per CbC group (aromatic group terminated by carbon atom) and 4.1 kJ/mol per “–CH₂(Cb)–” group (a “–CH₂–” group connected to an aromatic carbon) were found. The resultant standard deviation is about 2 kJ/mol, which is comparable to the average uncertainties in the experimental values.

In short, our analysis shows that the group additivity approach for correcting the extrapolated B3LYP computed enthalpies of formation works very well for the aliphatic compounds, the PAHs, and the substituted PAHs. The standard deviation between our corrected G3MP2B3 results and the experimental results for our limited training set focusing on simple classes was on the order of 3 kJ/mol, whereas for all of the molecules, many with complicated functionalities, the standard deviation was on the order of 6 kJ/mol.

It was found that the G3B3 method accurately computes energies with little systematic differences for molecules with well-established heats of formation (that is, deviations between calculations and experiment were within experimental uncertainties). This was found to hold for a range of hydrocarbons including acyclic aliphatic (alkanes, alkenes, alkynes, etc.) and cyclic aliphatic (cycloalkanes, cycloalkenes, etc.) hydrocarbons. Although the data were fewer for substituted aromatic hydrocarbons and PAH species, small differences were found between enthalpies of formation calculated using the G3B3 method and experimentally derived values. Use of the G3MP2B3 method for unsaturated aliphatic hydrocarbons and aromatics, however, produced computed enthalpies of formation that were consistently lower than those derived from experimental measurements (i.e., from enthalpies of combustion, heats of sublimation, etc.). The differences were found to be small but systematic and on the order of (1.0 to 1.5) kJ/mol per carbon atom.

The G3B3 method is a composite ab initio model chemistry method applicable to a wide range of molecules with reported average errors^163,164 of about 3–6 kJ/mol depending on the test set of molecules. The G3B3 method, however, is practically limited (at present) to PAH molecules with 12–18 carbon atoms (depending upon whether symmetry can be imposed) due to computer memory, scratch disk space limitations, and computational time. As a result, it is necessary to compute energies for larger molecules using a less computationally expensive method. The G3MP2B3 method uses a single MP2 calculation to approximate the composite total energies in the G3B3 method that are determined from a set of MP2, MP4, and QCISD(T) energies using different basis sets. The G3MP2B3 method itself is practically limited (at present) to PAH species with up to about 16–24 carbon atoms, depending on symmetry.

Data from G3MP2B3 calculations are presented in Table 17 (benzenoid and PAH compounds) and Table 18 (other compounds). Additional data from G3MP2B3 calculations for which no experimental data are available are given in Table S4, where some comparison is made to nonexperimental literature values.

Table 17.

Corrected Values of the Enthalpy of Formation ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}$ (kJ/mol) Computed Using the G3MP2B3 model chemistry

name	formula	CAS registry no.	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{expt}\right)$	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{corr}\right)$ G3MP2B3	residual
Benzene/Alkyls
benzene	C6H6	71-43-2	82.9 ± 0.9	84.5	1.6
toluene	C7H8	108-88-3	50.1 ± 1.1	52.1	2.0
ethylbenzene	C8H10	100-41-4	29.8 ± 0.8	30.3	0.5
prop-1-ylbenzene	C9H12	103-65-1	7.8 ± 0.8	7.7	−0.1
prop-2-ylbenzene	C9H12	98-82-8	3.9	3.1	−0.8
but-1-ylbenzene	C10H14	104-51-8	−13.8 ± 1.3	−13.7	0.1
but-2-ylbenzene	C10H14	135-98-8	−17.4 ± 1.4	−16.9	0.5
isobutylbenzene	C10H14	538-93-2	−21.5 ± 1.4	−23.2	−1.7
tert-butylbenzene	C10H14	98-06-6	−22.7 ± 1.4	−25.1	−2.4
Benzene/Alkyls-Multi
1,2-dimethylbenzene	C8H10	95-47-6	19.0 ± 1.1	18.9	−0.1
1,3-dimethylbenzene	C8H10	108-38-3	17.2 ± 0.8	17.5	0.3
1,4-dimethylbenzene	C8H10	106-42-3	17.9 ± 1.0	17.9	0.0
1-ethyl-2-methylbenzene	C9H12	611-14-3	1.2 ± 1.2	−0.7	−1.9
1-ethyl-3-methylbenzene	C9H12	620-14-4	−1.9 ± 1.2	−2.9	−1.0
1-ethyl-4-methylbenzene	C9H12	622-96-8	−3.3 ± 1.5	−1.5	1.9
1,2-diethylbenzene	C10H14	135-01-3	−19.5 ± 2.2	−21.7	−2.2
1,3-diethylbenzene	C10H14	141-93-5	−21.6 ± 2.2	−24.1	−2.5
1,4-diethylbenzene	C10H14	105-05-5	−22.1 ± 2.2	−23.2	−1.1
1,2,3-trimethylbenzene	C9H12	526-73-8	−9.6 ± 1.3	−8.8	0.8
1,2,4-trimethylbenzene	C9H12	95-63-6	−13.9 ± 1.1	−15.3	−1.4
1,3,5-trimethylbenzene	C9H12	108-67-8	−15.9 ± 1.3	−14.9	1.0
Benzene/Cycloalkyls
1-cyclopropyl-2-methylbenzene	C10H12	27546-46-9	125.5 ± 2.2	126.8	1.3
cyclohexylbenzene	C12H16	827-52-1	−16.7 ± 1.5	−19.8	−3.1
Naphthalene/Alkyls
naphthalene	C10H8	91-20-3	150.6 ± 1.6	149.4	−1.2
1-methylnaphthalene	C11H10	90-12-0	116.9 ± 2.7	116.7	−0.2
2-methylnaphthalene	C11H10	91-57-6	116.1 ± 2.6	115.6	−0.5
1-ethylnaphthalene	C12H12	1127-76-0	98.0 ± 5.0	97.1	−0.9
1,8-dimethylnaphthalene	C12H12	569-41-5	108.8 ± 3.0	109.5	0.7
2,3-dimethylnaphthalene	C12H12	581-40-8	79.9 ± 2.0	82.3	2.4
2,6-dimethylnaphthalne	C12H12	581-42-0	78.7 ± 2.5	82.0	3.3
2,7-dimethylnaphthalene	C12H12	582-16-1	79.5 ± 0.6	82.0	2.5
1-ethyl-8-methylnaphthalene	C13H14	61886-71-3	98.1 ± 1.5	96.5	−1.6
1,4,5,8-tetramethylnaphthalene	C14H16	2717-39-7	81.6 ± 3.6	80.7	−0.9
Naphthalene/Hydro
1,2-dihydronaphthalene	C10H10	447-53-0	124.8 ± 3.3	124.4	−0.4
1,4-dihydronaphthalene	C10H10	612-17-9	137.5 ± 3.2	136.8	−0.7
1,2,3,4-tetrahydronaphthalene	C10H12	119-64-2	24.0 ± 3.2	22.9	−1.1
trans-decalin	C10H18	493-02-7	−182.2 ± 2.3	−186.2	−4.0
Benzene/Benzocyclo
benzocyclobutane	C8H8	694-87-1	199.4 ± 0.9	199.8	0.4
indan	C9H10	496-11-7	60.9 ± 2.1	59.5	−1.5
4,6-dimethylindan	C11H14	1685-82-1	−5.8 ± 1.7	−6.4	−0.6
benzocyclobutene	C8H6	4026-23-7	406.0 ± 17.0	408.3	2.3
indene	C9H8	95-13-6	161.2 ± 2.3	159.8	−1.4
Naphthalene/Naphthacyclo
cyclopropa[b]naphthalene	C11H8	286-85-1	435.0 ± 5.0	440.4	5.4
acenaphthylene	C12H8	208-96-8	263.2 ± 3.7	260.9	−2.3
acenaphthene	C12H10	83-32-9	156.8 ± 3.1	155.7	−1.1
Benzene/Alkenyls
ethenylbenzene	C8H8	100-42-5	146.9 ± 1.0	148.4	1.5
(E)-propen-1-ylbenzene	C9H10	873-66-5	117.2	117.0	−0.2
(Z)-propen-1-ylbenzene	C9H10	766-90-5	121.4	124.2	2.8
propen-2-ylbenzene	C9H10	98-83-9	118.3 ± 1.4	117.0	−1.3
propen-3-ylbenzene	C9H10	300-57-2	133.8 ± 1.1	134.3	0.5
Benzene/Phenyl
phenylbenzene	C12H10	92-52-4	180.3 ± 3.3	178.1	−2.2
benzylbenzene	C13H12	101-81-5	162.3 ± 2.3	163.6	1.3
2-phenyltoluene	C13H12	643-58-3	152.8 ± 1.5	149.7	−3.1
phenylethylbenzene	C14H14	103-29-7	135.6 ± 1.3	139.9	4.3
PAH/Misc
biphenylene	C12H8	259-79-0	417.2 ± 1.9	415.8	−1.4
anthracene	C14H10	120-12-7	230.9 ± 3.7	229.7	−1.2
phenanthrene	C14H10	85-01-8	201.4 ± 3.5	206.6	5.2
pyrene	C16H10	129-00-0	225.5 ± 4.3	226.5	1.0
chrysene	C18H12	218-01-9	268.5 ± 2.8	269.2	0.7
benzo[c]phenanthrene	C18H12	195-19-7	295.3 ± 9.1	291.1	−4.2
perylene	C20H12	198-55-0	317.4 ± 3.5	315.6	−1.8
6,6-diphenylfulvene	C18H14	2175-90-8	402.0 ± 15.0	396.0	−6.0
fluoranthene	C16H10	206-44-0	291.4 ± 4.0	282.4	−9.0
coronene	C24H12	191-07-1	300.9 ± 9.9	294.9	−6.0
fluorene	C13H10	86-73-7	176.7 ± 3.1	179.4	2.4
Deviations (>3σ Low)
3-phenyltoluene	C13H12	643-93-6	152.5 ± 8.0	145.3	−7.2
benz[a]anthracene	C18H12	56-55-3	290.3 ± 6.0	279.8	−10.5
1,2-diphenylbenzene	C18H14	84-15-1	282.8 ± 3.2	273.2	−9.6
azulene	C10H8	275-51-4	308.0	292.1	−15.9
Deviations (>3σ High)
9-methylfluorene	C14H12	2523-37-7	148.0 ± 1.1	155.0	7.0
4-phenyltoluene	C13H12	644-08-6	138.2 ± 2.9	145.9	7.7
(E)-1,2-diphenylethene	C14H12	103-30-0	233.7 ± 2.0	239.4	5.7
(Z)-1,2-diphenylethene	C14H12	645-49-8	245.9 ± 1.3	252.9	7.0
ethynylbenzene	C8H6	536-74-3	306.6 ± 1.7	318.2	11.6
propyn-1-ylbenzene	C9H8	673-32-5	268.2 ± 2.2	277.2	9.0
Deviations (Large Low)
naphthacene	C18H12	92-24-0	340.7 ± 3.9	316.2	−24.5
corannulene	C20H10	5821-51-2	458.7 ± 9.1	427.0	−31.7
triphenylmethane	C19H16	519-73-3	276.1 ± 4.1	212.9	−55.1
Deviations (Large High)
pyracyclene	C14H8	187-78-0	408.6 ± 5.0	426.7	18.1
pyracene	C14H12	567-79-3	174.1 ± 5.1	190.2	16.1
diphenylethyne	C14H10	501-65-5	385.0 ± 2.7	405.1	20.1
triquinacene	C10H10	6053-74-3	224.0 ± 4.2	239.3	15.3
benzyne	C6H4	462-80-6	446.0 ± 13.0	456.2	10.2

Table 18.

Corrected Values of the Enthalpy of Formation ${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K},\text{corr}}^{°}$ (kJ/mol) Computed Using the G3MP2B3 Model Chemistry

name	formula	CAS registry no.	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{expt}\right)$	${\mathrm{\Delta }}_{\mathrm{f}}{H}_{\text{298K}}^{°}\left(\text{corr}\right)$ G3MP2B3	residual
Alkanes, Normal
ethane	C2H6	74-84-0	−84.4 ± 0.4	−84.3	0.1
propane	C3H8	74-98-6	−104.7 ± 0.6	−105.0	−0.3
butane	C4H10	106-97-8	−125.9 ± 0.4	−126.1	−0.2
pentane	C5H12	109-66-0	−146.8 ± 0.6	−147.1	−0.3
hexane	C6H14	110-54-3	−167.2 ± 0.8	−168.1	−0.9
heptane	C7H16	142-82-5	−187.8 ± 0.8	−189.2	−1.4
Alkanes, Branched
isobutane	C4H10	75-28-5	−134.4 ± 0.4	−134.4	0.0
isopentane	C5H12	78-78-4	−153.7 ± 0.6	−153.3	0.4
2-methylpentane	C6H14	107-83-5	−174.3 ± 1.0	−174.3	0.0
2-methylhexane	C7H16	591-76-4	−195.0 ± 1.3	−195.7	−0.7
neopentane	C5H12	463-82-1	−167.9 ± 0.6	−169.0	−1.1
2,2-dimethylbutane	C6H14	75-83-2	−185.6 ± 1.0	−185.2	0.4
2,2-dimethylpentane	C7H16	590-35-2	−206.2 ± 1.3	−206.4	−0.2
Alk-1-enes
ethene	C2H4	74-85-1	52.6 ± 0.2	50.1	−2.5
propene	C3H6	115-07-1	20.2 ± 0.4	18.6	−1.6
but-1-ene	C4H8	106-98-9	0.0 ± 0.5	−0.9	−0.9
pent-1-ene	C5H10	109-67-1	−21.3	−22.4	−1.1
hex-1-ene	C6H12	592-41-6	−42.1 ± 1.2	−43.7	−1.6
Alk-1-enes, Branched
3-methylbut-1-ene	C5H10	563-45-1	−27.7 ± 1.2	−29.4	−1.7
3-methylpent-1-ene	C6H12	760-20-3	−47.0 ± 1.1	−51.5	−4.5
3-methylhex-1-ene	C7H14	3404-61-3	−68.2 ± 1.5	−72.7	−4.5
4-methylpent-1-ene	C6H12	691-37-2	−49.4 ± 0.7	−49.9	−0.4
3-ethylpent-1-ene	C7H14	4038-04-4	−69.5 ± 2.0	−73.1	−3.6
3,3-dimethylpent-1-ene	C7H14	3404-73-7	−78.5 ± 1.7	−81.5	−3.0
3,3-dimethylbut-1-ene	C6H12	558-37-2	−59.7 ± 2.0	−61.7	−2.0
Alk-n-enes, (E)
(E)-but-2-ene	C4H8	624-64-6	−11.2 ± 0.5	−11.4	−0.2
(E)-pent-2-ene	C5H10	646-04-8	−33.1 ± 1.3	−31.3	1.8
(E)-hex-2-ene	C6H12	4050-45-7	−51.7 ± 2.0	−53.0	−1.3
(E)-hex-3-ene	C6H12	13269-52-8	−49.3 ± 1.1	−51.4	−2.1
(E)-4-methylpent-2-ene	C6H12	674-76-0	−60.1 ± 1.5	−60.1	0.0
Alk-n-enes, (Z)
(Z)-but-2-ene	C4H8	590-18-1	−7.3 ± 0.5	−6.5	0.8
(Z)-pent-2-ene	C5H10	627-20-3	−28.0 ± 0.8	−26.0	2.0
(Z)-hex-2-ene	C6H12	7688-21-3	−47.9 ± 2.0	−47.8	0.1
(Z)-hex-3-ene	C6H12	7642-09-3	−46.9 ± 2.0	−45.7	1.2
Isoalkenes
2-methylprop-1-ene	C4H8	115-11-7	−17.5 ± 0.5	−17.3	0.2
2-methylbut-1-ene	C5H10	563-46-2	−35.1 ± 0.8	−35.1	0.0
2-methylpent-1-ene	C6H12	763-29-1	−58.0 ± 1.1	−56.7	1.3
2-methylbut-2-ene	C5H10	513-35-9	−41.5 ± 0.9	−40.8	0.7
Alk-1-ynes
ethyne	C2H2	74-86-2	226.7 ± 0.8	227.5	0.8
propyne	C3H4	74-99-7	185.4 ± 0.9	184.9	−0.5
but-1-yne	C4H6	107-00-6	166.1 ± 2.1	166.4	0.3
pent-1-yne	C5H8	627-19-0	144.3 ± 2.1	144.7	0.4
Alk-1-ynes, Branched
isopentyne	C5H8	598-23-2	136.4 ± 2.1	139.2	2.8
tert-hexyne	C6H10	917-92-0	106.1	106.1	0.0
Alk-2-ynes
but-2-yne	C4H6	503-17-3	148.0 ± 1.5	147.9	−0.1
pent-2-yne	C5H8	627-21-4	128.9 ± 2.1	128.9	0.0
Alkadienes
penta-1,4-diene	C5H8	591-93-5	106.3 ± 1.3	102.8	−3.5
hexa-1,5-diene	C6H10	592-42-7	85.0 ± 2.0	81.8	−3.2
Alkadienes, Conjugated
(E)-buta-1,3-diene	C4H6	106-99-0	108.8 ± 0.8	108.8	0.0
(E)-penta-1,3-diene	C5H8	2004-70-8	75.8 ± 0.7	76.8	1.0
Alkatrienes
(E)-hexa-1,3,5-triene	C6H8	821-07-8	168.0 ± 3.0	163.9	−4.1
(Z)-hexa-1,3,5-triene	C6H8	2612-46-6	172.0 ± 3.0	170.1	−1.9
Alkenynes
1-buten-3-yne	C4H4	689-97-4	295.0 ± 3.0	288.0	−7.0
(E)-pent-3-en-1-yne	C5H6	2004-69-5	259.0 ± 3.0	252.7	−6.3
(Z)-pent-3-en-1-yne	C5H6	1574-40-9	258.0 ± 3.0	254.4	−3.6
2-methylbut-1-en-3-yne	C5H6	78-80-8	259.0 ± 1.3	253.1	−5.9
Alkadiynes
butadiyne	C4H2	460-12-8	464.0	454.5	−9.5
1,5-hexadiyne	C6H6	628-16-0	416.0	412.3	−3.7
Alkendiynes
(E)-hex-3-en-1,5-diyne	C6H4	16668-68-1	538.0 ± 3.0	524.8	−13.2
(Z)-hex-3-en-1,5-diyne	C6H4	16668-67-0	541.8 ± 3.0	525.6	−16.2

The G3MP2B3 method was found to be nearly as accurate as the G3B3 method for computing energies for saturated hydrocarbons (unsigned differences of less than 0.3 kJ/mol). For unsaturated species, however, a systematic deviation was found that correlated well with the number of unsaturated sites in the molecule. Slight differences in the correlations (close to being statistically insignificant) were observed for different for different types of unsaturated sites (i.e., alkenes, alkynes, aromatics). Enthalpies of formation for unsaturated species computed using the G3MP2B3 method were consistently lower than those computed using the G3B3 method, on the order of 2 kJ/mol per unsaturated bond.

Aliphatic Hydrocarbons – G3MP2B3 (Corrected)

Enthalpies of formation for the aliphatic hydrocarbons (alkanes, alkenes, and alkynes) were computed using both the G3MP2B3 and G3B3 methods and compared to experimental values. These data are presented in Table 18 for about 60 compounds. Only the G3MP2B3 results are presented here because the differences between the G3MP2B3 and G3B3 values (after corrections) were small (less than 1.0 kJ/mol). This systematic study was used to develop corrections for unsaturated bonds in aliphatic hydrocarbons that could be used in making corrections to alkenyl- and alkynyl-substituted aromatic hydrocarbons.

It is observed that the G3MP2B3 enthalpies of formation are consistently lower than the experimental values. Using linear regression, we found best fit values for coefficients (in kJ/mol) to correct the G3MP2B3 values of 0.69n_H, −1.43n_C, −0.32n_Cd, and −0.50n_Ct, where n_H, n_C, n_Cd, and n_Ct are the number of hydrogen atoms, total number of carbon atoms, number of sp²-hybridized carbon atoms (in double bonds), and number of sp-hybridized carbon atoms (in triple bonds), respectively. Equivalently, one could use corrections of +2.02 kJ/mol and +2.38 kJ/mol per double and triple bond, respectively.

It was found that the enthalpies of formation computed using the G3MP2B3 method after applying systematic corrections agreed well with the experimental values. The average uncertainty in the (quoted) experimental enthalpies of formation for this set of molecules is about 1.3 kJ/mol. The standard deviation of the differences between the corrected G3MP2B3 and the experimental values is 2.1 kJ/mol for the entire set and drops to 1.5 kJ/mol if one excludes those molecules with more than one unsaturated bond.

Inspection of the differences by the class of compound, one can see that the residuals for the alkadienes, alkadiynes, and alkenynes are consistently negative. We note that many of the experimental values were determined from heats of hydrogenation in the liquid phase, and to compute a gas-phase enthalpy of formation it was assumed that heats of hydrogenation in the liquid and gas phases were the same (i.e., identical enthalpies of vaporization for the saturated and unsaturated compounds). This could introduce a small systematic uncertainty—likely less than 1.0–1.5 kJ/mol. We note that the computed (corrected) values are lower than the experimental values and little change is observed whether the G3MP2B3 or G3B3 method is used. This suggests that that there may be systematic uncertainties in the heat of hydrogenation measurements (or systematic defects in the G3 methods), because any higher level calculations would likely only lower than computed enthalpy of formation.

Aromatic Hydrocarbons – G3MP2B3 (Corrected)

In Table 17, we present a list of about 150 aromatic hydrocarbon compounds where we have computed enthalpies of formation using the G3MP2B3 method (and after applying systematic corrections). Using linear regression, we found best fit values for coefficients (in kJ/mol) to correct the G3MP2B3 values of 1.25n_CbH, 0.93n_Cf (or n_Cp, n_Cg), 1.00n_Cd, and 1.20n_Ct. Here, CbH denotes peripheral aromatic carbon atoms (terminated by hydrogen atoms); Cf, Cp, and Cg denote ortho-fused, ortho- and peri-fused, and fused aromatic carbons contained as part of a non-six-membered ring, respectively. Cd and Ct denote aliphatic carbon atoms part of double and triple bonds, respectively.

We compared the corrected G3MP2B3 values with experimental values. The average (reported) uncertainty in the experimental values was about 2.4–2.8 kJ/mol with most of the uncertainties in the range 1–6 kJ/mol. We found that there were about 60 compounds where the corrected G3MP2B3 values were within about 2.0 kJ/mol (standard deviation) of the experimental values and another approximately 10 compounds that were within about 6 kJ/mol (3 standard deviations) of the experimental values. This can be considered excellent agreement. There were about another 10 compounds where there were large differences between the computed and experimental values. In these cases, there maybe an error in the computed values or in the experimental values.

In summary, we find that the G3MP2B3 method (after applying systematic corrections for the hybridization of each carbon site) can be used to produce enthalpies of formation for both aliphatic and aromatic hydrocarbons, including PAHs and substituted-aromatic hydrocarbons.

DISCUSSION

The results presented in the previous section demonstrate that quantum chemistry can produce good data on the enthalpy of formation for PAH molecules, particularly when empirical corrections such as the group based model are used. Given that the reliability of the present methodology has been established, various uses of the data generated by this methodology may be considered. Three such uses are presented below: the value of predictions of enthalpies of formation where none are available, the limitations of group additivity, and use as a screening tool.

Prediction

Predicted values (for which no experimental determinations are known to be available) are given in Tables S2, S3, and S4. These values may be regarded as the best available values until such time as they are supplanted by experimental data, more accurate calculations, or improved models. As the methodology developed in this article is straightforward and economical to apply, this methodology may be used to produce predictions of enthalpies of formation for any number of PAHs with reasonable accuracy. If and when additional experimental data become available, or improvements are made to some portion of the model, the present data set can be updated to yield more accurate predictions. These predicted values may be used for creating thermodynamic tables for PAHs and in modeling studies. Though it is impossible to place uncertainties on the predicted enthalpies of formation derived in this article, the mean unsigned deviation and the root-mean-square deviation may serve as guides in the assessment of the data quality.

It is unsurprising that the G3MP2B3 results are better than the B3LYP results; the G3 model chemistries have been carefully tuned to produce good thermochemical data. However, when the group additivity based correction is applied to the extrapolated B3LYP results, the quality of these results is significantly improved. When the data in Tables 17 and 18 are compared to experimental values, the mean unsigned deviation (MUD) and root-mean-square deviation (RMSD) are 3.8 and 8.0 kJ/mol, respectively. If the molecules with larger errors in Table 17 (that is the last 21 values, or those in the last four sections) are removed, these values decrease to 1.9 and 3.0 kJ/mol, respectively. For the extrapolated and corrected B3LYP results, these values are 6.8 and 18.3 kJ/mol, respectively (4.5 and 6.2 kJ/mol, respectively, when the same data are removed). If nonbenzenoid/non-PAH data are considered (Table 18), values of the MUD and RMSD are 2.2 and 3.7 kJ/mol, respectively, for the G3MP2B3 data versus 4.6 and 6.2 kJ/mol for the B3LYP results. Similarly, for the benzenoid and PAH compounds (Table 17) with the compounds with larger errors removed as above, values of the MUD and RMSD are 1.7 and 2.1 kJ/mol, respectively, for the G3MP2B3 results and 4.4 and 5.7 kJ/mol, respectively, for the B3LYP results. It is seen then that the deviations of the B3LYP set are approximately twice that of the G3MP2B3 set, a very good result considering that the B3LYP results require significantly less computer time and resources.

Group Additivity Based Empirical Corrections

Thermochemical data for a number of PAH species (and other hydrocarbons) have been estimated using group additivity methods (originally developed by Benson⁷⁵ and Cohen^76,77). For PAHs, an additivity approximation for neighboring groups may not be correct, because resonance stabilization energies are longer range, and ring strains cannot be readily predicted. Thus, such estimates may have high uncertainties, coupled with the fact that thermochemical data for reference species used to develop the groups may be uncertain. For many PAHs, there are significant uncertainties, on the order of 5–15) kJ/mol, in the condensed-phase enthalpies of formation and enthalpies of sublimation used to derived gas-phase enthalpies of formation.

The combination of quantum chemistry methods with group additivity corrections is particularly powerful, as seen in the present work. Many group additivity methods lack terms to account for important chemical effects such as the difference in (E) and (Z) isomers, the difference in ortho-, meta-, and para- substitution on benzene rings, and steric effects. These effects (and others) are all included in the quantum chemistry calculation, obviating the need for specific group additivity terms to account for specific chemistries. If the overall error can be ascribed in whole or in part to systematic deviations of specific chemical groups, then the group additivity model is appropriate for correcting the quantum chemistry results. The quality of the underlying quantum chemistry results will ultimately dictate the limits of the correction. In general, calculations made with larger basis sets, and more accurate or inclusive correlation methods will have smaller and more regular deviations from the correct experimental values. Such high-quality quantum chemistry results will typically result in a better fitting of the correction terms and thus in a more accurate set of results. This was seen in the present study wherein the G3MP2B3 results were corrected with a simpler model (fewer terms) and yielded smaller deviations from experiment.

Ultimately, the procedures used in the present work are limited by the uncertainty of the experimental data used to compute the model corrections. This points to the need for improved data for certain key compounds, and to the need for new measurements on PAH compounds.

Empirically-Corrected Quantum Calculations for Screening

Given the reliability that has been established for the present results, the use of these results as a check on the current experimental value is suggested. During the fitting of the correction term, it became apparent that including certain PAH compounds (e.g., azulene, naphthacene, pyracyclene, and triquinacene) in the fits reduced the overall quality of the results. (Note that an enthalpy of formation for naphthacene of 73.9 kcal/mol has recently been given by Karton and Martin using the W1–F12 ab initio computational thermochemistry method.¹⁶⁵) This result strongly suggests that some or all of the compounds may have substantial errors beyond their uncertainty limits, and a reevaluation of the reported enthalpies of formation is warranted. Such analysis might also be applied to new predictions based on group additivity or quantum chemistry techniques.

Molecules with Large Deviations

Computed enthalpies of formation for four sets of molecules are shown in Table 19. The first set of molecules have computed enthalpies of formation (after corrections) that differ significantly from the experimental values, but the lower level B3LYP and the higher level G3MP2B3 agree very well. This suggests (but does not prove) that the experimental values may be in error. Of particular concern are naphthacene, pyracene, and pyracyclene, which are highly prototypical molecules. Naphthacene is a simple molecule in the important basic series benzene, naphthalene, anthracene, and naphthacene. Pyracene and pyracyclene are representative of “ace” (ethylene) bridge aromatic hydrocarbons.

Table 19.

Comparison of Enthalpies of Formation at 298 K (kJ/mol) Computed Using the Corrected G3MP2B3 and Corrected B3LYP Methods

molecule	formula	CAS registry no.	expt	G3MP2B3 (corr)	dev	B3LYP (corr)	dev
Set 1
naphthacene	C18H12	92-24-0	340.7(±3.9)	316.2	−24.5	310.5	−30.2
benz[a]anthracene	C18H12	56-55-3	290.3(±6.0)	279.8	−10.5	277.1	−13.2
benzo[b]triphenylene	C22H14	215-58-7	331.0(±11)			348.0	17.0
pyracene	C14H12	567-79-3	174.1(±5.1)	190.2	16.1	191.4	17.3
pyracyclene	C14H8	187-78-0	408.6(±5.0)	426.7	18.1	438.2	29.6
Set 2
9-methylfluorene	C14H12	2523-37-7	148.0(±1.1)	155.0	7.0	150.9	2.9
(Z)-1,2-diphenylethene	C14H12	645-49-8	245.9(±1.3)	252.9	7.0	245.9	3.8
4-phenyltoluene	C13H12	644-08-6	138.2(±2.9)	145.9	7.7	142.9	4.7
diphenylethyne	C14H10	501-65-5	385.0(±2.7)	405.1	20.1	389.0	4.0
propyn-1-ylbenzene	C9H8	673-32-5	268.2(±2.2)	277.2	9.0	269.4	1.2
ethynylbenzene	C8H6	536-74-3	306.6(±1.7)	318.2	11.6	314.1	7.5
Set 3
3-phenyltoluene	C13H12	643-93-6	152.5(±8.0)	145.3	−7.2	143.3	−9.2
(E)-1,2-diphenylethene	C14H12	103-30-0	233.7(±2.0)	239.4	5.7	233.7	−5.1
Set 4
1,2-diphenylbenzene	C18H14	84-15-1	282.8(±3.2)	273.2	−9.6	290.5	7.7
corannulene	C20H10	5821-51-2	458.7(±9.1)	427.0	−31.7	498.5	39.8

The second set of molecules have computed enthalpies of formation (after corrections) from the lower level B3LYP method that agree well with the experimental values (deviations on the order of 4 kJ/mol), but the deviations from experiment for the higher level (and corrected) G3MP2B3 method are somewhat larger (on the order of 10 kJ/mol). This good agreement (for the B3LYP) method suggests that the experimental values are good but raises the question why the higher level G3MP2B3 method has higher deviations particular the alkynyl-substituted compounds (ethynyl- and propynylbenzene).

The third set of molecules have computed enthalpies of formation (after corrections) that differ from the experimental values by a relatively modest amount (6–8 kJ/mol) for both computational methods, but the experimental uncertainties and the deviations suggested that experimental (or computational) values with tighter uncertainties would be in order, and worthy of further experimental or computational studies. Of particular concern are fluoranthene and coronene, which are prototypical molecules. Coronene is a good reference for large PAHs and fluoranthene for five-membered ring fused systems.

The fourth set of molecules have substantial deviations between the computational methods and the experimental values, and further investigations are warranted. Of particular interest is corannulene, a highly strained “bowl-like” molecule, where there is a large difference between the computed methods.

In Table 19, there are a number of molecules with significant differences between the computed and experimentally derived enthalpies of formation. We will discuss several of them here. We believe in some cases that the experimental values may be in error whereas in others the computations may be in error.

There is only one reliable measurement for the enthalpy of formation of naphthacene. This value is about 25 kJ/mol higher than the G3MP2B3 computed value. The computed values for the series benzene, naphthalene, anthracene, and naphthacene appear to follow a simple trend, an incremental value of about 77 kJ/mol per each additional benzo ring with the difference in predicted and computed on the order of about 4–6 kJ/mol. The experimental values also follow this trend, except the value for naphthalene is about 25–30 kJ/mol higher. The consistency between the calculated and the “group additivity” incremental approach suggests that the experimental enthalpy of formation for naphthacene may be in error. There is no reason why an incremental approach should not be able to roughly predict the trend in this homologous series.

There is only one measurement for the enthalpy of formation of benz[a]anthracene and it is about 11 kJ/mol higher than the G3MP2B3 value. There are a number of enthalpies of combustion for similar molecules by Magnus and co-workers.¹⁶⁶ One of them is a determination for naphthacene that differs from the other measurement by about 50–60 kJ/mol. In addition, they also measured enthalpies of sublimation for a number of PAHs including benzo[a]anthracene, phenanthrene, triphenylene, and naphthacene that are lower than values measured by other groups by about 8–14 kJ/mol. This is on the order of the difference observed here.

There have been several determinations of the enthalpy of formation of pyracene and pyracyclene. These values are consistently lower than the computed G3MP2B3 value by about 15–20 kJ/mol. For these molecules, we believe that the computations may be in error, in part because the computed energies are higher. The structures of these molecules are influenced by the strain due to five-membered rings in the plane that would prefer to have asymmetric (non-D_2h symmetry), puckered, or skewed structures. However, loss of planarity and symmetry would destroy the energy gained by aromatic/delocalized electrons. It is possible that the structures we computed with low-level B3LYP/6-31G(d) calculations may not reflect the true structures. Furthermore, these molecules have a significant number of low frequency and anharmonic modes that are likely coupled to other modes in the molecules.¹⁶⁷ The difference between computed and experimental enthalpies of formation could simply be that our simple zero point energy (ZPE) correction using computed harmonic frequencies may be incorrect; a 15 kJ/mol difference corresponds to about 1300 cm⁻¹.

The G3MP2B3 and B3LYP computed enthalpies of formation for corannulene differ substantially form the available experimentally derived values (which appear to be very reliable). Given the high strain in this molecule, it is very possible that the computed geometries may not reflect the true structures and vibrational partition functions.

There are several other molecules in Table 19 where there are some differences between the computed and experimental values. One thing to note is that several of them involve aromatic structures modified by sp² (triple bond) substitution. Given the conjugation of the unsaturation with the aromatic ring, there may be unusual effects that could be reflected in both the computations and the experimental determinations. Interestingly, the B3LYP computed values seem to be more consistent with the experimental values than the higher-level G3MP2B3 calculations.

Without a detailed, systematic study of these molecules to explore the reasons where there are significant differences, we cannot draw any conclusion and simply propose the possible rational as given above.

Uncertainties in G3MP2B3 (Corrected) Enthalpies of Formation

We now provide a short discussion of the overall uncertainties in the G3MP2B3 (empirically corrected) enthalpies of formation of the PAHs, paying attention to several particular prototypical molecules.

The (corrected) enthalpy of formation for fluoranthene of 282–283 kJ/mol agrees (within about 1 kJ/mol) with the recommended value by Monte et al.¹⁶⁸ but differs from that of Roux et al.² by about 9 kJ/mol (see experimental values in Table 13). Given the uncertainty in the experimental values (about 4 kJ/mol) and the uncertainty in the computed value (estimated 6–8 kJ/mol), overall the agreement between experimental and computed values is good.

We computed G3MP2B3 (corrected) enthalpies of formation for ethynylbenzene and propyn-1-ylbenzene of 308–318 and 267–277 kJ/mol depending on the empirical fit parameters employed, respectively. These values agree within about 2–10 kJ/mol of the experimental values of 306.6 ± 1.7 and 268.2 ± 2.3 kJ/mol, respectively. Consequently, we consider that there is fair-to-good agreement between experimental and computed values. We computed a G3MP2B3 (corrected) enthalpy of formation of about 394–405 kJ/mol for diphenylethyne which is about 10–20 kJ/mol higher (depending on the empirical fit parameters employed) than the experimental value of 385.0 ± 2.7 kJ/mol derived from the heat of hydrogenation measurements by Davis et al.¹⁶⁹ and about 0–10 kJ/mol lower than the 404 ± 5 kJ/mol derived from the measurements by Flitcroft and Skinner¹⁷⁰ (see experimental values in Table 13). The gas-phase enthalpy of formation for this molecule was derived from the heat of hydrogenation of the liquid and solid phases in the Davis et al.¹⁶⁹ and Flitcroft and Skinner¹⁷⁰ experiments, respectively, and this procedure using the condensed-phase heats of hydrogenation introduces some uncertainties. The substantial difference between these two experimental values suggests that both the experimental and computational values should be reexamined.

We find that the G3MP2B3 (corrected) enthalpy of formation for benzyne is dependent upon how one treats the unsaturation in the molecule (modified aromatic or a cyclic compound with triple and double bonds). We find computed values that differ from the experimental value of 446 ± 13 kJ/mol by about 2–10 kJ/mol. Given the uncertainty in the experimental value, the agreement is good.

Overall, a good measure of the minimum uncertainty in the computed enthalpies of formation for the PAHs can be estimated from the small (three or four fused rings) PAHs anthracene, phenanthrene, chrysene, benzo[c]phenanthrene, and benzo[a]anthracene. The differences between the calculated and experimental values are −0.3 ± 3.7, +6.1 ± 3.5, +2.5 ± 2.8, −2.4 ± 9.1, and −8.8 ± 6.0 kJ/mol, respectively, where the uncertainties (±) given here are the experimental values. (See Tables 13 and 17 for the specific experimental and computed values.) These data suggest an uncertainty (2σ ≈ 95% coverage) in the enthalpies of formation of the small PAHs of about 3–4 kJ/mol, largely dominated by the uncertainties in the experimental values. Our estimate for the uncertainties (2σ ≈ 95% coverage) in the larger PAHs (e.g., coronene) rises to about 6–9 kJ/mol, due to the combined uncertainties in the experimental values and the fitted empirical corrections to the G3MP2B3 values.

CONCLUSION

In this article, an approach for computing enthalpies of formation for PAH and related compounds from relatively inexpensive ab initio calculations and using a chemical group based correction scheme has been presented. The values computed in this manner are compared to the available experimental data, to the results of higher-level G3B3 and G3MP2B3 calculations, and to other empirical models. The application of an energy extrapolation scheme significantly improved the quality of the results, and the application of a group based correction scheme produces results that are in good agreement with the available experimental data. This extrapolation–correction model is then used to predict enthalpies of formation for 810 compounds for which no experimental data are known to be available (or for which the experimental data was deemed unreliable). The G3B3 and G3MP2B3 methods are interesting in their own right, and the present study clearly establishes their reliability for predicting the thermochemistry of PAHs, particularly after a simple correction is applied. This collection of data represent perhaps the best-known values of the enthalpies of formation for PAH compounds (including substituted PAHs). The extrapolation–correction model is generally applicable to other PAHs and substituted PAH molecules and should be valuable for predicting enthalpies of formation for such compounds with reasonable accuracy.