Abstract
In this paper, optimum wing bending and torsion deformations are explored for a mission adaptive, highly flexible morphing aircraft. The complete highly flexible aircraft is modeled using a strain-based geometrically nonlinear beam formulation, coupled with unsteady aerodynamics and 6-dof rigid-body motions. Since there are no conventional discrete control surfaces for trimming the flexible aircraft, the design space for searching the optimum wing geometries is enlarged. To achieve high performance flight, the wing geometry is best tailored according to the specific flight mission needs. In this study, the steady level flight and the coordinated turn flight are considered, and the optimum wing deformations with the minimum drag at these flight conditions are searched by utilizing a modal-based optimization procedure, subject to the trim and other constraints. The numerical study verifies the feasibility of the modal-based optimization approach, and shows the resulting optimum wing configuration and its sensitivity under different flight profiles.
I. Introduction
THE improvement of aircraft operation efficiency needs to be considered over the whole flight plan, instead of a single point in the flight envelop, since the flight missions and conditions might vary during the flight. Therefore, it is natural to employ morphing wing designs so that the aircraft can be made adaptive to different flight missions and conditions. At the advent of recent development in advanced composites as well as sensor and actuator technologies, in-flight adaptive wing/aircraft morphing is now becoming a tangible goal. With the morphing technologies, aircraft performances (e.g., range, endurance, maneuverability, gust rejection, etc.) can be passively or actively tailored to different flight conditions, while maintaining the flight stability. As an example, in Refs. [1, 2], the roll performance of a highly flexible aircraft was tailored by using the piezoelectric actuations (e.g., micro-fiber composites) embedded in the skin for wing warping (bending and torsion) control. Traditionally, the discrete control surfaces were used to re-distribute the aerodynamic loads along the wing span during the flight, so as to tailor the aircraft performance. However, the deflection of discrete surfaces, while providing the desired lift control, may increase the aerodynamic drag. To address this issue, different techniques had been applied to explore more efficient approaches to control the wing loading, improve the aircraft performance, and reduce the drag. An effective alternative has been to introduce conformal wing/airfoil shape changes for the aerodynamic load control. FlexSys Inc., with the support from AFRL, developed a compliant trailing edge concept in their Mission Adaptive Compliant Wing (MACW) project [3]. With a piezoelectric actuator driving the compliant morphing mechanism, it was shown in Ref. [4] that the continuous wing trailing edge was able to deflect about ±10°. In Ref. [5], a cantilever wing platform was designed and experimentally tested for the camber changes with active piezoelectric actuations. In rotorcraft application, the optimal airfoil design was studied for the control of airfoil camber [6]. Recently, in an effort to achieve a low-drag, high-lift configuration, a flexible transport aircraft wing design utilizing the Variable Camber Continuous Trailing Edge Flaps (VCCTEFs) to vary the wing camber is being studied at NASA Ames Research Center. The studies showed that highly flexible wing, if elastically shaped in-flight by active control of wing twist and bending, may improve aerodynamic efficiency through drag reduction during cruise and enhanced lift performance during take-off and landing [7]. Nguyen and Ting identified the flutter characteristics of the wing using a linear beam formulation and vortex-lattice aerodynamics [8]. Their study also indicated the reduction of flutter boundary of the wing with increased structural flexibility.
In general, the airborne intelligence, surveillance, and reconnaissance (ISR) missions [9] or civilian atmospheric research [10] require the vehicle platforms with high-aspect-ratio wings, resulting in highly flexible aircraft. This is because the high-altitude, long endurance (HALE) flights of these aircraft demand for greater aerodynamic performance. The improvement of the flight performance of the aircraft may be achieved through the high-aspect-ratio wings, as well as the lightweight, highly flexible structures. The high flexibility associated with the wing structures brings some special requirements to the formulation applied to the analysis. From the previous investigations [11], the slender wings of highly flexible aircraft may undergo large deformations, although still under small strain, under normal operating loads, exhibiting geometrically nonlinear behavior. The structural dynamic and aeroelastic characteristics of the aircraft may change significantly due to the large deflections of their flexible wings. In addition, highly flexible aircraft usually see the coupling between the low-frequency elastic modes of their slender wings and the rigid-body motions of the complete aircraft [11–15]. Therefore, the coupled effects between the large deflection due to the wing flexibility and the aeroelastic/flight dynamic characteristics of the complete aircraft must be properly accounted for in a nonlinear aeroelastic solution.
In addition to the aerodynamic platform, the lightweight structure technology is also a critical enabling path in developing high-performance aircraft. The trend in aircraft industries has been to increase the usage of composite materials in overall aircraft structure to save mass and reduce fuel burn. For example, the structure of Boeing 787 Dreamliner consists of 80% composites by volume and 50% composites by weight. More recently, a novel aerostructure concept is under development by utilizing lattice-based composite materials and discrete construction techniques to realize high stiffness-to-density ratio structures [16]. Furthermore, this digital construction of aerostructure can potentially offer great adaptability for varying flight missions and conditions.
The high flexibility and large wing deformation may be pro-actively utilized to improve the aircraft performance. The active aeroelastic tailoring techniques would allow aircraft designers to take advantage of the wing flexibility to create the desired wing load distribution according to the mission requirement, so as to improve overall aircraft operating efficiency and performance, without using the traditional discrete control surfaces. In doing so, one needs to understand the optimum wing bending, torsion, and camber deformations at various flight profiles. Subsequently, the optimum wing deformations will need to be integrated with on-board flight control systems to ensure the desired wing shape is maintained at designated flight condition.
The objective of this paper is to explore the optimum wing bending and torsion deformations (camber is not considered in the current study) of a highly flexible aircraft in seeking the most efficient flight configuration at any given flight scenario. Without modeling the built-up wing structures, a homogenized set of aircraft properties will be used as inputs to a strain-based nonlinear aeroelastic formulation for the complete aircraft modeling. This formulation has been successfully used to design and analyze different highly flexible aircraft configurations [14, 15, 17]. To find the optimum wing shape among the complex space of the wing deformations, a modal-based optimization scheme will be developed, which satisfies the required trimming condition of the aircraft.
II. Theoretical Formulation
Solutions of the coupled aeroelasticity and flight dynamics using the strain-based geometrically nonlinear beam formulation have been discussed by Su and Cesnik [14, 15, 18]. An introduction of the strain-based aeroelastic equations is presented here, followed by the modal-based optimization formulation for searching the optimum wing geometries under different flight conditions.
A. System Frames
As shown in Fig. 1a, a fixed global (inertial) frame G is defined. A body frame B(t) is then built in the global frame to describe the vehicle position and orientation, with Bx(t) pointing to the right wing, By(t) pointing forward, and Bz(t) being cross product of Bx(t) and By(t). The position and orientation b and the time derivatives and of the B frame can be defined as
| (1) |
where pB and θB are body position and orientation, both resolved in the body frame B. Note that the origin of the body frame is arbitrary in the vehicle and it does not have to be the location of the vehicle’s center of gravity.
Fig. 1. Basic beam reference frames.

Within the body frame, a local beam frame w is built at each node along the beam reference line (Fig. 1b), which is used to define the nodal position and orientation. Vectors wx(s,t), wy(s,t), and wz(s,t) are bases of the beam frame, whose directions are pointing along the beam reference axis, toward the leading edge (front), and normal to the beam surface, respectively, resolved in the body frame. s is the curvilinear beam coordinate.
B. Elements with Constant Strains
In Ref. [19], a nonlinear beam element has been introduced to model the elastic deformation of slender beams. Strain degrees (curvatures) of the beam reference line are considered as the independent variables in the solution. The strain-based formulation allows simple shape functions for the element. Constant-value functions are used here. Thus, the strain vector of an element is denoted as
| (2) |
where εx is the extensional strain, κx, κy, and κz are the twist of the beam reference line, bending about the local wy axis, and bending about the local wz axis, respectively. The total strain vector of the complete aircraft is obtained by assembling the global strain vector:
| (3) |
where εei denotes the strain of the ith element. Transverse shear strains are not explicitly included in this equation. However, shear strain effects are included in the constitutive relation [20]. Complex geometrically nonlinear deformations can be represented by such a constant strain distribution over each element.
C. Equations of Motion
The equations of motion of the system are derived by following the principle of virtual work extended to dynamic systems (equivalent to Hamilton’s Principle). The total virtual work done on a beam is found by integrating the products of all internal and external forces and the corresponding virtual displacements over the volume, which is given as
| (4) |
where f represents general forces acting on a differential volume. This may include internal elastic forces, inertial forces, gravity forces, external distributed forces and moments, external point forces and moments, etc. δu is the corresponding virtual displacement. Following the same process described in Ref. [14], the elastic equations of motion are eventually derived as
| (5) |
where the components of the generalized inertia, damping, and stiffness matrices are found in Refs. [14, 15]. The generalized force vector is
| (6) |
where N, BF, and BM are the influence matrices for the gravity force, distributed forces, and distributed moments, respectively, which come from the numerical integration. The generalized force vector involves the effects from initial strains , gravity fields g, distributed forces , distributed moments , point forces , and point moments . The aerodynamic forces and moments are considered as distributed loads. The thrust force is considered as a point follower force. All the Jacobians can be obtained from the nonlinear strain-position kinematical relationship discussed in Refs. [13, 19].
D. Unsteady Aerodynamics
The distributed loads and in Eq. (6) are divided into aerodynamic loads and user-supplied loads. The unsteady aerodynamic loads used in the current study are based on the two dimensional (2-D) finite-state inflow theory provided in Ref. [21]. The theory calculates aerodynamic loads on a thin airfoil section undergoing large motions in an incompressible inviscid subsonic flow. The lift, moment, and drag of a thin 2-D airfoil section about its midchord are given by
| (7) |
where bc is the semichord and d is the distance of the midchord in front of the reference axis. The quantity is the angle of attack that consists of the contribution from both the pitching angle and the unsteady plunging motion of the airfoil. The different velocity components are shown in Fig. 2.
Fig. 2.

Airfoil coordinate systems and velocity components.
The inflow parameter λ0 accounts for induced flow due to free vorticity, which is the summation of the inflow states λ as described in Ref. [21] and given by
| (8) |
The aerodynamic loads about the midchord (as defined above) will be transferred to the wing elastic axis and rotated into the body frame for the solution of the equations of motion. To transfer the loads, one may use
| (9) |
Furthermore, the aerodynamic loads are rotated as
| (10) |
where is the transformation matrix from the local aerodynamic frame to the body frame. This matrix is determined by using the instantaneous nodal orientations and has to be updated from the kinematics at each solution steps and sub-steps.
The optimization solutions will search for the optimum wing geometry based on the steady flight performances. So the unsteady effects of the aerodynamic loads are not important at this stage. However, the unsteady effects should be included when the stability is considered in the optimization. In addition, the continuous time-domain simulations and the flight control development for the mission adaptive flights should also consider the unsteady effects.
E. Modal Representation of Aircraft Deformation
The strain field along the beam coordinate s is approximated by the combination of linear normal modes
| (11) |
where Φi are the linear normal strain modes of the aircraft and ηi are the corresponding magnitudes of the modes. To obtain the normal modes in strain, one may use the strain-based finite-element equation (Eq. 5) and perform an eigenvalue analysis with the stiffness and inertia matrices. As the stiffness matrix in Eq. (5) is singular, one can find six zero eigenvalues, which correspond to the free-free rigid-body modes. The remaining eigenvalues are the frequencies for the coupled elastic and rigid-body modes. For the eigenvectors of these coupled modes, they generally take the following form
| (12) |
where ΦF and ΦB denote the elastic and rigid-body components of the modes, respectively. Since the modal approximation in Eq. (11) only requires the elastic deformation, the rigid-body component of these modes are removed, i.e.,
| (13) |
One more note about the normal modes is that they are not necessarily obtained about the undeformed shape. One can find normal modes about a geometrically nonlinear deformation. In doing so, the nonlinear system equations should be linearized about the deformation.
F. Trimming of Aircraft
Trim solution can be performed for both traditional aircraft with discrete control surfaces and the deformable configuration without discrete surfaces. In this study, the aircraft is trimmed at either 1-g steady level flight or steady coordinated turn. For the steady level flight, the force balancing equation is
| (14) |
which includes the contributions from the aerodynamic loads on the main lifting surfaces (a), gravity (g), thrust (t), and additional loads from control input (u) in the longitudinal direction. For steady turns, the following balancing equation is used:
| (15) |
where the only non-zero inertial term (with superscript i) is the centrifugal force pointing to the center of the turn path, which is given by
| (16) |
where MA is the total mass of the aircraft, V is the turn speed, and R is the radius of the turn path. The roots of Eq. (14) or (15) give the trimmed state of the aircraft. For traditional aircraft with discrete control surfaces, the roots of Eq. (14) are searched over the solution space using the body angle of attack αB, the elevator deflection δe, and the thrust T. A Newton-Raphson scheme is used to search the roots. Figure 3 illustrates the entire trim procedure of level flight. For the trim of turns, the roots of Eq. (15) are searched over the solution space using the body pitch angle αB, the bank angle φB, the aileron deflection δa, the elevator deflection δe, the rudder deflection δr, and the thrust T. It has to be noted that when evaluating the perturbation of the force balancing function f and the Jacobian J = Δf/Δs, the static elastic equilibrium equation has to be satisfied, which can be deduced from Eq. (5) and given as
| (17) |
where the generalized loads on the right side of the equation correspond to the physical loads in Eq. (14) or (15).
Fig. 3.

Flowchart of trim of level flight with defined control parameters.
To trim the flexible wing aircraft (without control surfaces) follows the similar procedure. However, the control parameters of the discrete control surfaces (δa, δe, and δr) should be replaced by a new type of input. In this case, the control loads will be used to maintain a specific wing deformation but not to generate forces to balance the aircraft. Therefore, the corresponding terms with superscript u should be removed from Eqs. (14) and (15), while being kept in Eq. (17) for the equilibrium of the aircraft deformation. Since the specific control mechanism is yet to be developed, the load Ru in Eq. (17) for the new aircraft configuration is not available, even if the optimum wing shape is found.
The focus of this paper is to explore the optimum wing geometry for better in-flight performance. To facilitate the search for the optimum wing shape, a modal-based approach will be utilized, which makes use of the magnitudes of natural modes in the search process.
G. Optimization Problem
Because of the large design space associated with the flexible wing aircraft, the optimum trimmed wing geometry is explored by a modal-based optimization process. If the wing deformation is represented by a truncated series of the natural modes
| (18) |
Then the design variables of the optimization problem become
| (19) |
From flight mechanics, it is evident that the minimum drag is associated with many important flight performance metrics. For example, the flight range of a battery-powered, propeller-driven airplane is derived as
| (20) |
where the weight of the aircraft W is considered constant, V is the flight speed, ηt is the propulsion efficiency, and C represents the discharge of the capacity of the battery. The maximum range requires minimum D/L ratio, or the minimum drag with a constant lift. Therefore, the objective function in the optimization problem is defined as the drag force of the corresponding flight condition, given as
| (21) |
Several constraints have to be satisfied by the optimum solution. The first is the trim of the aircraft:
| (22) |
Again, the above condition is for the trim of general flights. It can be reduced for longitudinal flights. Ideally, it is necessary that the elastic equilibrium Eq. (17) be satisfied by the optimization solution. Assume an optimum wing deformation is identified and one can design a controller with enough control authority to satisfy Eq. (17). The problem now becomes how much of the control authority is required to maintain the optimum shape. To place a limit on the required control authority, the constraint of the strain energy associated with the wing deformation is considered:
| (23) |
where U(x) is the strain energy of the optimum wing shape and U0 is the strain energy of a shape that is known to be exact or close to at a trimmed condition. Note that satisfying C2 does not guarantee the elastic equilibrium equation Eq. (17), but at least it avoids some unrealistic solutions that demand extremely large control power. More details about the use of C2 will be provided in the numerical study. Furthermore, some variables should also be constrained within their search limits, such as
| (24) |
| (25) |
and
| (26) |
The optimum solutions can be obtained by using Matlab’s “fmincon” command. It is important to note that in order to avoid numerical instability, the optimization variable x must be properly scaled. For instance, the magnitude of higher-order modes may be orders of magnitude smaller than that of lower-order modes, and such difference in magnitude can cause numerical instability when formulating the gradient-based optimization solutions. Therefore, to improve numerical accuracy, the optimization variables xi are all scaled with the scalar quantities dxi according to
| (27) |
where dxi are determined based on the initial condition of the optimization, i.e.,
| (28) |
The objective function and constraints are also scaled accordingly by using the reference values from the initial shape, which also helps to improve the stability of the numerical solution.
III. Numerical Results
In this section, a highly flexible aircraft model is considered for the numerical study. The aircraft model is described first, followed by the introduction of linear modal analysis. The search for the optimum wing geometries under different flight conditions is based on the natural modes. Different optimum solutions are also compared in the study.
A. Description of the Baseline Highly Flexible Aircraft
The physical and geometrical properties of the aircraft members are shown in Fig. 4 and Table 1. The distance between the main wings and the tails is 10 m. The boom is considered rigid and massless. To keep the static stability, a point mass of 30 kg is attached to the boom at 0.75 m ahead of the main wings. The thrust force is applied at 2.5 m behind the main wings, which always points along the boom. Three sets of control surfaces are defined for the baseline vehicle, as illustrated in Fig. 4. The elevators are defined on the horizontal tails, running from the 1/3 span to the tip of the member. The rudder is defined on the vertical tail, also running from the 1/3 span to the tip of the member. The ailerons are defined on the main wings, running from 70% to 90% span of the member. All the control surfaces occupy 20% chord of the corresponding aircraft member.
Fig. 4.

Geometrical data of the baseline highly flexible aircraft.
Table 1.
Properties of the baseline highly flexible aircraft
| Wings | Tails | ||||
|---|---|---|---|---|---|
| Span | 16 | m | Span of horizontal tail | 2.5 | m |
| Chord | 1 | m | Span of vertical tail | 1.6 | m |
| Incidence angle | 2 | deg | Chord of tails | 0.5 | m |
| Sweep angle | 0 | deg | Incidence of horizontal tail | −3 | deg |
| Dihedral angle | 0 | deg | Incidence of vertical tail | 0 | deg |
| Beam ref. axis (from l.e.) | 50% | chord | Sweep of horizontal tail | 0 | deg |
| Cross-sectional c.g. (from l.e.) | 50% | chord | Sweep of vertical tail | 10 | deg |
| Mass per span | 0.75 | kg/m | Dihedral of horizontal tail | 0 | deg |
| Rotational moment of inertia | 0.1 | kg · m | Beam ref. axis (from l.e.) | 50% | chord |
| Torsional rigidity | 1.00 × 104 | N · m2 | Cross-sectional c.g. (from l.e.) | 50% | chord |
| Flat bending rigidity | 2.00 × 104 | N · m2 | Mass per span | 0.08 | kg/m |
| Edge bending rigidity | 4.00 × 106 | N · m2 | Rotational moment of inertia | 0.01 | kg · m |
| Torsional rigidity | 1.00 × 104 | N · m2 | |||
| Complete aircraft mass | 54.5 | kg | Flat bending rigidity | 2.00 × 104 | N · m2 |
| Edge bending rigidity | 4.00 × 106 | N · m2 |
The main wings are divided into 10 elements in the finite-element model, while the tail members are all divided into 3 elements. The baseline aircraft can be trimmed for different flight conditions, such as the straight and level flight and steady coordinated turn in a horizontal plane at different altitudes, as listed in Table 2. The level flight speeds at different altitudes are determined by the same dynamic pressure of the flight, while the turn speed is determined by reaching a similar wing tip deflection as the level flights, with a 150-m radius of the turn path. When the aircraft is trimmed for the straight and level flight, its body orientation and wing deformation are symmetric (Fig. 5) and elevators are the only control surfaces involved in the trim. However, this symmetry generally does not hold for the steady coordinated turn (Fig. 6), where all three types of control surfaces are engaged (Table 2). The wing tip deflection for the turn flight listed in the table is also the average of the left and right wings, as the wing geometry is asymmetric in the trimmed state.
Table 2.
Trim results of the baseline aircraft under different steady flight conditions
| Flight status | Straight | Straight | Straight | Turn |
|---|---|---|---|---|
| Altitude (m) | 0 | 8,000 | 20,000 | 20,000 |
| Speed (m/s) | 6.735 | 10.28 | 25.00 | 20.50 |
| Thrust (N) | 60.15 | 59.80 | 59.28 | 92.19 |
| Body pitch angle (deg) | 1.28 | 1.27 | 1.26 | 4.44 |
| Bank angle (deg) | – | – | – | 14.97 |
| Elevator angle (deg) | 6.76 | 6.76 | 6.75 | 0.572 |
| Aileron angle (deg) | – | – | – | 0.239 |
| Rudder angle (deg) | – | – | – | −0.346 |
| Wing tip deflection (%) | 32.56 | 32.46 | 32.32 | 32.04 |
Fig. 5.

Trimmed baseline aircraft for straight and level flight at 20,000 altitude.
Fig. 6.

Trimmed baseline aircraft for steady coordinated turn at 20,000 altitude.
B. Natural Modes and Frequencies
Since the focus of current study is to utilize the flexibility of the highly flexible wings to search for the optimum wing shape with the best performance under different flight conditions, the control surfaces are “removed” from the models, while the wings are allowed with the full extension/bending/torsion deformations. It is expected that with the optimum wing deformation, the vehicle’s performance can be improved. In consideration of the large design space involved in searching for the optimum wing shapes, the modal-based approach is used in the study, since an arbitrary wing deformation can be represented by a linear combination of fundamental mode shapes. Therefore, the natural modes and frequencies are explored here. The mode description and the natural frequencies of the first 20 modes from the linear modal analysis are listed in Table 3. Because of the slenderness of the wings, the lower-order bending modes are coupled with the plunge and pitch modes of the rigid-body. However, such coupling becomes weak and negligible for the higher-order modes.
Table 3.
Natural modes and frequencies of the highly flexible aircraft (in Hz) about its undeformed shape
| No. | 1 | 2 | 3 | 4 | 5 |
| Rigid-body | Plunge + pitch | Roll | Plunge + pitch | – | Plunge + pitch |
| Wing | 1st S Flat Bend | 1st A Flat Bend | 2nd S Flat Bend | 1st A Torsion | 1st S Torsion |
| Frequency | 0.4244 | 1.572 | 2.431 | 4.946 | 5.039 |
|
| |||||
| No. | 6 | 7 | 8 | 9 | 10 |
| Rigid-body | Roll | Lead | Plunge + pitch | Roll | plunge |
| Wing | 2nd A Flat Bend | 1st S Edge Bend | 3rd S Flat Bend | 3rd A Flat Bend | 4th S Flat Bend |
| Frequency | 5.156 | 5.915 | 6.698 | 10.92 | 13.47 |
|
| |||||
| No. | 11 | 12 | 13 | 14 | 15 |
| Rigid-body | – | – | Roll + yaw + side | Roll + yaw + side | – |
| Wing | 2nd A Torsion | 2nd S Torsion | 4th A Flat Bend + 1st Tail Bend | 4th A Flat Bend | 5th S Flat Bend |
| Frequency | 14.96 | 14.97 | 18.06 | 19.53 | 23.33 |
|
| |||||
| No. | 16 | 17 | 18 | 19 | 20 |
| Rigid-body | – | – | Roll | Lead | – |
| Wing | 3rd S Torsion | 3rd A Torsion | 5th A Flat Bend | 2nd S Edge Bend | 4th S Torsion |
| Frequency | 25.32 | 25.34 | 26.87 | 34.14 | 36.27 |
S = Symmetric (with shade), A = Anti-symmetric
C. Steady and Level Flight
In this study, the altitude of steady and level flight is kept at 20,000 m. The flight speed is initially fixed as 25 m/s. The trim results of the baseline aircraft are listed in Table 2. The elevators are removed from the aircraft model, while the body pitch angle and the thrust force are kept the same. Obviously, the aircraft will be unbalanced. This state is used as the initial condition of the optimization procedure, targeting to find out the new wing deformation that can minimize the drag, while regaining the balance (trim). In doing so, one may carry out a series of optimizations where the possible wing deformations are represented by different number of modes. As the wing deformation is always symmetric for the steady and level flight, only the symmetric modes are included in the optimization. Table 4 summarizes part of the optimization results using different number of the symmetric modes, while the modal magnitude data of the optimum shapes by using 3 to 10 symmetric modes are plotted in Fig. 7. From the results, it is evident that the modal-based optimization solution is converging, where the optimum (minimum) drag is about 51.3 N, while the drag at initial condition is about 59.8 N. When comparing the magnitude of each mode, it can be seen that Modes 1, 3, 5, and 12 contribute more than the rest of the modes. It is also of interest to note that there may be a discontinuity in the solution if a torsional mode is included, which can be observed from the results with 6 and 7 symmetric modes. So, one may truncate the modes by selecting the first 12 modes (first 7 symmetric modes) for future studies, while keeping the convergence of the solution. The optimization study herein have demonstrated that the modal-based optimization solution is promising in finding the trim condition of the aircraft while searching for the optimum flight performance – minimum drag in this case.
Table 4.
Initial and optimum wing shapes and trim results for steady and level flight
| 3 Modes | 6 Modes | 7 Modes | 8 Modes | 9 Modes | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||
| Initial | Opt. | Initial | Opt. | Initial | Opt. | Initial | Opt. | Initial | Opt. | |
| Body pitch angle(deg) | 1.2596 | 2.6619 | 1.2596 | 2.6580 | 1.2596 | 2.6380 | 1.2596 | 2.6379 | 1.2596 | 2.6357 |
| Thrust (N) | 59.2823 | 51.5123 | 59.2823 | 51.5205 | 59.2823 | 51.3974 | 59.2823 | 51.3976 | 59.2823 | 51.3715 |
| Mode 1 | 1.5654 | 0.2212 | 1.5654 | 0.2212 | 1.5654 | 0.1904 | 1.5654 | 0.1905 | 1.5654 | 0.1862 |
| Mode 3 | −0.0164 | −0.0161 | −0.0164 | −0.0161 | −0.0164 | −0.0161 | −0.0164 | −0.0161 | −0.0164 | −0.0161 |
| Mode 5 | 0.0071 | 0.0021 | 0.0071 | 0.0021 | 0.0071 | 0.0020 | 0.0071 | 0.0020 | 0.0071 | 0.0020 |
| Mode 7 | – | – | 0.0003 | 0.0003 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 |
| Mode 8 | – | – | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0005 |
| Mode 10 | – | – | −0.0002 | −0.0002 | −0.0002 | −0.0002 | −0.0002 | −0.0002 | −0.0002 | −0.0002 |
| Mode 12 | – | – | – | – | −0.0014 | −0.0014 | −0.0014 | −0.0014 | −0.0014 | −0.0015 |
| Mode 15 | – | – | – | – | – | – | 0.0001 | 0.0001 | 0.0001 | 0.0001 |
| Mode 16 | – | – | – | – | – | – | – | – | 0.0006 | 0.0006 |
| Drag (N) | 59.84 | 51.46 | 59.84 | 51.47 | 59.84 | 51.34 | 59.84 | 51.34 | 59.84 | 51.32 |
Fig. 7.

Magnitudes of symmetric modes in the optimum shape for steady and level flight.
If one converts the wing deformation from the modal magnitudes given in Table 4 to physical quantities, the resulting wing deformation is actually very small (Fig. 8). It is important to note that to attain the solutions shown in Table 4, no constraints, other than the force and moment balance of the aircraft under the straight and level flight C1, are applied. In other words, the optimizer has a large freedom to explore the design space defined by the natural modes to find the wing shape, as long as the external forces are balanced. Therefore, the optimum solution tends to be aggressive and difficult to achieve in reality. Actually, the uncontrolled wing geometry with the balance between the internal wing rigidity and the external gravity and aerodynamic loads will be a deep U-shape shown in Fig. 5. Hence, one will need less control authority to maintain the optimum wing shape if the shape is similar to the deep U-shape. On the contrary, if the optimum wing geometry is far from the U-shape, one needs significant amount of the control authority to fight against either the aerodynamic loads or the wing stiffness in order to keep the optimum wing shape in the flight. Therefore, additional design constraints should be considered in the optimization procedure to attain more feasible/realistic optimum wing geometry. This is achieved by introducing constraints C2 and C3, with the limits defined as
| (29) |
and
| (30) |
where the strain energy of the optimum wing shape is compared to the strain energy of the shape shown in Fig. 5, which also ensures the structural integrity of the aircraft under the combined loads. Note that the numbers in Eqs. (29) and (30) are selected to prove the optimization process is tractable, in real design problem, however, they should be chosen properly.
Fig. 8.

Optimum wing shape for steady and level flight with constraint C1.
Table 5 summarizes the modal magnitudes and the corresponding trim parameters of the optimum wing shapes when the two constraints C2 and C3 are applied in addition to C1. The results are also compared to the optimum solution with C1 only. Note that all the solutions compared in Table 5 involve 7 symmetric modes. Figures 9 and 10 illustrate the resulting optimum shapes. From these results, one can see the dominance of the first flat bending mode (Model 1), which results in the optimum wing shapes to look more like the initial wing shape but with significantly less drag. It should be noted that the optimum solutions are all under trimmed condition, while the initial condition is untrimmed with the removal of the elevators. In particular, as shown in Table 5, with inclusion of constraints C1, C2 and C3, the drag is reduced to 54.92 N, which is still a significant improvement from the initial drag.
Table 5.
Initial and optimum wing shapes for steady and level flight with constraints
| Initial Condition | Optimum solutions
|
|||
|---|---|---|---|---|
| Constraint C1 | Const. C1 and C2 | Const. C1, C2, and C3 | ||
| Body pitch angle (deg) | 1.26 | 2.64 | 2.84 | 3.21 |
| Thrust (N) | 59.28 | 51.40 | 51.67 | 55.00 |
| Mode 1 | 1.5654 | 0.1904 | 0.5046 | 1.3798 |
| Mode 3 | −0.0164 | −0.0161 | −0.1714 | −0.0708 |
| Mode 5 | 0.0071 | 0.0020 | 0.0009 | 0.0013 |
| Mode 7 | 0.0004 | 0.0004 | 0.0003 | 0.0004 |
| Mode 8 | 0.0005 | 0.0005 | 0.0005 | 0.0005 |
| Mode 10 | −0.0002 | −0.0002 | −0.0002 | −0.0002 |
| Mode 12 | −0.0014 | −0.0014 | −0.0001 | −0.0010 |
| Strain energy (J) | 439.8 | 10.04 | 395.8 | 395.8 |
| Drag (N) | 59.84 | 51.34 | 51.61 | 54.92 |
Fig. 9.

Optimum wing shape for steady and level flight with constraints C1 and C2.
Fig. 10.

Optimum wing shape for steady and level flight with constraints C1, C2, and C3.
The last study in this section is to consider the flight speed as a variable in the optimization process, while the altitude is held at 20,000 m. In the optimization, only the first 7 symmetric modes are involved and the constraints C1, C2, and C3 are applied. The optimum solution is then compared to the one with the fixed flight speed (Table 6). Obviously, introducing an additional variable in the optimization process offers a new design degree of freedom when searching for the best solution. The optimum solution sees a 59% reduction in drag, compared to the fixed-speed case, but at higher flight speed. The strain energy and bending/torsion curvature constraints are still satisfied, which ensures that the optimum wing geometry (Fig. 11) can be achieved with the available control authority. It is also interesting to notice from Fig. 11 that the aerodynamic lift force is redistributed – more lift is generated at the inner board of the wings, which is beneficial as the bending moment at the wing root may be reduced compared to the case where aerodynamic load is distributed evenly along the wing span. This load redistribution is attributed to the increased magnitude of the torsional modes (Modes 5 and 12) when the flight speed is a variable.
Table 6.
Initial and optimum wing shapes for steady and level flight with fixed and varying flight speeds
| Initial Condition | Fixed flight speed | Variable flight speed | |
|---|---|---|---|
| Speed (m/s) | 25.00 | 25 | 48.23 |
| Body pitch angle (deg) | 1.26 | 3.21 | 2.85 |
| Thrust (N) | 59.28 | 55.00 | 22.71 |
| Mode 1 | 1.5654 | 1.3798 | 1.4633 |
| Mode 3 | −0.0164 | −0.0708 | −0.0262 |
| Mode 5 | 0.0071 | 0.0013 | −0.0078 |
| Mode 7 | 0.0004 | 0.0004 | 0.0004 |
| Mode 8 | 0.0005 | 0.0005 | 0.0005 |
| Mode 10 | −0.0002 | −0.0002 | −0.0002 |
| Mode 12 | −0.0014 | −0.0010 | 0.0078 |
| Strain energy (J) | 439.8 | 395.8 | 395.8 |
| Drag (N) | 59.84 | 54.92 | 22.68 |
Fig. 11.
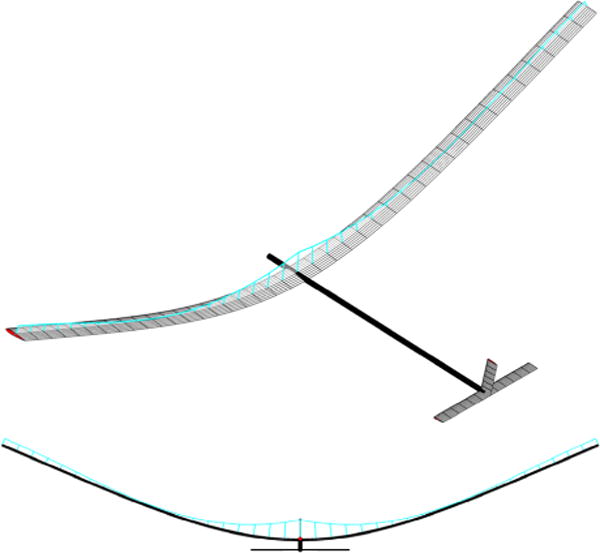
Optimum wing shape for steady and level flight with constraints C1, C2, and C3; flight speed is a variable.
Table 7 lists the components of the gradient vector of the objective function D with respect to each design variable obtained at the optimum solutions. This would indicate the sensitivity of optimum drag when subject to a small perturbation in the design variables. Note that the derivative components are calculated based on the scaled design variables so that they can be directly comparable. From Table 7, one can see that the sensitivity of the torsional mode (Mode 5) and the body pitch angle are dominant at steady level flight condition.
Table 7.
Components of the gradient vector at the optimum solutions for steady level flights
|
|
C1 | C1+C2 | C1+C2+C3 | C1+C2+C3+Variable speed | |
|---|---|---|---|---|---|
| Speed | – | – | – | 0.3930 | |
| Body pitch angle | 0.3906 | 0.3905 | 0.3900 | 0.3915 | |
| Thrust | 0 | 0 | 0 | 0 | |
| Mode 1 | 0.0010 | 0.0028 | −0.1637 | −0.0690 | |
| Mode 3 | 0.0106 | 0.0086 | 0.0135 | 0.0075 | |
| Mode 5 | 0.8487 | 0.8480 | 0.8605 | 0.6404 | |
| Mode 7 | 0.0001 | 0.0003 | −0.0002 | −0.0002 | |
| Mode 8 | −0.0020 | −0.0020 | −0.0021 | −0.0018 | |
| Mode 10 | −0.0001 | −0.0001 | −0.0001 | −0.0001 | |
| Mode 12 | 0.0174 | 0.0156 | 0.0166 | 0.0135 |
D. Steady Coordinated Turn
The optimum wing geometry is also explored for the steady coordinated turn flight. The altitude is still 20,000 m, while the nominal turn speed is set at 20.50 m/s. Two specific cases are studied here, subjected to all the constraints during the optimization process. The first case has the constant turn speed at nominal 20.50 m/s and the second case allows the turn speed to be a variable. It is important to note that in both cases the anti-symmetric modes must be included to represent the possible asymmetric wing geometry. In this study, the first 12 modes are included in the optimization solutions. For a coordinated turn, it is also necessary to set a constraint on allowable bank angle C4 to ensure the structural integrity, and in this study the limit is set as
| (31) |
Table 8 and Figs. 12 and 13 highlight the optimum solutions for the two cases, and the comparison with the initial condition (Table 8). It can be seen that the optimum wing geometry with the fixed turn speed is similar to the initial shape, hence similar drag. On the other hand, allowing the turn speed to vary during the optimization process results in a significant drag reduction of about 48%.
Table 8.
Initial and optimum wing shapes for steady coordinated turn with fixed and varying flight speeds
| Initial Condition | Fixed flight speed | Variable flight speed | |
|---|---|---|---|
| Speed (m/s) | 20.50 | 20.50 | 31.91 |
| Body pitch angle (deg) | 4.44 | 4.51 | 2.80 |
| Bank angle (deg) | 14.97 | 15.89 | 35.00 |
| Thrust (N) | 92.19 | 91.21 | 47.77 |
| Mode 1 | 1.5529 | 1.4813 | 0.8565 |
| Mode 2 | −0.0069 | 0.0005 | 0.0114 |
| Mode 3 | −0.0182 | −0.0188 | −0.1471 |
| Mode 4 | 0.0000 | 0.0000 | 0.0000 |
| Mode 5 | 0.0074 | 0.0070 | −0.0024 |
| Mode 6 | 0.0022 | 0.0025 | 0.0118 |
| Mode 7 | 0.0006 | 0.0006 | 0.0006 |
| Mode 8 | 0.0007 | 0.0007 | −0.0031 |
| Mode 9 | 0.0011 | 0.0011 | 0.0031 |
| Mode 10 | −0.0002 | −0.0002 | 0.0001 |
| Mode 11 | 0.0000 | 0.0000 | −0.0001 |
| Mode 12 | −0.0017 | −0.0016 | 0.0015 |
| Strain energy (J) | 434.98 | 395.8 | 395.8 |
| Drag (N) | 91.92 | 90.91 | 47.71 |
Fig. 12.

Optimum wing shape for steady and level flight with constraints C2, C3, and C4; flight speed is fixed.
Fig. 13.

Optimum wing shape for steady and level flight with constraints C2, C3, and C4; flight speed is variable.
Similarly, a sensitivity analysis is performed for the two cases. Table 9 lists the sensitivity of the drag with respect to the design variables calculated at the optimum solutions. It can be seen that the most sensitive design variables are still the body pitch angle and the torsional mode (Mode 5). It should be noted that the first bending mode (Mode 1) is becoming more sensitive in coordinated turns, compared to the straight flights.
Table 9.
Components of the gradient vector at the optimum solutions for steady coordinated turns
|
|
Fixed flight speed | Variable flight speed | |
|---|---|---|---|
| Speed | – | 0.6507 | |
| Body pitch angle | 0.8999 | 1.0653 | |
| Bank angle | 0 | 0 | |
| Thrust | 0 | 0 | |
| Mode 1 | −0.1972 | −0.0398 | |
| Mode 2 | −0.0000 | 0.0001 | |
| Mode 3 | 0.0141 | 0.0090 | |
| Mode 4 | −0.0000 | −0.0000 | |
| Mode 5 | 0.6237 | 0.6813 | |
| Mode 6 | −0.0000 | −0.0000 | |
| Mode 7 | −0.0003 | 0.0002 | |
| Mode 8 | −0.0021 | −0.0022 | |
| Mode 9 | −0.0000 | 0.0000 | |
| Mode 10 | −0.0001 | −0.0001 | |
| Mode 11 | −0.0000 | 0.0000 | |
| Mode 12 | 0.0112 | 0.0172 |
IV. Concluding Remarks
To determine the optimum wing geometry for a mission adaptive, highly flexible morphing aircraft, the optimum wing bending and torsional deformations are explored in this paper. The goal is to search for the most efficient wing configuration that produces the minimum drag at various flight profiles. The geometrically nonlinear effects of the highly flexible aircraft were modeled through a methodology that integrates a nonlinear strain-based beam model, unsteady aerodynamics, and the six-degree-of-freedom rigid-body equations. With the strain-based finite-element implementation of the formulation, the nonlinear wing deformations of the highly flexible aircraft were further represented by the linear normal modes. This allows for a quick and effective characterization of the contributing mode shapes to a specific wing deformation. Based on the modal representation, optimum wing geometries under different flight conditions were explored through an optimization procedure that considered the magnitude of each mode as a design variable. The objective was to minimize the drag at those flight conditions, while satisfying the trimming of the aircraft and other constraints. Since the control mechanism and control loads were not available, the flapless aircraft platform and the strain energy from wing deformations were used to place a constraint on the required control authority.
Two flight conditions were considered in the current study. One was the steady level flight and the other was the steady coordinated turn. To trim the highly flexible flapless morphing aircraft, the coupled wing bending and torsional deformations along the wing span were used to tailor the wing load distribution. In particular, the optimum solutions showed that tailored wing twist/torsion resulted in a significant drag reduction and improved performance. Furthermore, the sensitivity analysis also indicated the importance of torsional modes.
The numerical study demonstrated the feasibility of the modal-based optimization scheme for finding the optimum wing geometry. The significance of each mode in contributing to the optimum wing geometry was also identified from the optimal solution. This will benefit the future study on developing the reduced-order modal-based flight controllers. Further follow-up studies will include other flight performance metrics, such as flutter boundary, roll performance, etc., and the optimum wing shapes at these flight scenarios will be determined.
Acknowledgments
The first author acknowledges the sponsorship from the NASA Ames Research Center’s Summer Faculty Fellowship. The work was partially supported by the NASA ARMD’s Team Seedling Fund Project.
Nomenclature
- a0
local aerodynamic frame, with a0y axis aligned with zero lift line of airfoil
- a1
local aerodynamic frame, with a1y axis aligned with airfoil motion velocity
- B
body reference frame
- BF, BM
influence matrices for the distributed forces and moments
- b
positions and orientations of the B frame, as time integral of β
- bc
semichord of airfoil, m
- CFF, CFB, CBF, CBB
components of generalized damping matrix
- D
total drag of aircraft, N
- d
distance of midchord in front of beam reference axis, m
- F, M
forces and moments in physical frames
- F1, F2, F3
influence matrices in inflow equations with independent variables
- Fdist, Fpt
distributed and point forces g
- J
Jacobians
- KFF l, m, d
aerodynamic loads on an airfoil
- MA
mass of complete aircraft, kg
- Mdist, Mpt
distributed and point moments
- MFF, MFB, MBF, MBB
components of generalized mass matrix
- N
-
influence matrix for gravity force
number of linear natural modes selected to represent aircraft deformation
- pB, θB
position and orientation of B frame, as time integral of vB and ωB, respectively
- R
generalized load vector
- R
range of flight, m
- r
turn radius, m
- s
curvilinear coordinates of beam, m
- T
total engine thrust force, N
- U
strain energy, J
- V
turn speed, m/s
- vB, ωB
linear and angular velocities of B frame, resolved in B frame itself
- w
local beam reference frame defined at each node along beam reference line
- x
complete set of variables in optimization
airfoil translational velocity components resolved in a0 frame, m/s
airfoil angular velocity about a0x axis, rad/s
- αB
aircraft body pitch angle, deg
- β
body velocities, with translational and angular components, resolved in B frame
- δa, δe, δr
aileron, elevator, and rudder deflections (deg)
- ε
elastic strain/curvature vectors
- εx
Extensional strain beam members
- η
magnitudes of linear natural modes
- κx, κy, κz
torsional, flat bending, and edge bending curvatures of beam members, 1/m
- λ
inflow states, m/s
- λ0
inflow velocities, m/s
- ρ∞
air density, kg/m3
- Φ
mode shape of strain modes
- φB
aircraft bank angle, deg
Abbreviation
- c.g.
center of gravity
- l.e.
leading edge Subscript
- B
reference to B frame
- BB, BF
components of a matrix with respect to body/flexible differential equations of motion
- F
reference to flexible degrees of freedom
- FB, FF
components of a matrix with respect to flexible/body differential equations of motion
- hb
h vector with respect to motion of B frame
- hε
h vector with respect to strain ε
- mc
midchord
- pb
nodal position with respect to motion of B frame
- pε
nodal position with respect to strain ε
- ra
beam reference axis
- x, y, z
components of a reference frame
- θb
nodal rotation with respect to motion of B frame
- θε
nodal rotation with respect to strain ε
Contributor Information
Weihua Su, University of Alabama, Tuscaloosa, AL, 35487-0280.
Sean Shan-Min Swei, NASA Ames Research Center, Moffett Field, CA, 94035.
Guoming G. Zhu, Michigan State University, East Lansing, MI 48824.
References
- 1.Cesnik CES, Brown EL. “Modeling of High Aspect Ratio Active Flexible Wings for Roll Control,” AIAA-2002–1719. 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference; Denver, Colorado. Apr. 22-25, 2002. [Google Scholar]
- 2.Cesnik CES, Brown EL. “Active Wing Warping Control of a Joined-Wing Airplane Configuration,” AIAA-2003-1715. 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference; Norfolk, Virginia. Apr. 7-10, 2003. [Google Scholar]
- 3.Hetrick J, Osborn R, Kota S, Flick P, Paul D. “Flight Testing of Mission Adaptive Compliant Wing,” AIAA-2007-1709. 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference; Honolulu, HI. Apr. 23-26, 2007. [Google Scholar]
- 4.Kota S, Osborn R, Ervin G, Maric D, Flick P, Paul D. RTO Applied Vehicle Technology Panel (AVT) Symposium RTO-MP-AVT-168. Evora, Portugal: Apr 20-24, 2009. Mission Adaptive Compliant Wing - Design, Fabrication and Flight Test. [Google Scholar]
- 5.Bilgen O, Kochersberger KB, Inman DJ, Ohanian OJ. Novel, Bidirectional, Variable-Camber Airfoil via Macro-Fiber Composite Actuators. Journal of Aircraft. 2010;47(1):303–314. doi: 10.2514/1.45452. [DOI] [Google Scholar]
- 6.Gandhi F, Frecker M, Nissly A. Design Optimization of a Controllable Camber Rotor Airfoil. AIAA Journal. 2008;46(1):142–153. doi: 10.2514/1.24476. [DOI] [Google Scholar]
- 7.Kaul UK, Nguyen NT. Drag Optimization Study of Variable Camber Continuous Trailing Edge Flap (VCCTEF) Using OVERFLOW; 32nd AIAA Applied Aerodynamics Conference; Atlanta, GA. Jun. 16-20, 2014. [Google Scholar]
- 8.Nguyen NT, Ting E. “Flutter Analysis of Mission-Adaptive Wing with Variable Camber Continuous Trailing Edge Flap,” AIAA-2014-0839. 55th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference; National Harbor, MD. Jan. 13-17, 2014. [Google Scholar]
- 9.Tilmann CP, Flick PM, Martin CA, Love MH. RTO AVT-099 Symposium on Novel and Emerging Vehicle and Vehicle Technology Concepts. Brussels, Belgium: Apr 7-11, 2003. “High-Altitude Long Endurance Technologies for SensorCraft,” MP-104-P-26. [Google Scholar]
- 10.Noll TE, Ishmael SD, Henwood B, Perez-Davis ME, Tiffany GC, Madura J, Gaier M, Brown JM, Wierzbanowski T. NATO/RTO AVT-145 Workshop on Design Concepts, Processes and Criteria for UAV Structural Integrity. Florence, Italy: May 14-18, 2007. Technical Findings, Lessons Learned, and Recommendations Resulting from the Helios Prototype Vehicle Mishap. [Google Scholar]
- 11.Patil MJ, Hodges DH, Cesnik CES. Nonlinear Aeroelasticity and Flight Dynamics of High-Altitude Long-Endurance Aircraft. Journal of Aircraft. 2001;38(1):88–94. doi: 10.2514/2.2738. [DOI] [Google Scholar]
- 12.Livne E, Weisshaar TA. Aeroelasticity of Nonconventional Airplane Configurations - Past and Future. Journal of Aircraft. 2003;40(6):1047–1065. doi: 10.2514/2.7217. [DOI] [Google Scholar]
- 13.Shearer CM, Cesnik CES. Nonlinear Flight Dynamics of Very Flexible Aircraft. Journal of Aircraft. 2007;44(5):1528–1545. doi: 10.2514/1.27606. [DOI] [Google Scholar]
- 14.Su W, Cesnik CES. Nonlinear Aeroelasticity of a Very Flexible Blended-Wing-Body Aircraft. Journal of Aircraft. 2010;47(5):1539–1553. doi: 10.2514/1.47317. [DOI] [Google Scholar]
- 15.Su W, Cesnik CES. Dynamic Response of Highly Flexible Flying Wings. AIAA Journal. 2011;49(2):324–339. doi: 10.2514/1.J050496. [DOI] [Google Scholar]
- 16.Swei SS-M. Active Wing Shaping Control Concept Using Composite Lattice-based Cellular Materials. [online article], Url: http://nari.arc.nasa.gov/2015seminar [cited Apr. 07 2015]
- 17.Cesnik CES, Senatore P, Su W, Atkins E, Shearer CM. X-HALE: A Very Flexible Unmanned Aerial Vehicle for Nonlinear Aeroelastic Tests. AIAA Journal. 2012;50(12):2820–2833. doi: 10.2514/1.J051392. [DOI] [Google Scholar]
- 18.Su W, Cesnik CES. Strain-Based Analysis for Geometrically Nonlinear Beams: A Modal Approach. Journal of Aircraft. 2014;51(3):890–903. doi: 10.2514/1.C032477. [DOI] [Google Scholar]
- 19.Su W, Cesnik CES. Strain-Based Geometrically Nonlinear Beam Formulation for Modeling Very Flexible Aircraft. International Journal of Solids and Structures. 2011;48(16–17):2349–2360. doi: 10.1016/j.ijsolstr.2011.04.012. [DOI] [Google Scholar]
- 20.Palacios R, Cesnik CES. Cross-Sectional Analysis of Nonhomogeneous Anisotropic Active Slender Structures. AIAA Journal. 2005;43(12):2624–2638. doi: 10.2514/1.12451. [DOI] [Google Scholar]
- 21.Peters DA, Johnson MJ. Finite-State Airloads for Deformable Airfoils on Fixed and Rotating Wings. In: Friedmann PP, Chang JCI, editors. Proceedings of Symposium on Aeroelasticity and Fluid Structure Interaction Problems, ASME Winter Annual Meeting. Vol. 44. The American Society of Mechanical Engineers; New York, New York: 1994. pp. 1–28. AD. [Google Scholar]


