Single-Photon Nanoantennas

Abstract

Single-photon nanoantennas are broadband strongly scattering nanostructures placed in the near field of a single quantum emitter, with the goal to enhance the coupling between the emitter and far-field radiation channels. Recently, great strides have been made in the use of nanoantennas to realize fluorescence brightness enhancements, and Purcell enhancements, of several orders of magnitude. This perspective reviews the key figures of merit by which single-photon nanoantenna performance is quantified and the recent advances in measuring these metrics unambiguously. Next, this perspective discusses what the state of the art is in terms of fluoresent brightness enhancements, Purcell factors, and directivity control on the level of single photons. Finally, I discuss future challenges for single-photon nanoantennas.

This Perspective deals with single-photon nanoantennas, defined as the combination of a fluorescent quantum system and a resonant optical nanostructure. The quantum system ensures that the system can emit and absorb precisely a single photon at a time, while the nanostructure or “antenna” placed in its near field manipulates the coupling of the emitter to far field radiation channels.^1,2 This idea originates from the near-field microscopy community,³ in which the desire to boost the sensitivity of fluorescence microscopy and vibrational spectroscopy on the level of single molecules has been a main driver for plasmonic antenna research.⁴ Yet, the main motivation for single-photon nanoantennas stems from the desire to control light emission, detection, and amplification at the level of one or a few photons, at submicron length scales and subpicosecond time scales for envisioned quantum and classical information technology. This perspective focuses on antennas for emission, as amplification and detection at few photon levels are as yet out of reach for antennas.

Much stands in the way of turning a single emitter into a bright, fast, single-photon source.⁵ Quantum emitters are point-like objects that emit almost isotropically, and emitter decay rates are typically slow (nanosecond time scales), as fixed through their electronic structure. Hence, whether one considers cold atoms, single organic molecules, or semiconductor quantum dots, they are far from the ideal of a push-button source of single photons that are emitted on demand and then emerge with unit efficiency in a desired collection channel.⁵⁻⁸ Such an ideal source of photons is generally considered as an important enabling resource for quantum communication and a stepping stone for quantum information protocols on the basis of photons, or on the basis of matter qubits that are connected by light.⁶ Ideally, nanoantennas change the electromagnetic mode structure around an emitter to obtain a strongly enhanced light–matter interaction. This should ensure that the source emits its photons into a well-defined spatial mode that can be harvested with 100% efficiency and at accelerated (sub)-picosecond photon emission rates for minimum timing uncertainty between excitation and extraction of photons (Figure 1). This mission statement is indistinguishable from that of microcavities for quantum optics.⁶⁻⁸ For monolithic III–V photonic crystals and micropillar cavities, researchers demonstrated over 98% coupling efficiencies for single photons into chip-integrated photonic crystal waveguides,⁹ at spontaneous emission rate enhancement factors of around 10. Another important metric for quantum applications^10,11 is in how far single photons are indistinguishable. Recent advances in III–V microcavity sources have led to sources with 99% photon indistinguishability, while at the same time achieving 65% extraction efficiency. Given these astounding achievements, one must ask what distinctive role nanoantennas could play.

Figure 1.

Sketch of the single-photon nanoantenna concept, based on common motifs in literature: a fluorescent quantum system (black arrow), coupled to a photonic system, typically comprised by one or a few plasmonic resonators, for the purpose of controlling the coupling between the emitter and the far-field. A desirable single-photon nanoantenna source emits a stream of single photons, where the antenna provides control over how fast each photon is emitted after excitation of the emitter (LDOS control over rate and efficiency), and with what spatial mode profile (control over emission pattern). Narrow gaps, such as in the bow tie motif, generally enhance emission rate, while the emission pattern benefits from having an extended antenna, for instance, consisting of multiple secondary scatterers alongside the antenna feed element that is coupled to the emitter.

The distinguishing advantage of antennas over cavities is their bandwidth. Purcell’s formula states that the emission of a fluorophore in a dielectric resonator is accelerated over that in vacuum by a factor of F = 3/(4π²)λ³Q/V, where Q is the resonator quality factor and V/λ³ is the mode volume in cubic wavelengths. Microcavities have diffraction limited volumes, directly leading to the requirement of large quality factors (Q > 10⁴). For large Purcell factors, the paradigm of microcavities hence dictates narrow line widths, with significant drawbacks for control and scalability. These include the need to very precisely tune cavities to emitters and the need to keep their tuning stable. Also, high Q implies slow (picosecond to nanosecond) response times that could ultimately stand in the way of ultrafast switching. Antennas follow the converse philosophy: they are broadband, open systems with typically Q = 3–30. Enhancement of emission can occur across the entire room temperature spectrum of a typical organic dye or II–VI nanocrystal emitter. The required deeply subwavelength mode volume immediately implies that one must store electromagnetic energy in a material resonance, as opposed to using standing wave interference as in a microcavity. Thus, single-photon nanoantennas almost exclusively rely on plasmonic or polaritonic materials.² Thereby single-photon antennas trigger questions beyond simply replicating microcavity performance at larger bandwidth. Since plasmonic resonators are open and lossy, the standard formulation for the Purcell enhancement factor on the basis of a mode function and its mode volume needs to be generalized.^12,13 Plasmonics implies a fundamental and difficult trade off between material loss, emission rate enhancement, and efficiency.^14,15 Strong field gradients mean that one may break quantum mechanical selection rules.¹⁶ Furthermore, one may enter a new regime of quantum strong coupling (“quantum” pointing at vacuum Rabi splitting with a single emitter, as opposed to semiclassical strong coupling with many emitters¹⁷) that goes beyond the usual Jaynes-Cummings theory, owing to the open and lossy nature of antennas.¹⁸⁻²⁰

In this Perspective, I first review parameters of key importance for single-photon nanoantennas. Next, I summarize the two main recent breakthroughs, namely, (1) understanding how to unambiguously measure single-photon antenna performance, and (2) performance metrics of recently proposed optically driven single-photon nanoantenna designs. Finally, I speculate on future research directions.

Basic Figures of Merit

Given that no electrically driven plasmonic light emitting device has so far reached the quantum level,²¹ I focus particularly on optically driven single-photon nanoantennas. The concept of an optical nanoantenna with a single fluorophore as optically driven active element was proposed first in the near-field optics community.³ Around the year 2000, researchers used single fluorescent molecules as the ultimate point probe to quantify the electromagnetic field concentration of near field optics scanning tips. They noted that the radiation pattern of single molecules can be strongly modified by a metallized probe, that essentially acted as plasmonic nanoantenna.²² Two groups from the near-field optics community in two seminal 2006 papers clearly laid down the main figures of merit at play, illustrated by the only analytically solvable plasmon antenna, a nanosphere. Anger et al.²³ and Kühn et al.²⁴ monitored the fluorescence of a single molecule in a confocal microscope while approaching a spherical gold nanoparticle glued to a scanning probe tip to within tens of nanometers. The experiments clearly demonstrated three enhancement effects that occur for any optically driven nanoantenna, whose product determines the fluorescent count rate extracted from the emitter, and each of which involves the strongly varying electromagnetic field around the antenna:

1

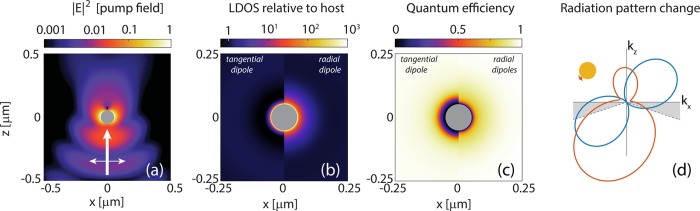
Here the argument r emphasizes the dependence on the emitter location, while ω_pump and ω_em indicate the optical pump and emission frequency, respectively. Figure 2 illustrates these factors for the seminal case of a metal nanosphere. The first factor, P_pump, corresponds to enhancement of excitation of the single fluorophore, in direct proportion to the local enhancement of pump field intensity at the location of the molecule. This factor (illustrated in Figure 2a) depends solely on the scattering properties of the antenna at the pump wavelength and can be controlled by matching illumination wavelength, polarization, and beam profile to the antenna resonance. Once the molecule is excited, the remaining factors come into play at the Stokes-shifted fluorescence wavelength. The collected signal depends on quantum efficiency φ(r), that is, on the likelihood that excitation of the emitter actually results in an output photon. Any quantum emitter decays from its excited state according to a total decay rate that is the sum of radiative and nonradiative decay rates γ_r and γ_nr, respectively, the ratio of which sets the intrinsic molecular quantum efficiency. Only the intrinsically radiative part is susceptible to acceleration by the electromagnetic mode structure around the emitter, through a quantity known as local density of optical states,²⁵ see Figure 2b. This is an emitter-independent electromagnetic quantity that depends on emission frequency, dipole position, and dipole orientation²⁶ with SI units (s/m³), indicating the volume-density (m^–3) of the number of optical states that are available per Hz. In plasmonics, its most convenient definition is through the so-called Green function, stating that for an emitter at r, oriented along unit vector p̂, LDOS = (6ω_em)/(πc²)[p̂̂^T·Im G(ω_em; r, r)·p̂]. The quantity ImG(ω_em; r, r) also appears in antenna engineering literature as the radiative impedance of a small antenna.²⁷ Literature is remarkably loose in the use of the term LDOS, usually using the term to indicate the LDOS normalized to its vacuum value, and variably using it as an orientation-averaged, or orientation-resolved quantity. Throughout this paper, I use LDOS to mean the local density of states normalized to that of the homogeneous background medium in absence of the antenna, and plot its value for particular dipole orientations as indicated. Nowadays, any LDOS effect on spontaneous emission rates is commonly but inappropriately referred to as “Purcell enhancement”, although Purcell himself⁹⁹⁷ never considered any case other than a cavity, and although the quantities Q and mode volume V in the Purcell factor are not well-defined for plasmonics.^12,13 In this work, I will follow this current, if inappropriately sloppy, custom of using LDOS and Purcell enhancement interchangeably. Since plasmonic metals necessarily absorb, the LDOS separates as a sum of a radiative (LRDOS) and nonradiative contributions. The fluorescence decay rate reads

2

Here, the rates γ_0,nr and γ_0,r (no spatial argument, subscript 0) are the nonradiative and radiative rates in absence of the antenna. A fluorescence lifetime experiment measures the total decay rate γ(r). The quantum efficiency (Figure 2c) reads φ(r) = γ_r(r)/γ(r). Note that the efficiency of an intrinsically efficient emitter (one photon out, per pump photon in) can never be improved, while conversely, the efficiency of a poor emitter (intrinsic quantum efficiency φ₀ ≪ 1 can be improved up to as much as 1/φ₀ or, more realistically, to an upper bound set by the ratio of LRDOS and LDOS (efficiency enhancement by a factor LRDOS/LDOS·1/φ₀). This fact has motivated Gill et al.²⁸ to go so far as to propose that fluorescence enhancement times φ₀ is a more objective figure of merit for an antenna.

Figure 2.

All contributors to fluorescence enhancement effects at optically driven nanoantennas strongly depend on position near a nanoantenna. This figure illustrates the textbook case of a 100 nm gold sphere in water, excited by a tight (NA = 1.3) laser focus at 567 nm wavelength, emitting at 600 nm. (a) Pump field distribution (first term in eq 1) for a wave incident from below, polarized along the x-axis. In addition to the dipolar lobes of the plasmon particle resonance, note that strongly scattering antennas will generally reflect laser light, in this case giving rise to a strong standing wave. (b). LDOS (eq 2) near the same Mie sphere (at emission wavelength 600 nm) is strongly enhanced at the metal surface, particularly for radial transition dipole moments. (c) Quantum efficiency (second term in eq 1) of emission assuming an intrinsicially efficient emitter is strongly reduced in a 10 nm radius shell around the metal. (d) Example of redistribution of radiation, in this case for an emitter (sketch top) almost tangential to, and 10 nm away from, the sphere, in the xz-plane (arbitrarily chosen geometry). The diagram shows the radiation pattern (probability density, i.e., probability per steradian for an emitted photon to end up in a given direction) as a polar plot for a bare emitter (blue curve), and emitter plus sphere (orange curve). The gray shaded area delimits the boundaries of the typical acceptance cone of a high NA objective. Depending on geometry, the collection probability can vary strongly (third term in eq 1).

Finally, a plasmon antenna can strongly redirect light (cf., Figure 2d). Engineering the radiation pattern (probability density per steradian to find the emitted photon in a particular far field solid angle (θ, ϕ)) can improve the fluorescence collection efficiency

3

if the antenna can be matched to a collection lens, fiber, or waveguide circuit.

The enhancement effects listed above define the list of challenges for optically driven single-photon nanoantennas as

• 1.How to independently control pump enhancement, quantum efficiency, and directivity enhancement effects to obtain meaningful performance benefits.
• 2.How to control the placement r and orientation of a single molecule and antenna with nanometric accuracy, given the strong position dependencies in eqs 1 and 2.
• 3.How to design antenna-emitter geometries that enhance decay rates yet optimize quantum efficiency.
• 4.How to rationally design antenna directivity.

This list is formulated for antenna design, yet can equally be read as a benchmark to strive for in experiments, simply replacing “how to design/control” with “how to fabricate and measure at the single molecule level”. Recently both the measurement and the design challenge have made great strides. Arguably, progress is even such that the field can now shift attention from quantifying and optimizing fluorescence enhancement characteristics to actual implementations as single-photon sources. In such implementations, one would likely operate in pulsed mode at high pump intensity, so that for each pulse, the emitter is surely excited. In that case, the actual pump field enhancement that one reaches is no longer relevant. Instead, the key performance factors that are left are the timing jitter for photon arrival after the driving pulse (minimized by a high LDOS) and the proportion of excitation pulses that actually results in a collected photon, as determined by the product of collection efficiency and system quantum efficiency. Moreover, the question will then arise if the spectrum of emission can be made stable and lifetime-limited in width, to reach indistinguishability for the stream of output photons. Given that plasmon-accelerated lifetimes could reach the picosecond domain, the relevant spectral widths would be in the range of tens of GHz, much narrower than the temperature-broadened spectra of the organic dyes and semiconductor nanocrystals at 300 K that are currently in use to demonstrate antenna-enhanced, single-photon emission. Irrespective of the fact that plasmon antennas allow some degree of spectral control over such broadband emitters²⁹ by spectral structure in LDOS, their THz line widths imply that the spectral purity should ultimately come from intrinsic emitter properties, not antenna physics.

Unambiguously Measuring Antenna Performance

There is an enormous variability in reported “fluorescence enhancement factors” even for similar antennas. The iconic “plasmonic bow tie antenna” might give anything from a 1000-fold molecular brightness increase³⁰ to a net decrease, depending on whether one probes with one ideally placed, intrinsically low efficiency fluorophore, or averages an ensemble of intrinsically efficient molecules. The main pitfall is ensemble averaging. Differently placed and oriented molecules within a volume equal to the diffraction limit of a confocal detection system will experience antenna enhancement factors that vary orders of magnitude for typical plasmon antennas (see Figure 3, a factor 1000 difference between LDOS and ensemble-averaged LDOS). Furthermore, molecules in an ensemble that experience the highest LDOS may contribute least to the signal, as they likely experience the most quenching. A second main cause of confusion is insufficient understanding of intrinsic fluorophore efficiency (intrinsic quantum efficiency φ₀). For intrinsically inefficient emitters, large Purcell factors directly improve quantum efficiency. Even if there is no effect of pump field or collection enhancement, brightness can shoot up by a factor up to 1/φ₀, owing to LDOS enhancement. Yet, at low φ₀, no large overall rate enhancement will be apparent in fluorescence decay traces, as the intrinsic nonradiative decay dominates. Conversely, for efficient emitters large Purcell factors imply large decay rate changes. Yet there need not be any brightness improvement, since still at most one photon per pump photon is emitted. These facts are well-known,³¹ yet still cw antenna brightness and LDOS enhancement are often confused.

Figure 3.

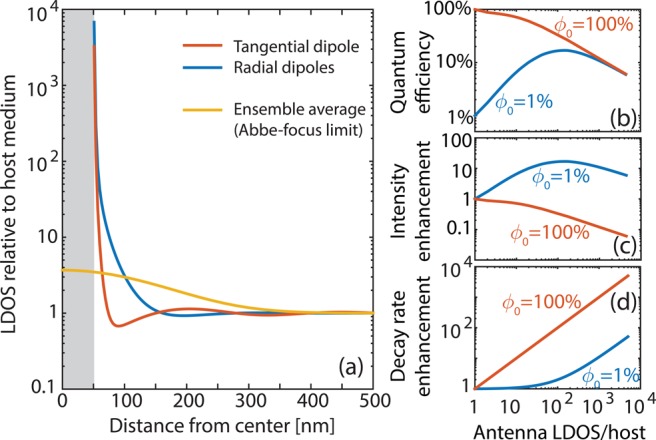
(a) LDOS dependencies for a single dipole emitter radial and tangential to a Au nanosphere antenna (100 nm diameter, in water) are strongly different, with LDOS rapidly varying with distance and exceeding 10⁴. The position and orientation ensemble-averaged LDOS over a confocal microscope detection volume scanned (position on the x-axis indicates position of the focus center relative to the particle center) over the antenna only shows enhancement up to a factor 5. Right, (b) apparent antenna quantum efficiency, (c) fluorescence brightness enhancement per absorbed pump photon, and (d) fluorescence decay rate change, as a function of LDOS near the same gold nanosphere antenna, for an intrinsically efficient and inefficient emitter (ϕ₀ = 100% and 1%). An efficient emitter will never appear brighter (per absorbed pump photon) when it is coupled to an antenna, even if its fluorescence decay trace shows a large change (compare middle and bottom panel). Conversely, large LDOS can result in large brightness gains for low quantum efficiency emitters, even if the fluorescence decay rate appears unaffected. This occurs because the system quantum efficiency can be raised to reach the albedo of the antenna (about 50%). At very large LDOS, quenching limits quantum efficiency. While this plot is specific for a nanosphere, the qualitative dependencies are generic.

A crucial recent achievement is to develop robust measurement protocols that avoid ensemble averaging, yet obtain statistically relevant data. This means collecting statistics on antennas with single molecules, one at a time. Deterministically mapping performance metrics with single molecules is an idea over 15 years old.^23,24,32,33 Several groups integrated either antennas or luminescent nanosources with near-field tips and demonstrated fluorescence decay rate imaging with deep subwavelength resolution.^{23,24,33−40} Unfortunately, probes are difficult to make yet easy to break, so only few teams persisted. Singh et al. recently demonstrated that one can map the near field of a plasmon dipole antenna fabricated at the end of a near field probe in a statistically relevant manner by scanning over many single molecules.³⁹ A less tedious alternative is localization microscopy.⁴¹ Localization microscopy hinges on fitting single-molecule locations in diffraction limited intensity images. While one usually only maps where molecules are located, localization microscopy can be coupled to, for example, time-correlated single-photon counting to map antenna performance, like LDOS, with 10–20 nm resolution.⁴² It does take a leap of faith to believe that antennas do not distort point spread functions, a problem that several groups have attempted to tackle.^43,44 On this proviso, one can perform super-resolution imaging with randomly deposited photoactivated fluorophores⁴⁵ or with fluorophores that sample space by diffusive or directed motion in a microfluidic cell,⁴⁶ in vein of super-resolution techniques like PALM and STORM.⁴¹ Finally, several authors have demonstrated sampling many random realizations of single-molecule, single-antenna pairs without even imaging their relative configuration. The tedious approach is to screen many nominally identical antennas with randomly sprinkled, immobilized emitters (at most one per antenna), as first done by Kinkhabwala.^30,47,48 The notion of nominally identical is unfortunately very problematic when nanometer-sized geometrical differences matter, as well appreciated by the SERS (surface enhanced Raman scattering) community.⁴⁹ The more elegant approach is to exploit random diffusion of fluorophores in a liquid around one single nanostructure.⁵⁰⁻⁵³ Fluorescence bursts occur whenever a molecule diffuses into the antenna hot spot volume, and from each burst one can determine brightness enhancements, and LDOS enhancements. None of the strategies outlined above form a viable route to reproducibly assemble single-photon nanoantennas. Likely, this is because lithographic approaches, such as two-step e-beam lithography⁵⁴⁻⁵⁶ have low throughput and are limited to 10–20 nm in alignment accuracy. Lithographic approaches to assemble antenna-emitter pairs are thus problematic for completely sampling antenna performance. Strong cards for deterministic assembly are held by colloidal antennas combined with DNA linkers and DNA origami strategies.⁵⁷⁻⁶¹ While quite specific to colloidal geometries and Au particles, this approach is the closest to deterministic fabrication of antenna-emitter pairs with nanometer control.

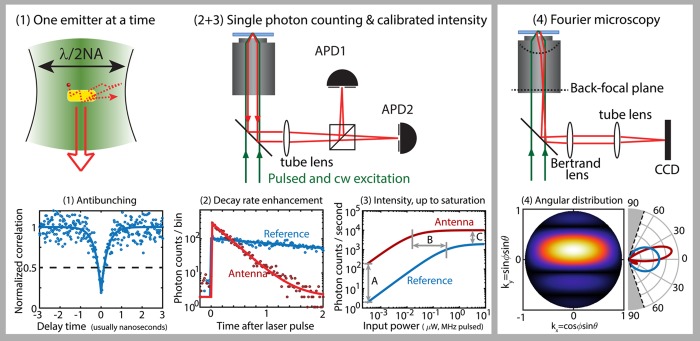
Even with single-molecule-at-a-time data it is no mean feat to separate pump rate, angular redistribution of photons, and emitter/antenna quantum efficiency. Only their product is measurable as fluorescence brightness (eq 1). Likewise, separating radiative and nonradiative decay rates is not trivial since a fluorescence decay rate measures only their sum (eq 2). Therefore, one requires a suite of measurements, as illustrated in Figure 4. None of these is unique, but the combination is unique to recent reports.^{30,48,50−52,62,63} Step 1 (Figure 4, left) is to demonstrate single emitter behavior, for example, through antibunching⁵ in a Hanbury-Brown and Twiss set up. Given the importance of demonstrating that a single-photon source is based on a single emitter, it is remarkable that very few papers actually report antibunching.^{48,55,60,61,64} Likely, this is associated with the fact that separating emitter fluorescence from background light is difficult, especially given that resonant plasmon particles also tend to fluoresce. Next, (step 2) one determines the [total] fluorescence decay rate γ(r) (far below saturation). Step 3 is to determine quantitative fluorescent count rates of the single-photon antenna versus pump intensity, ideally up to saturation. Ultrashort pulse excitation at saturation intensities means that the emitter emits up to one photon for each excitation pulse. Thus, overall set up collection efficiency should be measured using an efficient fluorophore in absence of any antenna, comparing measured count rates to the laser repetition frequency. Comparative measurements with and without antenna give access to the pump field enhancement (comparing saturation pump intensities) and fluorescence brightness enhancement (count rate comparison at low pump power). Step 4 is to measure the angular distribution of photons as modified by the antenna, by back-focal plane imaging.⁶⁵⁻⁶⁸ Quantitative intensity per steradian over an entire objective NA can be measured with excellent resolution (below 0.5°), using a CCD and the alignment protocols laid out by Kurvits et al.⁶⁸ One can now factorize out the pump enhancement P_pump in eq 1 (from saturation pump intensity), the collection efficiency (back-focal plane image partially maps in eq 3), and retrieve the quantum efficiency by correcting fluorescence brightness enhancement for the deduced pump and collection effects. Finally, given the quantum efficiency φ(r) and φ₀, the measured LDOS separates into radiative and quenching contributions according to eq 2. As a further consistency check, if one is able to drive the emitter in saturation using pulsed driving (excitation rate equals pump pulse repetition frequency f) and at the same pump wavelength also in cw (excitation rate is only limited by the emitter decay rate), the count rate ratio should directly provide γ(r) in units of f.

Figure 4.

Quantifying single-photon nanoantenna performance means (1) taking data with a single emitter at a time, (2) measuring decay rates with and without antenna using pulsed excitation, (3) mapping quantitatively collected photon counts vs input pump power up to saturation, and (4) Fourier microscopy to image radiation patterns (photons per second per steradian). To this end, one typically employs a confocal microscope scheme (sketch 2 + 3), imaging the antenna-emitter system (1) onto a Hanbury-Brown and Twiss APD configuration. Single emitter behavior is verified by measuring antibunching in the photon–photon correlation g⁽²⁾(τ) under cw or pulsed excitation (1), while time-correlated photon counting with pulsed excitation yields fluorescence decay rate enhancement (2). Some authors use dilute fluorophores diffusing in solvent around the emitter (indicated in (1) as dashed trajectory) to probe one antenna in different single-antenna single-emitter configurations. In a saturation experiment, (3) information is obtained from (A) fluorescence brighthness enhancement at low power (product of pump field enhancement, quantum efficiency enhancement and collection enhancement), (B) the change in saturation power (pump field enhancement), (C) the change in photon count rate in saturation. Note that (B) and (C) need accounting for whether the excitation is pulsed or cw. Diagram (4) shows that by insertion of one ”Bertrand” lens, a standard fluorescence imaging microscope (objective + tube lens) act as a Fourier or ”radiation pattern” imaging set up. Through the Bertrand lens the CCD images the objective back focal plane, not the sample plane. The data shown are not measured, but computer generated with Poisson noise at typical count rates included, for illustration purposes.

This approach only works if important criteria are met. First, as almost always in single-molecule microscopy, data in arbitrary units are not useful. Second, one needs stable emitter photophysics (no blinking), a well-known (high) intrinsic quantum efficiency, and access to saturation without photobleaching. These conditions are not easy to fulfill, for instance, quantum dots and dyes blink and bleach, and for emitters like NV centers, it is almost impossible to accurately know the (highly disperse) quantum efficiency.⁶⁹⁻⁷¹ The entire set of measurements easily exceeds the total fluorescence count budget of most single emitters. Third, proximity to the metal must not modify emitter wave functions, that is, one has to exclude electronic or chemical effects. As a fourth problem, the factorization of fluorescence brightness enhancement is not assumption free, since Fourier imaging only covers a fraction of all far-field radiation channels. Thus, quenching is indistinguishable from beaming out of the collection NA or emission into guided modes (the desired channel for waveguide-integrated plasmon antennas). Ideally, one strengthens the data set by probing the same antenna with different pump wavelengths to confirm the estimate of pump enhancement effects and probes an antenna with emitters of different efficiency to verify the assessment of LDOS changes.⁵³ Also, techniques like angle-resolved cathodoluminescence, that is, radiation pattern measurement using local point excitation with an electron beam,⁷²⁻⁷⁵ have been extremely helpful in confirming our understanding of antenna radiation patterns.

Survey of Reported Antenna Performances

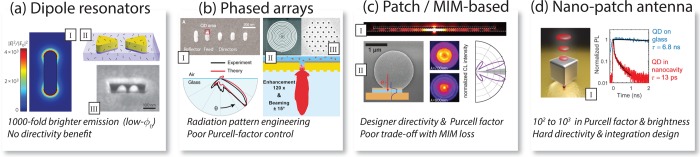
While reviews on plasmonic structures for field enhancement abound,^1,4 many structures that yield strong field enhancement will not yield efficient emission of light. In other words, requirements for “dark” plasmonics with huge local fields are very different from those for “bright” plasmonics. Here, I distinguish “bright” and “dark”, according to whether the ratio LRDOS/LDOS in eq 2 is close to unity (bright) or zero (dark plasmonics, useful when optimized for exciting guided plasmons or for high fields at the price of quenching). Reported antenna designs that can actually be classified as yielding bright plasmon-enhanced emission can be broadly understood as dipole antennas,⁷⁶ phased-array antennas,^{54,67,77−79} and so-called patch and nanopatch antennas.^{47,48,80−84}Figure 5 and Table 1 provide a showcase of these antennas and a tabulatation of figures of merit. Dipole antenna designs have been pivotal as model systems, but excel neither at emission directivity nor Purcell enhancement. Phased-array antennas master emission directivity control through intuitive design rules, yet are not particularly optimal for Purcell enhancement. Finally, patch antennas offer record high Purcell enhancements and some directivity control, though their functioning is least intuitive. In all instances, gold, silver, or aluminum nanoparticles for a strong plasmonic resonance in the visible to blue part of the spectrum are required. Similar antenna designs could be made in the infrared with other polaritonic or high-index dielectric materials. Yet, these fall out of the scope of single-photon nanoantennas owing to the dependence on efficient silicon single-photon detectors and good quantum emitters. Dielectric antennas at frequencies near multipole resonances tend to give directivity,⁸⁵⁻⁸⁷ can give significant fluorescence brightness enhancements,⁸⁸ yet strong Purcell enhancement is much harder to achieve.⁸⁹

Figure 5.

Single-photon nanoantenna classes of which metrics are reported in Table 1. (a) Dipole antennas like nanorods⁹⁹⁹ and dimer/gap antennas^30,50 have been reported to give 1000-fold fluorescence brightness enhancement for intrinsically poor emitters, in equal parts due to pump and LDOS enhancement. (b) Phased array nanoparticle⁵⁴ or nanohole antennas^67,93 impart directivity, usually with poor Purcell factor control. (c) Patch antennas^81,83 use the high confinement of metal insulator–metal waveguides for high LDOS. Emission leaking from the edge is directional, depending on patch size. (d) nanopatch natennas based on a metal nanoparticle-dielectric-spacer-metal according to Hoang et al.⁴⁸ display above 500-fold Purcell enhancement, and nearly 2000-fold brightness-enhancement even for intrinsically good emitters. While directional to some degree, the emission pattern is difficult to control. Image credits: Panel (a) I: Reprinted with permission from Nature Nanotechnology2012, 7, 379–382. Copyright 2012 Macmillan Publishers Ltd. Panel (a) II: Reprinted with permission from Nature Photonics2009, 3, 654–657. Copyright 2009 Macmillan Publishers Ltd. Panel (a) III: Reprinted with permission from Nature Nanotechnology2013, 8, 512–516. Copyright 2013 Macmillan Publishers Ltd. Panel (b) I: Reprinted with permission from Science2010, 329, 930–933. Copyright 2010 AAAS. The remaining figure parts are adapted or reprinted from the following American Chemical Society journals: panel b, part II (ref (67). Copyright 2011 American Chemical Society), panel c, part I (ref (81). Copyright 2013 American Chemical Society), and panel d (ref (48). Copyright 2016 American Chemical Society), panel b, part III (ref (93). Copyright 2013 American Chemical Society), and panel c, part II, (ref (83). Copyright 2014 American Chemical Society).

Table 1. Performance Metrics Extracted from Reported Experimental Data^a.

	analysis/assembly	source QE	system QE	brightness gain	pump	collection gain	rate enh.	LDOS	directiv.
nanosphere23,24	SNOM	φ0 = 100%	50%	13–20	25	none	22	∼22	[1.64]
nanorod51,52	burst/fcs	2	17	1000	130	none		∼9	[1.64]
lithographic bow tie30	random/fixed	2.5	20	1340	180	none	27	∼800	[1.64]
lithographic dimer50	burst/fcs	8	57	1100	144	none	4	∼315	[1.64]
DNA-bound dimer61	DNA, fixed	65	70	300		none	70		[1.64]
DNA-bound dimer59	DNA, fixed	65	80	475		none			[1.64]
same (quencher added)	DNA, fixed	<10	75	5000		none			[1.64]
Yagi-Uda54,94	litho								>3.6
bull’s eye67,93	burst/fcs	30	60	80	5	5	2		9
patch antenna80,81,83	litho	100	40			3	60–80	∼60–80	10
nanopatch antenna47,48	random, fixed	20	20–50	1900	170	5.5	>540	>2000	2.5

^aPump field enhancements of a factor 100–150 are routinely achieved. For inefficient emitters, an extra order of magnitude brightness enhancement (fluorescent count rate enhancement well below saturation) can be achieved through an LDOS-induced quantum efficiency change, even if measured rate changes do not show this. While numbers have been extracted from measured data where possible, it should be noted that some (especially quoted LDOS changes) are estimates. Quoted reported directivities are high only for metal nanoaperture and patch antennas (dipole: directivity D = 1.64, inserted in table as estimate, not measured). Effectively, collection efficiency gains are at best a factor 5.

The rationale of dipole antennas is evident: the simplest bright plasmon resonance is the strongly radiating dipole mode of a scatterer.^76,90 Plasmon particles above 50 nm in size will have up to 95% of their damping rate due to radiation into the far field, not absorption. This “albedo” also defines the maximum quantum efficiency that the single-photon nanoantenna can reach.⁹⁰ After a decade of intense study, it now appears that the best dipole antenna performance is achieved either with monocrystalline particles, such as self-assembled nanorods,^51,52,91 or with dimers that are self-assembled,⁶¹ or lithographically defined in a numerically optimized bow-tie shape, yet usually polycrystalline material.^30,50,92 Colloidal nanorods may not have a particularly optimized geometry, but the field enhancement at their distal end is strongly favored by the low material damping of monocrystalline nobel metal. In comparison, antennas composed of two elements with a controlled 10–20 nm gap benefit from a much cleverer geometry that exploits the lightning rod effect. However, once one uses lithography, the gains from geometry are negated by higher material loss of polycrystalline metal. Thus, in single-molecule studies, both systems show quite similar, up to 1000-fold, fluorescence count rate enhancements for intrinsically low efficiency fluorophores (reporting maximum performance in single molecule fluorescence burst (nanorods), respectively, best realization in random assembly). This enhancement factors in approximately a factor 100 from pump field enhancement, and the remainder due to a boost in quantum efficiency by accelerated spontaneous emission. Punj et al.⁵³ and Bideault et al.⁶¹ have studied systematically the performance as a function of gap size, demonstrating that it is crucial to reach gaps as narrow as ∼15 nm.

Dipole antennas offer almost no directivity control,²² as they impose a dipolar radiation pattern. This limitation is overcome by phased arrays in which the emitter excites an adjacent “feed” plasmon particle, which through its near field excites nearby plasmonic elements in a wavelength-sized oligomer.^{54,72,77−79} The radiation pattern of an antenna is the coherent sum of the dipole pattern directly emitted by the emitter, and the radiation pattern of the antenna elements that it excites. Similar physics holds for metal hole arrays and bull’s eyes, where the secondary radiators that make up the phased array antenna are holes or grooves excited through the guided surface plasmon polariton wave that the emitter launches. While the most publicized phased array is the Yagi-Uda antenna demonstrated by refs (54 and 72), it is not practical, as it is very sensitive to disorder.⁹⁴ Its property of beaming along the antenna axis is useful for waveguide-integrated realizations,⁹⁵ but not for extraction of light out of plane. For that purpose, the most successful directional phased array was developed for single emitter fluorescence spectroscopy, based on bull’s eye antennas in gold films.^67,93,96 These cause beaming of light from molecules inside the central aperture into a narrow cone of angles, reaching directivities close to 10. The directivity of plasmonic phased array antennas in such systems, as well as in particle oligomers can be modeled quantitatively with classroom-level diffraction physics, expressed in terms of an ”array factor” (Fourier transform of array geometry, that is, particle placement in the oligomers), multiplied with a “form factor” (radiation pattern of each element), convoluted with the k-content of the driving emission source field.^78,93 Accordingly, a prerequisite to make a directional beam is that the field is distributed over the plasmon structure over a wavelength-sized area. Directivity and Purcell enhancement do not combine naturally. Directional emission requires efficient radiation by plasmonic elements that are distributed over an extended, wavelength-sized volume, as opposed to requiring a very tightly confined field, as is beneficial for LDOS. Moreover, unidirectional performance, as in the Yagi-Uda antenna, specifically requires destructive interference of radiation into one-half-space, which reduces Purcell enhancement.⁷⁹ Still, the intrinsically poor Purcell factor can be overcome by replacing the feed element by a gap structure, like a bow tie. In my opinion, realistically the largest potential of plasmonic phased array antennas is not for single-photon applications with high Purcell factor but rather for fluorescence from source ensembles where efficiency counts, not rate enhancement. They can provide bright directional emission,⁹⁷ or even distributed feedback lasing in solid-state lighting scenarios.^98,99 As directivity control mainly utilizes the strong scattering of antenna elements, it is a function that could be very well performed by replacing metal with high-index dielectric. High-index dielectric nanoparticles can have similarly high, resonant scattering cross sections as metal particles, with the benefit of zero material loss.¹⁰⁰

Record breaking performance is achieved by plasmonic (nano)patch antennas. These stem from 2D metal–insulator–metal waveguides that afford tightly confined modes in the limit of vanishing (but nonzero) thickness of the insulator.^101,102 Since the gap in an MIM offers a very high LDOS enhancement, MIMs are naturally suited for “dark” quantum plasmonics where all light is funneled into guided plasmon modes, not free space. Esteban et al.⁸⁰ first proposed that truncation of one of the two metal layers to a finite sized patch results in reasonably efficient, directive antennas with high Purcell factors of up to 80.⁸¹⁻⁸³ If one tunes the gap to have 10–20 nm width, then the MIM LDOS is high, and an emitter midway the gap efficiently excites MIM plasmons without further quenching. Since outcoupling requires diffraction at the patch edge, Ohmic loss is dominated by the MIM propagation loss. A major surprise is that this patch geometry works even better if one shrinks the patch to a single Ag nanocube. Akselrod et al.⁴⁷ used template-stripped gold as ultrasmooth bottom layer, on which they deposited monocrystalline Ag cubes, separated from the gold by polymer spacings of nanometer-controlled thickness. While there is no way to deterministically control assembly with a single emitter, by random deposition of dilute emitters one can evidence instances with remarkable performance.⁴⁸ Reported Purcell enhancements as probed with single quantum dots are >500 times, while one can advantageously combine a modest efficiency gain, and a fivevold collection efficiency gain to obtain a large brightness gain of a factor 2000 compared to having the same emitters on a glass slide. It is remarkable that this Purcell factor is 2–3 orders of magnitude beyond that with which the field started a decade ago. More remarkable is the pairing of performance metrics, that is, Purcell enhancement, brightness, directivity, and reasonable efficiency (20–50% level). One could expect that modest further gains in efficiency and directivity could be made in this platform, for instance, by corrugating or layering the substrate to aid directivity, or if variation in antenna particle shape and material could reduce absorption.

Future Challenges

The recent breakthroughs in nanopatch/nanogap antennas^47,48,61 show that single-photon nanoantennas can realistically provide extremely high Purcell factor and brightness enhancement. One can furthermore create directional efficient sources by phased array design. For applications like antenna-enhanced single molecule microscopy and spectroscopy, this likely means that plasmon antennas have matured to a stage where one should focus on functionalization, not better antenna design. In terms of a roadmap for quantum optics, at current performance levels, plasmon antennas can compete with microcavity single-photon sources,⁷ in terms of sheer brightness and timing-performance, as the huge Purcell factors mean that picosecond lifetimes can be reached, even with “slow” emitters like quantum dot nanocrystals. Unexplored is whether the proposed concepts can be usefully operated as single photon sources, that is, stably running in a regime of pulsed driving in saturation for a prolonged period of time and with a high probability of capturing a photon for each pump pulse. Fundamentally problematic is the quantum efficiency for radiation into free space, which is not accurately known, with estimates for the nanopatch antenna in the 20–50% range.^48,103 An efficiency of 20% is in itself counterintuitively high for a plasmonic antenna with such a narrow gap. Yet it should be compared to the very high 98.4% β-factor reported for single-photon sources in III–V waveguides⁹ or, alternatively, the 65% photon capture efficiency reported by Somaschi et al.¹¹ for near-optimal high indistinguishability solid-state single photon sources. It is an unsettled theoretical question if efficiency can be pushed further up in any plasmonics-based design without sacrificing LDOS.^15,104 Dielectric nanoantennas so far have shown a similar potential to plasmon antennas when it comes to scattering strength and emission directionality, but not Purcell factor.¹⁰⁰ The nanopatch antenna geometry has as further practical drawback that the vertical-emission geometry is not easy to combine with on-chip integration. In fact, when examining the table of numbers in Figure 5, it stands out that all of the breakthrough performance antennas studied so far are optimized for radiation into free space. This table is undoubtedly biased by the fact that sofar the field was pushed mainly by single molecule microscopy, not photonic integration. While single emitters coupled to plasmonic waveguides have been widely studied, the physics of of nanoantennas coupled to dielectric waveguides have been limited to scattering studies^94,95 or designs,¹⁰⁵ not actual single molecule experiments. A method to design and deterministically fabricate plasmon antennas with such phenomenal light–matter interaction strengths, as in nanopatches, but directly matched to dielectric waveguides and preferably with electrical driving and electrical tuning would be extremely helpful.^21,106,107

An often touted advantage of nanoantennas over monolithic microcavity approaches is the freedom to match any emitter. Organic dyes, semiconductor nanocrystals, NV centers, and 2D materials have all been proposed for pairing with plasmonics. How to use this freedom in practice is as yet an open question. To demonstrate Purcell enhancement, one simply chooses whichever emitter has a convenient spectrum, efficiency, and lifetime. For a useful resource for quantum optics, one very often requires much more than just a Purcell factor. For instance, whether the photons are indistinguishable^7,8 is of fundamental importance. For indistinguishability, one needs the final source to have a spectral width limited only by the radiative decay rate without being broadened by dephasing. Generally, this requires select emitters at liquid helium temperatures to ensure MHz line widths. In the mature III–V microcavity platform, this is still a formidable challenge, with a recent study on micropillar cavities reporting >99% indistinguishability, yet at 65% photon extraction efficiency and a Purcell factor of 7.5.^10,11 The tremendous shortening of lifetime that one can obtain with huge LDOS enhancements, yet without entering quantum strong coupling, could be expected to ease this challenge. Figure 6a highlights the typical line width of an organic emitter like DBT¹⁰⁹ that rises from MHz (lifetime limited, nanosecond lifetime) at liquid helium temperature to several THz at room temperature. Even a 1000-fold Purcell enhancement would still result in a radiative line width of tens of GHzs, not several THz. Thus, any step toward an indistinguishable single-photon nanoantenna would still require low-temperature implementation, in my view at best at liquid nitrogen temperature, for instance, pairing plasmon antennas with organic molecules in a crystalline host.^5,109 This might be overcome if proposals¹¹⁰ for antennas with even orders of magnitude higher Purcell enhancement could be realized while still avoiding quantum strong coupling and quenching (see Figure 6).

Figure 6.

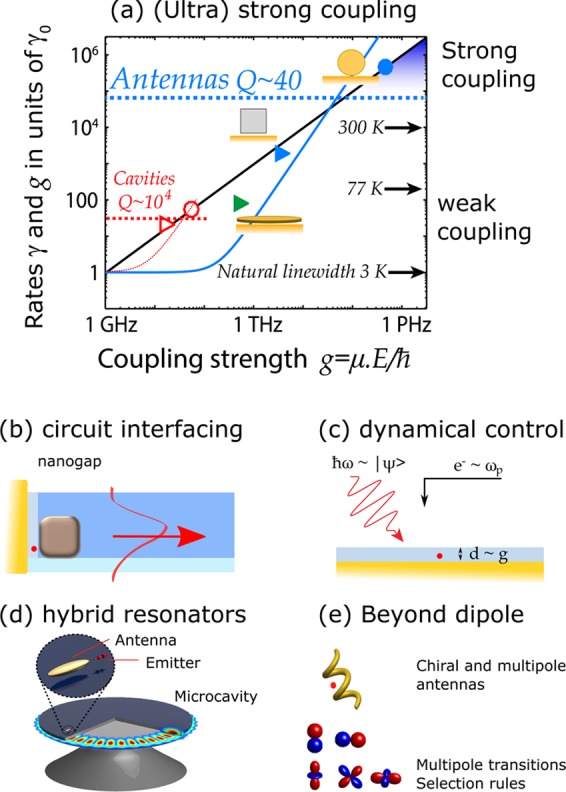
(a) Phase diagram to classify light–matter interaction strength in systems composed of a single emitter and a resonator compares characteristic decay rates as a function of the light–matter interaction strength g, i.e., the vacuum Rabi-frequency associated with the emitter dipole moment μ coupling to the single-photon field E. This diagram shows rates normalized to the emitter decay rate γ₀ in a homogeneous host (assumed as 1 GHz in this example) vs g. Plasmon antennas typically have Q ∼ 40 (meaning a resonator loss rate κ in the THz range), indicated by the blue dashed line. The spontaneous emission rate γ in eq 2 scales with g², as shown by the blue solid curve. Strong coupling occurs when the coupling rate g (black diagonal line g = g) exceeds the loss rate of the resonator (black line crossing horizontal dashed line) and the bare emitter decay rate. Solid symbols represent measured Purcell enhancements (triangles, weak coupling regime) for a plasmon patch antenna⁸¹ and nanopatch antenna⁴⁸ and measured coupling strength at strong coupling (circles) reported by Chikkaraddy.⁸⁴ For reference in the lower left corner, the typical numbers for microcavities (Q = 10⁴ (dashed horizontal red curve), corresponding enhanced rate, thin red dashed curve) are shown. The open triangle corresponds to a state-of-the-art photonic crystal single-photon source,⁹ and the open circle represents strong coupling in a micropillar dielectric cavity.¹⁰⁸ A source of indistinguishable single photons would require to be in weak coupling, but have a decay rate exceeding the emitter line width. For reference, arrows next to the right-hand axis indicate emitter line widths (typical values for the molecule DBT¹⁰⁹ at room temperature, liquid nitrogen, and liquid helium temperature (lifetime-limited), labeled 300, 77, and 3 K). Further open challenges include (b) the coupling of single-photon antennas to integrated dielectric photonic circuitry, (c) the dynamic modulation of single-photon antennas through controlling either the nanogap (controls g) or the plasmon resonance frequency ω_p, or by preparing the quantum state |Ψ⟩, for instance through optical control pulses. Panel (d) indicates the open challenge of controlling resonator Q to be arbitrary, with values between plasmonics and microcavities, through hybrid plasmonic-photonic structures. Panel (e): plasmon antennas to control or impart chirality or multipole character to single-photon emitters. Conversely, strong field gradients and the local vector structure of the field may overcome spectroscopic selection rules.

Novel physics can be reached if light–matter interaction is so strong that coupling rates exceed the plasmon and emitter line width. Recently, Chikkaraddy et al.⁸⁴ claimed to have reached this regime of single-molecule strong coupling with the vacuum field in a nanosphere-patch antenna geometry at room temperature. The basis of this claim is the observation of a distinct anticrossing between antenna and molecular resonance in extinction spectra of antennas that statistically have just one molecule. Whether this report indeed constitutes a vacuum Rabi splitting at the level of one molecule might still be disputed. The large antenna Purcell factor, quenching, and strong enhancement of Raman signals conspire to make a fluorescence (antibunching) measurement impossible, and according to some works, plasmon antenna scattering is not an unambiguous signature for strong coupling.¹¹¹ Nonetheless, it appears that the quantum strong coupling regime is in reach, with light–matter coupling strengths g on the 10s of THz level. This fact heralds new physics, well beyond repeating microcavity physics. At low Q and significant absorption, plasmon antennas should be very far from the well-tested Jaynes-Cummings theory for emitters and single mode closed cavities.^8,19 The concept of quantization underlying cavity QED presupposes single, normalizable optical mode functions, which mathematically do not exist for lossy open systems.¹² Recent reports attempt to salvage this through “quasi-normal modes”. Heated debates in literature indicate significant struggles, derived from the fact that these quasinormal modes are intrinsically divergent when moving away from the antenna, and disagreements result about how to obtain a proper normalization.^13,112−115 Building a fully quantum description on the basis of these modes is as yet a formidable task. Also, for experimentalists, new opportunities appear. A strongly coupled antenna-emitter system would be a strongly nonlinear scatterer, and one has to wonder what its scattering properties, radiation patterns, and spectral properties are, as well as its response in the time domain, that is, upon interrogation with few-cycle optical pulses. Also, one could envision cooperative effects in “few-photon nanoantennas”, where N emitters form coherent states through a shared antenna resonance.^19,116

If one believes that single-photon nanoantennas can lead to applications in integrated classical or quantum optics, their utility would be much enlarged if one would find mechanisms to dynamically modulate single nanoantennas. Two handles that one could envision for any emitter-resonator system are addressing of the emitter (i.e., femtosecond coherent control,¹¹⁷ or electric gating) and dynamic control of the resonator. For a high-Q microcavity, one can exert resonator control, even on time scales shorter than the cavity ring down time, by switching of refractive index (Kerr effect, free carrier absorption). For plasmon antennas, such switching mechanisms are not evident. Propositions that come to mind are to control electrostatically or electrochemically the charge density,^118−120 which can induce small (percent level) shifts in the plasma frequency of the metal and, thereby, in the plasmon resonance. Alternatively, one could switch the index of the dielectric spacer in the gap, or geometrically change the antenna gap.^121,122 Nanometer changes can give large differences in the light–matter interaction strength g.^50,61 How to reconcile such mechanisms with the extreme demands that low-dephasing single-photon emitters place on a (electrostatically) stable environment is, as yet, a completely open challenge. One alternative approach that we are pursuing is to create “practical-Q” antenna-cavity hybrids.^123−125 Modest-Q cavities coupled to nanoantennas can give Purcell factors at least as high as those of the antenna, yet at quality factors inherited from the cavity. This leads to a resonance that is sufficiently narrow that switching strategies to detune the antenna through detuning the cavity are effective. An added benefit is that quenching can be reduced in this system and that the hybrid system is naturally matched to integrated optics. The price one pays is that the positioning challenge doubles: one requires an emitter aligned to an antenna, aligned to a cavity.

Finally, I offer two observations on the single-photon nanoantenna field that fall outside the roadmap for broadband quantum optics. First, in 2006 many at the founding GRC Plasmonics conference chaired by Polman and Atwater relished the conceptual challenge of uniting quantum optics, multiple scattering of strongly scattering structures, and electrical engineering. By now, macroscopic quantum optics of antenna systems is being developed in full swing.¹⁸⁻²⁰ In contrast, electrical engineering has offered many design cues, especially for directional antennas, but in my view has not grown into an equal partner in pushing single-photon nanoantenna quantum optics. Mappings of calculated Purcell factors and directivity onto equivalent circuits² did not result into truly new insight in the crossover between electrical engineering and single-photon sources. Its main contribution in the future might lie at the interface with metamaterials (hyperbolic metamaterials, epsilon-near-zero (ENZ) platforms for antennas^126,127) or perhaps in the debate on quasinormal modes that parallels works in electrical engineering of C. E. Baum in the 1970s.¹²⁸ A second observation is that unexplored territory may also lie ahead in light–matter interaction mediated not by strong fields but by strong field gradients. Strong field gradients imply physics beyond the dipole approximation, intrinsically entailing the physics of multipole emitters and chirality. Of course, plasmon antennas could be designed such that a dipole emitter in an antenna spoofs a multipole emitter, using plasmon modes with a strong electric or magnetic multipole moment.^55,74 Spectrally, this would still be recognizable as light coming from an allowed dipole transition. Even in gap antennas, while the plasmon field is very strongly enhanced, it does not vary so sharply over the scale of a wave function that selection rules for other transitions appear to be broken. Only very particular emitters, such as quantum dots with extended wave functions and lanthanide ions, show notable emission beyond the electric dipole approximation that can to some degree be controlled by generalized photonic LDOS effects^129−132 Yet, a recent survey of highly confined plasmonic geometries suggests that some structures might allow to break selection rules, promoting usually forbidden transitions.¹⁶ Science right at the interface of strongly structured light, chirality and spin–orbit coupling in electromagnetic fields,¹³³ and light–matter interaction beyond the dipole approximation is a very interesting new topic that could ultimately also feed into (quantum) optics through the resulting entanglement of emission properties and internal degrees of freedom of the emitter.¹³⁴

The author declares no competing financial interest.