Emergence of Kondo lattice behavior in a van der Waals itinerant ferromagnet, Fe₃GeTe₂

Ferromagnetism and the Kondo effect are crucial for 3d electrons to become spin-separated and heavy at the same time.

Abstract

Searching for heavy fermion (HF) states in non–f-electron systems becomes an interesting issue, especially in the presence of magnetism, and can help explain the physics of complex compounds. Using angle-resolved photoemission spectroscopy, scanning tunneling microscopy, physical properties measurements, and the first-principles calculations, we observe the HF state in a 3d-electron van der Waals ferromagnet, Fe₃GeTe₂. Upon entering the ferromagnetic state, a massive spectral weight transfer occurs, which results from the exchange splitting. Meanwhile, the Fermi surface volume and effective electron mass are both enhanced. When the temperature drops below a characteristic temperature T*, heavy electrons gradually emerge with further enhanced effective electron mass. The coexistence of ferromagnetism and HF state can be well interpreted by the dual properties (itinerant and localized) of 3d electrons. This work expands the limit of ferromagnetic HF materials from f- to d-electron systems and illustrates the positive correlation between ferromagnetism and HF state in the 3d-electron material, which is quite different from the f-electron systems.

INTRODUCTION

Spins residing on a periodic lattice can exhibit peculiar behaviors when they are coupled to other interactions. For example, when spins are arranged periodically, magnetically ordered states arise (1). When spins scatter itinerant electrons within a Kondo scenario, Kondo singlet states emerge (2). In f-electron heavy-fermion (HF) systems, the localized f-spin is a necessary prerequisite for the appearance of magnetism and HF state, which originate from the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction and Kondo effect, respectively. Whereas for 3d-electron systems, the delocalization of d orbitals raises the question of whether the HF behavior and magnetism could be achieved in the same compound. Another imperative task is to understand the origin of the effective electron mass enhancement observed in d- and f-electron systems (3, 4). The driving forces of the enhancement are various, such as electron correlations (5), Kondo effect (2) or electron-bosonic mode coupling (6), and so on. Further investigation will be needed to understand the mass enhancement in 3d-electron ferromagnets.

Recently, a van der Waals ferromagnet, Fe₃GeTe₂ (FGT), with a Curie temperature of T_c = 230 K was synthesized (7, 8). The single-layer FGT reveals a significant uniaxial magnetocrystalline anisotropy energy (9), which could be applied for magnetic storage media such as tap and hard disks. Surprisingly, the value of the Sommerfeld coefficient of FGT has reached 135 mJ/(K²·mol) (7, 10–12), implying a large effective electron mass renormalization. However, theoretical calculations suggest that the remarkable mass enhancement is beyond naive band renormalizations (10, 11). By replacing Fe with Ni, the ferromagnetism of FGT disappears, and the Sommerfeld coefficient reduces to 9 mJ/(K²·mol) (10), implying correlations between ferromagnetism and electron mass. The critical behavior of FGT is close to the mean-field model, indicating a long-range ferromagnetic (FM) interaction around the critical point (13). Angle-resolved photoemission spectroscopy (ARPES) and scanning tunneling microscopy/spectroscopy (STM/STS) are ideal probes for resolving electronic structures in complex materials. In d- or f-electron systems, the two techniques have revealed both the magnetism and renormalizations of band dispersions, respectively (4, 5, 14, 15). These capabilities make FGT a promising candidate for investigating the relationship between effective electron mass and ferromagnetism.

Here, the coexistence of itinerant ferromagnetism and Kondo lattice behavior is observed in FGT. Exchange splitting induces a massive spectral weight transfer in the FM state revealed by ARPES. An additional Fano resonance feature observed by STM and the coherent-incoherent crossover exhibited in transport and magnetic measurements below a characteristic temperature T* indicate the emergence of a Kondo lattice behavior in FGT. Together with the first-principles calculations, the coexistence of the two phenomena can be well interpreted by the dual properties of 3d electrons. This work illustrates the positive correlation between ferromagnetism and Kondo lattice behavior in FGT and needs further advances in theoretical approaches for 3d-electron FM HF compounds.

RESULTS

Crystal and electronic structures

Figure 1 (A and B) depicts the schematic crystal structure of FGT. Its most pronounced character is the layered Fe₃Ge substructure sandwiched by two layers of Te atoms. The adjacent Te layers are connected by weak van der Waals interactions (7). Consequently, the most possible termination is the layer of Te atoms. The high quality and orientation of the as-grown facet of FGT are confirmed by the x-ray diffraction (XRD) pattern in Fig. 1D. One termination is observed exclusively, except for the few steps in Fig. 1E. The step height and nearest-neighbor atomic distance in Fig. 1 (F and H) agree well with the lattice parameters of FGT (P6₃/mmc, a = 0.399 nm, c =1.63 nm) (7).

Fig. 1. Crystal structure of FGT.

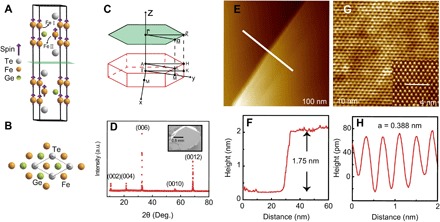
(A) Side and (B) top views of the crystal structure of FGT. Inequivalent Fe sites are labeled as I and II, respectively. The most possible cleaving plane parallel to the (001) surface is shown in green. (C) The bulk and projected Brillouin zones of FGT. (D) XRD pattern for the as-grown facet of FGT single crystals, with (001) diffraction peaks observed exclusively. The insert is an image of FGT compound revealed by scanning electron microscopy. a.u., arbitrary units. (E) STM step and (G) atomic resolution images (0.3 V, 100 pA) on the cleaved (001) surface of FGT. (F) The step height and (H) nearest-neighbor atomic distance are measured from the profiles of the line sections in (E) and (G), respectively.

The observed Fermi surface (FS) contour consists of a circular-shaped pocket (α), a hexagonal-shaped hole pocket (β) centered at the Γ point, and an elliptical-shaped pocket (γ) centered at the K point in Fig. 2 (A and B). The band α and hole-like band β cross E_F. Band θ extends to a higher binding energy (BE), and band ε is located at a 500- to 600-meV BE (Fig. 2C). When the light source becomes He I light, the band α disappears, and another hole-like band emerges around the Γ point in fig. S2. Around the K point in Fig. 2E, a nearly nondispersive band η is located at the 500-meV BE, indicating its localized nature. Band γ crosses E_F and connects band η with a much weaker spectral weight.

Fig. 2. Valence band structures of FGT.

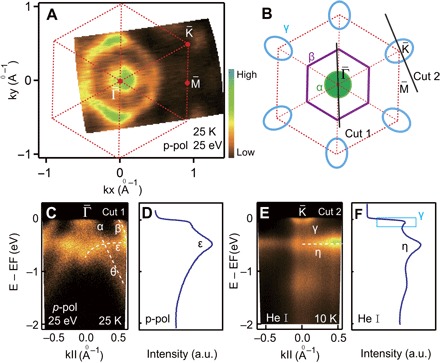
(A and B) Photoemission intensity map at E_F integrated over a window (E_F, − 10 and +10 meV) with p-polarized light and the corresponding FS sheets by tracking Fermi crossings. (C and D) Photoemission intensity plot and its angle-integrated photoemission spectroscopy (AIPES) with p-polarized light along cut 1 in (B). (E and F) Photoemission intensity plot and its AIPES with He I light along cut 2 in (B).

Spectral weight transfer in the FM state

To trace the origin of the effective electron mass enhancement in FGT, the temperature dependence of the electronic structure of band γ is exhibited in Fig. 3. Two-petalled band γ evolves into waterfall-like bands below a 40-meV BE in Fig. 3B1. With the increase of temperature, the two-petalled band weakens and totally disappears above 260 K. Meanwhile, spectral weight redistributions are observed with the increase of temperature in Fig. 3C. (i) The peak centered at a 50-meV BE weakens. (ii) The dip centered at a 200-meV BE starts to drain away. (iii) The hump centered at a 500-meV BE has a lower intensity.

Fig. 3. Spectral weight transfer in the FM state.

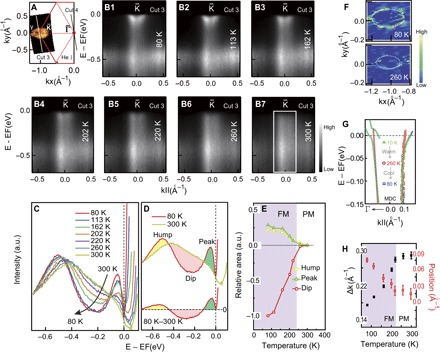
(A) Photoemission intensity map at E_F integrated over a window (E_F, −10 and +10 meV) around the K point with He I light at 80 K. (B) Temperature dependence of the band structure along cut 3 in (A), warming up from 80 to 300 K and then cooling back to 80 K. The nearly unchanged data quality excludes the possibility of surface aging as being responsible for the observed effect. (C) Temperature dependence of the AIPES divided by the Fermi-Dirac function and normalized at a 750-meV BE. The integrated range is marked by the solid rectangle in (B7). (D) The AIPES data at 80 and 300 K in (C). The curve in the lower panel corresponds to the AIPES spectrum at 80 K subtracted by that measured at 300 K. (E) Temperature dependences of the relative areas of the peak, dip, and hump in (D). The relative areas are normalized by the dip area at 80 K. (F) Curvature intensity maps around the K point at 80 and 260 K, respectively. The white dashed ellipses are visual guides. (G) Extracted momentum distribution curves (MDCs) dispersion of band γ. The solid and dotted lines represent the calculated and experimental results, respectively. The red lines represent the dispersions in the paramagnetic (PM) state, whereas other lines represent those in the FM state. (H) The temperature dependences of MDC peak widths at E_F (black squares) and MDC peak position shifts (red squares) of band γ. The peak position shifts are defined as k_F − k_{(150 meV)}, where k_F is the Fermi vector, and k_{(150 meV)} is the MDC peak position at a 150-meV BE.

The quantitative analysis of the redistribution is shown in Fig. 3E. Above T_c, the spectra do not exhibit significant changes. Below T_c, the redistribution of the spectra deepens with the decrease of temperature. Similar redistributions can be observed around the Γ point and other momentum position in fig. S2, indicating that the spectral weight transfer is independent of the details of band structures. For a FM metal, the exchange splitting follows the Stoner model, according to which the splitting emerges below T_c (1, 14). The spectral weight transfer, which is also observed in other ferromagnets [such as MnP and CoS₂ (14, 16)] to some extent, is a signature of the exchange splitting in FGT. For example, the enhanced density of state (DOS) at a 500-meV BE and suppressed DOS at a 200-meV BE in the FM state can be explained by the calculations (10) that support the Stoner model.

We find that the onset temperature of the FM transition is slightly higher than the bulk T_c in Fig. 3 (C and E). The spectral weight transfer already happens just above T_c. Broken symmetry at the surface is likely to influence the FM state due to the breakdown of the long-range FM interaction (13) and may account for the slightly increased onset transition temperature relative to that of the bulk material. The phenomena have already been observed in other magnetic materials, such as URu₂Si₂ (17) and MnP (14).

We extract the dispersion and peak width of band γ near E_F using the MDC analysis shown in Fig. 3 (G and H). The dispersion at 260 K is linear near E_F. When the temperature decreases, the band dispersion above a 40-meV BE bends to larger momentum values accompanied by smaller group velocities. By performing a conventional analysis (18), we fit straight lines in the dispersions between ±10 meV of E_F in Fig. 3G. We extract a quantity of ν_{F(260 K)}/ν_{F(80 K)} = 5.29 ± 0.95, where ν_{F(80 K)} and ν_{F(260 K)} are group velocities of band γ at 80 and 260 K, respectively. Consequently, we deduce an effective electron mass enhancement: m_{80 K}/m_{260 K} = ν_{F(260 K)}/ν_{F(80 K)} = 5.29. Furthermore, the quantitative analyses of the width at E_F and the position shift of MDC peak of band γ are shown in Fig. 3H. In the PM state, the position shift and the width of the MDC peak stay immobile. In the FM state, the width starts to decrease, and the position shift starts to increase monotonously. The marked suppression of the peak width and enhanced DOS near E_F of band γ indicate that the formation of a coherent state is below T_c. Besides, the increase of peak position shift in the FM state reveals that the enlarged FS volume and effective electron mass are directly related to the PM-FM transition.

The evolution of band γ as a function of temperature can be well explained by exchange splitting. Exchange splitting separates spin-up and spin-down channels of the electronic states and shifts the weakly dispersive valence bands to E_F in the FM state, which is highlighted by the calculation results in Fig. 3G. Specific heat measurements show a large effective electron mass enhancement of ~m*/m_b = 13.3 in FGT, where m_b is determined from density functional calculations or the nonmagnetic reference material Ni₃GeTe₂ (7, 10, 11). The calculation result allows an estimated effective mass of 2.61 m_b due to correlation-induced renormalization (10). Our observation of the ferromagnetism-related renormalization in band γ provides direct evidence of an effective electron mass enhancement of ~5.29 m_b. However, it is still insufficient to account for the total enhancement. More investigations should be made to illustrate this issue.

Emergence of Fano lattice behavior

Because of the lack of information about the unoccupied states revealed by ARPES, we perform STM to probe the total electronic structure around E_F. Two peaks can be observed in dI/dV spectra, whereas their intensities are highly dependent on the locations in Fig. 4C. The Fermi level is located at the edge of peak B at 6 K, indicating an enhancement of the DOS at E_F. This consequently induces another effective electron mass enhancement. In the dark area in Fig. 4 (A and B, points 1 to 3 and 8), the intensity of peak A (−50 meV) is much weaker than that of peak B (+25 meV), whereas in the bright area (points 4 to 7), the intensity of peak A is comparable with that of peak B. The excitation at a 50-meV BE is consistent with the peak near E_F, as revealed by ARPES in Fig. 3C, which originates from the PM-FM transition. As the temperature is raised, we find that the position of peak A is nearly unchanged, whereas peak B rapidly broadens in Fig. 4D. The two peaks respond differently to temperature and spatial locations (fig. S6), indicating their different origins. The behavior of peak B is reminiscent of the Fano resonance peak in Kondo systems (17). In a Kondo system, the Fano line shape naturally occurs because of the presence of two interfering tunneling pathing from the STM tip, one directly into the itinerant electrons and the other indirectly through the heavy quasi-particles. The Fano resonance line shape follows

$$\mathit{d}\mathit{I}/\mathit{d}\mathit{V}\propto \frac{{(\mathrm{\epsilon }+\mathit{q})}^2}{1+{\mathrm{\epsilon }}^2},\mathrm{\epsilon }=\frac{\mathit{e}\mathit{V}-{\mathrm{\epsilon }}_0}{\mathrm{\Gamma }}$$ (1)

Fig. 4. Emergence of the Fano resonance peak at low temperature.

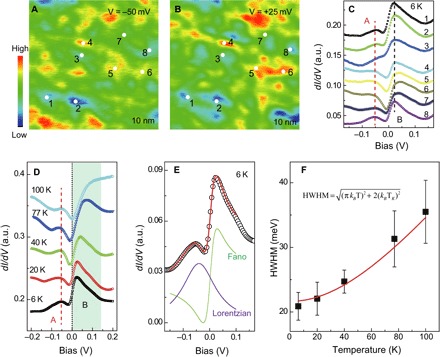
(A and B) dI/dV maps (200 pA) on the same field at 6 K with bias voltages of −50 and +25 mV, respectively. (C) Spatial-resolved low-energy dI/dV spectra measured at the eight locations marked in (A) and (B). Two peaks located at −50 meV (A) and +25 meV (B) are marked with dashed lines. (D) Spatially averaged dI/dV spectra taken at different temperatures. The two peaks are marked with the red dashed line and green shadow, respectively. (E) Theoretical simulation (red curve) of the experimental dI/dV spectrum (black dots) at 6 K. The simulated Fano feature (green curve) is subtracted from the raw data, and the remaining peak is fitted by a Lorentzian term (purple curve). The Fano and Lorentzian terms are shifted for clarity. (F) Temperature dependence of the Fano resonance width extracted from the fitting in (E). The red line represents the temperature dependence of the width for a single Kondo impurity.

Here, q reflects the quality of the ratio of probabilities between the two tunneling paths, ε₀ is the energy location of the resonance, and Γ is the resonance half width at the half maximum (HWHM).

We find that all the spectra around E_F can be well fit with a combination of the Fano resonance peak and the Lorentzian peak in Fig. 4E. The temperature dependence of HWHM of the Fano peak extracted from the fitting is shown in Fig. 4F. Fortunately, the width of peak B is nearly spatially independent, allowing us to extract a reliable HWHM at different temperatures. Results for the single-channel spin one-half Kondo impurity model (17, 19) in a Fermi liquid regime have been used to describe the temperature dependence of HWHM

$$\text{HWHM} =\sqrt{{(\mathrm{\pi }{\mathit{k}}_{\mathrm{B}}\mathit{T})}^2+2{({\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{K}})}^2}$$ (2)

and to extract the value of the Kondo temperature of FGT (T_K ≈ 190 ± 20 K). The success of this model at describing the spectra indicates the existence of a possible Kondo lattice behavior in FGT, which reveals that localized spins reside on the periodic lattice at high temperature and are coupled with itinerant electrons with reduced temperature. As the temperature is raised to 100 K, peak A is nearly unchanged, whereas the Fermi level shifts to the minimum in the two-peak structure in Fig. 4D, implying the diminution of peak B and decreased effective electron mass. The Fano line shape and width evolution as a function of the temperature of peak B agree well with the behaviors of the Kondo peak in HF systems.

Recently, another FM–antiferromagnetic (AFM) transition has been reported in FGT inside the FM state (20). However, the strength of the signal of antiferromagnetism is fairly weak and is 60 times smaller than that of its ferromagnetism. Besides, some electronic characterization methods, such as resistivity, specific heat, and thermal conductivity (7, 12) measurements, also fail to detect such a small magnetic signal, indicating that the weak transition is electronic state–insensitive. Consequently, we propose that the AFM transition cannot explain the Fano-shaped peak in our STS data, which are totally reflections of electronic states.

Although the Kondo lattice behavior is not the exclusive explanation of the Fano resonance peak observed in the dI/dV curves, we could confirm that the enhanced Sommerfeld coefficient or effective electron mass is highly related to the electronic contributions. Because STM and ARPES are tools to characterize the electronic states, the situation is quite different from some other layered magnetic compounds, such as CrCl₃, CrSiTe₃, CrI₃, and Mn₃Si₂Te₆ (21–24). These compounds have relatively large Sommerfeld coefficients but are electrically insulating, demonstrating that the large Sommerfeld coefficients of those compounds are independent of any charge carriers, probably related to magnetic excitations. The electronic structure differences between FGT and the other magnetic compounds mentioned above indicate that electronic excitations are responsible for the enhanced effective electron mass in FGT and not the magnetic excitations observed in the magnetic insulating compounds.

Coherent-incoherent crossover in the FM state

To further study the possible Kondo lattice behavior in FGT, we perform transport and magnetic measurements, as shown in Fig. 5. Except for the PM-FM transition at 230 K, a coherent-incoherent crossover at T* ~ 110 ± 20 and 150 ± 20 K is observed in resistivity and magnetic susceptibility curves in FGT, respectively. It should be mentioned that the line shapes of the measured curves in the crossover regions in Fig. 5 (A and B) are quite different from those at T_c, where the curves show abrupt kink structures. It implies that the physics associated with the crossover behavior is different from the PM-FM transition. Nevertheless, since Fe deficiency has been observed in the FGT single crystal (12), can this crossover behavior be a reflection of the Fe-deficient parts of the crystal? Recently, an Fe-deficient FGT compound, Fe_2.9GeTe₂, was synthesized and exhibits a Curie temperature of 178 K, which is largely suppressed compared with the transition temperature of the stoichiometric compound. Except for the abrupt change in the resistivity curve at 178 K, a crossover behavior has been observed below 80 K (25). A similar crossover behavior could also be observed in the magnetic susceptibility curve of the Fe-deficient FGT, except for the marked change at T_c (12). These phenomena indicate that the crossover behavior is different from the FM-PM transition in an Fe-deficient compound. The slopes of resistivity and magnetic susceptibility show significant changes below T*, similar to other d-electron HF systems, such as AFe₂As₂, CaCu₃Ir₄O₁₂, and LiV₂O₄ (3, 26, 27). We would like to emphasize that these crossover behaviors have been widely observed in f-electron HF materials and are related to the hybridization between local moments and conduction electrons (28–32). The great similarity to other d- and f-electron HF materials also strongly suggests a possible Kondo scenario for FGT.

Fig. 5. Coherent-incoherent crossover in the FM state.

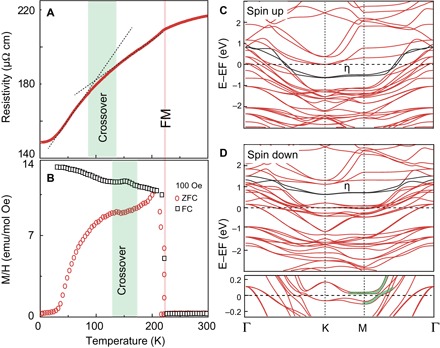
(A and B) Temperature dependence of resistivity and magnetic susceptibility for FGT. The dashed lines in (A) are two tentative T linear trends to extract the value of T*. The bold green and orange lines mark the crossover and PM-FM transition, respectively. (C) Spin-up and (D) Spin-down band structures of Te-terminated FGT. The black line is the experimentally observed flat band η in Figs. 2 and 3. The bold green lines in the lower panel in (D) represent the hybridization between strongly dispersive bands and weakly dispersive bands near E_F.

In the FGT compound, the coherent temperature T* is different from the Kondo temperature T_K ≈ 190 ± 20 K, which is extracted from the fitting of the Fano resonance peak. The separation of the two temperatures is widely observed in 4f- or 5f-electron materials, such as CeCoIn₅, URu₂Si₂, and USb₂ (17, 33–35). On the other hand, in HF systems, a scaling behavior is observed as follows (36)

$$\mathrm{\gamma }\approx \frac{\mathit{R}\text{log}2}{{\mathit{T}}_{\mathrm{K}}}\approx \frac{10000}{{\mathit{T}}_{\mathrm{K}}}[\mathit{m}\mathit{J}/({\mathit{K}}^2\cdot \text{mol})]$$ (3)

where γ is the Sommerfeld coefficient. For FGT, because there are three Fe atoms per formula unit, γ is about 135/3 = 45 mJ/(K²·mol Fe), and we can obtain the calculated Kondo temperature T_K ≈ 222 K, which is in excellent agreement with our experimental value. All these results further qualify the FGT compound as a d-electron HF system.

Being in the Kondo regime implies that the atoms must host, at least, a localized d-electron level whose magnetic moment is screened by conduction electrons. The last piece of the puzzle is the origin of the localized spins in FGT. For example, one pronounced characteristic of the electronic structure of FGT is the nearly nondispersive band η, which is confirmed by ARPES measurements in Fig. 2E and calculation results in Fig. 5 (C and D). The dispersion of band η is reminiscent of the f⁰ state located at a 2-eV BE in 4f-electron systems (37), which would act as local moments in HF materials. The hybridization between localized η band and conduction band is distinct in Fig. 5D. Except for band η, the hybridization between other weakly dispersive bands and the strongly dispersive band near E_F is also observed in the lower panel in Fig. 5D, which could induce a hybridization gap and enhance the effective electron mass of FGT. The similar hybridization has been widely observed in f-electron HF systems (33). Furthermore, the Rhodes-Wohlfarth ratio of FGT also indicates an FGT compound lying in the region between localized and itinerant ferromagnetism (7, 12, 38, 39). Exchange splitting plays a significant role for the formation of the Kondo lattice behavior in FGT. Exchange splitting separates the spin-up and spin-down channels of electronic states and shifts the weakly dispersive bands to E_F, providing a platform for the hybridization between localized state and itinerant state near E_F. The calculation results provide a direct vision of how heavy electrons emerge in an itinerant ferromagnet.

DISCUSSION

The flat band observed by ARPES in Fig. 2E demonstrates that when plentiful electrons are restricted in a small area, strong electronic correlations occur. According to the calculations of Zhu et al. (10), the strength of the Hubbard interactions in FGT is about U = 5 to 5.5 eV, which is similar to the values of other HF systems. For example, the strength of Hubbard interactions in a d-electron HF compound KFe₂As₂ is about U = 5 eV (40). The value in a classical f-electron HF compound CeIn₃ is U = 6.2 eV (41). The similar environment of the d- or f-local orbitals provides a platform for the formation of the similar properties, such as the HF state. Although the calculations merged with the single-site dynamical mean-field theory produce the magnetic moment nearly the same with the experimental value, the electron mass enhancement cannot be fully explained in these calculations (10). This indicates the existence of other interactions in this compound, except for the electronic correlations. Considering the existence of localized electrons, the suitable Hubbard interactions, the Fano line shape STS curves, the crossover behaviors in the transport and magnetic measurements, and the direct observation of hybridization between different bands in the calculations, we propose that the Kondo lattice behavior is present at low temperature in FGT.

To date, neither the local scenario nor the itinerant scenario is sufficient to account for the coexistence of itinerant ferromagnetism and Kondo lattice behavior in FGT. Both of them should be taken into account, which is somehow similar to the situations in f-electron systems (42). The coexistence between the Kondo lattice behavior and FM order has already been observed in f-electron systems, such as UTe (43), CePt (44), CeSi_x (45), CeAgSb₂ (46), URu_2−xRe_xSi₂ (47), UGe₂ (48), URhGe (49), and so on. However, the coherent temperature is usually higher than the Curie temperature in those materials, opposite to FGT. The relatively high Curie temperature in FGT may result from the higher degree of delocalization of the 3d states than f states (50). On the other hand, the magnetism of f-electron HF systems mainly results from the RKKY interaction. The Kondo effect and RKKY interaction exhibit clear anticorrelation (51). For FGT, the Kondo lattice behavior is highly related to its ferromagnetism. It deserves to be mentioned that the Kondo effect has already been observed in 3d-electron FM atomic contacts (Fe, Co, and Ni). The nanoscale size of the samples is a dominant factor for the formation of local moment and decrease of the FM coupling with neighboring atoms (52). Kondo lattice behavior in a 3d-electron bulk ferromagnet presents a brand new issue.

In summary, we perform ARPES, STM, transport, magnetic measurements, and the first-principles calculations to illustrate the electronic structure of the van der Waals ferromagnet FGT. The coexistence of itinerant ferromagnetism and Kondo lattice behavior is observed in this 3d-electron material. The ferromagnetism leads to a massive spectral weight transfer revealed by ARPES. The Kondo lattice behavior is confirmed by the Fano resonance feature revealed by STM, coherent-incoherent crossover by transport and magnetic measurements, and the calculation results. The dual nature of 3d electrons plays a significant role in the coexistence of the two phenomena. This work expands the limit of FM HF materials from f- to d-electron systems and clarifies the underlying coexistence of magnetism and Kondo lattice physics in 3d-electron bulk materials.

MATERIALS AND METHODS

Sample growth and characterization

High-quality single crystals of FGT were grown by the chemical transport method, with iodine as the transport agent (7). The chemical compositions of the single crystals were determined by energy-dispersive x-ray spectroscopy. XRD measurements were performed on a PANalytical X’Pert Pro diffractometer (Cu K_α radiation). The resistivity and dc magnetization measurements were performed with the Quantum Design Physical Property Measurement System.

STM measurements

STM experiments were performed with a low-temperature ultrahigh vacuum system. The FGT crystals were cleaved in the preparation chamber with pressure better than 5 × 10⁻¹¹ mbar at 77 K and then immediately transferred to the STM scanning stage cooled at 6 K with pressure better than 1 × 10⁻¹¹ mbar. A tungsten tip was used for the STM measurements. Before each measurement, the tip was treated and calibrated carefully with Cu(111) surface. After each measurement, the tip was rechecked with Cu(111) surface to exclude the tip states. The dI/dV spectra were acquired by the standard lock-in technique.

ARPES measurements

ARPES experiments with p-polarized (21.2-eV He Iα) light were performed at the National Synchrotron Radiation Laboratory in Hefei, China (with a home-built ARPES) using a VG ARUPS 10 (VG Scienta R4000) electron analyzer. The overall energy and momentum resolutions were 30 (10) meV and 0.012 (0.006) Å⁻¹, respectively. The samples were cleaved in situ along the (001) plane and measured under ultrahigh vacuum better than 8 × 10⁻¹¹ mbar. A freshly evaporated gold sample in electrical contact with the FGT sample was served to calibrate E_F. The surfaces of FGT were very stable and showed no signs of degradation over 24 hours.

First-principles calculations

The electronic structures of Te-terminated FGT for FM phase and PM phases were calculated with the projector-augmented wave method, as implemented in the Vienna ab initio simulation package within the local density approximation. The Ceperley-Alder functional was used to describe the exchange correlation potential, and the cutoff energy of plane wave was 700 eV. The Monkhorst-Pack grid was chosen as 18 × 18 × 2. The total energy was converged to 10⁻⁵ eV. The calculated average magnetic moment per Fe atom of FGT was 1.454 μ_B, within the range of experimental values (7, 8, 10).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/1/eaao6791/DC1

fig. S1. Hysteresis loop for H parallel to the c axis at 2 K.

fig. S2. Spectral weight transfer at other momentum locations.

fig. S3. Enlarged Fermi surface volume in the FM state.

fig. S4. Spatial-resolved low-energy dI/dV spectra at different temperatures.

fig. S5. Band structures of Te-terminated FGT in the PM state.

fig. S6. The positive correlation between ferromagnetism and Kondo lattice behavior.

References (53–65)