Sorting Things Out: Cell Sorting during Hydra Regeneration

Main Text

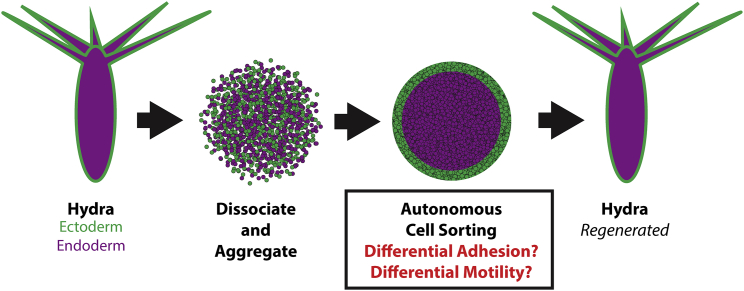
Hydra, a fascinating freshwater cnidarian famous for being able to regenerate fully after having been dissociated into single cells and recombined into a heterogeneous aggregate (1), plays an important role in our understanding of the process of cell sorting (2, 3). Cell sorting describes the phenomenon where a mixed population of cells spontaneously sorts into distinct tissues, and a crucial early step of Hydra regeneration is that the initially heterogeneous aggregate of cells spontaneously sorts into a sphere-within-a-sphere structure with ectodermal cells on the outside and endodermal cells within (see Fig. 1). How, precisely, such sorting occurs has been the subject of much research as identifying the mechanisms behind cell sorting has implications for better understanding how tissues and organs form and our future abilities to engineer such systems.

Figure 1.

Abbreviated Hydra regeneration cycle. (Left to right) A mature Hydra is dissociated into individual cells of either ectoderm (green, outer tissue) or endoderm (purple, inner tissue) lineages that are subsequently concentrated into a heterogeneous aggregate. Upon aggregation, the ectodermal cells sort to the outside of the aggregate and the endodermal cells concentrate in the interior, creating a sphere-within-a-sphere. Following this, a variety of developmental steps occur that eventually result in a fully regenerated Hydra. To see this figure in color, go online.

To date, two dominant hypotheses have been proposed to explain the phenomenon as it occurs in Hydra. First, referred to here as “differential adhesivity”, is a variant of the classic differential adhesion hypothesis that reflects relative differences in cell-cell adhesion/interfacial tensions between different cell types that make specific cell-cell arrangements more energetically favorable (4, 5). The second hypothesis is known as “differential motility”, and reflects relative differences in the active motion of endodermal and ectodermal cells during sorting (6, 7). Before now, there have been data to support both hypotheses in Hydra and other, related sorting systems (3). In the case of Hydra, experimental difficulties have arisen that make it difficult to pin down specific mechanisms, such as the fact that the properties of endodermal and ectodermal cells change markedly over time.

Cochet-Escartin et al. (8) set out to address these ambiguities using a methodical combination of in vivo experiments (e.g., two-photon imaging of regenerating Hydra aggregates), and computational models (e.g., 3D cellular Potts models). By tracking cell sorting and the migration trajectories of individual cells in real-time from the moment of reaggregation up through cellular sorting, the authors were able to establish complete trajectories of the cells involved in the process. These data, combined with physical parameters attained through a combination of biophysical assays including micropipette aspiration and aggregate fusion, were used to develop computational models capable of interrogating the relative contributions of both differential adhesivity and differential motility.

Their findings indicate that, contrary to the assumption that both differential adhesivity and differential motility play some role in initial ectoderm/endoderm sorting in Hydra, differential adhesivity alone was sufficient to explain the data. Moreover, the authors noted no apparent differential motility between endodermal and ectodermal cells in the time-lapse imaging data according to a variety of metrics including the mean-squared-displacement of cellular trajectories, mean cellular speeds, and persistence of cellular motion within the aggregates. Although there could still be sorting interactions mediated by the extracellular matrix that forms between the two tissue types in the mature animal, the authors performed antibody staining experiments to rule this out; noting that significant extracellular matrix synthesis appears to occur only much later in the regeneration program. Together, these data make it unlikely that differential motility drives cell sorting in Hydra—a statement further supported by computational modeling demonstrating that differential adhesivity should be sufficient. Significantly, the authors also found that the geometric context under which regeneration occurs can have a marked impact on the observed phenomena. Whereas many previous Hydra models have been developed in a 2D context with well-defined geometries and boundary conditions (9), the Hydra aggregates studied here began as flattish disks that, over the course of regeneration, changed shape to the fully developed sphere-within-a-sphere structure. Such differences over time likely account for variations in the parameters measured in this study versus prior work and serve to highlight the importance of, and difficulty in, studying tissues and organisms in their natural 3D forms.

Although the data do not favor differential motility and appear to strongly support differential adhesivity, a major open question is how such adhesive interfaces between Hydra cells develop. A core assumption of classical differential adhesion is that the process is mediated by cell-cell adhesion proteins, typically those of the cadherin superfamily. Although such interactions are very well characterized in other systems, cell-cell adhesion in Hydra is not well understood (although a putative cadherin has been identified (10)). Future work to understand such interactions will help better isolate how different cellular components contribute to cell sorting—knowledge that will not only improve our biological and biophysical understanding of the system, but also our ability to precisely manipulate such sorting processes to control and design tissues in the future.

Overall, Cochet-Escartin et al. (8) present a cogent and elegant study that demonstrates how differential adhesivity is sufficient to explain the fundamental cell sorting process that initiates Hydra regeneration. Beyond advancing developmental biology and the biophysics of cell sorting, this work also illustrates the value and excitement that quirky model organisms such as Hydra bring to the table and will hopefully spark future studies with these fascinating creatures.

Editor: Celeste Nelson.