Infectious disease prediction with kernel conditional density estimation

Abstract

Creating statistical models that generate accurate predictions of infectious disease incidence is a challenging problem whose solution could benefit public health decision makers. We develop a new approach to this problem using kernel conditional density estimation (KCDE) and copulas. We obtain predictive distributions for incidence in individual weeks using KCDE and tie those distributions together into joint distributions using copulas. This strategy enables us to create predictions for the timing of and incidence in the peak week of the season. Our implementation of KCDE incorporates two novel kernel components: a periodic component that captures seasonality in disease incidence, and a component that allows for a full parameterization of the bandwidth matrix with discrete variables. We demonstrate via simulation that a fully parameterized bandwidth matrix can be beneficial for estimating conditional densities. We apply the method to predicting dengue fever and influenza, and compare to a seasonal autoregressive integrated moving average (SARIMA) model and HHH4, a previously published extension to the generalized linear model framework developed for infectious disease incidence. KCDE outperforms the baseline methods for predictions of dengue incidence in individual weeks. KCDE also offers more consistent performance than the baseline models for predictions of incidence in the peak week, and is comparable to the baseline models on the other prediction targets. Using the periodic kernel function led to better predictions of incidence. Our approach and extensions of it could yield improved predictions for public health decision makers, particularly in diseases with heterogeneous seasonal dynamics such as dengue fever.

1. Introduction

With the maturation of digital disease surveillance systems in recent years, accurate and real-time infectious disease prediction has become an achieveable goal in many contexts. These predictions provide valuable information to public health officials planning disease prevention and control measures [1]. For example, interventions designed to reduce person-to-person transmission of disease have been associated with diminished outbreak intensity [2]. Accurate predictions can help target such interventions more effectively.

In this work, we use a semi-parametric approach that combines a non-parametric method for conditional density estimation referred to as kernel conditional density estimation (KCDE) with a parametric method for modeling joint dependence structures known as copulas. We apply this method to make predictions for three targets chosen by the United States Centers for Disease Control (CDC) as relevant to public health:

1. Incidence h time steps in the future (at “prediction horizon” h).

2. Timing of the week of the current season with the highest incidence.

3. Incidence in the week of the current season with the highest incidence.

These quantities have emerged as being targets of particular utility in making planning decisions [3, 4], and variations on these targets have been set as the quantities of interest in recent prediction contests [5].

We model the first of these prediction targets directly; predictions for the second and third prediction targets are derived from a joint predictive distribution of incidence in each remaining week of the season. Using data available up through time t*, we employ KCDE to obtain separate predictive distributions for disease incidence in each subsequent week of the season. We then combine those marginal distributions using copulas to obtain joint predictive distributions for the trajectory of incidence over the following weeks. Without a technique like copulas to introduce correlation among week-specific predictions the predictions would not realistically represent the time-series nature of infectious disease dynamics. Predictive distributions relating to the timing of, and incidence at, the peak week can be obtained from this joint predictive distribution. Methods combining non-parametric estimates of marginal densities with copulas have been considered previously for other applications such as economic time series [6].

In addition to the novel application of these methods to predicting disease incidence, our contributions include the use of a periodic kernel specification to capture seasonality in disease incidence and a method for obtaining multivariate kernel functions that handle discrete data while allowing for a fully parameterized bandwidth matrix. Previous implementations of kernel methods involving discrete variables have employed a kernel function that is a product of univariate kernel functions [7, 8, 9, 10, 11, 12, 13, 14, 15]. This approach forces the kernel function to be oriented in line with the coordinate axes. Motivated by results showing that multivariate kernel functions with a bandwidth parameterization allowing for flexible orientations can result in improved continuous density estimates [16], we introduce an approach that allows for flexible orientation of discrete kernels by discretizing an underlying continuous kernel function.

In a time-series context, KCDE is a local method in the sense that the density estimate for observations at future time points conditional on covariates is a weighted combination of contributions from previous observations with similar covariate values. Using such local methods is a natural idea in predicting nonlinear systems because it imposes little structure on the assumed relationship between conditioning and outcome variables. The covariates we condition on could include historical observations from the time series we are predicting as well as other variables such as weather or the time of the season.

Applications range from similar infectious disease settings where nearest neighbors regression has been used to make point predictions for incidence of measles [17] and influenza [18] to sports analytics where a version of nearest neighbors regression predicts the career trajectories of current NBA players [19]. We note that KCDE can be seen as a distribution-based counterpart of nearest neighbors regression. For example, the point prediction obtained from nearest neighbors regression is equal to the expected value of the predictive distribution obtained from KCDE if a particular kernel function is used in the formulation of KCDE (e.g., Hastie et al.[20] discuss the connection between nearest neighbors and kernel methods for regression).

KCDE has not previously been applied to obtain predictive distributions for infectious disease incidence, but it has been successfully used for prediction in other settings such as survival time of lung cancer patients [10], female labor force participation [10], bond yields and value at risk in financial markets [21], and wind power [22], among others. Similar methods can also be formulated in the Bayesian framework. For example, Zhou et al.[23] model the time to arrival of a disease in amphibian populations using Dirichlet processes and copulas.

There is also a long history of using other modeling approaches for infectious disease prediction, including agent-based models, compartmental models [24, 25], and more generic regression-based time series models such as seasonal autoregressive integrated moving average (SARIMA) models [26, 27, 28] and generalized linear models with autoregressive terms [29, 30], among others. Previous work has also explored a variety of covariates that can be used for infectious disease prediction, including measures of access frequency for Wikipedia articles [31], data derived from Twitter [32, 33], and climatological variables [34]. These models need not be used in isolation; some work has been done on ensemble methods combining predictions from multiple model specifications [24, 35]. Unkel et al.[36] is a recent reviews of work on forecasting infectious disease, and describes these alternative approaches in more detail. Additionally, Chretien et al.[37] and Nsoesie et al.[38] are reviews focusing on prediction methods for influenza.

Little research has been done comparing the predictive performance of more detailed and disease-mechanistic modeling approaches (agent-based or compartmental models) to more generic models (regression or SARIMA). One difficulty in making comparisons to agent-based models is that these models are often highly parameterized and difficult to independently reproduce or replicate. An additional challenge with agent-based and compartmental models is that expert knowledge is required to tailor them to the specific disease being modeled, and details of the assumed model specification can have a large impact on the quality of predictions [39].

One of the most well-developed modern statistical frameworks suitable for infectious disease prediction is the “HHH4” model [30, 40, 41, 42, 43], a specific extension of a generalized linear model developed for infectious disease. Another commonly used and widely studied approach is the seasonal autoregressive integrated moving average (SARIMA) model. However, both of these approaches have limitations that also hamper generalizability. The HHH4 model specifies a discrete distribution for the observed incidence measure, an appropriate assumption for some data sets, but not for others. The standard SARIMA specification is based on continuous distributions which means that it cannot be directly applied to modeling discrete case count data if low case counts are observed [36].

Several key features distinguish our approach from existing methods commonly used for predicting infectious disease incidence. First, we generate full predictive distributions to fully characterize uncertainty in the predictions. Compared to point predictions, this gives decision makers additional information in situations where the predictive distribution is skewed or has multiple modes. Second, unlike many methods common in the infectious disease literature, KCDE makes minimal assumptions about the underlying system governing disease dynamics. This flexibility makes KCDE suitable for application to a wide variety of time series, including diseases with different latent dynamics. Third, the method can easily be used with either discrete or continuous data by substituting one kernel function specification for another.

One of the few previous methods that shares these characteristics is an Empirical Bayes method employed by Brooks et al.[44] and van Panhuis et al.[45] that also gives a joint predictive distribution for incidence in each remaining week in the season. Their approach contrasts with ours in that it takes a “top-down” approach to constructing that predictive distribution, saying that the general trend in incidence over the course of the season will look like a modified version of the season-long trend in incidence from a previous season. On the other hand, the approach we discuss in the present article is a “bottom-up” method that first constructs predictive distributions for incidence in individual weeks and then ties those marginal distributions together to obtain a joint distribution for incidence in all weeks of the season. It seems likely that both of these approaches have something to offer in predicting disease incidence; we will return to this point in the conclusions.

The remainder of this article is organized as follows. First, we describe our approach to prediction using KCDE and copulas. Next, we present the results of a simulation study comparing the performance of KCDE for estimating discrete conditional distributions using a fully parameterized bandwidth matrix and a diagonal bandwidth matrix. We then illustrate our methods by applying them to predicting disease incidence in two data sets: one with a discrete measure of weekly incidence of dengue fever in San Juan, Puerto Rico and a second with a continuous measure of weekly incidence of influenza in the United States. We conclude with a discussion of these results.

2. Method Description

Suppose we observe a measure z_t of disease incidence at evenly spaced times indexed by t = 1, …, T. Our goal is to obtain predictions relating to incidence after time T using time series of incidence up to time T as well as time series of covariates up to time T. Broadly, our model works in two stages. In the first stage, KCDE is used to obtain separate predictive distributions for incidence in each remaining week of the season; this will be described in detail in Subsection 2.1. Second, we use copulas to model the dependence in incidence across different weeks; this will be described in detail in Subsection 2.2. These two model components together yield a joint predictive distribution for the trajectory disease incidence over the rest of the season, and predictive distributions for the targets of interest can be obtained from this joint distribution for disease incidence. We introduce notation and give a more detailed statement of the overall structure of the model here, and describe its components and parameter estimation in more detail in the following Subsections.

We allow the incidence measure to be either continuous or discrete and use the term density to refer to either the probability density function or probability mass function as appropriate. We will use a colon notation to specify vectors: for example, z_s:t = (z_s, …, z_t). The variable t* ∈ {1, …, T} will be used to represent a time at which we desire to form a predictive distribution, using observed data up through t* to predict incidence after t*. When we apply the method to perform prediction for incidence after time T, t* is equal to T; however, t* takes other values in the estimation procedure we describe below.

At time t*, our model approximates f (z_{(t*+1):(t*+Ht*)} | t*, z_1:t*) by conditioning only on the time at which we are making the predictions and observed incidence at a few recent time points with lags given by the non-negative integers l₁, …, l_M: f (z_{(t*+1):(t*+Ht*)} | t*, z_t*−l1, …, z_t*−lM). For notational simplicity, we take l_M to be the largest of these lags. The model represents this density as follows:

$$f(z_{(t^{\ast }+1):(t^{\ast }+H_{t^{\ast }})}|t^{\ast },z_{t^{\ast }-l_1},\dots ,z_{t^{\ast }-l_M})=c^{H_{t^{\ast }}}\{f^1(z_{t^{\ast }+1}|t^{\ast },z_{t^{\ast }-l_1},\dots ,z_{t^{\ast }-l_M};{\mathit{\theta }}^1),\dots ,f^{H_{t^{\ast }}}(z_{t^{\ast }+H_{t^{\ast }}}|t^{\ast },z_{t^{\ast }-l_1},\dots ,z_{t^{\ast }-l_M};{\mathit{\theta }}^{H_{t^{\ast }}});{\mathit{\xi }}^{H_{t^{\ast }}}\}.$$ (1)

Here, each f^h (z_t*+h | t*, z_t*−l1, …, z_t*−lM; θ^h) is a predictive density for one prediction horizon obtained through KCDE. The distribution for each prediction horizon depends on a separate parameter vector θ^h. The function c^H_t* (·) is a copula used to tie these marginal predictive densities together into a joint predictive density, and depends on parameters ξ^H_t*. In our applications, we will obtain a separate copula fit for each trajectory length H_t* of interest for the prediction task.

Let W denote the number of time points in a disease season (e.g., W = 52 if we have weekly data). For each time t*, let S_t* denote the time index of the last time point in the previous season, so that the times in the same season as t* are indexed by S_t* + 1, …, S_t* + W. Finally, let H_t* = W − (t* − S_t*) denote the number of time points after t* that are in the same season as t*. H_t* gives the largest prediction horizon for which we need to make a prediction in order to obtain predictions for all remaining time points in the season.

We obtain predictive distributions for each of three prediction targets. We will model the first of these prediction targets directly and frame the second and third as suitable integrals of a predictive distribution f (z_{(t*+1):(t*+Ht*}) | t*, z_1:t*) for the trajectory of incidence over all remaining weeks in the season:

1. Incidence in a single future week with prediction horizon h ∈ {1, …, W}:

   $$f(z_{t^{\ast }+h}|t^{\ast },{\mathbf{z}}_{1:t^{\ast }})$$
2. Timing of the peak week of the current season, w* ∈ {1, …, W}:

   $$P(\text{Peak Week}=w^{\ast })=P(Z_{S_{t^{\ast }}+w^{\ast }}=\underset{w}{\text{max }}{Z}_{S_{t^{\ast }}+w}|t^{\ast },{\mathbf{z}}_{1:t^{\ast }})={\int }_{\{{\mathbf{z}}_{(t^{\ast }+1):(t^{\ast }+H_{t^{\ast }}):z_{S_{t^{\ast }}+w^{\ast }}={\text{max}}_{w}z{S}_{t^{\ast }}+w}\}}f({\mathbf{z}}_{(t^{\ast }+1):(t^{\ast }+H_{t^{\ast }})}|t^{\ast },{\mathbf{z}}_{1:t^{\ast }})\mathrm{d}{\mathbf{z}}_{(t^{\ast }+1):(t^{\ast }+H_{t^{\ast }})}.$$ (2)
3. Binned incidence in the peak week of the current season:

   $$P(\text{Incidence in Peak Week}\in [a,b))=P(a\le \underset{w}{\text{max}}{Z}_{S_{t^{\ast }}+w}<b|t^{\ast },{\mathbf{z}}_{1:t^{\ast }})={\int }_{\{({\mathbf{z}}_{(t^{\ast }+1):(t^{\ast }+H_{t^{\ast }})}):a\le {\text{max}}_w{z}_{S_{t^{\ast }}+w}<b\}}f({\mathbf{z}}_{(t^{\ast }+1):(t^{\ast }+H_{t^{\ast }})}|t^{\ast },{\mathbf{z}}_{1:t^{\ast }})\mathrm{d}{\mathbf{z}}_{(t^{\ast }+1):(t^{\ast }+H_{t^{\ast }})}.$$ (3)

In predicting binned incidence in the peak week, we are following the precedent set in prediction competitions run by the CDC [3, 4]. In practice, we use Monte Carlo integration to evaluate the integrals in Equations (2) and (3) by sampling incidence trajectories from the joint predictive distribution.

2.1. KCDE for Predictive Densities at Individual Prediction Horizons

We now discuss the use of KCDE to obtain f^h(z_t*+h | t*, z_t*−l1, …, z_t*−lM; θ^h), the predictive density for disease incidence at a particular horizon h after time t*. To simplify the notation, we define two new variables: $Y_t^h=Z_{t+h}$ represents the prediction target relative to time t, and X_t = (t, Z_t−l1, …, Z_t−lM) represents the vector of predictive variables relative to time t. With this notation, the distribution we wish to estimate is $f^h(y_{t^{\ast }}^h|{\mathbf{x}}_{t^{\ast }};{\mathit{\theta }}^h)$.

To estimate this distribution, we use the observed data to form the pairs (x_t, $y_t^h$) for all t = 1 + l_M, …, T − h (for smaller values of t there are not enough observations before t to form x_t and for larger values of t there are not enough observations after t to form $y_t^h$). We then regard these pairs as a (dependent) sample from the joint distribution of (X, Y^h) and estimate the conditional distribution of Y^h | X via KCDE:

$${\hat{f}}^h(y_{t^{\ast }}^h|{\mathbf{x}}_{t^{\ast }})=\frac{{\sum }_{t\in \mathit{\tau }}{K}^{\mathbf{X},Y}\{({\mathbf{x}}_{t^{\ast }},y_{t^{\ast }}^h),({\mathbf{x}}_t,y_t^h);{\mathit{\theta }}^h\}}{{\sum }_{t\in \mathit{\tau }}{K}^{\mathbf{X}}({\mathbf{x}}_{t^{\ast }},{\mathbf{x}}_t;{\mathit{\theta }}^h)}$$ (4)

$$=\sum _{t\in \mathit{\tau }}{\zeta }_{t^{\ast },t}^h{K}^{Y|\mathbf{X}}(y_{t^{\ast }}^h,y_t^h|{\mathbf{x}}_{t^{\ast }},{\mathbf{x}}_t;{\mathit{\theta }}^h),\text{where}$$ (5)

$${\zeta }_{t^{\ast },t}^h=\frac{K^{\mathbf{X}}({\mathbf{x}}_{t^{\ast }},{\mathbf{x}}_t;{\mathit{\theta }}^h)}{{\sum }_{s\in \mathit{\tau }}{K}^{\mathbf{X}}({\mathbf{x}}_{t^{\ast }},{\mathbf{x}}_s;{\mathit{\theta }}^h)}.$$ (6)

Here we are working with a slightly restricted specification in which the kernel function K^X,Y can be written as the product of K^X and K^Y|X. With this restriction, we can interpret K^X as a weighting function determining how much each observation (x_t, $y_t^h$) contributes to our final density estimate according to how similar x_t is to the value x_t* that we are conditioning on. These weights are the ${\zeta }_{t^{\ast },t}^h$ in Equations (5) and (6). K^Y|X is a density function that contributes mass to the final density estimate near $y_t^h$. The parameters θ^h control the locality and orientation of the weighting function and the contributions to the density estimate from each observation. In Equations (4) through (6), τ ⊆ {(1 + l_M), …, (T − h)} indexes the subset of observations used in obtaining the conditional density estimate; we return to how this subset of observations is defined in the discussion of estimation below.

We take the kernel function K^Y,X to be a product kernel with one component being a periodic kernel in time and the other component capturing the remaining covariates, which are measures of disease incidence:

$$K^{\mathbf{X},Y}\{({\mathbf{x}}_{t^{\ast }},y_{t^{\ast }}^h),({\mathbf{x}}_t,y_t^h);{\mathit{\theta }}^h\}=K^{\text{per}}(t^{\ast },t;{\mathit{\theta }}_{\text{per}}^h)K^{\text{inc}}\{(z_{t^{\ast }-l_1},\dots ,z_{t^{\ast }-l_M},z_{t^{\ast }+h}),(z_{t-l_1},\dots ,z_{t-l_M},z_{t+h});{\mathit{\theta }}_{\text{inc}}^h\}.$$

Here we have set ${\mathit{\theta }}^h=({\mathit{\theta }}_{\text{per}}^h,{\mathit{\theta }}_{\text{inc}}^h)$ where θ^h encompasses parameters both about the periodicity and incidence.

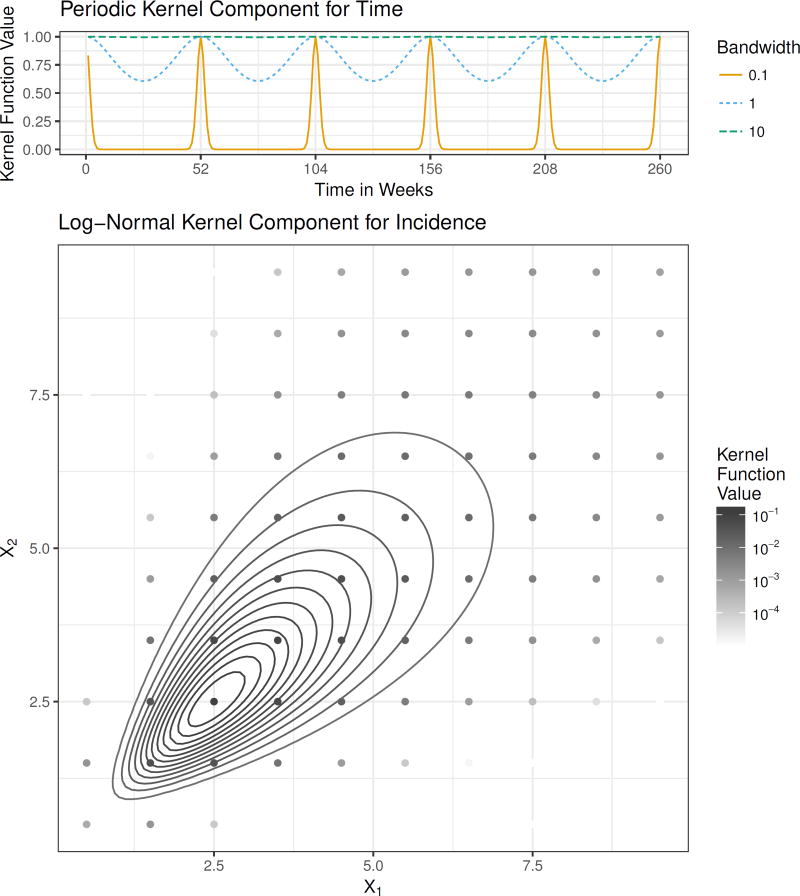
The periodic kernel function was originally developed in the literature on Gaussian Processes [46], and is defined by

$$K^{\text{per}}(t^{\ast },t;{\rho }^h,{\eta }^h)=\text{exp }[-\frac{{\text{sin}}^2\{{\rho }^h(t^{\ast }-t)\}}{2{({\eta }^h)}^2}].$$ (7)

We illustrate this kernel function in Figure 1. It has two parameters: ${\mathit{\theta }}_{\text{per}}^h=({\rho }^h,{\eta }^h)$, where ρ^h determines the length of the periodicity and η^h determines the strength and locality of this periodic component in computing the observation weights ${\zeta }_{t^{\ast },t}^h$. In our applications, we have fixed ρ^h = π/52, so that the kernel has period of length 1 year with weekly data. Using this periodic kernel provides a mechanism to capture seasonality in disease incidence by allowing the observation weights to depend on the similarity of the time of year that an observation was collected and the time of year at which we are making a prediction.

Figure 1.

The components of the kernel function. The top panel shows the periodic kernel function illustrated as a function of time in weeks with ρ = π/52 and three possible values for the bandwidth parameter η. The lower panel shows the log-normal kernel function in the bivariate case. The curves indicate contours of the continuous kernel function and the points indicate the discrete kernel function, which is obtained by integrating the continuous kernel function. The kernel is centered at (2.5, 2.5) and has bandwidth matrix $\left[\begin{array}{cc}\hfill 0.2\hfill & \hfill 0.15\hfill \\ \hfill 0.15\hfill & \hfill 0.2\hfill \end{array}\right]$.

The second component of our kernel is a multivariate kernel incorporating all of the other variables in x_t and $y_t^h$. In our applications, these variables are measures of incidence; for brevity of notation, we collect them in the column vector z̃_t = (z_t−l1, …, z_t−lM, z_t+h)′. These incidence measures are continuous in the application to influenza and discrete case counts in the application to dengue fever. In the continuous case, we have used a multivariate log-normal kernel function parameterized in terms of its mode rather than its mean (Figure 1). Using the mode ensures that the contribution to the conditional density is largest near z_t+h. This kernel specification automatically handles the restriction that counts are non-negative, and approximately captures the long tail in disease incidence that we will illustrate in the applications Section below. This kernel function has the following functional form:

$$K_{\text{cont}}^{\text{inc}}({\stackrel{\sim }{\mathbf{z}}}_{t^{\ast }},{\stackrel{\sim }{\mathbf{z}}}_t;\mathbf{B})=\frac{\text{exp}[-\frac{1}{2}\{\text{log}({\stackrel{\sim }{\mathbf{z}}}_{t^{\ast }})-\text{log}({\stackrel{\sim }{\mathbf{z}}}_t)-\mathbf{B}\underset{¯}{1}\}\prime {\mathbf{B}}^{-1}\{\text{log}({\stackrel{\sim }{\mathbf{z}}}_{t^{\ast }})-\text{log}({\stackrel{\sim }{\mathbf{z}}}_t)-\mathbf{B}\underset{¯}{1}\}]}{{(2\pi )}^{\frac{M+1}{2}}{|\mathbf{B}|}^{\frac{1}{2}}{z}_{t^{\ast }+h}{\prod }_{m=1}^M{z}_{t^{\ast }-l_m}}$$ (8)

In this expression,1̱ is a column vector of ones. The matrix B is a bandwidth matrix that controls the orientation and scale of the kernel function. Subtracting B1̱ in the numerator has the effect of placing the mode of the kernel function at z_t+h. This bandwidth matrix is parameterized by ${\mathit{\theta }}_{\text{inc}}^h$. In this work we have considered two parameterizations: a diagonal bandwidth matrix, and a fully parameterized bandwidth based on the Cholesky decomposition [47]. To obtain the discrete kernel (Figure 1), we integrate an underlying continuous kernel function over hyper-rectangles containing the points in the range of the discrete random variable (see supplement for details). According to Equations (4) through (6), $K_{\text{cont}}^{\text{inc}}$ makes a contribution to calculation of the observation weights by measuring the similarity of the lagged observations of incidence included in z̃_t* and z̃_t, and contributes mass to the predictive density for future incidence z_t*+h near the observed incidence z_t+h.

We estimate the bandwidth parameters θ^h by numerically maximizing the cross-validated log score of the predictive distributions for the observations in the training data. For a random variable Y with observed value y the log score of the predictive distribution f_Y is log{f_Y (y)}. A larger log score indicates better model performance. In obtaining the cross-validated log score for the predictive distribution at time t*, we leave the year of training data before and after the time t* out of the set τ in Equations (4) through (6). Our primary motivation for using the log score as the optimization target during estimation is that this is the criteria that has been used to evaluate and compare prediction methods in two recent government-sponsored infectious disease prediction contests [3, 4]. We apply our method to the data sets from those competitions in the applications section below, and report log scores to facilitate comparisons with other results from those competitions that may be published in the future. In general, the log score is a strictly proper scoring rule; i.e., its expectation is uniquely maximized by the true predictive distribution [48]. However, its use as an optimization criterion has been criticised for being sensitive to outliers [48]. In the kernel density estimation literature, this approach to estimation is referred to as likelihood cross-validation, and similar criticisms have been made regarding its performance in handling outliers and estimating heavy-tailed distributions [49, 50]. This is relevant to application of the method to infectious disease prediction, as the distribution of disease incidence tends to be skewed right with a long upper tail. It is possible that the use of cross-validated log scores in estimation could lead to too-large bandwidth estimates, in turn inflating the width of the predictive distribution. We will return to this possibility in our conclusions.

2.2. Combining Marginal Predictive Distributions with Copulas

We use copulas [51] to tie the marginal predictive distributions for individual prediction horizons obtained from KCDE together into a joint predictive distribution for the trajectory of incidence over multiple time points. The copula is a parametric function that captures the dependence relations among a collection of random variables and allows us to compute the joint distribution from the marginal distributions. Supplemental Figure 7 shows that the copula induces positive correlation in the predictive distributions for incidence in nearby weeks, so that high incidence in one week is more likely to be followed by high incidence in weeks soon after.

To describe our methods for both continuous and discrete distributions, it is most convenient to frame the discussion in this Subsection in terms of cumulative distribution functions (CDF) instead of density functions. We will use a capital C to denote the copula function for CDFs and a lower case c to denote the copula function for densities. Similarly, the predictive densities $f^h(y_{t^{\ast }}^h|{\mathbf{x}}_{t^{\ast }};{\mathit{\theta }}^h)$ we obtained in the previous Subsection naturally yield corresponding predictive CDFs $F^h(y_{t^{\ast }}^h|{\mathbf{x}}_{t^{\ast }};{\mathit{\theta }}^h)$.

Our model specifies the joint CDF for $(Y_{t^{\ast }}^1,\dots ,Y_{t^{\ast }}^{H_{t^{\ast }}})$ as follows:

$$F^{H_{t^{\ast }}}(y_{t^{\ast }}^1,\dots ,y_{t^{\ast }}^{H_{t^{\ast }}}|{\mathbf{x}}_{t^{\ast }};{\mathit{\theta }}^1,\dots ,{\mathit{\theta }}^{H_{t^{\ast }}},{\mathit{\xi }}^{H_{t^{\ast }}})=C^{H_{t^{\ast }}}\{F^1(y_{t^{\ast }}^1|{\mathbf{x}}_{t^{\ast }};{\mathit{\theta }}^1),\dots ,F^{H_{t^{\ast }}}(y_{t^{\ast }}^{H_{t^{\ast }}}|{\mathbf{x}}_{t^{\ast }};{\mathit{\theta }}^{H_{t^{\ast }}});{\mathit{\xi }}^{H_{t^{\ast }}}\}$$ (9)

The copula function C^H_t* maps the marginal CDF values to the joint CDF value. We use the isotropic normal copula implemented in the R [52] package copula [53]. The copula function is given by

$$C^H(u_1,\dots ,u_H;{\mathit{\xi }}^H)={\mathrm{\Phi }}_{{\sum }^H}({\mathrm{\Phi }}^{-1}(u_1),\dots ,{\mathrm{\Phi }}^{-1}(u_H)),$$ (10)

where Φ⁻¹ is the inverse CDF of a univariate normal distribution with mean 0 and variance 1 and Φ_Σ^H is the CDF of a multivariate normal distribution with mean 0̱ and covariance matrix Σ^H. The isotropic specification sets ${\sum }^H=[{\sigma }_{i,j}^H]$, where

$${\sigma }_{i,j}^H=\{\begin{array}{c}1\text{ if }i=j,\hfill \\ {\xi }_d^H\text{ if }|i-j|=d\hfill \end{array}$$ (11)

Intuitively, ${\xi }_d^H$ captures the amount of dependence between incidence levels at future times that are d weeks apart.

We obtain a separate copula fit for each value of H from 2 to W (note that a copula is not required for “trajectories” of length H = 1). Estimation for the model parameters proceeds in two stages: first we estimate the parameters for KCDE separately for each prediction horizon h = 1, …, H as described in the previous Section, and second we estimate the copula parameters while holding the KCDE parameters fixed. We give a more detailed description of this estimation procedure in the supplement. In general the two-stage approach may result in some loss of efficiency relative to one-stage methods, but this efficiency loss is small for some model specifications [54]. Also, it results in a large reduction in the computational cost of parameter estimation.

3. Simulation Study

One component of the KCDE model specification outlined in Subsection 2.1 is the parameterization of the bandwidth matrix. We conducted a simulation study to examine the utility of using a fully parameterized matrix specification instead of a diagonal bandwidth matrix when estimating discrete conditional distributions with KCDE. The simulation study is motivated by the simplest case of predicting incidence in a single week using KCDE: predicting incidence at time t + h given incidence at time t. A central characteristic of the disease incidence data we analyze in the next Section is the presence of positive correlation between incidence in nearby time points (Supplemental Figure 2). In this simulation study we demonstrate that in the presence of such correlation, using fully parameterized bandwidth matrices can improve conditional density estimates over using a diagonal bandwidth.

There are many factors that determine the relative performance of KCDE estimators with different bandwidth parameterizations. In this simulation study, we vary just one of these factors: the sample size (N = 100 or N = 1000). These sample sizes are roughly similar to the number of observations in the training data sets used in the applications in Section 4 (where we have training sets of size 692 in the application to influenza and 988 in the application to dengue fever).

We conducted 500 simulation trials for each sample size. In each trial, we simulated N observations of a discretized bivariate normal random variable X with mean 0̱ and covariance matrix Σ where Σ has 1 on the diagonal and 0.9 off of the diagonal (see Supplement for further detail). Using these observations as a training data set, we estimated the bandwidth parameters for two variations on a KCDE model for the conditional distribution of X₁ | X₂: one with a diagonal bandwidth matrix specification and one with a fully parameterized bandwidth matrix. In this simulation study, the kernel function was obtained by discretizing a multivariate normal kernel function rather than a log-normal kernel function as in the applications below. Otherwise, the method is as described previously.

We evaluated the conditional density estimates by an importance sampling approximation of the Hellinger distance of the conditional density estimate from the true conditional density, integrated over the range of the covariates (see supplement). The Hellinger distance lies between 0 and 1, with smaller values indicating that the density estimate is better. It has been argued that the Hellinger distance is preferred to other measures of the quality of kernel density estimates such as integrated squared error [55]. For each combination of the training set sample size, dimension, and simulation trial, we compute the difference between the Hellinger distance from the true conditional distribution achieved with a diagonal bandwidth matrix and with a fully parameterized bandwidth matrix.

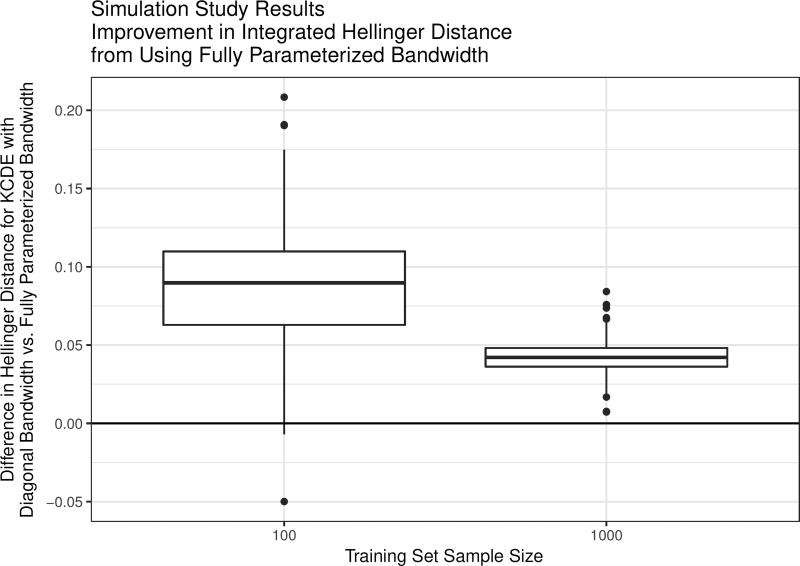
The results indicate that in the presence of correlation between the conditioning variable and the density estimation target, using a fully parameterized bandwidth matrix instead of a diagonal bandwidth generally yields improved density estimates as measured by the integrated Hellinger distance (Figure 2). The average improvement from using a fully parameterized bandwidth matrix is larger with a sample size of N = 100 instead of N = 1000, but there is also more variation in performance with the smaller sample size. This suggests that using a fully parameterized bandwidth may be helpful in applications similar to infectious disease prediction where there is correlation between the quantity being predicted (e.g., future incidence) and the quantities that we condition on in order to make the predictions.

Figure 2.

Box plots of results from the simulation study. Positive values indicate simulation trials where the full bandwidth specification outperformed the diagonal bandwidth specification with the same training data set, as measured by Hellinger distance from the target conditional density.

4. Applications

In this Section, we illustrate our methods through applications to prediction of infectious disease incidence in two examples with real disease incidence data sets. We begin with a discussion of the data, then we describe the models we compare and the evaluation procedures before discussing the results.

4.1. Data

We apply our methods to two infectious disease data sets (Figure 3). The first data set consists of a weekly count of reported cases of dengue fever in San Juan, Puerto Rico. The second data set consists of a composite indicator of flu activity generated by the CDC and referred to as the weighted influenza-like illness (wILI) index. The wILI is calculated as the proportion of doctor visits at clinics participating in the U.S. Outpatient Influenza-like Illness Surveillance Network (ILINet) where the patient had influenza-like illness. The measured proportions are weighted by state population and combined into region-level scores. We did not attempt to replicate this weighting scheme and instead used wILI directly in our models. These data sets were used in two recent prediction competitions sponsored by the United States federal government [3, 4].

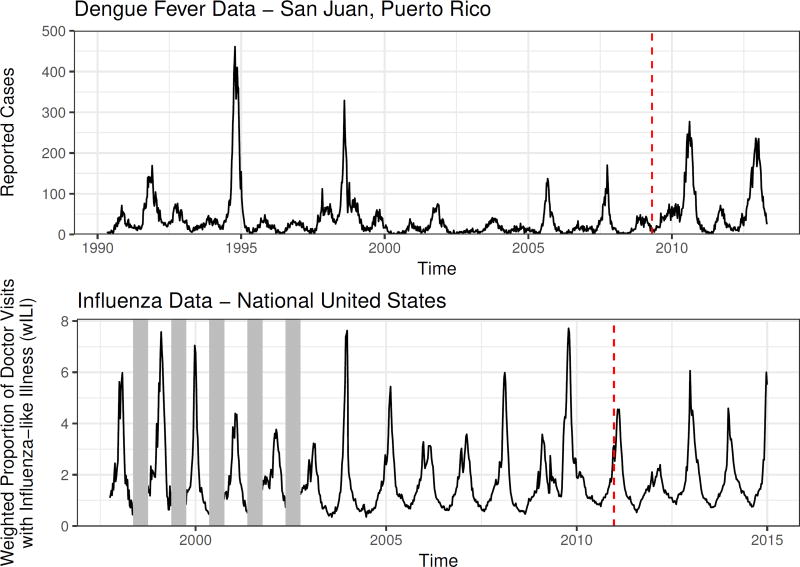
Figure 3.

Plots of the data sets we apply our methods to. In each case, the last four years of data are held out as a test data set; this cutoff is indicated with a vertical dashed line. For the flu data set, low-season incidence was not recorded in early years of data collection. These missing data are indicated with vertical grey bars.

An important feature of both of these time series is that they exhibit fairly regular seasonal trends: incidence of dengue fever usually reaches a peak during the summer months and a nadir during the winter months, while influenza typically peaks during the winter and reaches a nadir during the summer months. However, within these general trends there is variation in the timing and severity of the disease seasons, with more variability across different seasons for dengue than for influenza. For the purposes of making predictions of seasonal targets with the dengue data, we have used the definition of a season used by the competition administrators: the season begins in the week starting on April 29th or April 30th (depending on the year); historically, this has been near the week of the year with lowest dengue incidence. For the influenza data, we define the season as beginning in the 30th week of the year; which is the week starting on July 29th or July 30th. Again, historically the lowest incidence of influenza has tended to occur near that time.

4.2. Prediction targets and evaluation criteria

We use the three prediction targets described in Section 2 (Supplemental Figure 3). As discussed there, we make predictions for binned incidence in the peak week. For the dengue data set, the bins are [0, 50), [50, 100), …, [500, ∞). For the influenza data set, the bins are [0, 0.5), [0.5, 1), …, [13, ∞). Our predictions for incidence in individual weeks are for the raw, unbinned, incidence measure.

We divided each data set into two subsets. The last four years of each data set are reserved as a test set for evaluating model performance. The size of the test set was determined by the dengue prediction competition administrators. In the influenza data set, the last four years of data included only observations for three full seasons. The first period is used as a training set in estimating the model parameters. For the influenza data, we had 14 years of training data (1997 through 2010); for the dengue data, we had 19 seasons of training data (1990/1991 through 2008/2009). All predictions are made as though in real time, assuming that once cases are reported they are never revised and that there are no delays in reporting. Specifically, we use only data up through a given week to make predictions for incidence after that week.

We evaluated model performance using log scores for predictions in the test phase for each data set (log scores were defined previously in Section 2.1). For each season in the testing period, we examined the log scores for predictions made in all weeks of the season, as well as for smaller subsets of those weeks that are most relevant to decision makers using predictions to set public health policy. Specifically, for incidence in individual weeks, we examined model performance for predictions of incidence in the weeks where the eventually observed incidence was at least 2/3 of the maximum incidence observed in the testing phase. For predictions of incidence in the peak week and the timing of the peak week, we evaluated performance of predictions made before the peak actually occurred. Additionally, for predictions of incidence in individual weeks, we considered the coverage rate of predictive intervals obtained from each method.

We considered two summaries of the log scores of these predictions for each target: 1) the mean log score across all weeks (and across all prediction horizons, in the case of predictions of incidence in individual weeks); and 2) the minimum log score across all weeks and prediction horizons. The mean log score is a strictly proper score, and its expected value is uniquely maximized by the true conditional distribution for Y |X. The minimum log score is not a proper score, and therefore relative performance of the different models according to this metric should be interpreted cautiously. The minimum log score can be viewed as a measure of worst-case performance of a given method. We contend that consideration of worst-case performance is important for predictions that may be used by public health officials as inputs to setting public policy. For example, [5] note that “[p]ublic health actions informed by forecasts that later prove to be inaccurate can have negative consequences, including the loss of credibility, wasted and misdirected resources, and, in the worst case, increases in morbidity or mortality.” It is therefore important that predictions for key times such as the season peak assign non-negligible probability to the outcome that eventually occurs, and this is what the minimum log score measures. However, we emphasize that the minimum log score should only be considered as a secondary measure to characterize methods that have demonstrated good overall performance as measured by the mean log score.

4.3. Models

Our applications evaluate four variations on KCDE model specifications:

1. The “Null KCDE” model omits the periodic component of the kernel function and uses a diagonal bandwidth matrix specification for the incidence kernel.

2. The “Full Bandwidth KCDE” model omits the periodic component of the kernel function and uses a fully parameterized bandwidth matrix specification for the incidence kernel.

3. The “Periodic KCDE” model includes the periodic component of the kernel function and uses a diagonal bandwidth matrix specification for the incidence kernel.

4. The “Periodic, Full Bandwidth KCDE” model includes the periodic component of the kernel function and uses a fully parameterized bandwidth matrix specification for the incidence kernel.

We include three baseline models for comparison to our methods. The first is a seasonal autoregressive integrated moving average (SARIMA) model. In fitting this model, we first transformed the observed incidence measure to the log scale (after adding 1 in the dengue data set, which included some observations of 0 cases); this transformation makes the normality assumptions of the SARIMA model more plausible. We then performed first-order seasonal differencing, and obtained the final model fits using the auto.arima function in R’s forecast package [56]; this function uses a stepwise procedure to determine the terms to include in the model. This procedure resulted in a SARIMA(2,0,0)(2,1,0)₅₂ model for the influenza data and a SARIMA(3,0,2)(1,1,0)₅₂ model for the dengue data. In applying this model to the dengue data, we have discretized the predictive distributions obtained from SARIMA using the same methods that we used for KCDE. This discretization was not used in model estimation since it is not available in the standard estimation software.

The second baseline model is the “HHH4” model for infectious disease incidence [30, 41, 42], available in the surveillance [57] package in R. This is an extension to the generalized linear model framework with either a Poisson or Negative Binomial family. The majority of work with this model has focused on modeling multiple time series, with models for a single time series (as considered in the present article) obtained as a special case. Although the primary focus of development of this model has been for multivariate time series, and further refinements to the model are possible, it provides a good baseline for comparison. The mean is modeled with a linear combination of autoregressive and sinusoidal components. We followed the model selection and estimation procedures outlined in [42], working with a restricted version of the model for a single time series (see Supplement for details). The prediction target for dengue data is discrete case counts and easily implemented in the HHH4 software. The prediction target for flu requested by the CDC is proportion of doctor visits with flu-like illness weighted by state population. Implementing this in HHH4 would require weighting state-level predictions. As we did not attempt to make state level predictions we did not use HHH4 as a reference model for the flu data.

For predictions of peak timing and binned peak incidence, we considered a third naive baseline that assigned equal probability to all bins (where for peak timing, there is one bin for each week in the season).

4.4. Results

4.4.1. For predictions of incidence in individual weeks, KCDE outperforms the baseline models (Table 1)

Table 1.

Summaries of model performance for predictions of incidence in individual weeks. The “All Weeks” group summarizes log scores for all combinations of prediction horizon and target week in the test period; the “High Incidence” group summarizes log scores for predictions of indience in weeks where the observed incidence was at least two thirds of the maximum weekly incidence in the test period.

			Summary of Log Scores
Disease	Subset	Model	Min	Mean
Dengue	All Weeks	Null KCDE	−9.981	−5.147
		Full Bandwidth KCDE	−10.373	−5.165
		Periodic KCDE	−11.047	−5.021
		Periodic, Full Bandwidth KCDE	−10.851	−5.019
		HHH4	−16.201	−5.369
		SARIMA	−14.416	−5.456
	High Incidence	Null KCDE	−9.981	−8.235
		Full Bandwidth KCDE	−10.373	−8.339
		Periodic KCDE	−11.047	−7.841
		Periodic, Full Bandwidth KCDE	−10.851	−7.791
		HHH4	−14.665	−9.046
		SARIMA	−14.416	−9.380
Influenza	All Weeks	Null KCDE	−4.430	−1.039
		Full Bandwidth KCDE	−5.004	−0.993
		Periodic KCDE	−3.660	−0.668
		Periodic, Full Bandwidth KCDE	−3.850	−0.642
		SARIMA	−6.385	−0.666
	High Incidence	Null KCDE	−4.430	−2.887
		Full Bandwidth KCDE	−5.004	−3.025
		Periodic KCDE	−3.660	−2.404
		Periodic, Full Bandwidth KCDE	−3.850	−2.447
		SARIMA	−6.385	−2.345

The model in bold font had the highest mean log score within each combination of disease and weeks subset. The model in italicized and underlined font had the lowest minimum log score within each combination of disease and weeks subset. In some cases, the same model had both the highest average log score and the lowest worst-case log score.

KDCE specifications including a periodic kernel component consistently had the highest or close to the highest mean log scores for both data sets whether aggregating across all weeks or only high incidence weeks. Additionally, the worst-case performance of the HHH4 and SARIMA models was much lower than the worst-case performance of any of the KCDE specifications for all combinations of the data set and the subset of weeks considered.

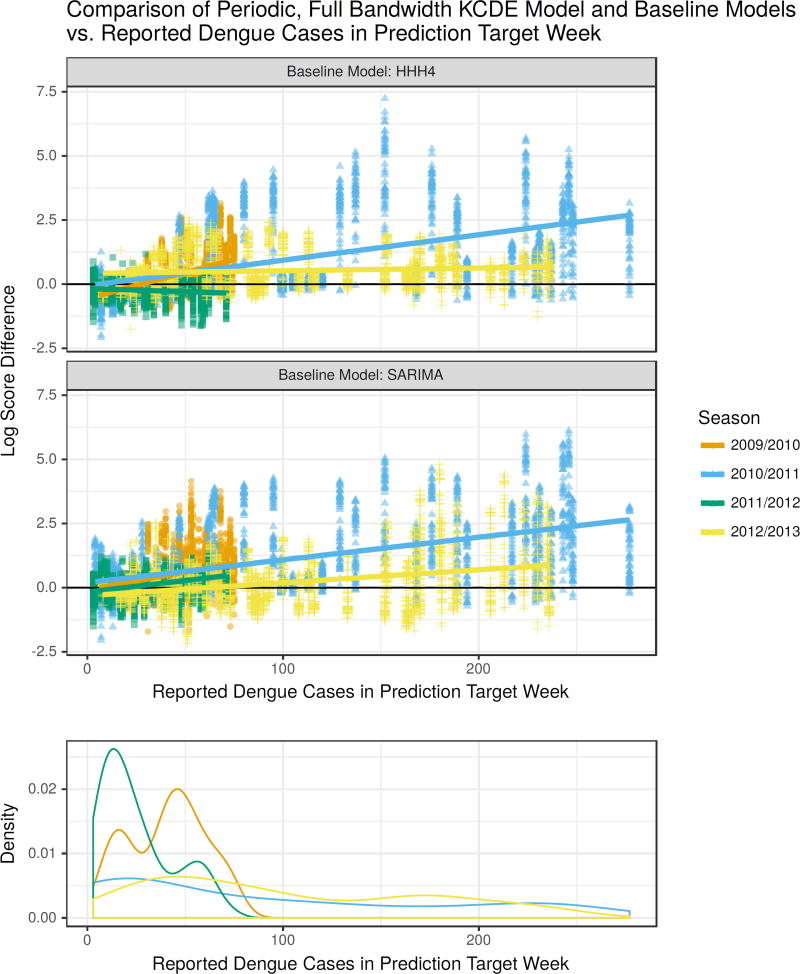
In the application to dengue fever, KCDE offered the largest improvements relative to the baseline models for predictions in weeks with high incidence near the season peaks (Table 1, Figure 4). For example, in weeks with more than 184 reported cases (two thirds of the maximum weekly case count in the testing period), the median log score difference between the predictions from the Periodic, Full Bandwidth KCDE model and SARIMA was about 1.48 (Q₁ = 0.25, Q₃ = 2.72) where values greater than zero show KCDE making more accurate predictions than SARIMA (Supplemental Table 1). The median log score difference relative to HHH4 for these weeks was about 0.94 (Q₁ = 0.41, Q₃ = 1.95). Translating to a probability scale, in these periods of high incidence this KCDE specification assigned about 5 times higher probability to the observed outcome as SARIMA on average and about 1.25 times higher probability as HHH4 on average. Moreover, there were cases where the KCDE model assigned up to about 450 times as much probability to the realized outcome as SARIMA, and over 1300 times as much probability as HHH4. Across all weeks in the test period and all prediction horizons, neither baseline model ever outperformed this KCDE specification by a factor of more than 9. Similar patterns also hold with the other KCDE specifications. For the application to influenza, there were not consistent trends in the relative performance of the models in low and high incidence weeks.

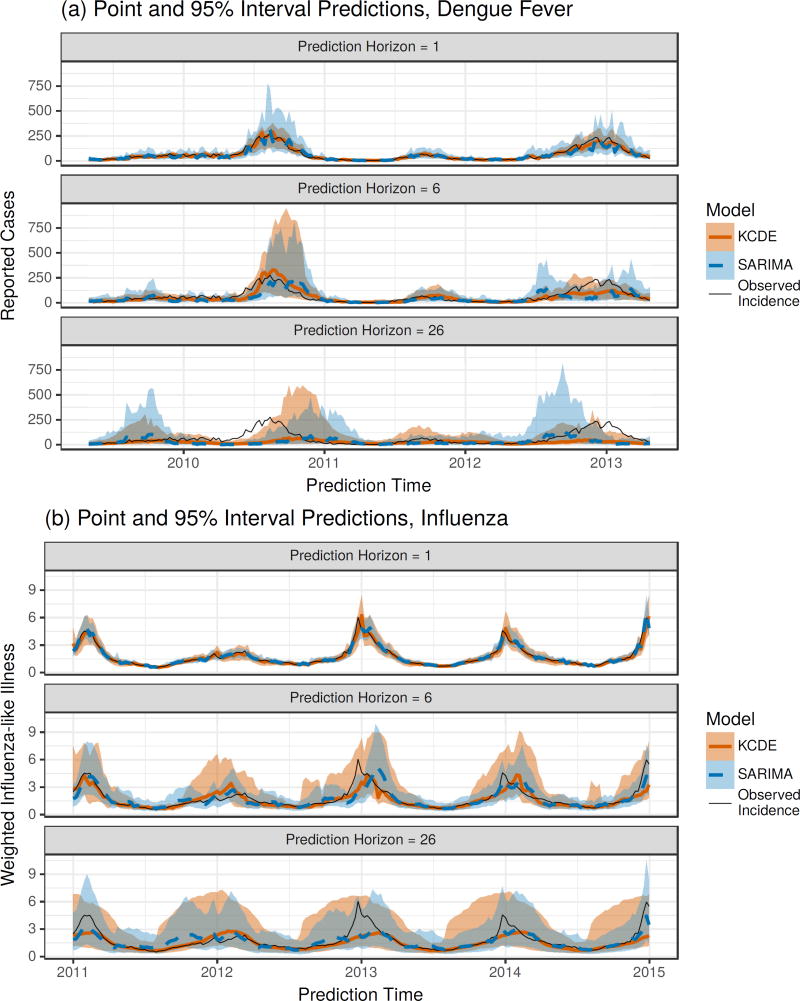
Figure 4.

Differences in log scores for the weekly predictive distributions obtained from the Periodic, Full Bandwidth KCDE model and the baseline models, plotted against the observed incidence in the week being predicted. For reference, a log score difference of 2.3 (4.6) indicates that the predictive density from KCDE was about 10 (100) times as large as the predictive density from the baseline model at the realized outcome. Each point corresponds to a unique combination of prediction target week and prediction horizon. The lower panel displays a density estimate of incidence levels in each week of the season separately for each season in the test phase.

In both applications, the predictive intervals for incidence in individual weeks are quite wide for all of the methods we considered (Figure 5). However, for dengue fever the coverage rates in the test phase were actually lower than the nominal coverage rate for all methods (Table 2). The KCDE models were generally closer to the target coverage rates than the baseline models, indicating that the width of the predictive intervals from KCDE give an appropriate representation of uncertainty about future dengue incidence. For predictions of influenza, the coverage rates for all KCDE specifications as well as the baseline SARIMA model were too large. For this application, none of the models had consistently better or worse performance than the others as measured by coverage rates of the predictive intervals.

Figure 5.

Plots of point and interval predictions from SARIMA and the Periodic, Full Bandwidth KCDE model. The point prediction is the median of the predictive distribution for incidence in the given week. The interval prediction is a percentile interval; for example, the endpoints of the 95% prediction interval are the 2.5th percentile and the 97.5th percentile of the predictive distribution.

Table 2.

Coverage rates for predictions of disease incidence in individual weeks during the test time frame. For each model specification, we have obtained the overall proportion of predictive intervals that contained the realized outcome, combining across all prediction horizons and all times in the test period at which the prediction was made. For each combination of disease and target coverage rate, the result for the model with actual coverage rate closest to the target coverate rate is highlighted.

		Nominal Coverage
Disease	Model	50%	95%
Dengue	Null KCDE	40.958	91.827
	Full Bandwidth KCDE	38.794	89.571
	Periodic KCDE	44.749	87.343
	Periodic, Full Bandwidth KCDE	41.901	86.418
	HHH4	40.163	78.217
	SARIMA	38.637	79.919
Influenza	Null KCDE	69.580	99.457
	Full Bandwidth KCDE	70.896	99.420
	Periodic KCDE	77.374	99.678
	Periodic, Full Bandwidth KCDE	76.150	99.485
	SARIMA	73.270	99.384

4.4.2. For predictions of peak incidence the KCDE models with periodic kernel components had better mean performance than the baseline models in the application to dengue fever, and in both applications the KCDE models had more consistent performance across seasons than the baseline models (Table 3, Figure 6)

Table 3.

Summaries of model performance for predictions of incidence in the peak week. The “All Weeks” group summarizes results for all combinations of target week in the test period and prediction horizon; the “Before Peak” group summarizes results for predictions in weeks before the actual peak for the given season.

			Summary of Log Scores
Disease	Subset	Model	Min	Mean
Dengue	All Weeks	Null KCDE	−3.221	−0.973
		Full Bandwidth KCDE	−3.239	−0.933
		Periodic KCDE	−3.037	−0.771
		Periodic, Full Bandwidth KCDE	−2.802	−0.739
		HHH4	−4.816	−0.901
		SARIMA	−3.088	−0.836
		Equal Bin Probabilities	−2.398	−2.398
	Before Peak	Null KCDE	−3.221	−1.570
		Full Bandwidth KCDE	−3.239	−1.531
		Periodic KCDE	−3.037	−1.315
		Periodic, Full Bandwidth KCDE	−2.802	−1.282
		HHH4	−4.816	−1.600
		SARIMA	−3.088	−1.361
		Equal Bin Probabilities	−2.398	−2.398
Influenza	All Weeks	Null KCDE	−3.487	−1.423
		Full Bandwidth KCDE	−3.483	−1.311
		Periodic KCDE	−4.528	−1.337
		Periodic, Full Bandwidth KCDE	−4.678	−1.313
		SARIMA	−5.714	−1.140
		Equal Bin Probabilities	−3.296	−3.296
	Before Peak	Null KCDE	−3.487	−2.538
		Full Bandwidth KCDE	−3.483	−2.363
		Periodic KCDE	−4.528	−2.518
		Periodic, Full Bandwidth KCDE	−4.678	−2.471
		SARIMA	−5.714	−2.190
		Equal Bin Probabilities	−3.296	−3.296

The model in bold font had the highest mean log score within each combination of disease and weeks subset. The model in italicized and underlined font had the lowest minimum log score within each combination of disease and weeks subset. In some cases, the same model had both the highest average log score and the lowest worst-case log score. There were 42 weeks before the peak in the 2009/2010 dengue season, 15 in the 2010/2011 dengue season, 19 in the 2011/2012 dengue season, 31 in the 2012/2013 dengue season, 23 in the 2011/2012 influenza season, and 12 in each of the 2012/2013 and 2013/2014 influenza seasons.

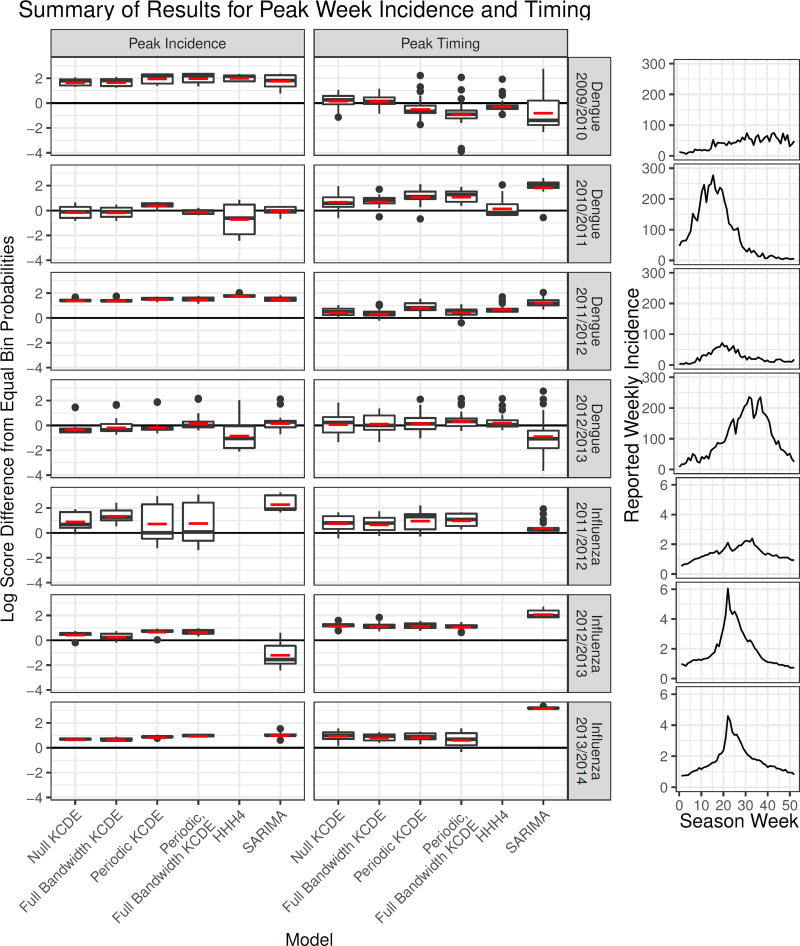
Figure 6.

A summary of performance of each method for predicting incidence in the peak week and peak week timing. Each boxplot summarizes all predictions made by a method in a given season in weeks before the actual peak week for that season. The vertical axis is the difference in log scores between the given method and a naive approach assigning equal probability to each week of the year. Positive values indicate cases when the method did better than using equal bin probabilities. The horizontal red dash indicates the mean log score for those predictions made before the peak within each season. The plots on the right display the trajectory of incidence over each season. There were 42 weeks before the peak in the 2009/2010 dengue season, 15 in the 2010/2011 dengue season, 19 in the 2011/2012 dengue season, 31 in the 2012/2013 dengue season, 23 in the 2011/2012 influenza season, and 12 in each of the 2012/2013 and 2013/2014 influenza seasons.

In the application to dengue fever, the HHH4 model struggled to predict peak incidence in the two test phase seasons with the highest peak, generally performing worse than a naive approach using equal bin probabilities in those seasons (Figure 6). The SARIMA model did well at predicting peak incidence for dengue, with overall performance that was only slightly lower than the Periodic, Full Bandwidth KCDE specification and similar performance in all four test phase seasons. However, in the application to influenza the SARIMA model struggled in the test phase season with highest incidence, with performance levels generally falling below the approach using equal bin probabilities. Meanwhile, the KCDE specifications had much more consistent performance across all test phase seasons, and never did much worse than using equal bin probabilities. For dengue fever the Periodic, Full Bandwidth KCDE specification had the highest average log scores and best worst-case log scores for predictions of peak incidence (Table 3), while in the application to influenza the KCDE models did only a little worse than SARIMA overall, and did much better in the influenza season with highest incidence.

4.4.3. For predictions of peak week timing made before the peak actually occurred, the KCDE models without periodic kernel components had the best performance in the application to dengue fever, but the SARIMA model had the best performance in the application to influenza

For dengue fever, both the SARIMA and HHH4 models consistently underperformed relative to the naive approach using equal bin probabilities for predictions of peak timing. On the other hand, the KCDE models, and particularly those that did not use a periodic kernel component, generally outperformed this baseline. There was quite a bit of variability in the timing of peak dengue incidence between test phase seasons, and the models including seasonal terms sometimes failed badly when the peak occurred relatively early or late (Figure 6). The KCDE specifications without periodic terms were more robust to this variation in season timing. There was less variability in the timing of the season peak in the three complete test phase seasons in our influenza data, and the SARIMA model was the overall best performing model in that application. However, the SARIMA model was still outperformed by the KCDE models in the influenza season with the latest peak. All methods we evaluated tend to converge rapidly on the truth once the peak week has passed.

4.4.4. In most cases, including a periodic kernel component in the KCDE specification led to improved predictions

KCDE specifications including a periodic kernel component had better average performance than the corresponding KCDE specification without a periodic kernel component for predicting incidence in individual weeks in all combinations of the data sets and the subset of weeks considered. The periodic kernel also led to better predictions of peak incidence in every case except for early season predictions in the application to influenza when the bandwidth matrix for the incidence kernel component was fully parameterized. For predictions of peak timing, including the periodic kernel component was helpful in the application to influenza, but led to worse performance for early-season predictions of the peak timing for dengue incidence.

4.4.5. We have seen that the KCDE model outperformed the baseline models in the application to dengue, but the SARIMA model generally had higher mean performance than the KCDE models in the application to influenza (although SARIMA had less consistent performance for predictions of incidence in individual weeks or at the peak week in both applications)

We believe that the difference in relative performance of KCDE and the baseline models for prediction in the dengue and influenza data sets can be explained to a great extent by differences in the underlying disease processes and how they relate to the model specifications. The most salient difference between the two time series is the much greater season-to-season variability in the dengue data set relative to the influenza data set (Figure 3). For dengue, the peak incidence in the largest season is about 30 times larger than the peak incidence in the smallest season; this ratio is only about 3 for influenza. It may be the case that the restrictive structure of the SARIMA and HHH4 models means that they are not able to capture the dynamics of dengue incidence accurately. For example, Held and Paul [42] discuss the fact that the seasonal structure in the HHH4 model does not explicitly allow for different amplitudes in different seasons. Relaxing that structure by using a non-parametric approach such as KCDE may yield improved capability to represent the disease dynamics. This is less of an issue in predicting influenza where there is much more consistency across different seasons – but even in that case, SARIMA was outperformed by KCDE for predicting peak incidence in the season with the highest incidence and for predicting peak timing in the season with the latest peak (Figure 6).

5. Conclusions

Prediction of infectious disease incidence at horizons of more than a few weeks is a challenging task. We have presented a semi-parametric approach to doing this based on KCDE and copulas and found that it is a viable method that can yield improved predictions relative to commonly employed methods in this field. In predicting incidence of dengue fever in individual weeks, our approach offered consistent and substantial performance gains relative to a SARIMA model and the HHH4 model, particularly in periods of high incidence near the season peak that are of most interest to public health decision makers. In the application to influenza our method did about as well as SARIMA on average for this prediction target, but there were some cases where the SARIMA model assigned a very low probability density to the eventually observed outcome; the KCDE model was more consistent in this regard.

Across both data sets, our method also offered more consistency than the baseline models in predictions for incidence in the peak week. Both baseline models suffered in one or more seasons with high incidence where they made substantially worse predictions than a naive model assigning equal probability to each incidence bin, whereas KCDE never did much worse than this naive model. For pre-peak predictions of peak week timing, there were multiple seasons where the SARIMA model consistently underperformed relative to the naive approach of assigning equal probability to each week of the year; KCDE and HHH4 were more consistently at or above the level of this naive approach.

The lack of appropriate statistical methods to analyze model performance limits our ability to draw formal conclusions about relative model performance. Challenges arise when attempting to apply standard methods for formal model comparisons (such as the Diebold-Mariano test [58]). For example, the standard Diebold-Mariano test assumes that the differences in model performance have a fixed mean and variance. However, Figures 4 and 6 indicate that the mean and variance of log score differences are different in each season, and are likely a function of variables such as the timing and severity of the season peak. Additionally, due to the limited amount of real data available, we have only a small number of testing seasons to evaluate; this makes fitting a more flexible linear mixed effects model with a realistic variance structure difficult. Therefore, many of the conclusions about relative model performance are based on exploratory and graphical summaries of performance metrics. Despite the lack of a formal statistical test, we believe that the graphical summaries in Figures 4 and 6 show clear patterns of model performance, and in particular highlight the benefits of flexible methods for heterogeneous data.

The goal of making predictions of infectious disease is to provide information to public health officials planning interventions several weeks or months before the disease season begins or peaks. Predictions that assign very low probability to the eventually observed outcome may lead public health agencies to misdirect limited resources, potentially resulting in increased disease incidence [5]. Across all three prediction targets, our method consistently delivers non-negligible predictive probabilities for the eventually observed events. This improved reliability of predictions from KCDE relative to the baseline models is an important benefit of the proposed method. However, since year-to-year variation is substantial, continued evaluation of these methods on datasets with longer prospective testing phases could provide better information about long-run performance of all of these methods.

We have introduced the use of a periodic kernel component that led to substantial improvements in the predictive distributions for incidence in individual weeks, and more moderate improvements to predictions for peak incidence in both applications and predictions of peak timing in the application to influenza. Periodic kernels have not otherwise been used in the KCDE literature despite their importance for prediction in seasonal systems. This advance improves the applicability of KCDE to infectious disease prediction in general and we demonstrate how it leads to improved performance for CDC’s chosen prediction targets. An exception to this was for predictions of peak timing in the application to dengue fever, where KCDE specifications without the periodic kernel component outperformed KCDE specifications with the periodic kernel component (and both of the baseline models, which also included seasonal terms) for predictions made before the peak occurred. This may be due to the fact that there was quite a bit of variability in the timing of the season peak in the test phase seasons for dengue. In future work, we plan to consider methods for adapting the strength of the seasonal weighting according to how well incidence so far in the current season matches the predominant historical seasonal trends.

We also introduced application of KCDE with a fully parameterized bandwidth matrix to discrete data. Much infectious disease case data is discrete and small discrete counts can be indicative of transmission dynamics driven by stochasticity. Handling this important case directly makes our method widely applicable to infectious disease data, particularly when combined with the periodic kernel.

While taking advantage of a fully parameterized bandwidth matrix did not lead to consistent improvements in our test data, we have demonstrated through a simulation study that the fully parameterized bandwidth can be helpful in some conditional density estimation tasks. This general method for obtaining discrete kernel functions may be beneficial in other applications of KCDE.

An advantage of the approach we have outlined is its flexibility in terms of cleanly handling both discrete and continuous data and a variety of underlying disease mechanisms. Our method consistently yielded reasonable predictions for all three prediction targets in both applications. As we have seen, the HHH4 model is formulated in terms of discrete case counts and so could not be directly applied to the influenza data where the disease measure was continuous. Even in the data set where it could be used, the HHH4 model underperformed relative to KCDE in predictions for incidence in individual weeks and incidence in the peak week. Similarly, the standard SARIMA model is formulated in terms of continuous distributions, which are not appropriate for use with case count data when small integer numbers of cases are reported. The resulting continuous predictive distributions can be discretized as we have done in this article, but without extra coding effort this discretization is not accounted for during the estimation process so that different models are effectively used during estimation and prediction. Furthermore, our approach consistently equalled or exceeded the performance SARIMA across the applications to dengue and influenza.

There is room for extensions and improvements to the methods we have outlined in this article. One limitation of our work lies in the selection of covariates for the predictive model. We have simply used incidence at the two most recent time points, and possibly the observation time, as covariates. In theory, the method could accommodate the use of additional covariates; however, in practice we are limited by the computationally demanding estimation procedure. We considered using a stepwise variable selection approach to select the model specification, but we found this to be too computationally expensive to be practical; the full grid search suggested by De Gooijer and Gannoun [59] in similar settings with only one bandwidth parameter would be far too slow for our methods. In future work, we plan to consider methods for combining predictive distributions from multiple small KCDE models that each use a small subset of the possible covariates; this strategy should reduce the overall computational complexity of estimation with multiple covariates. If successful, this would also enable further exploration of using other predictive variables such as weather or incidence measures from neighboring locations in the model.

Another method for improving our ability to use covariates would be to replace variable selection with shrinkage. [10] show that when cross-validation is used to select the bandwidth parameters in KCDE using product kernels, the estimated bandwidths corresponding to irrelevant covariates tend to infinity asymptotically as the sample size increases. We conjecture that by introducing an appropriate penalty on the elements bandwidth matrix, bandwidths for irrelevant covariates could be driven to infinity at lower sample sizes. This technique should allow us to include more (possibly irrelevant) covariates in the model.

In many disease incidence data sets, we observe multiple incidence time series simultaneously. For example, in addition to the national level wILI index used in this article, the influenza-like illness data from the CDC contain measures of incidence for 10 smaller regions within the United States, and break down incidence within four age groups. The methods described in this article could be applied to make predictions with multiple time series. For example, one possible approach to this would be to fit a separate predictive model for each time series, using the other time series as covariates that are conditioned on. If a joint distribution of these time series were required, we could use the copula to estimate joint dependence structure across all of the time series; as we mentioned in the introduction, similar approaches have been developed in the economics literature [6]. Another option would be to use KCDE to directly estimate the joint distribution of a random vector of the values of all time series in future time points. Although this is beyond the scope of the current article, we have begun exploratory work in this area, and some preliminary results from separate KCDE models for influenza fit to each region in the United States are available from [60].

Another aspect of our method that should be explored further is the use of log score in estimation. We used log scores in this work to match the use of log scores in evaluating and comparing the performance of different models. The log score has the advantage of defining a proper scoring rule, but it has the disadvantage of being sensitive to extreme values. Previous authors have suggested the use of other loss functions in estimation for kernel-based density estimation methods that reduce these effects, such as variations on integrated squared error [21] or the continuous ranked probability score [22]. Despite discussion in the literature of the potential limitations of using log scores for estimation with kernel-based methods, there is not conclusive evidence that use of log scores caused any difficulties in our application. For example, while the predictive interval coverage rates were too high in the application to influenza, coverage rates were too low in the application to dengue fever. Nevertheless, details of the loss function used in estimation could impact the utility of the resulting predictions.

In the present article, we have simplified the disease prediction task by assuming that the disease incidence measure is reported accurately and without delay. This allowed us to focus on the narrower methodological question of examining whether KCDE is able to capture infectious disease dynamics. However, in order to apply the methods in a real time setting it will be crucial to relax this assumption. We envision two ways that this could be done. First, we could model the relationship between initial reports of incidence and the final revised incidence measure. Using that model, we could use initial reports of incidence at any given time to predict the revised incidence at that time. These incidence “nowcasts” could then be used as inputs to the KCDE prediction model outlined in this article. This approach is similar in spirit to the methods used by Brooks et al.[44]. An alternative approach could use KCDE to directly learn a relationship between initial, unrevised, reports of disease incidence and the final incidence measure in future weeks.

The KCDE modeling framework could also be applied to directly model the joint distribution of incidence in multiple future weeks without the use of a copula. If we were to directly model incidence in all remaining weeks of the season with KCDE the method would operate more similarly to the approach of Brooks et al.[44], who directly model the trajectory of incidence over the course of the season. However, we believe that this line would have limited success since fully nonparametric estimation of the joint distribution of incidence in 40 future weeks (for example) given only about 15 to 20 years of past data will be challenging. Another possible approach would be to use KCDE to obtain a joint predictive density of incidence in smaller groups of weeks (for example, 2 – 5 weeks at a time) and then combine those predictive densities using a mechanism such as a copula. Such an intermediate approach might be able to capture more information about medium-term trends in incidence such as holiday effects than the method we have presented in this article without suffering from the curse of dimensionality as much as direct application of KCDE to an entire season at a time.

There is also a long history of using other modeling approaches such as compartmental models for infectious disease prediction. KCDE is distinguished from these approaches in that it makes minimal assumptions about the data generating process. This can be either an advantage or a disadvantage of KCDE. On the positive side, these minimal assumptions are what make KCDE appropriate for use with a wide variety of disease processes with minimal changes to the model specification. On the other hand, we believe that a well-specified mechanistic model might outperform KCDE in certain circumstances. However, rather than selecting one “preferred” modeling framework or model formulation, we believe it may be fruitful to incorporate the methods developed in this paper as components of an ensemble with several different types of models. An appropriately constructed ensemble incorporating predictions from KCDE as well as other methods might perform better than any of the component models on their own, and would be a valuable approach for maximizing the utility of these predictions to public health decision makers.

6. Software

The estimation methods were implemented in R and C. All source code and data are available in R packages hosted on GitHub [61].

7. Supplementary Material

The reader is referred to the on-line Supplementary Materials for technical details and additional figures with further information about the results.

Table 4.

Summaries of model performance for predictions of peak week timing. The “All Weeks” group summarizes results for all combinations of target week in the test period and prediction horizon; the “Before Peak” group summarizes results for predictions in weeks before the actual peak for the given season. The model in bold font had the highest mean log score within each combination of disease and weeks subset.

			Summary of Log Scores
Disease	Subset	Model	Min	Mean
Dengue	All Weeks	Null KCDE	−5.298	−2.135
		Full Bandwidth KCDE	−5.279	−2.116
		Periodic KCDE	−5.684	−2.107
		Periodic, Full Bandwidth KCDE	−7.824	−2.197
		HHH4	−4.867	−2.115
		SARIMA	−7.601	−2.297
		Equal Bin Probabilities	−3.951	−3.951
	Before Peak	Null KCDE	−5.298	−3.645
		Full Bandwidth KCDE	−5.279	−3.656
		Periodic KCDE	−5.684	−3.759
		Periodic, Full Bandwidth KCDE	−7.824	−3.940
		HHH4	−4.867	−3.814
		SARIMA	−7.601	−4.001
		Equal Bin Probabilities	−3.951	−3.951
Influenza	All Weeks	Null KCDE	−4.374	−1.689
		Full Bandwidth KCDE	−4.193	−1.708
		Periodic KCDE	−4.227	−1.568
		Periodic, Full Bandwidth KCDE	−4.283	−1.601
		SARIMA	−3.868	−1.258
		Equal Bin Probabilities	−3.951	−3.951
	Before Peak	Null KCDE	−4.374	−3.014
		Full Bandwidth KCDE	−4.193	−3.094
		Periodic KCDE	−4.227	−2.945
		Periodic, Full Bandwidth KCDE	−4.283	−3.000
		SARIMA	−3.868	−2.383
		Equal Bin Probabilities	−3.951	−3.951

The model in italicized and underlined font had the lowest minimum log score within each combination of disease and weeks subset. In some cases, the same model had both the highest average log score and the lowest worst-case log score. There were 42 weeks before the peak in the 2009/2010 dengue season, 15 in the 2010/2011 dengue season, 19 in the 2011/2012 dengue season, 31 in the 2012/2013 dengue season, 23 in the 2011/2012 influenza season, and 12 in each of the 2012/2013 and 2013/2014 influenza seasons.