Channel Density Distributions Explain Spiking Variability in the Globus Pallidus: A Combined Physiology and Computer Simulation Database Approach

Abstract

Globus pallidus (GP) neurons recorded in brain slices show significant variability in intrinsic electrophysiological properties. To investigate how this variability arises, we manipulated the biophysical properties of GP neurons using computer simulations. Specifically, we created a GP neuron model database with 100,602 models that had varying densities of nine membrane conductances centered on a hand-tuned model that replicated typical physiological data. To test the hypothesis that the experimentally observed variability can be attributed to variations in conductance densities, we compared our model database results to a physiology database of 146 slice recordings. The electrophysiological properties of generated models and recordings were assessed with identical current injection protocols and analyzed with a uniform set of measures, allowing a systematic analysis of the effects of varying voltage-gated and calcium-gated conductance densities on the measured properties and a detailed comparison between models and recordings. Our results indicated that most of the experimental variability could be matched by varying conductance densities, which we confirmed with additional partial block experiments. Further analysis resulted in two key observations: (1) each voltage-gated conductance had effects on multiple measures such as action potential waveform and spontaneous or stimulated spike rates; and (2) the effect of each conductance was highly dependent on the background context of other conductances present. In some cases, such interactions could reverse the effect of the density of one conductance on important excitability measures. This context dependence of conductance density effects is important to understand drug and neuromodulator effects that work by affecting ion channels.

Introduction

The external globus pallidus (GP) is a central nucleus in the indirect pathway of the basal ganglia and plays an important role in controlling basal ganglia activity through inhibitory output connections to the subthalamic nucleus, internal pallidum, substantia nigra, and striatum. GP neurons in awake animals have high spontaneous firing rates and frequently exhibit short spike bursts and pauses (Delong, 1971). This bursting is irregular and uncorrelated between GP neurons in normal animals but switches to synchronized bursting with loss of dopamine in Parkinson's disease (PD) (Bergman et al., 1994; Nini et al., 1995; Wichmann et al., 1999). In brain slices, rat GP neurons show spontaneous slow regular firing with variable intrinsic electrophysiological properties such as spike adaptation and rebound firing (Nambu and Llinas, 1994, 1997; Cooper and Stanford, 2000). Transitions to bursting can be induced with pharmacological interventions including the application of apamin, a blocker of small-conductance calcium-activated potassium (SK) channels (Loucif et al., 2005). At the present time, it remains unknown to what degree intrinsic GP neuron properties contribute to the observed shifts in network activity in PD. It is known, however, that dopamine has direct effects on calcium channels in the GP (Stefani et al., 2002), and other modulators and mechanisms of excitability plasticity are likely to be present as well. Such modulation of GP excitability is, in principle, well suited to strongly affect basal ganglia network activity because of the high interconnectivity of this nucleus with other structures.

Recently, measurements have shown that different neurons of a given type typically show twofold to fivefold variability in the density of their voltage-gated conductances, resulting in considerable variations of their dynamical behavior (Golowasch et al., 1999; Prinz et al., 2003; Bucher et al., 2005). In the present study, we addressed the question of whether such variability in conductance densities could explain the variability of GP neuron properties observed in slice recordings, and we examined how interactions between different channel types may have important consequences on excitability and neuromodulation. Although experimental studies are well suited to assess the presence and kinetics of specific membrane conductances and determine the action of modulators, it is not possible to determine the resulting interplay of multiple conductances in a spatially complex neuron. Conductance-based compartmental neuron models using realistic cell morphologies that build on the detailed knowledge of experimental studies, in contrast, provide a tool that allows one to fill in this gap and examine the interactions between multiple voltage-gated conductances of a neuron in generating complex activity patterns (Herz et al., 2006). In the present study, we first obtained recordings from 146 GP neurons in vitro to collect data on their spiking behavior and variability. We then constructed a morphologically realistic GP model that included nine membrane conductances found in GP neurons to replicate the most “typical” physiological properties of our in vitro recordings. We then used a brute-force parameter search and database (DB) approach (Prinz et al., 2003) to make a GP neuron model DB of 100,602 models with varying conductance densities centered on the original model. We analyzed the model DB with automated Matlab routines to determine how electrophysiological properties such as spike rate and spike shape depend on multiple conductances. We found that this model DB generally showed smoothly varying properties replicating physiological variability. Importantly, the effect of any specific conductance density change strongly depended on the combination of other conductances present.

Materials and Methods

Electrophysiology

Coronal slices 300 μm in thickness were prepared from 16- to 21-d-old male Sprague Dawley rats according to procedures described previously (Hanson et al., 2004). Briefly, rats were anesthetized with halothane and decapitated. The brain was rapidly removed and immersed in ice-cold artificial CSF containing (in mm) 124 NaCl, 3 KCl, 1.9 MgSO₄, 1.2 KH₂PO₄, 26 NaHCO₃, 2 CaCl₂, and 20 d-glucose, bubbled continuously with a mixture of 95% O₂/5% CO₂. After cutting, slices were incubated at 32°C until use. Whole-cell recordings were obtained using an Axoclamp-2B amplifier (Molecular Devices) at 32°C. Borosilicate pipettes (#8250; AM Systems) were pulled and filled with (in mm) 140 K-gluconate, 6 NaCl, 2 MgCl₂, 0.2 EGTA, 4 Na₄ATP, 0.4 Na₃GTP, 5 glutathione, 0.5 spermine, 0.02 Alexa-568, and 10 HEPES, pH 7.3 with KOH. All animal procedures complied with the National Institutes of Health and other federal rules on animal use and were approved by the Emory University Institutional Animal Care and Use Committee.

Construction of the baseline GP neuron model

Membrane properties.

The procedures used to match the passive electrical properties of reconstructed rat GP neurons were described in a previous publication (Hanson et al., 2004), and additional details are given in the supplemental material (available at www.jneurosci.org). The resulting passive parameter values were as follows: C _M = 0.024 F/m², R _M = 1.47 Ωm², and R _A = 1.74 Ωm, which were used throughout this study. Eight different types of voltage-dependent conductances and one calcium-dependent conductance based on experimental evidence for these channel types in GP neurons were included in the simulations. All voltage-dependent gates were assumed to be independent and were modeled using standard Hodgkin–Huxley equations. The calcium-dependent gate was modeled using the Hill equation. The voltage-gated conductance kinetics were modeled to match kinetics described in the following sources: fast transient sodium (NaF) (Raman and Bean, 2001; Khaliq et al., 2003; Hanson et al., 2004); persistent sodium (NaP) (Magistretti and Alonso, 1999, 2002); fast delayed rectifier potassium of the Kv3 family (Baranauskas et al., 1999, 2003); slow delayed rectifier potassium of the Kv2 family (Baranauskas et al., 1999); A-type, transient potassium of the Kv4 family (Tkatch et al., 2000); M-type potassium of the KCNQ family (Gamper et al., 2003; Prole and Marrion, 2004); calcium-dependent potassium of the SK family (Hirschberg et al., 1998, 1999; Keen et al., 1999); high-threshold, noninactivating calcium (CaHVA) reflecting a mixture of L, N, and P/Q-type calcium channel types (Surmeier et al., 1994); and HCN, which gives rise to the hyperpolarization-activated, cyclic nucleotide-modulated, mixed cation conductance (Wang et al., 2002; Chan et al., 2004). Kv4 was modeled as two separate channel populations with identical activation and deactivation properties but different inactivation kinetics (Tkatch et al., 2000). HCN was also modeled as two separate channel populations, which differed in both their steady-state and kinetic properties (Chan et al., 2004). The equations and parameters defining the simulation of each conductance type are fully listed in supplemental Tables 1 and 2 (available at www.jneurosci.org as supplemental material).

Incorporation of conductances into reconstructed morphologies.

Three morphological reconstructions of differently sized GP neurons (Fig. 1 B) were used interchangeably to model GP neuron properties to cover the range of input resistances found in our slice recordings of GP neurons. Using the CVAPP software (www.compneuro.org), these reconstructions were divided into 585, 643, and 615 compartments, respectively, to obtain a near-equal passive electrotonic length of 0.02 lambda for each compartment. A value of 0.1 lambda is small enough to approximate the continuous cable solution for dendritic cylinders (Holmes et al., 1992), and our value of 0.02 allows for a fivefold membrane conductance increase attributable to voltage-gated conductance activation.

Figure 1.

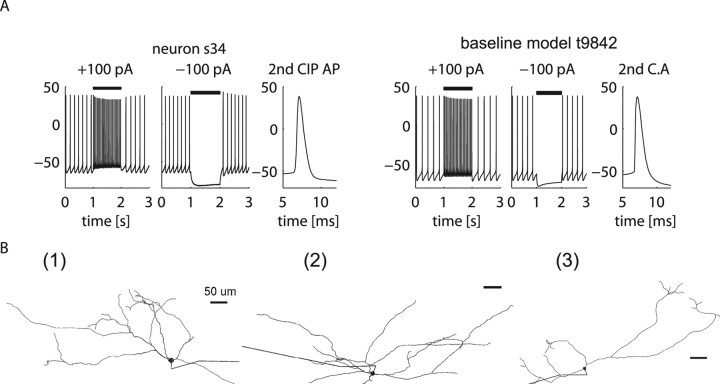
The baseline GP neuron model reflects typical features of GP neurons. A, A representative GP neuron (s34) and the baseline model (t9842) that matches its electrophysiological characteristics such as firing rate, AP shape, and envelope of AP amplitude decay during a depolarizing current injection. B, Anatomical heterogeneity in the GP is represented in our DB study by three reconstructed GP neuron morphologies. The length of the axons is truncated in this depiction.

The compartments in the reconstructed neurons were grouped into three functional regions: soma, axon, and dendrites. Axonal reconstructions were not available from our dye-filled cells, and instead a default axon was used (Shen et al., 1999) that contained two different compartment types: myelinated compartments, which had no ion channel conductances but a 100-fold reduced capacitance attributable to myelin, and unmyelinated compartments (including the axon initial segment and nodes of Ranvier) that were highly excitable.

The dendrites contained three subdivisions based on dendritic diameter: thick dendrites had diameters >1 μm, medium dendrites had diameters ranging from 0.5 to 1 μm, and thin dendrites had diameters <0.5 μm. These subdivisions differed in only one parameter: the calcium channel density was 3 times higher in the thin dendrites than the thick dendrites, and 1.5 times higher in the medium dendrites than the thick dendrites (Hanson and Smith, 2002). The somatic, dendritic, and axonal regions were allowed to have different conductance densities from each other, whereas conductance densities were uniform within each region, except for the differences mentioned above.

We constrained the GP model neuron to have uniform densities of sodium and K _DR channels (Kv2 and Kv3) throughout the soma and dendrites after our recent study demonstrating voltage-gated sodium channel expression in rat GP dendrites with immunolabeling, and with whole-cell recordings from rat brain slices indicating that excitatory synaptic inputs could trigger propagating sodium spikes in GP dendrites (Hanson et al., 2004). The exact densities and distributions of channels were obtained by a semiautomated tuning process to match electrophysiological characteristics such as spike shape and spike rate–current (fI) curves from rat brain slice recordings [a representative neuron (s34) is shown in Fig. 1 A]. See supplemental material (available at www.jneurosci.org) for the details of this tuning process and the resulting parameter settings.

DB construction

Stimulation protocol.

Both experiments and simulations used a current injection pulse (CIP) stimulation protocol. In this protocol, a current injection period would follow an initial period of spontaneous activity. This allowed us to track electrophysiological changes when a depolarizing or hyperpolarizing current was applied. Simulations consisted of a 4 s recording, in which the first second before reaching the steady state was discarded. The remaining 3 s consisted of 1 s for spontaneous activity, followed by a 1 s CIP period and a 1 s recovery period.

Measurements of electrophysiological characteristics.

Measurements from recorded or simulated voltage traces were obtained automatically with our custom PANDORA Toolbox (available from the SimToolDB repository; http://senselab.med.yale.edu/SimToolDB) (C. Günay and D. Jaeger, unpublished observation) within the Matlab environment (MathWorks). Approximately 20 primary measurements were collected from different periods of the CIP protocol and for different levels of injected current, yielding a total of ∼300 measures for each real or model neuron. The firing rate for each period (spontaneous, CIP, recovery) was calculated as the inverse of averaged interspike intervals (ISIs). Action potential (AP) amplitude was measured as the voltage from the AP threshold (see supplemental material, available at www.jneurosci.org) to the peak voltage of the AP. The afterhyperpolarization (AHP) depth was measured as the difference between the AP threshold and the voltage minimum during the AHP. The half-width of the AP was measured at the half-amplitude voltage. Spike frequency adaptation was calculated as the ratio of ISIs from the beginning and end of the 100 pA CIP period, indicating the change in firing rate. A sag during −100 pA CIP was measured as the voltage difference between the lowest voltage reached early in the CIP response and the steady-state voltage reached at the end. The rebound ratio was measured as the ratio between the initial firing rate during the recovery period after a −100 pA hyperpolarizing CIP and the spontaneous firing rate. For AP shape measurements, each AP was measured separately and averaged to give a mean and SD for that measure. For each measure, we selected a sample of near-average and extreme outcomes from the DB and visually checked the original raw data traces to test for correct performance of the respective Matlab algorithm. This testing, in particular, led to a fine-tuning process of the spike-threshold detection, because the standard method of 15 mV/ms threshold crossing of the first voltage derivative (slope) produced poor results for some spike waveforms (see supplemental material, available at www.jneurosci.org).

Conductance parameter space to create model DB.

The model DB was created by changing conductances by factors of 2, 5, or 10, from values in the baseline model. Only three or four values were selected for each parameter to create a coarse-grained search grid that could be completed in a reasonable amount of time with available computational resources. The chosen conductance values bracketed the values used in the baseline model, and in each case added higher and lower than baseline values that were still within physiologically plausible ranges (Table 1). Each conductance density combination was also simulated with three different morphologies (Fig. 1 B). However, the lowest values for NaF, KCNQ, and HCN were used only for the two morphologies with higher input resistances, resulting in some missing combinations of parameter values. The total number of models was 100,602, which is less than the number of all possible conductance density combinations, 3⁷ × 4³ = 139,968. To avoid a combinatorial explosion of parameter combinations, the relative axonal, somatic, and dendritic densities were kept constant throughout all simulations. See supplemental material (available at www.jneurosci.org) for additional details.

Table 1.

Conductance density parameter values used to generate the model DB

Parameters	Name	Values (S/m2)
NaF	Fast, transient Na	125, 250, 500, 1000
NaP	Persistent Na	0.5, 1, 2
Kv2	Slow delayed rectifier	0.1, 1, 10
Kv3	Fast delayed rectifier	2, 10, 50
Kv4f	A-current	10, 20, 40
KCNQ	M-current	0.08, 0.4, 2, 10
SK	Ca-activated AHP K	2, 4, 8
HVA	High-threshold Ca	0.03, 0.3, 3
HCN	H-current	0.04, 0.2, 1, 5
Morph	Morphology	1, 2, 3

DB construction of 146 GP neurons recorded in brain slices.

A physiology DB was constructed by evaluating current-clamp data from 146 GP neurons, which were subjected to a CIP injection protocol as described above for simulations. The same Matlab analysis routines were used to determine measures of physiological properties in the pool of recorded neurons as in the simulations. The analysis routines had to be improved for processing noisy experimental data compared with noiseless simulation data, and thus we tested and fine tuned analysis procedures such as finding the AP threshold that can behave differently in the presence of recording noise. Because physiological responses to a given CIP stimulus can be variable, we used an average measure across several trials. The physiology DB was analogous to the model DB, except that additional values were inserted to keep track of the SD of measures across trials.

Neuron-matching algorithm and distance metrics.

To find best matching model candidates to a given physiological recording, a matching algorithm was used to rank model neurons according to their similarity to that recording. The matching algorithm worked by calculating a distance metric between a set of corresponding measures for two neurons, which could be either simulations or recordings. The metric was defined as the sum of absolute differences between corresponding measures, each normalized by the inverse of the SD of the measure found in our physiology DB of 146 neurons. Each normalized measure difference gives the distance between the two neurons in number of SDs. This normalization allows balancing contributions from measures with different units and different scales of amplitude (e.g., AP width in few milliseconds versus AP amplitude in tens of millivolts). This normalization also had the effect that highly variable features in our recordings did not need to be mapped very accurately in our simulations to provide a reasonable match. For example, the spontaneous firing rate of neurons had a SD of 5.9 Hz, so our distance metric would be increased only by 1.0 if a model neuron had a spontaneous spike rate 5.9 Hz higher than a given recorded neuron. See supplemental material (available at www.jneurosci.org) for a complete list of measurements included in the calculation of the distance metric.

Results

Physiological heterogeneity of GP neurons

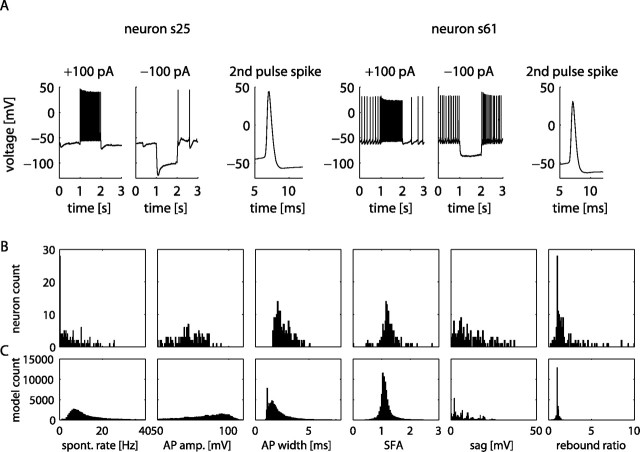
The electrophysiological heterogeneity among neurons in a brain structure is likely to have important consequences on signal processing. To quantitatively characterize the electrophysiological heterogeneity among GP neurons, we formed a DB of measured electrophysiological properties from 146 neurons recorded in brain slices. Properties such as AP threshold, AP amplitude, AP width, spike rate, spike rate adaptation, etc., were quantified from current-clamp data using custom Matlab (MathWorks) scripts (see Materials and Methods). The neurons exhibited a high degree of variability in these physiological properties (Fig. 2 A,B). The frequency of spontaneous firing ranged between 0 and 25.51 Hz (mean, 5.45 Hz; SD, 5.89 Hz), and measures such as spike frequency adaptation, rebound, and sag attributable to HCN also showed severalfold ranges of variation (Fig. 2 B). However, each measure showed a broad unimodal distribution that did not allow for a clear classification into distinct cell types. Thus, although we confirm the spread of different physiological properties in GP neurons reported in previous studies (Nambu and Llinas, 1994, 1997; Cooper and Stanford, 2000), we found no clear separation of the recorded pool of neurons into distinct physiological classes. In part, this difference to previous studies may be attributable to a selection bias in our recordings. In particular, we avoided recording from very large neurons indicative of cholinergic cells present in GP (Schwaber et al., 1987; Gritti et al., 1993); thus it is plausible that type C neurons as defined by Cooper and Stanford (2000) and similarly type III neurons described by Nambu and Llinas (1994) are absent from our DB. Because cholinergic cells in GP belong to a different functional circuit than the GABAergic output neurons, this absence does not limit the use of our data in examining heterogeneity in the indirect pathway of the basal ganglia.

Figure 2.

Electrophysiological and anatomical heterogeneity in the GP is replicated in the model DB. A, Electrophysiological heterogeneity in the GP is shown by two example neurons (s25 and s61) that exhibit distinct characteristics such as the occurrence of a voltage “sag” with hyperpolarizing current stimulus and different spontaneous firing rates. B, C, Histograms of electrophysiological measurements from the physiology neuron DB (B) compared with the histograms of measurements from the model DB (C). The bins representing models with no spontaneous spiking were omitted for clarity in the rate and rebound histograms. spont. rate, Spontaneous rate; AP amp., AP amplitude; SFA, spike frequency accommodation.

GP physiological heterogeneity can be replicated with models of varying conductance densities

To test the hypothesis that electrophysiological heterogeneity in GP may be attributable to variations in channel densities, we constructed a computer model of a GP neuron with nine ion channel types (eight voltage gated and one calcium gated) known to be present in GP neurons to match typical in vitro properties (Fig. 1 A) (see Materials and Methods for details). Three morphological reconstructions were used (Fig. 1 B) that spanned the typical range of input resistances found in recordings. To simulate physiological heterogeneity of GP neurons, we varied the nine conductance densities for all possible combinations of three to four selected values (see Materials and Methods). This brute-force approach to scan all parameter combinations resulted in 100,602 distinct models, the measured properties of which were collected in a model DB. The range of data values for our physiological measures in the model DB (Fig. 2 C) was similar to the distributions found in the physiology DB (Fig. 2 B). As in the physiology DB, individual measured properties such as AP amplitude, AP width, AHP depth, and firing rates in spontaneous activity and in response to CIPs showed broad distributions in the model DB (Fig. 2 C). However, the proportion of models without spontaneous spike activity (56%) was much higher than the proportion of physiological recordings without spontaneous spiking (19%). This finding is congruent with previous studies indicating that biological neurons use homeostatic plasticity mechanisms that keep neurons within specific excitability ranges (Desai et al., 1999) and thus would avoid random conductance density combinations found in our brute-force DB that lead to nonspiking behaviors. In contrast to the physiological data, our simulations also showed only very few models (250 of 100,602) with very low spontaneous spike rates between 0 and 3 Hz (Fig. 2 B,C). This could again be attributable to biological plasticity mechanisms that encourage conductance densities leading to such activity, but may also suggest that the complement of voltage-gated kinetics used in our model is missing a feature that would stabilize very slow firing. Most measures, however, showed good matches not only in the range of values seen but in the peak and shape of the distributions found. It may be surprising at first that measured properties were distributed smoothly in our simulations despite the coarse grid of only three to four density values used for each conductance. Two main factors contributed to the smoothing of measured properties. First, the same conductance density combinations led to different outcomes in the three morphologies used. This mechanism, in particular, smoothed distributions of spike amplitude and sag during negative CIPs, which were otherwise dominated by the discrete settings of the NaF and HCN densities, respectively (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). Second, most measured properties were influenced by multiple conductances (see below), thus no single discrete conductance setting dominated such measures. In some cases, however, a particular value of one conductance could result in non-unimodal distributions of measured properties. The clearest case we observed was the control of spike width at half-amplitude. The half-width histogram showed a peak of narrow spike width values (Fig. 2 C), which was entirely attributable to the highest density of Kv3 used (supplemental Fig. 2, available at www.jneurosci.org as supplemental material).

Most physiological properties were controlled by multiple conductances

An influence of multiple conductances on physiological properties has been observed previously in single-compartment models using multiple Hodgkin–Huxley conductances (Foster et al., 1993). In our full morphological GP neuron model, we found a similar dependence of physiological properties on multiple conductances (Fig. 3). For example, the spike width was strongly affected by both NaF and Kv3 channels (Fig. 3 A); the spike AHP involved CaHVA, Kv2, and NaF channels (Fig. 3 B); and the spike rate during a depolarizing current injection was dependent on both KCNQ and SK channels (Fig. 3 C).

Figure 3.

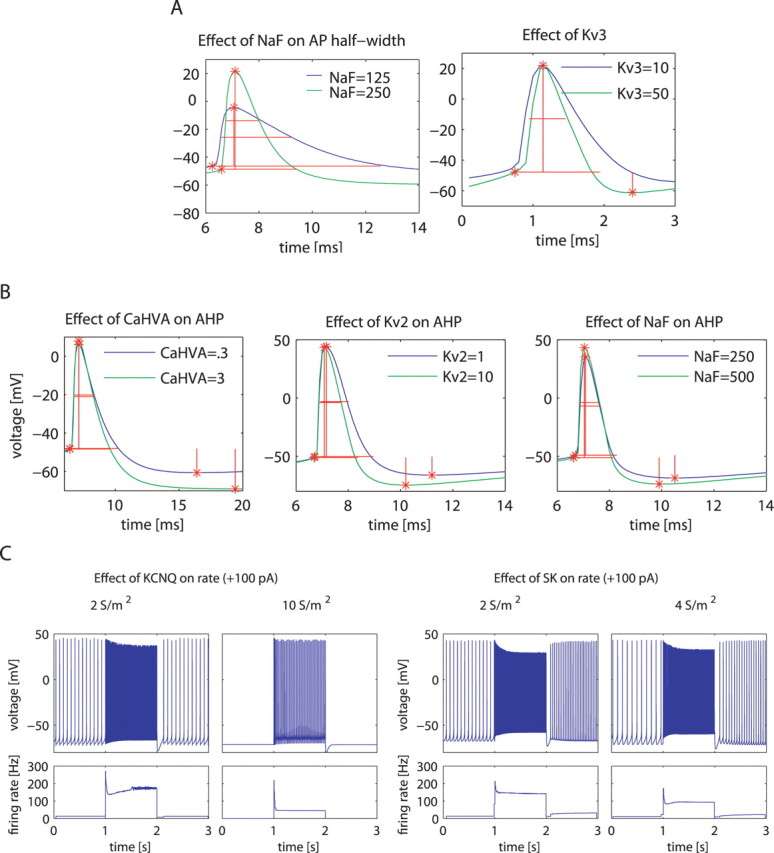
Examples of how a change in the density of a particular conductance affects multiple individual measurements of model neuron properties and how each property is affected by multiple conductances. A, Effects of NaF and Kv3 on the AP half-width. B, Effects of CaHVA, Kv2, and NaF on AHP magnitude. C, Effects of KCNQ and SK on firing rate (see supplemental Table 3, available at www.jneurosci.org as supplemental material, for the conductance density parameters of these example models).

A full analysis of the model DB with respect to average effects of channel density increases on each measured property revealed a complex matrix of each channel influencing multiple measures (Fig. 4 C). In fact, the only property that we found to be almost entirely controlled by a single conductance was the sag of the voltage trajectory during a negative CIP, which was attributable to HCN. Rebound spiking after hyperpolarization was increased both by NaP and by HCN conductances, but not others. Thus, our analysis predicts that in GP, an increase in these two conductances could be important for network-bursting behavior because of rebound spiking. The spontaneous spike rate was positively influenced primarily by NaP conductance but also by Kv3, whereas it was primarily negatively influenced by KCNQ conductance, but also by Kv4, SK, and CaHVA. Notably, the control of the steady-state spike rate during +100 pA current injection was different from the control of the spontaneous spike rate, indicating a difference in channel contributions to spike rates at different membrane potentials. In particular, during CIP-induced depolarization, NaF played an increased role in enabling higher spike rates, and the Kv2 conductance actually reversed its effect of slowing down spontaneous spiking to allowing faster spiking during positive current injection. Further analysis of this effect showed that Kv2 prevented the development of depolarization block during 100 pA current injection. From the total population of 100,602 models, depolarization block developed in 25,688 (26%) during 100 pA current injection, therefore an impact on depolarization block became an important effect of conductance manipulations. Our results indicate that an increase in Kv2 conductance would also lead to an increase in AP amplitude, an increase in AHP depth, and a decrease in spike width and would affect other physiological properties as well (Fig. 4 C). This multiplicity of effects leads to the prediction that channel modulation, even when limited to a single conductance type, will have complex consequences on single-neuron dynamics.

Figure 4.

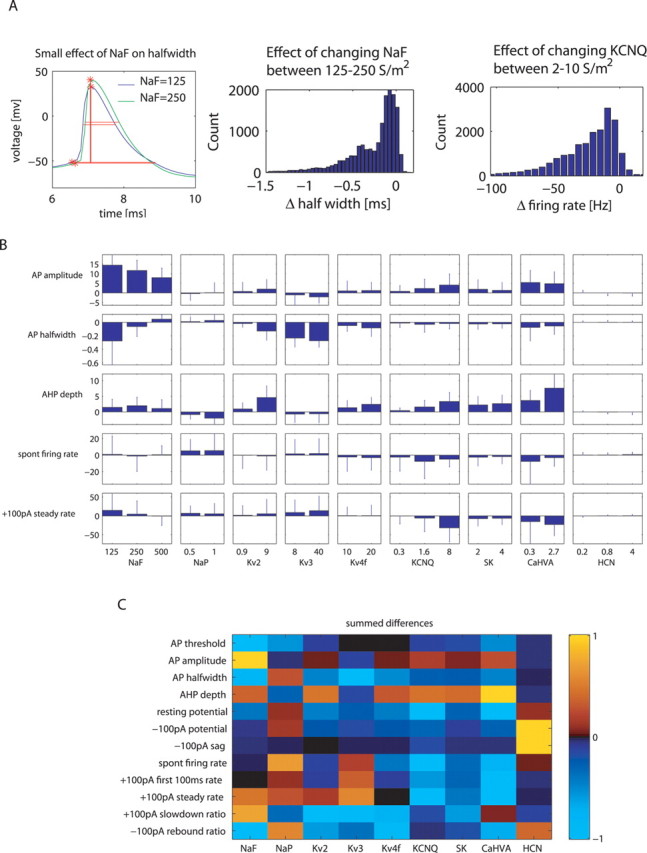
Context dependence of channel effects on measures in the entire model DB. A, As an example of context-dependent effect, this model had a smaller effect of NaF on AP half-width (left) than the model shown in Figure 3 A. The histogram of change in AP half-width with NaF conductance increases (middle) shows that the effect of NaF on the AP half-width varied between −1.5 and 0 ms based on the background context. As another example, the histogram of changes in firing rate during +100 pA CIP with KCNQ over all combinations of background conductances also showed broadly distributed values. The S/m² ranges above the plots indicate the change in the conductance value. B, Error-bar plot representing mean and SD of the distribution of the effect caused on some important measures by change in conductance (including the examples from A). Each bar indicates the effect caused by a conductance increase of the magnitude indicated on the x-axis (i.e., the bar labeled with 125 S/m² NaF shows the effects of increasing the conductance from 125 to 250 S/m²). C, Table representing context-independent total effect on measure value with change of conductance value from its lowest to highest level. The color of each box represents the sum of mean effect in B for each measure–conductance pair. Each row of the table is normalized to a maximal value of +1.0 or −1.0 for the largest absolute change seen for the respective measure.

Context dependence of channel effects in the control of spike shape and excitability

Although information on averaged conductance density effects on physiological properties (Fig. 4 C) is highly desirable for understanding the effects of channel modulation, this information is inadequate for predicting the outcome of such modulation when the density levels of other voltage-gated conductances are different. A simple example of this sort is the strong effect of CaHVA on deepening the AHP (Fig. 4 B), which is mediated by the activation of a SK. Thus, the high variability of the effect of CaHVA on AHP depth (Fig. 4 B) was mostly caused by the variable density of the SK conductance (supplemental Fig. 3, available at www.jneurosci.org as supplemental material). Channel interactions, however, were usually more complex than a pairwise dependency. When we examined the effects of different conductances on AP half-width (Fig. 4 B, second row), we found that NaF had a large mean effect when its density was increased from 125 to 250 S/m², but for many individual backgrounds of other conductances, this increase actually had almost no effect (Fig. 4 A). Because a large effect on spike width was also caused by Kv3 (Fig. 4 B), it was interesting to understand how NaF and Kv3 interacted in controlling spike width. Scatter plots of AP amplitude versus half-width for different levels of Kv3 and NaF (supplemental Fig. 2) revealed a nonlinear interaction of effects. NaF had a primary effect on AP amplitude, whereas Kv3 had a primary effect on AP half-width. However, AP amplitude and half-width were related to each other because larger spikes activated much more Kv3 because of its depolarized activation range. Thus, high levels of NaF resulted in large spikes, and the voltage dependence of Kv3 led to a pronounced narrowing of large spikes, but only when Kv3 was also at a high density.

The control of spike rate by active properties is of particular functional relevance because it determines overall excitability and responsiveness to synaptic input. Thus, we more closely analyzed the average effects of different channel types on spike rate described above. We focused our analysis on the spike rate during +100 pA current injection, which had a mean value of 36 Hz in our model DB, closely resembling the 31–36 Hz average spike rate of GP neurons in awake rats (Ruskin et al., 1999; Urbain et al., 2000). The largest effect on this measure by a single conductance change was found for an increase in the level of KCNQ from medium to high. This KCNQ increase resulted, on average, in a large reduction in spike rate (Fig. 4 B). However, for individual combinations of other conductances present, this effect varied smoothly from large to nonexistent (Fig. 4 A, right). In a few cases, the effect was even in the opposite direction, and the spike rate increased slightly with added KCNQ. In fact, every conductance in the model could show opposite effects on spike rate when it was increased depending on the background of other conductances present. In the cases of KCNQ, NaP, Kv3, and SK, only a few outliers showed opposite effects compared with the mean, but for NaF, Kv2, Kv4f, and CaHVA conductances, this was the case for >10% of all models (see supplemental Table 6, available at www.jneurosci.org as supplemental material, for percentage of models with opposite effects). This type of context dependence of channel modulation effects could present a basis for bidirectional effects of neuromodulation, such as the upregulation or downregulation of spike rate in different neurons by serotonin in substantia nigra pars reticulata (Invernizzi et al., 2007), which bear many similarities to GP neurons. It should be noted, however, that our model DB covered all permutations of different conductance settings in a coarse search grid. Some areas of this parameter space may not be visited by biological neurons because of homeostatic plasticity rules (see Discussion).

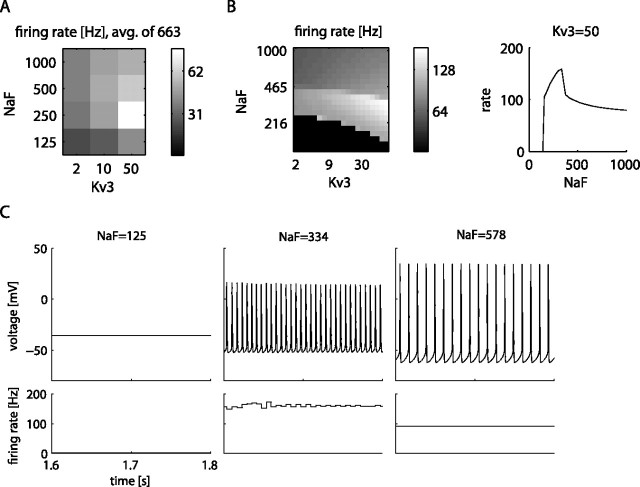
Another possible explanation for inconsistent drug effects is given when two successive increases of one conductance (low to medium, then medium to high) produce opposite effects on spike rate although all other conductances remain the same. NaF presented a good candidate for a conductance producing such effects, because many more models showed an increase in spike rate when NaF was increased from 125 to 250 S/m² than for an additional increase to 500 S/m² (supplemental Table 6, available at www.jneurosci.org as supplemental material). We specifically queried the DB for models in which the spike rate increased for a conductance increase to 250 S/m², but for an additional increase to 500 S/m² showed a decrease of at least 20%. We found that these conditions were predominantly fulfilled by model conductance backgrounds with a high level of Kv3 (n = 663 of 10,206 backgrounds; 6.5%) (Fig. 5 A). To examine this reversal of spike rate change at a NaF density near 250 S/m² and its dependency on Kv3 more closely, we picked one of the models showing this effect and used it as a starting point to create a finer-grained model DB to fill in the coarse search grid of the original DB. To create this finer-grained DB, we used 20 levels of both NaF and Kv3 densities on a logarithmic scale covering the density range of the coarse-grained DB. Even at the finer resolution, we found that the increase and then decrease in spike rate with increasing NaF were dominated by sudden boundaries in spiking behavior (Fig. 5 B). Representative raw data traces show that the model first underwent a change from depolarization block to fast spiking with increasing NaF and then underwent a second transition to a slower spiking mode with a different spike shape.

Figure 5.

Analysis of the effect of NaF and Kv3 channels on the firing rate. A, Change of spike rate with four NaF and three Kv3 levels, averaged over the 663 models with strongly reversing effects in the DB. Rate is measured during the 100 pA current injection period. avg., Average. B, Left, Same landscape from A, in a DB created with finer-grade values of 20 steps each for NaF and Kv3 for one of the 663 models (see supplemental Table 4 for the selected model parameters). Right, Line plot of spiking frequency for increasing values of NaF when Kv3 is held at 50 S/m². C, Example voltage traces from the three distinct regions of spike frequencies shown in B.

Multiple combinations of channel density could lead to similar activity

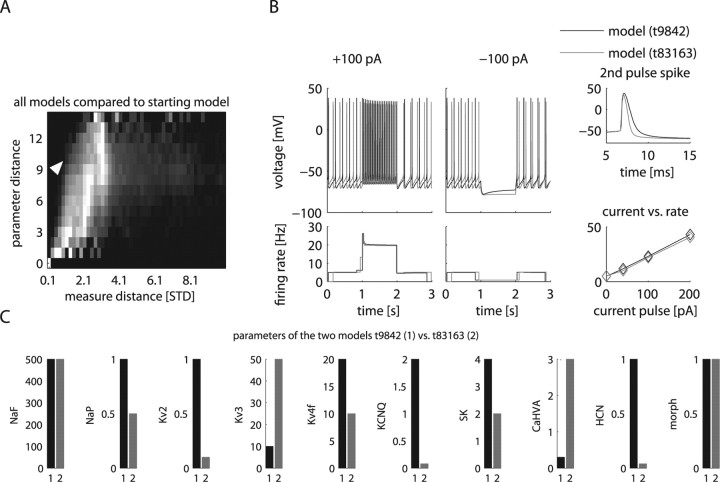
Experimental studies have shown that homeostatic plasticity can lead to neurons showing similar electrophysiological properties by choosing different combinations of conductance densities (Golowasch et al., 1999; Bucher et al., 2005). Similarly, in computer simulations, different combinations of conductance densities can lead to similar electrophysiological properties (Bhalla and Bower, 1993; Foster et al., 1993; DeSchutter and Bower, 1994; Goldman et al., 2001; Prinz et al., 2003; Achard and De Schutter, 2006). Thus, constructing an “ideal” computer model of a given type of neuron with the “correct” set of conductances presents an ill-posed problem. A more general approach to understand which conductance densities can result in a desired behavior is to assess the space of solutions in close proximity to a given electrophysiological set of properties. We used a systematic approach to find GP models in our DB that were maximally disparate in parameters but minimally different in measured properties to our original model. To quantify the similarity in neuronal activity, we defined an overall “distance” metric between neuron representations in our DB by combining measured distances of a comprehensive set of electrophysiological properties. Each measure was weighted in inverse proportion to its SD in the physiology DB with the option of weighting particular properties more heavily (see supplemental material, available at www.jneurosci.org). We then calculated distances of all model neurons to the baseline model that replicated typical GP neuron properties. We plotted these data as a distance matrix along the dimensions of parameter distance and measured property distance (Fig. 6 A). This overall landscape of parameter distance versus measure distance relative to our reference model confirmed that measure distance generally increased with parameter distance. It also showed that many models existed with a relatively high parameter distance and a low measure distance seen from the light-colored areas on the left of the distance matrix. From this distance landscape of the model DB, we searched for models with a large parameter distance (e.g., 10) and low measure distance. Of 7121 models with parameter distance 10, 54 models had <1 SD of measure distance. From the top 10 models with lowest measure distances, we picked an example model with highly similar spiking activity to the baseline model, whereas eight of nine of its conductance parameters differed (Fig. 6 B,C). Although a general analysis of how similar activity can emerge from different parameter settings is beyond the scope of this study, an examination of conductance density differences between the example and baseline models (Fig. 6 C) in reference to the average effect of each conductance (Fig. 4 C) suggests some specific compensatory mechanisms. For example, the picked model differed by an increase in CaHVA conductance and a decrease in SK conductance from the baseline one. The increased CaHVA conductance will activate the remaining SK conductance more strongly and may lead to a comparable overall SK current. Thus, many different matched combinations of CaHVA and SK current could result in similar model behaviors. Similarly, the observed reduction in NaP is expected to lead to a decrease in spike rate, as well as affect other measures. These effects could be compensated for by the observed decrease in KCNQ, because these two conductances have opposite effects on most measures (Fig. 4 C). It is important to note that disparate parameter combinations leading to similar electrophysiological properties are not an artifact of computer simulations but have been observed experimentally as well (Golowasch et al., 1999). Nevertheless, these neurons or models are not functionally identical, because the different background conductances would cause them to respond differently to neuromodulation that upregulates or downregulates specific channels (see above). Our analysis here specifically predicts that conductance densities in GP could be highly variable while overall behavior is maintained because of compensatory changes. The presence of variability in GP conductances can be experimentally tested by using current-clamp and voltage-clamp analysis in brain slices. Our modeling results also indicate that such an analysis is important to understand the variability in the effect of drugs on different GP neurons.

Figure 6.

Models with different channel densities could lead to similar behavior. A, The landscape of relationship between distances in model parameters and in electrophysiological properties of all models compared with the starting model showed regions where models were similar in activity but disparate in parameters. The grayscale color in this two-dimensional histogram indicated the percentage of models out of all models with a parameter distance that fall within the range of property distance denoted on the x-axis. Each row in the histogram was normalized by the bin with maximal number of models indicated with the brightest white (see supplemental Table 5, available at www.jneurosci.org as supplemental material, for the normalization coefficients). For example, there are only very few models with a very small parameter distance to the original model, and all of these show a small distance in properties (bottom left corner of plot). There are also only a small number of models with a maximal distance in parameter space, and most of these show an intermediate property distance (top row). There are many models with intermediate parameter distances, and these show a large range of property distances, among them the largest observed total property distances (middle rows). STD, Standard deviation. B, C, The baseline model is compared with the model found from the landscape in A (white arrow) with the largest discrepancy between parameter distance (10) while showing a small property distance (0.7) to the baseline model. Raw traces show the overall similarity between these two models (B). Nevertheless, eight of the nine conductance parameters are substantially different between the two models, whereas only the level of NaF and the morphology of the neuron remained the same (C).

The model DB approach allows finding models that best match the properties of individual recordings

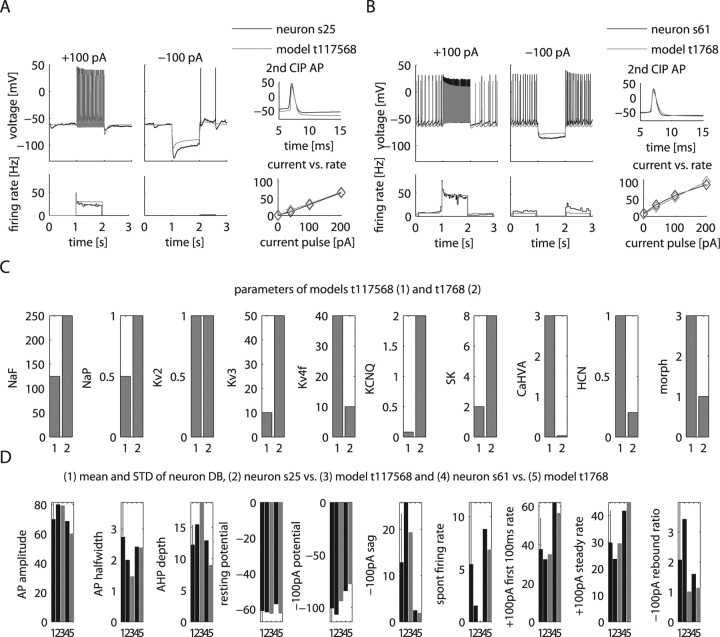
As shown in Figure 2, our physiology DB of 146 recorded GP neurons shows a large range in property distances. To better understand how conductance density differences could explain the physiological properties of individual neurons, we used the distance metric defined above to compare recordings and models. In particular, we identified the best matches in the model DB for the two distinct GP neurons shown in Figure 2 A by their minimal property distance to the recordings. These best matches in the model DB fit the distinguishing features in the two real neurons such as the sag, firing rate, the fI relationship, and rate adaptation quite well (Fig. 7 A,B). A comparison of the conductance parameters of the DB models best matching each recording showed differences in eight of nine channel density parameters (Fig. 7 C). An understanding of some of the conductance differences between the best matching models can be gained by comparing density changes with the matrix in Figure 4 C that predicts the mean effect of conductances on physiological properties. Sag during hyperpolarization was greater in neuron s25 than neuron s61, and this greater sag was matched by a model with higher HCN density, as expected. Similarly, but less intuitively, the higher spontaneous spike rate of neuron s61 was matched by a model with higher NaP and Kv3 conductance and lower CaHVA conductance, because these were the major conductances affecting this measure in the average effect matrix. However, KCNQ was not lower in this model despite its strong influence on spontaneous spike rate. This demonstrates that best matches between recordings and models cannot be obtained from just combining average channel effects on individual properties, because each channel also influences multiple other properties.

Figure 7.

Models that best match the distinguishing features of the two GP neurons s25 and s61 from Figure 2 A. A, B, Comparison of the two recorded neurons and models selected for best matching their pronounced differences in physiological properties. The raw data traces for ±100 pA CIP are aligned with instantaneous firing rate plots shown below. Additional plots show the shapes of the second AP during the +100 pA CIP period and a graph of the firing rate versus injected current (fI curve). C, Comparison of conductance values between the two models matching the two different recordings highlight their distinctions. D, Comparison of measures between the neurons and matching models. The mean and standard deviation (STD) of the physiology DB is shown in the first column to allow a comparison of the selected neurons with the sample mean and variance. The STD of the physiology DB also indicates the relative weight of the measure used in our matching algorithm (see Materials and Methods).

Despite the overall good match between recorded neurons and best-matching models, a detailed comparison of the measurements showed remaining quantitative differences between the selected neurons and matching models (Fig. 7 D). These differences may be partly attributable to the coarse granularity of our search grid, and matches might be improved with gradient descent searches in the local parameter neighborhood of our identified best matches. Nevertheless, we expect remaining differences even after such searches because of inherent model limitations such as simplified intracellular Ca²⁺ handling and missing pump currents. In contrast to just creating a single “optimized” model, the DB approach allows the identification of mismatches that are not caused by conductance density settings, and it facilitates the eventual incorporation of additional processes into the model that best address such mismatches.

Comparison of multiple models that match specific recorded neurons

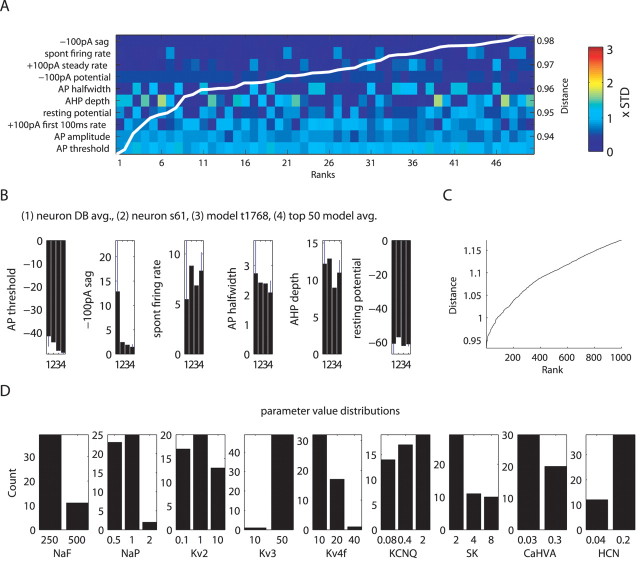
Given our above findings of multiple models with similar physiological properties, we expected to find multiple good candidate models in our DB that match the behavior of particular recorded neurons. Many candidate models were indeed similar, because the distance between the example target neuron s61 and matching models only increased from a mean of 0.93 SDs (SD determined from variance in DB of 146 recorded neurons) for the selected set of properties to 0.98 SD for the 50th ranked model (Fig. 8 A) and to 1.15 SD for the 1000th ranked model (Fig. 8 C). The distances of these top-ranking candidate models were significantly lower than the mean distance of 2.5 and its SD of 1.1 obtained from all matches to this neuron in the model DB. The individual measure distances showed that all top 50 ranking models tended to best match the same properties of the target neuron s61 (Fig. 8 A). For this neuron, the most closely matched feature was the sag at −100 pA CIP period throughout the ranks, whereas the worst matched feature, by far, was the AP threshold during the +100 pA current injection period. This threshold had only a small SD in the physiology DB (Fig. 8 B), and models in the DB generally showed a lower AP threshold, which is potentially attributable to a mismatch in the NaF kinetics or voltage dependence. The matches to this neuron also showed an interesting interaction between the AP half-width and AHP depth measures because no model was able to match both of these measures well at the same time, and thus different models switched between solutions that satisfied one or the other (Fig. 8 A). To determine the range of conductance densities that could account for model behaviors similar to neuron s61, we plotted the conductance level distribution of the top 50 matches (Fig. 8 D). We found that some conductances were constrained primarily to one (NaF, Kv3, HCN) or two (NaP, Kv4, CaHVA) levels, whereas the remaining ones (Kv2, KCNQ, SK) took on all three possible conductance levels in a considerable number of models matching neuron s61. Again, these findings highlighted the point that multiple conductance combinations could result in similar physiological properties because each property is controlled by multiple conductances.

Figure 8.

Multiple similar models matching neuron s61 were found. A, Color plot of measure distances of top 50 ranking models to the recorded neuron shows the similarities between models. The colors are scaled by the standard deviation (STD) of the respective measure in the DB of 146 recorded neurons. The measures on the y-axis were sorted to have better matching measures at the top. The superimposed white-line plot shows the cumulative distance measure of each of the models, the scale bar of which appears to the right. B, Quantitative comparison of actual measure values between the physiology DB, neuron s61, best-matching model t1768, and the mean and SD of the top 50 models. avg., Average. C, Plot of sorted cumulative measure distance for the 1000 best-matching models shows that distance to the target neuron increases more steeply in the lower ranks. D, Differences in conductance densities found in the top 50 models are shown with distribution plots of conductance parameters.

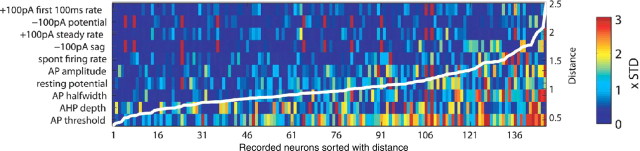
To test the hypothesis that manipulating channel conductance densities can completely explain the observed variability in GP neuron recordings, we applied the best-matching algorithm to each of the 146 recorded GP neurons (Fig. 9). The results indicated that we were able to match >80 recordings within 1.0 SD averaged across properties. Thus, the model DB approach is generally suited to find models for individual recordings and to generate future network models that incorporate the natural heterogeneity of recorded populations of neurons.

Figure 9.

Model DB of varying conductance densities can provide matches to all 146 GP neurons. Best-matching models to each of the 146 recorded GP neurons were shown in the same way as in Figure 8 A, except that the measures were sorted differently according to overall match to all recorded neurons. Also, the neurons are sorted from most easily matched to most difficult match on the x-axis. The superimposed white-line plot indicates the cumulative distance value of the best matches to each neuron. STD, Standard deviation.

Experimental testing of a key modeling prediction: variability of channel block outcomes

A key finding of our modeling results was that the effect of changing the density of an individual conductance on a given measure, such as spike width or spike rate, should be quite variable because of the interaction with the combination of other conductances present (Figs. 3, 4 A,B, 5). Even conductances that are generally expected to have a consistent effect on spiking behavior, such as NaF and delayed rectifiers (e.g., Kv3), showed highly variable effects on these behaviors in the presence of different conductance backgrounds. The prediction of variable effects of reduced channel densities is testable by applying partial block concentrations of toxins in a set of biological neurons, which presumably would also display some variability in conductance density backgrounds. Because Na⁺ current is a major contributor to spiking behavior and showed conductance background-dependent effects in our model, we undertook partial block experiments of Na⁺ current by adding low concentrations of tetrodotoxin (TTX; 7–15 nm; n = 7) to the slice perfusate during a GP recording after having established baseline spiking behavior. TTX blocks both fast and persistent Na⁺ current (Crill, 1996), therefore the matching model comparison to partial TTX block consists of a joint reduction in NaF and NaP conductances. At the concentrations used, the Na⁺ conductance should be reduced by 50–80% (Osorio et al., 2005; Mercer et al., 2007). In the model, a joint reduction in NaF and NaP conductance led to a variable reduction in spike rate during 100 pA current injection (Fig. 10 A,C), but only in very rare cases to an increase. Our experiments revealed a similar distribution of effects (Fig. 10 C) ranging from no effect to a dramatic reduction (see supplemental Fig. 4, available at www.jneurosci.org as supplemental material, for effects on individual cells). The most extreme reductions in spike rate occurred both in experiments and in the model because of developing depolarization block for low effective Na⁺ conductance densities (Fig. 10 A). A similar match between experiments and simulations was also observed for variable reductions in spike amplitude and increases in spike width (Fig. 10 B,C). Thus, overall a good match between NaF/NaP reductions in the model and partial TTX block in slice recordings was found. This supports the notion that neuromodulators that upregulate or downregulate Na⁺ channels will have different effects on different neurons and affect many aspects of spiking dynamics simultaneously. Nevertheless, cases of reversing effects that were present in a very small population of models were generally not found in our experiments, possibly because one might need hundreds of recordings to find such cases. It is also possible that the conductance backgrounds associated with reversing effects of Na⁺ channel density on spike rate are not found in biological GP neurons. The only reversing effect seen in a TTX block experiment was the increase in spike amplitude in one neuron during 100 pA current injection after TTX application (Fig. 10 C). On closer inspection, this was likely attributable to absence of spontaneous spiking preceding the 100 pA current injection, which can lead to increased sodium channel availability at the onset of the CIP because of the removal of slow inactivation in the preceding period.

Figure 10.

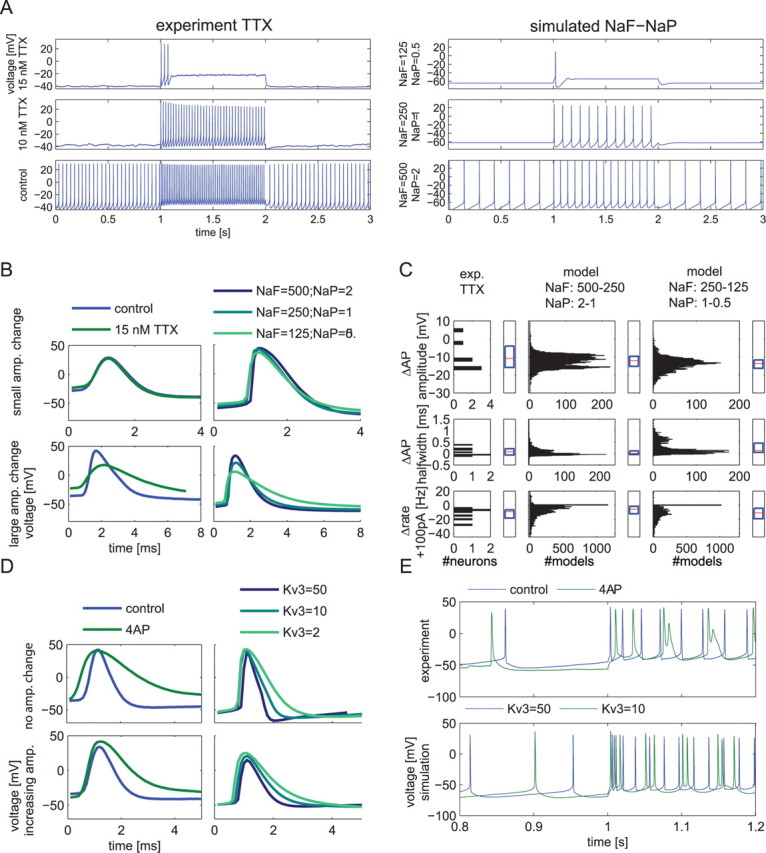
Comparison between variable effects of NaF/NaP or Kv3 density reductions in the model and matching partial block experiments using TTX or 4-AP in brain slices. A, Examples of firing rate changes in whole-cell recordings after application of 10 and 15 nm TTX (left) and in the model when the two sodium conductances (NaF and NaP) were reduced twofold or fourfold with the same remaining conductance background (right). B, D, Examples of spike shape changes after TTX or 4-AP application (left panels) or reduction of NaF/NaP or KV3 conductances in the model (right panels). For the 4-AP and Kv3 manipulation, increases in spike amplitude (amp.) were seen in some recordings and in some models with specific combinations of other conductances present. Note that the spike width increased in all cases, but to a different degree. TTX application matched Na⁺ conductance manipulation in the model as smaller spike amplitudes resulted only in some recordings and for some model conductance backgrounds. C, Statistics of measure changes obtained after applying TTX in slice recordings (left column; n = 7 neurons; 7–10 nm TTX). The effects of multiple measures for all seven neurons recorded with one or two concentrations of TTX are given in supplemental Figure 4 (available at www.jneurosci.org as supplemental material). The range of observed effects of TTX on key measures generally matched the effect of a joint lowering of NaF and NaP conductance in model backgrounds (n = 10,206 models). In these box plots, red lines denote the population median, and the blue box denotes upper and lower quartiles. TTX, Experiment TTX. E, Two of eight recorded neurons exhibited doublets during 100 pA current injection after application of 4-AP, as did 4 of 11 model backgrounds randomly picked out of 1155 conductance backgrounds when their Kv3 conductance was lowered from 50 S/m². This feature was searched for manually because a measure of doublets was not present in our DB. In the example shown, the second spike in each doublet was more attenuated in amplitude in the experiment than the model. An additional reduction from 250 to 125 S/m² of the NaF conductance in the model also led to pronounced amplitude attenuation of second spikes in doublets (data not shown). Parameter backgrounds of the example models are listed in supplemental Table 7 (available at www.jneurosci.org as supplemental material).

Whereas TTX blocks two conductances present in the model, a low concentration of 100 μm 4-aminopyridine (4-AP) results in selective and approximately half-maximal block of Kv3 channels in GP neurons (Baranauskas et al., 1999). Thus, as a second test of our model predictions, we used 100 μm 4-AP block in some GP neurons (n = 8). The model DB predicted that reduced Kv3 conductance should result in a pronounced but variable spike width increase, a small but highly variable spike amplitude increase, and a highly variable spike rate increase during +100 pA current injection (Fig. 4 B). The experimental findings confirmed these major predictions (Fig. 10 D,E), although the median effects and the amount of variability were not identical. In particular, the spike width increase was generally larger in the experimental data than in the model, even when Kv3 was reduced 25-fold (Fig. 10 C). In fact, the effects after application of 100 μm 4-AP were generally better matched by a much larger than twofold reduction in Kv3 in the model, suggesting that Kv3 is somewhat underrepresented in the default model (see Discussion). Some unexpected findings emerged as well. Two of the eight recordings showed doublet spike firing during +100 pA CIP injection after application of 4-AP (Fig. 10 E). This led to a post hoc search in the model DB, which also revealed a transition to doublet firing during 100 pA current injection for some models after reduction of Kv3 (Fig. 10 E). This similarity between model and experiments as to the induction of doublet firing by partial Kv3 block for some conductance backgrounds gives additional confidence in the mapping of the dynamical behaviors between the two domains and illustrates the back and forth between experiment and simulation to gain new insights in the range of GP neuron behaviors.

Discussion

We used a brute-force DB search approach (Prinz et al., 2003) to examine the dependence of the physiological properties of a morphologically realistic GP neuron model on the density of nine different membrane conductances that are known to be expressed in GP neurons. By building a Matlab DB of 100,602 models with different parameter combinations, we could use graphical methods and search algorithms to determine the interactions between membrane conductances and measured electrophysiological properties. The construction of a physiology DB of 146 GP neuron recordings containing measures of the same properties allowed us to make a detailed comparison between the variability found in real neurons and the variability found in a model by changing conductance densities. Finally, we were able to confirm the variability of physiological effects of conductance density changes by partial block experiments of NaF/NaP and Kv3 currents.

Model DB indicates that conductance density variations can account for most physiological variability within the GP

Our finding that distributions of characteristic properties (e.g., spike rate, spike width, spike frequency adaptation, sag) were similar in the model and physiology DBs indicates that conductance density and morphological variability can account, to a large degree, for the experimentally observed spread of electrophysiological behaviors in GP neurons. This assessment is supported by experimental studies that find a severalfold conductance density variability in different types of neurons (Turrigiano et al., 1995; Desai et al., 1999; MacLean et al., 2005; Marder and Bucher, 2007). Nevertheless, conductance parameters such as activation curves and time constants are also variable because of modulation. For example, NaP half-activation can be modulated by dopamine (Gorelova and Yang, 2000), and glial cell line-derived neurotrophic factor decreases the activation time constant of CaHVA channels in dopamine neurons (Wang et al., 2003). Varying these parameters will introduce additional effects on neural dynamics, which could be similar to or distinct from the variability found with conductance density modulation.

The model DB allowed us to match individual GP recordings with models showing a high degree of similarity in properties. However, the matches were nonunique in that multiple models with quite different conductance density combinations could result in equally close matches to a given recording. Multiple channel combinations that result in a similar target behavior have also been found in Purkinje cell models (Achard and De Schutter, 2006). Such nonuniqueness is expected from theoretical and modeling studies of homeostatic plasticity, which have shown that homeostatic mechanisms do not lead to a single fixed combination of channel densities, but rather to a range of different channel combinations that can all achieve the appropriate target behavior (Liu et al., 1998; Abbott, 2003; MacLean et al., 2005). The model DB approach is well suited to explore the consequence of nonuniqueness in biological neurons for effects of neuromodulation and synaptic integration in networks. Specifically, the dynamic variability in individual GP neurons will be important to consider in network simulations that explore the causes of network bursting observed in PD (Bergman et al., 1994; Wichmann et al., 1999).

The GP model DB generates novel insights into the control of physiological properties by multiple voltage-gated conductances

The model DB approach enabled us to perform an analysis of the interdependence between multiple conductances in controlling seemingly distinct physiological properties of GP neurons such as spike width, spontaneous spike rate, and fI curves. Previous work in single-compartment models of invertebrate burst pattern generation (Prinz et al., 2003) has shown that many electrophysiological properties are affected by multiple conductances. Similarly, we found that most GP properties are affected by multiple, if not all, conductances present (Fig. 4 C). In turn, a change in the density of any given conductance had a pleiotropic effect on multiple physiological properties. Given the set of conductances found in GP, the context dependence of the effect of changing any given conductance on physiological properties was surprisingly large, because severalfold differences and even reversals of effects were found for different conductance backgrounds. Although such context dependence would seem to make the results of neuromodulation and plasticity random, it also generates a rich repertoire of outcomes, the most useful of which could be stabilized through selection, a mechanism that has been hypothesized to be the cornerstone of biological learning rules (Edelman and Gally, 2001; Seth and Edelman, 2007). A selection of conductance backgrounds through homeostatic plasticity resulting in particular behaviors also makes it unlikely that biological neurons exhibit all possible combinations of conductance densities that are present in our complete grid of parameter combinations in the model DB. Constraints on channel density combinations in biological neurons have been found and were present on homeostatic plasticity mechanisms (MacLean et al., 2005; Schulz et al., 2007) as well as neuromodulators (Khorkova and Golowasch, 2007). Thus, the dynamical behaviors of some of our random conductance combinations are likely nonbiological and should be interpreted with this perspective.

Specific predictions resulting from the GP model DB about possible roles of neuromodulators in changing intrinsic GP properties

Many insights into possible mechanisms of PD were made possible by a model of differential effects of dopamine on the spike rate in the direct and indirect pathway of the basal ganglia (Albin et al., 1989; Delong, 1990), but the exact mechanisms of rate changes in GP remain elusive. Our model DB suggests that the persistent sodium (NaP) and M-type (KCNQ) channels have a predominant but opposite effect on spike rate. Both of these channels are known to be affected by neuromodulation through protein kinase A and PKC pathways (Brown and Yu, 2000; Shen et al., 2005; Scheuer and Catterall, 2006). Because many neuromodulators affect these pathways, the change in the neuromodulatory milieu in PD and/or the treatment with levodopa could lead to a change in KCNQ and/or NaP conductances. Interestingly, our analysis also showed an effect of NaP conductance on the strength of rebound after hyperpolarization. Because rebound behavior can support bursting, this effect may be interesting with respect to the emergence of synchronized GP bursting in PD (Raz et al., 2000). A second conductance we found to affect rebound behavior was HCN, which has previously been implicated in the synchronization behavior of GP in PD (Chan et al., 2004). This finding is notable in light of recent reports that HCN channels in GP neurons are modulated by serotonin (Chen et al., 2008; Hashimoto and Kita, 2008). Serotonin is of significant clinical interest in drug-induced dyskinesias (Brotchie, 2005).

Validation of GP neuron model construction from model DB approach

The match between specific models in our DB and different recordings suggests that the kinetics of GP conductances we derived from the literature provided a good starting point to simulate GP neuron behavior. We found the model DB approach very useful in identifying remaining mismatches between model behavior and recordings that could not be compensated for by channel density variations. The most obvious mismatch was given by a lower spike threshold in the model, which could be caused by a difference in sodium channel properties. Sodium channel activation is notoriously hard to determine experimentally and to model accurately (Naundorf et al., 2006), and clearly our model will benefit from future revisions of NaF kinetics. In fact, the model DB approach is well suited to address this problem by building a DB that parameterizes NaF and Kdr (Kv2 and Kv3) kinetics to find improved spike-threshold matches with recordings. The use of morphologically complete neurons is important in this regard as well, because the spatial distribution of sodium channels in axonal and dendritic structures in addition to the soma has a large impact on AP shape and threshold (McCormick et al., 2007; Shu et al., 2007).

High-dimensional conductance-based neuron models have sometimes been criticized for providing arbitrary solutions to matching experimental data. The model DB approach addresses this criticism by revealing the space of possible matches to a given experimental set of data. Although the potential search space is very large, this effort is helped by the observation that physiological properties generally vary smoothly over large areas of a parameter space made of multiple Hodgkin–Huxley conductances (Foster et al., 1993; Olypher and Calabrese, 2007). Our results make the specific prediction that partial block of specific conductances in slice recordings will lead to variable effects in different neurons, even if they show similar baseline activity. Such partial block experiments cannot only be used to validate model predictions, but also have important implications for the effect of neuromodulation and drugs used in the treatment of disease. We used two types of partial block experiments with the application of 7–15 nm TTX or 100 μm 4-AP in brain slice recordings to selectively reduce NaF/NaP or Kv3 conductance in GP by 50–80%. We could indeed verify that biological GP neurons show variable responses to drug application in the direction predicted by the model. The match of a combined NaF/NaP reduction between model and experiment was generally quite good, whereas reduction of Kv3 currents in the model had smaller effects than in the experiments. This could be attributable to the relatively low density of Kv3 conductance in the original hand-tuned model (10 S/m² compared with 500 S/m² of NaF), so that only the largest values of Kv3 in the DB (50 S/m²⁾ could show significant impact after reduction. In addition, it is possible that the fast inactivation of NaF in the biological neurons was somewhat slower than in the simulated NaF kinetics, so that broader spike-waveforms were possible after the elimination of Kv3 current. Such remaining small differences between experimental outcomes and modeling predictions are expected because of the many simplifications and parameter choices inherent to the process of creating detailed compartmental models and lead to a fruitful process of model improvement that parallels our improved understanding of the underlying neural dynamics. It is important to note that an ongoing feedback cycle between modeling and experimentation provides the basis for this process.