Abstract
A surrogate endpoint in a randomized clinical trial is an endpoint that occurs after randomization and before the true, clinically meaningful, endpoint that yields conclusions about the effect of treatment on true endpoint. A surrogate endpoint can accelerate the evaluation of new treatments but at the risk of misleading conclusions. Therefore, criteria are needed for deciding whether to use a surrogate endpoint in a new trial. For the meta-analytic setting of multiple previous trials, each with the same pair of surrogate and true endpoints, this article formulates five criteria for using a surrogate endpoint in a new trial to predict the effect of treatment on the true endpoint in the new trial The first two criteria, which are easily computed from a zero-intercept linear random effects model, involve statistical considerations: an acceptable sample size multiplier and an acceptable prediction separation score. The remaining three criteria involve clinical and biological considerations: similarity of biological mechanisms of treatments between the new trial and previous trials, similarity of secondary treatments following the surrogate endpoint between the new trial and previous trials, and a negligible risk of harmful side effects arising after the observation of the surrogate endpoint in the new trial. These five criteria constitute an appropriately high bar for using a surrogate endpoint to make a definitive treatment recommendation.
Keywords: Meta-analysis, Prentice Criterion, Randomized trial, Surrogate endpoint
1. Introduction
A true endpoint is a clinically meaningful endpoint that usually reflects “how a patient feels, functions, or survives.”1 A surrogate endpoint in a randomized trial is an endpoint that (i) occurs after randomization and before the true endpoint and (ii) yields conclusions about the effect of treatment on true endpoint. Examples of surrogate endpoints include molecular, cellular, or tissue changes when the true endpoint is cancer incidence, bone mineral density when the true endpoint is bone fracture, fetal heart rate when the true endpoint is fetal brain oxygenation, and progression-free survival when the true endpoint is overall survival. A surrogate endpoint can accelerate innovation and the dissemination of a new treatment to patients, but only if it yields the correct conclusions about the effect of treatment on the true endpoint. A notable example of a surrogate endpoint yielding an incorrect conclusion was the approval of drugs incorrectly thought to reduce mortality based on a surrogate endpoint of ventricular arrhythmia.2 Therefore, it is important to carefully evaluate a surrogate endpoint before its use in clinical decision-making, often with a checklist of criteria.
Commonly used criteria for evaluating surrogate endpoints have various limitations. Perhaps the most commonly used criteria for evaluating a surrogate endpoint are the Prentice Criteria. In a landmark 1989 article, Prentice proposed three criteria for valid hypothesis testing extrapolation (rejecting the null hypothesis of no treatment effect on the surrogate endpoint implies rejecting the null hypothesis of no treatment effect on the true endpoint): (i) the effect of the surrogate endpoint on the true endpoint does not vary with randomization group, (ii) the surrogate endpoint affects the true endpoint, and (iii) the effect of treatment on the surrogate endpoint changes the average effect of treatment on true endpoint.3 The Prentice Criteria refer to the first two original criteria of Prentice with additional easily-satisfied criteria that treatment affects both surrogate and true endpoints. The Prentice Criteria guarantee valid hypothesis testing extrapolation for binary surrogate and true endpoints but can yield incorrect hypothesis testing extrapolation when the surrogate endpoint is not binary.4, 5 A proposed modified version of the Prentice Criteria that is applicable to continuous surrogate and true endpoints consists of the first original criterion and a criterion that an increase in the surrogate endpoint implies an increase in the true endpoint. See the Supplementary Material for a graphical justification of the Prentice Criteria and the modified Prentice Criteria.
The main limitation of the criteria of Prentice is that the first criterion, which is often called the Prentice Criterion, is unlikely to hold to the degree necessary for valid hypothesis testing extrapolation. In terms of biological mechanism, the Prentice Criterion implies that treatment only affects true endpoint via a pathway through the surrogate endpoint. For example, in the evaluation of cholesterol level as a surrogate endpoint for heart disease, the Prentice Criterion implies that different drugs lower the incidence of heart disease only by lowering the cholesterol level and not by another pathway. Not surprisingly, the in-depth understanding of the biology needed to establish the Prentice Criterion is almost invariably lacking. When using a small trial with a surrogate endpoint (such as cell proliferation) to replace a large trial with a true endpoint (such as cancer incidence or mortality), a very small deviation from the Prentice can invalidate hypothesis testing extrapolation making conclusions from such a relatively small surrogate endpoint trial particularly tenuous.6, 7
A commonly used criterion for evaluating a surrogate endpoint based on single previous trial with surrogate and true endpoints is the proportion of treatment effect that is explained by the surrogate endpoint.8, 9 A drawback of this criterion is that confidence intervals are typically too wide to be informative.10, 11 In the statistical literature, there is growing interest in criteria based on principal stratification.12, 13 While principal stratification is appealing in theory, identifiability requires restrictive assumptions, such as monotonicity, which may not hold.14, 15 Another criterion is the individual-level correlation between surrogate and true endpoints within each arm of the trial. However, this criterion is not recommended because, even with perfect individual-level correlation, the estimated treatment effects for the surrogate and true endpoints can have opposite signs.16
While early work on evaluating surrogate endpoints focused on data from a single previous trial with a surrogate and true endpoint, the more recent trend has been toward the evaluation of surrogate endpoints in a more informative meta-analytic setting involving a set of previous trials, each with the same pair of surrogate and true endpoints. The set of trials should involve the same disease and the treatments in all of the trials should involve the same mechanism of action. A simple meta-analytic criterion is a trial-level correlation coefficient relating the effect of treatment on the surrogate endpoint to the effect of treatment on the true endpoint. A recent review of 65 sets of oncology trials found that 34 had correlation coefficients less than 0.7, called low strength, 16 had correlation coefficients between 0.7 and 0.85, called medium strength, and 15 had correlation coefficients greater than 0.85, called high strength.17 A related meta-analytic criterion is R2trial, a trial-level correlation arising from a random effects model applied to individual-level data.18 A downside to using R2trial is the difficulty of computation under some random effects models.18 While R2trial (or the trial-level correlation coefficient) is informative, there are concerns about determining a threshold value that would indicate acceptability of the surrogate endpoint.19. A commonly used supplement to R2trial is the surrogate threshold effect, which is the minimum effect of treatment on the surrogate endpoint necessary to predict a statistically significant effect of treatment on the true endpoint.18–20
This article formulates five criteria in the meta-analytic setting for using a surrogate endpoint in a new trial to predict the effect of treatment on the true endpoint in the new trial. The first two criteria are statistical considerations, namely easily computed and interpretable metrics derived from a simple but novel statistical model. The last three criteria are biological and clinical considerations that are important for extrapolating results from previous treatments to a new treatment.
2. Statistical model
This section discusses the statistical model underlying the two statistical criteria. For the ith trial in a set of previous trials, let yi denote the estimated effect of treatment on true endpoint. The form of yi depends on the type of data and how it is analyzed. One example of yi is a difference in survival probabilities between randomization groups. Another example of yi is the estimated proportionality constant relating the hazard functions in the two randomization groups. Let xi denote the estimated effect of treatment on the surrogate endpoint in the ith trial. Let wi denote the estimated variance of the estimated effect of treatment on the true endpoint in the ith trial. The zero-intercept random effects linear model is
| (1) |
The model includes a random effects μ, with mean 0 and unknown between-trial variance σ2. to capture the variability over trials of the different treatments.
Unlike most models involving the meta-analysis of surrogate endpoints, the model does not include a sub-model of the form xi = θi + ψ, where θi is the underlying effect of treatment on the surrogate endpoint and ψ is a random error.21,22 If the sub-model involving θi were included, the goal of the analysis would shift to estimating the relationship between θi and the independent variable yi. When the goal is prediction, as it is here, the sub-model involving θi is not appropriate because prediction directly involves the observed dependent variable xi. For example, in a prediction context, if xi were randomly larger than its underlying value θi (as opposed to being equal to θi), the increased value of xi should translate into an increase value for yi. Carroll et al. make a related point that measurement error models are not suitable for prediction.23
The error variable εi is the sampling error when measuring the observed effect of treatment on the true endpoint in the ith trial. Unlike most models for the meta-analysis of surrogate endpoints, the variance of the error term, wi, is estimated from observed data on the true endpoint prior to model fitting. This approach has the advantage of directly separating the overall variance into a within-trial sampling variance, wi, and a between-trial variance, σ2. Under the model, the sample size of the new trial affects only wi, and not, σ2, a desirable attribute.
Another distinctive feature of the model is the lack of an intercept term. Statisticians typically include an intercept in a linear model to improve the fit of the model. However, the zero-intercept formulation has two desirable implications that outweigh a poorer model fit. First, a zero-intercept ensures that no change in a surrogate endpoint implies no change in a true endpoint, an intuitively reasonable condition for a correctly specified model. Second, a zero-intercept avoids logical problems and errors when labeling randomization groups as control or experimental.24,25 If one trial compares treatments A and B, and another trial compares treatments B and C, the choice of label for treatment B (control or experimental) is arbitrary. If the model included an intercept, then whether treatment B is declared a control group or declared an experimental group would affect estimation. A line through the origin avoids the labeling problem by making the difference in true endpoints proportional to the difference in surrogate endpoints, so that reversing the labels multiplies both differences by negative one, leaving β unchanged. Thus, a zero-intercept avoids miss-specification of the model by incorrect labels of control and experimental groups.
2.1 Approximate maximum likelihood estimates
Maximum likelihood estimates (MLEs) for this model require iterative numerical calculations. Fortunately, it is possible to obtain an excellent approximation to the maximum likelihood estimate in closed-form. The derivation starts with a maximum likelihood approach involving a parameter that is not in the original model. The kernel of the log-likelihood is
| (2) |
Treating αi as a parameter (instead of σ2) and taking the derivatives of the log-likelihood with respect αi and β gives
| (3) |
| (4) |
Setting equations (3) and (4) equal to zero yields the following simultaneous equations for the maximum likelihood estimates of αi and β,
| (5) |
| (6) |
Based on equations (5) and (6), an approximate maximum likelihood estimate for αi is
| (7) |
Based on equation (7), approximate maximum likelihood estimates for the parameters of interests, β, and σ2, are, respectively,
| (8) |
| (9) |
2.2 Predicted treatment effects and prediction bands
For a new trial of size nNEW with surrogate endpoint x, the estimated predicted treatment effect and its distribution have the following form
| (10) |
Let wNEW denote the sampling variance of the effect of treatment on the true endpoint in the new trial. Because the true endpoint is not observed in the new trial, it is necessary to predict wNew from the set of wi while adjusting for differences in sample sizes between the new and previous trials. For the usual case of equal-sized arms in each trial, let ni denote the sample size of each arm of the ith previous trial, and let nNEW denote the sample size of each arm of the new trial. Also let k denote the number of previous trials. For each person in randomization group g in the ith trial, let wig denote the variance of the person’s observed true endpoint. Then wi= Σg wi(g) / ni. Assuming the average value of wi(g) over previous trials applies to the new trial, the sampling variance of the effect of treatment on the true endpoint in the new trial is
| (11) |
Because the estimated variance of yi is hi, the estimated variance of b is
| (12) |
Based on the quantities derived in the equations (11) and (12), the estimated variance of the predicted treatment effect in equation (10) is
| (13) |
The predicted treatment effect and the 95% prediction band are
| (14) |
| (15) |
Let xNEW denote the effect of treatment on the surrogate endpoint in a new trial.
Substituting x =xNEW into equations (14) and (15) yields the predicted treatment effect and its 95% prediction interval for the new trial, which are the quantities of interest when applying the model to a new surrogate endpoint trial.
2.3 Examples
Figures 1 and 2 depict predicted treatment effects and 95% prediction bands. For additional insight, the graphs show the point estimates and the 95% confidence intervals for the observed effect of treatment on the true endpoint. The prediction bands in these figures correspond to a new trial with sample size equal to the median sample size of the previous trial. If the sample size of the new trial were known, one could graph prediction bands corresponding to that sample size.
Figure 1.
Model fits with to data from 4 hypothetical sets of trials. The dashed blue diagonal lines are 95% prediction bands. The solid black vertical lines at the points are 95% confidence intervals for the observed effect of treatment on true endpoint. A prediction separation score larger than 1 says that leftmost and rightmost prediction intervals (represented by the dashed red vertical lines) do not overlap (indicated by no intersection with the horizontal dashed green line).
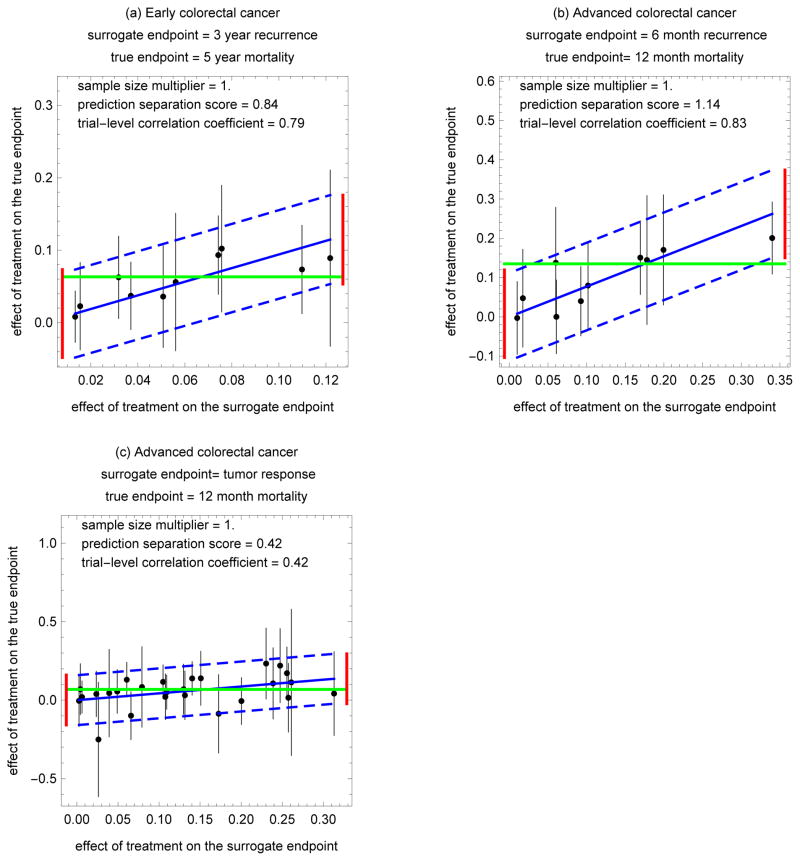
Figure 2.
Model fits to data from 3 colorectal cancer treatment trials. The dashed blue diagonal lines are 95% prediction bands. The solid black vertical lines at the points are 95% confidence intervals for the observed effect of treatment on true endpoint. A prediction separation score larger than 1 says that leftmost and rightmost prediction intervals (represented by the dashed red vertical lines) do not overlap (indicated by no intersection with the horizontal dashed green line).
Figure 1 applies to hypothetical data which was randomly generated. Figure 1(a)–1(d) corresponds to (β=0.9, σ2=25), (β=0.9, σ2=4), (β=2, σ2=25), (β=2, σ2=4), respectively, with 10 trials, ni =100, and wi = 9.
Figure 2 applies actual data from colorectal cancer treatment trials. See Tables 1–3, where xi and yi are differences in fractions, ni is the average sample size in the two arms, and wi is a binomial variance for a difference in fractions. Computations for of xi, yi, and wi are based on published estimated counts.15 Because the published estimated counts have the same estimates and similar variances as counts directly obtained from individual level survival data, the values of xi, yi, and wi account for censoring.15 Figure 2(a) corresponds to 10 randomized trials for early-stage colon cancer, where the surrogate endpoint indicates cancer recurrence before 3 years, and true endpoint indicates of overall mortality before 5 years.26 Figure 2(b) corresponds to 10 randomized trials for advanced-stage colorectal cancer, where surrogate endpoint indicates cancer recurrence at 3–6 months, and true endpoint indicates overall mortality before 12 months.27 Figure 2(c) corresponds to 27 randomized trials for advanced-stage colorectal cancer, where surrogate endpoint indicates tumor response at 3–6 months, and the true endpoint indicates overall mortality before 12 months.28
Table 1.
Trials for the treatment of early colorectal cancer. The surrogate endpoint indicates cancer recurrence (or not) before 3 years, and true endpoint indicates overall mortality (or not) before 5 years.26 The estimated treatment effects are differences in fractions that account for censoring.15
| Trial | Estimated effect of treatment on the surrogate endpoint | Estimated effect of treatment on the true endpoint | Average sample size per arm | Estimated sampling variance of the effect of treatment on the true endpoint |
|---|---|---|---|---|
| i | xi | yi | ni | wi |
| 1 | 0.0133209 | 0.00810028 | 2136 | 0.000327462 |
| 2 | 0.0154465 | 0.0227297 | 878 | 0.000946246 |
| 3 | 0.031803 | 0.0625501 | 896 | 0.00084016 |
| 4 | 0.0370214 | 0.0370513 | 1390 | 0.000564888 |
| 5 | 0.0507431 | 0.0359503 | 724 | 0.00128489 |
| 6 | 0.0560784 | 0.0560784 | 408 | 0.00234467 |
| 7 | 0.0741955 | 0.0932471 | 1042 | 0.000764536 |
| 8 | 0.0756713 | 0.102222 | 456 | 0.00198833 |
| 9 | 0.109814 | 0.0733984 | 926 | 0.000967199 |
| 10 | 0.121802 | 0.0890725 | 248 | 0.00385288 |
Table 3.
Trials for the treatment of advanced colorectal cancer. The surrogate endpoint indicates tumor response (or not) between 3 and 6 months. The true endpoint indicates with overall mortality (or not) by 12 years.28 The estimated treatment effects are differences in fractions that account for censoring.15
| Trial | Estimated effect of treatment on the surrogate endpoint | Estimated effect of treatment on the true endpoint | Average sample size per arm | Estimated sampling variance of the effect of treatment on the true endpoint |
|---|---|---|---|---|
| i | xi | yi | ni | wi |
| 1 | 0.00264784 | −0.00423654 | 158 | 0.00697091 |
| 2 | 0.00424809 | 0.0698386 | 162 | 0.00684591 |
| 3 | 0.00630874 | 0.0196868 | 356 | 0.00275263 |
| 4 | 0.0236874 | 0.0393162 | 180 | 0.00544156 |
| 5 | 0.0262514 | −0.250522 | 26 | 0.034631 |
| 6 | 0.0393375 | 0.044984 | 46 | 0.020156 |
| 7 | 0.0491228 | 0.0555556 | 184 | 0.00503523 |
| 8 | 0.0607485 | 0.130383 | 306 | 0.0032042 |
| 9 | 0.0658915 | −0.0989863 | 164 | 0.00604527 |
| 10 | 0.0792541 | 0.0839161 | 60 | 0.0170716 |
| 11 | 0.104938 | 0.116667 | 324 | 0.00304328 |
| 12 | 0.107668 | 0.0213607 | 180 | 0.0055205 |
| 13 | 0.109419 | 0.0510577 | 382 | 0.00308951 |
| 14 | 0.129886 | 0.0696033 | 148 | 0.00663814 |
| 15 | 0.131535 | 0.0311355 | 156 | 0.00625076 |
| 16 | 0.140312 | 0.13857 | 248 | 0.00295039 |
| 17 | 0.150871 | 0.139344 | 124 | 0.0076863 |
| 18 | 0.172547 | −0.0864888 | 62 | 0.0162696 |
| 19 | 0.200272 | −0.00567514 | 174 | 0.00577375 |
| 20 | 0.230317 | 0.233328 | 64 | 0.0132916 |
| 21 | 0.238828 | 0.10696 | 74 | 0.0133953 |
| 22 | 0.238828 | 0.10696 | 74 | 0.0133953 |
| 23 | 0.247371 | 0.22021 | 64 | 0.0144687 |
| 24 | 0.255682 | 0.171875 | 130 | 0.00723255 |
| 25 | 0.257433 | 0.0154741 | 80 | 0.0124803 |
| 26 | 0.261034 | 0.113493 | 16 | 0.0565146 |
| 27 | 0.313043 | 0.042029 | 52 | 0.0185411 |
2.4 Simulations
A simulation involving 1000 iterations investigated the properties of estimates from the zero-intercept random effects linear model. Under the simulation each previous trial has a sample size per arm of ni =100, a slope of β =2, a within-trial sampling variance for the effect of treatment on the true endpoint of wi =9, and an effect of treatment on the surrogate endpoint of xi equal to integers from 1 to the number of trials. A key desideratum for the simulation was to have one value for between-trial variance, σ2, larger than wi and one value smaller than wi. Another desideratum was to investigate the performance of estimates for a small new trial as well as an average size new trial. A third desideratum was to investigate the effect of the number of trials on the performance of the estimates. The simulation involved 8 scenarios defined by the ratio of the size of the new trial to the average size the previous trials (1 or 0.2), the number of trials (10 or 30), and the between-trial variance σ2 (4 or 25). The coverage of the prediction interval is the fraction of simulated prediction intervals that enclosed the predicted effect of treatment on true endpoint, β x+ μ, evaluated at x equal to the median value of the xi.
Table 4 summarizes the simulation results. For the both the slope β and the between-trial variance σ2, the approximate and actual MLE’s (under the constraint that σ2≥ 0) were almost identical. For the slope β, the mean value over the simulations of the approximate MLE was virtually identical to its true value. For the between-trial variance σ2, the mean value over the simulations of the approximate MLE was less than the true value, and with 30 versus 10 trials the estimate was closer to the true value. The bias in estimating σ2 had negligible impact on the validity of the prediction band, as the coverages of the 95% prediction intervals were acceptable, ranging from 0.93 to 1.00 over the scenarios. Software written in Mathematica for creating the figures and performing the simulation can be found at https://prevention.cancer.gov/about-dcp/staff-search/stuart-g-baker-scd/predicting-treatment-effect.
Table 4.
Properties of estimates based on 1000 simulations. Estimates are mean values over simulations. The sample size ratio is the size of the new trial divided by the average size of the previous trials. The 95% prediction was computed at the median value of the effect of treatment on the surrogate endpoint among the previous trials.
| Sample size ratio | Number of trials | Between-trial standard error =σ | Slope = β | Coverage of the 95% prediction interval | ||||
|---|---|---|---|---|---|---|---|---|
| True | Approximate MLE | MLE | True | Approximate MLE | MLE | |||
| 1.0 | 10 | 5 | 4.37 | 4.37 | 2 | 2.00 | 2.01 | 0.93 |
| 2 | 1.41 | 1.41 | 2 | 2.00 | 2.00 | 0.99 | ||
| 30 | 5 | 4.80 | 4.80 | 2 | 2.00 | 2.00 | 0.96 | |
| 2 | 1.67 | 1.67 | 2 | 2.00 | 2.01 | 1.00 | ||
| 0.2 | 10 | 5 | 4.37 | 4.37 | 2 | 2.00 | 2.00 | 1.00 |
| 2 | 1.41 | 1.41 | 2 | 2.00 | 2.00 | 1.00 | ||
| 30 | 5 | 4.80 | 4.80 | 2 | 2.00 | 2.00 | 1.00 | |
| 2 | 1.67 | 1.67 | 2 | 2.00 | 2.00 | 1.00 | ||
3. Statistical criteria
The following two statistical criteria for the meta-analytic evaluation of surrogate endpoints are based on the zero-intercept linear random effects model.
3.1 Acceptable sample size multiplier
Often investigators use a surrogate endpoint to reduce the sample size relative to that for a true endpoint. The reduction in sample size in this scenario arises because (i) investigators use the surrogate endpoint trial to estimate the effect of treatment on the surrogate endpoint, and (ii) the effect size for the surrogate endpoint is larger than the effect size for the true endpoint. However, interpretation of the effect of treatment on the surrogate endpoint is difficult because it is rarely possible to translate the effect size on a surrogate endpoint to an effect size on a true endpoint. Also, as mentioned previously, hypothesis testing extrapolation for small surrogate endpoint trials relative to large true endpoint trials is sensitive to small deviations from the Prentice Criterion.6,7 For these reasons, a surrogate endpoint trial substantially smaller than the corresponding true endpoint trial does not yield rigorous conclusions about the effect of treatment on true endpoint.
In contrast, the predictive modeling approach uses the surrogate endpoint trial to predict the effect of treatment on the true endpoint. The effect size for the predicted treatment effect based on the surrogate endpoint trial is the same as the effect size for the observed treatment effect in the true endpoint trial. Because the predicted effect of treatment on the true endpoint has more variability than the observed effect of treatment on the true endpoint, the sample size for the surrogate endpoint trial is larger than the sample size for the true endpoint trial (with the same power and type I error).
The sample size multiplier is the ratio of the new trial sample size based on the predicted effect of treatment on the true endpoint to the new trial sample size based on the observed effect of treatment on the true endpoint. Keeping the power, type I error and effect size fixed, the ratio of two sample sizes equals the ratio of the variances for the estimated treatment effects. Therefore, under the zero-intercept linear random effects model,
| (16) |
where xmedian and nmedian are median values in previous trials. The sample size multiplier is conceptually related to a previously proposed standard error multiplier that required leave-one-out resampling.15
The acceptable threshold for a sample size multiplier depends on the availability of patients and enrollment costs. Suppose that a surrogate endpoint trial that is less than 50% larger than a true endpoint trial would be acceptable. Figures 1(b), 1(d), 2(a), 2(b), and 2(c) illustrate acceptable standard error multipliers in this context, as they are less than 1.5.
3.2 Acceptable prediction separation score
A flat line for the predicted effect of treatment on the true endpoint can correspond to a small sample size multiplier if there is little between-trial variability. However, a flat line is not useful for predicting the effect of treatment on the true endpoint. Thus, in evaluating a surrogate endpoint, it is also necessary to also consider the amount of predictive information in the model, which depends on the slope of the line, b, relative to the variance of the predicted treatment effect, varYNEW(x, nNEW). The prediction separation score captures this signal-to-noise consideration. The prediction separation score is the maximum change in the predicted treatment effect (over the observed range for the effect of treatment on the surrogate endpoint) divided by the width of the prediction band (at the median value of the treatment effect on the surrogate endpoint among the previous trials). Under the zero-intercept linear random effects model,
| (17) |
An acceptable prediction separation score has a value greater than 1, which implies that the upper bound of the leftmost prediction interval is less than the lower bound of the rightmost prediction interval, so that the prediction intervals at the extremes of the horizontal axis (for effect of treatment on the surrogate endpoint) do not overlap. (The non-overlapping of the prediction intervals at the extremes of the horizontal axis assumes the width of the prediction band is the same at the median as the extremes; otherwise there may be a little overlap).
A comparison of the prediction separation score with the trial-level correlation coefficients is instructive. A prediction separation score greater than 1 (indicating acceptability) corresponded to a trial-level correlation coefficient of 0.78 or greater in Figures 1(c), 1(d), and 2(b). A prediction separation score less than 1 (indicating unacceptability) corresponded to a trial-level correlation coefficient of 0.66 or less in Figures 1(a), 1(b), and 2(c). A discrepancy between these two metrics is shown in Figure 2(a) where an unacceptable prediction separation score of 0.84 corresponded to a high trial-level correlation coefficient of 0.79. The reason for the discrepancy is that the wide confidence intervals for the observed effect of treatment on the true endpoint, which contribute to the prediction separation score, are not reflected by the distribution of points used to compute the trial-level correlation coefficient.
4. Biological and clinical criteria
It is a mistake to think that statistical criteria alone are sufficient for evaluating a surrogate endpoint. The reason is that prediction of the treatment effect in a new trial requires consideration of the biological and clinical aspects of the new treatment versus the treatments in the new previous trials, and this consideration cannot be summarized in a statistical model. These clinical and biological aspects lead to the following three criteria.
4.1 Similarity of biological mechanism of treatments
The biological mechanism for the way in which treatment affects the true endpoint should be similar for the new trial and the previous trials in the meta-analysis.29 At one extreme, if the biological mechanisms were identical between the new treatment and previous treatments, there would be no need to the study the new treatment. At the other extreme, if the new treatment were so innovative that its biological mechanism was unknown, one should not use a surrogate endpoint because the experience with previous treatments would not provide useful informative for evaluating the new treatment. Between these extremes is a middle ground in which previous treatments and new treatment involve related but not identical biological mechanisms. There is generally less concern about biological mechanism if the surrogate endpoint were an intermediate clinical endpoint, such as progression-free survival, than if the surrogate endpoint were a biomarker, such as the level of a protein in the blood.
4.2 Similarity of secondary treatments following the surrogate endpoint
Any treatment given in response to the surrogate endpoint should be similar for the treatment in the new trial and the treatments in the previous trials. Otherwise, there could be bias in the predicted treatment effect. For example, if tumor response or prostate-specific antigen level is the surrogate endpoint and prostate cancer mortality is the true endpoint, then the type of therapy following either of these surrogate endpoints could change over time, so surrogate endpoints in previous trials are not good predictors for the true endpoint in a new trial. Moreover, it is not just the change in treatment in response to the surrogate endpoint that can lead to bias, but a change in efficacy over time that (hopefully) accompanies the change in treatment. In the case of prostate cancer and several other cancers, an indicator of change in efficacy over time would be good evidence that systemic treatments for recurrent disease have improved, as documented in randomized trials.
4.3 Negligible risk of harmful side effects after the observation of the surrogate endpoint
A trial with a surrogate endpoint will not detect a harmful side effect that occurs after the observation of the surrogate endpoint and before the observation of the true endpoint. Failure to detect such a side effect when using a surrogate endpoint could lead to misleading conclusions. For example, a drug that shrunk tumors and delayed progression of cancer led to worse overall survival due to cardiotoxicity.29 Another real-life situation occurred in colorectal cancer prevention trials when COX-2 inhibitors were shown to decrease the number of polyps, but an increase in cardiovascular events was noted before any delayed decrease in colorectal cancer incidence could be observed.30 As with the criterion involving similarity of biological mechanisms, this criterion also argues against using a surrogate endpoint to evaluate a truly innovative new treatment.
5. Discussion
There is a tendency in the statistical literature on surrogate endpoints to fit increasingly complicated models for the statistical evaluation of surrogate endpoints. However, it is important to realize that clinical and biological criteria are at least as important as the statistical criteria because the use of surrogate endpoints fundamentally involves an extrapolation to a new trial. There is a danger that complex statistical metrics could lead investigators to overly focus on statistical issues and downplay the biological and clinical considerations, which would be a mistake. The proposed statistical criteria are easy to compute and interpret, which may facilitate a greater appreciation of the biological and clinical considerations. The biological and clinical criteria may be difficult to evaluate, but not knowing whether some of these criteria hold is also important and should be explicitly stated.
The five proposed criteria constitute a high bar for the use of a surrogate endpoint to evaluate a new treatment, particularly when the new treatment represents a major departure from previous treatments. This high bar is appropriate for the definitive evaluation of a new treatment for direct recommendation to patients. For a preliminary evaluation, where the result leads to another trial and not an immediate treatment recommendation, the bar need not be so high and some of the criteria might be relaxed.
Supplementary Material
Table 2.
Trials for the treatment of advanced colorectal cancer. The surrogate endpoint indicates cancer progression (or not) between 3 and 6 months. The true endpoint indicates overall mortality (or not) by 12 years.27 The estimated treatment effects are differences in fractions that account for censoring.15
| Trial | Estimated effect of treatment on the surrogate endpoint | Estimated effect of treatment on the true endpoint | Average sample size per arm | Estimated sampling variance of the effect of treatment on the true endpoint |
|---|---|---|---|---|
| i | xi | yi | ni | wi |
| 1 | 0.0101776 | −0.00300867 | 434 | 0.00223822 |
| 2 | 0.0175788 | 0.0474206 | 272 | 0.0040373 |
| 3 | 0.0600888 | 0.137713 | 184 | 0.00516377 |
| 4 | 0.0609015 | 0.0000155292 | 490 | 0.00228519 |
| 5 | 0.0925625 | 0.0398926 | 488 | 0.00202247 |
| 6 | 0.1018 | 0.079676 | 310 | 0.00320678 |
| 7 | 0.169392 | 0.15072 | 422 | 0.00229129 |
| 8 | 0.178005 | 0.144626 | 136 | 0.00701305 |
| 9 | 0.199408 | 0.170422 | 206 | 0.00510997 |
| 10 | 0.339943 | 0.200604 | 148 | 0.00219454 |
Acknowledgments
Funding
This research was supported by the National Cancer Institute.
References
- 1.Biomarkers Definitions Working Group. Biomarkers and surrogate endpoints: preferred definitions and conceptual framework. Clin Pharmacol Ther. 2001;69(3):89–95. doi: 10.1067/mcp.2001.113989. [DOI] [PubMed] [Google Scholar]
- 2.Fleming TR, DeMets DL. Surrogate end points in clinical trials: are we being misled? Ann Intern Med. 1996;125(7):605–613. doi: 10.7326/0003-4819-125-7-199610010-00011. [DOI] [PubMed] [Google Scholar]
- 3.Prentice RL. Surrogate endpoints in clinical trials: Definitions and operational criteria. Stat Med. 1989;8:431–430. doi: 10.1002/sim.4780080407. [DOI] [PubMed] [Google Scholar]
- 4.Berger VW. Does the Prentice criterion validate surrogate endpoints? Stat Med. 2004;27(10):1571–8. doi: 10.1002/sim.1780. [DOI] [PubMed] [Google Scholar]
- 5.Buyse M, Molenberghs G. Criteria for the validation of surrogate endpoints in randomized experiments. Biometrics. 1998;54(3):1014–29. [PubMed] [Google Scholar]
- 6.Baker SG, Kramer BS. Surrogate endpoint analysis: An exercise in extrapolation. J Natl Cancer Inst. 2013;105(5):316–320. doi: 10.1093/jnci/djs527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Baker SG, Kramer BS. The risky reliance on small surrogate endpoint studies when planning a large prevention trial. J R Stat Soc, Series A. 2013;176(2):603–608. doi: 10.1111/j.1467-985X.2012.01052.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Freedman LS, Graubard B, Schatzkin A. Statistical validation of intermediate endpoints for chronic diseases. Stat Med. 1992;11(2):167–178. doi: 10.1002/sim.4780110204. [DOI] [PubMed] [Google Scholar]
- 9.Royce TJ, Chen M, Wu J, et al. Surrogate end points for all-cause mortality in men with localized unfavorable-risk prostate cancer treated with radiation therapy vs radiation therapy plus androgen deprivation therapy. A secondary analysis of a randomized clinical trial. JAMA Oncol. 2017;3(5):652–658. doi: 10.1001/jamaoncol.2016.5983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Freedman LS. Confidence intervals and statistical power of the ‘Validation’ ratio for surrogate or intermediate endpoints. J Stat Plan Inference. 2001;96:143–153. [Google Scholar]
- 11.Molenberghs G, Buyse M, Geys H, Renard D, Burzykowski T, Alonso A. Statistical challenges in the evaluation of surrogate endpoints in randomized trials. Control Clin Trials. 2002;27(6):607–25. doi: 10.1016/s0197-2456(02)00236-2. [DOI] [PubMed] [Google Scholar]
- 12.Tanaka S, Matsuyama Y, Ohashi Y. Validation of surrogate endpoints in cancer clinical trials via principal stratification with an application to a prostate cancer trial. Stat Med. 2017;36(19):2963–2977. doi: 10.1002/sim.7318. [DOI] [PubMed] [Google Scholar]
- 13.Frangakis CE, Rubin DB. Principal stratification in causal inference. Biometrics. 2002;58:21–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Baker SG, Kramer BS, Lindeman KL. Latent class instrumental variables: A clinical and biostatistical perspective. Stat Med. 2016;35(1):147–160. doi: 10.1002/sim.6612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Baker SG, Sargent DJ, Buyse M, Burzykowski T. Predicting treatment effect from surrogate endpoints and historical trials: an extrapolation involving probabilities of a binary outcome or survival to a specific time. Biometrics. 2012;68(1):248–257. doi: 10.1111/j.1541-0420.2011.01646.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Baker SG, Kramer BS. A perfect correlate does not a surrogate make. BMC Med Res Methodol. 2003;3:16. doi: 10.1186/1471-2288-3-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Prasad V, Kim C, Burotto M, Vandross A. The strength of association between surrogate end points and survival in oncology: A systematic review of trial-level meta-analyses. JAMA Intern Med. 2015;175(8):1389–1398. doi: 10.1001/jamainternmed.2015.2829. [DOI] [PubMed] [Google Scholar]
- 18.Buyse M, Molenberghs G, Paoletti X, Oba K, Alonso A, Van der Elst W, Burzykowsk T. Statistical evaluation of surrogate endpoints with examples from cancer clinical trials. Biom J. 2016;58:104–132. doi: 10.1002/bimj.201400049. [DOI] [PubMed] [Google Scholar]
- 19.Burzykowski T, Buyse M. Surrogate threshold effect: an alternative measure for meta-analytic surrogate endpoint validation. Pharm Stat. 2006;5(3):173–186. doi: 10.1002/pst.207. [DOI] [PubMed] [Google Scholar]
- 20.Lassere MN, Johnson KR, Schiff M, Rees D. Is blood pressure reduction a valid surrogate endpoint for stroke prevention? An analysis incorporating a systematic review of randomised controlled trials, a by-trial weighted errors-in-variables regression, the surrogate threshold effect (STE) and the Biomarker-Surrogacy (BioSurrogate) Evaluation Schema (BSES) BMC Med Res Methodol. 2012;12:27. doi: 10.1186/1471-2288-12-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Torri V, Simon R, Russek-Cohen E, Midthune D, Friedman M. Statistical model to determine the relationship of response and survival in patients with advanced ovarian cancer treated with chemotherapy. J Natl Cancer Inst. 1992;84(6):407–414. doi: 10.1093/jnci/84.6.407. [DOI] [PubMed] [Google Scholar]
- 22.Weir CJ, Walley RJ. Statistical evaluation of biomarkers as surrogate endpoints: a literature review. Stat Med. 2006;25(2):183–203. doi: 10.1002/sim.2319. [DOI] [PubMed] [Google Scholar]
- 23.Carroll RJ, Ruppert D, Stefanski LA, Crainceanu CM. Measurement Error in Nonlinear Models: A Modern Perspective. 2. Boca Raton, FL: Chapman and Hall; 2006. p. 38. [Google Scholar]
- 24.Daniels MJ, Hughes MD. Meta-analysis for the evaluation of potential surrogate markers. Stat Med. 1997;16(17):1965–1982. doi: 10.1002/(sici)1097-0258(19970915)16:17<1965::aid-sim630>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 25.Freedman L. Commentary on assessing surrogates as trial endpoints using mixed models. Stat Med. 2005;24(2):183–185. doi: 10.1002/sim.1857. [DOI] [PubMed] [Google Scholar]
- 26.Sargent DJ, Wieand HS, Haller DG, et al. Disease-free survival versus overall survival as a primary end point for adjuvant colon cancer studies: individual patient data from 20,898 patients on 18 randomized trials. J Clin Oncol. 2005;27(34):8664–670. doi: 10.1200/JCO.2005.01.6071. [DOI] [PubMed] [Google Scholar]
- 27.Meta-Analysis Group in Cancer. Modulation of fluorouracil by leucovorin in patients with advanced colorectal cancer: an updated meta-analysis. J Clin Oncol. 2004;22:3766–3775. doi: 10.1200/JCO.2004.03.104. [DOI] [PubMed] [Google Scholar]
- 28.Burzykowski T, Molenberghs G, Buyse M. The validation of surrogate end points by using data from randomized clinical trials: a case-study in advanced colorectal cancer. J R Stat Soc, Series A. 2004;167:103–124. [Google Scholar]
- 29.Ellenberg SS. Surrogate endpoints. Br J Cancer. 1993;68:457–459. doi: 10.1038/bjc.1993.369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Solomon SD, McMurray JJ, Pfeffer MA, et al. Cardiovascular risk associated with celecoxib in a clinical trial for colorectal adenoma prevention. N Engl J Med. 2005;352(11):1071–80. doi: 10.1056/NEJMoa050405. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.