Modeling Rater Diagnostic Skills in Binary Classification Processes

Summary

Many disease diagnoses involve subjective judgments by qualified raters. For example, through the inspection of a mammogram, MRI, or ultrasound image, the clinician himself becomes part of the measuring instrument. To reduce diagnostic errors and improve the quality of diagnoses, it is necessary to assess raters’ diagnostic skills and to improve their skills over time. This paper focuses on a subjective binary classification process, proposing a hierarchical model linking data on rater opinions with patient true disease-development outcomes. The model allows for the quantification of the effects of rater diagnostic skills (bias and magnifier) and patient latent disease severity on the rating results. A Bayesian Markov chain Monte Carlo (MCMC) algorithm is developed to estimate these parameters. Linking to patient true disease outcomes, the rater-specific sensitivity and specificity can be estimated using MCMC samples. Cost theory is utilized to identify poor- and strong-performing raters and to guide adjustment of rater bias and diagnostic magnifier to improve the rating performance. Furthermore, diagnostic magnifier is shown as a key parameter to present a rater’s diagnostic ability because a rater with a larger diagnostic magnifier has a uniformly better receiver operating characteristic (ROC) curve when varying the value of diagnostic bias. A simulation study is conducted to evaluate the proposed methods, and the methods are illustrated with a mammography example.

1 Introduction

In the practice of clinical medicine, many screening and diagnostic tests involve a subjective image analysis such as reading a mammogram, MRI, or ultrasound image. For this type of clinical practice, the supervision and evaluation of radiologists’ performance is very important. However, the performance evaluation of radiologists is usually less objective and relies highly on a peer review process.¹

In the literature of diagnostic accuracy analysis, comparing the sensitivity and specificity combined with receiver operating characteristic (ROC) curve and its various indices are common tools to evaluate the diagnostic tests (raters). Earlier traditional methods^2,3 rely on the existence of a binary reference test or gold standard. Mossman⁴ and Obuchowski et al.⁵ among others extended ROC methods to the estimation of diagnostic test accuracy when the gold standard is nominal- or ordinal-scale. Obuchowski⁶ proposed a non-parametric estimator of accuracy for diagnostic tests with continuous-scale gold standards. Shiu and Gatsonis⁷ extended the binormal ROC model⁸ for binary gold standard to a conditional normal model to accommodate continuous gold standards and investigated the effects on the estimated sensitivity, specificity, and ROC curves when varying threshold on the reference standard. Another branch of literature about estimating diagnostic accuracy is using latent class analysis⁹ when there is no gold standard. For example, Qu et al.¹⁰ proposed random effects models in latent class analysis to accommodate conditional dependence among multiple tests (raters). A review of this branch of methods refers to Collins and Albert.¹¹

In this paper, we focus on binary diagnostic results linking with patients’ true binary disease-development outcomes. Instead of directly modeling sensitivity and specificity as the previous reviewed literature, we propose a new model where the probability of a rater’s positive rating and the probability of the patient’s true positive outcome are modeled. These two probabilities are connected by a common latent variable, and thus sensitivity and specificity can be accordingly formulated. Instead of using sensitivity and specificity to evaluate a rater’s diagnostic performance, we specify the rater’s diagnostic skills as diagnostic bias and diagnostic magnifier for the rating process and quantify their connection to sensitivity and specificity.

The motivating data set was collected by Beam et al.,¹² who studied variability in the interpretation of mammograms by radiologists in the United States. One hundred and seven radiologists for the study came from a stratified random sample of mammography facilities accredited by the U.S. Food and Drug Administration. Index mammograms of good technical quality were obtained from 146 women randomly sampled from a large screening program affiliated with the University of Pennsylvania. Of these, 82 were cancer-free and 64 had malignancies. The true disease status of the women screened was determined by a biopsy examination or a minimum follow-up period of two years. Every radiologist interpreted all mammograms in a controlled reading environment during two 3-hour periods. A modified 5-point Breast Imaging Reporting and Data System (BI-RADS) scale¹³ was used for the radiologists to record the results: 1=normal, return to normal screening; 2=benign, return to normal screening; 3= probably benign, 6-month follow-up; 4=possibly malignant, biopsy recommended; 5=probably malignant, biopsy strongly recommended. Although an ordinal scale rating is more informative, in many clinical settings such as breast cancer screening, dichotomization is very commonly practiced. For example, on the webpage http://breast-cancer.ca/bi-rads/, it states that “After the initial breast cancer screening, a followup or diagnostic mammography is often recommended if the BI-RADS category is 3 or higher. By a huge majority, most breast cancer screening mammograms are classified as either BI-RADS 1 or BI-RADS 2 and those categories are nothing to worry about and require no further treatment”. A common classification made in a medical screening test setting is whether or not patients should be “recalled” for further testing (yes/no), where BI-RADS classifications are dichotomized accordingly.

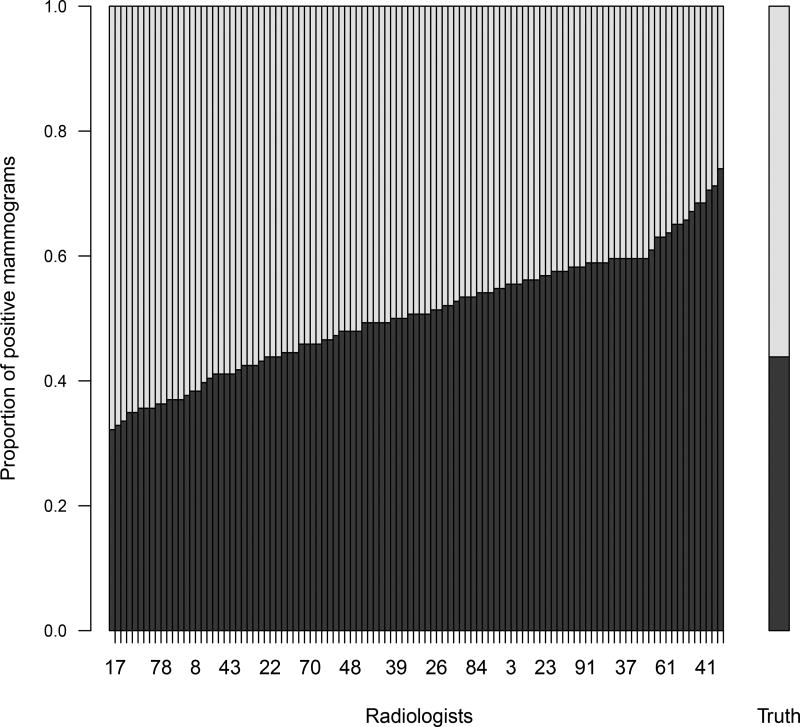
Figure 1 presents the mammogram data, where radiologist ratings are dichotomized with “BI-RADS ≥ 3” as a positive result. The main part of the figure shows the proportion of positive ratings of each radiologist in an ascending order. The right bar of the figure shows the true proportion of positive mammograms. From Figure 1, it is clear that radiologists do not always give consistent or correct diagnostic decisions on disease status and that some radiologists gave more positive decisions than others, indicating rater biases and different diagnostic abilities.

Figure 1.

The mammography data: 107 radiologists and 146 mammograms. The main part of the plot shows the proportion of positive ratings for each radiologist in an ascending order. The right bar shows the true proportion of positive mammograms.

For this type of dichotomized item-rater data with true disease statuses known, using empirical sensitivity and specificity combined with ROC curve methods^14,15,16 is a common and simple practice to evaluate individual raters’ overall performance. In this paper, we analyze this type of data from a new perspective. Aiming to directly access diagnostic skills, we model and estimate a rater’s diagnostic skills as diagnostic bias and diagnostic magnifier directly. Diagnostic bias reflects a rater’s innate tendency to rate a patient “diseased.” Diagnostic magnifier reflects a rater’s diagnostic ability. A strong-performing rater would magnify a patient’s latent disease state in a correct direction and therefore have a higher chance of making a correct decision. An analogous modeling idea can be found in two-parameter item response models^17,18 in the psychology literature, wherein the item with a larger discrimination parameter is more useful for separating examinees into different ability levels. Instead of using the ROC curve, cost theory is adopted to provide a more complete and flexible method to rank individual raters’ overall performance and to provide a guide to improve their performance in terms of the adjustment of their diagnostic bias and magnifier. Another important property of our model is that a rater with a larger diagnostic magnifier has a uniformly better ROC curve when varying the value of diagnostic bias. Therefore, diagnostic magnifier provides a more convenient method than the conventional ROC curve method to compare raters’ diagnostic performance.

The techniques presented in this paper provide a fundamental analysis for investigating raters’ diagnostic skills. The model can be extended to investigate the effects of significant factors on diagnostic bias and diagnostic magnifier by incorporating these factors into the hierarchical model. Our approach can be widely used because this type of item-rater data is common for many disease diagnoses that involve subjective judgments from raters, such as the use of the Gleason grading scale for diagnosing prostate cancer,¹⁹ the comparison of diagnostic instruments for the detection of liver cancer,²⁰ and the assessment of slides by pathologists for the detection of carcinoma in situ of the uterine cervix.²¹ This type of data can also arise from multi-reader multi-case (MRMC) studies²² for the comparison of several diagnostic tests. Our proposed Bayesian approach is useful even when the true patient outcomes are unknown, and can be easily modified when the data is unbalanced, that is, some raters only rate a partial set of items.

The remainder of this paper is organized as follows. Section 2 presents the primary model, establishing identifiability, and specifying the priors for Bayesian analysis. Section 3 provides details about the Bayesian computational algorithm and the estimation of related parameters. Section 4 investigates techniques to identify strong raters based on cost theory. Section 5 shows a simulation study to illustrate the efficiency of the proposed methods. Section 6 applies our proposed approach to analyze the mammogram data set in Beam et al.¹² Section 7 concludes with a discussion.

2 Proposed model

Motivated by the mammogram data set, we propose a hierarchical model where rater decisions are linked with patient true disease outcome through a common latent variable, patient latent disease severity. Meanwhile, we allow rater diagnostic ability and patient latent disease severity to interactively affect the rater’s decision. Denote by D_i the true disease outcome of patient i within a practical time frame and W_ij the diagnostic binary classification of patient i by rater j, both with 1 for a positive result. The following primary model is proposed:

$$P(D_i=1|u_i)=\mathrm{\Phi }(u_i),$$

$$P(W_{\mathit{\text{ij}}}=1|u_i)=\mathrm{\Phi }(a_j+b_j{u}_i),$$ (1)

for i = 1, …, m; j = 1, …, n, where Φ(·) is the cumulative distribution function of a standard normal random variable. In general, Φ(·) can be replaced by any other cumulative distribution function (CDF), such as a standard logistic CDF. Here, we choose Φ(·) to ease the computation by introducing normal latent variables as illustrated in Section 3.

In the model, u_i represents a continuous latent variable, reflecting the latent disease severity for patient i. Though u_i is univariate, it can be understood as a univariate index based on a multidimensional profile of a patient. For example, it can be a linear combination of a set of related variates. Through this common latent variable, the rater decision W_ij and patient disease outcome D_i are linked together. A large value of u_i indicates a large probability that the patient has the disease and increases the chance that a qualified rater (with b_j > 0) will classify the patient as diseased. The correct judgment is also affected by the rater’s bias and diagnostic magnifier through terms a_j and b_j. The intercept term a_j reflects the innate tendency (bias) of clinician j to say “disease” when u_i = 0, i.e. when there is a 50–50 chance of disease development. The rater-specific magnifier term b_j reflects the clinician’s diagnostic ability. A qualified rater should “magnify” the patient latent disease severity in the same direction as it is, that is, have b_j > 0. A strong-performing rater should be more adept at detecting the potential for the disease, that is, have b_j > 1.

Although model (1) looks similar as the latent class models described in Qu et al.¹⁰ and Dendukuri and Joseph,²³ where they adopted a latent variable to model the conditional dependence among different tests or raters, their models directly model the conditional probabilities, i.e., sensitivity and specificity, to access a rater’s diagnostic ability, while our proposed method models the probability of giving a positive rating instead and aims to estimate a rater’s diagnostic skills as diagnostic bias and magnifier. Through the patient latent disease severity u_i, the probability of positive rating P(W_ij = 1) is connected with the probability of true positive disease status P(D_i = 1), and therefore rater sensitivity and specificity can also be calculated as shown at the end of Section 3.

The second layer of the model is to assume distributions for the patient latent variable and the rater’s diagnostic skills. We assume that u_i’s independently follow a standard normal prior distribution. The rater effects a_j and b_j are independently assumed to follow normal and truncated normal priors, respectively:

$$a_j~N({\mu }_a,{\tau }_a^{-1});$$

$$b_j~N({\mu }_b,{\tau }_b^{-1})1_{(b_j>0)},$$ (2)

for j = 1, …, n, where b_j is restricted to be positive because in practice the ability or skill of a qualified rater may not classify a patient accurately, but it is unlikely that this effect would be magnified in the opposite direction. For a diagnostic process, the rater overall mean of diagnostic skills and the variability of diagnostic skills among raters are naturally of interest. Correctly assessing these quantities is important. In the priors, the rater overall mean of diagnostic bias and magnifier are reflected by μ_a and μ_b, respectively, and the precision of rater bias and diagnostic magnifier are naturally quantified by τ_a and τ_b, respectively. To allow for the estimation of these key parameters, we assign conventional non-informative/diffuse hyper priors. Specifically, we assign normal priors N(0, τ⁻¹) to μ_a and μ_b with τ a small value such as 0.01, and gamma priors Ga(γ, γ) to τ_a and τ_b with γ a small value such as 0.01.

It is worth mentioning that the choice of the prior of u_i is not critical. In simulation studies and the analysis of the mammography data, it is observed that the standard normal prior distribution is overwhelmed by the data, resulting in a bimodal posterior for the u_i’s that coincides nicely with diseased and non-diseased patients, respectively. For rater effects a_j and b_j, we may assume a bivariate normal type prior if we care about the correlation between a_j and b_j.

Although the rater bias and diagnostic magnifier and patient latent effect are modeled as random effects in the above model, the Bayesian Markov chain Monte Carlo (MCMC)²⁴ estimation algorithm developed in the next section allows estimation of rater-specific and patient-specific effects. One advantage of this paper is actually to provide an approach that allows assessment of rater-specific diagnostic skills and even patient-specific latent disease severity. The following proposition proves the identifiability of model (1) when all parameters are fixed and supports the estimation of each rater-specific and patient-specific parameter.

Proposition 1

Model (1) with u_i’s, a_j’s, and b_j’s as unknown constants is identifiable if the u_i’s are not all equal.

The proof of Proposition 1 is in the appendix. From the proof, we can see that the existence of D_i’s (the gold standard knowledge of disease presence/absence) makes the model mathematically identifiable, and it is clear that without D_i’s the model is no longer identifiable. Though the D_i’s render the model mathematically identifiable, stable estimation of the model parameters is still challenging due to no replication of D_i and the multiplicative term b_ju_i in the model. The bulk of the likelihood function (the part not depending on the D_i’s),

$$\prod _{i=1}^m\prod _{j=1}^{n}P(W_{\mathit{\text{ij}}}=1|u_i)=\prod _{i=1}^m\prod _{j=1}^n\mathrm{\Phi }(a_j+b_j{u}_i),$$

has the same value for $a_j^{\prime }=a_j-{\mathit{\text{db}}}_j/c,b_j^{\prime }=b_j/c$, and $u_i^{\prime }={\mathit{\text{cu}}}_i+d$ for any choice of positive constants c and d. As a result, conventional likelihood and Bayesian estimation methods usually do not converge to meaningful values. To solve this problem, we rescale the mean and standard deviation of the u_i’s equal to 0 and 1 at each MCMC iteration.

3 Bayesian estimation

For notational convenience, we denote D_i as W_i0. Then model (1) is simplified as

$$P(W_{\mathit{\text{ij}}}=1|u_i)=\mathrm{\Phi }(a_j+b_j{u}_i),$$

for i = 1, …, m; j = 0, 1, …, n, with known a₀ = 0 and b₀ = 1. For probit models such as this, it is a common strategy to introduce normal latent variables to simplify Bayesian computation.^25,26 For each W_ij, a normal latent variable

$$Z_{\mathit{\text{ij}}}|u_i~N(a_j+b_j{u}_i,1)$$

is introduced. Then it is clear that for each pair of W_ij and Z_ij, for i = 1, …, m; j = 0, 1, …, n, we have P(Z_ij > 0| u_i) = P(W_ij = 1| u_i). Therefore, the augmented joint density function of w = (w₁₀, w₁₁, …, w_mn) and z = (z₁₀, z₁₁, …, z_mn) is

$$p(\mathit{w},\mathit{z}|\mathit{a},\mathit{b},\mathit{u})=\prod _{i=1}^m\prod _{j=0}^n\varphi (z_{\mathit{\text{ij}}}-(a_j+b_j{u}_i)){[I_{(z_{\mathit{\text{ij}}}>0)}]}^{w_{\mathit{\text{ij}}}}{[I_{(z_{\mathit{\text{ij}}}\le 0)}]}^{1-w_{\mathit{\text{ij}}}},$$ (3)

where a = (a₁, …, a_n), b = (b₁, …, b_n), and u = (u₁, …, u_m).

Gibbs sampling^27,28 is one of the most widely used Markov chain Monte Carlo (MCMC)²⁹ algorithms for Bayesian computation. It repeatedly and sequentially generates all unknown parameters and latent variables from their full conditional distributions. The MCMC theory guarantees that the limiting distribution of the samples from a Gibbs sampler is the same as the joint posterior distribution under certain regularity conditions.²⁹ We adopt Gibbs sampling for our posterior computation and derive the full conditional distributions of all parameters and latent variables by combining the augmented likelihood (3) and the priors. After specifying the initial values of the unknown parameters, our Gibbs sampler iterates through the following steps.

1. Sample z_ij, for i = 1, …, m; j = 0, 1, …, n,

   $$z_{\mathit{\text{ij}}}~\{\begin{array}{c}N(a_j+b_j{u}_i,1)I_{(z_{\mathit{\text{ij}}}>0)},\text{ when }{w}_{\mathit{\text{ij}}}=1,\hfill \\ N(a_j+b_j{u}_i,1)I_{(z_{\mathit{\text{ij}}}\le 0)},\text{ when }{w}_{\mathit{\text{ij}}}=0.\hfill \end{array}$$
2. Sample u_i, for i = 1, …, m,

   $$u_i~N(\frac{{\sum }_{j=0}^n{b}_j(z_{\mathit{\text{ij}}}-a_j)}{1+{\sum }_{j=0}^n{b}_j^2},\frac{1}{1+{\sum }_{j=0}^n{b}_j^2}).$$
3. Sample a_j, for j = 1, ⋯, n,

   $$a_j~N(\frac{{\sum }_{i=1}^m(z_{\mathit{\text{ij}}}-b_j{u}_i)+{\mu }_a{\tau }_a}{m+{\tau }_a},\frac{1}{m+{\tau }_a}).$$
4. Sample b_j, for j = 1, ⋯, n,

   $$b_j~N(\frac{{\sum }_{i=1}^m{u}_i(z_{\mathit{\text{ij}}}-a_j)+{\mu }_b{\tau }_b}{{\sum }_{i=1}^m{u}_i^2+{\tau }_b},\frac{1}{{\sum }_{i=1}^m{u}_i^2+{\tau }_b})I_{(b_j>0)}.$$
5. Sample μ_a,

   $${\mu }_a~N(\frac{{\tau }_a\sum _{j=1}^n{a}_j}{n{\tau }_a+\tau },\frac{1}{n{\tau }_a+\tau }).$$
6. Sample τ_a,

   $${\tau }_a~\mathit{\text{Ga}}((\gamma +\frac{n}{2}),(\gamma +\frac{1}{2}\sum _{j=1}^n{(a_j-{\mu }_a)}^2)).$$
7. Sample μ_b using the adaptive rejection Metropolis sampling (ARMS)^30,31 method. The full conditional distribution of μ_b is proportional to

   $${[\mathrm{\Phi }({\tau }_b^{\frac{1}{2}}{\mu }_b)]}^{-n}\text{ exp}\{-\frac{{\tau }_b}{2}\sum _{j=1}^n{(b_j-{\mu }_b)}^2-\frac{\tau }{2}{\mu }_b^2\}.$$
8. Sample τ_b using the ARMS^30,31 method. The full conditional distribution of τ_b is proportional to

   $${\tau }_b^{\frac{n}{2}+\theta -1}{[\mathrm{\Phi }({\tau }_b^{\frac{1}{2}}{\mu }_b)]}^{-n}\text{ exp}\{-{\tau }_b[\frac{1}{2}\sum _{j=1}^n{(b_j-{\mu }_b)}^2+\gamma ]\}.$$

The above Gibbs sampler is fast and easy to execute because all of the steps can be updated either from a standard distribution or by using the automatic ARMS method. Readers who do not want code the algorithm can choose to use WinBUGS³² to run the Bayesian fitting by specifying the model and priors. The R³³ code and JAGS³⁴ code can be found as online supplements for this paper or at the first author’s webpage http://people.stat.sc.edu/lin.

When the MCMC chains in the Gibbs sampler converge, the samples from the Gibbs sampler can be treated as samples from the true joint posterior distribution. The mean of the MCMC samples of a parameter is then the estimate of the posterior mean of the parameter. The quantiles of the MCMC samples can naturally construct credible intervals for the parameter. For example, the 2.5 and 97.5 percentiles of a converged MCMC chain of a parameter delimit a 95% credible interval for the parameter. Therefore, parameter vectors a, b, and u can be easily estimated using the MCMC samples.

Furthermore, the MCMC samples can be used to estimate functions of these parameters. For example, the model-based sensitivity and specificity of individual rater j

$${\mathit{\text{Se}}}_j=P(W_{·j}=1|D_{·}=1)=\frac{\underset{u}{\int }\mathrm{\Phi }(u)\mathrm{\Phi }(a_j+b_{j}u)\mathit{\text{dF}}(u)}{\underset{u}{\int }\mathrm{\Phi }(u)\mathit{\text{dF}}(u)}$$ (4)

and

$${\mathit{\text{Sp}}}_j=P(W_{·j}=0|D_{·}=0)=\frac{\underset{u}{\int }[1-\mathrm{\Phi }(u)][1-\mathrm{\Phi }(a_j+b_{j}u)]\mathit{\text{dF}}(u)}{1-\underset{u}{\int }\mathrm{\Phi }(u)\mathit{\text{dF}}(u)},$$ (5)

where F(u) denotes the true distribution of the latent disease severity u, can be estimated by

$${\widehat{\mathit{\text{Se}}}}_j=\frac{1}{L}\sum _{l=1}^L\left[\frac{{\sum }_{i=1}^m\mathrm{\Phi }(u_i^{(l)})\mathrm{\Phi }(a_j^{(l)}+b_j^{(l)}{u}_i^{(l)})}{{\sum }_{i=1}^m\mathrm{\Phi }(u_i^{(l)})}\right]$$

and

$${\widehat{\mathit{\text{Sp}}}}_j=\frac{1}{L}\sum _{l=1}^L\left[\frac{{\sum }_{i=1}^m(1-\mathrm{\Phi }(u_i^{(l)}))(1-\mathrm{\Phi }(a_j^{(l)}+b_j^{(l)}{u}_i^{(l)}))}{{\sum }_{i=1}^m(1-\mathrm{\Phi }(u_i^{(l)}))}\right],$$

respectively, where the superscript (l) denotes the lth MCMC sample in the Gibbs sampling iteration after the burn-in period, and L is the total number of MCMC samples used for the estimation. Credible intervals for rater-specific sensitivity and specificity can be constructed based on the quantiles of the L elements within the average calculation.

4 Identification of strong-performing raters

Rater-specific sensitivities and specificities can be used to identify strong raters via a receiver operating characteristic (ROC) curve. The ROC curve is created by plotting true positive rate (sensitivity) over false positive rate (one minus specificity) for each rater. One simple criterion to apply is that strong raters are those with short distances to the point (0, 1).³⁵ However, the above simple method assumes that the proportions of truly diseased and not diseased are the same and that false negative and false positive errors result in the same costs. In reality, a false negative decision and a false positive often result in different costs.¹⁴ Suppose the cost of a false negative is a fixed constant C_FN (≥ 0), the cost of a false positive is a fixed constant C_FP (≥ 0), and the cost ratio of C_FN over C_FP is denoted by θ. Then according to model (1), the total expected cost TC for an individual rater is as follows (suppressing subscripts i and j):

$$\mathit{\text{TC}}=C_{\mathit{\text{FN}}}P(W=0|D=1)P(D=1)+C_{\mathit{\text{FP}}}P(W=1|D=0)P(D=0)=C_{\mathit{\text{FN}}}P(W=0,D=1)+C_{\mathit{\text{FP}}}P(W=1,D=0)=C_{\mathit{\text{FN}}}{\int }_u\mathrm{\Phi }(u)[1-\mathrm{\Phi }(a+\mathit{\text{bu}})]\mathit{\text{dF}}(u)+C_{\mathit{\text{FP}}}{\int }_u(1-\mathrm{\Phi }(u))\mathrm{\Phi }(a+\mathit{\text{bu}})\mathit{\text{dF}}(u)\propto \theta {\int }_u\mathrm{\Phi }(u)[1-\mathrm{\Phi }(a+\mathit{\text{bu}})]\mathit{\text{dF}}(u)+{\int }_u(1-\mathrm{\Phi }(u))\mathrm{\Phi }(a+\mathit{\text{bu}})\mathit{\text{dF}}(u).$$ (6)

A strong rater should have a small total expected cost. In practice, individual raters’ TCs can be estimated by inserting the estimates of rater diagnostic bias and magnifier and patient disease severities into (6). Then, the total cost for rater j is estimated as

$${\widehat{\mathit{\text{TC}}}}_j\propto \frac{1}{m}\{\theta \sum _{i=1}^m\mathrm{\Phi }({\hat{u}}_i)(1-\mathrm{\Phi }({\hat{a}}_j+{\hat{b}}_j{\hat{u}}_i))+\sum _{i=1}^m(1-\mathrm{\Phi }({\hat{u}}_i))\mathrm{\Phi }({\hat{a}}_j+{\hat{b}}_j{\hat{u}}_i)\}.$$

Proposition 2 below guides the optimal adjustment of rater bias to achieve minimal expected cost when the rater magnifier is fixed.

Proposition 2

Given a fixed rater magnifier b, the total cost (6) will be minimized if the rater bias a* satisfies the following conditions:

$${\int }_u[1-(\theta +1)\mathrm{\Phi }(u)]\varphi (a^{\ast }+\mathit{\text{bu}})\mathit{\text{dF}}(u)=0,$$

$${\int }_u[1-(\theta +1)\mathrm{\Phi }(u)]\varphi (a^{\ast }+\mathit{\text{bu}})(a^{\ast }+\mathit{\text{bu}})\mathit{\text{dF}}(u)<0.$$ (7)

The proof of Proposition 2 is straightforward using differentiation of TC. For a given rater magnifier, the first equation of (7) can be approximated by inserting the estimates of patient-specific disease severities as below:

$$\frac{1}{m}\sum _{i=1}^m[1-(\theta +1)\mathrm{\Phi }({\hat{u}}_i)]\varphi (a^{\ast }+b{\hat{u}}_i)=0.$$

For this, the R³³ function uniroot can be applied to solve for the optimal bias.

Intuitively, a rater with a large magnifier b tends to lead to correct decisions and reach small costs; Proposition 3 confirms this.

Proposition 3

Assume b > 0. If the optimal rater bias a* is used as defined in Proposition 2, then the total cost TC is a decreasing function of the rater’s magnifier b.

The proof of Proposition 3 is in the appendix. It is worth mentioning that although the cost theory is useful to identify strong-performing raters, objective costs or cost ratio θ are not easy to define in many cases. Therefore, in practice researchers may still prefer to know the sensitivity and specificity of each rater to identify strong raters than use the combined measure based on costs. The corollary below shows that a rater with a larger magnifier b has a uniformly better ROC curve. The proof of Corollary 1 is in the appendix. Although the proof of the corollary is based on Proposition 2 and 3, the corollary itself does not involve any cost theory.

Corollary 1

Define an ROC curve, ROC(b), by the points [1 − Sp(a, b), Se(a, b)] for a fixed rater magnifier b and varying rater bias a, where the model-based Se(a, b) and Sp(a, b) are calculated as in equations (4) and (5), respectively. If b₁ ≥ b₂, then ROC(b₁)≥ROC(b₂).

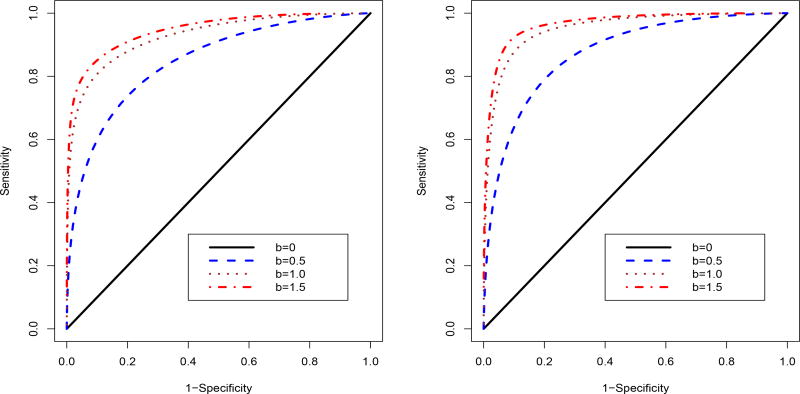
This result confirms the importance of using diagnostic magnifier b to present a rater’s diagnostic ability. While rater bias is relatively easy to justify in clinical practice, increasing diagnostic magnifier should be more important to improve a rater’s diagnostic performance. Figure 2 illustrates the corollary result, where the sensitivity and specificity are calculated based on equations (4) and (5) with F(u) following a two component normal mixture distribution.

Figure 2.

Comparison of ROC curves for different values of diagnostic magnifier b when varying the value of diagnostic bias a. A two component normal mixture distribution F(u) = pΦ(u; −2, 1) + (1−p)Φ(u; 2, 1) is adopted for calculating the sensitivity and specificity, where p = 0.8 and 0.5 for the left and right panels, respectively.

5 Simulation study

A simulation study was conducted to evaluate the model and the proposed estimation methods. We chose two sample size scenarios: m = 50 patients and n = 50 raters, and m = 150 patients and n = 100 raters. The second one is close to the size of the mammogram data. For each scenario, we generated 200 data sets in the following manner based upon model (1). For each data set, n raters evaluate each of m patients. True diagnostic biases a_j, j = 1, …, n, were independently sampled from a normal distribution N(0, 0.5²), while true diagnostic magnifiers b_j, j = 1, …, n, were independently sampled from a truncated normal distribution N(1.2, 0.3²)1_(bj>0). In order to assess the estimation of rater-specific parameters, the same raters were used across all of the 200 data sets. For each data set, patients’ unobserved disease severity u_i, i = 1, …, m, were independently sampled from a bimodal normal distribution $0.5N(-\sqrt{0.8},0.2)+0.5N(\sqrt{0.8},0.2)$. Then based on the simulated a_j, b_j, and u_i, the variables D_i and W_ij were generated for i = 1, …, m and j = 1, …, n. The main purpose of the simulation is first to evaluate the estimation algorithm for different quantities, such as rater-specific diagnostic bias, magnifier, sensitivity, and specificity. A second purpose is to illustrate the robustness of the method for estimating a non-normal distribution of patient disease severity u_i’s.

Figure 3 shows the estimation of rater-specific bias a_j and diagnostic magnifier b_j for the two sample size scenarios. The point estimates shown in the figure are the average of 200 posterior means from the 200 simulations for each individual rater. The corresponding line connects the smallest lower bound and the largest upper bound of the corresponding 200 95% credible intervals from the simulations. For both two sample size scenarios, the estimation of a_j and b_j is good with most the point estimates (shown as points in the figure) near the true values (shown as crosses in the figure) and all the true values covered within the credible intervals. The larger sample size scenario provides more accurate estimation results with the most point estimates overlaying the true values and narrower credible intervals.

Figure 3.

Simulation study: plot of point estimates and 95% credible intervals of rater bias a_j and diagnostic magnifier b_j for the raters. True values of a_j and b_j for each rater are plotted as ×. Left panel is for the sample size m = n = 50; right panel is for the sample size m = 150 and n = 100.

Figure 4 shows the estimation of rater-specific sensitivity and specificity for the two sample size scenarios. The point estimates, the average of 200 posterior means, track the true values closely, especially for the larger sample size scenario.

Figure 4.

Simulation study: plot of point estimates of sensitivity and specificity vs. true values of sensitivity and specificity. Left panel is for the sample size m = n = 50; right panel is for the sample size m = 150 and n = 100.

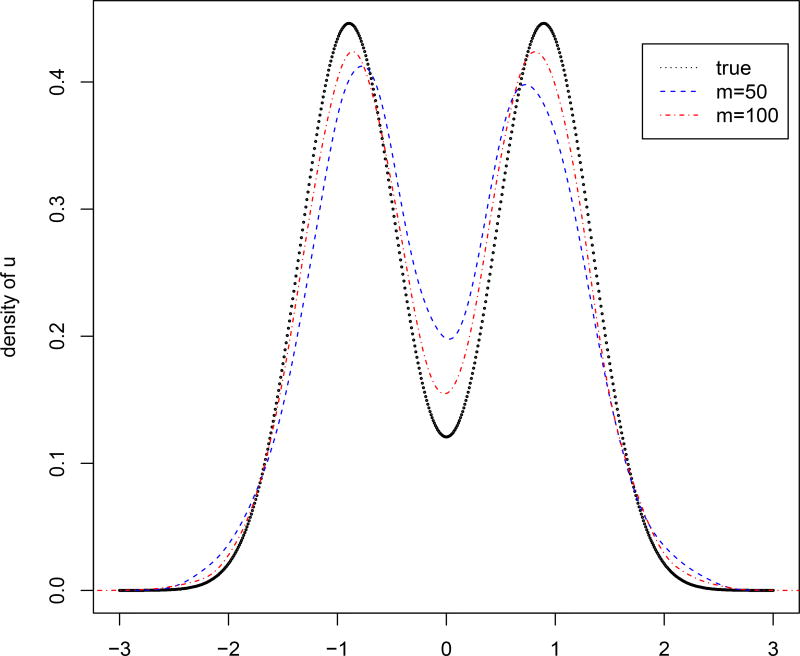
Figure 5 shows the estimation of the distribution of patient disease severity, using a density estimation on the posterior means of u_i’s. It is clear that the estimated density curve catches the bimodal shape of the true density curve for both two sample size scenarios, which implies that the posterior estimation reflects the true distribution of patient latent disease severity despite the N(0, 1) prior specification on u_i.

Figure 5.

Simulation study: estimation of the distribution of patient latent disease severity u. The dotted line is the true density of the generated u_i; the dashed line is the estimated density for the sample size m = n = 50; the dotdashed line is the estimated density for the sample size m = 150 and n = 100.

6 Application to the mammogram data

In this section, we apply our proposed method to analyze the mammogram data set introduced in Section 1. We summarize results based on 8000 Gibbs iterations after 2000 iterations as a burn-in. The assessment of convergence of MCMC chains was carried out using various convergence criteria in the R package coda.³⁶

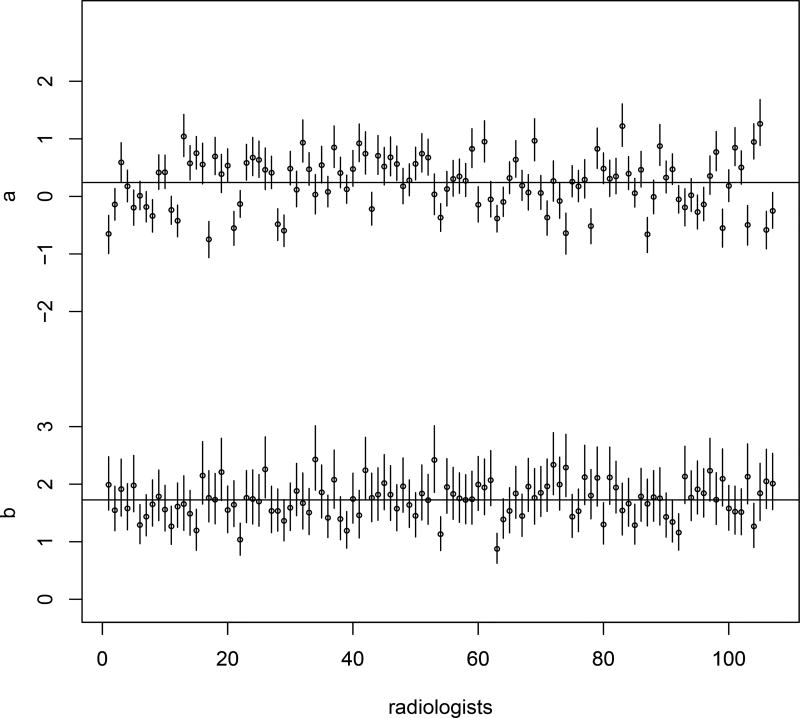
The posterior mean of the rater overall mean bias μ_a is 0.241, showing that there is a slight positive diagnostic bias over the whole group of radiologists. The posterior mean of μ_b, the rater overall mean diagnostic magnifier of the group, is 1.727. The posterior means of ${\tau }_a^{-\frac{1}{2}}$ and ${\tau }_b^{-\frac{1}{2}}$ are 0.494 and 0.395, reflecting the variation of diagnostic bias and diagnostic magnifier, respectively, for the whole group. More specifically, Figure 6 gives the estimation of rater-specific diagnostic biases and magnifiers. It is noted that most of the raters have estimated diagnostic biases between −1 and 1 and all of the raters have estimated diagnostic magnifiers greater than 1.

Figure 6.

The mammography data: estimation of diagnostic bias a_j and diagnostic magnifier b_j for the 107 radiologists. The two horizontal lines show the mean of estimated a_j’s and b_j’s, respectively.

Based on the total cost criterion, the three strongest-performing raters are identified using different values of the cost ratio θ. The estimated diagnostic bias, diagnostic magnifier, sensitivity, and specificity and their corresponding credible intervals for these raters are presented in Table 1. The results show that when the cost ratio is not too small or too large (0.5 ≤ θ ≤ 2), identified strong raters usually have large (> 2) diagnostic magnifiers and rater biases are more sensitive to the change of the cost ratio. The optimal bias a* is found according to Proposition 2 and presented in Table 1 for each identified rater under different values of the cost ratio. The optimal bias can guide good raters themselves to further improve their performance. These identified strong raters can also help other raters to improve their diagnostic skills, thus to increase the average diagnostic skills and to reduce the inter-rater variability over time.

Table 1.

The mammogram data: estimation of diagnostic bias a, diagnostic magnifier b, sensitivity, and specificity for the 3 identified strongest raters for the mammogram data based upon different values of cost ratio θ.

θ	rater	a*	a	b	sensitivity	specificity
0.5	74	−1.208	−0.639 (−1.007, −0.291)	2.287 (1.749, 2.924)	0.614 (0.563, 0.661)	0.861 (0.824, 0.892)
	1	−1.144	−0.643 (−0.9966,0.3097)	2.0312 (1.573,2.575)	0.600 (0.546,0.651)	0.862 (0.821,0.895)
	99	−1.162	−0.557 (−0.892, −0.230)	2.109 (1.635, 2.666)	0.618 (0.565, 0.665)	0.853 (0.812, 0.886)
1	34	−0.223	0.032 (−0.319, 0.388)	2.453 (1.882, 3.131)	0.614 (0.563, 0.661)	0.861 (0.824, 0.892)
	53	−0.226	0.034 (−0.312, 0.383)	2.416 (1.886, 3.039)	0.703 (0.660, 0.742)	0.789 (0.739, 0.831)
	93	−0.250	−0.181 (−0.500, 0.145)	2.161 (1.668, 2.745)	0.672 (0.623, 0.717)	0.809 (0.762, 0.849)
2	42	0.777	0.745 (0.397, 1.137)	2.246 (1.707, 2.848)	0.788 (0.751, 0.822)	0.658 (0.593, 0.718)
	26	0.787	0.478 (0.135, 0.832)	2.281 (1.773, 2.861)	0.756 (0.717, 0.792)	0.713 (0.655, 0.766)
	79	0.743	0.830 (0.486, 1.175)	2.120 (1.648, 2.620)	0.802 (0.765, 0.837)	0.625 (0.554, 0.690)
5	105	3.062	1.273 (0.879,1.709)	1.860 (1.359,2.413)	0.866 (0.831,0.896)	0.468 (0.390,0.543)
	83	2.957	1.217 (0.859,1.615)	1.532 (1.076, 2.026)	0.877 (0.841,0.907)	0.416 (0.336,0.494)
	13	2.988	1.059 (0.707,1.423)	1.666 (1.203,2.1645)	0.850 (0.813,0.882)	0.490 (0.411,0.566)

The values in parentheses are the corresponding credible intervals.

For each identified rater, a* is the solved optimal diagnostic bias.

Finally, the estimated distributions of patient disease severity are plotted in Figure 7. It is clear that the patients who are cancer free and who have malignancies have separate distributions of disease severity.

Figure 7.

The mammography data: estimation of the distribution of patient latent disease severity u. The estimated distributions are drawn separately for the patients with D = 0 (no disease) and for the patients with D = 1 (disease). The reference line is the standard normal density, used as the prior for u in the estimation algorithm.

7 Discussion

In this paper, we propose a hierarchical model linking raters’ decisions with patients’ disease-development outcomes for a binary subjective disease diagnostic process. The proposed model specifies a rater’s diagnostic skills as diagnostic bias and diagnostic magnifier and allows rater diagnostic magnifier and patient latent disease severity to interactively affect the decision-making. It is the first application of this model in diagnostic medical testing.

Our proposed approach can be very useful in the performance evaluation of clinicians. Not only can it access the overall diagnostic performance on the entire group of raters (analogous to measures of inter-rater reliability), but can also estimate rater-specific bias and diagnostic ability. Strong raters can be identified using the proposed cost theory. The optimal adjustment of rater bias can be achieved through the minimization of the expected cost. While rater bias is relatively easy to justify, diagnostic magnifier more fundamentally presents a rater’s diagnostic skill. A rater with a larger diagnostic magnifier has a uniformly better ROC curve. Identified strong raters can help others to improve the diagnostic ability; investigating strong raters helps to find important factors that affect the diagnostic accuracy. For future research, we can augment the model by adding a layer of regression analysis on the diagnostic bias and magnifier to find significant covariates.

The proposed approach is also useful for investigating the nature of the disease development by estimating the patient-specific latent disease severity and the distribution of the disease severity for the whole group of patients. For future research, we may incorporate patient covariates, such as patient age, gender, etc. to further investigate the nature of the disease development.

Our proposed methods are applicable even when patients’ true disease outcomes D’s are not observed. For the model fitting, the Gibbs sampler algorithm in Section 3 remains the same except dropping the j = 0 terms in steps 1 and 2. The estimation of sensitivity and specificity and the other results in Section 4 also remain the same as long as the part of model, P(D_i = 1|u_i) = Φ(u_i), conceptually holds. The supporting web materials include the comparison of estimated a’s, b’s, sensitivities, and specificities between using and not using D′s for a further simulation study (with 30 raters rating 30 patients) and the analysis for the mammogram data. The figures there show that without using D’s, the estimation of rater abilities remains almost the same except there is a little influence on the estimated b’s, that is, the estimated b’s are overall slightly larger when not using D’s.

In practice, many diagnostic results lie on an ordinal scale, such as the BI-RADS scale in the mammogram data. Although dichotomization is a common clinic practice, it does lose some useful rating information. Our future research will extend our approach to ordinal-rating responses.

Appendix

Proof of Proposition 1

Suppose the joint density of the data (D, W) is always the same for (u, a, b) as for (u′, a′, b′). In particular the marginal distributions of D_i’s are the same for any i, so ${\mathrm{\Phi }}^{-1}(u_i)\equiv {\mathrm{\Phi }}^{-1}(u_i^{\prime })$. Therefore, $u_i\equiv u_i^{\prime }$. If the u_i are not all equal, without loss of generality let u₁ ≠ u₂. For any j,

$${\mathrm{\Phi }}^{-1}(a_j+b_j{u}_1)={\mathrm{\Phi }}^{-1}(a_j^{\prime }+b_j^{\prime }{u}_1)$$

$${\mathrm{\Phi }}^{-1}(a_j+b_j{u}_2)={\mathrm{\Phi }}^{-1}(a_j^{\prime }+b_j^{\prime }{u}_2)$$

Therefore,

$$a_j+b_j{u}_1=a_j^{\prime }+b_j^{\prime }{u}_1$$

$$a_j+b_j{u}_2=a_j^{\prime }+b_j^{\prime }{u}_2$$

Subtracting the equations we find that $b_j(u_1-u_2)=b_j^{\prime }(u_1-u_2)$. Hence $b_j=b_j^{\prime }$ because u₁ − u₂ ≠ 0. Thus $a_j=a_j^{\prime }$. Since j is arbitrary, identifiability is established.

Proof of Proposition 3

$$\frac{\mathit{\text{dTC}}}{\mathit{\text{db}}}\propto {\int }_u[1-(\theta +1)\mathrm{\Phi }(u)]\varphi (a^{\ast }+\mathit{\text{bu}})\mathit{\text{udF}}(u)$$ (8)

When the optimal rater bias a* is used, according to the definition of the optimal rater bias, the following two facts hold:

$${\int }_u[1-(\theta +1)\mathrm{\Phi }(u)]\varphi (a^{\ast }+\mathit{\text{bu}})\mathit{\text{dF}}(u)=0,\text{ and}$$

$${\int }_u[1-(\theta +1)\mathrm{\Phi }(u)]\varphi (a^{\ast }+\mathit{\text{bu}})(a^{\ast }+\mathit{\text{bu}})\mathit{\text{dF}}(u)<0.$$

These facts imply that $\frac{\mathit{\text{dTC}}}{\mathit{\text{db}}}<0$ and the conclusion follows.

Proof of Corollary 1

For ease of notation, define

$$I_1={\int }_u\mathrm{\Phi }(u)\mathit{\text{dF}}(u),$$

$$I_2(a,b)={\int }_u\mathrm{\Phi }(u)\mathrm{\Phi }(a+\mathit{\text{bu}})\mathit{\text{dF}}(u),$$

$$I_3(a,b)={\int }_u\mathrm{\Phi }(a+\mathit{\text{bu}})\mathit{\text{dF}}(u).$$

Then true positive rate, that is, sensitivity in equation (4), can be denoted as

$$\mathit{\text{Se}}(a,b)=\frac{I_2(a,b)}{I_1};$$

false positive rate, that is, one minus specificity in equation (5), can be denoted as

$$1-\mathit{\text{Sp}}(a,b)=\left(\frac{1}{1-I_1}\right)[I_3(a,b)-I_2(a,b)];$$

and total cost in equation (6) for a given cost ration θ > 0, up to a positive multiplier, can be denoted as

$$\mathit{\text{TC}}(a,b)=\theta I_1-(1+\theta )I_2(a,b)+I_3(a,b).$$

For any given b₁ ≥ b₂ and θ > 0, let $a_1^{\ast }$ be the optimal choice of a for the θ and b₁, that is, $a_1^{\ast }$ minimizes total cost using proposition 2; and let a₂ be the value of a such that $1-\mathit{\text{Sp}}(a_1^{\ast },b_1)=1-\mathit{\text{Sp}}(a_2,b_2)$. This value of a₂ exists because 1 − Sp(a, b₂) is continuous and strictly increasing from 0 to 1 as a ranges from −∞ to ∞. Plugging I₁, I₂, and I₃ in the equation $1-\mathit{\text{Sp}}(a_1^{\ast },b_1)=1-\mathit{\text{Sp}}(a_2,b_2)$, we can derive that

$$[I_3(a_1^{\ast },b_1)-I_3(a_2,b_2)]=[I_2(a_1^{\ast },b_1)-I_2(a_2,b_2)].$$ (9)

Next, for such defined $a_1^{\ast }$ and a₂, we show that $\mathit{\text{Se}}(a_1^{\ast },b_1)\ge \mathit{\text{Se}}(a_2,b_2)$. By Proposition 3, since $a_1^{\ast }$ is optimal for b₁, and b₁ ≥ b₂, we have $\mathit{\text{TC}}(a_1^{\ast },b_1)\le \mathit{\text{TC}}(a_2,b_2)$, that is,

$$0\le \mathit{\text{TC}}(a_2,b_2)-\mathit{\text{TC}}(a_1^{\ast },b_1)=\{\theta I_1-(1+\theta )I_2(a_2,b_2)+I_3(a_2,b_2)\}-\{\theta I_1-(1+\theta )I_2(a_1^{\ast },b_1)+I_3(a_1^{\ast },b_1)\}=(1+\theta )\{I_2(a_1^{\ast },b_1)-I_2(a_2,b_2)\}-\{I_3(a_1^{\ast },b_1)-I_3(a_2,b_2)\}=\theta \{I_2(a_1^{\ast },b_1)-I_2(a_2,b_2)\}\text{ By equation }(9)=I_1\theta \{\mathit{\text{Se}}(a_1^{\ast }{b}_1)-\mathit{\text{Se}}(a_2{b}_2)\}.$$

To summarize, for any b₁ ≥ b₂ and θ > 0, we can find $a_1^{\ast }$ and a₂ such that $1-\mathit{\text{Sp}}(a_1^{\ast },b_1)=1-\mathit{\text{Sp}}(a_2,b_2)$ and $\mathit{\text{Se}}(a_1^{\ast },b_1)\ge \mathit{\text{Se}}(a_2,b_2)$. Varying θ over its entire range (0, ∞) will generate all values of $a_1^{\ast }$, hence all ordinates $1-\mathit{\text{Sp}}(a_1^{\ast },b_1)$ between 0 and 1 for the ROC curve. This establishes the dominance of the entire curve ROC(b₁) over ROC(b₂).