Evaluation of Fitting Models for Prostate Tissue Characterization Using Extended-Range b-Factor Diffusion-Weighted Imaging

Abstract

Purpose

To compare the fitting and tissue discrimination performance of biexponential, kurtosis, stretched exponential, and gamma distribution models for high b-factor diffusion-weighted images in prostate cancer.

Methods

Diffusion-weighted images with 15 b-factors ranging from b = 0 to 3500 s/mm² were obtained in 62 prostate cancer patients. Pixel-wise signal decay fits for each model were evaluated with the Akaike Information Criterion (AIC). Parameter values for each model were determined within normal prostate and the index lesion. Their potential to differentiate normal from cancerous tissue was investigated through receiver operating characteristic analysis and comparison with Gleason score.

Results

The biexponential slow diffusion fraction f_slow, the apparent kurtosis diffusion coefficient ADC_K, and the excess kurtosis factor K differ significantly among normal peripheral zone (PZ), normal transition zone (TZ), tumor PZ, and tumor TZ. Biexponential and gamma distribution models result in the lowest AIC, indicating a superior fit. Maximum areas under the curve (AUCs) of all models ranged from 0.93 to 0.96 for the PZ and from 0.95 to 0.97 for the TZ. Similar AUCs also result from the apparent diffusion coefficient (ADC) of a monoexponential fit to a b-factor sub-range up to 1250 s/mm². For kurtosis and stretched exponential models, single parameters yield the highest AUCs, whereas for the biexponential and gamma distribution models, linear combinations of parameters produce the highest AUCs. Parameters with high AUC show a trend in differentiating low from high Gleason score, whereas parameters with low AUC show no such ability.

Conclusion

All models, including a monoexponential fit to a lower-b sub-range, achieve similar AUCs for discrimination of normal and cancer tissue. The biexponential model, which is favored statistically, also appears to provide insight into disease-related microstructural changes.

INTRODUCTION

In the past decade, there has been a major increase in the application of MRI for detection and characterization of prostate cancer. Now there are increasing demands for advanced characterization of suspicious tissue by improving the specificity of the MR techniques. A typical clinical prostate MR exam is multiparametric, consisting of high-resolution T₁- and T₂-weighted imaging for anatomical details and lesion localization, as well as diffusion-weighted imaging (DWI), dynamic contrast-enhanced MRI (DCE-MRI) and/or MR spectroscopic imaging for further characterization of pathologic changes (1–3). The resulting parameter maps provide quantitative information related to water diffusion hindrance within the cellular environment, tissue perfusion, and metabolite distributions. PI-RADSv2 is an assessment system for prostate MRI established by an international team of experts(4). PI-RADSv2 defines the approach to assessment of suspicious lesions using a qualitative scoring approach. The DWI sequence is given most weight for assessing peripheral zone lesions.

According to PI-RADSv2, the qualitative evaluation shall be performed with an apparent diffusion coefficient (ADC)-map and a diffusion-weighted image. It is recommended that the ADC map is obtained by monoexponential fitting over a narrow range of b-factors under 1000 s/mm² and that the diffusion-weighted image is acquired with b ≥ 1400 s/mm². At low b-factors (0–250 s/mm²), a deviation of the signal decay from a simple monoexponential decay can be observed. This deviation is attributed to intravoxel incoherent motion (IVIM) of blood and may possibly be used to estimate tissue perfusion (5,6). Besides a deviation from a simple monoexponential decay in the low b-factor range, a departure from a monoexponential decay can also be observed at high b-factors (>1000 s/mm²) (7). The nonmonoexponential diffusion signal decay in prostate tissue can be attributed to the presence of different compartments, such as extracellular, intracellular, and intranuclear compartments that exhibit different water diffusion characteristics, which also depend on the size of the respective compartments. The presence of distinct water pools has also been confirmed by ex vivo prostate DWI studies (8). Several models have been proposed, such as the biexponential model (7), the kurtosis model (9), the stretched exponential model (10), and the gamma distribution model (11), to describe and fit the observed diffusion in tissues.

Although the monoexponentially derived ADC-map is of major importance for prostate cancer diagnosis and staging with MR imaging, the PI-RADS committee strongly encourages the development of novel promising DWI techniques to further improve prostate cancer management (4). To this end, the present study evaluates prostate high b-factor scans (up to 3500 s/mm²) with full-range biexponential, kurtosis, stretched exponential and gamma distribution model analysis, and partial-range monoexponential model analysis. For each model, the relative fit quality in terms of information content and the ability of the resulting parameters to differentiate tumors from normal tissue in both the peripheral zone (PZ) and transition zone (TZ) of the prostate is determined. As the low b-factor images may include a perfusion component, we also evaluate the effect of the b = 0 images on the fitted parameters.

METHODS

Patients

This HIPAA-compliant study was approved by the Institutional Review Board at Brigham and Women’s Hospital (Boston, MA). Written informed consent was prospectively obtained from each patient. In total, 62 patients, who were scheduled for a clinical multiparametric MR exam, were recruited. Review of medical records was performed in all cases to determine prior and post-MRI biopsies, prior and post-MRI treatment, as well as all pathology results.

Of the 62 patients enrolled in this study, 6 patients had undergone prior therapy and were retrospectively excluded. Of the remaining 56 patients, 50 had a prior TRUS-guided biopsy, 4 patients had no prior biopsy, and for 2 patients, documentation regarding prior diagnostic measures was not available. For the 56 included patients, the age ranged from 43 to 77 years with a mean of 62 years. The mean serum prostate specific antigen (PSA) level of these patients was 8.8 ng/mL (range, 0.37–46 ng/mL). In 9 of the 50 (9/50) patients with prior TRUS-guided biopsy, pathology results were benign. In one (1/50) patient, a high-grade prostatic intraepithelial neoplasia (HGPIN), a precursor of prostate cancer, was diagnosed. In the remaining 40 (40/50) patients the highest Gleason score in the biopsy samples was: 3 + 3 (n = 23), 3 + 4 (n = 9), 4 + 3 (n = 5), 4 + 4 (n = 1), 3 + 5 (n = 1) and 4 + 5 (n = 1).

The radiologist identified 40 index lesions that appeared suspicious for tumor. Of these, 27 were located in the PZ and 13 in the TZ. If a lesion extended over both zones, it was assigned to the zone that contained the largest volume of the lesion. In 10 of the 40 (10/40) patients with identified index lesion, updated Gleason scores were available from radical prostatectomy, in 5 (5/40) patients from MR-guided biopsy, and in 7 (7/40) patients from follow-up TRUS biopsy. The final Gleason scores in the patients with identified index lesion were: benign (n = 7), HGPIN (n = 1), 3 + 3 (n = 7), 3 + 4 (n = 12),4 + 3 (n = 5), 4 + 4 (n = 1), 3 + 5 (n = 1), and 4 + 3 + 5 (n = 2), In four cases, a Gleason score was not available.

MRI Acquisition

All patients underwent a standard multiparametric MR exam (1) with an additional diffusion-weighted sequence on a GE 3 Tesla Discovery MR750 scanner. For all examinations, an endorectal coil (Medrad, Pittsburgh, PA) in combination with pelvic phased array coils (General Electric Medical Systems, Milwaukee, WI) was used for signal reception. Patients were administered glucagon to minimize peristalsis. Each MR exam began with fast gradient-echo imaging for coil and patient anatomy localization. This scan was followed by T₂-weighted fast spin-echo imaging at 0.6 mm isotropic in plane resolution and 3 mm slice thickness without gap in three orthogonal plane orientations. The remainder of the MR exam consisted of spoiled gradient recalled T₁-weighted imaging, clinical DWI, DCE-MRI and extended-range b-factor DWI. For the DWI sequences only the endorectal coil was used for signal reception.

Two clinical DWI sequences (matrix size 96 × 96, field of view 140 × 140 mm, slice thickness 4 mm without gap, TR > 5800 ms), one with b = 0 (1 acquisition) and b = 500 s/mm² (8 averages) and the other with b = 0 (1 acquisition) and b = 1400 s/mm² (16 averages), were performed. Diffusion-weighted images were obtained for each of three orthogonal diffusion encoding directions. Scan time for DWI varied with coverage, but was at least 2.5 min for the b = 500 s/mm² scan and at least 5 min for the b = 1400 s/mm² scan. From the clinical diffusion-weighted images, conventional, i.e., monoexponential ADC maps were generated using the standard scanner software. The clinical DWI data was used to find and grade lesions, yet because of different diffusion time, resulting quantitative ADC values were not considered in the analysis. A third DWI sequence (matrix size 64 × 64, field of view 280 × 280 mm, slice thickness 5 mm without gap, TR 4000 ms) was performed over an extended b-factor range; 15 b-factors equally spaced in 250 s/mm² increments from b = 0 to 3500 s/mm² along each of three orthogonal diffusion encoding directions were used. Scan time for the extended-range b-factor scan was 3 min. A relatively long echo time (~ 100 ms) was required to accommodate the high diffusion weighting with gradient times δ = 37 ms and Δ = 47 ms and accordingly a diffusion time Δ-δ/3 = 35 ms.

Ice-Water Phantom Measurements

An ice-cooled water phantom (12,13) with predictable Gaussian diffusion was used to determine if any deviations from monoexponential decays would be observed as a consequence of system related artifacts or b-factors deviating from prescribed values over the extended-range b-factor range. The inner tube of the phantom containing distilled water was cooled to 0°C by packing an outer container with ice and ice water. The cooling to 0°C resulted in a diffusion coefficient of around 1.1 μm²/ms along the length of the 22-cm-long inner tube. Two sets of DW images were obtained from the phantom and fitted to a monoexponential decay curve. The first set was the extended-range b-factor DWI as described above (echo time [TE] = 99 ms), the second set included only low b-factors, i.e., b = 0, 20, 30, 40, 50, 60, 70, 80, 90, 100, 120, 250 s/mm² (TE = 52 ms). For both sets, the average ADC was determined for five regions of interest (ROIs) along the inner tube each 2–3 cm apart. Deviations from monoexponential decays were ascertained by visual inspection of semilog plots of signal versus b-factor.

Selection of Regions of Interest

All MR examinations were performed as part of the patient’s clinical care and prospectively interpreted and reported. These clinical reports and all MR images, except the extended-range b-factor images, were re-evaluated separately by one radiologist. This analysis included: (i) Identification and localization of an index lesion (defined as the most dominant lesion in terms of size or potential aggressiveness). (ii) In cases of disagreement with the clinical report, the radiologist consulted with a second radiologist until consensus was reached. (iii) The position of each index lesion was indicated on the axial T₂-weighted slice where it had the largest cross-sectional expansion. (iv) Normal appearing PZ and TZ tissue regions were also identified in all cases. (v) Anatomically corresponding regions of interest (ROIs) of the index lesion and normal appearing PZ and TZ tissue were outlined on the b = 0 image of spatially matching sections with the public domain 3D Slicer software (14). In consideration of glucagon administration, low spatial resolution and a relatively short scan time, a coregistration of the individual diffusion images was not performed.

Models and Fitting Algorithms

The biexponential, gamma distribution, and stretched exponential model are physically motivated models; the biexponential model insinuates two distinct components, one with a slow and one with a fast diffusion coefficient. The kurtosis model is an empirical model that estimates how the distribution of the diffusion-related displacement deviates from a simple Gaussian distribution as observed in plain water. The gamma distribution and stretched exponential models assume a continuous distribution of components with diffusion coefficients from 0 to infinity, rather than a discrete number of components. For the stretched exponential, the distribution ρ_s(D) with a distributed diffusion coefficient (DDC) and a stretching exponent α can be computed from the series expansion:

$${\mathrm{\rho }}_s(D)=\frac{1}{\mathrm{\pi }}{\displaystyle \sum _{k=1}^{\text{∞}}\frac{{(-1)}^{k+1}}{k!}\text{sin}\left(\mathrm{\pi }\mathrm{\alpha }k\right)\frac{\mathrm{\Gamma }(\mathrm{\alpha }k+1)}{{(D/\mathit{DDC})}^{\mathrm{\alpha }k+1}},\mathit{with}0<\mathrm{\alpha }\le 1,}$$ [1]

where Γ is the gamma function (15–17).

The gamma distribution ρ_g(D) for the diffusion coefficient D is given by:

$${\mathrm{\rho }}_g(D)=\frac{1}{\mathrm{\Gamma }(k){\mathrm{\theta }}^k}{D}^{k-1}{e}^{-\frac{D}{\mathrm{\theta }}},$$ [2]

where k describes a shape parameter and θ a scale parameter. It should be emphasized that these distributions do not describe the observed signal decay, but rather the relative signal contribution for any given diffusion coefficient.

With the biexponential model, the signal decay is fitted with a function of the form:

$$S(b)=S_0[(1-f_{\mathit{slow}})e^{-b{D}_{\mathit{fast}}}+f_{\mathit{slow}}{e}^{-b{D}_{\mathit{slow}}}],$$ [3]

where f_slow represents the fraction of the slow diffusion component and D_fast and D_slow components with fast and slow diffusion, respectively.

With the kurtosis model, the signal is fitted with a Taylor expansion of the decaying exponential, whereby the series is truncated to a second-order polynomial in b according to the following equation:

$$S(b)=S_0{e}^{-\mathit{bAD}{C}_K+\frac{1}{6}{b}^{2}AD{C}_K^{2}K},$$ [4]

where ADC_K is the apparent kurtosis diffusion coefficient and K the excess kurtosis factor. The stretched exponential model results in the following exponential signal decay function:

$$S(b)=S_0{e}^{-{(\mathit{bDDC})}^{\mathrm{\alpha }}},$$ [5]

where DDC is the distributed diffusion coefficient and the stretching coefficient α introduces the deviation from a monoexponential decay. The gamma distribution model produces nonexponential signal decays of the following form:

$$S(b)=\frac{S_0}{{(1+\mathrm{\theta }b)}^k},$$ [6]

where k represents shape parameter and θ the scale parameter of the gamma distribution.

For each voxel, the signal decay recorded in the geometric mean images was directly fitted with the biexponential, kurtosis, stretched exponential and gamma distribution models using a nonlinear least square fitting (Levenberg-Marquardt) algorithm. Based on initial testing, suitable starting parameters were provided that together with 15 measurement points and overall data quality within the prostate region appeared to consistently provide a fit with a global minimum of the cost function. Parameter limits were not set. For comparison with clinically used ADC values, the monoexponential ADC was determined for the extended-range b-factor diffusion-weighted images by fitting the signal decay to a subset of b up to 1250 s/mm² to a monoexponential fit.

Fitting algorithms were implemented within the 3D Slicer Prostate extension. In consideration of perfusion effects, for each model the fitting was performed twice, once with signal values of all b-factors and once excluding the signal value at b = 0. The following parameter maps were generated: D_slow, D_fast, and f_slow for the biexponential model, ADC_K and K for the Kurtosis model, DDC and α for the stretched exponential, and k and θ for the gamma distribution model. In addition, each model generated an estimate of S₀. An IVIM estimate of the blood perfusion fraction was obtained by using the computed biexponential S₀ parameter for signal values with b ≥ 0 and b ≥ 250 s/mm² in the following equation:

$$f_{\mathit{perfusion}}=\frac{S_{0(b\ge 0)}-S_{0(b\ge 250)}}{S_{0(b\ge 0)}}.$$ [7]

To test the goodness of each fit, χ² was determined and normalized with number of fitted b-factors N_b and the number of parameters N_p in the following way:

$${\mathrm{\chi }}_n^2=\frac{{\mathrm{\chi }}^2}{N_b-N_p-1}.$$ [8]

Because fitting was performed with magnitude data, there is a concern that Rician noise (18) may introduce a signal bias at high b-factors. Because an endorectal coil was used, signal is expected to vary widely across the volume of interest. Surface coil intensity correction (SCIC) had been applied to correct for nonuniform coil sensitivity, which precluded a simple measurement of Rayleigh noise within signal-free areas. To obtain measures of noise with the collected data, noise was estimated for each voxel as the square root of the normalized χ². To correct for the folded normal distribution of $\sqrt{{\mathrm{\chi }}^2}$ the noise was adjusted by the factor $\sqrt{\mathrm{\pi }/2}$ and signal-to-noise ratio (SNR) was estimated for b = 0 data as:

$$\mathit{SNR}=S_0\sqrt{\frac{2}{{\text{πχ}}_n^2}.}$$ [9]

The effect of signal bias introduced by Rician noise was reduced by only considering voxels where the signal intensity at b = 3500 s/mm² exceeded twice the estimated noise level (18) in the final analysis. Moreover, voxels with negative D_slow were excluded from biexponential analyses.

Statistical Analysis

For each of the four fitting models, the percentage of voxels within each ROI was determined that could be included based on the two-fold signal-to-noise level criterion. To compare fits with the different models, AIC (19) was evaluated for each voxel. For limited sample sizes, i.e., when the resulting ratio between number of fitted b-factors N_b and the number of parameters N_p falls below 40, it is more appropriate to use a corrected AIC, termed AICc (19):

$$\mathit{AI}{C}_C=N_b\text{ln}\left(\frac{{\mathrm{\chi }}^2}{N_b}\right)+2N_p+\frac{2N_p(N_p+1)}{N_b-N_p-1}.$$ [10]

The biexponential model uses four fit parameters, whereas the other three models use three fit parameters. For each ROI, the percentage of voxels was determined for which the biexponential model had a lower AIC_C, where a lower AIC_C indicates a model with higher information content and thus the additional fitting parameter of the biexponential model is justified.

For each parameter and each tissue type, the mean value was determined within the voxels of the ROI that met the two-fold signal-to-noise level criterion. In addition, for the stretched exponential and gamma distribution the mode, i.e., the peak position of the distribution, was derived from the mean parameter values. For the stretched exponential this was accomplished by searching the maximum of ρ_s(D) with a fast converging algorithm (17) over a wide range of D-values. For the gamma distribution, the mode is directly computed with the analytic expression (k−1)θ. Subsequently, for each tissue type the standard deviation of all mean values was computed. The mean values for each tissue type were compared using analysis of variance (ANOVA) and Tukey’s posthoc test.

To study the performance of discrimination between normal and tumor tissue identified with multiparametric MRI, a receiver operating characteristic (ROC) curve was obtained and the area under the curve (AUC) was calculated for each parameter. The standard deviation of the AUC was estimated according to the method of Hanley and McNeil (21). Youden’s index was used to determine optimal cutoff values. Furthermore, it was investigated whether the performance could be improved by combining up to three parameters p₁, p₂, and p₃ of a model. To this end, a distribution-free rank-based approach for optimizing the area under the ROC curve was used to compute the linear combination factors r and r′ (22). The cutoff value y₀ for the optimal discriminator line p₁ + rp₂ + r′ p₃ = y₀ was also determined with Youden’s index. Additionally, tumor parameter values were classified into a first group with a combined Gleason score of 7 or higher and a second group with a combined Gleason score of 6 or below. For each parameter, a two sided t-test was performed to test for a significant difference between the two groups sorted according to Gleason score.

For all tests, a P-value of 0.05 was used to indicate a significant difference. The statistical analysis was performed in Matlab (version 8.2; Mathworks, Natick, MA) and Graphpad Prism (La Jolla, CA).

RESULTS

Ice-Water Phantom Measurements

The mean and standard deviation of the ADC excluding the signal value at b = 0 in the fit for the five ROIs in the tube at different positions along the magnet main axis was 1.14 ± 0.06 μm²/ms for the extended-range b-factor diffusion-weighted images and 1.05 ± 0.10 μm²/ms for the low b-factor diffusion-weighted images (P = 0.12). Visual inspection of the data points and associated fits showed that the signal intensity strictly followed a monoexponential decay; however, in a large part of the voxels the intensity at b = 0 s/mm² was clearly higher than indicated by the monoexponential fit. Due to the much smaller range in signal intensity, this was most evident for the low b-factor diffusion-weighted images: In the five ROIs investigated, the signal deviation from the fitted line at b = 0 ranged from + 1.27% to + 2.43%, without any clear association to iso-center distance.

Patient Image Data

In general, image quality was deemed adequate (see Fig. 1). However, due to image distortions, in one patient a tumor PZ ROI and in another patient a normal TZ ROI could not be outlined.

FIG. 1.

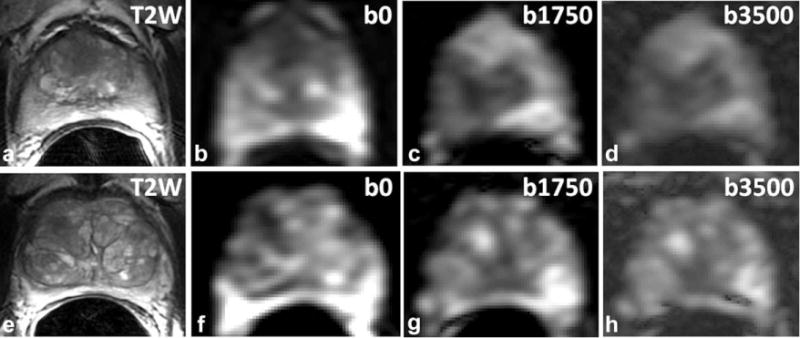
Two MR datasets showing the quality of extended-range b-factor DWI at b = 0, b = 1750, and b = 3500 s/mm². (a) T₂-weighted image showing a hypointense region in the TZ. (b–d) Corresponding b = 0, b = 1750 and b = 3500 s/mm² images of the extended-range b-factor DWI. (e) T₂-weighted image without a clearly suspicious region (PSA level of 2.4 ng/mL and a 3 + 3 Gleason score on biopsy). On the clinical ADC map, a suspicious region in the right TZ was observed. (f,g) Corresponding b = 0, b = 1750, and b = 3500 s/mm² images of the extended-range b-factor DWI. In both cases, the suspicious region is more conspicuous on the b = 0 image than on the T₂-weighted image (TE 93 ms/TR 4758 ms). All image intensities are scaled for optimal contrast.

Diffusion Signal Fits and Resulting Parameters

An example of the observed signal decays and associated fits is presented Figure 2. Average SNR of the geometric mean data at b = 0 amounts to 180 ± 52 in normal PZ ROIs, 119 ± 23 in normal TZ ROIs, 108 ± 37 in tumor PZ ROIs and 74 ± 18 in tumor TZ ROIs. The fraction of voxels in each ROI that could be included according to the two-fold signal-to-noise level criterion is approximately the same for the gamma model and the biexponential model, i.e., irrespective of b = 0 signal inclusion or exclusion around 94%. In comparison, when signal values of all b-factors are included, the kurtosis and stretched exponential model have only 80 to 90% voxels accepted by the signal-to-noise criterion. In this case, when compared with the biexponential model, the χ² values are on average 1.9 times higher for the kurtosis model and 1.3 times higher for the stretched exponential model. In contrast, exclusion of the b = 0 signal value results in similarly high acceptance rate of approximately 94%. In 32 subjects, biexponential fits with substantial fractions of negative D_slow values and exceedingly high D_fast values were observed in approximately 5% of the voxels. Based on the negative D_slow criterion, these voxels were excluded from further analysis. An evaluation of parameter histograms did not reveal any other occurrence of improbable parameter values or clustering at starting parameters.

FIG. 2.

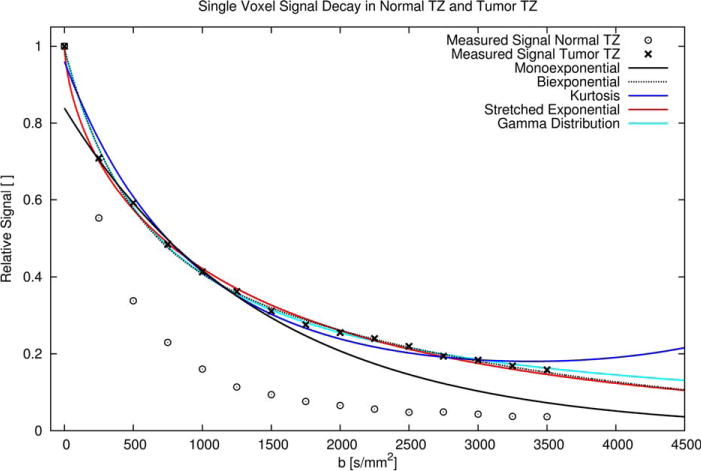
Diffusion related signal decays measured in individual voxels of normal TZ and tumor TZ. In the normal TZ compared with the tumor TZ the signal decay with increasing b-factor is faster. For the tumor TZ all model fits are shown: The monoexponential model fit (b 250–1250 s/mm²) shows a clear deviation from the measured data for b = 0 and b > 1250 s/mm². The biexponential and gamma distribution fit (b 0–3500 s/mm²) appear to match the measured decay and each other very closely. Only for b > 3000 s/mm² do the fitted curves separate, with the gamma distribution model upholding a slower decay than the biexponential model. The stretched exponential model curve (fitted for b 0–3500 s/mm²) matches the biexponential model curve for b > 1500 s/mm², but features the steepest decent of all curves for b < 250 s/mm². Finally, the kurtosis model curve (fitted for b 0–3500 s/mm²), appears to exhibit a suboptimal fit, with a curve that three times clearly crosses the most likely path of signal decay. Moreover, there is an implausible signal rise with increasing b-factor for b > 3500 s/mm².

The percentages of voxels for which AIC_C of the biexponential model is superior are reported in Table 1. Evidently fits obtained with the biexponential model, compared with fits obtained with the kurtosis and stretched exponential models, are statistically preferred, particularly when signal values measured at b = 0 are included. The biexponential model and gamma distribution model yield in terms of AIC_C approximately equally good fits; when the b = 0 signal is included in the fit, the gamma distribution model appears to perform slightly better. Focusing on particular tissues, fits with the gamma distribution model result in a lower AIC_C for tumors in the TZ. In none of the specific tissues, does the kurtosis model outperform the biexponential model in terms of AIC_C ranking.

Table 1.

AIC: Percentage of Voxels for Which the Biexponential Model Results in a Lower AIC_c.^a

Model	b-Factors [s/mm2]	Normal PZ (n = 56)	Tumor PZ (n = 27)	Normal TZ (n = 56)	Tumor TZ (n = 13)	All ROIs (n = 152)
Kurtosis (%)	0–3500	86 ± 20	89 ± 18	94 ± 15	87 ± 19	89 ± 25
	250–3500	79 ± 25	74 ± 27	80 ± 19	55 ± 31	76 ± 25
Stretched	0–3500	92 ± 12	82 ± 20	87 ± 13	61 ± 28	86 ± 18
exponential (%)	250–3500	83 ± 21	65 ± 26	81 ± 19	43 ± 17	76 ± 24
Gamma	0–3500	62 ± 20	41 ± 24	35 ± 22	28 ± 15	45 ± 25
distribution (%)	250–3500	69 ± 28	44 ± 29	54 ± 20	22 ± 13	55 ± 28

^aData are given as mean ± standard deviation.

Examples of parameter maps and ROI outlines are presented in Figure 3. Mean parameter values for each tissue type are listed in Table 2. For the parameters ADC, f_slow, ADC_K, K, all four tissue types investigated (normal PZ, normal TZ, tumor PZ and tumor TZ) exhibit significantly different values (see Table 2 and Fig. 4). For DDC, stretched exponential mode, and gamma distribution mode, this is only the case if the signal measured at b = 0 is included. Exclusion of the signal measured at b = 0 results in less stable fits and particularly the parameter DDC exhibits excessively high values with high variability. For the other parameters, only some or none of the specific tissue values differ significantly (see Table 2). Overall, exclusion of the b = 0 signal has the effect of lowering monoexponential ADC, the biexponential parameters f_slow, D_slow, and D_fast, the kurtosis diffusion coefficient ADC_K, and the stretched exponential model parameter α, but raising the gamma distribution model scaling parameter θ and the mode of the continuous distribution models. The kurtosis parameter K does not appear to be influenced by b = 0 signal exclusion. Diffusion coefficient spectra of the physically motivated models, which result from average parameters of normal and tumor tissue in the PZ, are shown in Figure 5.

FIG. 3.

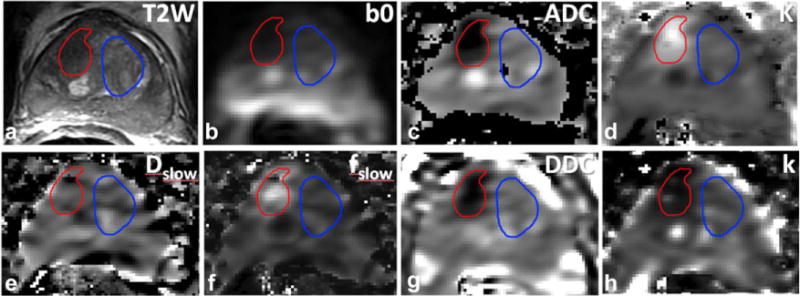
MR data of a 77-year-old patient with a PSA level of 13.8 ng/mL and a Gleason score 4 + 3 tumor on biopsy. (a) T₂-weighted image with a tumor suspicious region outlined in red in the right TZ and normal appearing TZ tissue, outlined in blue. (b) b = 0 s/mm² image of extended-range b-factor DWI. (c) Map of ADC derived from the monoexponential fit of the data (mean value tumor ROI: 0.78 μm²/ms and normal TZ ROI: 1.46 μm²/ms). (d) Map of K derived from the kurtosis model fit excluding b = 0 (mean value tumor ROI: 0.90 μm²/ms and normal TZ ROI: 0.53 μm²/ms). (e) Map of D_slow of the biexponential model fit excluding b = 0 (mean values for tumor ROI: 0.24 μm²/ms and normal TZ: 0.32 μm²/ms). (f) Map of f_slow derived from the biexponential fit excluding b = 0 (mean value tumor ROI: 0.40 and normal TZ: 0.16). (g) Map of DDC derived from the stretched exponential model fit including b = 0 (mean value tumor ROI: 0.85 μm²/ms and normal TZ ROI: 1.78 μm²/ms). (h) Map of k obtained from the gamma distribution model fit excluding b = 0 (mean value tumor ROI: 1.12 and normal TZ ROI: 1.81).

Table 2.

Mean Parameter Values for Each Tissue Type and Model.^a

Model	Parameter	b-Factors [s/mm2]	Normal PZ (n = 56)	Tumor PZ (n = 27)	Normal TZ (n = 55)	Tumor TZ (n = 13)
Monoexponential	ADC	0–1250	2.01 ± 0.28†	1.37 ± 0.29†	1.70 ± 0.20†	1.10 ± 0.30†
		250–1250	1.71 ± 0.27†	1.14 ± 0.27†	1.39 ± 0.15†	0.89 ± 0.25†
Biexponential	fslow	0–3500	0.19 ± 0.06†	0.33 ± 0.10†	0.28 ± 0.05†	0.45 ± 0.12†
		250–3500	0.14 ± 0.05†	0.28 ± 0.09†	0.20 ± 0.05†	0.36 ± 0.13†
	Dslow	0–3500	0.52 ± 0.11	0.41 ± 0.10*,**	0.53 ± 0.08	0.40 ± 0.11*,**
		250–3500	0.40 ± 0.11	0.33 ± 0.10*,**	0.39 ± 0.06	0.29 ± 0.07*,**
	Dfast	0–3500	2.81 ± 0.29	2.58 ± 0.47	2.86 ± 0.37	2.97 ± 1.34
		250–3500	2.49 ± 0.34	2.09 ± 0.36*	2.21 ± 0.21*	2.01 ± 0.53*
	fperfusion	–	0.06 ± 0.04	0.06 ± 0.05	0.08 ± 0.04	0.07 ± 0.05
Kurtosis	ADCK	0–3500	2.21 ± 0.30†	1.51 ± 0.32†	1.87 ± 0.18†	1.23 ± 0.34†
		250–3500	2.06 ± 0.32†	1.36 ± 0.32†	1.67 ± 0.19†	1.05 ± 0.31†
	K	0–3500	0.47 ± 0.07†	0.67 ± 0.14†	0.55 ± 0.05†	0.78 ± 0.15†
		250–3500	0.48 ± 0.07†	0.67 ± 0.13†	0.55 ± 0.06†	0.77 ± 0.16†
Stretched exponential	Mode	0–3500	0.89 ± 0.18†	0.56 ± 0.19†	0.74 ± 0.11†	0.41 ± 0.15†
		250–3500	1.77 ± 1.06	0.90 ± 0.70*	0.98 ± 0.38*	0.69 ± 0.66*
	DDC	0–3500	2.02 ± 0.29†	1.38 ± 0.36†	1.75 ± 0.20†	1.08 ± 0.35†
		250–3500	25.3 ± 32.9	12.3 ± 11.9	13.2 ± 20.8	5.84 ± 7.07*
	α	0–3500	0.70 ± 0.03	0.68 ± 0.05*	0.69 ± 0.03	0.66 ± 0.05*
		250–3500	0.44 ± 0.06	0.45 ± 0.09	0.46 ± 0.05	0.51 ± 0.10*
Gamma distribution	Mode: (k−1)·θ	0–3500	1.61 ± 0.40†	0.75 ± 0.46†	1.17 ± 0.27†	0.38 ± 0.38†
		250–3500	2.74 ± 4.63	0.82 ± 0.57*	1.20 ± 0.33*	0.58 ± 0.38
	k	0–3500	2.42 ± 0.61	1.65 ± 0.56*	1.90 ± 0.32*	1.32 ± 0.31*,**
		250–3500	2.06 ± 0.49	1.61 ± 0.53*	1.82 ± 0.29*	1.54 ± 0.63*
	θ	0–3500	1.23 ± 0.28	1.41 ± 0.43	1.37 ± 0.28	1.40 ± 0.43
		250–3500	3.43 ± 7.12	1.63 ± 0.59	1.60 ± 0.58	1.52 ± 1.34
ROI Volume	mm3	–	850 ± 400	630 ± 540	1920 ± 1210	800 ± 300

^aData are given as mean ± standard deviation. Units for diffusion coefficients, θ, and Mode are μm²/ms. All significances with P < 0.05:

^*significantly different from normal appearing PZ;

^**significantly different from normal appearing TZ;

^†all four tissue types are significantly different.

FIG. 4.

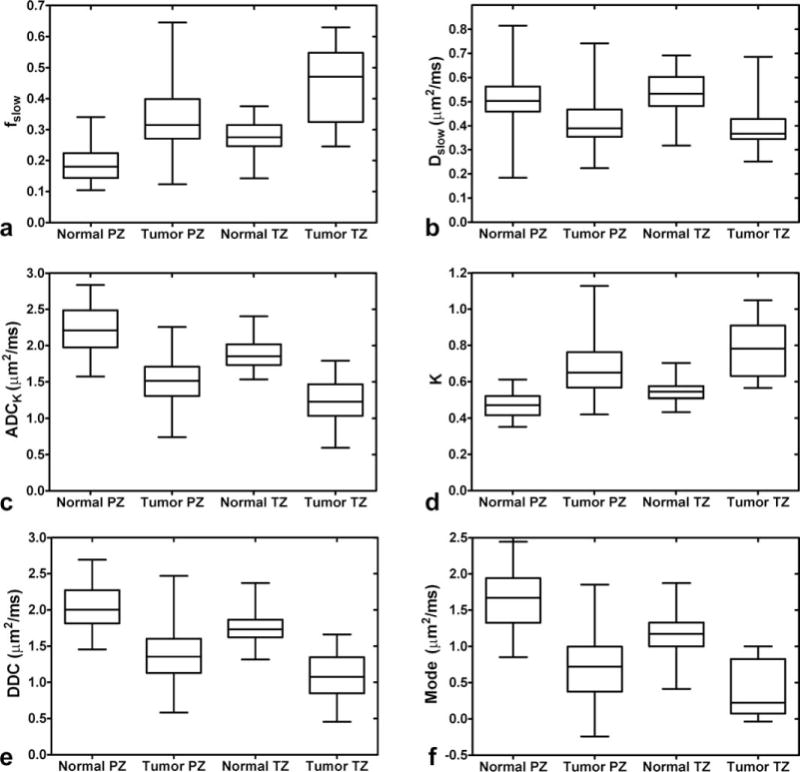
Boxplots of the median, 25^th and 75^th percentile with whiskers indicating the minimum and maximum ROI values observed for f_slow (a), D_slow (b), ADC_K (c), K (d), DDC (e), and gamma distribution mode (f) with all b-values included. For f_slow, ADC_K, K, DDC and mode, all tissue types are significantly different from each other (P < 0.05). For D_slow, tumors in the PZ and TZ do not differ significantly, but each tumor zone is significantly different from both normal PZ and normal TZ (P < 0.05).

FIG. 5.

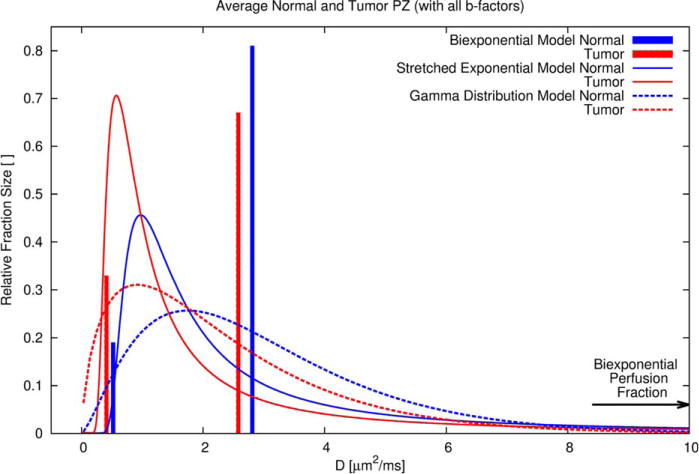
Distributions of the diffusion coefficient D obtained with the inclusion of all b-factor measurements for the biexponential, stretched exponential, and gamma distribution model in the average normal (blue) and tumor (red) PZ. The area under the curves equals 1. The vertical bars representing the biexponential model indicate the fractions at respective discrete diffusion values. The perfusion fraction, which was estimated with the biexponential model, is indicated by a horizontal arrow at a relative fraction size of 0.06 (see also Table 2). This perfusion fraction cannot be associated with a particular diffusion coefficient, because the sparse sampling close to b = 0 precludes computation of the perfusion-related D. The presence of a sizeable fast decaying component is also evident on the exemplary decay curve shown in Figure 2, where for low b-factors the stretched exponential exhibits the steepest signal descent. On the other end of the diffusion spectrum, the presence of a sizeable slow diffusion fraction for the gamma distribution and the absence of such fraction for the biexponential and stretched exponential, explains the slightly different estimated signal decay as seen in Figure 2 at very high b-factors.

The AUC values indicative for the performance of each parameter to discriminate normal tissue from tumor in the PZ and TZ are provided in Table 3. Also listed are AUC values for cases where the linear combination of two or three parameters results in an improvement over AUC values with a single parameter. For each model, parameters and their combinations are listed approximately according their diagnostic performance, with the highest performing discriminator on top. Of the single parameters, f_slow, ADC_K, DDC, and k result in the best discrimination. Of these, only ADC_K (irrespective of b = 0 signal value inclusion or exclusion) and stretched exponential DDC (only for all b-factors) produce AUCs that are comparable to or slightly exceed the AUC obtained with basic monoexponential analysis. For the biexponential or gamma distribution model, only parameter combination produces AUCs that match or exceed the AUC of a monoexponential analysis. For the kurtosis and stretched exponential model, the linear combination of parameters results in no or only negligible improvement (results not shown in table).

Table 3.

AUC of the ROC Curves for Discriminating Normal and Tumor Tissue for Each Prostatic Zone and Model Parameter, Including Combined Model Parameters.^a

			AUC		Cutoff value		r/r′
Model	Parameter	b-Factors [s/mm2]	PZ (nN=56, nT=27)	TZ (nN=55, nT= 13)	PZ (nN=56, nT= 27)	TZ (nN=55, nT= 13)	PZ (nN=56, nT=27)	TZ (nN=55, nT=13)
Monoexponential	ADC	0–1250	0.95 ±0.03	0.97 ±0.03	1.66	1.49	–	–
		250–1250	0.94 ±0.03	0.95 ±0.04	1.37	1.08	–	–
Biexponential	fslow + r·Dslow + r·′Dfast	0–3500	0.95 ±0.03	0.97 ±0.03	0.00	−0.05	−0.20/−0.07	−1.54/0.11
		250–3500	0.94 ±0.03	0.97 ±0.03	−0.27	0.10	0.09/−0.22	−1.61/0.18
	fslow + r·Dslow	0–3500	0.94 ±0.03	0.97 ±0.03	0.05	−0.06	−0.45	−0.85
		250–3500	0.93 ±0.03	0.93 ±0.05	0.08	0.01	−0.34	−0.69
	fslow + r·Dfast	0–3500	0.94 ±0.03	0.91 ±0.06	−0.06	0.23	−0.13	−0.04
		250–3500	0.94 ±0.03	0.88 ±0.06	−0.19	−0.49	−0.18	−0.39
	fslow	0–3500	0.90 ±0.04	0.88 ±0.06	0.24	0.36	–	–
		250–3500	0.91 ±0.04	0.87 ±0.07	0.20	0.30	–	–
	Dslow + r·Dfast	0–3500	0.81 ±0.06	0.95 ±0.04	0.47	0.20	0.01	−0.09
		250–3500	0.84 ±0.05	0.91 ±0.06	−2.24	0.12	−1.15	−0.10
	Dslow	0–3500	0.80 ±0.06	0.86 ±0.07	0.44	0.43	–	–
		250–3500	0.72 ±0.06	0.88 ±0.06	0.32	0.34	–	–
	Dfast	0–3500	0.73 ±0.06	0.60 ±0.09	2.65	2.58	–	–
		250–3500	0.83 ±0.05	0.77 ±0.08	2.24	2.15	–	–
	fperfusion	–	0.52 ±0.07	0.62 ±0.09	0.08	0.05
Kurtosis	ADCK	0–3500	0.95 ±0.03	0.97 ±0.04	1.88	1.67	–	–
		250–3500	0.95 ±0.03	0.96 ±0.04	1.64	1.32	–	–
	K	0–3500	0.92 ±0.04	0.95 ±0.04	0.55	0.60	–	–
		250–3500	0.89 ±0.04	0.88 ±0.06	0.58	0.66	–	–
Stretched exponential	DDC	0–3500	0.93 ±0.04	0.97 ±0.04	1.71	1.47	–	–
		250–3500	0.72 ±0.06	0.80 ±0.08	8.46	5.06	−	−
	Mode	0–3500	0.91 ±0.04	0.96 ±0.04	0.63	0.62	–	–
		250–3500	0.85 ±0.05	0.81 ±0.08	0.97	0.65	–	–
	α	0–3500	0.66 ±0.07	0.68 ±0.09	0.67	0.66	–	–
		250–3500	0.52 ±0.07	0.65 ±0.09	0.47	0.46	–	–
Gamma	Mode: (k−1)·θ	0–3500	0.92 ±0.04	0.95 ±0.04	1.02	1.00	–	–
distribution		250–3500	0.96 ±0.04	0.88 ±0.06	1.07	0.91	–	–
	k + r· θ	0–3500	0.89 ±0.04	0.98 ±0.03	2.71	2.67	0.67	0.73
		250–3500	0.87 ±0.05	0.86 ±0.07	2.36	1.70	0.42	0.09
	k	0–3500	0.85 ±0.05	0.90 ±0.06	1.59	1.33	–	–
		250–3500	0.79 ±0.06	0.84 ±0.07	1.49	1.58	–	–
	θ	0–3500	0.60 ±0.07	0.55 ±0.09	1.55	1.32	–	–
		250–3500	0.60 ±0.07	0.66 ±0.09	1.18	1.38	–	–

^aAUC data are given as mean ± standard deviation (20).

Units for diffusion coefficients, θ, and Mode are μm2/ms.

n_N = number of normal tissue ROIs; n_T = number of tumor tissue ROIs.

It should be emphasized that differences among the highest achievable AUCs are not significant. Figure 6 shows actual TZ data points with optimized separation lines for the linear combinations with the biexponential, gamma distribution and kurtosis model. For ADC, ADC_K, DDC, stretched exponential mode and gamma distribution mode, optimal AUC cutoff values according to Youden’s index, are clearly lower in the TZ. On the other hand, for f_slow and K, optimal AUC cutoff values are lower in the PZ.

FIG. 6.

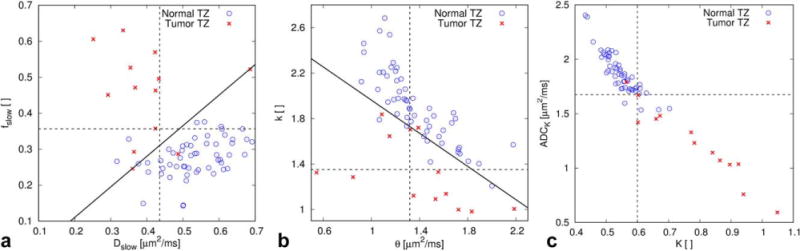
Examples of combined analysis with TZ parameter data. All b-factors were used to calculate the parameters considered for combination. The linear combination with the highest AUC is indicated by a solid line and each parameter cutoff value by a dotted line. (a) For the biexponential model, linear combination of f_slow (AUC = 0.88) and D_slow (AUC = 0.86) improves the AUC to 0.94. (b) For the gamma distribution model, linear combination of k (AUC = 0.90) and θ (AUC = 0.55) improves the AUC to 0.98. (c) For the kurtosis model, linear combination of ADC_K (AUC = 0.97) and K (AUC = 0.95) does not result in any improvement. A correlation coefficient r² for ADC_K versus K of 0.92 indicates a high normalized covariance between the two variables. In contrast, r² for f_slow versus D_slow is 0.06 and for k versus θ it is 0.36.

The probability of each parameter to predict low versus high Gleason score of PZ tumors is provided in Table 4. Parameters with high AUC compared with parameters with low AUC follow a clear trend of better prediction of low versus high Gleason score. For the TZ, the smaller number of cases and the lack of Gleason scores in some cases preclude a meaningful statistical analysis.

Table 4.

Probability of Parameters to Predict Low (≤3 + 3, n = 10) Versus High (≥3 + 4, n = 14) Gleason Score for PZ Tumors.

Model	Parameter	b-Factors [s/mm2]	PZ P-value of prediction Gleason low versus high
Monoexponential	ADC	0–1250	0.07
		250–1250	0.03
Biexponential	fslow	0–3500	0.05
		250–3500	0.03
	Dslow	0–3500	0.39
		250–3500	0.84
	Dfast	0–3500	0.73
		250–3500	0.84
Kurtosis	ADCK	0–3500	0.03
		250–3500	0.03
	K	0–3500	0.03
		250–3500	0.04
Stretched exponential	DDC	0–3500	0.06
		250–3500	0.16
	Mode	0–3500	0.07
		250–3500	0.12
	α	0–3500	0.38
		250–3500	0.81
Gamma distribution	Mode: (k−1)·θ	0–3500	0.07
		250–3500	0.03
	k	0–3500	0.15
		250–3500	0.34
	θ	0–3500	0.78
		250–3500	0.64

DISCUSSION

With the present MR protocol, using b-factors up to 3500 s/mm², whole-gland diffusion-weighted images were obtained with reasonable spatial resolution at acceptable SNR. Compared with protocols with external coil arrays, the endorectal coil used in the present study results in overall higher but nonuniform SNRs. Others have either used lower b-factors (23–27), or lower spatial resolution (7,28), when performing extended-range b-factor DWI in the prostate. The present study clearly differs from studies that used measurements over the typical clinical b-factor range with monoexponential signal extrapolation to obtain computed high b-factor images with raised lesion conspicuity (29).

Different models were used to fit the extended-range b-factor DWI data acquired in suspected prostate cancer patients. Particular attention was paid to the effect of including or excluding the signal measured at b = 0, which, unlike the other measured signals at b ≥ 250 s/mm², can be strongly affected by blood perfusion (5,6). The phantom experiments demonstrate that signal deviation can occur even without the presence of blood flow. The most likely source of this deviation are issues with pulse sequence design, such as unwanted weighting effects originating from gradient cross-terms. The deviation, however, is lower than previously reported perfusion fraction values (5,6) and the estimated perfusion fractions of the present study. Nonetheless, the deviation requires a cautious interpretation of the estimated perfusion fractions.

In general, in prostate tissues, the observed lower AIC_C favors the biexponential model and gamma distribution model, i.e., two physically motivated models, over the other models. The removal of voxels that are significantly affected by Rician noise is deemed critical, because otherwise the average parameter generated from an ROI tends to be dominated by far-off fit results of those voxels. A minimum SNR criterion readily avoids Rician noise; but a reliable measure of noise is not trivial to obtain. It is possible to use the square root of the normalized χ² as a measure of noise, provided the model perfectly describes the signal decay. For the present study, noise estimates of different models, not all of them fitting equally well, were used. In the worst case, i.e., for data with b = 0 signal inclusion, this resulted on average in a relative increase of the signal-to-noise criterion from 2 to 2.75 $(2\cdot \sqrt{1.3})$for the kurtosis model and to 2.3 $(2\cdot \sqrt{1.9})$ for the stretched exponential model. This minor inconsistency seems reasonable in view of an overall rather low SNR criterion and rules that also hold in the case where only a subset of models is investigated.

Key observations made with the typical signal decay curves (Fig. 2), the information content ranking (Table 1) and the average parameters of the models (Table 2), are better understood by looking at the diffusion coefficient spectrum of the physically motivated models, i.e., the biexponential, stretched exponential and gamma distribution model (Fig. 5). In tumors compared with normal tissue, a substantial shift of the biexponential fraction sizes toward the slow fraction and a small reduction of both diffusion coefficients can readily be appreciated. For the stretched exponential and the gamma distribution, these changes are similarly reflected in an elevation of the peak and a shift of the peak position (mode) toward lower diffusion values.

The usage of the stretched exponential to describe tissue diffusion MR signal decays was initially proposed by Bennett et al (10) and it has subsequently also been applied to diffusion signal analysis in vivo in normal prostate and prostate cancer (27) as well as ex vivo in prostate specimens (30). The stretched exponential has proven useful in a wide range of scientific analyses, such as studies of physical relaxation processes (16), word-frequencies, earthquake magnitudes and socio-economic studies about city sizes, currency exchange rate variations, and the success rate of Hollywood blockbusters, musicians, and scientists (31). For these applications, the stretched exponential is well justified by a wide range of decays or variations that underlie the same physical or socio-economic process.

Although diffusion is the common physical process in the present application, it is likely that physically distinct compartments, like intranuclear, intracellular, extracellular, and intravascular contribute to the nonmonoexponential diffusion signal decay. Here the monoexponential and biexponential models definitely fall short of fully characterizing the observed decay. The mean values for D_fast when b = 0 is included (see Table 3) come close to the value for free diffusion of water at 37°C, which is 3.0 μm²/ms. Although water molecules in the prostatic fluid of the luminal space probably have quite some freedom of movement, it seems unlikely that the tissue water diffusion of a voxel (representing multiple tissue components) is similar to free water diffusion, but that the observed diffusion is rather the result of including the very high-D intravascular compartment. The two continuous distributions exhibit sizable fractions at very high D-values, which may explain the inferior fitting for data sets excluding the signal measured at b = 0. For D-values higher than approximately 7 μm²/ms, the fraction size of the stretched exponential distribution exceeds the fraction size of the gamma distribution, which may explain the even lower fitting stability of the stretched exponential model, when the signal measured at b = 0 is excluded.

The stretched exponential with its extended tail of high diffusion coefficients is unlikely to realistically describe the observed intravascular component. Modified stretched exponential functions with a less pronounced distribution tail have been proposed (16,17). The gamma distribution seems to provide a good compromise with a continuous distribution that reasonably matches fraction sizes across distinct physical compartments. Given the number of distinct compartments and a certain exchange among them, a physically motivated model with at least three dissimilar diffusion coefficients and respective fractions would seem the most sensible fitting approach. That signal fraction sizes should not be interpreted as true compartment sizes, due to potential differences in T₂ relaxation and the possibility of exchange between compartments should be emphasized as one of many imaginable confounding details.

The present study demonstrates that a simplified IVIM analysis can provide an estimate of the intravascular compartment size, in addition to the size and diffusion coefficient of the fast and slow diffusion compartments. The VERDICT model (32) uses three compartments and, moreover, probes diffusion time dependence. However, VERDICT scan protocols require longer scan time and fixing of the intracellular and intravascular diffusion coefficients may be necessary to achieve fitting stability (32). The potential detrimental consequences of such parameter fixing have recently been spotlighted by Mulkern et al. (33). A major obstacle in fitting three compartments is the limited SNR; with the biexponential values reported in Table 2 it can be extrapolated that for b = 3500 s/mm² the signal in normal PZ decays to 3.1% of S₀. This requires high SNR that typically only can be achieved with endorectal coils. Fitting procedures that rely on ROI signal averaging to boost SNR (34) are likely to result in parameters heavily influenced by signal bias caused by the Rician noise distribution.

The analysis of the diffusion coefficient spectrum cannot be applied to the empirical kurtosis model, because such a spectrum does not exist. Inspection of the decay curve shown in Figure 2 nevertheless reveals the shortcomings of the model for the purpose of fitting, i.e., an inferior fit when the signal value at b = 0 is included and the implausible increase with b-factor of the signal at higher b-factors. With an even further extended-range of b-factors this might become a more limiting issue. On the other hand, a further extension of b-factors might help to reveal the existence of very slow diffusion compartments that the gamma distribution model is particularly well suited to account for (see Fig. 2).

An entirely different aspect of the model fits, which is not reflected in the AIC_c, is the suitability of the associated parameters to differentiate disease from normal tissue. For the present experimental setup, the kurtosis model, which proved to be inferior in terms of fitting the measured data, performs well, even without linear parameter combination. Also remarkable about this model, at least for the parameter ADC_K, is the robustness to inclusion or exclusion of b = 0. Noteworthy is the solid performance of the simple monoexponential model, particularly considering that it is based on a subset of the extended b-range data. The individual parameters of the biexponential and gamma distribution model have an inferior tissue differentiation performance. However, some of the linear parameter combinations bring back the tissue discrimination performance to levels observed in the kurtosis and mono-exponential model, although an easy clinical application obviously favors a single parameter discriminator over a linear combination. Furthermore, minor differences among the highest achievable AUCs among respective models cannot be considered significant. The absence of improvement for linear combinations with the kurtosis model is explained by the very high normalized covariance of the parameters (see Fig. 6). In general, the resulting improvement in discrimination power is significant, if the combined parameters exhibit low normalized covariance.

The observation that the physically motivated biexponential model results in the best AIC_C ranking, and thus more closely follows the signal decay measured over an extended b-factor range, begs an explanation in terms of the tissue microstructure, an explanation not as accessible with an empirical model. Toward this end, we observed that the fraction of the slow component appears to reflect low versus high Gleason score. However, future studies with larger number of tumors are needed to confirm this finding with statistical significance. For fixed tissue, it has been shown that luminal, epithelial and stromal components exhibit different diffusion properties (8) and their relative sizes change with Gleason score (35). Even if parameter maps from the simpler models with fewer fit parameters may perform equally well or even better for tissue discrimination, the biexponential model has, perhaps, a distinct advantage in that its slow fraction parameter may reflect and so provide an estimate of the degree of malignant invasion within a given voxel. This is a measurement that may be useful in determining the aggressiveness of the tumor and/or for monitoring patients during active surveillance protocols or for determining the effects and/or efficacies of sundry therapies available for treating prostate cancer patients.

The findings made in this study are also in line with other studies that compared the fitting of the biexponential model with the kurtosis, stretched exponential and monoexponential models (23,30). Quentin et al. (24), who for a low-b range of 0–800 s/mm² noted superior fitting of the biexponential and kurtosis model over the monoexponential model, also observed a strong performance of the monoexponential ADC for discrimination of normal prostate tissue from tumor.

The present study distinguishes between tumors originating in the PZ and tumors originating in the diagnostically more challenging TZ. All models investigated were able to differentiate tumors in each prostatic zone from its normal appearing counterpart. Previous studies did not distinguish the location of the tumors (24,27,28), or only studied TZ tumors (26). The present study establishes different optimal cutoff values for PZ and TZ. It should be emphasized, however, that optimal cutoff values strongly depend on the diffusion encoding times and b-factor range used, as already evident from the significant changes that some of the cutoff values undergo when b = 0 is excluded.

The current study has some limitations. Repeatability was not evaluated. Despite smooth muscle relaxant administration, low spatial resolution and short scan time, motion may have resulted in image registration errors. Due to ill-defined ROI boundaries on the low-resolution diffusion-weighted images and rather thick slices, partial-volume errors are likely. The ROIs were based on conspicuity of the prostate tissue on multiparametric MRI and were not based on whole-mount histopathology of prostatectomy samples. Whole-mount histopathology processing is not performed at our institution for routine prostatectomy cases. When interpreting prostate exams, DWI plays a major role in categorizing the suspiciousness of a lesion, especially in the PZ (4). Therefore, there might be a bias in this study toward lesions that are well delineated on ADC maps. This was also a reason to exclude the conventional diffusion scan data from the ANOVA and ROC analysis. The good discrimination between tissue types with several parameters might thus not be reproducible in a prospective setting. However, the main focus on this study was comparing different fitting models for extended-range b-factor diffusion-weighted data. It should be emphasized that model performance in terms of AIC and ROC also depends on the experimental setup, such as the setup of receiver coils, imaging parameters, and particularly b-factor range and diffusion encoding time. Finally, the number of TZ tumors in this study was limited (13 of 41 tumor suspicious lesions) and TZ tumors that are challenging to pick up by the radiologists on multiparametric MRI may have been missed due to the study design.

CONCLUSIONS

To conclude, this study in prostate cancer patients was able to obtain extended-range b-factor DWI data of good quality and sufficient SNR up to 3500 s/mm². Based on the resulting normalized χ² and AIC_C criterion, biexponential and gamma distribution models produce statistically preferred fits. However, though all evaluated models are equally capable of discriminating tumor from normal prostate tissue, some models require linear parameter combination to achieve full diagnostic performance. To the best of our knowledge this is the first paper that provides both an information-based (AIC) comparison of models together with a comparison of the cancer prediction performance of each model. The equally good tissue discrimination performance observed with the b-factor subrange 0–1250 s/mm², hints that for the diffusion time investigated here, signal averaging over that range may be preferable over sampling the entire range 0–3500 s/mm². Further experiments are needed to verify if one of the parameters with high AUC clearly outperforms other parameters in the prediction of Gleason score.