Three-part joint modeling methods for complex functional data mixed with zero-and-one inflated proportions and zero inflated continuous outcomes with skewness

Abstract

We take a functional data approach to longitudinal studies with complex bivariate outcomes. This work is motivated by data from a physical activity study that measured two responses over time in five-minute intervals. One response is the proportion of time active in each interval, a continuous proportions with excess zeros and ones. The other response, energy expenditure rate in the interval, is a continuous variable with excess zeros and skewness. This outcome is complex because there are three possible activity patterns in each interval (inactive, partially active and completely active), and those patterns, which are observed, induce both non-random and random associations between the responses. More specifically, the inactive pattern requires a zero value in both the proportion for active behavior and the energy expenditure rate; a partially active pattern means that the proportion of activity is strictly between zero and one and that the energy expenditure rate is greater than zero and likely to be moderate, and the completely active pattern means that the proportion active is exactly one, and the energy expenditure rate is greater than zero and likely to be higher. To address these challenges, we propose a three-part functional data joint modeling approach. The first part is a continuation-ratio model to reorder the ordinal valued three activity patterns. The second part models the proportions when they are in interval (0, 1). The last component specifies the skewed continuous energy expenditure rate with Box-Cox transformations when they are greater than zero. In this three-part model, the regression structures are specified as smooth curves measured at various time-points with random effects that have a correlation structure. The smoothed random curves for each variable are summarized using a few important principal components, and the association of the three longitudinal components is modeled through the association of the principal component scores. The difficulties in handling the ordinal and proportional variables are addressed using a quasilikelihood type approximation. We develop an efficient algorithm to fit the model which also involves the selection of the number of principal components. The method is applied to physical activity data and is evaluated empirically by a simulation study.

1. Introduction

Our methodology is motivated by data from Kozey-Keadle et al. [1] which used a body-worn device to record aspects of individuals’ physical activity over time. The study had 60 participants and each has 36 consecutive records that summarize physical activity information over five minute intervals. For each interval, the device used in the study recorded estimates of both the proportion of active behavior and the energy expenditure rate in the interval. The proportion ranges from zero to one. The energy expenditure rate is expressed in metabolic equivalent unites (METs), and we use METs−1.25 which is a non-negative continuous measurement. As illustrated in Table 1, there are three types of five minute intervals among all observations, approximately a third of each type. The energy expenditure rate for the inactive intervals is zero, and the energy expenditure rates are 0.42 and 1.19 for partially active and active intervals, respectively.

Table 1.

Summary for the our physical activity data structure. Displayed are the possible activity patterns for a five minute interval and the corresponding percentages among all observations. Proportion and EE rate are the value ranges for the proportion for active behavior and the energy expenditure rate, respectively.

Pattern	Proportion	EE Rate	Example
Inactive (37.6%)	0	0	Sitting/lying down for five minutes
Partially active (31.4%)	(0, 1)	(0, +∞)	Sitting for two minutes and walking for three minutes
Completely active (31.0%)	1	(0, +∞)	Walking for five minutes

Figure 1 shows more detail for the data from Kozey-Keadle et al. [1]. Panels (a) and (b) show the two factors over time from one individual. Panel (c) contains a histogram of the active time proportions across all subjects, and illustrates an excess of zeros (inactive intervals) and ones (completely active intervals). Panel (d) contains a histogram for the energy expenditure rate values. It shows that the continuous measurement also has repeated zero values of energy expenditure (inactive intervals), and other values that are skewed to the right. Panel (e) is a line chart for the percentages of inactive, partially active and completely active intervals in each time interval, respectively. Panels (f) and (g) are line charts for the average proportion of active behavior and energy expenditure rate in inactive, partially active and completely active intervals for each five minute interval, respectively.

Figure 1.

(a) Sample data from subject with ID 1 for the proportion of time spent in active behavior in each five-minute interval from minute −60 to 115. (b) Sample data from subject with ID 1 for energy expenditure rate (METs−1.25) in each five-minute interval from minute −60 to 115. See Section 5 for more explanation of the data. (c)(d) histograms for all of the observations in proportion and energy expenditure rate (METs−1.25), respectively. (e) Line chart for the percentages for inactive, partially active and completely active intervals. (f)(g) Line charts for the average proportion for active behavior and energy expenditure rate in inactive, partially active and completely active intervals, respectively. For (e)(f)(g), dotted line, thin solid line and thick solid line represent inactive, partially active and completely active intervals, respectively.

The proportion of active behavior and the energy expenditure rate give separate and related insights into both an individual’s physical activity pattern and how that expenditure changes over time. Consideration of both of these aspects of activity is important because the energy expenditure rate and how often a person is sedentary are both hypothesized to be related to health [2]. Therefore, the main purposes of this study are to develop functional data analysis methods to jointly model the two factors, and this involves a novel functional association structure that includes deterministic and random dependencies depending on the pattern of activity or inactivity in an interval. This has many potential uses for physical activity studies. In this manuscript, the association will facilitate efficient estimation of the energy expenditure rate for active behaviors, physical activity energy expenditure (PAEE). Additionally, as an illustration, we also require the intervals to include more than 2.5 minutes of activity. Statistically, that is a conditional expectation for the ratio of the energy expenditure rate divided by the proportion for active behavior given (a) the interval is partially or completely active, and (b) the proportion for active behavior is greater than 0.5. That conditional expectation could be directly estimated by using observations with active proportion greater than 0.5, but that method would lead to a critical loss of information because only 45.4% of the intervals meet the criterion.

Zero inflated data, zero-or-one inflated data, functional data, and random effects have all individually received a lot of attention in the literature, but, as far as we know, methodology does not exist to handle our problem where all occur simultaneously. Kipnis et al. [3] discuss a two-part model to address a zero inflated outcome, but the method cannot be directly applied in functional data analysis. Buu et al. [4] propose a zero-inflated Poisson model with functional forms in predictors, but the model uses two random intercepts to link variables, and that is too restrictive for our situation. Ospina and Ferrari [5] discuss a class of beta regression models for zero-or-one inflated continuous proportions. The use of a beta distribution combined with our functional data scenario and random effects could be computationally prohibitive [6]. For functional data studies, Hall et al. [7] proposed a functional model for non-Gaussian data, but this method does not cover the bivariate functional data case. Das and Daniels [8] discuss a simultaneous covariance estimation for bivariate outcomes. Huang et al. [9] study a joint modeling and clustering method to handle paired binary responses. Li et al. [10] propose a bivariate functional model mixed with a skewed continuous variable and a binary measurement. Ye et al. [11] discuss a jointly modeling framework for a functional data response and a time-to-event outcomes. Tidemann-Miller et al. [12] propose a multivariate mixed-response functional data model. Kowal et al. [13] study a multivariate functional dynamic linear model under a Bayesian framework. However, these models do not address the zero inflated aspect of our continuous response, and they are not compatible with the zero-or-one inflated proportional data.

To solve this problem, we develop a model that has three components. The model’s first component, which we note is based on observed data, is an ordinal variable to indicate if an observed interval is sedentary, partially active, or fully active. When the individual is partially active, the model’s second component specifies the proportion of active time in the interval. In addition, the third component has a non-negative continuous variable to reflect energy expenditure rate above resting when the interval contains at least some active time.

To model the ordinal response for the first component, we choose a continuation-ratio modeling based on the study from Molenberghs and Verbeke [14]. This method is computationally convenient because it avoids potential restrictions for the functional curves. For the second component with proportions, a quasilikelihood type approximation is employed, following the suggestions of Cox [15], which does not need to use a full distribution but only models for the first and second moments. Finally, the third component for the continuous variable assumes a normal distribution after Box-Cox transformation.

The model’s three components are possibly correlated within an individual at a given time point and over time. A simple approach would be to ignore the possible correlation and treat the three components independently. A slightly more complicated alternative method would be to use two random intercepts to link components [3, 4]. However, as we will show in the simulation studies, both approaches can lead to biased curve estimations. To build a more flexible model, we use functional random curves summarized by a few principal components, where possible correlation between the three components is induced by correlation across the principal component scores from each factor. This general approach has been discussed by Zhou et al. [16] and Li et al. [10]. We extend that methodology to our three component model framework.

The computational algorithm has to jointly estimate an ordinal component, a proportional component that is constrained to be between zero and one, and a non-negative skewed component. Perhaps somewhat surprisingly, these components can be well-approximated by the penalized quasilikelihood framework proposed by Breslow and Clayton [17]. The approximation takes nonlinear variables into “pseudo” normal responses, which can be seen as the classical model for longitudinal data analysis [18] and functional data analysis [e.g. 16]. Then we extend the methods discussed in Li et al. [10] to use a combination of Newton-Raphson and an EM procedure to obtain smoothed fixed and random effect curves. An eigen-decomposition step is included in the iterations to reduce the dimension and select important principal components for three components, respectively.

The remainder of the paper is organized as follows. Section 2 describes the three component model, and Section 3 describes the algorithm to fit the model. A simulation study is discussed in Section 4. Section 5 contains an analysis of the physical activity data, and conclusions are in Section 6.

2. Model

Let {P_i(t), Y_i(t)} be the observed proportion and continuous measurement for time interval t and subject i = 1, …, n, and let t_ij for j = 1, …, m_i be the observation times. The observed ordinal component is C_i(t) where C_i(t) ∈ {1, 2, 3}, which represent inactive, partially active, and completely active intervals respectively. Note that P_i(t) = 0 when C_i(t) = 1, 0 < P_i(t) < 1 when C_i(t) = 2, and P_i(t) = 1 when C_i(t) = 3. Moreover, Y_i(t) = 0 when C_i(t) = 1, and Y_i(t) > 0 otherwise. We develop a model for the functional pattern of the three components {C_i(t), P_i(t), Y_i(t)} next in Section 2.1.

2.1. The Three Component Model

2.1.1. The Model for Category C_i(t)

We use the continuation-ratio model suggested by Molenberghs and Verbeke [14] to model the ordinal outcomes C_i(t). Letting H(·) denote the logistic distribution function, the functional model for C_i(t) is

$$\text{pr}\{C_i(t)>\ell |C_i(t)\ge \ell ,{\mathbf{U}}_{C_{\ell },i}(t)\}=H\{{\mu }_{C_{\ell }}(t)+{\mathbf{U}}_{C_{\ell },i}(t)\},\ell =1,2,$$ (1)

where μ_Cℓ(t) and U_Cℓ,i(t) are fixed and random curves, respectively. The model in (1) has two levels. When ℓ = 1, it is the unconditional probability that the interval is at least partially active. When ℓ = 2, it is the probability that time interval t is completely active given that the interval is at least partially active.

Remark 1

The most important reason to use continuation-ratio model is that it allows the functional curves μ_C1(t) + U_C1,i(t) and μ_C2(t) + U_C2,i(t) to be estimated without restrictions. Molenberghs and Verbeke [14] also suggest a proportional odds logistic regression model, pr{C_i(t) ≤ ℓ|U_Cℓ,i(t)} = H{μ_Cℓ(t) + U_Cℓ,i(t)} (ℓ = 1, 2). A drawback of that approach though is that it would require μ_C1 (t) + U_C1,i(t) ≤ μ_C2(t) + U_C2,i(t) for all t which would complicate estimation.

The continuation-ratio model in (1) can be formulated equivalently using two binary responses, $C_i^{(\ell )}(t)$ (ℓ = 1, 2) where

$$\text{pr}\{C_i^{(1)}(t)=1|{\mathbf{U}}_{C_{\ell },i}(t)\}=\text{pr}\{C_i(t)>1|{\mathbf{U}}_{C_{\ell },i}(t)\}\text{ and }\text{pr}\{C_i^{(2)}(t)=1|C_i^{(1)}(t)=1,{\mathbf{U}}_{C_{\ell },i}(t)\}=\text{pr}\{C_i(t)>2|C_i(t)\ge 2,{\mathbf{U}}_{C_{\ell },i}(t)\}.$$ (2)

We will use the notation of $C_i^{(\ell )}(t)$ in the following discussions. Unless otherwise specified, ℓ has ℓ = 1, 2 in our manuscript.

2.1.2. The Model for Proportion P_i(t)

For the modeling of continuous proportions, we use the Beta regression suggested in Ferrari and Cribari-Neto [19]. According to our model, P_i(t) ∈ (0, 1) if $C_i^{(1)}(t)=1$ and $C_i^{(2)}(t)=0$. Thus, given $C_i^{(1)}(t)=1$ and $C_i^{(2)}(t)=0$, we model the density function for P_i(t) by

$$\frac{\mathrm{\Gamma }(\varphi )}{\mathrm{\Gamma }\{{\kappa }_i(t)\varphi \}\mathrm{\Gamma }[\{1-{\kappa }_i(t)\}\varphi ]}{\{P_i(t)\}}^{{\kappa }_i(t)\varphi -1}{\{1-P_i(t)\}}^{\{1-{\kappa }_i(t)\}\varphi -1},$$

where Γ(·) is the gamma function, κ_i(t) represents the mean curve $E\{P_i(t)|C_i^{(1)}(t)=1,C_i^{(2)}(t)=0,{\mathbf{U}}_{P,i}(t)\}$, and we reparameterize ϕ into ${\sigma }_P^2=1/(1+\varphi )$ for ease of computation. Based on the Beta regression model, we have $\text{var}\{P_i(t)|C_i^{(1)}(t)=1,C_i^{(2)}(t)=0,{\mathbf{U}}_{P,i}(t)\}={\sigma }_P^2{\kappa }_i(t)\{1-{\kappa }_i(t)\}$ and further postulate the mean curve by

$${\kappa }_i(t)=E\{P_i(t)|C_i^{(1)}(t)=1,C_i^{(2)}(t)=0,{\mathbf{U}}_{P,i}(t)\}=H\{{\mu }_P(t)+{\mathbf{U}}_{P,i}(t)\},$$ (3)

where μ_P(t) and U_P,i(t) are fixed and random curves, respectively. The mean function of P_i(t) has 0 < E{P_i(t)|U_P,i(t)} < 1, which is appropriate for the continuous proportions.

2.1.3. The Model for Continuous Variable Y_i(t)

Let d_tr(·; λ) be the Box-Cox transformation function with transformation parameter λ. According to the definition, Y_i(t) > 0 if $C_i^{(1)}(t)=1$. Therefore, we specify the functional model for Y_i(t) as

$$d_{\text{tr}}\{Y_i(t)|C_i^{(1)}(t)=1,C_i^{(2)}(t),{\mathbf{U}}_{Y,i}(t);\lambda \}={\mu }_{Y_1}(t)+I\{C_i^{(2)}(t)=1\}{\mu }_{Y_2}(t)+{\mathbf{U}}_{Y,i}(t)+{\epsilon }_{Y,i}(t),$$ (4)

where μ_Y1(t) and μ_Y2(t) are fixed effect curves, U_Y,i(t) is random effect curve, and ε_Y,i(t) denotes random noise with mean zero and variance ${\sigma }_Y^2$.

Equations (2)–(4) combine to build a three component model for $C_i^{(\ell )}(t)$, P_i(t) given $C_i^{(\ell )}(t)$, and Y_i(t) given $C_i^{(\ell )}(t)$ where the functionally fixed curves are respectively μ_Cℓ(t), μ_P(t) and μ_Yℓ(t), and the functionally random curves are U_Cℓ,i(t), U_P,i(t) and U_Y,i(t). We allow U_Cℓ,i(t), U_P,i(t) and U_Y,i(t) to be correlated and further assume that, given the random effects curves, the three components are independent. Thus, the correlation structures between the three components are determined by the correlations between the three random curves.

2.2. Reduced Rank Model

We employ a set of smooth basis functions to represent the fixed effect functions {μ_Cℓ(t), μ_P(t), μ_Yℓ(t)} and the random effect functions {U_Cℓ,i(t), U_P,i(t), U_Y,i(t)}. Let b(t) = {b₁(t), …, b_q(t)}^T be a vector of orthogonal B-spline basis functions evaluated at t, which can be computed using an exact approach found in the R package “orthogonalsplinebasis” [20, 21]. This means that ∫ b(t)b^T(t) dt = I_q, where I_q is the q × q identity matrix. In this approach, and similar to Zhou et al. [16] and Li et al. [10], we summarize the fixed effects by

$${\mu }_{C_{\ell }}(t)=b^{\mathrm{T}}(t){\beta }_{C_{\ell }};{\mu }_P(t)=b^{\mathrm{T}}(t){\beta }_P;{\mu }_{Y_{\ell }}(t)=b^{\mathrm{T}}(t){\beta }_{Y_{\ell }},$$

where β_Cℓ, β_P and β_Yℓ are q × 1 regression coefficients.

We summarize the random effects by a few important principal components as

$${\mathbf{U}}_{C_{\ell },i}(t)={\sum }_{s=1}^{k_{C_{\ell }}}{f}_{C_{\ell },s}(t){\alpha }_{C_{\ell },i,s};{\mathbf{U}}_{P,i}(t)={\sum }_{s=1}^{k_P}{f}_{P,s}(t){\alpha }_{P,i,s};{\mathbf{U}}_{Y,i}(t)={\sum }_{s=1}^{k_Y}{f}_{Y,s}(t){\alpha }_{Y,i,s},$$ (5)

where f_Cℓ,s(t), f_P,s(t) and f_Y,s(t) are orthogonal principal component functions with constraints ∫ f_Cℓ,s(t) f_Cℓ,s*(t) dt = ∫ f_P,s(t) f_P,s*(t) dt = ∫ f_Y,s(t) f_Y,s*(t) dt = I(s = s*), with I(·) denoting an indicator function. (α_Cℓ,i,1, …, α_Cℓ,i,kCℓ), (α_P,i,1, …, α_P,i,kP) and (α_Y,i,1, …, α_Y,i,kY) are principal component scores. We require the principal component scores to follow var(α_Cℓ,i,1) > ⋯ > var(α_Cℓ,i,kCℓ) and α_Cℓ,i,s to be independent across s. Similarly, let var(α_P,i,1) > ⋯ > var(α_P,i,kP) and α_P,i,s be independent across s, and let var(α_Y,i,1) > ⋯ > var(α_Y,i,kY) and α_Y,i,s be independent across s. The inequalities are for identifiability.

We further summarize the principal component functions by orthogonal B-spline basis functions as

$$f_{C_{\ell },s}(t)=b^{\mathrm{T}}(t){\theta }_{C_{\ell },s};f_{P,s}(t)=b^{\mathrm{T}}(t){\theta }_{P,s};f_{Y,s}(t)=b^{\mathrm{T}}(t){\theta }_{Y,s},$$

where θ_Cℓ,s, θ_P,s and θ_Y,s are q × 1 principal components vectors subject to the orthogonality constraints, respectively.

Denote Θ_Cℓ = (θ_Cℓ,1, …, θ_Cℓ,kCℓ), Θ_P = (θ_P,1, …, θ_P,kP) and Θ_Y = (θ_Y,1, …, θ_Y,kY). Thus, Θ_Cℓ, Θ_P and Θ_Y are q × k_Cℓ, q × k_P and q × k_Y principal components matrices subject to the orthogonality constraints. Let α_Cℓ,i = (α_Cℓ,i,1, …, α_Cℓ,i,kCℓ)^T, α_P,i = (α_P,i,1, …, α_P,i,kP)^T and α_Y,i = (α_Y,i,1, …, α_Y,i,kY)^T be k_Cℓ × 1, k_P × 1 and k_Y × 1 principal component scores, respectively. The random effect curves U_Cℓ,i(t), U_P,i(t) and U_Y,i(t) can be written as

$${\mathbf{U}}_{C_{\ell },i}(t)=b^{\mathrm{T}}(t){\mathrm{\Theta }}_{C_{\ell }}{\alpha }_{C_{\ell },i};{\mathbf{U}}_{P,i}(t)=b^{\mathrm{T}}(t){\mathrm{\Theta }}_{P\alpha P,i};{\mathbf{U}}_{Y,i}(t)=b^{\mathrm{T}}(t){\mathrm{\Theta }}_Y{\alpha }_{Y,i}.$$

The models (2)–(4) are thus

$$\text{pr}\{C_i^{(1)}(t)=1|{\mathbf{U}}_{C_1,i}(t)\}=H\{b^{\mathrm{T}}(t){\beta }_{C_1}+b^{\mathrm{T}}(t){\mathrm{\Theta }}_{C_1}{\alpha }_{C_1,i}\},\text{ and }\text{pr}\{C_i^{(2)}(t)=1|C_i^{(1)}(t)=1,{\mathbf{U}}_{C_2,i}(t)\}=H\{b^{\mathrm{T}}(t){\beta }_{C_2}+b^{\mathrm{T}}(t){\mathrm{\Theta }}_{C_2}{\alpha }_{C_2,i}\}$$ (6)

$$E\{P_i(t)|C_i^{(1)}(t)=1,C_i^{(2)}(t)=0,{\mathbf{U}}_{P,i}(t)\}=H\{b^{\mathrm{T}}(t){\beta }_P+b^{\mathrm{T}}(t){\mathrm{\Theta }}_P{\alpha }_{P,i}\},$$ (7)

$$d_{\text{tr}}\{Y_i(t)|C_i^{(1)}(t)=1,C_i^{(2)}(t),{\mathbf{U}}_{Y,i}(t);\mathrm{\lambda }\}=b^{\mathrm{T}}(t){\beta }_{Y_1}+I\{C_i^{(2)}(t)=1\}{b}^{\mathrm{T}}(t){\beta }_{Y_2}+b^{\mathrm{T}}(t){\mathrm{\Theta }}_Y{\alpha }_{Y,i}+{\epsilon }_{Y,i}(t).$$ (8)

We denote the covariances of α_Cℓ,i, α_P,i and α_Y,i as Δ_CℓCℓ, Δ_PP and Δ_YY. Since the principal component scores for each outcome are assumed to be mutually independent, the covariance matrices are diagonal matrices with the variances of the corresponding principal component scores sorted in decreasing order along their diagonals.

In addition, we combine the vector of principal component scores for subject i in ${\alpha }_i={({\alpha }_{C_1,i}^{\mathrm{T}},{\alpha }_{C_2,i}^{\mathrm{T}},{\alpha }_{P,i}^{\mathrm{T}},{\alpha }_{Y,i}^{\mathrm{T}})}^{\mathrm{T}}=\text{Normal}(0,\mathrm{\Delta })$. The $({\sum }_{\ell =1}^2{k}_{C_{\ell }}+k_P+k_Y)\times ({\sum }_{\ell =1}^2{k}_{C_{\ell }}+k_P+k_Y)$ covariance matrix Δ for α_i includes block diagonal elements Δ_CℓCℓ, Δ_PP and Δ_YY, and off-diagonal elements Δ_C1C2, Δ_CP, Δ_CY, and Δ_PY.

Remark 2

We also consider two simplified models for the random effect curves U_Cℓ,i(t), U_P,i(t) and U_Y,i(t). The first approach specifies them as random-intercepts [4]

$${\mathbf{U}}_{C_{\ell },i}(t)=u_{C_{\ell },i};{\mathbf{U}}_{P,i}(t)=u_{P,i}\text{ and }{\mathbf{U}}_{Y,i}(t)=u_{Y,i},$$

where u_Cℓ,i, u_P,i and u_Y,i are scalar random effects. The second approach follows our random effect curve framework with principal components, but it assumes that U_Cℓ,i(t), U_P,i(t) and U_Y,i(t) are independent, which implies Δ_C1C2, Δ_CP, Δ_CY and Δ_PY are matrices of zeros. We show in the simulation study that both methods can lead to biased results.

The models described in equations (6)–(8) involve the following parameters: the Box-Cox transformation parameter λ; the B-spline coefficients for the fixed effects β_Cℓ, β_P and β_Yℓ; the dispersion parameters ${\sigma }_P^2$ and ${\sigma }_Y^2$; the number of principal components: k_Cℓ, k_P, and k_Y; the B-spline coefficients for principal component functions Θ_Cℓ, Θ_P and Θ_Y; and the principal component scores’ covariance matrix Δ.

2.3. Linear Approximation

Parameter estimation for (6)–(8) is difficult since the three components are non-linear functions of variables of different types. One approach to this problem is to linearly approximate using the penalized quasilikelihood framework proposed by Breslow and Clayton [17] and further improved by Goldstein and Rasbash [22] who used a quadratic Taylor expansion for non-linear responses. Since H(·) is logistic distribution function, the first and second derivative of H(·) are H′(·) = H(·){1 − H(·)}, and H″(·) = {1 − 2H(·)}H′(·).

Given known values of (β̂_Cℓ, Θ̂_Cℓ, α̂_Cℓ,i), we approximate the ordinal factors as

$$C_i^{\ast (\ell )}(t)=[1/H\prime \{{\hat{\eta }}_{C_{\ell },i}(t)\}][C_i^{(\ell )}(t)-H\{{\hat{\eta }}_{C_{\ell },i}(t)\}]+{\hat{\eta }}_{C_{\ell },i}(t)-[1/2H\prime \{{\hat{\eta }}_{C_{\ell },i}(t)\}]H″\{{\hat{\eta }}_{C_{\ell },i}(t)\}\{b^{\mathrm{T}}(t){\hat{\mathrm{\Theta }}}_{C_{\ell }}\widehat{\text{var}}({\alpha }_{C_{\ell },i}-{\hat{\alpha }}_{C_{\ell },i}){\hat{\mathrm{\Theta }}}_{C_{\ell }}^{\mathrm{T}}b(t)\}\approx b^{\mathrm{T}}(t){\beta }_{C_{\ell }}+b^{\mathrm{T}}(t){\mathrm{\Theta }}_{C_{\ell }}{\alpha }_{C_{\ell },i}+{\epsilon }_{C_{\ell },i}(t),\text{ given }{C}_i^{(1)}(t)=1\text{ for }\ell =2,$$ (9)

where η̂_Cℓ,i(t) = b^T(t)β̂_Cℓ + b^T(t)Θ̂_Cℓα̂_Cℓ,i and ε_Cℓ,i(t) = Normal[0, 1/H′{η̂_Cℓ,i(t)}].

Similarly, given known values of (β̂_P, Θ̂_P, α̂_P,i), we approximate P_i(t) as

$$P_i^{\ast }(t)=[1/H\prime \{{\hat{\eta }}_{P,i}(t)\}][P_i(t)-H\{{\hat{\eta }}_{P,i}(t)\}]+{\hat{\eta }}_{P,i}(t)-[1/2H\prime \{{\hat{\eta }}_{P,i}(t)\}]H″\{{\hat{\eta }}_{P,i}(t)\}\{b^{\mathrm{T}}(t){\hat{\mathrm{\Theta }}}_P\widehat{\text{var}}({\alpha }_{P,i}-{\hat{\alpha }}_{P,i}){\hat{\mathrm{\Theta }}}_P^{\mathrm{T}}b(t)\}\approx b^{\mathrm{T}}(t){\beta }_P+b^{\mathrm{T}}(t){\mathrm{\Theta }}_P{\alpha }_{P,i}+{\epsilon }_{P,i}(t),\text{ given }{C}_i^{(1)}(t)=1,C_i^{(2)}(t)=0,$$ (10)

where η̂_P,i(t) = b^T(t)β̂_P + b^T(t)Θ̂_Pα̂_P,i and ${\epsilon }_{P,i}(t)=\text{Normal}[0,{\sigma }_P^2/H\prime \{{\hat{\eta }}_{P,i}(t)\}]$.

Finally, if we denote $Y_i^{\ast }(t)=d_{\text{tr}}\{Y_i(t);\lambda \}$, equation (8) becomes

$$Y_i^{\ast }(t)=b^{\mathrm{T}}(t){\beta }_{Y_1}+I\{C_i^{(2)}(t)=1\}{b}^{\mathrm{T}}(t){\beta }_{Y_2}+b^{\mathrm{T}}(t){\mathrm{\Theta }}_Y{\alpha }_{Y,i}+{\epsilon }_{Y,i}(t),\text{ given }{C}_i^{(1)}(t)=1.$$ (11)

Equations (9)–(11) show that the binary response $C_i^{(\ell )}(t)$, proportional response P_i(t) can be approximately transformed into normally distributed $C_i^{\ast (\ell )}(t)$ and $P_i^{\ast }(t)$. Moreover, the Box-Cox transformed continuous variable $Y_i^{\ast }(t)$ has a normal distribution too. Therefore, the three component model with different types of responses can be unified into an approximately joint normal model which facilitates estimation of model’s parameters.

3. Model Estimation Procedure

3.1. Link to the Linear Mixed Effects Model

If we rewrite the principal component part of the reduced rank model as γ_Cℓ,i = Θ_Cℓα_Cℓ,i, γ_P,i = Θ_Pα_P,i and γ_Y,i = Θ_Yα_Y,i. The models in (9)–(11) become

$$C_i^{\ast (\ell )}(t)=b^{\mathrm{T}}(t){\beta }_{C_{\ell }}+b^{\mathrm{T}}(t){\gamma }_{C_{\ell },i}+{\epsilon }_{C_{\ell },i}(t),\text{ given }{C}_i^{(1)}(t)=1\text{ for }\ell =2;$$ (12)

$$P_i^{\ast }(t)=b^{\mathrm{T}}(t){\beta }_P+b^{\mathrm{T}}(t){\gamma }_{P,i}+{\epsilon }_{P,i}(t)\text{ given }{C}_i^{(1)}(t)=1,C_i^{(2)}(t)=0;$$ (13)

$$Y_i^{\ast }(t)=b^{\mathrm{T}}(t){\beta }_{Y_1}+I\{C_i^{(2)}(t)=1\}{b}^{\mathrm{T}}(t){\beta }_{Y_2}+b^{\mathrm{T}}(t){\gamma }_{Y,i}+{\epsilon }_{Y,i}(t)\text{ given }{C}_i^{(1)}(t)=1.$$ (14)

Equations (12)–(14) share identical formulations as commonly used multivariate linear mixed effect model [18]. Based on this similarity, we build our estimation algorithm on an ECME model fitting framework [23] with necessary extensions to address our entire model.

For ease of model estimation, we define random effect vector ${\gamma }_i={({\gamma }_{C_1,i}^{\mathrm{T}},{\gamma }_{C_2,i}^{\mathrm{T}},{\gamma }_{P,i}^{\mathrm{T}},{\gamma }_{Y,i}^{\mathrm{T}})}^{\mathrm{T}}$ and the corresponding covariance structure as Ψ = cov(γ_i). Although the random effect γ_i and its covariance matrix Ψ are not the model parameters to be estimated in Section 2.2, they play important intermediate roles in our estimation procedure. Firstly, the ECME procedure easily provides estimates of γ_i and Ψ, which is convenient for computation. Furthermore, based on the estimates of Ψ, the parameters in our principal components can be easily derived. For example, for the diagonal block matrices in Ψ, we have ${\mathrm{\Psi }}_{C_{\ell }{C}_{\ell }}=\text{var}({\gamma }_{C_{\ell },i})={\mathrm{\Theta }}_{C_{\ell }}{\mathrm{\Delta }}_{C_{\ell }{C}_{\ell }}{\mathrm{\Theta }}_{C_{\ell }}^T,{\mathrm{\Psi }}_{\mathit{\text{PP}}}=\text{var}({\gamma }_{P,i})={\mathrm{\Theta }}_P{\mathrm{\Delta }}_{\mathit{\text{PP}}}{\mathrm{\Theta }}_P^T$, and ${\mathrm{\Psi }}_{\mathit{\text{YY}}}=\text{var}({\gamma }_{Y,i})={\mathrm{\Theta }}_Y{\mathrm{\Delta }}_{\mathit{\text{YY}}}{\mathrm{\Theta }}_Y^T$. Similar equations link the off-diagonal block matrices in Ψ with the off-diagonal elements of Δ.

3.2. Additional Implementation Details

Based on suggestions from Ruppert [24] and Zhou et al. [25], degree two or three splines with 10 to 20 knots are commonly sufficient to fit many datasets adequately. Therefore, we use a cubic orthogonal B-spline basis function with 10 equally spaced knots in our simulation study and data application, which yields satisfactory results.

We set the initial numbers of principal components to be k_Cℓ = k_P = k_Y = q. Our methods also requires initial values for parameters λ, β_Cℓ, β_P, β_Yℓ, ${\sigma }_P^2,{\sigma }_Y^2$, Ψ and γ̂_i. To be specific, λ is selected based on the profile log likelihoods in the Box-Cox power transformation by assuming non-zero continuous independent observations without random effects. Our selection for λ is implemented by the “boxcox” function in the R package “MASS” [26, 21]. β_Cℓ and β_P are obtained from a generalized linear models fit without random effects. β_Yℓ and ${\sigma }_Y^2$ are obtained from a linear model fit without random effects with a Box-Cox transformation using the initial λ applied to the responses. We also set ${\sigma }_P^2$ to be 0.01. Following the discussion in Breslow and Clayton [17], all elements in γ̂_i are specified to be 0 as starting values, and we set the diagonal elements in the covariance matrix Ψ to be 0.1 and off-diagonal elements to be 0.

The iteration procedure first updates λ, β_Cℓ, β_P, β_Yℓ, ${\sigma }_P^2$ and ${\sigma }_Y^2$ with Newton-Raphson. The second step updates Ψ using an EM method. The third step then updates k_Cℓ, k_P, k_Y, Θ_Cℓ, Θ_P, Θ_Y and Δ with an eigen-decomposition of Ψ. For computational stability, the Steps 1 and 2 are set to loop five times, and then the three steps are iterated until convergence. It can be seen that this is an ECME procedure which iteratively uses Newton-Raphson and EM method. As such, its general convergence properties are discussed in Liu and Rubin [27]. The details of Steps 1 to 3 are described in the Online Supplementary Material.

Remark 3

A feature of our proposed algorithm is that, the numbers of principal components k_Cℓ, k_P and k_Y are automatically updated during the iteration procedure. When the algorithm converges, the numbers of principal components are also selected. Therefore, the algorithm avoids a four-dimensional grid searching problem, which improves computational efficiency.

3.3. Maximum Penalized Likelihood

The previous discussion focused on the modeling of the response variables using basis functions. It is necessary however, to introduce roughness penalties to regularize the fits of functions [28]. Let θ_Cℓ,j, θ_P,j and θ_Y,j denote the j^th columns of Θ_Cℓ, Θ_P and Θ_Y, respectively.

We use penalized maximum likelihood for parameter estimation and maximize

$${ℒ}_{\mathit{\text{pen}}}=ℒ-{\tau }_{\beta }({\sum }_{\ell =1}^2{\beta }_{C_{\ell }}^{\mathrm{T}}D{\beta }_{C_{\ell }}+{\beta }_P^{\mathrm{T}}D{\beta }_P+{\sum }_{\ell =1}^2{\beta }_{Y_{\ell }}^{\mathrm{T}}D{\beta }_{Y_{\ell }})-{\tau }_{\theta }({\sum }_{\ell =1}^2{\sum }_{s=1}^{k_{C_{\ell }}}{\theta }_{C_{\ell },s}^{\mathrm{T}}D{\theta }_{C_{\ell },s}+{\sum }_{s=1}^{k_P}{\theta }_{P,s}^{\mathrm{T}}D{\theta }_{P,s}+{\sum }_{s=1}^{k_Y}{\theta }_{Y,s}^{\mathrm{T}}D{\theta }_{Y,s}),$$ (15)

where ℒ is defined in Online Supplementary Material, τ_β and τ_θ are penalty parameters, and the penalty matrix is D = ∫ b″(t)b″(t)^T dt. The penalty parameters are selected using a grid search from candidate sets with a five-fold cross-validation approach and profile likelihood as discussed in Lee and Phillips [29]. Using maximum penalized likelihood requires a slight modification of the algorithms described in Section 3.2. We describe this modification in detail in Online Supplementary Material.

4. Simulation Studies

We use a simulation experiment with 500 runs to assess the performance of our method. This Monte Carlo sample size was sufficient to discern differences between our proposed methods and other approaches. Following identical settings in our application data, let n = 60 subjects and each subject have 36 equally spaced visits, t_ij = j, j = 1, …, 36. At visit time t, subject i has observations {C_i(t), P_i(t), Y_i(t)} corresponding to the model described in Section 2. Follow the identical settings as in Section 2, we set the ordinal categories C_i(t) ∈ {1, 2, 3}, which leads to two binary variables $C_i^{(\ell )}(t)$ (ℓ = 1, 2). Using functions that are generally similar to what we expected to see in our application, they are generated by

$$\text{pr}\{C_i^{(1)}(t)=1|{\mathbf{U}}_{C_1,i}(t)\}=H\{{\mu }_{C_1}(t)+f_{C_1,1}(t){\alpha }_{C_1,i,1}\};$$

$$\text{pr}\{C_i^{(2)}(t)=1|{\mathbf{U}}_{C_2,i}(t)\}=H\{{\mu }_{C_2}(t)+f_{C_2,1}(t){\alpha }_{C_2,i,1}\}\text{ given }{\mathrm{C}}_{\mathrm{i}}^{(1)}(\mathrm{t})=1,$$

where μ_C1(t) = exp(t/4 − 4)/{1 + exp(t/4 − 4)} + 0.5, μ_C2(t) = −0.5 − exp(t/4 − 4)/{1 + exp(t/4 − 4)}, $f_{C_1,1}(t)=\text{sin}\{2\pi (t-1)/35\}/\sqrt{17.5},f_{C_2,1}(t)=\text{cos}\{2\pi (t-1)/35\}/\sqrt{17.5}$, and Δ_C1C1 = var(α_C1,i,1) = Δ_C2C2 = var(α_C2,i,1) = 12.

Given $C_i^{(1)}(t)=1$ and $C_i^{(2)}(t)=0$, the continuous proportions are generated from the beta distribution described in Section 2.1.2. In particular, the mean curve function in (3) is specified as

$${\kappa }_i(t)=E\{P_i(t)|C_i^{(1)}(t)=1,C_i^{(2)}(t)=0,{\mathbf{U}}_{P,i}(t)\}=H\{{\mu }_P(t)+f_{P,1}(t){\alpha }_{P,i,1}+f_{P,2}(t){\alpha }_{P,i,2}\},$$

where ${\mu }_P(t)=\{(t-1)/35-1\}/\sqrt{35/3},f_{P,1}(t)=\text{sin}\{4\pi (t-1)/35\}/\sqrt{17.5},f_{P,2}(t)=\text{cos}\{4\pi (t-1)/35\}/\sqrt{17.5}$. We further set Δ_PP,1 = var(α_P,i,1) = 12, Δ_PP,2 = var(α_P,i,2) = 6 and ${\sigma }_P^2=1/30$.

Given $C_i^{(1)}(t)=1$, we generate the skewed continuous outcome with function conditional on U_Y,i(t) as

$$d_{\text{tr}}\{Y_i(t)|{\mathbf{U}}_{Y,i}(t);\mathrm{\lambda }\}={\mu }_{Y_1}(t)+I\{C_i^{(2)}(t)=1\}{\mu }_{Y_2}(t)+f_{Y,1}(t){\alpha }_{Y,i,1}+f_{Y,2}(t){\alpha }_{Y,i,2}+{\epsilon }_{Y,i},$$

where μ_Y1(t) = 4 + t/100 + exp{−(t − 18)²/100}, μ_Y2(t) = 0.5, $f_{Y,1}(t)=\text{sin}\{2\pi (t-1)/35\}/\sqrt{17.5},f_{Y,2}(t)=\text{cos}\{2\pi (t-1)/35\}/\sqrt{17.5}$, Δ_YY,1 = var(α_Y,i,1) = 12, Δ_YY,2 = var(α_Y,i,2) = 6, λ = 0.5 and ${\epsilon }_{Y,i}=\text{Normal}(0,{\sigma }_Y^2)$ with ${\sigma }_Y^2=0.25$.

For a comparison to our method, two naive approaches are explored as discussed in Remark 2. The first approach (labeled as NAIVE1) uses a random-intercept model for U_Cℓ,i(t), U_P,i(t) and U_Y,i(t). The second method (labeled as NAIVE2) follows our principal component framework, but it ignores the association across the three responses by assuming that the three random effect curves are independent.

In Section 1 we said that estimation for energy expenditure rate for active behaviors (PAEE) is one of our research interests. As we will discuss in Section 5, estimation of PAEE is equivalent to estimation of the conditional expectation $E\{Y_i(t)/P_i(t)|C_i^{(1)}=1,P_i(t)>0.5\}$. In this simulation study, our proposed method and two naive methods are used to fit simulated data. Based on the estimates, the conditional expectation is calculated by averaging the outcomes from 500,000 Monte Carlo samples, which yielded acceptable precision.

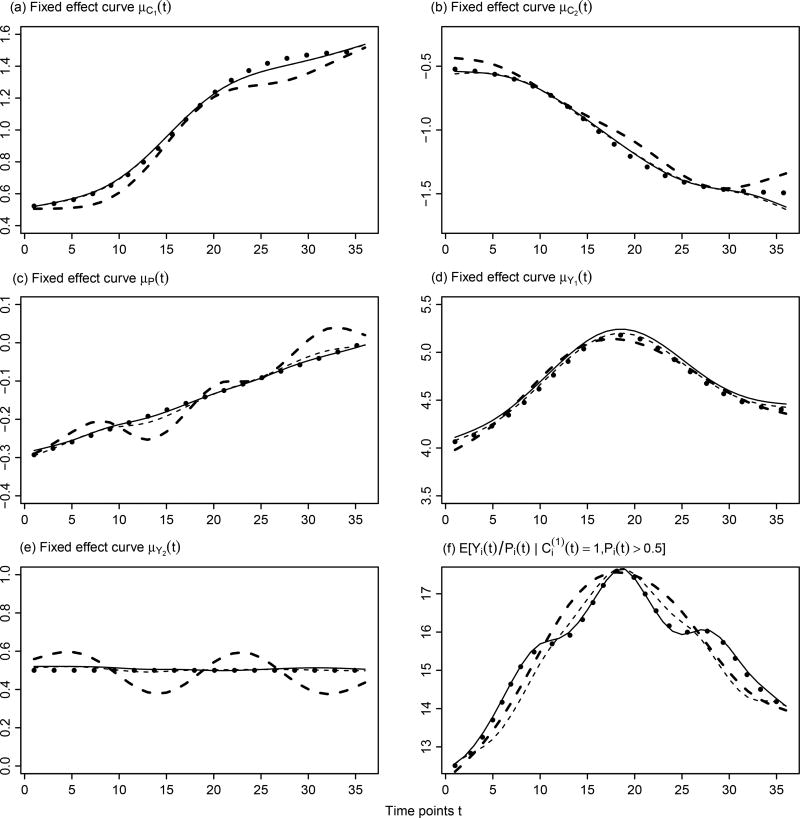
Figures 2(a)–(e) display the true fixed curves, and the average estimates of the three methods. They indicate that NAIVE1 approach lead to biased outcomes for μ_Cℓ(t), μ_P(t) and μ_Yℓ(t). Figure 2(f) presents the true and estimated curves for $E\{Y_i(t)/P_i(t)|C_i^{(1)}=1,P_i(t)>0.5\}$, and there are obvious biases for both NAIVE1 and NAIVE2 methods. On the other hand, our proposed approach has relatively small bias for all curves. Figures 3(a)–(f) represent the performance of our approach in principal component curves. Our method generally leads to correct patterns for all true curves.

Figure 2.

Fitted fixed effects curves and average curves for 500 simulated data sets: (a) fixed effects curve of μ_C1(t), (b) fixed effects curve of μ_C2(t), (c) fixed effects curve of μ_P(t), (d) fixed effects curve of μ_Y1(t), (e) fixed effects curve of μ_Y2(t), (f) average curve for $E\{Y_i(t)/P_i(t)|C_i^{(1)}=1,P_i(t)>0.5\}$. Dotted lines denote the true curves. Solid lines represent the average values of the fitted curves from our proposed method. Thick dashed and thin dashed lines represent the average fitted curves by NAIVE1 and NAIVE2 methods, respectively.

Figure 3.

Fitted principal component curves for 500 simulated data sets: (a) principal component curve f_C1,1(t); (b) principal component curve f_C2,1(t); (c)(d) principal component curves for f_P,1 and f_P,2(t), respectively; (e)(f) principal component curves for f_Y,1 and f_Y,2(t), respectively. Dotted lines denote the true curves. Solid lines represent the averaged values of the fitted curves from our proposed method. The upper and lower dashed lines are the 10% and 90% quantiles of the fitted values over the 500 simulated data sets.

Let f(t) be a true curve and let f̂_r(t) be the estimated curve evaluated at time t for simulation run r. We define the mean square error (MSE) for the estimation of f(t) as ${\sum }_{r=1}^{500}{\sum }_{t=1}^{36}{\{{\hat{f}}_r(t)-f(t)\}}^2/500$. Table 2 displays the MSE for our proposed method as well as NAIVE1 and NAIVE2 methods. It indicates that the proposed approach has smallest MSE in the three methods among all estimated curves. The NAIVE1 method has largest MSE in three approaches, which is caused by biased estimates. The NAIVE2 method has comparable MSE with our proposed method in the estimates of the fixed effect curves, but it leads to a larger MSE for the estimate of the conditional expectation.

Table 2.

Simulation results for mean square errors (MSE) defined in Section 4. Displayed are the MSE obtained from our proposed method (labeled as Propose), the approach using random-intercept model (labeled as NAIVE1) and the method of assuming independence across three processes (labeled as NAIVE2). The “CE” denotes the conditional expectation $E\{Y_i(t)/P_i(t)|C_i^{(1)}=1,P_i(t)>0.5\}$.

	Method	MSE
	Propose	0.660
μC1(t)	NAIVE1	0.810
	NAIVE2	0.672
	Propose	0.955
μC2(t)	NAIVE1	1.015
	NAIVE2	0.976
	Propose	0.340
μP(t)	NAIVE1	0.478
	NAIVE2	0.352
	Propose	5.500
μY1(t)	NAIVE1	7.362
	NAIVE2	5.605
	Propose	0.403
μY2(t)	NAIVE1	0.971
	NAIVE2	0.418
	Propose	9.361
CE	NAIVE1	15.222
	NAIVE2	13.951

In summary, the simulation results suggest that the NAIVE1 with misspecified random effect structure, will lead to biased results in both fixed effect curves and conditional expectations. The NAIVE2 approaches, which has correct random effect structure but assumes independence across three processes, provides acceptable estimates of the fixed effect curves, but it leads to misleading conclusions about the conditional expectations. On the other hand, our proposed approach has satisfactory results for both the curves and the conditional expectation.

5. Application to Physical Activity Data

In this section we apply our methods from Section 2 and 3 to data from Kozey-Keadle et al. [1] where a wearable monitor (ActivPAL™, www.paltech.plus.com) was used to estimate aspects of physical activity and sedentary behavior over a period of time. The data are summarized in five minute intervals. The device is worn on the thigh, and accelerometers are used to detect when the wearer is sedentary (a horizontal thigh indicates sitting or lying down) or active (standing or stepping). For active behaviors, data from the accelerometers are used to estimate energy expenditure above resting.

The unit of energy expenditure recorded by the device is the metabolic equivalent (MET). A MET is defined equivalently in several ways. One is that one MET is a person’s resting energy expenditure and X Mets is X times the resting expenditure. Additionally, if a person is at one MET for one hour, then that person will use one times the person’s body mass in kilograms in kilocalories. An activity with METs greater than or equal to 3 is defined as moderate to vigorous physical activity (MVPA). To illustrate our methods, we extract data for one hour before and two hours after a bout of MVPA (36 five-minute intervals) for each individual. We set minute −60 to be one hour before the MVPA bout, minute 0 to be the start time for the MVPA bout and minute 115 to be two hours after the MVPA bout started. Referring to the notation in Section 2, for subject i in the t^th time interval, C_i(t) = 1, 2, 3 means a completely sedentary interval, an interval with mixed sedentary and active behaviors, and a fully active interval, respectively. P_i(t) is the proportion of time used for active behaviors. P_i(t) = 0 represents a fully sedentary interval, while P_i(t) = 1 is a completely active interval. Y_i(t) is the energy expenditure rate with METs minus 1.25. Y_i(t) = 0 occurs if the interval is completely sedentary, and it is a positive continuous outcome otherwise.

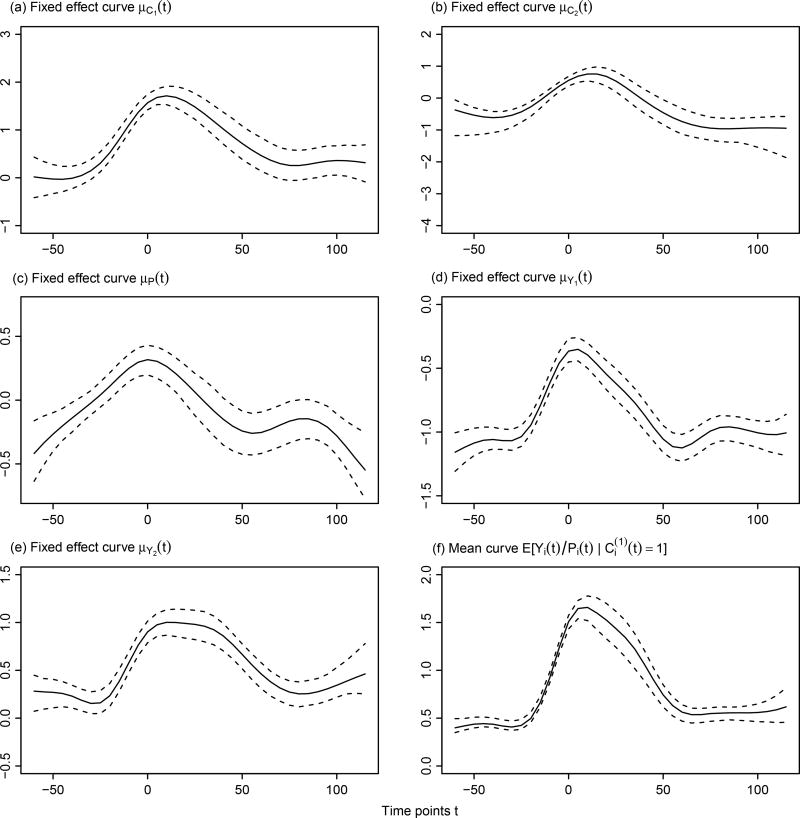
The model and estimation algorithm discussed in Sections 2 and 3 are used to fit the data. Figures 4 (a)–(e) present fixed effects for μ_C1(t), μ_C2(t), μ_P(t), μ_Y1(t) and μ_Y2(t). The plots illustrate that the probability of the occurrence for active behavior increases significantly at about 10 minutes before the MVPA bout, and returns to the initial level after an hour from the bout. Given the occurrence of active behavior, the probability for fully active behavior also increases at the time of MVPA bout, and reduces after the bout to just below the starting level. The proportion of active behavior starts to increase from one hour before the MVPA bout, reaches its peak at the MVPA bout, and then turns to decrease. The energy expenditure rate follows the pattern of the occurrence for active behavior, which raises before the bout of MVPA, and goes down after the bout. Comparing with partial active interval, the fully active interval has higher energy expenditure rate, especially during the one hour around the MVPA bout.

Figure 4.

Fixed effects for the physical activity data in Section 5: (a)(b) fixed effect curve for ordinal categorical outcomes: the occurrence of active interval, and the occurrence of fully activity given an interval is active, respectively, (c)(d)(e) fixed effect curves for proportions of time used and intensity in active behavior, respectively, (f) mean curve for energy expenditure. Solid lines represent the fitted curves. The upper and lower dashed lines are the 10% and 90% quantiles of the fitted values across 500 bootstrap estimates.

In this application, the term Y_i(t)/P_i(t) represents energy expenditure rate for active behaviors (PAEE −1.25). This expression can be derived from the relationship: Y_i(t) + 1.25 = 1.25 × {1 − P_i(t)} + P_i(t)PAEE_i(t). The conditional expectation $E\{Y_i(t)/P_i(t)|C_i^{(1)}=1,P_i(t)>0.5\}$ allows the PAEE to be calculated (1) for intervals with partially or complete active behaviors and (2) for active behaviors use more than 2.5 minutes in each five minute interval. Figure 4 (f) reports the curve for the conditional expectation. The active behavior specific energy expenditure rate also shares similar features with the active behavior rate in these data.

Our method leads to the number of principal components to be k_C1 = k_C2 = k_P = 1 and k_Y = 2. Figures 5 (a)–(d) present the first principal component curves for ordinal, proportional and continuous outcomes, respectively. The plots indicate that the major variabilities of ordinal category outcomes occur from 30 minutes after the MVPA bout. In addition, the correlation coefficient of the principal component scores from two ordinal responses are estimated to be 0.76, which indicates subjects with active intervals after MVPA bouts are more likely to have fully active intervals. The variabilities of proportion and continuous outcomes mainly occur between 30 to 60 minutes after a MVPA bout. The correlation coefficient between the occurrence of full active interval and the first principal component of energy expenditure rate is 0.16. It suggests that if a subject has higher rates of having fully active intervals from the MVPA bout to one hour after MVPA, he/she would have a higher energy expenditure rate for physical activity in those intervals.

Figure 5.

First principal component curves for the physical activity data in Section 5: (a)(b) first principal component curves for ordinal categorical variables, (c) first principal component curves for proportional response, (d) first principal component curves for continuous response. Solid lines represent the fitted curves. The upper and lower dashed lines are the 10% and 90% quantiles of the fitted values across 500 bootstrap estimates.

In the Online Supplementary Material, we also compare our joint modeling approach with the method that assumes the three processes to be independent. The fitted fixed effect curves from the two methods are similar, but the independent model approach underestimates the conditional expectation after the MVPA bout relative to the proposed joint modeling approach. Based on the conclusions obtained from our simulation studies, the joint model fitting results are more appropriate.

6. Discussion

We have proposed a three-part joint modeling and estimation strategy for functional data with complicated structure. The model can handle data with zero-and-one inflated proportions and zero inflated normal observations with skewness. The simulation results show that compared with commonly used naive methods, our proposed approach has little bias. The application of our method to the physical activity data illustrates utility in a real application.

Our motivating dataset illustrates that assessing physical activity and sedentary behavior with an accelerometer involves more than one response over time, and those responses can have a non-standard association structure. This has been recognized in the subject matter literature, see for instance Keadle et al. [30]. Our proposed methods illustrate that it can be beneficial to model these responses jointly over time. In addition to the expected benefits of borrowing strength across related responses, a joint model also can yield improved estimates of quantities that are derived from more than one response. We illustrate this by estimating the energy expenditure rate for active behaviors (PAEE), the conditional expectation of a ratio of two our responses.

One potential limitation for our proposed algorithm is that it could be sensitive to initial values. In an unreported simulation study, when we arbitrarily set fairly large or small initial values for some parameters (e.g. the Box-Cox transformation parameter λ and the dispersion parameters ${\sigma }_Y^2$), the algorithm sometimes failed to converge or gave biased results. In order to avoid that problem, we proposed a detailed approach for selecting initial values in Section 3.2. This method works well in our simulation and application studies, but it would still be interesting to improve the selection for the initial covariance matrix Ψ from original data. This could be addressed by the procedure proposed by Wolfinger and O’Connell [31], for instance.

The estimation of the three-part functional data model is based on a penalized quasilikelihood method. Rodriguez and Goldman [32] show that this approach could lead to biased estimates. However, the asymptotic properties of this approach are derived in Vonesh et al. [33], which confirms that a consistent estimator can be obtained as the number of individuals (n) and the number of time intervals (m_i) go to infinity. Goldstein and Rasbash [22] also suggest that our second order approximation greatly improves the estimation results. The simulation studies in this manuscript agree with these conclusions, where the bias for fixed effect and principal component curves is small. On the other hand, estimation via Monte Carlo approaches is widely used in multivariate or multilevel functional data analysis [9, 34]. These approaches have high computational costs, and they cannot be directly applied to our data structure, but it would be interesting to adapt them our our situation in future studies.

Finally, we used orthogonal B-splines in this manuscript. This method has satisfactory performance in our simulation and application studies, and orthogonality provided great simplifications in Section 2.2. That said, other bases such as restricted cubic splines or fractional polynomials ([35] and [36]) could be considered.