Jointly characterizing epigenetic dynamics across multiple human cell types

Abstract

Advanced sequencing technologies have generated a plethora of data for many chromatin marks in multiple tissues and cell types, yet there is lack of a generalized tool for optimal utility of those data. A major challenge is to quantitatively model the epigenetic dynamics across both the genome and many cell types for understanding their impacts on differential gene regulation and disease. We introduce IDEAS, an integrative and discriminative epigenome annotation system, for jointly characterizing epigenetic landscapes in many cell types and detecting differential regulatory regions. A key distinction between our method and existing state-of-the-art algorithms is that IDEAS integrates epigenomes of many cell types simultaneously in a way that preserves the position-dependent and cell type-specific information at fine scales, thereby greatly improving segmentation accuracy and producing comparable annotations across cell types.

INTRODUCTION

With a plethora of epigenetic data sets generated by advanced sequencing technologies (1,2), a key challenge is to build quantitative models elucidating how epigenomic variation across both the genome and different cell types relates to gene expression changes and phenotypic diversity (3,4). A popular approach for characterizing epigenetic landscapes is genome segmentation (5,6), which assigns states to genomic segments exhibiting unique combinatorial patterns of chromatin marks. The inferred epigenetic states have proven useful for studying gene regulation and disease, since hypotheses based on these state assignments have been confirmed by functional experiments (7).

Existing genome segmentation tools (5,6,8,9) were mostly developed for segmenting a single genome. Genome-concatenation (5) and data stacking (5,10) strategies have been used to apply single genome segmentation methods to analyze multiple cell lines. While the genome-concatenation approach uniformly segments multiple cell types together, it ignores the position dependency of regulatory events. For example, a DNA segment that acts as a promoter in one cell type is likely to be a promoter in other cell types, but without consideration of position dependency, that segment may be assigned to a spurious state across cell types. In contrast, the data stacking approach takes position specificity into account, but it does not produce segmentations for each cell type individually. Interpreting the states learned from stacked data can be a challenging task, especially when data from a large number of cell types is stacked. Also, both strategies treat multiple cell types equally, which may over-train on closely related cell types at the expense of distant ones.

Extensions from single genome segmentation tools have been developed to borrow local information across cell types. TreeHMM (11) uses a Bayesian network to combine information across cell types at each position. Two limitations of treeHMM are that it requires a known cell type hierarchy that is invariant across the genome, and it requires data binarization. A bigger issue is that exact inference of treeHMM is computationally intractable for analyzing a large numbers of cell types. Variational approximation is therefore used to obtain approximate solutions, which unfortunately has no upper bounds for inference errors. HiHMM (12) handles multiple epigenomes via infinite-state hidden Markov models (iHMM (13)). Each epigenome has its own iHMM parameters to account for cell type specificity, and these iHMM parameters share information across cell types via a common prior. HiHMM however ignores the position-dependent events across cell types. GBR (14) uses position-pair graphs to transfer information between pairs of interacting genomic positions and across cell types. GBR takes existing segmentations as input, and it relies on the user to choose the cell types from which information will be transferred. Also, GBR still segments one genome at a time by using other cell types as priors, and thus it does not develop a coherent segmentation model for all cell types jointly.

We introduce IDEAS, an integrative and discriminative epigenome annotation system, to jointly segment multiple genomes by quantitatively modeling position-dependent and cell type-specific epigenetic events at fine scales. Our approach is a 2D segmentation method that identifies co-occurrence patterns of epigenetic features (and inferred regulatory events) both along the genome and across cell types. Horizontally along the genome within each cell type, the method identifies positional organization of inferred regulatory events in a region that are commonly observed in many cell types. For instance, if an enhancer is observed upstream of a target gene, it would be intuitively more likely to observe transcriptional activity at the gene, even though the two loci may be 100 kb away. Vertically across cell types at each position, we also detect co-occurrence of inferred regulatory events. For instance, a transcription initiation event at a locus in one cell type may increase our confidence for observing similar activities in other cell types, but reduce our expectation for seeing transcription termination events at the position. IDEAS can capture these horizontal and vertical state correlations that help to improve segmentation accuracy.

MATERIALS AND METHODS

Overview of the IDEAS model

The IDEAS model has three key components. First, it locally partitions cell types into groups based on similarity of their local epigenetic landscapes, and assumes that local regulatory regimes are similar among cell types in the same group. This step effectively borrows information across cell types, but selectively, i.e. only from cell types exhibiting similar epigenetic landscapes in a local region. This approach bypasses the direct modeling of complex cell type dependencies, thereby producing computationally tractable models even if the number of cell types grows large. Secondly, the model assigns genomic positions into classes based on distinct and reoccurring position-dependent epigenetic profiles learned from all cell types. Many genomic positions are epigenomically conserved among cell types due to their underlying DNA sequences, such as regions ubiquitously bound by transcription factors, transcription start sites, and non-functional regions in the genome. This step captures the major co-occurrence patterns of epigenetic events among cell types at each position, thereby improving segmentation accuracy as well as state comparability across cell types at the position. Thirdly, the model assigns epigenetic states to each position in each cell type, conditioning on the previous two components. Taken together, our model can gain power when position and cell type specificity are present in the data (see simulation study in Supplementary Note Section 1).

The IDEAS method not only outputs the genome segmentations as similarly produced by existing tools, but also reports local cell type clusters and position classes that capture the co-occurrence pattern of epigenetic states both along the genome and among cell types. The output of IDEAS thus can be used to describe complex epigenetic architectures among multiple cell types, identify potential regulatory loci in the genome and their cell type specificity, and reveal changes in cell type relationships. An illustration of the IDEAS model is shown in Figure 1A.

Figure 1.

Illustration of IDEAS model. (A) Rationale for the IDEAS method. Input data include multiple epigenetic marks in many cell types. IDEAS updates three model components iteratively: clustering cell types by local epigenetic landscape similarity; classifying genomic positions based on regulatory profiles learned from all cell types; and conditionally inferring epigenetic states at each position in each cell type. The output of the IDEAS model includes genome segmentation in each cell type, local cell type clusters, genomic position classes, and co-occurrence patterns of epigenetic states. (B) An illustrative hierarchy of the IDEAS model assuming five cell types. Unknown model parameters are shown in hollow shapes and observations are shown in filled circles. Arrows indicate model dependency. Only a small set of example connections between the cell type clustering component and the epigenetic state component are shown. Other model parameters such as emission and hyper model parameters are not displayed.

Model implementation

Let denote the data of p epigenetic marks collected from N cell types at L genomic locations. We allow replicate data, so the total sample size is M = n₁+…+n_N, where n_i ≥ 1 denotes the number of replicates for cell type i. We describe the joint distribution of by a Bayesian mixture of multivariate Gaussian density functions. Let denote the data (n_ip values) observed in cell type i at position j, 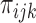denote the corresponding mixture distribution (for all possible states k in cell type i at position j), and denote the density function for state k with parameter 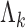. We express the IDEAS model in form of

where the inner product is taken over replicates r = 1,…,n_i. The parameter space for 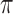is much larger than the sample size and hence requires regularization. Also, we want to borrow information across cell types and the genome. This is achieved by treating as random measures with Bayesian hierarchical priors. Specifically, we impose two constraints: (i) 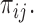are identical for all cell types i that are in the same cell type cluster at position j; and (ii) have the same prior distribution of states given by the class of position j. While the first constraint borrows information from locally related cell types, the latter constraint combines genome-wide information to identify distinct and recurring co-occurrence pattern of epigenetic states.

We use a set of infinite-state hidden Markov models (iHMM) (13) to realize both local cell type clustering and position classification. For cell type clustering, we implement one iHMM for each cell type. The states in an iHMM denote the cell-type cluster membership. That is, at each position, the cell types in the same iHMM states belong to the same cluster. For position classification, we implement another iHMM with its state representing the position classes. The cell type clustering and position classification combined together represent a latent structure in the data, in which each latent class has a distinct emission probability of epigenetic states that are cell type and position specific. We use a Dirichlet process (15,16) to model the number of epigenetic states. Finally, the observed data is emitted from those epigenetic states, conditionally independent of cell type relationships and position classes. Our utility of iHMMs and Dirichlet processes means that the model by itself can choose the number of states to fit the data, and via Bayesian regularization, we will always obtain finite model sizes in finite samples. The user however can fix the number of states in the model if needed, thereby allowing other model selection procedures to be applied. An illustration of IDEAS model hierarchy is shown in Figure 1B.

Our setup of the model allows us to analytically integrate out the position and cell type specific state distribution parameters π, the space of which is in principle infinite. This leads to a collapsed model that is inference-wise substantially simplified for multi-genome segmentations. IDEAS has a linear time complexity with respect to the number of cell types analyzed, and thus it is capable for segmenting up to hundreds of cell types jointly even if the cell type relationships are complex. Yet simultaneously, our model is substantially richer than existing methods that can powerfully capture the multi-cellular epigenetic dynamics at fine details. We use Markov chain Monte Carlo sampling methods, followed by maximization, to train the IDEAS model. Additional details of the IDEAS model and its inference can be found in online Supplementary Methods.

Input data set of chromatin marks

We applied IDEAS to an ENCODE dataset containing 14 epigenetic marks (H3K4me1, H3K4me2, H3K4me3, H3K9ac, H3K27ac, H3K27me3, H3K36me3, H4K20me1, POL2RA, CTCF, Duke DNase, UW DNase, FAIRE and Control) in six human cell types (GM12878, H1-hESC, HeLa-S3, HepG2, HUVEC and K562). The 84 ENCODE data sets (Supplementary Table S1) were downloaded from https://sites.google.com/site/anshulkundaje/projects/wiggler. The data sets from the website have already been uniformly processed and normalized by the ENCODE pipeline. We followed the same procedure taken in (17) to take the maximum signal per 200bp window as the input to our method, and we took log₂(x+1) transformation of the input data to reduce signal skewness. However, we want to point out that both ChromHMM and IDEAS are not restricted to 200bp window sizes. We removed repetitive regions and blacklist regions as provided in (17) The final input data matrix for IDEAS consisted of 13 763 197 windows and 84 tracks of data. Additional data sets used for comparison and validation in this study were obtained from the sources listed in Supplementary Methods online.

Assignment of mnemonics to IDEAS states

We overlapped the states generated by IDEAS with the states generated by ChromHMM (5) on the same data, and we calculated the fold enrichment of overlap for each state pair relative to random matching. If a pair of states had both the maximum absolute overlap and the maximum fold enrichment, we assigned the mnemonics of the ChromHMM state to the corresponding IDEAS state. We assigned mnemonics to the remaining IDEAS states by comparing their mean signal patterns of the epigenetic marks with those of ChromHMM (Supplementary Figure S1) and selecting the closest match. If multiple states of IDEAS matched to one ChromHMM state, we added numerical indices to the mnemonics to distinguish them. For a few states involving strong CTCF signals, we assigned different mnemonics to reflect their enriched chromatin signatures and spatial relationships to genes. A summary of the mnemonics assigned to IDEAS states and the rationales are provided in Supplementary Table S2.

Reproducibility of segmentation

We evaluated the reproducibility of the segmentation of IDEAS presented in this paper by generating three additional segmentation results using independently and randomly initialized model parameters. We calculated an overall agreement between a pair of segmentation results by rand index. We further quantified the reproducibility of each state using correlation coefficients. In particular, for each state to be replicated (a target state), we converted the segmentation matrix into a binary vector with 1s denoting the instances of the state, and 0s denoting the instances of all other states. For each state in a replication run (a replicate state), we similarly generated a binary vector and we calculated the correlation coefficient between the two binary vectors. We did this for all replicate states and identified the one with the highest correlation coefficient with the target state as a ‘match’. We recorded the correlation coefficients between the target and replicate runs in a square matrix R, with each element R_ij in the matrix denoting the correlation coefficient between the ith target state and the replicate state that best matched to the jth target state. In this way, the diagonal elements in R quantified the reproducibility of each target state, but the off diagonal elements in each column in R quantified the cases where different target states were captured by a single replicate state, and the off diagonal elements in each row in R quantified the cases where a target state was split into multiple replicate states. Due to large sample size, a non-reproducible state would have a near 0 correlation coefficient even though we used the largest correlation as the best match. Finally, we took average of the correlation matrices from the three independent runs.

Gene expression analysis

To estimate state effects on gene expression (with genes defined by GENCODE (18) version19), we first calculated the percentage of states in a region of interest. We then regressed gene expression values in two replicates of each cell type on the percentage of states in the same cell type using a linear regression model. State effects on gene expression were measured by regression coefficients. To quantify the relationship between differential gene expression and state assignments across cell types, we performed ANOVA analysis by partitioning the 12 expression values per gene into groups. Grouping was based on the states assigned to each cell type at a position of interest, i.e. expression values of cell types assigned with the same states were grouped together. We then quantified the amount of expression variability explained by the state assignments at the position by r².

Enhancer and CTCF analysis

For EP300 analysis, we pooled the Enh, Enh1 and Enh2 states of Segway together, as they all represented strong enhancers but had different mnemonics in different cell types. Both IDEAS and ChromHMM had a single Enh state denoting strong enhancers in all cell types. For the precision recall analysis, we evaluated enhancer predictions in each cell type separately. For FANTOM5 enhancers (19), we matched the cell types of our predictions and the reference enhancers. For VISTA enhancers (20) tested in transgenic mice, there was no cell type information. We therefore overlapped our predicted enhancers in each cell type with the same set of VISTA enhancers. Our rationale for comparing to the developmental enhancers from the VISTA enhancer browser was that several enhancers were shared across cell types, so they could be useful to evaluate the predicted enhancers in the cell types in this study. We pooled all results from all cell types together to calculate an overall precision and recall value. Recall was calculated as the percentage of positive enhancer regions overlapped with the corresponding states by each program. Genome-wide fold enrichment was calculated as the ratio between the observed basepair coverage of enhancer regions and the expected basepair coverage in the genome-scale by chance. Note that fold enrichment is proportional to one minus false discovery rate, and thus a large fold enrichment indicates a small false discovery rate. Precision was calculated as the percentage of basepairs in the states within the reference regions (including both positive and negative enhancers) overlapped with positive enhancer regions.

For CTCF analysis, the cell types for manually curated and non-ENCODE CTCF sites obtained from CTCFBSDB2.0 (21) did not match with the ENCODE cell types. We therefore merged the CTCF states in the six cell types together and then compared with the reference CTCF sites. Again, our rationale for comparing CTCF occupancy in different cell types is that CTCF binding sites are often commonly bound in many cell types. If two CTCF states overlapped, we used the mnemonics of the CTCF state with the larger mean CTCF signals. Power was calculated as the percentage of CTCF sites overlapped with a predictor state by at least 1basepair. Genome-wide fold enrichment was calculated as the ratio between the observed basepair coverage of CTCF regions and the expected basepair coverage in the genome-scale by chance.

GWAS enrichment analysis

We used both the lead SNPs from GWASCatalog (22) and their proxy SNPs obtained from SNAP (23) as ‘disease variants’ in the enrichment analysis. Fold enrichment was calculated as the ratio between the number of disease SNPs within the prediction regions and the number of disease SNPs within randomly shuffled regions. We shuffled the prediction regions randomly within each chromosome and we kept the size distribution of those regions. The p-values of enrichment were estimated by randomly shuffling the prediction regions 10 000× and checking how frequent the number of disease SNPs within the shuffled regions were greater than or equal to the number observed in the original prediction regions. FDR was calculated by p.adjust() in R.

RESULTS

We applied IDEAS to an ENCODE dataset containing 14 epigenetic marks in six human cell types (see Methods). This dataset has been previously analyzed (17) by two state-of-the-art algorithms, ChromHMM (5) and Segway (6). While ChromHMM trained a 25-state model via genome concatenation, Segway segmented each cell type separately and assigned 55 mnemonics to the segments in all cell types. IDEAS generated a 36-state model (Figure 2A). On average 90.3% of the IDEAS segmentation was concordant with the segmentations obtained from additional runs using independent and random initial values of model parameters. As shown in Figure 2B, a majority of the 36 states by IDEAS were reproducible, especially for states carrying strong signals in at least one epigenetic mark. A few states (DnaseD1, Low2, Repr1, H4K20) were not reproduced in additional runs of IDEAS, which had relatively low signals in all marks and were rare (<0.2% in total) in the genome. Some states with similar epigenetic profiles were merged or split in other runs of IDEAS. The 36-state segmentation by IDEAS can be accessed at http://main.genome-browser.bx.psu.edu under Regulation → IDEAS36.

Figure 2.

IDEAS model generated 36 states in ENCODE data. (A) Heatmap of the mean signals of the 14 marks in 36 IDEAS states. State mnemonics are shown on the right. (B) Reproducibility for the corresponding states shown in (a), measured by correlation coefficients. Reproducible states have high correlation coefficients along the diagonal; off diagonal strong correlation coefficients within a row indicates that the target state was split into multiple states in replication; off diagonal strong correlation coefficients within a column indicates that multiple target states were merged in one state in replication. (C) Boxplot of the methylation levels in IDEAS states, sorted by median. (D) Heatmap of the estimated state effects on gene expression by regressing gene expression on the percentage of states within 2 kb upstream of transcription start sites.

Many of the 36 states inferred by IDEAS shared common signatures as captured by other methods (Supplementary Figure S1). Comparison with orthogonal datasets revealed that the functional roles inferred for the IDEAS's states were consistent with known patterns of DNA methylation (Figure 2C), spatial distribution relative to genes (Supplementary Figure S2), and effects on RNA output (Figure 2D; Supplementary Figure S3), thereby confirming the ability of IDEAS to detect known function-associated states, such as enhancers, promoters, repressors, transcription elongation, and heterochromatin. IDEAS also detected some novel states, including distinct chromatin signatures at CTCF occupancy sites enriched near transcription start sites (TSS), promoter flanking regions, and transcription end sites (TES) (Figure 2A; Supplementary Figure S2).

Consistent segmentation across cell types improves annotation accuracy

IDEAS's state assignments were considerably more homogeneous across cell types than those produced by other methods (Figure 3A). The greater homogeneity improved the accuracy of genome segmentation. We first evaluated enhancer prediction by IDEAS using EP300 datasets, which were not used in the training data. All three methods captured 71–75% EP300 peaks in four or five states, but the state compositions overlapping EP300 differed among methods (Supplementary Figure S4). More of the EP300 peaks were covered by enhancer-labeled states for IDEAS (65% in Enh, EnhF and EnhWF) than for ChromHMM (48% in Enh, EnhW and EnhF) or Segway (59% in Enh, EnhF1, EnhPr and EnhF3) (Supplementary Figure S4). For all three methods, the other states capturing substantial numbers of EP300 peaks had features of TSS. A TSS-labeled state from IDEAS, TssCtcf, had both a TSS signature and CTCF occupancy, potentially revealing a state with enhancer activity (EP300) and cohesin (a frequent partner of CTCF) close to a TSS. When further tested with validated enhancers in the VISTA enhancer library (20), FANTOM5 enhancers, and CAGE usage data (19), IDEAS yielded notably better predictions by its enhancer-labeled states (Enh, EnhF, EnhW) than by other methods (Supplementary Figures S5 and S6). IDEAS also performed better in FANTOM5 and CAGE data when compared with EnhancerFinder (24), a supervised method that was trained on VISTA enhancers, suggesting an advantage of using unsupervised approaches to identify novel enhancers that are not represented in the training data. We note, however, that EnhancerFinder was trained on a different set of predictors and cell types, and it was specifically developed for predicting developmental enhancers, which may contribute to the performance difference observed here.

Figure 3.

Homogeneity of state assignments and similarity of state effects on expression across cell types. (A) Each heatmap shows the correlation coefficients of pairs of states assigned at the same positions across cell types. (B) Barplot of the average cosine similarity of state effects on gene expression estimated between pairs of cell types. In each cell type and at each genomic interval relative to genes (defined in Supplementary Figure S2), we linearly regressed gene expression on the state composition. State effects are the regression coefficients. Cosine similarity for a state between a pair of cell types was then calculated from the vectors of state effects over all genomic intervals. We finally averaged the cosine similarity across all pairs of cell types. The insert shows the distribution of cosine similarity for all states.

We next evaluated CTCF occupancy prediction using manually curated CTCF sites and experimentally validated CTCF sites from non-ENCODE studies in CTCFBSDB2.0 (21). The CTCF-labeled states for IDEAS captured substantially more CTCF sites (57.7%) than for ChromHMM (21.2%) and Segway (25.0%), respectively, on the manually curated CTCF. Similarly, the CTCF-labeled states for IDEAS also captured more CTCF sites (93.3%) than for the other two methods (73.9% and 78.0%, respectively) on the non-ENCODE CTCF. In addition, IDEAS yielded similar or better fold enrichments than ChromHMM and Segway (Supplementary Figures S7 and S8). Taken together, the results suggest that IDEAS had a better sensitivity and specificity for predicting CTCF occupancy than the other two methods. Among all positions carrying at least one CTCF-labeled state in the six cell types, 29.2% of those positions for IDEAS were ubiquitous (with the same CTCF-labeled state assignments in all six cell types, Supplementary Figure S9), denoting common occupancy of CTCF in all cell types. The variance of CTCF signals at those ubiquitous CTCF sites was notably smaller than those at the variable CTCF sites (Supplementary Figure S10). In comparison, the proportions of ubiquitous CTCF binding predicted by ChromHMM and Segway were much smaller (5.3% and 11.4%, respectively).

We further used RNA-seq data to evaluate the predictive power of epigenetic states on gene expression. Each epigenetic state potentially represents a cis-regulatory module (CRM) that may promote or repress the expression of its target genes. Should the inferred states be a good predictor for CRMs, the effect of a state on gene expression would be only related to its occurrence around the gene, but not depend on cell types. Using a linear regression model, we predicted gene expression by the states within a region of fixed distance to each gene (Supplementary Figure S11). In all cell types and at various distances to genes, the segmentations from IDEAS consistently yielded the best prediction of gene expression compared to those of other methods, with the largest power gain in H1hESC. Importantly, comparing between cell types, IDEAS produced the most homogeneous state effect estimates on gene expression (Figure 3B).

We also examined the impact of using epigenetic data in stacked mode in ChromHMM, which does preserve position specific information. The drawback to this mode is that data from all cell types are used simultaneously but without the cell type identity being considered. To interpret the resulting states, Mortazavi et al. (10) trained self-organizing maps (SOMs), which did uncover cell-specific candidate regulatory regions. We compared our enhancer predictions to those from the ChromHMM-SOM maps, and found substantial concordance in the results (Supplementary Figure S12). The GM12878-specific enhancer predictions from IDEAS also identified an additional cluster of states in the SOM not described in Mortazavi et al. Thus the single coherent model from IDEAS can recapitulate and expand on results from analysis by running in series ChromHMM (stacked mode) followed by SOMs.

Dynamic segmentations predict differential gene expression

Our improved state assignments across cell types enabled robust detection of epigenomically constitutive and variable positions. We define a genomic position as epigenomically ‘variable’ if the cell types received different state assignments at the position. IDEAS marked 46.6% of the genome epigenomically ‘variable’, which was a much smaller proportion than the 84.4% and 99.1% variable positions by ChromHMM and Segway, respectively. The nearly 100% differentially annotated positions by Segway was due to its disjoint segmentation done in each cell type separately, which created inconsistent state inference between cell types. The variable positions inferred by IDEAS were enriched in enhancer and repression states, whereas the constitutive sites mainly contained low signal, elongation and TSS states (Supplementary Figure S13).

We evaluated the reliability of our variable and constitutive state assignments at each position using independent gene expression data. As epigenetic states have different impacts on gene expression, we expected that genes differentially expressed among cell types would have more dynamic state assignments at their nearby positions across cell types; and vice versa, silent genes or genes ubiquitously expressed among cell types would have more constitutively assigned states at their nearby positions across cell types. We calculated state assignment heterogeneity, which is the probability that two randomly selected cell types will have different state assignments at a position, at different positions within genes and at varying distances from genes. As shown in Figure 4A, IDEAS produced a dynamic pattern of state assignment heterogeneity as a function of distance to genes and differential gene expression. Specifically, the states assigned by IDEAS were more heterogeneous among cell types at positions near highly differentially expressed genes, as compared to distant positions to genes or at genes not differentially expressed among cell types. In comparison, ChromHMM yielded a similar pattern but had a weaker signal-to-noise ratio. Segway results showed a very different pattern with heterogeneous states assigned at most positions among cell types, except for the TSS regions of non-differentially expressed genes. This result again reflected the inconsistent state assignments produced by disjoint segmentation in each cell type separately. In addition, the state assignment heterogeneity for IDEAS had the strongest correlation with gene expression variability across cell types (Supplementary Figure S14).

Figure 4.

Differential gene expression explained by state assignments across cell types. (A) Each plot shows the mean state assignment heterogeneity (the probability of two randomly selected cell types having different state assignments at a position) as a function of distance to gene (x-axis, see Supplementary Figure S2 for details) and standard deviation of expression changes across cell types (y-axis). Since the state heterogeneity values for different methods are very different, we show relative heterogeneity by subtracting the minimum value, which is indicated in the color legend. The same color map is used for all methods in this panel. (B) Mean proportion of differential gene expression (r²) explained by state assignments across cell types, as a function of distance to gene and standard deviation of expression changes. The same color map is used for all methods in this panel.

We further performed analysis of variance (ANOVA) to relate position-wise state assignments to gene expression changes across cell types. At each position and for a target gene, we grouped cell types by the state assignments at the position, and we calculated r² for the expression variability of the target gene explained by the state assignments. As shown in Figure 4B, for all methods, the differential expression patterns of genes were best explained by the state assignments near TSS and within genes. In addition, the greater the changes in gene expression among cell types, the more they were explainable by the state assignments. Comparing the r² values for all methods between TSS and distal regions to genes, and between differentially expressed and ubiquitous genes, IDEAS yielded the strongest signal-to-noise ratio. In contrast, the overall large r² values for Segway reflected over fitting in small samples (12 expression values per gene).

Cell type specific regions are enriched of GWAS variants

About 75% of the epigenomically variable sites marked by IDEAS were locally clustered, forming epigenomically ‘variable regions’, which were captured by IDEAS's local cell type clustering. We refer to a genomic region for which the cell types were clustered in at least two groups as an epigenomically variable region, and otherwise the region is constitutive. Defining ‘cell type specific regions’ as regions with one cell type forming a cluster and the other cell types forming another cluster, we obtained the cell type specific regions for each cell type. A substantially larger proportion (29.6%) of the genome was unique to H1hESC than the proportions (1–4%) unique to other cell types. The H1hESC-specific regions were driven by weak enhancer, Pol2 and H4K20 states (Supplementary Figure S15). Overall, cell type specific regions were enriched either in enhancers or near but not at TSS (Supplementary Figure S16).

The cell type specific positions and regions identified by IDEAS were enriched for disease and trait-associated genetic variants in the NHGRI GWAS Catalog (22) (Figure 5). The enriched traits were highly unique and relevant to the corresponding cell types. GM12878, for instance, is a lymphoblastoid cell line. Positions and regions with epigenetic marks specific to GM12878 were enriched in genetic variants associated with many autoimmune diseases, including multiple sclerosis, rheumatoid arthritis, Crohn's disease, type 1 diabetes and celiac disease. HepG2 is derived from a liver carcinoma and has been used to study metabolism disorders. Positions and regions with epigenetic marks specific to HepG2 were enriched in variants for metabolism-related traits such as iron levels, cholesterol levels, metabolite levels, gamma-glutamyl transpeptidase and fibrinogen. K562 is derived from a chronic myeloid leukemia patient and has both erythoid and megakaryocytic properties. Positions and regions with epigenetic marks specific to K562 were enriched in variants for blood-related traits, coagulation and erythroid phenotypes. For some traits, the rationale is less obvious for why genetic variants associated with those traits were enriched in particular cell type specific positions and regions. These cases may represent novel trait-cell type relationships and may be better understood by incorporating additional cell types. Finally, we performed the same analysis on the cell type specific positions derived from the results for ChromHMM and Segway. While the results for ChromHMM revealed a substantially smaller number of enriched traits and less intuitive trait-cell type relationships (Supplementary Figure S17), we obtained no significant results for cell type specific positions predicted by Segway.

Figure 5.

Enrichment of trait-associated variants in IDEAS cell type specific positions and regions. Both (A) P-value and (B) fold enrichment of the enriched traits are shown, but only including traits with fold change ≥3 and FDR ≤0.02 in at least one column in the heatmap. Row colors on the side mark the groups of traits most significantly enriched in the corresponding cell types.

DISCUSSION

We introduced a powerful new tool, IDEAS, for jointly segmenting multiple genomes. While our approach globally share information across both the genome and cell types, it also preserves local position specific and cell type specific information. IDEAS can be broadly utilized in a range of studies involving one or multiple chromatin marks in one or many cell types, tissues and conditions (see method evaluation in Supplementary Note Section 2). For one cell type, IDEAS reduces to a quantitative hidden Markov model, but it can model replicate data without taking averages. For multiple cell types, IDEAS can scale up to segment more than 100 cell types simultaneously. We tested IDEAS using the 127 epigenomes in the Roadmap Epigenomics project (6) on chromosome 21 (Supplementary Note Section 3) and obtained comparable segmentations to those released by the Roadmap Epigenomics project. As the number of cell types increases, however, we expect fewer regions will be unique to each cell type, for which advanced testing methods (25) will become useful for testing state enrichment in groups of cell types.

While IDEAS can produce more favorable results than the current state-of-the-art algorithms and other methods (Supplementary Note Section 4), it is also computationally efficient. A runtime comparison using the ENCODE data on chromosome 22 showed that IDEAS ran as fast as ChromHMM and 20∼30 times faster than Segway using a single core computer, and IDEAS supports parallel computing (Supplementary Note Section 5). The computational efficiency of IDEAS is significant considering the richness of its model. Our approach avoided the exponentially growing model complexity with respect to the number of cell types, which would be required by standard methods that model both position and cell type dependence. Importantly, we used local cell type clustering to flexibly account for complex cell type relationships that may further change along the genome by functions of the underlying DNA sequences. We note, however, that our current model for position classification is a standard approach that has quadratic complexity with respect to the number of position classes involved, which is another target for improvement.

Genome segmentation methods, including IDEAS, are clustering algorithms that have local mode issues in general, i.e. segmentations generated in independent runs of the algorithm may not be identical. Segmentation results may vary depending on the initial values of the model parameters. While a majority of the states generated by IDEAS in this study were reproduced in independent runs, especially for the states carrying strong signals in at least one mark, a few states were not reproduced either due to low signals or similar epigenetic profiles with other states. For the latter case, the union of those similar states could be more concordant between runs than evaluated individually. We will implement and evaluate advanced methods for alleviating these local mode issues in the future. Potential solutions include simulated annealing (26) and methods that combine results from different runs followed by model retraining.

While we used the same scales for comparisons, we note that the color maps used in this manuscript may exaggerate some of the differences or similarities between methods (27). Also, due to limitation of the model assumptions, some epigenetic states inferred by IDEAS may not correspond to biologically functional elements. Furthermore, genome segmentation is an unsupervised method that may not work as well than some specialized methods for calling specific types of regulatory elements, such as enhancers. IDEAS currently uses Gaussian densities in its mixture model, for which we suggest using log₂ transformation on very skewed data. Alternatively, other probability functions (28) that better account for the variance inflation in sequencing read counts may be more appropriate. While IDEAS encourages homogeneous state assignments, it may miss subtle signal variation across cell types. To improve the accuracy and sensitivity of IDEAS, we may further incorporate known cell type relationships and model the enrichment of epigenetic states in some reoccurring subsets of cell types. Nevertheless, our ENCODE data application has demonstrated the utility of IDEAS for characterizing functional classes of DNA sequences, detecting cell type similarity and specificity, and relating epigenetic landscapes to phenotypes.

AVAILABILITY

The software implementing the IDEAS method is available at the corresponding author's website http://stat.psu.edu/∼yuzhang/IDEAS/ and also at GitHub https://github.com/yuzhang123/IDEAS

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health (NIH) [R01DK065806 and R56DK065806 (to Y.Z., R.C.H.), R01HG004718 (to Y.Z.), RC2HG005573 and U54HG006998 (to R.C.H.)]; U01CA176063, U01CA200060, PhRMA Foundation and Penn State CTSI (to F.Y.); National Science Foundation [OCI-0821527 in part] (the Penn State CyberSTAR and BioSTAR computers); NIH [R01HG004718 to Y.Z.]. Funding for open access charge: NIH [R01HG004718].

Conflict of interest statement. None declared.