Abstract
Multimode fibers can guide thousands of modes capable of delivering spatial information. Unfortunately, mode dispersion and coupling have so far prevented their use in endoscopic applications. To address this long-lasting challenge, we present a robust scanning fluorescence endoscope. A spatial light modulator shapes the input excitation wavefront to focus light on the distal tip of the fiber and to rapidly scan the focus over the region of interest. A detector array collects the fluorescence emission propagated back from the sample to the proximal tip of the fiber. We demonstrate that proper selection of the multimode fiber is critical for a robust calibration and for high signal-to-background ratio performance. We compare different types of multimode fibers and experimentally show that a focus created through a graded-index fiber can withstand a few millimeters of fiber distal tip translation. The resulting scanning endoscopic microscope images fluorescent samples over a field of view of 80µm with a resolution of 2µm.
OCIS codes: (110.1080) Active or adaptive optics, (110.7050) Turbid media, (060.2310) Fiber optics
1. Introduction
Endoscopic imaging is typically based on single mode fiber bundles, GRIN lenses or hybrid systems of fiber optics and mechanical actuators [1]. The cross section of these devices typically ranges from half a millimeter up to a few millimeters, which makes them unsuitable for the most demanding biological applications such as deep live neuron imaging and optogenetics. Lately, the ability to control light propagation in complex media has restored the old idea [2] of transmitting images through a multimode fiber (MMF). MMFs have the advantage of a small cross section down to tens of microns and the ability to bend into small angles. On the other hand, the excitation of multiple transverse modes with different propagation velocities produces a speckle field, product of the interference among all of the propagating modes, dismissing the MMFs as a standalone imaging device. Lately, a variety of new ideas using digital phase conjugation [3,4] and wavefront shaping techniques [5–9] have demonstrated the possibility of controlling the propagation of these modes showing their imaging potential. Papadopoulos et al. [3] use digital optical phase conjugation to calibrate a MMF and create a focus in every point at the tip of the fiber, converting the MMF into a scanning fluorescence microscope. Their method is capable of imaging in-vitro neurons with 1-3µm lateral resolution. A different approach [5] calibrates the input-output relation of the MMF using an orthonormal set of illumination patterns. The calibrated MMF can be used for fluorescence imaging and optical trapping. A further different method measures and stores each speckle field created at the proximal tip of a MMF for various input fields at the distal tip, enabling the reconstruction of the brightness of an object placed at the distal tip [6].
Unfortunately, none of these techniques has so far overcome the problems arising from fiber perturbations (e.g. shape changes, temperature) that produce mode coupling. Two solutions have been proposed to compensate for such perturbations. One of them uses a real-time re-focusing system, based on feedback and wavefront control, able to focus light at the distal tip while the fiber is bent [9]. Still, the requirement of accessing the distal tip, makes it difficult to implement in vivo. A second creative solution uses a single mode fiber and a holographic film in conjunction with the MMF to create a virtual beacon source at the distal tip of the fiber [4] enabling digital phase conjugation compensation of fiber bending. Furthermore, recent advances in theoretical models [10] have shown the possibility of predicting the bending angle based on the analysis of the transmission matrix of the fiber, and its potential for image correction.
As an alternative, it would be useful to reduce the effect of perturbations in the fiber calibration. In this manuscript, we evaluate the effect of perturbations at the distal tip of the fiber, and show how a proper fiber selection and system design can mitigate the mode coupling/dispersion so that the fiber calibration becomes robust to such changes. Furthermore, we show the importance of the speckle contrast in MMF to produce a high signal-to-background scanning foci and relate it to the specific fiber type.
The manuscript is divided as follows: in Sec. 2 we revise the transmission matrix approach used in the experiments and in Sec. 3 we present the optical setup to calibrate the MMF and to evaluate the robustness of the calibration. In Sec. 4 we compare the performance of four different MMF. In Sec. 5 we explore the relation between speckle contrast and the enhancement of a focus created with knowledge of the transmission matrix. In Sec. 6 we show the capabilities of the MMF used as a scanning fluorescence endoscopic microscope and evaluate its performance. In the last section, we discuss the implications of this work for the advancement of microendoscopy.
2. Principle of operation
Using a MMF as an optical element requires knowledge of the relation between any optical field launched at the proximal tip of the fiber and the resulting optical field at the distal tip. Theoretically, MMFs can be modeled as uniformly cylindrical waveguides, solving the wave equation to find the analytic expression of the propagating eigenmodes, which depend on the index distribution [11]. However, modes propagate with different velocities, generating a complex interference pattern at the output of the fiber resulting from the scramble of the relative phases of the modes. Furthermore, the coupling among modes as they propagate along the fiber is hard to predict because of fabrication defects, bends and temperature changes. Therefore, an experimental calibration that measures the relation between the corresponding optical fields at the proximal tip and at the distal tip is required. Typically, this relation is represented by the transmission matrix (TM), t, part of the more general scattering matrix, S, which also includes the reflection terms, r. The relation is expressed mathematically as
| (1) |
where a+ and b- are the input fields launched at the closer and distal tips respectively, and a- and b+ are the output fields from the closer and distal tips respectively (Fig. 1).
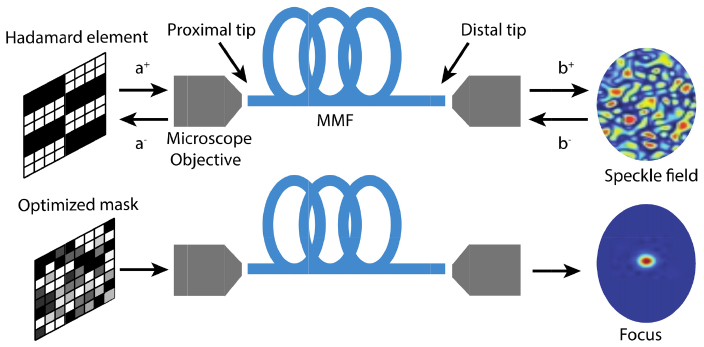
Fig. 1.
Calibration of and focusing through a MMF. Top: Scheme of the calibration procedure. During the calibration, each Hadamard element illuminates the proximal tip of the MMF and produces a different speckle pattern at the distal tip. We extract the phase of each output mode to build the TM. Bottom: The TM provides information to calculate an optimized mask that creates an optical focus at the distal tip.
Because only a discrete set of modes can propagate inside the MMF, the optical field at the distal tip is determined by the summation of each mode’s contribution
| (2) |
To measure t experimentally, instead of using the theoretical eigenmodes of a given MMF, we implement a similar approach to the one developed in the context of focusing light through scattering media [12]. We divide the incident wave into N spatial input modes, where each spatial mode is defined by a squared macro-pixel in the spatial light modulator. We use the elements of a Hardamard basis set as the input fields. This approach is more suitable for our experiment because of the square geometry of the phase-only spatial light modulator. Each Hadamard element projected is surrounded by a constant phase frame that switches its phase value between 0, π/2 and π. From the intensity measurements at the distal tip for each of the three different frame phase values, we reconstruct the field exiting the distal tip of the fiber [13,14]. Therefore, the element of the experimental transmission matrix [12] corresponding to the n Hadamard element is calculated using
| (3) |
After all the elements of the basis set are measured, we can calculate the optimal phase mask using .
3. Experimental setup
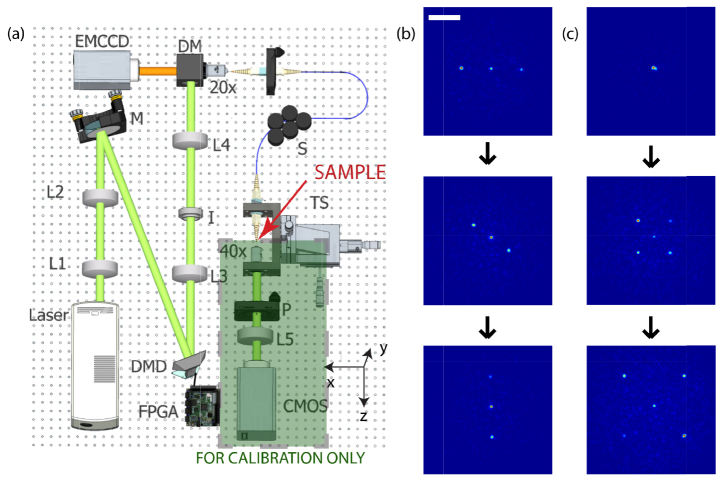
To use a MMF as an endoscope, we first calibrate it measuring its transmission matrix using the experimental apparatus shown in Fig. 2(a). A digital micro-mirror device (DMD TI-DLP Discovery 4100) controls the phase of the input wavefront using off-axis computer-generated holography [14]. A custom driver designed to interface the FPGA board from the DMD using Matlab allows for high-speed feedback operation. The FPGA board receives the phase values via USB and uses a lookup table with Lee Holograms corresponding to eight phase values between 0 and 2π to send the correct pattern onto the DMD [15]. Using this approach, the data sent through the USB cable is minimized to increase the refresh rate of the DMD when feedback is required. The spatial light modulator is imaged onto the back aperture of a 20x microscope objective, which couples the light onto the MMF. The distal tip of the fiber sits on a 2D translation stage and is imaged onto a CMOS camera using a 40x microscope objective. The system allows us to controls up to 4096 spatially independent input modes to measure the transmission matrix of the MMF using a Hadamard orthonormal basis set [12,14], as explained in the previous section. With knowledge of the transmission matrix, it is possible to create almost arbitrary intensity distributions at the distal tip of the MMF. Figures 2(b) and 2(c) show two examples of multiple foci generation.
Fig. 2.
Fiber endoscope system and scanning capability. (a) Experimental apparatus to calibrate the MMF, measure the speckle statistics and perform fluorescence imaging. The laser beam illuminates L1,L2,L3,L4 and L5: lenses; I: Iris; S: Scrambler; TS: Translation stage; P: Polarizer. BS: Beam splitter. (b-c) Different dynamic patterns created at the distal tip consisting of three and five focus spots. In the left column three spots rotate clockwise, while in the right column five spots expand from the center of the fiber. A movie of the foci moving can be found in the supplementary material (Visualization 1 (216.6KB, MOV) and Visualization 2 (119.2KB, MOV) ). Scale bar is 25µm.
In particular, for fluorescence imaging, we scan a focus spot across the sample, which defines the pixel location in the final image. The distal tip of the MMF collects the fluorescence emitted photons, which are directed to an EMCCD (Andor iXon3) at the proximal tip of the fiber. A dichroic mirror (Thorlabs DMLP567 longpass at 567nm) and a fluorescence filter are used to reject the excitation photons. Note that the EMCCD could be substituted with an avalanche photodiode or photomultiplier tube for faster operation because it acts as a bucket photon collector of the fluorescence photons coming back through the fiber. After the focus scanning is finished, a fluorescence image is reconstructed. The DMD scans the focus at high speed by direct control of the local FPGA. The theoretical resolution of the system is limited by the size of the speckle created by the MMF, which is a function of the illumination wavelength and the numerical aperture of the fiber.
4. Robustness of the endoscope calibration
An important aspect to consider in a MMF endoscope is the resilience of the calibration to external perturbations. The part of the endoscope that is most likely to suffer those perturbations is the distal tip of the MMF, for instance when inserted into the sample. We compare four different commercial MMFs that are representative of the options readily available: 200µm core diameter step-index (Thorlabs FT200EMT, 0.39NA), 100µm core diameter step-index (Thorlabs UM22-100, 0.22NA), 100µm core diameter graded-index (Newport F-MLD, 0.29NA) and 50µm core diameter graded-index (Corning® ClearCurve®). Table 1 summarizes the V-number, defined as , where NA is the numerical aperture, a is the radius and is the wavelength, as well as the number of propagating modes of each MMF. All the fibers except the 50µm core graded-index one have a number of modes larger than the number of input modes of our setup controls. The length of all the fibers is ~1.5m.
Table 1. Summary of V-number and Number of Propagating Modes for the Tested MMFs.
| MMF model | Core diameter (µm) | V-number | Number of propagating modes |
|---|---|---|---|
| Thorlabs FT200EMT | 200 | 460 | 85758 |
| Thorlabs UM22-100 | 100 | 129 | 6744 |
| Newport F-MLD | 100 | 171 | 7331 |
| Corning® ClearCurve® | 50 | 59 | 871 |
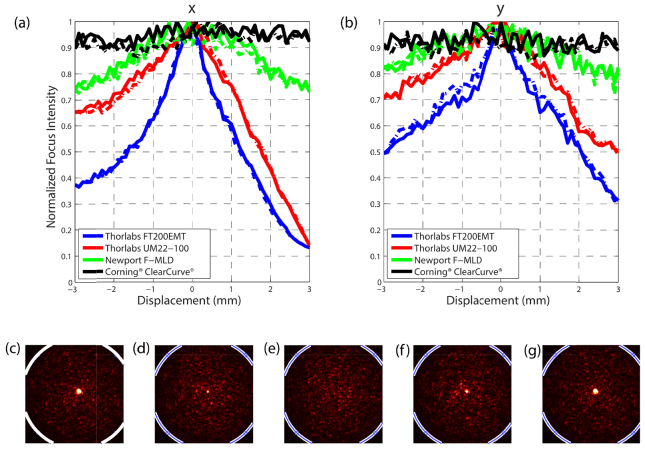
To quantify robustness to distal tip perturbations, we analyze the variation of the focus intensity while the distal tip of the fiber is moved. First, we calibrate the MMF measuring the TM, followed by projection onto the DMD of a hologram calculated to create a focus at the distal tip. We place the distal tip of the MMF on a translation stage and move it in the x and y plane as shown in Fig. 2. To obtain a more uniform speckle distribution at the output of the fiber we use a mode scrambler 20cm away from the distal tip. Additionally, the mode scrambler helps maintain the position of the rest of fiber fixed. We record the intensity of the focus for every 100µm of displacement. Figures 3 (a) and (b) shows the variation of the normalized focus intensity value. The solid line indicates the displacement from the origin and the dashed line indicates the displacement towards the origin to show we recover the original maxima. Both graded-index MMF show a more resilient focus intensity to movements up to 3 mm in both, x and y directions.
Fig. 3.
Multimode fiber resilience to distal tip perturbation. Intensity of the focus created using wavefront shaping as the distal tip is translated (a) in x and (b) y direction. The solid line indicates the intensity as the fiber moves away from the initial position. The dashed line indicates the intensity as the fiber moves towards the initial position. (c-g) Focus evolution while the Newport F-MLD MMF is perturbed (pressed with a finger) and released. The image is saturated to appreciate better the focus and the speckle field at the same time. The white curve delimits the border of the MMF.
A fully quantitative simulation of these results would require the specific profile of the fibers and the curvature function of each fiber. However, the result would be representative only for a given fixed curvature function. At a more fundamental level, these results can be explained using mode-coupling theory. If the bending produced to the MMF is a small perturbation, we can assume the shape of the eigenmodes in the bent region is (essentially) the same as in the straight part. The bending of the MMF can produce two effects: a change in the propagation constants of the modes in the bent fiber with respect to the straight fiber, and a coupling between propagating modes. The change in the propagation constants produces a small change in the output field since the perturbation is produced mostly at the end of the fiber. This effect is shown in Figs. 3(a) and 3(b) as the slow decrease of the peak intensity in both graded-index MMFs. To evaluate the difference in mode coupling between both types of MMF, we use the power mode-coupling equation [16]
| (4) |
which describes the evolution of the power of the eigenmodes, where is the modal power, is the attenuation coefficient and is the coupling coefficient between modes with principal mode numbers m and m’. The principal mode number m is defined as m = 2μ + |ν|, where μ is the radial index and ν the azimuthal index of the eigenmodes of the MMF. We assume the attenuation is negligible for the length of the fiber we use. The coupling strength favors coupling only between modes with [17]. Olshansky derived the coupling coefficient for both cases, graded index (GI) and step-index (SI) MMF:
| (5) |
where n is the core refractive index, k is the wave number in free space, a is the radius, m is the mode family number, M2 is the total number of modes, and is the power spectrum of the curvature function that depends inversely on the mode propagation constant difference between the two modes that are coupling. Coupling between nonadjacent family modes characterized by have a that is at least twice as large as the for and therefore a weaker coupling. The propagation constants of a step-index and a graded-index MMF of similar size and index values have values of the same order of magnitude while , resulting in a stronger coupling between modes in the step index fiber case. Therefore, we can infer the step index MMF exhibit greater mode coupling causing the intensity peak to decrease faster than in the graded index fibers.
Additionally, we test the validity of the calibration in a more uncontrolled case, namely when the fiber comes back to its original position after a perturbation. Figures 3(c)-3(g) show five snapshots of Visualization 3 (21.7MB, AVI) , corresponding to the intensity at the distal tip of the Newport F-MLD fiber as it is pressed with a finger and released. We observe the focus regains its primary enhancement without re-calibration.
5. Speckle intensity contrast and enhancement
We now investigate the relation between the fiber structure and the speckle pattern it produces, as well as the effect on wavefront shaping focusing enhancement. Examining the speckle pattern created by the various MMFs (Fig. 4) we observe different characteristic features. A common parameter used to characterize the speckle is the intensity contrast, C, defined as
| (6) |
where 〈⋯〉 indicates an ensemble average and σI denotes the variance of the intensity [18]. A fully developed speckle created by the interference of a vast number of partial waves with phases uniformly distributed over 2π has associated a contrast value of 1. A lower value of C indicates deviations from this fully developed speckle regime and can be caused by the combination of a large number of phasors with a nonuniform phase statistics, which is usually referred as a partially developed speckle [19]. Because wavefront shaping combines multiple speckle output modes to create a bright focus, a higher contrast enables a larger constructive interference among different speckles, while a lower contrast produces the opposite effect and hence a lower intensity enhancement factor.
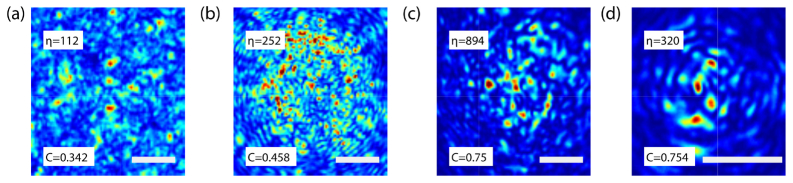
Fig. 4.
Speckle intensity image, speckle contrast, and enhancement at the distal tip of different fibers. (a) Thorlabs FT200EMT, (b) Thorlabs UM22-100, (c) Newport F-MLD, (d) Corning® ClearCurve®. The bottom insets indicate the speckle contrast, C, for each fiber while the top insets indicate the mean of the enhancement of the focus created at 1000 different output modes. Scale bar is 25µm.
We record the intensity of the light exiting the distal tip of the fiber for each Hadamard element projected in the DMD and calculate C for each intensity image. It is important to notice the polarizer between the distal tip of the fiber and the camera used to measure only one polarization. The pixel size in each case is smaller than the speckle grain. Figures 4(a)-4(d) shows the normalized intensity image of the speckle at the distal tip of different MMFs under similar illumination conditions (during the TM measurement). Undoubtedly, each fiber produces a speckle pattern that has distinctive contrast and intensity distributions. We calculate the mean contrast value for each MMF and display it at the bottom inset of each plot. From those values, we can determine that the graded index fibers (c) and (d), produce speckle fields closer to a fully developed speckle compared to the other two step-index fibers.
For each fiber we also calculate the mean enhancement for foci created at 1000 different output modes, each corresponding to a different location. As expected, there is a significant correlation between the intensity contrast and the mean focus enhancement.
Note also, that the focus spot size for each fiber is defined by the speckle grain size, which is determined by the wavelength and the NA of the fiber. In the four cases studied here this spot size is within 10% difference.
It is interesting to notice that while in modal noise experiments, the aim is to reduce the contrast to 0 and destroy the speckle structure to avoid errors [20], in our case we look to maximize this contrast.
6. Fluorescence microscopy
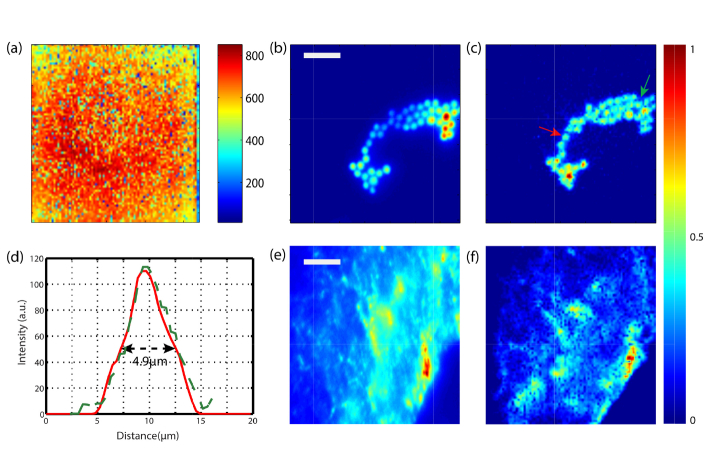
To demonstrate the feasibility of the MMF as an endoscope, we image different fluorescence samples. We select the Newport F-MLD due to the large diameter core and good performance in terms of enhancement and robustness. Once the measurement of the TM is finished, and the MMF calibrated, we create a focus at the distal tip in every output mode at a time. Figure 5(a) shows a colormap of the peak to background ratio achieved in each of the 7392 foci points created at the distal tip using 4096 input modes. The plot reflects the intensity of the focus created is consistent and quite uniform, both characteristics required to have a working scanning microscope. After the calibration, we place a fluorescence sample ~100µm far from the distal tip, corresponding to the output plane where the MMF had been calibrated. We project all the input patterns corresponding to the scanning focus at the distal tip and measure the fluorescence signal that is emitted back through the fiber using an EMCCD. This approach converts the MMF into a scanning fluorescence microscope. The field of view of the endoscope is related to the core diameter, the numerical aperture and the distance from the distal tip to the imaging plane. In our experiment, the field of view is 80µm x 80µm. The numerical aperture of the fiber limits the size of the focus and ultimately the resolution achievable by the endoscope. Figure 5(b) shows an experimental image of a sample composed of 4µm diameter fluorescence beads, imaged with a fluorescence widefield microscope. Afterwards, we image the same sample using the MMF endoscope obtaining the image shown in Fig. 5(c). The difference in the location of the intensity maxima between both images is because the beads lay in different planes. To demonstrate the endoscope can resolve the beads, Fig. 5(d) plots a line scan of two fluorescence beads pointed by the red and green arrows in Fig. 5(c). The full with at half maximum of the line scans corresponds to 4.9µm. The spot size is uniform across the field of view as shown in Fig. 5(d). Therefore, the corresponding point spread function of the system and the resolution is close to 2µm. Additionally, Figs. 5(e) and 5(f) show a more interesting and complex sample, a monkey brain slice labeled with Cy3, again imaged with a widefield fluorescence microscope and using the MMF endoscope respectively. The correspondence between both images demonstrates the capacity of the endoscope to image this type of samples.
Fig. 5.
Demonstration of the single-fiber endoscope. (a) Colormap of the peak-to-brakground ratio of each focus created at the distal tip of the fiber. (b) Sample of 4µm fluorescence beads imaged with fluorescence widefield microscope. (c) The same sample imaged with the MMF scanning endoscope. (d) Line scan of two beads pointed by the red and green arrows in (c). (e) A brain monkey slice labeled with Cy3 imaged using a fluorescence widefield microscope and (f) using the MMF scanning endoscope. Scale bar is 20µm
7. Discussion and conclusions
We experimentally demonstrated the feasibility of converting a single MMF into a fluorescence scanning endoscope. Although the MMF calibration is sensitive to external perturbation, the selection of the right fiber plays an important role. Comparing four different MMF (two step-index MMF and two graded-index MMF) we show that both graded-index fibers are more robust to displacements at the distal tip. Remarkably, the focus created after the calibration can withstand more than 3 mm translation of the fiber distal tip in the x and y directions. Similar experiments have shown robustness of the fiber to displacements along the axial direction as well [21].
In addition, we showed the enhancement of a focus created with the TM information depends on the fiber characteristics. The number of propagating modes of the fiber is not as critical as the speckle contrast. Different MMFs create a speckle field with distinct intensity contrast. Examining the intensity contrast of the speckle we can infer how good the quality and enhancement of the focus will be. It is important to notice that, in our study, the graded-index outperformed the step-index MMFs considered.
This study opens up the possibility to predict the performance of other MMFs based on the value of the intensity speckle contrast. A deeper study could reveal the relation of the statistics of the fiber speckle with its physical parameters, which could help predict the performance or guide the design of the optimal MMF.
Furthermore, the high-speed modulation offered by the DMD implementation is key to many imaging experiments such as in the use of calcium indicators for neuron activity studies [22]. Despite the current system using the EMCCD requires a few seconds to obtain the complete florescence image, updating the system with a fast photomultiplier tube and a data acquisition card would allow video frame rates as required for in-vivo experiments. Besides imaging only one axial plane, the system can also be extended to image multiple planes by calibrating the fiber at multiple output planes. This, in turn, allows scanning the focus in the axial direction by just modifying the input wavefront.
These results are promising towards the implementation of a MMF endoscope that could be used for example to image the brain in small rodents, with only a small part of the MMF introduced inside the animal.
Supplementary Material
Acknowledgments
We thank Dr. Shay Ohayon for useful discussions and the preparation of the brain monkey sample.
Funding
National Institute of Health (NIH) Award REY026436A.
References and Links
- 1.Oh G., Chung E., Yun S. H., “Optical fibers for high-resolution in vivo microendoscopic fluorescence imaging,” Opt. Fiber Technol. 19(6), 760–771 (2013). 10.1016/j.yofte.2013.07.008 [DOI] [Google Scholar]
- 2.Gover A., Lee C. P., Yariv A., “Direct transmission of pictorial information in multimode optical fibers,” J. Opt. Soc. Am. 66(4), 306–311 (1976). 10.1364/JOSA.66.000306 [DOI] [Google Scholar]
- 3.Papadopoulos I. N., Farahi S., Moser C., Psaltis D., “High-resolution, lensless endoscope based on digital scanning through a multimode optical fiber,” Biomed. Opt. Express 4(2), 260–270 (2013). 10.1364/BOE.4.000260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Farahi S., Ziegler D., Papadopoulos I. N., Psaltis D., Moser C., “Dynamic bending compensation while focusing through a multimode fiber,” Opt. Express 21(19), 22504–22514 (2013). 10.1364/OE.21.022504 [DOI] [PubMed] [Google Scholar]
- 5.Čižmár T., Dholakia K., “Exploiting multimode waveguides for pure fibre-based imaging,” Nat. Commun. 3, 1027 (2012). 10.1038/ncomms2024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Choi Y., Yoon C., Kim M., Yang T. D., Fang-Yen C., Dasari R. R., Lee K. J., Choi W., “Scanner-free and wide-field endoscopic imaging by using a single multimode optical fiber,” Phys. Rev. Lett. 109(20), 203901 (2012). 10.1103/PhysRevLett.109.203901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bianchi S., Di Leonardo R., “A multi-mode fiber probe for holographic micromanipulation and microscopy,” Lab Chip 12(3), 635–639 (2012). 10.1039/C1LC20719A [DOI] [PubMed] [Google Scholar]
- 8.Mahalati R. N., Gu R. Y., Kahn J. M., “Resolution limits for imaging through multi-mode fiber,” Opt. Express 21(2), 1656–1668 (2013). 10.1364/OE.21.001656 [DOI] [PubMed] [Google Scholar]
- 9.Caravaca-Aguirre A. M., Niv E., Conkey D. B., Piestun R., “Real-time resilient focusing through a bending multimode fiber,” Opt. Express 21(10), 12881–12887 (2013). 10.1364/OE.21.012881 [DOI] [PubMed] [Google Scholar]
- 10.Plöschner M., Tyc T., Čižmár T., “Seeing through chaos in multimode fibres,” Nat. Photonics 9(8), 529–535 (2015). 10.1038/nphoton.2015.112 [DOI] [Google Scholar]
- 11.Saleh B. E. A., Teich M. C., Fundamentals of Photonics, 2nd ed. (Wiley, 2007). [Google Scholar]
- 12.Popoff S. M., Lerosey G., Carminati R., Fink M., Boccara A. C., Gigan S., “Measuring the transmission matrix in optics: an approach to the study and control of light propagation in disordered media,” Phys. Rev. Lett. 104(10), 100601 (2010). 10.1103/PhysRevLett.104.100601 [DOI] [PubMed] [Google Scholar]
- 13.Schreiber H. B., “Phase shifting interferometry,” in Optical Shop Testing, Malacara D. (John Wiley & Sons, 2007), pp. 547–666. [Google Scholar]
- 14.Conkey D. B., Caravaca-Aguirre A. M., Piestun R., “High-speed scattering medium characterization with application to focusing light through turbid media,” Opt. Express 20(2), 1733–1740 (2012). 10.1364/OE.20.001733 [DOI] [PubMed] [Google Scholar]
- 15.Caravaca-Aguirre A. M., Niv E., Piestun R., “High-speed phase modulation for multimode fiber endoscope,” in Imaging and Applied Optics 2014, OSA Technical Digest (Online) (Optical Society of America, 2014), p. ITh3C.1. [Google Scholar]
- 16.Kaminow I., Li T., Willner A. E., Optical Fiber Telecommunications VI: Components and Subsystems (Academic Press, 2013). [Google Scholar]
- 17.Olshansky R., “Mode coupling effects in graded-index optical fibers,” Appl. Opt. 14(4), 935–945 (1975). 10.1364/AO.14.000935 [DOI] [PubMed] [Google Scholar]
- 18.Apostol A., Dogariu A., “Non-Gaussian statistics of optical near-fields,” Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 72(2), 025602 (2005). 10.1103/PhysRevE.72.025602 [DOI] [PubMed] [Google Scholar]
- 19.Goodman J., Speckle Phenomena in Optics, 1st ed. (Roberts and Company Publishers, 2010). [Google Scholar]
- 20.Ha W., Lee S., Jung Y., Kim J. K., Oh K., “Acousto-optic control of speckle contrast in multimode fibers with a cylindrical piezoelectric transducer oscillating in the radial direction,” Opt. Express 17(20), 17536–17546 (2009). 10.1364/OE.17.017536 [DOI] [PubMed] [Google Scholar]
- 21.Aguirre A. M. C., Piestun R., “Robustness of multimode fiber focusing through wavefront shaping,” in Latin America Optics and Photonics Conference (2014), Paper LTh4A.23 (Optical Society of America, 2. 014), p. LTh4A.23. [Google Scholar]
- 22.Martial F. P., Hartell N. A., “Programmable illumination and high-speed, multi-wavelength, confocal microscopy using a digital micromirror,” PLoS One 7(8), e43942 (2012). 10.1371/journal.pone.0043942 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.