In situ calibration of position detection in an optical trap for active microrheology in viscous materials

Abstract

In optical trapping, accurate determination of forces requires calibration of the position sensitivity relating displacements to the detector readout via the V-nm conversion factor (β). Inaccuracies in measured trap stiffness (k) and dependent calculations of forces and material properties occur if β is assumed to be constant in optically heterogeneous materials such as tissue, necessitating calibration at each probe. For solid-like samples in which probes are securely positioned, calibration can be achieved by moving the sample with a nanopositioning stage and stepping the probe through the detection beam. However, this method may be applied to samples only under select circumstances. Here, we introduce a simple method to find β in any material by steering the detection laser beam while the probe is trapped. We demonstrate the approach in the yolk of living Danio rerio (zebrafish) embryos and measure the viscoelastic properties over an order of magnitude of stress-strain amplitude.

1. Introduction

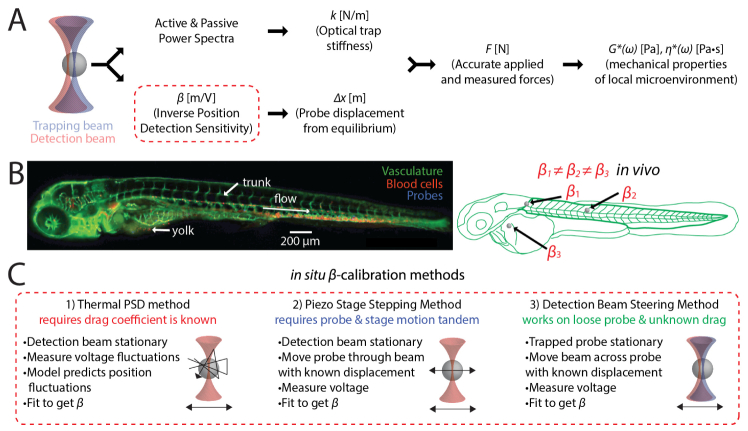
Optical trapping is of broad utility in characterizing molecular and microscale biophysical interactions [1, 2]. In this phenomenon, the electric field gradient of light confines dielectric particles [3–5]. The technique can accurately measure pN-scale forces at length scales from µm to nm [6, 7]. In optical trap-based active microrheology, mechanical properties of the local microenvironment are determined by measuring the induced motion of a trapped particle due to the applied force [8–14]. Briefly, near infrared light is used to apply spring-like oscillations that drive embedded probes used as local mechanical sensors. Many biomaterials and specimens commonly exhibit nonlinear viscoelasticity [15, 16]. This method can reveal the mechanical properties of three-dimensional (3D) tissue microenvironments in vivo. Viscoelastic response is accessible across a broad range of frequencies. By modulating the forces on the trapped particle, it can probe stress-strain behavior. Quantitation of the underlying tissue rheological properties depends on accurate application and measurement of forces. This requires knowledge of the optical trap stiffness, k, and ∆x, the probe’s displacement from equilibrium. We can determine ∆x by calibrating the position sensitivity of the detector, 1/β, a parameter that allows conversion of the voltage detected to the probe’s displacement (in nanometers). The ability to measure forces in biological materials including tissues is non-trivial as both k and β vary from probe to probe due to intrinsic optical and mechanical heterogeneities. Using an average value of either k or β (from either a proxy material or even the experimental sample) results in up to 20-fold overestimation of tissue material properties, as we showed previously [15]. This necessitates in situ calibration of k and β, i.e. on-the-fly calibration of each bead. Mechanical properties of viscoelastic samples can be determined from the thermal power spectrum and the active power spectrum (obtained by oscillating the trap position), as shown in Fig. 1(a) [15–20]. An advantage of this approach is that k is determined in situ from the spectra of each probe. However, β is not given by the spectra and requires an additional measurement for samples like the optically heterogeneous tissues of the zebrafish embryo in Fig. 1(b). In this manuscript, we focus on the determination of β in viscous materials.

Fig. 1.

Calibration for active microrheology in vivo. (a) Determining micromechanical properties requires calibration of the optical trap stiffness, k, and the inverse position detection sensitivity β (i.e. the V-nm conversion factor) of the detection system used to measure probe displacements. (b) in vivo (such as in the depicted zebrafish embryo), probes lie in different positions along the beam axis and in regions with different optical properties. Thus, both calibrations must be conducted for every probe measured. In some regions, probes may be free to fluctuate in position because they are not tightly confined (e.g. in the viscous yolk), or are subject to flow (as in perivasculature). (c) Two common methods used to calibrate β are (1) the thermal power spectral density (PSD) method and (2) the piezo stage stepping method. In the PSD method, the probe is trapped and allowed to fluctuate due to thermal motion while the voltage on the detector is recorded. Fluctuations in voltage are related by β to position fluctuations predicted by a fluctuation-dissipation model that requires knowledge of the probe radius and the drag coefficient. In the piezo stage stepping method, the probe is stepped through the detection beam as the stage is moved through known distances, while the voltage on the detector is recorded. This works well unless the probe and stage motions are not in tandem. (3) To calibrate under these conditions, the trap holds the probe stationary while the detection beam scans across it.

A common and effective way to measure probe displacements in optical traps is by back focal plane interferometry [6, 7]. When a probe of diameter d is trapped at the center of the beam waist of a laser with wavelength λ focused by an objective in its image plane, some light undergoes scattering due to light-probe interactions and (in the dipole limit d < λ) produces spherical waves [21]. This scattered light slightly diverges from the fraction of light that does not undergo scattering. Thus, shifts in relative phase between these two wavefronts give rise to a pattern of constructive and destructive interference fringes. The light is collected by a high numerical aperture (NA) condenser aligned for Köhler illumination. The image planes of the field diaphragm iris and the objective are conjugate and image into each other (forming a Keplerian telescope) [22]. Behind the condenser, a dichroic mirror reflects the detection beam onto a detection lens that is positioned to relay the image at the back focal plane of the condenser onto a quadrant photodiode (QPD). In this configuration, displacements of the probe cause rotation of the detection beam in the image plane and corresponding translations of the beam at both the back-aperture of the condenser and on the detection QPD. The interference pattern is mapped onto the QPD, so lateral displacements of the probe relative to the detection beam in the imaged plane result in changes in voltage. The voltage response ∆S_x is linearly related to probe translations for small displacements (∆x ~150 nm from the probe center). Thus, calibrating the position detection sensitivity consists in finding the V-nm relation ∆x = β•S_x in the linear response regime.

A number of methods may be used to calibrate β, with each applicable in different circumstances as outlined in Fig. 1(c). When the temperature and the Brownian dynamics of the probe and material are known, methods based on recording the thermal power spectrum are frequently used. But since these depend on independent knowledge of the dynamic viscosity or related frictional terms, they are generally inapplicable to microrheology [23]. Additionally, biomaterials may exhibit glassy dynamics that lie outside the regime of thermal equilibrium [24]. In another method, the trap is moved rapidly while the impulse response of the QPD is tracked as the probe relaxes to its new position, but this too relies on the drag coefficient [25]. In materials like tissue with physical properties which are not known a priori, determination of β requires other methods. Tolić-Nørrelykke et al. demonstrated that by imposing a known oscillating flow in combination with the power spectrum method, both the drag coefficient and β can be determined [26]. This approach requires that the induced motion in the liquid be synchronized with an imposed low-frequency stage, which may not be the case in biphasic materials. Hence, this method will not work in samples that show nonlinearities or elastic effects. A direct method is to scan the probe across the waist of the detection beam by employing a piezoelectric nanopositioning system (NPS) to step the sample stage with known displacements [7]. This ‘piezo method’ requires calibration of the NPS, which can be accomplished by imaging displaced probes with a camera of known pixel size. This method works in nonlinear or elastic materials where the probe motions are confined and remain correlated to the stage displacements, including some tissues with fine meshwork [15, 16]. However, this is not the case in more fluid-like environments, wherein yet other methods must be used. Dutov and Scheiber’s dual trapping method employs a fixed and moving trap and a pair of QPDs. β is found by displacing the probe with the movable trap while holding with the fixed trap, and additionally trapping the probe in both traps separately [27]. In a simpler method for single beam setups, the fast-sweeping method of Vermeulen et al. oscillates the trapping laser at frequencies sufficiently high to impart little appreciable motion on the probe [28]. However, for materials with unknown drag coefficient, especially at high laser power, this motion may be appreciable. Here we employ a similar beam steering approach, but instead use a weak secondary detection beam to scan across the probe while it is confined in the trap. This method is applicable to probes that are either weakly attached to or freely moving through the microenvironment, such as in the perivascular microenvironment in the zebrafish trunk. It also works for probes that are strongly attached or confined in a solid-like microenvironment, and the microenvironment may be nonlinear, viscous, elastic or viscoelastic with unknown Brownian dynamics. We first test the method in water, reconstituted collagen and surrogate basement membrane hydrogels, and a liquid silicone solution. The method produces independent β measurements in good agreement with the power spectrum method and the piezo scanning method. We then use it to perform active microrheology measurements in the fluid-like yolks of living zebrafish embryos.

2. Methods and materials

2.1 Optical trapping

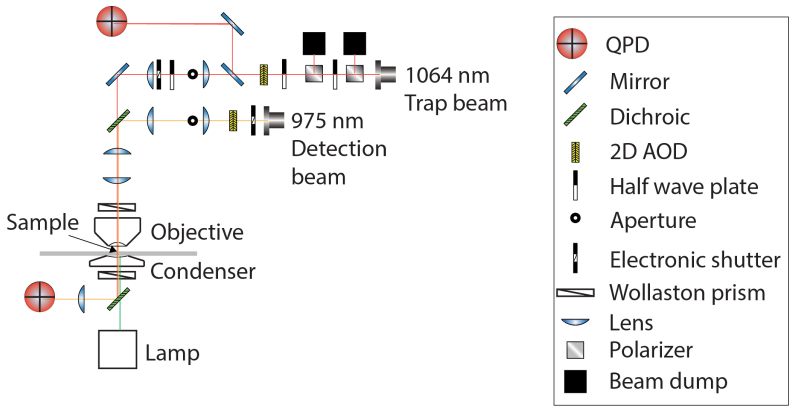
Our optical setup is depicted in Fig. 2. A 1064 nm trapping beam (IPG Photonics, #YLR- 20-1064-Y11) and a 975 nm detection beam (Lumics, #LU0975M00-1002F10D) are each steered with dual axis acousto-optic deflectors (AODs) (IntraAction, DTD274HD6). In both cases, the doubly diffracted (1st order in both dimensions) beam is selected with an iris. Signals are sent to the AODs by radio frequency (RF) generating cards (Analog Devices, #AD9854/PCBZ) with onboard temperature controlled crystal oscillators (TCXO) (Anodyne Components, ZKG10A1N-60.000M). The cards are controlled by digital outputs from a data acquisition (DAQ) card (National Instruments, PCIe-5871R FPGA). AODs are mounted on 5-axis adjustable mounts (Newport, New Focus 9081) to facilitate alignment to meet the Bragg condition. Each beam is shuttered electronically (Uniblitz, VS1452Z0R3). Polarizing beam splitter cubes (Thorlabs, PBS23) linearly polarize the trapping beam. Before entering the AOD, the beam is attenuated manually by half-wave plates (Thorlabs, WPH05M-1064) or electronically via analog output from a data acquisition (DAQ) card (National Instruments, PCIe-5871R FPGA). To detect trap displacement, a beam sampler mirror (Thorlabs, BSF10-C) and neutral density (ND) filter (Thorlabs, NENIR210B) after the AOD direct a small amount of power (~1%) onto the ‘trap’ quadrant photodiode (QPD) (First Sensor, QP154-Q-HVSD). This QPD is not in a conjugate plane, so changes in QPD voltage are correlated to beam displacements. The trapping beam is expanded by a lens pair (Thorlabs, LA1509-C, 100 mm; AC508- 200-B, 200 mm) and directed into the microscope (Nikon, Eclipse Ti-U) backport with a broadband mirror (Thorlabs, BB1- EO3IR). The detection beam is expanded by a lens pair (Thorlabs, LA1131-C, 50 mm; AC508- 200-B, 200 mm) and then coupled into and aligned with the trapping beam by a dichroic mirror (Chroma, T1020LPXR). A third lens pair (Thorlabs, LA1131-C, 50 mm; LA1384-CA, 125 mm) expands both beams so the trapping beam slightly overfills the back aperture of the objective (Nikon, (MRDO7602 CFI-PLAN-APO VC60XA WI 1.2NA). A dichroic filter cube (Chroma, ZT1064rdc-2p) sends both beams into the objective. A high numerical aperture (NA), long working distance (WD) condenser (Nikon, WI 0.9NA) collects the light from the objective. Behind the condenser, a dichroic mirror (Chroma, ZT1064RDC-2P) directs the detection beam through a relay lens that is positioned to image the back focal plane of the condenser onto the detection QPD. The trapping beam is removed from the path to the QPD with a bandpass filter (Chroma, ET980/20X). Time-correlated trap and probe QPD signals are collected by analog inputs of the DAQ card. Control and data collection are conducted in custom programs (National Instruments, LabVIEW). A charge-coupled device (CCD) camera (Andor, Ixon DU-897E-C50-#BV) is mounted to the optical table. This enables position adjustments in X, Y and Z to place the camera in a plane conjugate to the trap beam AOD, back-aperture of the condenser, and detection QPD.

Fig. 2.

Schematic of the optical path of dual beam-steering optical trapping microscope. Both the primary trapping beam and the secondary detection beam have two-dimensional acousto-optical deflectors (AOD) in the optical path. Two telescope lens pairs collimate, expand and image the back focal plane of the objective onto both AODs. First, a probe is trapped and the secondary beam is steered across it while the detection QPD signal is recorded to calibrate β. Then the trap beam is alternately oscillated and held stationary in a sequential measurement for both the active-passive calibration of trap stiffness and for broadband active microrheology measurements.

2.2 Preliminary setup and $\beta$ calibration by thermal power spectrum (PSD) method

Prior to experiments, the Hz-nm conversion is calibrated by attenuating and focusing the beam on a coverslip and imaging the backscattered beam on the CCD camera. Before each experiment, beams are aligned using a control sample of carboxylated beads (1μm diameter) in water. First, the trapping beam is oscillated and centered on the trap QPD by adjusting the relay mirror between the trap QPD and the beam sampler mirror. Next, the XYZ motorized stage (Prior, #77011201) moves a bead into the trap. As the AOD oscillates the trap, the detection beam is co-aligned with the trapping beam by adjusting the dichroic mirror that couples the trapping and detection beams. Oscillation and adjustment are conducted iteratively in each lateral dimension. Finally, the detection QPD is adjusted so the signal from a trapped bead in equilibrium falls on its center. After beam alignment, the thermal power spectrum is recorded (blocking with eight separate measurements) while the trap is oscillated at 500 Hz with an amplitude of 50 nm. Position-time data is Fourier transformed into the frequency domain. We measure the viscosity and β by fitting the spectrum to a Lorentzian to check the setup and alignment of the microscope. Finally, the bead position on the CCD camera is determined by centroid-fitting an image of the bead on the camera, and this position is used as the lateral trap position.

2.3 Trap centering and $\beta$ calibration by detection beam steering (FFT) method

After alignment, measurements are then conducted in the sample material. A probe (bead) is selected and brought to the lateral trap position by moving the XYZ piezo stage (Mad City Labs, #77046501). With the objective focus in the specimen plane, the condenser is adjusted to Köhler illumination. To axially center the probe, the objective steps vertically through 49 steps and a bright field image is taken with the CCD camera at each step. The probe is then moved into the plane with the highest intensity image. Once the probe is centered, the stage, trap, and probe are held stationary. The detection beam position then scans across the center of the probe. During this scan, the beam oscillates sinusoidally for a measurement time t_msr of 1 s while the detection QPD records the voltage at a sampling rate of 80 kHz. The frequency f_drive is 1 kHz and the displacement amplitude is 55 nm. The resulting voltage time series are then Fourier transformed into the frequency domain with a frequency bandwidth ∆f of 1 Hz, giving a voltage frequency spectrum, which exhibits a strong peak at f_drive. Because the drive period (1 ms) divides evenly into t_msr, the peak is a single datum rather than having finite width [26]. The voltage at f_drive is then divided into the displacement amplitude of the detection beam to give β in nm•V⁻¹. The process can be conducted consecutively in each dimension.

2.4 Active-passive trap stiffness calibration and active microrheology

Following β calibration, a set of measurements is conducted to give both k and the complex modulus of the microenvironment over a range of frequencies and stress-strain amplitudes. In dynamic mechanical analyses, applying oscillatory stress σ = σ₀ sin(ωt + δ) to a material results in a strain ε = ε₀ sin(ωt), where t is time, f is oscillation frequency, ω = 2πf is the angular frequency, ε₀ and σ₀ are the stress and strain amplitudes respectively, and δ is the angular phase by which strain response lags stress perturbation. For purely elastic responses δ = 0 and for purely viscous responses δ = π/2; for viscoelastic responses 0 > δ > π/2. The complex modulus G* ≡ σ₀/ε₀ separates into a purely elastic component, the shear storage modulus G’ ≡ G*cos(δ), and a purely viscous component, the shear loss modulus G” ≡ G*sin(δ), since G* ≡ G’ + iG” and i² ≡ −1.

To measure the complex modulus with an optical trap, we get the probe’s passive and active power spectra from its passive motion and active motion, as described previously [15–19]. First, the probe’s position time series x_U(t) is recorded with the trap stationary to get the passive power spectrum, $P_U(\omega )\equiv 〈{\left|{\tilde{x}}_U(\omega )\right|}^2〉$, where brackets denote the time average and ${\tilde{x}}_U(\omega )$is the Fourier transform of x_U(t). Then, we oscillate the trap over a range of frequencies while the position-time series of both the trapping laser, x_L(t), and probe, x_dr(t), are recorded. These are Fourier transformed to ${\tilde{x}}_L(\omega )$ and ${\tilde{x}}_{dr}(\omega )$ respectively to yield the active power spectrum, ${\tilde{R}}_L(\omega )\equiv \frac{{\tilde{x}}_{dr}(\omega )}{-i\omega {\tilde{x}}_L(\omega )}$. The trap stiffness k is then found from the spectra via the relation $k=\frac{\text{Re}\{{\tilde{R}}_L(\omega )\}}{P_U(\omega )}$, where $\text{Re}\left\{\right\}$ denotes the real component. The friction relaxation spectrum ${\tilde{\gamma }}_D(\omega )$ is found by solving the equation ${\tilde{\gamma }}_D(\omega )+i\omega m=-\frac{k}{i\omega }\left(\frac{1}{i\omega {\tilde{R}}_L(\omega )}+1\right)$, where m is the probe’s mass. The complex modulus is given by the equation $G*(\omega )=\frac{i\omega {\tilde{\gamma }}_D(\omega )}{6\pi a}$, where a is the probe radius.

In the active measurements, we displace the trap with a complex waveform that allows multiple frequencies to be probed simultaneously (multiplexed) to reduce measurement time. The waveform consists of 20 superposed sine waves of equal amplitude at frequencies ranging 2 Hz – 12,809 Hz. The frequencies form a set of logarithmically distributed prime numbers to ensure distinct harmonics. Each frequency was alternately offset in phase by 0°, 45°, −45°, or 90° to minimize the maximum trap displacement, which was 200 nm, within the linear regime of the trapping and detection lasers. Each measurement consisted of 7 sequential pulses, where each pulse consisted of 2 s active motion followed by 2 s passive motion. Pulses were processed separately and resulting moduli were averaged for each probe. The optical trapping potential is harmonic near the trap center (within ~400 nm or half the beam waist). Accordingly F = -k∆x, where k is the trap stiffness, ∆x is the probe’s displacement from the trap center, and F is the optical force on the probe. This assumption holds if the mesh size is sufficiently small in comparison to the size of the bead. To examine the stress-strain behavior of these materials, we keep the laser power constant but modulate the trap oscillation amplitude. Since trap displacements modulate both stress and strain concurrently, we report the stress-strain amplitude in terms of trap displacement amplitude (per frequency) in nanometers. Measurements were conducted at successively higher amplitudes, first with waveforms composed of sines with amplitudes 2 nm, then with 5 nm, and 20 nm per frequency. The data from the detection QPD was acquired at a sampling rate of 80 kHz. In all samples, we measured only probes at distances exceeding ~30 µm away from the cover slip surface to minimize drag in consideration of Faxén’s law [1].

2.5 Silicone solutions

Polydimethylsiloxane (PDMS) (Dow Corning Sylgard 184 silicone elastomer base) was combined with Sylgard 184 silicone curing agent at a 10:1 ratio in a weighing boat on a digital scale. 20 µl of bead/sterile PBS solution of 5 × 10⁸ beads/mL of monodisperse 1 µm rhodamine carboxylated fluorospheres (Thermofisher #F8821) was added during 10 min of thorough mixing with a pipette tip. A flow chamber was made using two strips of double sided scotch tape, a No. 1.5 cover slip and a microscope slide. With vacuum pressure applied to one end of the chamber, a small volume of the solution was pulled in from the other end so no air bubbles remained. Samples were measured immediately and only within 30 min of initial mixing. Basement membrane ECM hydrogels (Matrigel^®, Corning #354230, Lot# 3032578) were prepared as previously described [12]. Rat tail collagen I hydrogels (BD Biosciences, San Jose, CA, USA) were prepared as previously described [16, 29, 30].

2.6 Animal studies

Animal studies were conducted under protocols approved by the National Cancer Institute, National Institute of Child Health and Human Development and the National Institutes of Health Animal Care and Use Committee. Wild type and transgenic (Tg(fli-1:eGFP)/Tg(gata-1:dsRed)) zebrafish (Danio rerio) were maintained at 28.5°C on a 14 h light/10 h dark cycle according to standard procedures and as previously described [15, 31]. Transgenic fish were kindly provided by Dr. Raman Sood, NHGRI core. Embryos were obtained from natural spawning and raised at 28.5°C and maintained in egg water containing 0.6 g sea salt per liter of DI water. 2 nL of monodisperse of 1 µm rhodamine carboxylated fluorospheres (Thermofisher #F8821) at 5 × 10⁸ beads/mL in sterile PBS was microinjected into the zebrafish embryo yolk. Between 10 and 16 h post fertilization (hpf), embryos were transferred to egg water. To inhibit melanin formation and increase optical transparency, egg water was supplemented 1:4500 with a solution of 7.5% w/v phenylthiourea (PTU, Sigma P5272) in DMSO. Embryos were then returned to the incubator at 28.5°C and checked for normal development and widely dispersed beads daily using fluorescence microscopy. The embryo shown in Fig. 1(b) was imaged on a Zeiss LSM780 confocal fluorescence microscope 144 h post fertilization (hpf). Mechanical characterization was performed 48 hpf. Zebrafish embryos were anesthetized in 0.4% buffered tricaine, then embedded in a lateral orientation in 1% low melting point agarose (NuSieve GTG agarose, Lonza), and allowed to polymerize on a 50 mm glass- bottom dish with cover glass no. 1.5 thickness. Egg water supplemented with tricaine was added to the agarose hydrogel for the entire time of data acquisition and used as the immersion medium. The maximum time of data acquisition on each embryo did not exceed 4 h.

2.7 Small angle oscillatory shear bulk rheology

All bulk rheology measurements were carried out at Georgetown University Institute for Soft Matter Synthesis and Metrology using an Anton Paar Physica MCR 301 rheometer equipped with a PP-50 measuring plate (parallel, 50 mm diameter). PDMS was mixed with crosslinking agent as above and de-gassed under vacuum for 20 minutes. 450 µl of the solution was spread onto the surface. The parallel plate was lowered into contact with the sample to a height 0.5 mm above the surface, and excess fluid was removed from the periphery. Measurements were carried out in triplicate.

3. Results

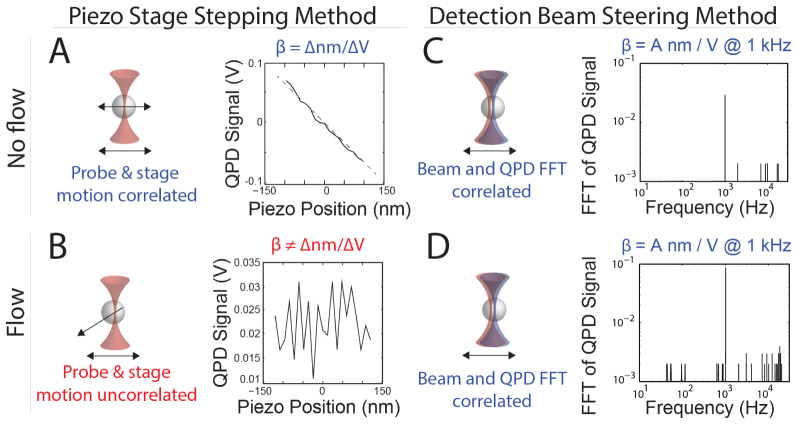
Figure 3 shows representative data comparing β calibrations by the piezo stage stepping and detection beam steering methods. Figures 3(a) and 3(c) show data from probes injected into a solid-like region of the tail of a zebrafish embryo. Figures 3(b) and 3(d) show data from a fluid-like region of the yolk. During piezo calibration, the probe in the tail was confined and moved in tandem with the piezo stage, shown in Fig. 3(a). The resulting QPD signal, in V, in the dimension parallel to the stage movement is plotted against the position in nm. β is determined simply by fitting a line in the central, linear response region ( ± ~150 nm from the probe center). Multiple samples of the voltage are averaged before fitting to reduce noise. This is performed in each lateral dimension. The piezo calibration fails for unconfined probes. Figure 3(b) shows the resulting signal for the probe in the yolk, which is noisy as it is likely that during acquisition the bead cannot be continuously observed in the detection beam path. To overcome this limitation, we instead employ the detection beam steering (FFT) method. The method works both for confined probes as in the zebrafish tail in Fig. 3(c), or unconfined probes as in the zebrafish yolk in Fig. 3(d). To avoid noise at lower frequencies (below ~60 Hz), we oscillate at a single high frequency of 1 kHz. The signal-to-noise ratio can be improved by increasing the collection time, or by averaging a number of separate measurements.

Fig. 3.

Methods for calibrating the V-nm conversion factor β. In the piezo stage stepping method, QPD voltage is recorded while the stage is stepped through the detection beam in defined steps of 12 nm by moving the sample stage via the piezo controller. (a) In viscoelastic solids, the probe moves with the sample stage, so the recorded voltage correctly corresponds to the linear response of the detector to the interference pattern in the back focal plane of the condenser caused by the probe. Linear regression is used to get β from the voltage and position data. Data from the solid-like region in the tail of a zebrafish embryo. (b) In liquid or liquid-like samples, such as the zebrafish yolk, the probe may move freely and is not constrained to move in tandem with the stage, so the signal cannot be used to find the positional sensitivity. In the detection beam steering method, the probe is first trapped and held stationary. The detection beam is then steered using an acousto-optic deflector, oscillating across the probe center with an amplitude of 55 nm and frequency of 1 kHz while the QPD Voltage signal is recorded. To get β, the signal is Fourier transformed to find the voltage at the drive frequency. The method works in solid-like regions as in the tail of a zebrafish embryo (c) or in fluid-like regions as in the yolk (d).

The piezo method is generally applicable where motions of the material do not give rise to net displacements of the bead exceeding ~20 nm•s⁻¹, including elastic solids, dense networks of fibers, and jammed colloidal suspensions. We performed a direct comparison for β values obtained using the detection beam steering (FFT) and piezo stage (Piezo) methods. Using phantom models made of rat-tail type I collagen hydrogels (2 mg•ml⁻¹ initial concentration; polymerized at 37°C). We employed both methods on confined 1 µm diameter carboxylated polystyrene microspheres embedded in the collagen meshwork to calculate β, as shown in Fig. 4(a). The ratio of the two values was taken for each probe, giving a value of 1.04 ± 0.09 (Gaussian fit parameters, mean ± standard deviation), a discrepancy falling below the range of other sources of error.

Fig. 4.

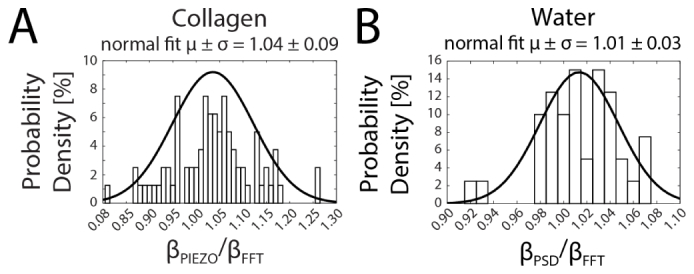
Histograms comparing V-nm conversion factors (β) of carboxylated polystyrene microspheres in collagen hydrogel and water obtained by Piezo, PSD and FFT methods. (A) In a collagen hydrogel, β was determined for each probe consecutively by the Piezo and FFT methods. First, the probe was centered in the trap position with the trap off and stepped through the detection beam. Then the detection beam was oscillated across the probe center with frequency 1 kHz and amplitude 55 nm, Fourier transformed and used to calculate β. The ratios of the values are plotted in a histogram and the distribution of ratios was fitted to a normal distribution, giving 1.04 ± 0.09 (mean ± standard deviation). (B) In water, each probe was trapped and the passive motion was recorded, Fourier transformed and fitted to a Lorentzian power spectrum model with the drag coefficient of water to calculate β by the PSD method. Then the detection beam was oscillated across the probe center with frequency 1 kHz and amplitude 55 nm, Fourier transformed and used to calculate β. The ratios of the values are plotted in a histogram and the distribution of ratios was fitted to a normal distribution, giving 1.01 ± 0.03 (mean ± standard deviation). At the 5% significance level, Lilliefors statistical tests suggest the data in (A) and (B) were normally distributed (A: h = 0, p = 0.50; B: h = 0; p = 0.32).

We next sought to compare the thermal power spectrum (PSD) method to the FFT method. We performed measurements for probes in two different samples: water and laminin-rich extracellular matrix (Matrigel^®) hydrogels. We assumed the drag coefficient of water in both cases. As expected, the PSD method cannot be used in elastic or viscoelastic materials such as Matrigel^®, because the drag coefficient is incorrect and the spectrum does not fit a Lorentzian function. When calculated under these inappropriate conditions, values for $\beta$ were found to be as much as nearly 100-fold greater than those calculated for the same probes by the FFT method (data not shown). However, in water, as shown in Fig. 4(b), the two methods produce similar values. The PSD method resulted in values 1% greater on average than the FFT method, with a standard deviation less than 4%.

We next sought to compare active microrheology using the FFT calibration method to small angle oscillatory shear (SAOS) bulk rheology, which acts on the mm length scale. We used uncured polydimethylsiloxane (PDMS) in the initial stage of polymerization as a phantom for a complex fluid that is out of equilibrium, akin to tissue. We used the FFT method in active microrheology measurements and conducted bulk experiments on parallel samples with beads at the same concentration. For microrheology, we calibrated β and k in situ at each probe and performed multiplexed frequency sweeps (2 Hz – 12.8 kHz) at stress-strain (trap position displacement) amplitudes of 20 nm per frequency. For bulk rheology, we conducted frequency sweeps (0.1 – 100 Hz) at 1% shear strain using parallel plates with 1% shear strain. Figure 5(a) shows the resulting elastic (G’, squares) and viscous (G”, triangles) components of the complex shear modulus from both microrheology (red) and bulk rheology (black). The overlapping frequency domain (shaded region in Fig. 5(a)) is shown in Fig. 5(b). The bulk data gave similar frequency dependence for G’ and G”. G” and G* were very similar in magnitude to optical trapping at 20 nm amplitudes in the overlapping frequency range. Values of G’ were significantly lower in bulk, by 3 orders of magnitude at ~1 Hz and 1 order of magnitude at 100 Hz. To test whether the probes’ presence influenced the mechanical response, we conducted bulk measurements on solutions with no probes; G’ differed insignificantly (p = 0.10; two-way ANOVA; data not shown). However, solutions with tenfold increased probe concentration resulted in nearly eightfold higher G’ values (p = 0.05; two-way ANOVA; data not shown). G” in bulk was not affected by probe concentrations (p > 0.60; two-way ANOVA).

Fig. 5.

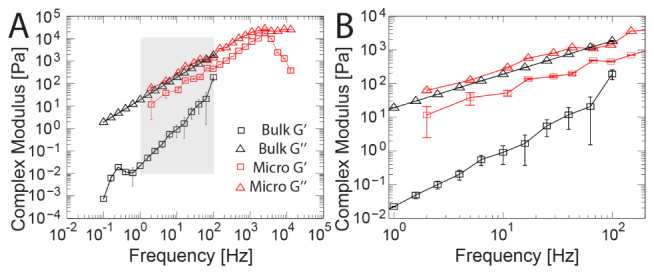
Active Microrheology and small angle oscillatory shear (SAOS) bulk rheology data of probes in uncured PDMS. (A) Active microrheology measurements (red) were conducted from 2 Hz – 12,809 Hz, with multiplexed frequencies at stress-strain amplitudes of 20 nm trap displacement per frequency. Bulk rheology (black) frequency sweeps were conducted from 0.1 – 100 Hz at 1% shear strain. The elastic (G’, squares) and viscous (G”, triangles) components of the complex modulus calculated from both methods are shown. (B) The moduli in the overlapping frequency range (shaded in B). The moduli increased significantly with increasing stress-strain amplitude (p < 0.0001, two-way ANOVA). Values of G” are similar across length scales, whereas values of G’ in bulk are lower than microscopic values by three orders of magnitude at ~1 Hz and one order of magnitude at 100 Hz.

To examine the microscale stress-strain behavior of a complex fluid, we performed active microrheology at multiple stress-strain (trap position displacement) amplitudes, as depicted in Fig. 6(a). Uncured PDMS measured at 2 nm, 5 nm, and 20 nm applied stress-strain amplitudes showed nonlinear viscoelasticity. Across the entire frequency range, both G’ and G” increase approximately one order of magnitude with an order of magnitude increase in amplitude (two-way ANOVA, p < 0.0001), as shown in Fig. 6(b). At 2 Hz, the complex viscosity was approximately 0.4 Pa•s, 0.5 Pa•s, and 5 Pa•s at 2 nm, 5 nm, and 20 nm amplitudes, respectively. The onset of shear thinning occurred at a critical shear rate of ~1 kHz.

Fig. 6.

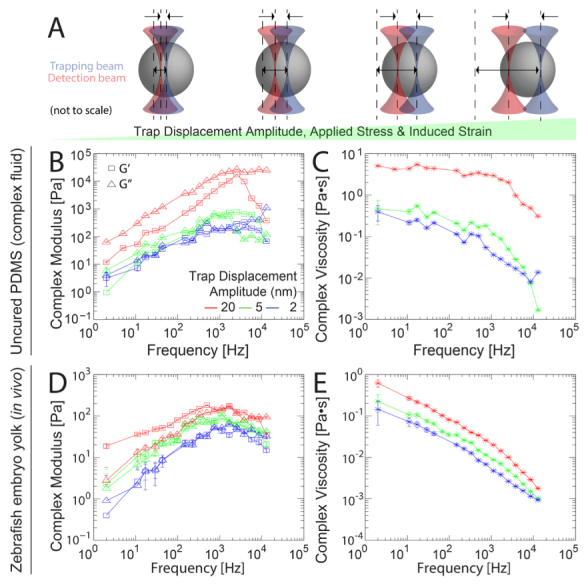
Microscale stress-strain behavior of zebrafish embryo yolk and uncured PDMS measured by active microrheology. (a) Sinusoidal oscillations of the trap position with increasing amplitudes of trap displacement increases applied force, stress, bead displacement and induced strain on the surrounding material. Probe displacements remain within the linear response regimes of both the detector and optical trapping potential but the material response is nonlinear. (b–e) Active microrheology measurements were conducted from 2 Hz – 12,8 kHz, with multiplexed frequencies at stress-strain amplitudes of 2 nm (blue), 5 nm (green) and 20 nm (red) trap displacement per frequency. (b, d) The elastic (G’, squares) and viscous (G”, triangles) components of the complex modulus are shown. (c, e) Corresponding complex viscosities η*. In both PDMS (b, c) and inside the yolks of living zebrafish embryos (d, e), the moduli show nonlinear viscoelasticity, increasing significantly with increasing stress-strain amplitude (p < 0.0001, two-way ANOVA).

We then proceeded to perform active microrheology measurements in the yolks of anesthetized zebrafish embryos 48 h post fertilization. In order to probe the nonlinear stress-strain response, we oscillated the trap at stress-strain amplitudes of 2 nm (blue), 5 nm (green), and 20 nm (red) per frequency. The moduli increase significantly with increased applied stress across the frequency range (two-way ANOVA, p < 0.0001), as shown in Fig. 6(d). G’ increased from ~2 Hz – 750 Hz, decreasingly slightly with frequency thereafter. At stress-strain amplitudes of 20 nm, G’ rose from 20 Pa – 200 Pa, falling again at the highest frequencies. In response to modulating the stress-strain amplitude, G’ varied more at lower frequencies: G’ at 20 nm amplitudes was ~40-fold greater than 2 nm amplitudes at 2 Hz, while only ~4-fold greater at 12.8 kHz. G” increased from 2 Hz – 1 kHz, leveling off at higher frequencies. In response to modulating the stress-strain amplitude, G” varied less than G’, and the variance was also less dependent on frequency: G” at 20 nm amplitudes rose from ~2 Pa – 100 Pa, ~2 – 3-fold greater than at 2 nm amplitudes across the frequency range. The corresponding complex viscosity $\eta *$ decreased from ~0.6 Pa•s – 0.002 Pa•s at 20 nm and ~0.1 Pa•s – 0.001 Pa•s at 2 nm, as shown in Fig. 6(e).

4. Discussion

The microscale mechanical properties of biomaterials and tissue microenvironments are important to physiological functions including gene expression, cell signaling, and motility [32–34]. One outstanding question in the field of mechanobiology is determining how the tissue mechanics impact cell fate, as many tissues exhibit nonlinear viscoelastic responses [1, 11, 12]. Optical trap based active microrheology is well suited and is increasingly used for biomechanical measurements [11–16, 35]. Complex materials including reconstituted ECM hydrogels and tissues in vivo feature intrinsic heterogeneities in optical properties. We and others have previously demonstrated the need for in situ calibration of each probe to obtain accurate forces and delineate mechanical properties of in these samples [15–20, 22, 23]. A variety of methods have been proposed for calibrating position detection in optical traps, each relying on different experimental configurations (e.g. single vs. dual beam optical traps), experimental measurements, and theoretical assumptions. PSD methods presuppose a Newtonian fluid with Langevin dynamics, a condition that does not hold generally in many biomaterials [36]. In cases where the material properties are unknown and cannot be assumed, some form of direct measurement of the V-nm conversion factor is desirable. Tissues may feature heterogeneous microdomains of various sizes. In this environment, some beads will be firmly confined by fibers or other solid-phase material, while others are free to diffuse, and the remainder are in an intermediate regime of partial confinement. The piezo stage-stepping method for in situ position detection calibration cannot be uniformly applied per bead under these circumstances.

AOD beam steering of the secondary detection laser across the trapped probe center (i.e. the FFT method) is a straightforward alternative method to find β, the V-nm conversion factor of a probe, that can be used in liquid or liquid-like material with nonlinear viscoelastic effects. We performed direct comparisons between the FFT, Piezo and PSD methods (Fig. 4). The FFT method gives results in good agreement with the power spectrum density and piezo stage stepping methods and expands the range of materials in which in situ calibration is possible. If the underlying structure of the material influences the detection beam over the length scale of its displacement, then there may be some systematic noise associated with the displacement of the detection beam. This is also true of the piezo method and back-focal-plane interferometry generally since it is sensitive not only to scattering by the probe but also to other objects in the beam path. As the detection beam is moved during this calibration process, it may be modulated by scattering from local optical inhomogeneities that introduce a potential source of uncertainty. We examined this possibility by measuring the signal on the detection QPD while oscillating the detection beam in the absence of a trapped probe at a number of random locations. Across the length scale of the oscillation, the signals were found to be indistinguishable.

We also tested the FFT method in a common material, PDMS. While curing, it is a dynamic, two-phase complex fluid out of equilibrium. We chose to measure the material while polymerizing to better approximate the dynamics of living tissue. For 2 nm, 5 nm, and 20 nm stress-strain amplitudes, complex viscosities were ~0.4 Pa•s, 0.5 Pa•s and 5 Pa•s respectively, at 2 Hz. The manufacturer-specified typical viscosity is 3.5 Pa•s at the 10:1 mix ratio used here. Small angle oscillatory shear (SAOS) rheology measurements with a parallel plate bulk rheometer at 1% strain gave values and frequency dependence for G” and G* similar to optical trap measurements using oscillations of amplitude 20 nm. Interestingly, the bulk values for G’ were considerably lower than even those measured optically at amplitude 2 nm. Using a cone-and-plate rheometer “LO” (linear oil) PDMS was previously found to have G’ of 5 Pa at ~1 Hz rising to ~1 kPa at 10² Hz; η had a plateau of 10² Pa•s from 10⁻¹ Hz – 10² Hz, dropping thereafter to 10¹ Pa•s at 10⁴ Hz [37]. We observe similar frequency dependence and values in the same range for both $G^{\prime }$ and η*. Kinetic viscosities were also reported to be 0.34 Pa•s – 56.3 Pa•s, a range in which our microrheology values fall up to ~1 kHz [38]. Other reports at higher frequencies found G’ at 10⁴ Hz (the lowest frequency probed there) to range from 10³ – 10⁵ Pa, increasing to nearly 10⁸ Pa at over 10⁸ Hz [39]. At 118 MHz, others more recently found values of 10⁵ – 10⁷ Pa for G’ and G” [40]. It is important to keep in mind that mechanical measurements by various apparatus at different frequencies, length scales, and strains are likely to differ for a number of reasons. For other complex fluids, order-of-magnitude differences in rheological properties have been observed between different length scales [41]. Discrepancies between bulk rheology and microrheology measurements stem from a number of distinctions [42]. The perturbation in SAOS induces a bulk flow, whereas active microrheology induces a microscopic flow. In the latter case, the strain field has both shear and uniaxial components, whereas SAOS induces no extensional deformations. Complex materials including gels and tissue exhibit structural heterogeneity within and across length scales, so measurements at different length scales may also differ due to intrinsically scale-dependent mechanical properties [43]. Bulk measurements are sensitive to interactions at the boundary of the material and the instrument surfaces, so sample loading and edge effects are considerable. In particle tracking microrheology techniques, the probe is subject to direct collisions from bath particles, adhesion due to specific or nonspecific binding, and hydrophobic and size exclusion effects [44]. If the mesh size of the material is larger than the probe, diffusion may become greater than predicted by continuum models based on generalized Stokes-Einstein relations [45]. Moreover, the presence of microscale probes can introduce steric and electrostatic effects that alter the local composition of the material. To address this possibility, we conducted bulk measurements in absence of probes but found similar results. The polymer solution may be intrinsically more elastic at the µm scale than at the mm scale, but bulk measurements may also be insensitive to any local microscopic effects due to probe presence.

We then applied the method for active microrheology by optical trapping in vivo in the yolks of zebrafish embryos 48 h post fertilization. Physical properties like cell stiffness, viscosity, and cortical tension are critical to cell migration, adhesion, and division in during embryonic development [45]. Various reports of avian egg viscosity range from 10⁻² Pa•s – 1 Pa•s, within which range our measurements fall [46]. For avian egg albumin, viscosities measured over the range 1 Hz – 102 Hz by parallel plate shear rheology were previously observed to decrease from ~5 Pa – 0.5 Pa. Frequency dependence with power law exponent 0.60 ± 0.08 was indicative of shear thinning [46]. To date, the relatively sparse mechanical data on zebrafish tissues published in the literature come from diverse experimental techniques, length scales, strains, and frequencies, which compounds the difficulty in drawing direct comparisons. Zebrafish yolk and embryo elasticity measured at much higher (GHz) frequencies by Brillouin scattering spectroscopy are ~2 – 3 GPa [47]. AFM indentation measurements found the surface tension of zebrafish embryonic cells to be ~66 pN•µm-1, and a cortical bulk elastic modulus of 1.9 kPa [48]. The corresponding shear modulus G’ ~633 Pa is within an order of magnitude of our measurements. Diffusion constants of cleavage-stage zebrafish embryos of ~6 × 10⁻⁹ cm²•s⁻¹ have been measured with gold nanoparticles, corresponding to viscosity η ~4 × 10⁻³ Pa•s [49]. Zebrafish whole blood viscosity was found to be ~3.5 × 10⁻³ Pa•s [50]. On greater length scales (~20 µm), fluorocarbon oil droplets were used to measure stresses in the zebrafish embryo, also finding viscosities of ~100 Pa•s at frequencies ~10⁻² Hz [51]. We recently measured extracellular matrix viscoelasticity in vivo in zebrafish brain and tail tissue, finding G’ and G” rising from ~1 Pa – 1 kPa over the frequency range 3 Hz – 15 kHz [15]. In the yolk, we find similar behavior up to several hundred Hz. In contrast to the brain and tail tissues, the moduli in the yolk feature a plateau at ~100 Pa from ~1 kHz – 12.8 kHz, corresponding to the onset of increased shear thinning. The yolk exhibited a nonlinear stress-strain response, with as much as a 40-fold increase in G’ at low frequencies in response to a 10-fold increase in stress-strain amplitude. Our observation of nonlinearity in vivo at microscopic strains may fall in the so-called toe or heel regions of the stress-strain curve. Nonlinearities in these regimes are different to large-strain nonlinearities arising from either strain-stiffening or softening induced by slippage and rupture found in many biomaterials. They may be associated with the uncrimping of fibrils and straightening of kinks in fibrillar gels [52–54]. Further study is needed to identify the mechanisms responsible for microscale nonlinearities in heterogeneous tissue.

5. Conclusion

Optical trap based active microrheology enables in vivo measurement of microscale tissue viscoelasticity over a broad band of frequencies and can probe nonlinear stress-strain behavior by varying the trap displacement amplitude. Back focal plane interferometry can be used detect probe displacements with nm resolution. For complex samples with intrinsic heterogeneities including tissues in vivo, accurate position detection requires in situ calibration. Calibrations based on thermal power spectra are largely accurate in samples where the material properties are known. Piezo stage stepping methods can be used in samples where the probes are firmly embedded in the underlying tissue architecture such that the probe moves in tandem with the stage. Here we present a straightforward in situ position detection method for a dual-beam optical traps with back focal plane interferometry. It enables measurement of probes in complex fluid environments by adding an AOD in the beam path of the detection laser. We show that in conditions where the thermal power spectrum and stage stepping methods are suitable, our method agrees well. We then go a step further to employ this approach in samples where the probes are not confined and where the underlying rheological properties are not known using in vitro surrogate and in vivo tissues. Direct comparison between active and bulk measurements in a silicone fluid revealed distinct elastic but similar viscous shear moduli across overlapping frequencies of both modalities. These results underscore the importance of length scale dependence on rheological properties in nonlinearly viscoelastic tissue. In vivo active microrheology measurements were then conducted inside the yolks of living zebrafish embryos.

Funding

This effort was supported by the Intramural Research Program of the National Institutes of Health, the National Cancer Institute.