Abstract
The fluorescence spectra of titanium doped sapphire (Ti:Sapphire) crystals were measured for temperature ranging from 300K to 77K. The resulting gain cross-section line shapes were calculated and used in a three-dimensional amplification model to illustrate the importance of the precise knowledge of these fluorescence spectra for the design of cryogenic cooled Ti:Sapphire based chirped-pulse laser amplifiers.
OCIS codes: (140.3280) Laser amplifiers; (140.3590) Lasers, titanium; (140.6810) Thermal effects
1. Introduction
When designing and developing Chirped Pulse Amplification (CPA) laser amplifiers for applications requiring high peak power and short pulses, Ti:Sapphire (Ti:Al2O3) is a material that has many advantages, which makes it a very good candidate for high peak power laser systems [1–6]. Its excellent thermal conductivity helps in managing the thermal loading induced by the pumping process. This thermal loading is caused by quantum defect – the energy mismatch between the seed and the pump photons – and the existence of non-radiative deexcitation to the ground level. Thermal loading can lead to thermo-optical distortion and lensing that are generally managed by water cooling for low average power systems. High average power chirped-pulse laser amplifiers often require the use of cryogenic cooling [2,7–10]. When cooling a Ti:Sapphire (Ti:Sa) crystal to temperatures below 150K the thermal conductivity increases [11,12], dn/dT is reduced [13] and the quantum efficiency [14–16] increases. Collectively these changes decrease thermally-induced effects from the optical pumping and result in better amplification. Even when thermal loading is not an issue, it may be tempting to consider cryogenic cooling for its benefit in term of energy extraction. At 77K, the quantum efficiency value is equal to 1 [14–16], which means that no more absorbed pump photon will contribute to non-radiative transitions and better energy extraction is possible.
Nevertheless, a drawback of cryogenic temperature is the modification in the line shape of the Ti:Sa fluorescence and gain cross-section, which can have detrimental effect on the amplified laser spectrum. After compression, a loss in spectrum width will lead to longer pulse duration and a loss of laser peak intensity. The gain in pulse energy given by cryogenic cooling could then be negated by the increase in pulse duration. Hence, the knowledge of the fluorescence and gain cross-section line shape at cryogenic temperature is critical for designers of CPA laser systems for modeling the amplification process and the laser system performance. Previously reported characterization of Ti:Sa fluorescence spectra as a function of temperature [14,17] are not precise enough to accurately model modern, single cycle carrier-enveloped phase-locked cryogenically cooled systems. Gachter et al. [17] have presented fluorescence spectra at 10K, 78K and 300K, but their room temperature fluorescence spectrum is not consistent with many other published values of fluorescence peaking between 750 nm and 760 nm at room temperature [15,16,18,19]. Byvik et al. [14] have measured the fluorescence spectrum from 13K to 578K, but the exact line shape for the fluorescence spectrum was not described and the spectral detector used had a rapid drop in response above 870 nm.
This paper presents a quantitative measurement of the change in Ti:Sa fluorescence and gain cross-section line shape from 300K to 77K. Section 2 describes the measurement of the fluorescence spectra that have been performed for temperature ranging from 77K to 300K. Section 3 then presents the calculations of the gain cross-section line shapes and corresponding fit parameters that can be readily used for the modeling of CPA amplification. Section 4 finally presents some simulation of multipass amplifiers with the gain line shapes presented in section 3 for cryogenic and room temperature. To illustrate quantitatively the effect of the modification of the gain cross-section line shapes with temperature, three temperatures (77K, 120K and 300K) and two case studies are considered: the first stage high-gain pre-amplifier and the second stage high-energy extraction power amplifier of a 100 TW laser system [8].
2. Measurement of Ti:Sa fluorescence spectra from 77K to 300K
The characterization of emission fluorescence was performed using the crystal of a second stage, nitrogen-cooled, multipass amplifier whose characteristics were previously described [10]. The laser crystal (16 mm diameter, 15 mm long, α532 = 2.1 cm−1) was held in a copper cold finger and cooled initially to 77K for several hours. The cooling was stopped and four pump laser beams - totaling 80W of pump power at 532 nm - were sent to the crystal without laser extraction. This resulted in a slow raise in temperature over several tens of hours (cf. Figure 1), which provided enough time to measure fluorescence spectra at a steady temperature values along the increase back to room temperature.
Fig. 1.
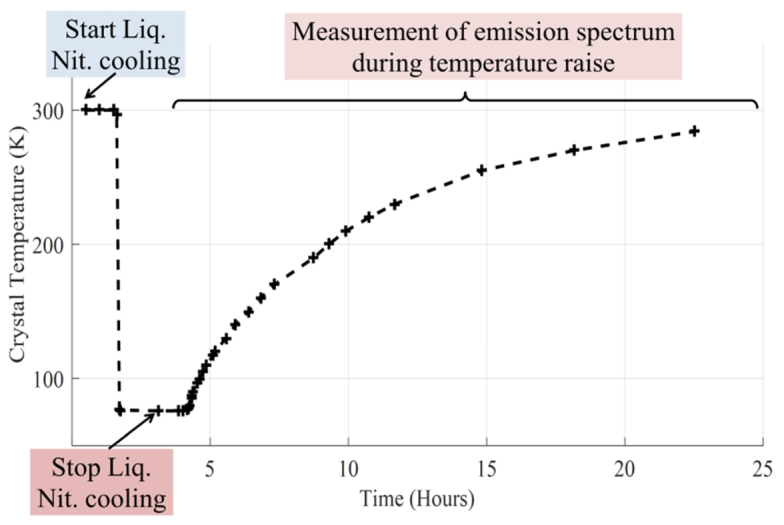
Temperature increase in the Ti:Sa crystal with cooling stopped. The crosses correspond to the temperature values where fluorescence spectra were recorded
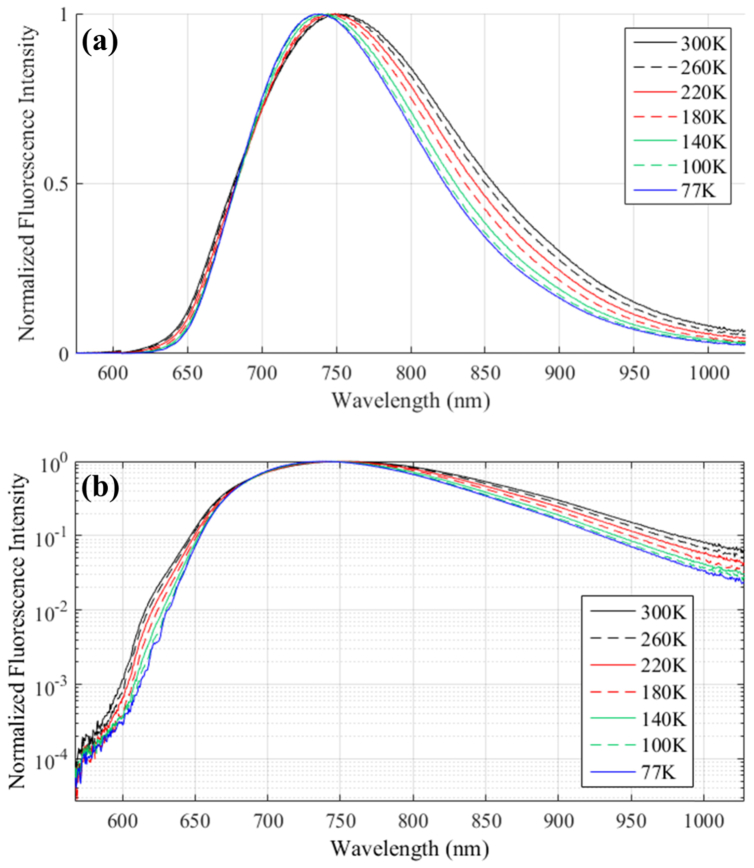
The 2D imaging spectrometer used to collect the emission fluorescence had grating reflectivity suited for wavelengths above 900 nm, to avoid the drop in sensitivity above 870 nm of previously reported measurements of the emission fluorescence spectra [14]. To collect the fluorescence, a lens was placed as close as possible to the crystal. Each collected 2D spectrum was composed of a bidimensional space and wavelength image that was integrated in the spatial domain in order to improve signal to noise. Finally, the overall response of the collecting system as function of wavelength was corrected using a known broadband source using the same collecting optics. The measured fluorescence spectra as a function of temperature are shown in Fig. 2. At room temperature (300K), the fluorescence peaks at 753 nm, and its Full Width Half Maximum (FWHM) value is 174 nm. Taking a comparative look into other published reports of the emission fluorescence spectrum at room temperature, with peak fluorescence values ranging from 750 nm to 760 nm and FWHM values from 165 nm to 188 nm [15,16,18,19], the agreement in values is confirming the validity of the collecting system calibration procedure.
Fig. 2.
Measured emission fluorescence spectra as a function of crystal temperature. Measurements were performed every 10K. (a) Linear scale, (b) Logarithmic scale
As is apparent in Fig. 2, with decreasing temperature, both the width of the fluorescence line shape and its peak wavelength value decrease. At a temperature of 77K, there are clear changes to the Ti:Sa fluorescence spectrum compared with room temperature, with a peak wavelength at 738 nm and a FWHM value of 143 nm. We found a similar trend than Byvik et al. [14], but the sensitivity of our collecting system up to 1050 nm permits the use of the experimental values of emission spectra for quantitative simulation of amplification. In order to use this information on the fluorescence emission as input parameter in the simulation of multipass amplification, one needs to deduce the gain cross-section line shape σg(λ) from the fluorescence emission line shape.
3. Gain cross-section line shape from 77K to 300K
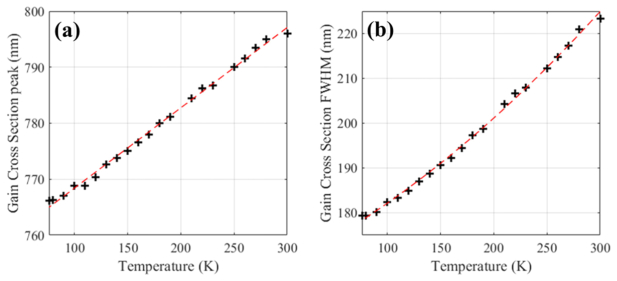
The gain cross-section can be obtained by multiplying the fluorescence emission spectrum by a factor of λ5 [16,20]. Using this multiplication factor and the measured emission fluorescence spectra shown in Fig. 2, the gain cross-section line shapes were calculated from 300K to 77K and normalized (cf. Figure 3). As evidenced before with the emission fluorescence data, a similar trend is observed regarding the gain cross-section line shape when the crystal temperature decreases. Details of the evolution of the gain line shape peak wavelength and FWHM are displayed in Fig. 4, with a 30-nm shift in the peak value from 796 nm at 300K to 766 nm at 77K, and a 43-nm decrease of the FWHM from 222 nm at 300K to 179 nm at 77K. In both Fig. 4(a) and 4(b), the crosses represent values obtained from the gain cross-section spectra and the red dashed lines polynomial fits that were performed to provide the peak and FWHM values at any temperature ranging from 77K to 300K. The polynomial coefficients fit parameters are indicated in Eq. (1) and (2).
| (1) |
| (2) |
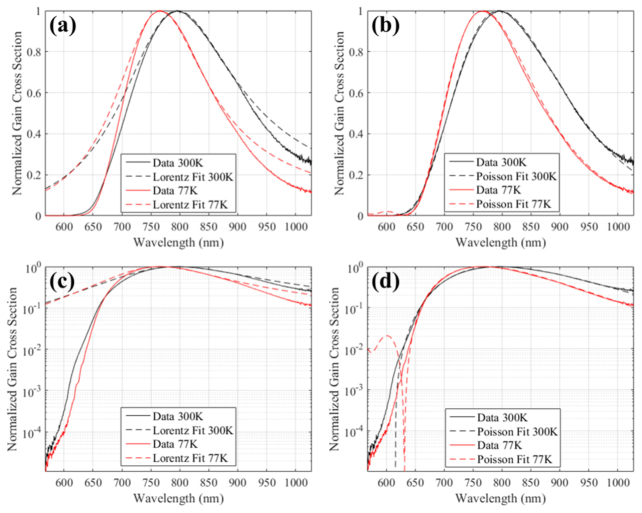
These results provide an excellent understanding of the evolution of the gain line shape with temperature between 77K and 300K. It may be tempting to use these values of gain peak wavelength and width to model the gain in the simulation of multipass amplification using a Lorentzian line shape as is done for homogeneous atomic transitions [21]. For Ti:Sa, this would result into an inaccurate representation of the measured gain cross section, as illustrate the two fits with Lorentzian distribution for the 77K and 300K gain cross sections shown in Fig. 5(a) and 5(c). A spectral profile following a Poisson distribution is better suited [20].
Fig. 3.
Calculated gain cross-section line shapes as a function of crystal temperature (T) using measured emission fluorescence spectra. (a) Linear scale, (b) logarithmic scale
Fig. 4.
Evolution with crystal temperature of: (a) Gain cross-section maximum peak wavelength and (b) the Full Width Half Maximum (FWHM) of the gain cross-section. The dashed lines represent linear and quadratic fit whose values are given in Eqs. (1) and (2)
Fig. 5.
Gain Cross-Section: (a), (c) Lorentzian distribution fit, (b), (d) Poisson distribution fit
The Poisson distribution is defined by three parameters: m, ν0 and νp, as shown in Eq. (3). The wavelength dependency is contained in the parameter P by expressing it in term of frequency ν, and the mathematical Gamma function Γ can be used instead of factorial to obtain a continuous distribution.
| (3) |
For temperature ranging from 300K to 77K, the three parameters m, ν0 and νp were found by fitting the experimental gain cross-section using least square fit method. The values of these parameters are shown in Table 1.
Table 1. Poisson distribution parameters m, ν0 and νp for selected temperatures.
| Temperature (K) | m | ν0 (cm−1) | νp (cm−1) |
|---|---|---|---|
| 300 | 5.5 | 15685 | 621 |
| 260 | 5.2 | 15571 | 621 |
| 220 | 4.7 | 15398 | 633 |
| 180 | 4.1 | 15195 | 657 |
| 140 | 3.5 | 15002 | 694 |
| 100 | 3.0 | 14835 | 737 |
To obtain m, ν0 and νp for any temperature between 77K and 300K, polynomial fits of the evolution of these parameters with temperature were performed, and the results are shown in Eq. (4), (5) and (6).
| (4) |
| (5) |
| (6) |
Using Eqs. (3) to (6) allows defining accurately the gain cross-section line shape for any temperature between 77K and 300K.
4. Effect of the gain cross-section changes for CPA multipass amplifiers
The design of CPA amplifiers is based on simulation of how the amplified (seed) laser is transformed when extracting energy after each pass in the gain medium. For Ti:Sa, the simulation of amplification can be made using a pair of rate equations [22–24] to describe qualitatively how the energy is evolving after each pass. These models can be extended to highly stretched chirped pulses by use of the instantaneous frequency formalism [25,26], to describe how the seed spectrum evolves during amplification. Finally, to describe the changes in spatial profile, and the effect of diffraction, and obtain a quantitative prediction of the extracted energy after each pass, these 1D models can be extended to 3D models [27].
Cryogenic cooling affects many parameters of the multipass amplification simulation. If the same pump and seed beam sizes are used, the cryogenic cooling increases the stored energy. This improves the gain and the extracted energy at each pass, which increases how fast the amplifier saturates. Cryogenic cooling also reduces the thermal lensing, and changes the shape of the gain cross-section. Both affect the seed spatial profile and spectral modification during amplification.
The purpose of this section is to show how significant the change in the amplified laser spectrum can be, when cryogenic cooling is used. Two multipass amplifier stages from an existing 100 TW laser system [8,27] are used as case-studies, and the simulation are based on a 3D amplification model [27]. Because cryogenic cooling causes a better energy extraction, the pump and seed beam sizes are adjusted so that the energy extraction stays the same for all three cooling temperatures after the same number of passes. For each amplifier, three temperatures are considered: Room temperature (300K), cryogenic cooling at 120K (typical of cryogenic cooling by compression of a cooling gas) and cryogenic cooling at 77K (by liquid Nitrogen). The first amplifier is a high-gain 8-passes pre-amplifier which attains saturation only in the last 2 passes, and the second stage a 5-passes power amplifier in which saturation occurs earlier and most of the pump energy deposited in the medium is extracted. Detailed parameters for these multipass amplifiers can be found in [8,27].
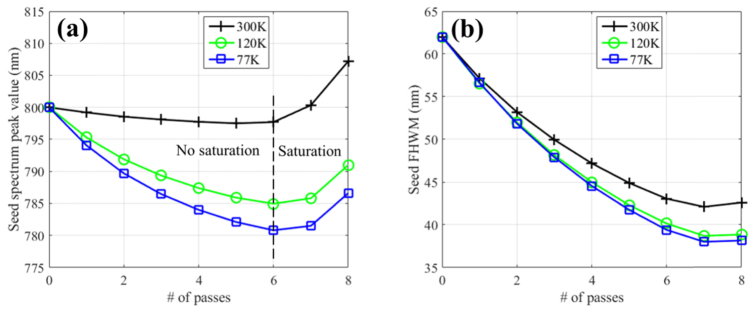
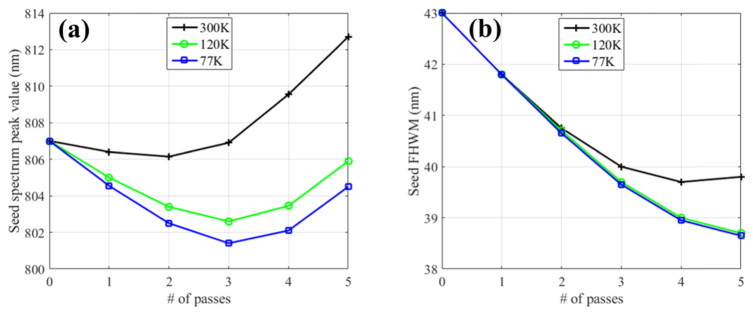
Figure 6 presents the change in the amplified peak wavelength and amplified spectrum width (FWHM) as a function of the number of passes in the high-gain pre-amplifier. At 300K, this pre-amplifier has an initial small-signal gain of 10 and amplify the energy of the infrared laser chirped pulse from 0.2 nJ to 2.0 mJ [8,27]. The amplified laser spectrum exhibits an initial shift of its peak wavelength (cf. black curves in Fig. 6(a)) toward the resonance wavelength of the gain cross-section up to pass number 6, when the pulse fluence is still low compared to the medium saturation fluence and no saturation occurs. It is then followed by a shift toward higher wavelength values due to the saturation of the gain which favors the amplification of red-shifted wavelength inside the chirped pulse. This effect is often referred as “gain shifting” or “gain saturation” [1,8,25–27]. Figure 6(b) shows how the width (FWHM) of the amplified laser spectrum narrows from 62 nm before the amplifier to 43 nm after the amplifier, an effect known as “gain narrowing” [1,8,25–27].
Fig. 6.
Evolution of the seed laser peak and FWHM spectrum value in high-gain pre-amplifier for three temperatures: 300K (black crosses), 120K (green circles), and 77K (blue squares)
The change in the gain cross-section for different cooling temperatures should affect the amount of “gain narrowing” and “gain shifting”. This is exactly what is observed for the 120K and 77K cryogenically cooled amplifiers, as shown by the green circle and blue square values in Fig. 6. All three cooling temperatures show similar trend but the shift toward the resonance is more significant at cryogenic temperature with around 20 nm shift for the 77K amplifier after pass number 6. The gain narrowing (Fig. 6(b)) is also affected, with an added reduction of spectrum width of 5 nm at 77K.
The second stage amplifier has an input seed laser spectrum centered at 807 nm, a pulse energy of 0.5 mJ, an initial small signal gain at 300K equal to 5, and amplify the near-infrared laser up to 200 mJ after 5 passes [8,27]. This amplifier is a good illustration of the modifications in the amplified laser spectrum for an amplifier which reaches saturation earlier. As shown in Fig. 7, similar effects and similar difference to the spectrum shift and width are seen, but as the saturation occurs in earlier passes, the shift toward the resonance wavelength is less striking, as is the difference between spectrum peak values and width between the cryogenic and room temperature.
Fig. 7.
Evolution of the seed laser peak and FWHM spectrum value in power amplifier for three temperatures: 300K (black crosses), 120K (green circles), and 77K (blue squares)
What are the implications for the design of CPA multipass laser amplifiers? Such a drastic effect as the 20 nm amplified spectrum shift seen in the pre-amplifier, is significant and needs to be taken into account to avoid problem in the matching of the stretcher and compressor pair in the CPA laser amplifier system. When saturation occurs during several passes, as in the 5-passes power amplifier considered in this section, the shift in the spectrum peak value is still the parameter that undergoes the most significant change between the different cooling temperatures. Both the shift in peak wavelength and the reduction in spectral width during amplification can be counteracted by actively shaping the input seed pulse spectrum out of the oscillator [8,26]. When using such a method, the complexity of the change in the amplified spectrum for multistage CPA laser necessitates the simulation of amplification using the gain cross-section as detailed in section 3, to predict correctly which input pulse spectrum optimizes the output spectrum bandwidth.
5. Conclusion
In this paper, we presented the quantitative measurement of the fluorescence spectrum of Ti:Sa with cooling temperatures from 300K down to 77K and deduced the corresponding gain cross-section. From these gain line shapes, relevant parameters were extracted to allow designer of CPA multipass or regenerative amplifiers to predict with confidence the transformation happening during amplification on the laser amplified spectrum. We have shown with two case-studies that the magnitude of these effects are significant and should not be neglected, and that the room-temperature gain cross-section cannot be used to predict accurately the spectral output of an amplified laser pulse in a CPA system. Using the correct gain cross-section presented in section 3 will allow designers of CPA amplifiers to balance the positive aspects of cryogenic cooling - improved wavefront quality, removal of thermal lensing, increase in energy extraction - and its negative aspects - cost, operational challenge, and possible increase in laser output pulse duration.
Funding
National Science Foundation (NSF CREST award 1242067); NASA URC (Group-V award NNX09AU90A); National Institute of Health NIH NIGMS IDeA program (grant #P20 GM1030446).
References and links
- 1.Backus S., Durfee C. G., III, Murnane M. M., Kapteyn H. C., “High power ultrafast lasers,” Rev. Sci. Instrum. 69(3), 1207–1223 (1998). 10.1063/1.1148795 [DOI] [Google Scholar]
- 2.Seres J., Müller A., Seres E., O’Keeffe K., Lenner M., Herzog R. F., Kaplan D., Spielmann C., Krausz F., “Sub-10-fs, terawatt-scale Ti:sapphire laser system,” Opt. Lett. 28(19), 1832–1834 (2003). 10.1364/OL.28.001832 [DOI] [PubMed] [Google Scholar]
- 3.Bahk S.-W., Rousseau P., Planchon T. A., Chvykov V., Kalintchenko G., Maksimchuk A., Mourou G. A., Yanovsky V., “Generation and characterization of the highest laser intensities (10(22) W/cm2),” Opt. Lett. 29(24), 2837–2839 (2004). 10.1364/OL.29.002837 [DOI] [PubMed] [Google Scholar]
- 4.Aoyama M., Yamakawa K., Akahane Y., Ma J., Inoue N., Ueda H., Kiriyama H., “0.85-PW, 33-fs Ti:sapphire laser,” Opt. Lett. 28(17), 1594–1596 (2003). 10.1364/OL.28.001594 [DOI] [PubMed] [Google Scholar]
- 5.Yanovsky V., Chvykov V., Kalinchenko G., Rousseau P., Planchon T., Matsuoka T., Maksimchuk A., Nees J., Cheriaux G., Mourou G., Krushelnick K., “Ultra-high intensity- 300-TW laser at 0.1 Hz repetition rate,” Opt. Express 16(3), 2109–2114 (2008). 10.1364/OE.16.002109 [DOI] [PubMed] [Google Scholar]
- 6.Sung J. H., Lee S. K., Yu T. J., Jeong T. M., Lee J., “0.1 Hz 1.0 PW Ti:sapphire laser,” Opt. Lett. 35(18), 3021–3023 (2010). 10.1364/OL.35.003021 [DOI] [PubMed] [Google Scholar]
- 7.Backus S., Bartels R., Thompson S., Dollinger R., Kapteyn H. C., Murnane M. M., “High-efficiency, single-stage 7-kHz high-average-power ultrafast laser system,” Opt. Lett. 26(7), 465–467 (2001). 10.1364/OL.26.000465 [DOI] [PubMed] [Google Scholar]
- 8.Pittman M., Ferré S., Rousseau J.-P., Notebaert L., Chambaret J.-P., Cheriaux G., “Design and characterization of a near-diffraction-limited femtosecond 100-TW 10-Hz high-intensity laser system,” Appl. Phys. B 74, 529–535 (2002). 10.1007/s003400200838 [DOI] [Google Scholar]
- 9.Ramanathan V., Lee J., Xu S., Wang X., Williams L., Malphurs W., Reitze D. H., “Analysis of thermal aberrations in a high average power single-stage Ti:sapphire regenerative chirped pulse amplifier: Simulation and experiment,” Rev. Scient. Instrum. 77, 103103 (2006). [Google Scholar]
- 10.Planchon T. A., Amir W., Childress C., Squier J. A., Durfee C. G., “Measurement of pump-induced transient lensing in a cryogenically-cooled high average power Ti:sapphire amplifier,” Opt. Express 16(23), 18557–18564 (2008). 10.1364/OE.16.018557 [DOI] [PubMed] [Google Scholar]
- 11.Eilers H., Hömmerich U., Yen W. M., “Temperature-dependant beam-deflection spectroscopy of Ti3+ - doped sapphire,” J. Opt. Soc. Am. B 10(4), 584–586 (1993). 10.1364/JOSAB.10.000584 [DOI] [Google Scholar]
- 12.Burghartz S., Schulz B., “Thermophysical properties of sapphire, AIN and MgAl2O4 down to 70K,” J. Nucl. Mater. 212–215, 1065–1068 (1994). 10.1016/0022-3115(94)90996-2 [DOI] [Google Scholar]
- 13.DeFranzo A. C., Pazol B. G., “Index of refraction measurement on sapphire at low temperatures and visible wavelengths,” Appl. Opt. 32, 2224–2234 (1993). [DOI] [PubMed] [Google Scholar]
- 14.Byvik C. E., Buoncristiani A. M., “Analysis of Vibronic Transitions in Titanium Doped Sapphire Using the Temperature of the Fluorescence Spectra,” J. Quantum Electron. 21(10), 1619–1624 (1985). 10.1109/JQE.1985.1072564 [DOI] [Google Scholar]
- 15.Albers P., Stark E., Huber G., “Continuous-wave laser operation and quantum efficiency of titanium-doped sapphire,” JOSA B 3(1), 134–139 (1986). 10.1364/JOSAB.3.000134 [DOI] [Google Scholar]
- 16.Moulton P. F., “Spectroscopic and laser characteristics of Ti:Al2O3,” J. Opt. Soc. Am. B 3(1), 125–133 (1986). 10.1364/JOSAB.3.000125 [DOI] [Google Scholar]
- 17.Gächter B. F., Koningstein J. A., “Zero phonon transitions and interacting Jahn-Teller phonon energies from the fluorescence spectrum of alpha-Al2O3:Ti3+,” J. Chem. Phys. 60(5), 2003–2006 (1974). 10.1063/1.1681307 [DOI] [Google Scholar]
- 18.Lacovara P., Esterowitz L., Kokta M., “Growth, Spectroscopy, and Lasing of Titanium-Doped Sapphire,” J. Quantum Electron. 21(10), 1614–1618 (1985). 10.1109/JQE.1985.1072563 [DOI] [Google Scholar]
- 19.Powell R., Caslavsky J., AlShaieb Z., Bowen J. M., “Growth, characterization, and optical spectroscopy of Al2O3:Ti3+,” J. Appl. Phys. 58(6), 2331–2336 (1985). 10.1063/1.335955 [DOI] [Google Scholar]
- 20.DeShazer L. G., Eggleston J. M., Kangas K. W., “Oscillator and amplifier performance of Ti:Sapphire,” in Tunable Solid-State Lasers II (Springer, 1986) pp. 228–234. [Google Scholar]
- 21.Siegman A. E., Lasers, (University Science Books, 1986), Chaps. 3 and 7. [Google Scholar]
- 22.Frantz L. M., Nodvik J. S., “Theory of Pulse Propagation in a laser amplifier,” J. Appl. Phys. 34(8), 2346–2349 (1963). 10.1063/1.1702744 [DOI] [Google Scholar]
- 23.Bellman R., Birnbaum G., Wagner W. G., “Transmission of monochromatic radiation in a two-level material,” J. Appl. Phys. 34(4), 780–782 (1963). 10.1063/1.1729535 [DOI] [Google Scholar]
- 24.Lowdermilk W. H., Murray J. E., “The multipass amplifier: Theory and numerical analysis,” J. Appl. Phys. 51(5), 2436–2444 (1980). 10.1063/1.328014 [DOI] [Google Scholar]
- 25.Le Blanc C., Curley P., Salin F., “Gain-narrowing and gain-shifting of ultra-short pulses in Ti:sapphire amplifiers,” Opt. Commun. 131(4-6), 391–398 (1996). 10.1016/0030-4018(96)00262-3 [DOI] [Google Scholar]
- 26.Cha Y. H., Kang Y. I., Nam C. H., “Generation of a broad amplified spectrum in a femtosecond terawatt Ti:sapphire laser by a long-wavelength injection method,” J. Opt. Soc. Am. B 16(8), 1220–1223 (1999). 10.1364/JOSAB.16.001220 [DOI] [Google Scholar]
- 27.Planchon T. A., Burgy F., Rousseau J. P., Chambaret J. P., “3D Modeling of amplification processes in CPA laser amplifiers,” Appl. Phys. B 80(6), 661–667 (2005). 10.1007/s00340-005-1787-4 [DOI] [Google Scholar]