Abstract
We present a new 1060 nm Fourier domain mode locked laser (FDML laser) with a record 143 nm sweep bandwidth at 2∙ 417 kHz = 834 kHz and 120 nm at 1.67 MHz, respectively. We show that not only the bandwidth alone, but also the shape of the spectrum is critical for the resulting axial resolution, because of the specific wavelength-dependent absorption of the vitreous. The theoretical limit of our setup lies at 5.9 µm axial resolution. In vivo MHz-OCT imaging of human retina is performed and the image quality is compared to the previous results acquired with 70 nm sweep range, as well as to existing spectral domain OCT data with 2.1 µm axial resolution from literature. We identify benefits of the higher resolution, for example the improved visualization of small blood vessels in the retina besides several others.
OCIS codes: (170.4500) Optical coherence tomography; (170.3880) Medical and biological imaging; (170.4460) Ophthalmic optics and devices; (120.3890) Medical optics instrumentation; (140.3510) Lasers, fiber
1. Introduction
Optical Coherence Tomography (OCT) [1] enables non-invasive three dimensional imaging of animate and inanimate objects. Since its development, it has found a wide range of applications ranging from ophthalmology [2–4], cardiology [5], gastroenterology [6], pulmonology [7], dentistry [8], dermatology [9] to monitoring of industrial processes [10, 11]. Also, the economic impact of OCT has been significant [12]. Despite of all the different applications, the major application is still ophthalmic imaging. Here, OCT provides the unique capability to create high-resolution cross-sectional images of the retina for diagnosing diseases of the human eye.
A major feature of OCT is that the transverse and axial resolution are decoupled. The transverse resolution, like for most other ophthalmic devices, is a function of the optics [13]. While in non-retinal OCT the use of high numerical aperture (NA) microscope objectives is possible [14], imaging the posterior eye requires the light passing through the lens of the eye, which limits the maximum achievable NA and causes additional aberrations. However, with the help of adaptive optics it is possible to correct these aberrations and to visualize individual photoreceptors [15] – even at A-scan rates in the MHz-range [16]. In contrast to the transverse resolution, the axial resolution Δz scales with the square of the center wavelength λ0 and the inverse of the bandwidth Δλ of the applied light source. Regarding the different OCT technologies with respect to the resolution, time domain OCT (TD-OCT) and spectral domain OCT (SD-OCT) generally are superior to swept source OCT (SS-OCT) regarding its axial resolution, as non-sweeping light sources usually feature a significantly higher bandwidth and often also a shorter center wavelength than swept laser sources [17–19]. This is because spectral multiplexing can be applied very easily in the case of superluminescent diodes or the spectral broadening effects of non-linear optical processes can be used by high-intensity pulses. With TD-OCT in ophthalmic imaging, axial resolutions down to 2-3 µm have been demonstrated [20] and images from a SD-OCT system with 2.1 µm [21] and 2.5 µm axial resolution were shown [22]. In contrast, to the best of our knowledge, the best axial resolution with a SS-OCT system demonstrated to date is 5.3 µm [23]. However, SS-OCT in general features significantly higher line rates than SD-OCT and TD-OCT [24–26]. Currently, the main reason for this is the limited read out rates for line cameras needed for SD-OCT compared to the speed in photodiodes and digitizers used in SS-OCT. This trend will probably continue in the future because of the increasing need for fast telecommunication and the simpler implementation of dual balanced detection required for shot-noise limited detection in case of SS-OCT [27].
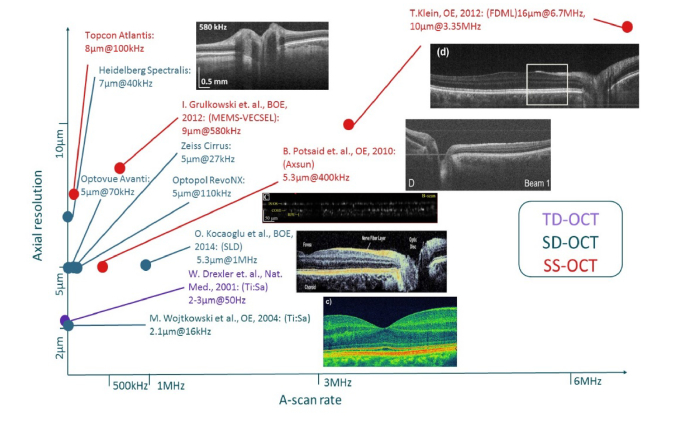
An overview of line rate versus axial resolution for various research systems as well as commercial systems with flying spot approaches can be found in Fig. 1. It clearly visualizes that there is a trade-off between speed and axial resolution. This raises the question, which axial resolution and imaging speed is required. As most manufactures provide axial resolutions on the range of 5-8 µm, we assume that this is sufficient for the diagnosis of most diseases. However, many applications like ultra-widefield imaging [28] or live video rate 4D OCT [29, 30] benefit from A-scan rates on the order of MHz as it has been discussed extensively in [24].
Fig. 1.
Overview of imaging speed versus axial resolution for different research and commercial systems with flying spot approaches. TD-OCT, SD-OCT and SS-OCT systems are color-coded. Data from commercial systems are obtained from manufacturer’s websites. Research systems are [20, 21, 23, 24, 31].
Our goal was to push the axial resolution of our MHz-OCT system, while maintaining the high imaging speed. We use a swept source OCT system, based on a Fourier Domain Mode Locked (FDML) laser. Due to their stationary mode of operation [32], FDML lasers have the unique advantage that they can combine very narrow, picometer scale linewidth [33, 34], meter range coherence [35, 36], stable polarization [37–40] and very high sweep rates [41]. The dynamic Doppler shift of the light wave inside the FDML cavity by the moving mirror of the intra-cavity Fabry Perot filter enables modehop-free tuning [42] and ultra-low intensity noise [36]. Due to the comparably high output power and low phase noise, FDML lasers are also well suited for OCT angiography [43, 44], photoacoustic sensing [45] as well for non-OCT imaging like combined fiber based stimulated Raman and 2-photon systems [46–49].
Therefore, we increased the sweep bandwidth of our Fourier-domain mode-locked (FDML) laser [50] significantly. Additionally, we carefully investigated the benefits of the higher axial resolution in the OCT images acquired with our system at various sweep bandwidths and compared them to previous results.
2. Experimental
We built an FDML laser based on the design already presented in [24], however without the Yb-amplifier as already shown in [28]. Figure 2(A) shows the basic setup together with the optical buffer stage [51]. We optimized three critical components, to enhance the sweep bandwidth:
Fig. 2.
A) Setup of the employed FDML laser. LDC: Laser diode controller; AWG: Arbitrary waveform generator; OSA: Optical spectrum analyzer; PD: Photodiode; PC: Polarization controller; cFBG: Chirped fiber-Bragg grating, ISO: Optical isolator; BFP-TP: Tunable Fabry-Perot Filter, SOA: Semiconductor optical amplifier. B) Spectrum achieved with 417 kHz FDML and with 1.67 MHz FDML. The 120 nm spectrum was attenuated for better visualization.
-
1.)
The chirped fiber-Bragg grating (cFBG) used for dispersion compensation in [52] had a maximum reflectivity bandwidth of about 70 nm and was therefore the main limiting factor for an increased sweep bandwidth. Due to a new manufacturing process of the supplier (Teraxion), gratings with reflectivities of 50% to 70% with 200 nm bandwidth centered at 1050 nm can now be manufactured.
-
2.)
The original semiconductor optical amplifier (SOA, Innolume SOA-1070-70-HI-24dB) had a 3 dB gain bandwidth of 70 nm. The new SOA (Innolume SOA-1020-110-HI-27dB) has not only a 40 nm wider gain bandwidth, but also a 3 dB higher maximum gain.
-
3.)
A new home-built Fabry-Perot filter with a free spectral range (FSR) of ~180 nm and a resonance frequency of 417 kHz in combination with very low losses of around 2 dB is employed. Older filters had FSRs of about 100 nm and higher losses.
With these modifications, the sweep bandwidth was increased to 143 nm at 2∙417 kHz = 834 kHz sweep rate (no buffering) and to 120 nm at 1.67 MHz (4-times buffering) as shown in Fig. 2(B). The difference in sweep range between buffered and unbuffered operation is probably due to the low modulation bandwidth of the SOA in the cavity. Measurements of the ASE with an open resonator and modulated operation showed a delay in amplification due to the rise time of the SOA, which is too slow for a proper modulation of the FDML laser and therefore limiting its output bandwidth. An exchange of the laser diode driver (Wieserlabs LDC10D), which is specified with a modulation bandwidth of 10 MHz, for a model with a higher bandwidth of 400 MHz (Picolas BFS-VRM 03 HP) did not result in any changes of this behavior. Therefore, the internal modulation bandwidth of the SOA is dominant in our case and not the driving electronics.
For all measurements in this paper we used 4-times buffering, 1.67 MHz sweep rate and 120 nm bandwidth because the detection electronics of our setup is designed for these speeds. We used the 60° field of view imaging configuration presented in [28], but the fiber collimator has a focal length of 18.4 mm instead of 11 mm. This way we were able to increase the transverse resolution (full width at half maximum (FWHM) of the beam on the retina) from 12.5 µm to 7.5 µm. The data acquisition card was an AlazarTech ATS9360 with an acquisition rate of 1.8 GS/s and a sampling depth of 12 bit. The photodiode was a Wieserlabs BPD1GA with an analog detection bandwidth of 1 GHz. This results in an imaging range of 2.5 mm in air.
3. Characterization of the new FDML laser
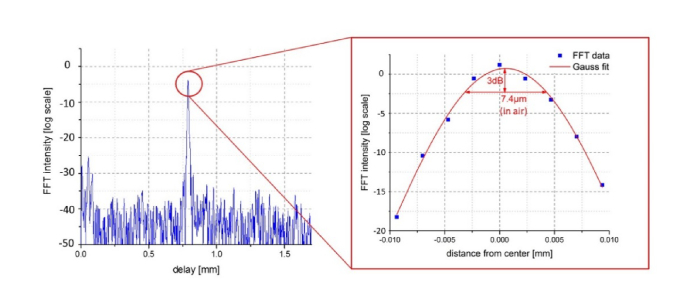
To measure the axial resolution of our new laser, a mirror at a depth of 800 µm was imaged. Figure 3 shows the results of our measurement. The FWHM of the point spread function is 7.4 µm. If one takes the refractive index of water (n = 1.33) into account, this results in an axial resolution of 5.6 µm. The theoretical value resulting from Δz = 0.44∙λ02 / Δλ is 3 µm with λ0 = 1050 nm und Δλ = 120 nm. However, the aforementioned equation is only valid for Gaussian shaped spectra, which are typical for simple superluminescent diodes (SLD) used in TD-OCT. With the introduction of ultra-broadband femtosecond lasers, swept laser sources and multiplexed SLDs or modern single SLDs which use two band transitions of the semiconductor in parallel in order to increase the bandwidth, the spectra of most of today’s light sources are not perfectly Gaussian shaped. In SD-OCT and SS-OCT this may not be to critical, because numerical apodization in post processing is simpler than in TD-OCT. Spectral shaping even allows to increase the 3dB bandwidth, however, of course with a noise penalty. Hence, it makes sense that most publications, especially in OCT quote the total bandwidth. However this makes it necessary to perform a Fourier transformation of the spectrum in order to obtain the true axial resolution [13] as we will do in the following. With the FWHM alone one cannot make a prediction about the axial resolution of the system.
Fig. 3.
Point spread function of a mirror imaged at 800 µm depth. Zoom-in shows the FFT together with a Gaussian fit. The FWHM in air is 7.4 µm.
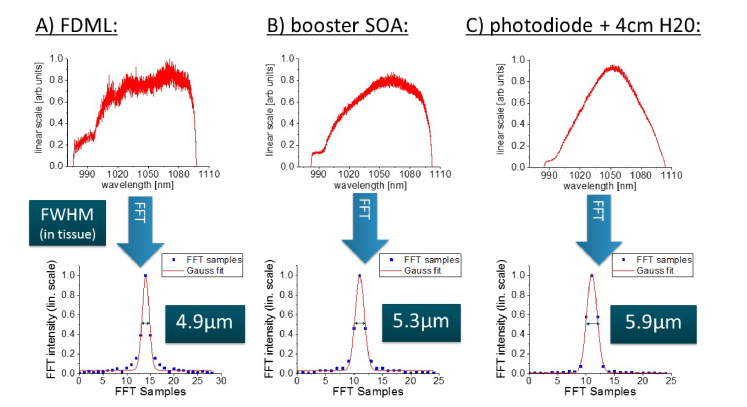
For this reason, we analyzed the theoretically achievable axial resolution more closely. We measured the optical spectrum of our FDML laser at three separate locations with an optical spectrum analyzer (OSA, Yokogawa AQ6370): Directly after the FDML laser, after the booster-SOA and in front of the photodiodes of our interferometer, where we included a 2 cm cuvette of water and a mirror in the sample arm to simulate an eye. The spectra were linearized in frequency (as we do not need to use k-clocking, see [25]), Fourier-transformed, the amplitude values were fitted with a Gaussian and the FWHM was calculated. This value was converted to the actual resolution by taking the known position of the mirror as a reference.
Figure 4 shows the spectra and the respective Fourier-transforms. The spectrum directly after the FDML laser results in an axial resolution of 4.9 µm (in tissue, as also for all following values). After the light passed the booster-SOA, the resolution deteriorated to 5.3 µm. Therefore the measured value of 5.6 µm is close to the theoretical minimum, whereby one has to consider, that the light passes a couple of optical components, which influence the spectrum further. Directly in front of the photodiode and including the 4 cm of water, we get a theoretical resolution of 5.9 µm. This value should be very close to what we get in retinal OCT measurements with our system. The decrease in axial resolution is, as one can see in the individual spectra, caused by a change of the spectral shape and a reduction of the 3dB bandwidth. In order to increase the axial resolution, it should be possible to modulate the current of the SOA in the FDML resonator or the booster-SOA [53, 54], such that the spectrum results in a higher axial resolution. Especially at the short wavelength end of the spectrum, we see potential for increasing the spectral intensity by increasing the current. However, we did not implement any modulation as we were concerned about an additional risk to exceed the ANSI safety limits by unintended changes in the spectrum.
Fig. 4.
Top row shows spectra measured A) directly after the FDML laser, B) after the booster SOA and before the photodetector after passing 4 cm of water. The bottom row shows the Fourier-transform of each spectrum together with the FWHM in tissue.
The strong change in the spectrum between the measurement after booster-SOA and the measurement in front of the photodiode results from the absorption characteristics of water [55]. It features a local minimum around ~ 1060 nm, which coincides quite well with the maximum of our spectrum. Therefore, retinal OCT data acquired at 1050 nm does usually not require any apodization. For a more detailed analysis, also the other components of the eye and temperature effects need to be taken into account, but the deviation from pure water is rather small [56].
Additionally, we characterized the roll-off of our new FDML laser. The results of our measurements of the point spread functions are displayed in Fig. 5. We identify the 6 dB roll-off point at 1.5 mm delay. Regarding the thickness of the structures in the posterior eye of ~1 mm, we consider this value as sufficient for retinal imaging.
Fig. 5.
Roll-off measurement of the FDML laser with 120 nm bandwidth and 1.67 MHz sweep rate. The amplitude of the FFT decreased by 6 dB after 1.5 mm.
4. OCT imaging
A healthy 30-year-old male healthy volunteer was imaged with the new FDML laser. No dilation of the pupil was performed. All in vivo retinal imaging experiments were performed in accordance to the tenets of the Declaration of Helsinki. The ethics committee of the University of Lubeck approved the experiments. Informed consent was obtained from the volunteer prior to the measurements. In order to investigate the effects of the enhanced sweeping bandwidth, the imaging was performed with the new 120 nm as well as the original 70 nm bandwidth. For this, only the amplitude of the Fabry-Perot filter had to be changed while everything else remained identical. For the 70 nm, a 10 µm resolution in tissue was determined. A sensitivity of 89 dB at a power of 1.6 mW incident on the cornea was measured. 1900 A-scans were acquired per B-scan, with a B-scan separation of 6 µm in order to get a slight oversampling. A field of view of about 35° was captured, which results in a distance of 5.5 µm between the A-scans and a quasi-isotropic sampling. In post-processing, we payed special attention to a correct linearization of the FDML phase and the numerical correction of the dispersion differences between sample arm (including the eye) and the reference arm, as these can significantly influence the axial resolution and the image quality.
A typical B-scan of each OCT data set with a four times flying average can be found in Fig. 6. Higher averaging leads to a decrease in visibility of fine structures. The labeling of the retinal layers is based on [57]. We would like to note that there is quite a controversy about the naming of the outer retinal layers [58]. For a more detailed analysis, a section around the RPE including the choroid (blue) and the top layers with fine blood vessels (red) was magnified. There is no significant difference visible in the layers around the RPE and the separation of the individual layers and the ELM on top is identical for both sweep ranges. Taking a closer look at the choroid, there is a slightly higher amount of detail with the higher sweeping range. The most significant difference, even though it is hardly notable, is visible in the bright white dots in the top layers of the retina. Based on en face reconstructions of our data sets and OCT angiography images from literature [59], we identify these structures as fine blood vessels. For a quantitative analysis, we determined the point spread function of a specular reflex at the interface of the retina and vitreous body to evaluate the actual axial resolution of our retinal images [60]. The measurement resulted in a width of 6.0 µm of the specular reflex, which confirms the theoretical value of 5.9 µm.
Fig. 6.
Representative B-scan of the OCT imaging with 120 nm and 70 nm sweeping bandwidth and a four times flying average. An area around the RPE and around the top retinal layer is magnified in the blue and red boxes.
Additionally, we compared our imaging results with the highest resolving retinal OCT images to date [21]. We took a comparable section from our OCT images with a theoretical axial resolution of 5.9 µm and compared it with a B-scan from the publication by Wojtkowski et al. [21] with an axial resolution of 2.1 µm in Fig. 7. All marked layers including the fine blood vessels above the RPE show a nearly identical separation and amount of detail. The only difference is visible in the outer segments of photoreceptors, which are better resolved with the higher resolution. However, it could also be possible that this is due to the different eyes investigated. Interestingly, there is no difference in the definition of the RPE and the interdigitation zone in both cases. We assume that the refractive index differences are not high enough, to provide a significant contrast of the scattering.
Fig. 7.
Comparison of our OCT imaging with 5.9 µm axial resolution with the highest resolving ophthalmic flying spot OCT images to date [21].
Finally, there remains the question when regarding all the OCT imaging results, which sweeping bandwidth or axial resolution is necessary. Between the data sets with 10 µm (FDML with = 70 nm), 5.9µm (FDML with = 120 nm) and 2.1 µm (SD-OCT system [21]) only marginal differences are visible when analyzing the B-scans. Due to this, we believe that most diseases are diagnosable with around 10 µm axial resolution. Higher resolutions around 6 µm should be beneficial for analyzing fine structures such as small vessels in the retina, which show a better definition here. In all cases, one has to take into account that an increase in axial resolution always leads to a decrease in imaging range if sweep rate and acquisition rate of the digitizer are kept constant. Therefore, the chosen sweep range is a compromise between axial resolution and maximum imaging range. At MHz imaging speeds, we already need to use the fastest digitizer cards available and for applications such as ultra-widefield imaging [28] or live video rate 4D OCT [29, 30] rather high imaging ranges are required. Hence, we consider 70 nm to be a good compromise for our experiments requiring high imaging ranges while 120 nm could be beneficial for analyzing vessel morphology.
5. Summary and outlook
In this paper, we show a new record regarding the combination of a high sweep bandwidth and MHz sweep rates of a tunable light source with a center wavelength of 1060 nm. 120 nm spectral bandwidth was demonstrated with our FDML laser at an A-scan rate of 1.67 MHz, and even 143 nm at 417 kHz. We were able to show that the resulting axial resolution most importantly depends on the shape of the spectrum and not on the spectral bandwidth alone. Especially the water absorption in the eye has a significant impact on the spectral shape. With the new FDML laser, OCT data of a human retina was captured and compared at two sweep ranges as well as with literature images of an SD-OCT system with very high axial resolution. The differences were only marginal regarding the definition of detail of the individual layers. The greatest benefit of high resolution is visible in the fine blood vessels in the top layers of the retina. For most applications, we think that 70 nm at MHz sweep rates are sufficient, as they are a good compromise between axial resolution and imaging range. Only for analyzing the morphology of small vessels we see a possible benefit in using the 120 nm sweep range. Here, we expect to see a better definition of small blood vessels. In each case, one has to be careful at the post-processing of the data to ensure a proper linearization in k-space and numerical dispersion compensation, as these parameters influence the perceived axial resolution significantly.
For future work, a modulation of the current of the buffer stage SOA in our setup for the optimization of the spectrum could be implemented, as far as appropriate safety precautions are taken.
Funding
European Union project ENCOMOLE-2i (Horizon 2020, ERC CoG no. 646669); German Research Foundation (DFG project HU1006/6 and EXC 306/2); European Union within Interreg Deutschland-Danmark from the European Regional Development Fund in the project CELLTOM.
Disclosures
Jan Philip Kolb, Tom Pfeiffer, Matthias Eibl, Hubertus Hakert declare that there are no conflicts of interest related to this article. Robert Huber declares the following potential conflicts of interest: Optores GmbH (I, P, R), Optovue Inc. (I, R), Abbott (I, R).
References and links
- 1.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Fujimoto J. G., “Optical Coherence Tomography,” Science 254(5035), 1178–1181 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fercher A. F., Hitzenberger C. K., Drexler W., Kamp G., Sattmann H., “In vivo optical coherence tomography,” Am. J. Ophthalmol. 116(1), 113–114 (1993). [DOI] [PubMed] [Google Scholar]
- 3.Puliafito C. A., Hee M. R., Lin C. P., Reichel E., Schuman J. S., Duker J. S., Izatt J. A., Swanson E. A., Fujimoto J. G., “Imaging of macular diseases with optical coherence tomography,” Ophthalmology 102(2), 217–229 (1995). [DOI] [PubMed] [Google Scholar]
- 4.Swanson E. A., Izatt J. A., Hee M. R., Huang D., Lin C. P., Schuman J. S., Puliafito C. A., Fujimoto J. G., “In vivo retinal imaging by optical coherence tomography,” Opt. Lett. 18(21), 1864–1866 (1993). [DOI] [PubMed] [Google Scholar]
- 5.Tearney G. J., Brezinski M. E., Bouma B. E., Boppart S. A., Pitris C., Southern J. F., Fujimoto J. G., “In vivo endoscopic optical biopsy with optical coherence tomography,” Science 276(5321), 2037–2039 (1997). [DOI] [PubMed] [Google Scholar]
- 6.Tearney G. J., Brezinski M. E., Southern J. F., Bouma B. E., Boppart S. A., Fujimoto J. G., “Optical biopsy in human gastrointestinal tissue using optical coherence tomography,” Am. J. Gastroenterol. 92(10), 1800–1804 (1997). [PubMed] [Google Scholar]
- 7.Hanna N., Saltzman D., Mukai D., Chen Z., Sasse S., Milliken J., Guo S., Jung W., Colt H., Brenner M., “Two-dimensional and 3-dimensional optical coherence tomographic imaging of the airway, lung, and pleura,” J. Thorac. Cardiovasc. Surg. 129(3), 615–622 (2005). [DOI] [PubMed] [Google Scholar]
- 8.Colston B., Sathyam U., Dasilva L., Everett M., Stroeve P., Otis L., “Dental OCT,” Opt. Express 3(6), 230–238 (1998). [DOI] [PubMed] [Google Scholar]
- 9.Schmitt J. M., Yadlowsky M. J., Bonner R. F., “Subsurface imaging of living skin with optical coherence microscopy,” Dermatology (Basel) 191(2), 93–98 (1995). [DOI] [PubMed] [Google Scholar]
- 10.Wiesauer K., Pircher M., Götzinger E., Bauer S., Engelke R., Ahrens G., Grützner G., Hitzenberger C., Stifter D., “En-face scanning optical coherence tomography with ultra-high resolution for material investigation,” Opt. Express 13(3), 1015–1024 (2005). [DOI] [PubMed] [Google Scholar]
- 11.Zhang J., Williams B. M., Lawman S., Atkinson D., Zhang Z., Shen Y., Zheng Y., “Non-destructive analysis of flake properties in automotive paints with full-field optical coherence tomography and 3D segmentation,” Opt. Express 25(16), 18614–18628 (2017). [DOI] [PubMed] [Google Scholar]
- 12.Swanson E. A., Fujimoto J. G., “The ecosystem that powered the translation of OCT from fundamental research to clinical and commercial impact Invited,” Biomed. Opt. Express 8(3), 1638–1664 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Drexler W., Fujimoto J. G., Optical coherence tomography: technology and applications (Springer, 2008). [Google Scholar]
- 14.Izatt J. A., Hee M. R., Owen G. M., Swanson E. A., Fujimoto J. G., “Optical Coherence Microscopy in Scattering Media,” Opt. Lett. 19(8), 590–592 (1994). [DOI] [PubMed] [Google Scholar]
- 15.Zawadzki R. J., Jones S. M., Olivier S. S., Zhao M., Bower B. A., Izatt J. A., Choi S., Laut S., Werner J. S., “Adaptive-optics optical coherence tomography for high-resolution and high-speed 3D retinal in vivo imaging,” Opt. Express 13(21), 8532–8546 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kocaoglu O. P., Turner T. L., Liu Z., Miller D. T., “Adaptive optics optical coherence tomography at 1 MHz,” Biomed. Opt. Express 5(12), 4186–4200 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chinn S. R., Swanson E. A., Fujimoto J. G., “Optical coherence tomography using a frequency-tunable optical source,” Opt. Lett. 22(5), 340–342 (1997). [DOI] [PubMed] [Google Scholar]
- 18.Golubovic B., Bouma B. E., Tearney G. J., Fujimoto J. G., “Optical frequency-domain reflectometry using rapid wavelength tuning of a Cr4+:forsterite laser,” Opt. Lett. 22(22), 1704–1706 (1997). [DOI] [PubMed] [Google Scholar]
- 19.Yun S., Tearney G., de Boer J., Iftimia N., Bouma B., “High-speed optical frequency-domain imaging,” Opt. Express 11(22), 2953–2963 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Drexler W., Morgner U., Ghanta R. K., Kärtner F. X., Schuman J. S., Fujimoto J. G., “Ultrahigh-resolution ophthalmic optical coherence tomography,” Nat. Med. 7(4), 502–507 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wojtkowski M., Srinivasan V., Ko T., Fujimoto J., Kowalczyk A., Duker J., “Ultrahigh-resolution, high-speed, Fourier domain optical coherence tomography and methods for dispersion compensation,” Opt. Express 12(11), 2404–2422 (2004). [DOI] [PubMed] [Google Scholar]
- 22.Leitgeb R., Drexler W., Unterhuber A., Hermann B., Bajraszewski T., Le T., Stingl A., Fercher A., “Ultrahigh resolution Fourier domain optical coherence tomography,” Opt. Express 12(10), 2156–2165 (2004). [DOI] [PubMed] [Google Scholar]
- 23.Potsaid B., Baumann B., Huang D., Barry S., Cable A. E., Schuman J. S., Duker J. S., Fujimoto J. G., “Ultrahigh speed 1050nm swept source/Fourier domain OCT retinal and anterior segment imaging at 100,000 to 400,000 axial scans per second,” Opt. Express 18(19), 20029–20048 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Klein T., Wieser W., Reznicek L., Neubauer A., Kampik A., Huber R., “Multi-MHz retinal OCT,” Biomed. Opt. Express 4(10), 1890–1908 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Klein T., Wieser W., Eigenwillig C. M., Biedermann B. R., Huber R., “Megahertz OCT for ultrawide-field retinal imaging with a 1050 nm Fourier domain mode-locked laser,” Opt. Express 19(4), 3044–3062 (2011). [DOI] [PubMed] [Google Scholar]
- 26.Wieser W., Biedermann B. R., Klein T., Eigenwillig C. M., Huber R., “Multi-megahertz OCT: High quality 3D imaging at 20 million A-scans and 4.5 GVoxels per second,” Opt. Express 18(14), 14685–14704 (2010). [DOI] [PubMed] [Google Scholar]
- 27.Rosa C. C., Podoleanu A. G., “Limitation of the achievable signal-to-noise ratio in optical coherence tomography due to mismatch of the balanced receiver,” Appl. Opt. 43(25), 4802–4815 (2004). [DOI] [PubMed] [Google Scholar]
- 28.Kolb J. P., Klein T., Kufner C. L., Wieser W., Neubauer A. S., Huber R., “Ultra-widefield retinal MHz-OCT imaging with up to 100 degrees viewing angle,” Biomed. Opt. Express 6(5), 1534–1552 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Kolb J. P., Klein T., Wieser W., Draxinger W., Huber R., “Full volumetric video rate OCT of the posterior eye with up to 195.2 volumes/s,” in 2015), 931202–931202–931207.
- 30.Wieser W., Draxinger W., Klein T., Karpf S., Pfeiffer T., Huber R., “High definition live 3D-OCT in vivo: design and evaluation of a 4D OCT engine with 1 GVoxel/s,” Biomed. Opt. Express 5(9), 2963–2977 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Grulkowski I., Liu J. J., Potsaid B., Jayaraman V., Lu C. D., Jiang J., Cable A. E., Duker J. S., Fujimoto J. G., “Retinal, anterior segment and full eye imaging using ultrahigh speed swept source OCT with vertical-cavity surface emitting lasers,” Biomed. Opt. Express 3(11), 2733–2751 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jirauschek C., Biedermann B., Huber R., “A theoretical description of Fourier domain mode locked lasers,” Opt. Express 17(26), 24013–24019 (2009). [DOI] [PubMed] [Google Scholar]
- 33.Biedermann B. R., Wieser W., Eigenwillig C. M., Klein T., Huber R., “Direct measurement of the instantaneous linewidth of rapidly wavelength-swept lasers,” Opt. Lett. 35(22), 3733–3735 (2010). [DOI] [PubMed] [Google Scholar]
- 34.Todor S., Biedermann B., Wieser W., Huber R., Jirauschek C., “Instantaneous lineshape analysis of Fourier domain mode-locked lasers,” Opt. Express 19(9), 8802–8807 (2011). [DOI] [PubMed] [Google Scholar]
- 35. Kolb J. P., Klee J., Pfeiffer T., Huber R., “1060nm FDML laser with centimeter coherence length and 1.67 MHz sweep rate for full eye length and retinal ultra-widefield OCT,” in European Conferences on Biomedical Optics, (International Society for Optics and Photonics, 2017), 104160J–104160J–104166. [Google Scholar]
- 36. Pfeiffer T., Draxinger W., Wieser W., Klein T., Huber R., “Analysis of FDML lasers with meter range coherence,” in SPIE BiOS, (SPIE, 2017), 100531T. [Google Scholar]
- 37.Jirauschek C., Huber R., “Modeling and analysis of polarization effects in Fourier domain mode-locked lasers,” Opt. Lett. 40(10), 2385–2388 (2015). [DOI] [PubMed] [Google Scholar]
- 38.Jirauschek C., Huber R., “Efficient simulation of the swept-waveform polarization dynamics in fiber spools and Fourier domain mode-locked (FDML) lasers,” J. Opt. Soc. Am. B 34, 1135–1146 (2017). [Google Scholar]
- 39.Torzicky T., Marschall S., Pircher M., Baumann B., Bonesi M., Zotter S., Goetzinger E., Trasischker W., Klein T., Wieser W., Biedermann B., Huber R., Andersen P., Hitzenberger C. K., “Retinal polarization-sensitive optical coherence tomography at 1060 nm with 350 kHz A-scan rate using an Fourier domain mode locked laser,” J. Biomed. Opt. 18, 026008 (2013). [DOI] [PubMed] [Google Scholar]
- 40.Wieser W., Palte G., Eigenwillig C. M., Biedermann B. R., Pfeiffer T., Huber R., “Chromatic polarization effects of swept waveforms in FDML lasers and fiber spools,” Opt. Express 20(9), 9819–9832 (2012). [DOI] [PubMed] [Google Scholar]
- 41.Klein T., Huber R., “High-speed OCT light sources and systems,” Biomed. Opt. Express 8(2), 828–859 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jirauschek C., Huber R., “Wavelength shifting of intra-cavity photons: Adiabatic wavelength tuning in rapidly wavelength-swept lasers,” Biomed. Opt. Express 6(7), 2448–2465 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Blatter C., Klein T., Grajciar B., Schmoll T., Wieser W., Andre R., Huber R., Leitgeb R. A., “Ultrahigh-speed non-invasive widefield angiography,” J. Biomed. Opt. 17, 0705051 (2012). [DOI] [PubMed] [Google Scholar]
- 44.Blatter C., Weingast J., Alex A., Grajciar B., Wieser W., Drexler W., Huber R., Leitgeb R. A., “In situ structural and microangiographic assessment of human skin lesions with high-speed OCT,” Biomed. Opt. Express 3(10), 2636–2646 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Blatter C., Grajciar B., Zou P., Wieser W., Verhoef A.-J., Huber R., Leitgeb R. A., “Intrasweep phase-sensitive optical coherence tomography for noncontact optical photoacoustic imaging,” Opt. Lett. 37(21), 4368–4370 (2012). [DOI] [PubMed] [Google Scholar]
- 46.Eibl M., Karpf S., Weng D., Hakert H., Pfeiffer T., Kolb J. P., Huber R., “Single pulse two photon fluorescence lifetime imaging (SP-FLIM) with MHz pixel rate,” Biomed. Opt. Express 8(7), 3132–3142 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Eigenwillig C. M., Wieser W., Todor S., Biedermann B. R., Klein T., Jirauschek C., Huber R., “Picosecond pulses from wavelength-swept continuous-wave Fourier domain mode-locked lasers,” Nat. Commun. 4, 1848 (2013). [DOI] [PubMed] [Google Scholar]
- 48.Karpf S., Eibl M., Wieser W., Klein T., Huber R., “A Time-Encoded Technique for fibre-based hyperspectral broadband stimulated Raman microscopy,” Nat. Commun. 6, 6784 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Karpf S., Eibl M., Wieser W., Klein T., Huber R., “Shot-Noise Limited Time-Encoded Raman Spectroscopy,” J. Spectrosc. 2017, 9253475 (2017). [Google Scholar]
- 50.Huber R., Wojtkowski M., Fujimoto J. G., “Fourier Domain Mode Locking (FDML): A new laser operating regime and applications for optical coherence tomography,” Opt. Express 14(8), 3225–3237 (2006). [DOI] [PubMed] [Google Scholar]
- 51.Huber R., Adler D. C., Fujimoto J. G., “Buffered Fourier domain mode locking: Unidirectional swept laser sources for optical coherence tomography imaging at 370,000 lines/s,” Opt. Lett. 31(20), 2975–2977 (2006). [DOI] [PubMed] [Google Scholar]
- 52.Wieser W., Klein T., Adler D. C., Trépanier F., Eigenwillig C. M., Karpf S., Schmitt J. M., Huber R., “Extended coherence length megahertz FDML and its application for anterior segment imaging,” Biomed. Opt. Express 3(10), 2647–2657 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Akcay A. C., Rolland J. P., Eichenholz J. M., “Spectral shaping to improve the point spread function in optical coherence tomography,” Opt. Lett. 28(20), 1921–1923 (2003). [DOI] [PubMed] [Google Scholar]
- 54.Marschall S., Klein T., Wieser W., Biedermann B. R., Hsu K., Hansen K. P., Sumpf B., Hasler K.-H., Erbert G., Jensen O. B., Pedersen C., Huber R., Andersen P. E., “Fourier domain mode-locked swept source at 1050 nm based on a tapered amplifier,” Opt. Express 18(15), 15820–15831 (2010). [DOI] [PubMed] [Google Scholar]
- 55.Hale G. M., Querry M. R., “Optical Constants of Water in the 200-nm to 200-µm Wavelength Region,” Appl. Opt. 12(3), 555–563 (1973). [DOI] [PubMed] [Google Scholar]
- 56. Maher E. F., “Transmission and absorption coefficients for ocular media of the rhesus monkey,” (School of Aerospace Medicine Brooks AFB TX, 1978). [Google Scholar]
- 57.Staurenghi G., Sadda S., Chakravarthy U., Spaide R. F., International Nomenclature for Optical Coherence Tomography (IN•OCT) Panel , “Proposed lexicon for anatomic landmarks in normal posterior segment spectral-domain optical coherence tomography: the IN*OCT consensus,” Ophthalmology 121(8), 1572–1578 (2014). [DOI] [PubMed] [Google Scholar]
- 58.Jonnal R. S., Kocaoglu O. P., Zawadzki R. J., Lee S.-H., Werner J. S., Miller D. T., “The Cellular Origins of the Outer Retinal Bands in Optical Coherence Tomography Images,” Invest. Ophthalmol. Vis. Sci. 55(12), 7904–7918 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hussain N., Hussain A., Zhang M., Su J. P., Liu G., Hwang T. S., Bailey S. T., Huang D., “Diametric measurement of foveal avascular zone in healthy young adults using Optical Coherence Tomography Angiography,” Int J Retina Vitreous 2(OCT), 27–36 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Cense B., Nassif N., Chen T., Pierce M., Yun S.-H., Park B., Bouma B., Tearney G., de Boer J., “Ultrahigh-resolution high-speed retinal imaging using spectral-domain optical coherence tomography,” Opt. Express 12(11), 2435–2447 (2004). [DOI] [PubMed] [Google Scholar]
- 61.Makita S., Hong Y., Yamanari M., Yatagai T., Yasuno Y., “Optical coherence angiography,” Opt. Express 14(17), 7821–7840 (2006). [DOI] [PubMed] [Google Scholar]
- 62.Wang R. K., Jacques S. L., Ma Z., Hurst S., Hanson S. R., Gruber A., “Three dimensional optical angiography,” Opt. Express 15(7), 4083–4097 (2007). [DOI] [PubMed] [Google Scholar]