High-resolution imaging in two-photon excitation microscopy using in situ estimations of the point spread function

Abstract

We present a technique for improving the spatial resolution of two-photon excitation microscopy; our technique combines annular illumination with an in situ estimation of the point spread function (PSF) used for deconvolution. For the in situ estimation of the PSF, we developed a technique called autocorrelation scanning, in which a sample is imaged by the scanning of two excitation foci that are overlapped over various distances. The image series obtained with the variation of the distance between the two foci provides the autocorrelation function of the PSF, which can be used to estimate the PSF at specific positions within a sample. We proved the principle and the effectiveness of this technique through observations of a fluorescent biological sample, and we confirmed that the improvement in the spatial resolution was ~1.7 times that of typical two-photon excitation microscopy by observing a mouse brain phantom at a depth of 200 µm.

1. Introduction

Two-photon excitation fluorescence microscopy is a technique used for the imaging of thick samples; it utilizes a nonlinear optical process, namely, two-photon absorption [1]. This technique has made it possible to obtain cellular and molecular information from thick tissue and from deep within living animals [2–6]. The optics used for detecting the fluorescence photons in two-photon excitation microscopes are simpler than those used in confocal single-photon excitation microscopes because they do not consist of pinholes accompanied by relay lenses. However, with the use of a longer wavelength for excitation, the spatial resolution of two-photon excitation fluorescence microscopes becomes lower than that of confocal microscopes. Furthermore, the imaging quality of two-photon excitation microscopes is easily affected by the optical properties of the samples and aberrations when imaging in deep regions. As a result, it is important for the spatial resolutions of two-photon excitation microscopes to be improved.

Recently, several super-resolution imaging techniques have been developed [7]. Structured illumination microscopy (SIM) is a useful technique to maximize the frequency capabilities of imaging optics [8]. It expands the cut-off frequency of wide-field microscopes by a factor of two, and it does this by illuminating high-frequency structured patterns that shift the spatial frequencies of images at the detector; this results in the patterns being observed as moiré fringes. The SIM concept has also been applied to two-photon excitation microscopy through the modulation of the intensity of excitation beams used to produce structured illuminations [9,10]. Furthermore, SIM has been combined with temporal focusing techniques so that it can remove background fluorescence signals [11]. Although SIM has proven to be effective, it is difficult to apply to typical two-photon excitation microscopes; this is because it requires a two-dimensional (2D) detector to be used for fluorescence detections. On the other hands, super-resolution imaging techniques based on laser scanning, such as stimulated emission depletion (STED) microscopy, are suitable for two-photon excitation microscopy. STED microscopy uses doughnut-shaped beams to produce an excitation point spread function (PSF) that is spatially confined beyond the diffraction limit by a stimulated-emission effect [12]. STED microscopy has been done with two-photon excitation and has achieved a spatial resolution of ~60 nm in optical systems with two lasers [13–15] and a single laser [16,17]. However, the imaging depth of two-photon STED microscopy is still limited to being less than ~100 µm. A super-resolution method called saturated excitation (SAX) microscopy is also applicable to two-photon excitation microscopy. It extracts only the saturation component of the fluorescence emissions and, in doing so, makes the effective PSF small; it also has a nonlinear dependence on the excitation intensity in addition to the non-linearity caused by the two-photon absorption [18,19]. Although it more than doubles the cut-off frequency and improves the spatial resolution, a high-power excitation beam has to be used, which may damage samples. There is a technique with modulation of two overlapping laser spots in two-photon excitation microscopy, which is called spatial overlap modulation nonlinear optical microscopy (SPOMNOM); this was proposed as a way for background fluorescence signals to be reduced [20,21], which would enable the image contrast in deep tissue imaging to be improved.

Aberrations generated in samples also degrade fluorescence images, especially when those images are obtained from a position deep within a thick sample. Aberration corrections by adaptive optics techniques have been found to be effective and practical approaches for the improving of spatial resolutions in deep tissue imaging [22]. These techniques have also been applied to two-photon excitation microscopy, and the correction of aberrations, especially those caused by refractive index mismatches, has been demonstrated for fluorescent beads in water [23]. Adaptive optics techniques use dynamic feedback loops that consist of deformable mirrors or spatial light modulators; these correct the aberrations in different ways [22]; one way is that they monitor the intensities or wave front distributions of fluorescent light [24–27], while another is that they detect back-scattered excitation light using a coherence-gated technique or a pinhole-filtered Shack–Hartmann sensor [28,29]. Recently, a new method called focus scanning holographic aberration probing (F-SHARP) has been developed and proved to be effective for correcting aberration in turbid medium, which utilizes iteration process of electric-field PSF estimation with two excitation lasers with different intensities and aberration correction by spatial light modulator [30]. These adaptive optics techniques can effectively correct the aberrations and produce nearly diffraction-limited PSFs in thick samples. However, the resolutions obtained using these techniques cannot exceed those of conventional PSFs that do not suffer from aberrations.

To enhance the spatial resolution obtained by deep imaging conducted by conventional two-photon excitation microscopes, we can also turn to PSF engineering [31–33]. This approach enhances the high-frequency component of an excitation PSF and, in doing so, produces sharp peaks and keeps high-frequency component against scattering in a sample. It often involves the sidelobes of a PSF, as these can negatively affect an image. Deconvolution techniques can be used to suppress the sidelobes of a PSF and enhance the resolution of two-photon excitation microscopes [34,35]. Deconvolution is an image processing method that can deblur images, but it often requires PSF information. Although a PSF can be readily characterized by a simulation when an image is taken of the surface of a sample, it is difficult to measure the PSF deep within a sample because it is often distorted by the refraction or scattering of light within the sample. Several approaches have been developed to estimate the PSF within samples; however, these require fluorescent beads to be embedded within a sample or phantom [36–38]. Furthermore, although adaptive optics techniques offer information about aberrations, they do not themselves directly provide accurate PSFs.

In this paper, we present an imaging technique that combines PSF engineering with an in situ estimation of the PSF required for a deconvolution. We utilized an annular illumination, which enhanced the high-frequency component of the excitation. In addition, we propose a method for estimating the PSF within a sample when two-photon excitation microscopes are used. Notably, our proposed method does not require any additional materials, such as fluorescent beads, to be used; rather, it utilizes autocorrelation scanning with two excitation foci. We looked to improve the spatial resolution of a two-photon excitation microscope by using the PSF we estimated for the deconvolution of the fluorescent images obtained by the annular illumination. We confirmed the principle of this method using both a simulation and experiments that were carried out on a biological sample and a mouse brain phantom. The results in our study show that our method can accurately estimate a PSF for both annular excitations and deep tissue imaging.

2. PSF estimation method

In this section, we demonstrate the principle behind the method used to directly estimate the PSF of a sample. We assumed that two excitation beams were focused onto a sample that had been stained with a fluorescent material. To simplify this model, we first assumed that the two excitation beams were incoherent, and we also assumed that the sample contained a uniform distribution of a fluorescent material. When the intensity distributions, I, of the two beams were equal and the position of one beam was displaced from the other by a distance of u in the x-direction, the intensity of the fluorescent light emitted from the two spots through two-photon excitation is represented by the following equation:

$$I_{fl\_2PE}(u)\propto {\displaystyle \iiint \left\{I^2(x,y,z)+I^2(x+u,y,z)+2I(x,y,z)I(x+u,y,z)\right\}dxdydz}.$$ (1)

In Eq. (1), the first and second terms in the integral show the excitation distributions of each excitation spot, and the third term represents an overlap of the two spots. The third term takes the form of an autocorrelation function, which is shown in Eq. (2); this form can also be expressed as a convolution in the $x$ -direction by assuming that I is symmetric in the x-direction ($I(x,y,z)=I(-x,y,z)$):

$$G(u)={\displaystyle \iiint I(x,y,z)I(x+u,y,z)dxdydz}.$$ (2)

$$F\left[G(u)\right]={\left(F\left[I(u)\right]\right)}^2.$$ (3)

$$I(u)=F^{-1}\left\{{\left(F\left[G(u)\right]\right)}^{1/2}\right\}.$$ (4)

Under this assumption, the Fourier transform of G simply gives the square of the Fourier transform of I, as shown in Eq. (3); therefore, the inverse Fourier transform of the square root of the Fourier transform of the G that is measured simply provides the distribution of the excitation beam spot in the x-direction as shown in Eq. (4). The PSF profile of the two-photon excitation is then obtained as I². By assuming that I is centrosymmetric in the focal plane, a 2D-PSF can be obtained by plotting I² with a rotation around the geometrical focus. In the above consideration, we described the case with using the same intensity for two foci, which provide a minimum offset in the correlation.

Under practical conditions, it would be reasonable to assume that the two excitation beams are generated from a single laser and are coherent with one another. As a result, Eq. (1) can be modified to give the following equation:

$$\begin{array}{ll}{I}_{fl\_2PE}(u)& \propto {\displaystyle \iiint \{I^2(x,y,z)+I^2(x+u,y,z)+2I(x,y,z)I(x+u,y,z)}\\ & +2\left(I(x,y,z)+I(x+u,y,z)\right)\left(E^{*}(x,y,z)E(x+u,y,z)+E(x,y,z)E^{*}(x+u,y,z)\right)\\ & +{\left(E^{*}(x,y,z)E(x+u,y,z)+E(x,y,z)E^{*}(x+u,y,z)\right)}^2\}dxdydz.\end{array}$$ (5)

Equation (5) includes the electric field, E (and its complex conjugate, E*), of the laser spot, which represents the interference between the two beams. By assuming that the polarization of the two beams is perpendicular, we can neglect the interference term; as a result, the intensity becomes similar to that of Eq. (1). However, a high-NA objective lens produces a PSF with different profiles on the x- and y- axes; this causes a mismatch between the actual 2D-PSF and the estimated one given by the rotational plot of I(x). As described below, we found that the estimated 2D-PSF matches the circular polarization well, which is reasonable given that a PSF profile with a circular polarization corresponds to the PSF profile with a linear polarization at an angle of 45° from the polarization axis [39].

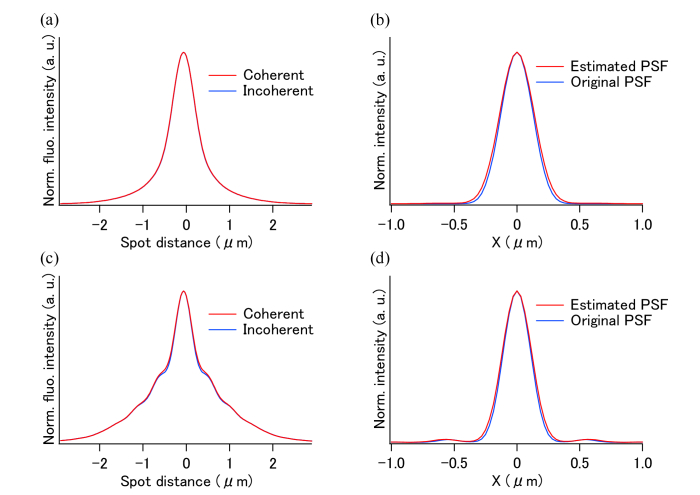
We confirmed the effect of the perpendicular polarization and the validity of the PSF estimation by using a simulation. Figure 1(a) shows the autocorrelation curve, the two-photon excited fluorescence intensities calculated by Eq. (5) as functions of the distance between the two excitation spots. The offset components, which correspond to the first and second terms of Eq. (5), are omitted in the plot. The calculation of the fluorescence intensity from the two excitation spots was performed in 3D space using a vector-based calculation [40] for an objective lens with 30 × magnification and a silicon immersion (whose refractive index was 1.4) with an NA of 1.05. The excitation laser wavelength was set to 800 nm. In a practical model, the excitation light enters the pupil of the objective lens as a uniformly distributed plane wave. To make a comparison, the autocorrelation curve with incoherent excitation beams was calculated by Eq. (1); the offset components of the first and second terms were also omitted from it. At a spot distance of zero, the curves peaked, because the overlapping of the two spots became maximum at this distance and produced the highest fluorescence intensity. In Fig. 1(a), the coherent and incoherent results are identical, which indicates that the interference term was too small for a clear distinction to be made between the two conditions.

Fig. 1.

(a, c) Autocorrelation curves for the circular and annular illuminations; in these images, the coherent and incoherent conditions are compared. (b, d) Comparison of the estimated PSFs for two-photon excitation and original PSFs with circular polarization for circular and annular illuminations. The estimated PSFs in (b) and (d) were calculated from the autocorrelation curves shown in (a) and (c).

Figure 1(b) shows the profile of the PSF estimated from the autocorrelation curves shown in Fig. 1(a). The estimated PSF and the PSF with the circular polarization show similar profiles on the x-axis. This result shows that the 2D-PSF with the circular polarization can be estimated by using the autocorrelation signal prepared using two foci with perpendicular polarizations. We also applied the PSF estimation method to a laser focus with an annular illumination, as shown in Figs. 1(c) and 1(d). Figure 1(c) shows the autocorrelation curves obtained with annular illumination, which is masking 62.5% of the objective's pupil diameter at the center. This result also shows that the PSFs obtained from the coherent and incoherent conditions are almost the same. In Fig. 1(d), the sidelobes characteristic for annular illumination are well estimated by the proposed method.

To perform the PSF estimation mentioned above, we had to consider a sample with a non-uniform distribution of the fluorescent material, as this distribution could influence and distort the autocorrelation curves. To obtain autocorrelation curves unaffected by the fluorescence distributions, we performed autocorrelation scanning, as this scans a sample with two spots separated by a distance u to integrate the fluorescence signal in the scanning area. By scanning the sample with different focal separations, G can be obtained as in Eq. (6), where ρ is the distribution of the fluorescent material. When the scanning area is sufficiently larger than the focal separation, ρ is integrated so as to be a constant coefficient for the different focal separations, and G can provide the autocorrelation curve of the two excitation spots even in non-uniform samples:

$$G(u)={\displaystyle \iint \rho (x,y,z)dxdy}{\displaystyle \iiint I(x,y,z)I(x+u,y,z)dxdydz}.$$ (6)

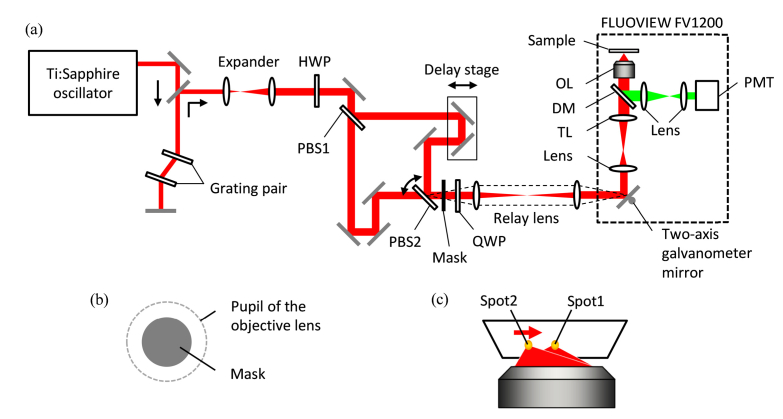
The experimental system shown in Fig. 2 was used to demonstrate the PSF estimation technique. We used a Ti:sapphire laser (Chameleon-XR, Coherent Inc.) with a repetition rate of 90 MHz and a pulse width of <140 fs for the two-photon excitation. Laser pulses of 800 nm wavelength were introduced into a pre-chirper with a grating pair to compensate for the wavelength dispersion in the optics. The magnification of the beam expander was set so as to overfill the pupil of the objective lens with the laser beam. The laser beam was split into two by a polarized beam splitter (PBS1), and the separated beams were merged by another PBS (PBS2) through a delay stage; this stage was used to ensure that the optical pass lengths of both beams were equal. PBS2 was mounted onto a stage whose tilting angle could be controlled by a computer to change the separation of the two excitation foci at a sample. For the experiment using annular illumination, a mask was placed after PBS2. Two-axis galvanometer mirrors in a laser scanning microscope system (FLUOVIEW FV1200 with IX83, Olympus Corp.) were used to perform autocorrelation scanning and fluorescence image acquisition. We used an objective lens with a NA of 1.05 (UPLSAPO 30XSIR, Olympus Corp.) and a non-descanned detector with a photo multiplier tube (PMT). For the imaging, we set the scanning speed to 200 µs/pixel, which was relatively slow, but useful to obtain images with a high signal-to-noise ratio and to suppress photobleaching with using a moderate excitation intensity. With this setup, two beams were focused by objective lens onto the sample, and one spot was scanned against another to perform the autocorrelation scanning. By rotating the half-wave plate, we were able to switch the experimental conditions between a two-beam configuration (for the autocorrelation scanning) and a one-beam configuration (for sample imaging) without losing any excitation power. The quarter-wave plate was used only for the one-beam configuration to make circular polarization and was removed in the two-beam configuration.

Fig. 2.

(a) Schematic of the experimental setup. In it, HWP means half-wave plate, PBS means polarized beam splitter, QWP means quarter-wave plate, TL means tube lens, DM means dichromic mirror, OL means objective lens, PMT means photo multiplier tube, and FLUOVIEW FV1200 represents the laser scanning microscope system (Olympus corp.). The mask is placed very close to PBS2. The dashed line implies that the relay lens makes an image of PBS2 (and mask) on the two-axis galvanometer mirror in FLUOVIEW FV1200. The red and green lines indicate excitation and fluorescent light, respectively. (b) The mask used for the annular illumination. The excitation beam inner below 62.5% in diameter is blocked at the pupil of the objective lens. (c) A schematic diagram of the excitation beam focused by the objective lens. The intensity of the two spots I corresponds to that given in Eq. (5). Spot2 can be scanned against spot1 by tilting PBS2 in (a), and both spots can be scanned together by the two-axis galvanometer mirror in FLUOVIEW FV1200.

3. Cell imaging

We performed the technique for an in situ PSF estimation during an observation of a biological sample. We used fixed HeLa cells of which the actin fibers were stained with Rhodamine 6G for the sample. The optical setup shown in Fig. 2 was used for this experiment.

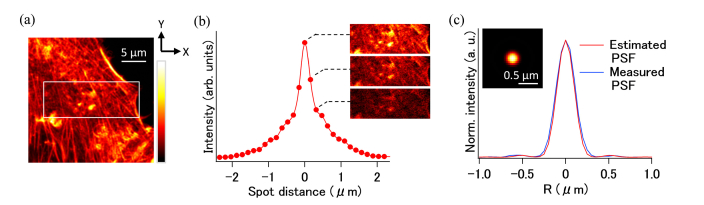
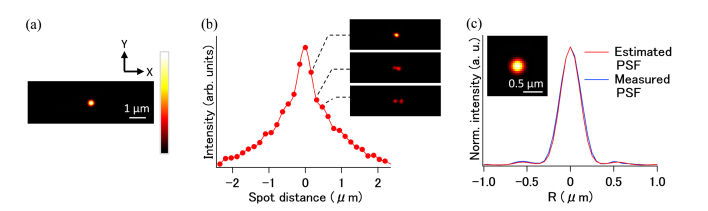
Figures 3(a)–(c) show the experimental results for an in situ estimation of the PSF with annular illumination. Figure 3(a) shows a fluorescence image of the sample obtained with one excitation beam. A box in the figure indicates the area for autocorrelation scanning with two excitation beams. Figure 3(b) shows the autocorrelation curve obtained by summing the signal in the fluorescence images obtained with different spot distances. The inset shows examples of the fluorescence images obtained by using two excitation beams. To estimate the signals of the offset components (i.e., the first and second terms of Eq. (5)), a series of images was captured without a temporal overlap of the excitation spot, which was realized by tuning the optical length at the delay stage. By subtracting the fluorescence signals without the temporal overlaps from those with the overlaps, an autocorrelation curve without any offset components was produced; this is shown in Fig. 3(b). To estimate the 2D-PSF, the autocorrelation curve was plotted as a rotation along the geometrical focus, and a 2D Fourier transformation and low-pass filtering to remove high-frequency noise above the cut-off of the objective lens were applied. Figure 3(c) shows the profile and a 2D image of the estimated PSF. In the figure, we have also, for the sake of comparison, plotted the profile of a two-photon excitation PSF obtained by the measuring of a fluorescent bead with diameters of 100 nm with a single circularly polarized beam. The two profiles show similar signal distributions, including their sidelobes, which indicates that our technique can make in situ estimations of the PSFs of actual biological samples.

Fig. 3.

PSF estimation process with experimental data from HeLa cells. (a) Image of HeLa cells (512 × 512 pixels, 0.05 µm/pixel) taken using annular illumination. Autocorrelation scanning was performed in the boxed area (128 × 48 pixels, 150 µm/pixel). The laser power was 0.7 mW. (b) Autocorrelation curve. Insets are images taken by two spots with corresponding spot distances, where the sum of the signal is plotted in the curve. The curve was averaged five times to improve the signal-to-noise ratio. (c) Profile of the PSF estimated from the autocorrelation curve. A PSF measured with a fluorescence bead (called Measured PSF) is compared against.

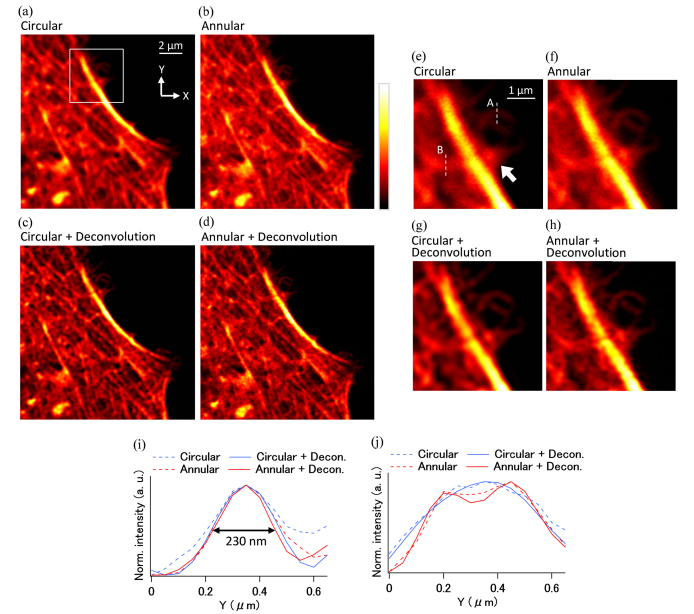
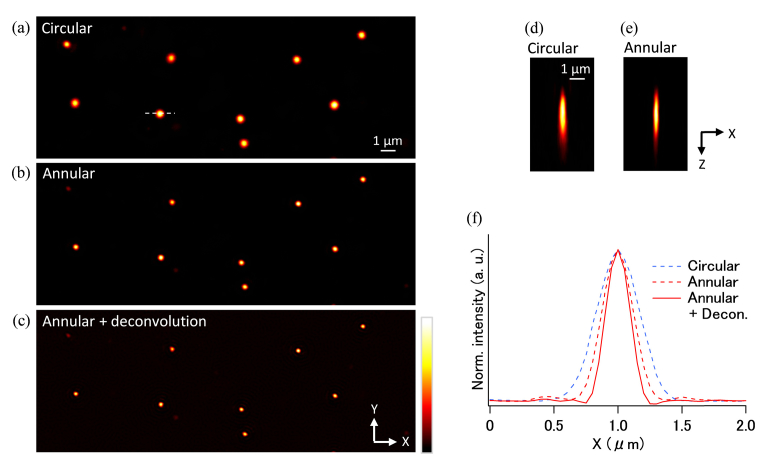
By using the estimated PSF in this observation, we were able to perform deconvolution on the image to retrieve the contrast of the high spatial frequency component. Figures 4(a)–(d) show the images obtained with circular illumination, annular illumination, circular illumination with deconvolution, and annular illumination with deconvolution, respectively. The one-beam excitation configuration with the circular polarization was used for these imagings. We used a Wiener filter as the deconvolution algorithm. To reduce the ringing effect, we added a Hann window with a cut-off frequency of the objective lens. From the figures, it would appear that the image obtained with the annular illumination with deconvolution provided the best resolution. Figures 4(e)–(h) show expanded views of the boxed area in Fig. 4(a). The actin structure indicated by the arrow head in Fig. 4(e) is blurred in the image obtained with the circular illumination. In the image obtained with the annular illumination, although the high-frequency component is more visible than in the one obtained by the circular illumination, the fine structure is still blurred. One possible reason for this is that the sidelobes of the PSF produced by the annular illumination reduced the contrast of the structures surrounded by the bright part of the image. By applying a deconvolution with the estimated PSF to the image of the annular illumination, we found that the effect of the sidelobes was reduced and the images of the fine structures became clearer. In Fig. 4(i), the normalized intensity profiles of the position indicated by the dashed line A in Fig. 4(e) are shown. The annular illumination was found to improve the two-point resolution laterally and the deconvolution further enhanced it. The full width at half maximum (FWHM) of a peak of the annular illumination with deconvolution was ~230 nm, which was 1.4 times greater than the peak obtained using the circular illumination. The normalized intensity profiles at the dashed line B in Fig. 4(e) are also shown in the Fig. 4(j). The profile of the circular illumination with deconvolution can show the only one peak. In contrast, the annular illumination with deconvolution can resolve the structure with two clearly visible peaks owing to the higher two-point resolution of the annular illumination. Significantly, this result indicates that the technique presented in this paper allows us to perform deconvolution by using the PSF estimated in situ, and no additional measurements with beads or complicated simulations are required. Furthermore, it confirmed that combining annular illumination and deconvolution with the estimated PSF is effective in improving the lateral spatial resolution of two-photon excitation fluorescence microscopes.

Fig. 4.

Imaging results of HeLa cells (300 × 300 pixels, 0.05 µm/pixel) (a)–(d) Images observed using circular illumination, annular illumination, a deconvolution image of circular illumination, and a deconvolution image of annular illumination, respectively. (e)–(h) Expanded images (91 × 91 pixels) of the area indicated by the small box in (a). (i, j) Normalized line profiles of the position shown by the dashed line A and B in (e), respectively.

4. Brain phantom imaging

To confirm the applicability of the in situ PSF estimation technique for deep tissue imaging, we imaged a mouse brain phantom made by a gel material with polystyrene beads as scattering medium into which 100-nm-diameter fluorescent beads (F8800, Invitrogen) were added. The optical properties of the phantom, such as its refractive index and scattering coefficient, were tuned to that of mouse brain tissue at a wavelength of 800 nm (refractive index: 1.36, scattering coefficient µ_s: 75 cm⁻¹). A critical angle method and Lambert-Beer law were utilized for measuring refractive index and scattering coefficient, respectively, in order to simply estimate the light attenuation and the degradation of PSF during propagation. This estimation cannot be applied to complicated tissue samples, however it is useful to know a sample conditions that affect the degradation of imaging quality in two-photon excitation microscopy. The distribution of refractive index and scattering coefficient was homogeneous in the phantom.

The results of the estimation of the two-photon excitation PSF are shown in Fig. 5. An autocorrelation curve was obtained from a single bead at a depth of 200 µm, as shown in Fig. 5(a). Figure 5(b) shows that the autocorrelation curve obtained by images in which the distances between the two excitation spots were varied. The inset images show the overlapping condition of the two excitation spots during autocorrelation scanning. After the signal processing, the two-photon excitation PSF was estimated; it is shown in Fig. 5(c). The line profile of the estimated PSF was almost the same as that of the measured PSF in the same phantom; this indicated that the PSF estimation worked for observations made deep within a tissue sample.

Fig. 5.

PSF estimation process with experimental data of mouse brain phantom. (a) Image of a bead in the phantom (151 × 51 pixels, 0.05 µm/pixel) taken by annular illumination at depth of 200 µm for autocorrelation scanning. The laser power was 22 mW. (b) Autocorrelation curve. Insets are images taken by two spots with correspondent distance. The curve was 10 times averaged. (c) Line profile and 2D image of estimated PSF. Line profile of the measured PSF at same depth is compared.

Lastly, we compared images of fluorescent beads embedded in the mouse brain phantom under different illumination conditions. The results are shown in Figs. 6(a)–(c). All of the images were taken using one excitation beam with circular polarization. The correction collar of the objective lens was adjusted at the surface of the sample and kept for deep imaging so that it would match with the actual condition of volume imaging. In the circular illumination condition shown in Fig. 6(a), the size of the PSF was broader than on the surface due to a spherical aberration. Figure 6(b) shows the image taken using annular illumination, where the PSF is shown as a smaller spot than that of the circular illumination; this was because the annular illumination was less sensitive to the spherical aberration due to the use of the narrow-band spatial frequency component at the pupil of the objective lens. The comparison of the XZ images of a single fluorescent bead obtained with the circular illumination and the annular illumination in Figs. 6(d) and 6(e) indicates that both illumination modes have almost a same axial resolution due to the spherical aberration at the depth of 200 µm in our experimental condition. By applying a Wiener filter in the same manner as we did with the cell sample, we found that the size of the bead images became smaller, as shown in Fig. 6(c). Figure 6(f) compares normalized intensity profiles of the position demarcated by the dashed line in Fig. 6(a). Similar to the result obtained for the cell sample, the annular illumination improved the lateral resolution of the image, while the deconvolution effectively enhanced the spatial resolution. Although a small ringing effect persisted, the sidelobes mostly disappeared after the deconvolution. The FWHM values found under both the circular illumination and annular illumination with deconvolution conditions were ~390 and ~230 nm, respectively. The combination of annular illumination and a deconvolution resulted in a lateral resolution that was 1.7 times better than that achieved using circular illumination, and there was no loss in the resolution quality of the image obtained from the surface.

Fig. 6.

Imaging results (512 × 192 pixels, 0.05 µm/pixel) of mouse brain phantom at depth of 200 µm by (a) circular illumination, (b) annular illumination, and (c) a deconvolution image of annular illumination. (d, e) XZ images of one bead taken by circular and annular illuminations. (f) Normalized line profiles at a dashed position in (a).

5. Discussion and conclusions

We proposed techniques for estimating an excitation PSF in situ in two-photon excitation microscopy to enhance the spatial resolution with a deconvolution in practical conditions. We proposed a technique, specifically that of autocorrelation scanning, which would allow for the estimation of an excitation PSF when non-uniform fluorescence samples, such as biological samples, are used. We also demonstrated that the estimated PSF can be used to effectively deconvolve fluorescent images and improve the contrast of high spatial frequency component in these images. This technique was combined with annular illumination, and it was used to successfully improve the lateral resolution of an observation that was made of a region deep within a tissue sample. We also confirmed that, for a mouse brain phantom, the spatial resolution of this technique was ~1.7 times better than that of circular illumination at a depth of 200 µm.

In this study, the autocorrelation scanning was performed in one direction under the assumption that PSF was centrosymmetric. For asymmetric PSF like simple elliptical distribution, 2D autocorrelation scanning can be applicable. However, if refractive index has distorted distribution and therefore PSF is complexly asymmetric, the technique cannot be applied. Autocorrelation scanning always provides symmetric function and replacement of autocorrelation and convolution requires the assumption of symmetric PSF as mentioned above, then PSF must be symmetric in each direction of autocorrelation scanning to apply this method. Furthermore, when the PSF is not the same everywhere in the field-of-view, autocorrelation scanning should be performed at several areas in the field-of-view. And the PSF estimation method was demonstrated in the lateral plane. Therefore, the PSF information is limited to a 2D-PSF, and the information in an axial direction is not taken into account. However, because a simple PSF made by a Gaussian and annular distribution at the pupil of objective lens has almost the same profile at different axial positions in a PSF, the estimation errors due to the integrated axial information should be small. Although we demonstrated our technique at the depth of 200 µm of the mouse brain phantom, the depth is not the limit and can be deeper where samples can be imaged with annular illumination. The combination of PSF estimation and deconvolution is also effective to enhance the resolution of circular illumination, however, combination of annular illumination and deconvolution is better since two-point lateral resolution of annular illumination is better than that of circular illumination. In addition, our PSF estimation method can be used for other microscopic techniques; for adaptive optics techniques, estimated PSFs allow for evaluating a pupil phase applied for correction without additional modifications in a sample.

Disclosures

The authors declare that there are no conflicts of interest related to this article.