Abstract
Fluorescence imaging through a turbid layer holds great promise for various biophotonics applications. Conventional wavefront shaping techniques aim to create and scan a focus spot through the turbid layer. Finding the correct input wavefront without direct access to the target plane remains a critical challenge. In this paper, we explore a new strategy for imaging through turbid layer with a large field of view. In our setup, a fluorescence sample is sandwiched between two turbid layers. Instead of generating one focus spot via wavefront shaping, we use an unshaped beam to illuminate the turbid layer and generate an unknown speckle pattern at the target plane over a wide field of view. By tilting the input wavefront, we raster scan the unknown speckle pattern via the memory effect and capture the corresponding low-resolution fluorescence images through the turbid layer. Different from the wavefront-shaping-based single-spot scanning, the proposed approach employs many spots (i.e., speckles) in parallel for extending the field of view. Based on all captured images, we jointly recover the fluorescence object, the unknown optical transfer function of the turbid layer, the translated step size, and the unknown speckle pattern. Without direct access to the object plane or knowledge of the turbid layer, we demonstrate a 13-fold resolution gain through the turbid layer using the reported strategy. We also demonstrate the use of this technique to improve the resolution of a low numerical aperture objective lens allowing to obtain both large field of view and high resolution at the same time. The reported method provides insight for developing new fluorescence imaging platforms and may find applications in deep-tissue imaging.
OCIS codes: (180.0180) Microscopy, (170.0110) Imaging systems, (110.0113) Imaging through turbid media
1. Introduction
Imaging through turbid layer holds great promise for many biophotonics applications. Various approaches have been reported in recent years, including wavefront shaping techniques [1–9], measurement of the transmission matrix [10], object recovery from its autocorrelation [11, 12], accumulation of single-scattered waves [13], among others. In the context of wavefront shaping, a common strategy is to generate a pre-distorted wavefront that creates focus at the target plane. Since there is no direct access to the target plane, different guide stars can be used as reference beacons for wavefront shaping. Once the correct wavefront is found, the focus spot is raster scanned at the target plane using the optical memory effect [14–16]. Despite exciting progress on the development of wavefront shaping techniques, finding the correct wavefront without direct access to the target plane remains a challenge. In addition, the field of view is limited by the angular [14] or the translational range [15] of the single focused spot.
In this work, we explore a new strategy for improving imaging resolution through a turbid layer with a large field of view using speckle illumination and iterative recovery. Our setup is shown in Fig. 1(a), where a fluorescence sample is sandwiched between two turbid layers. Instead of generating one focus spot on the sample via wavefront shaping, we use an unshaped beam to illuminate the turbid layer and generate an unknown speckle pattern on the sample. By tilting the input wavefront, we then raster scan the unknown speckle pattern via the memory effect and capture the corresponding low-resolution fluorescence images through the turbid layer (Visualization 1 (3.7MB, mov) ). Different from the wavefront-shaping-based single-spot scanning, the proposed approach employs many spots (i.e., speckles) in parallel. Based on all captured images, we jointly recover the fluorescence object and the unknown speckle pattern. Without direct access to the object plane or knowledge of the illumination pattern, we achieve one order of magnitude resolution enhancement using the reported strategy (Fig. 1(b)-1(c), will be discussed later).
Fig. 1.
The reported strategy for imaging through turbid layer (Visualization 1 (3.7MB, mov) ). (a) The experimental setup. The inset shows the fluorescence USAF target through the turbid layer (a scotch tape). (b) The captured raw fluorescence images through the turbid layer. (c) The recovered images with one order of magnitude resolution gain.
The use of illumination patterns to encode high-resolution information into low-resolution measurements is well-known and has been demonstrated in various types of structured illumination (SI) setups [16–21]. Typical linear SI techniques are targeted at 2-fold resolution improvement with known system point spread function (PSF). With certain support constraints, 3-fold resolution gain has been reported [22]. However, getting at least one order of magnitude resolution improvement with neither direct access to the targeted object nor the PSF has not been addressed before. In this work we explore such super resolution by relying on the memory effect which allows to obtain many images from a single unknown speckle pattern. This strategy is different from previous SI demonstrations which uses multiple speckle patterns and allows us to achieve more than one order of magnitude resolution gain without direct access to the object plane.
This paper is structured as follows: in Section 2, we discuss the forward modeling and recovery methods of the reported scheme. Section 3 reports experimental results and demonstrates a 13-fold resolution gain through turbid layers. In Section 4, we discuss the use of the proposed scheme to improve the resolution of a regular fluorescence microscope platform. We demonstrate the use of a 0.1 numerical aperture (NA) objective lens to achieve the resolution of a 0.4 NA. Finally, we summarize the results and discuss future directions in Section 5.
2. Modeling and simulation
We model the effect of the turbid layer in Fig. 1(a) as an unknown low-pass filter, with the point-spread-function (PSF) denoted as PSF(x, y). In the acquisition process, the captured image can be expressed as
| (1) |
where In(x, y) is the nth fluorescence intensity measurement (n = 1,2,3…), Object(x, y) is the fluorescence object we wish to recover, Punknown(x, u) is the unknown illumination pattern on the sample, (xn, yn) is the nth positional shift of the illumination pattern, and ‘*’ stands for convolution. In our experiment, we tilt the incident angle of the laser light to shift the unknown speckle pattern to different positions on the sample. For each position of the speckle pattern, the resulting fluorescence signal is detected through the turbid media (i.e., convolved with the PSF). The goal of our imaging scheme is to recover Object(x, y) from many measurements In(x, y) (n = 1, 2, 3…), a problem referred to as blind deconvolution.
In Eq. (1), there are four unknown terms in the right-hand side: the fluorescence object Object(x, y), the illumination pattern generated by the turbid layer Punknown(x, y), the PSF of the turbid layer PSF(x, y), and the step size of the positional shift. To jointly recover the first three unknown terms, we seek to minimize the cost function where
| (2) |
For efficient implementation, we perform stochastic gradient descent to update the three unknowns which leads to the iterations:
| (3) |
| (4) |
| (5) |
where ‘a’, ‘b’ and ‘c’ are step sizes. This stochastic gradient descent scheme is able to accelerate the recovery process [23, 24] and it is similar to our previous demonstrations of jointly recovering the object and speckle patterns [25, 26]. In our implementation, we choose
| (6) |
| (7) |
| (8) |
where FT denotes the Fourier transform. These step sizes are chosen based on the ptychographic algorithm [27] and are related to Lipschitz constants [28]. A detailed implementation can be found in the Appendix.
We initialize the object by averaging all measurements, i.e., , where N is the total number of acquired images. We initialize the unknown pattern by setting it to an all-ones matrix. To initialize the unknown PSF(x, y), we first perform a Fourier transform on the initialized object. We estimate the cutoff frequency fcutoff to be the point where the Fourier spectrum intensity drops to 5% of its maximum. The PSF is then initialized as an Airy function with a cutoff frequency fcutoff. To obtain the step size of the positional shift, we assume the step size is the same for all measurements so that we only need to recover one parameter. In our implementation, we define the convergence index as the difference between the measurements and the generated low-resolution data from the recovery [29]. We then iterate over different step sizes and pick the one that generates the highest convergence index. Figure 2 summarizes the recovery process.
Fig. 2.
Outline of the recovery process.
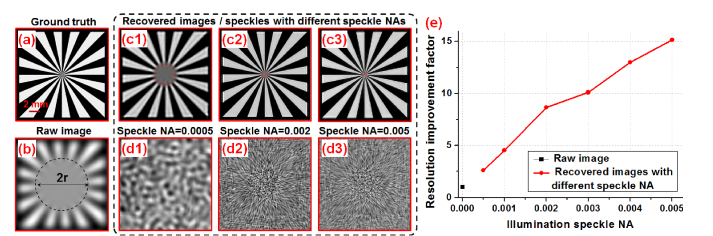
Figure 3 shows a simulation result of the resolution-improvement scheme. Figure 3(a) shows the simulated ground truth. We model the turbid layer as a low-pass filter for fluorescence emission of the object and Fig. 3(b) shows the low-resolution measurement through the turbid layer. Figures 3(c) and 3(d) show the recovered object and the unknown translated speckle patterns with different speckle NAs. The resolution of the raw image and the recovery can be quantified by the radius of the dashed lines in Fig. 3(b) and 3(c1)-(c3). The resolution improvement factor is shown in Fig. 3(e), where the resolution gain increases as the speckle pattern cutoff frequency increases. In our imaging setting, the detection NA is much smaller than the speckle NA, and thus, the final achievable resolution is determined by the speckle NA. As shown in Fig. 3(e), we can achieve one order of magnitude resolution gain without knowledge of the speckle pattern or the system PSF.
Fig. 3.
Simulation of the proposed strategy for improving resolution through turbid layer. (a) The simulation ground truth. (b) The simulated raw image through the turbid layer. (c) The recovered images with different speckle NAs. 81 by 81 raw images are used for recovery in this simulation. (d) The recovered speckle patterns. (e) The resolution improvement factor as a function of different speckle NAs.
For the unknown incoherent PSF, we assume it is shift-invariant across the entire field of view. As such, we only need to update one PSF in each iteration. In our implementation, the PSF updating process was performed in the Fourier domain, i.e., we updated the optical transfer function (OTF) of the turbid layer in each iteration. Figure 4(a) shows the ground-truth recovery assuming the OTF is known. Figure 4(b) and 4(c) show a comparison between the cases with and without the OTF updating process. In Fig. 4(b), we set the initial OTF cutoff frequency to be 1.5 times larger than that of the ground truth. By updating the OTF in the gradient descent process, we can recover both the object and the correct OTF in Fig. 4(b1) and 4(b2). Figure 4(b3) and 4(b4) show the results without updating the OTF. Similarly, we set the initial OTF cutoff frequency to be half of that of the ground truth in Fig. 4(c). Figure 4(c1) and 4(c2) show the results with the OTF updating process. Figure 4(c3) and 4(c4) show comparisons without updating the OTF.
Fig. 4.
Simulation of the proposed strategy for updating the object (top row) and the unknown incoherent OTF (bottom row). (a) The ground-truth recovery assuming the OTF is known. (b) We set the cutoff frequency of the initial OTF to be 1.5 times larger than that of the ground truth. The results with (b1-b2) and without (b3-b4) the OTF updating process. (c) We set the cutoff frequency of the initial OTF to be half of that of the ground truth. The results with (c1-c2) and w/o (c3-c4) the OTF updating process.
Figure 5 shows the process for recovering the step size of the positional shift. Figure 5(a1)-5(a3) shows the recovered object image with different step size errors. In Fig. 5(b1), the convergence index [29] increases as the loop number increases. To recover the step size, we iterate over different step sizes and pick the one that generates the highest convergence index, as shown in Fig. 5(b2).
Fig. 5.
Simulation of the proposed strategy for recovering the step size. (a) The recovered object images with different step size errors. (b1) The convergence index as a function of loop number. (b2) The convergence index as a function of different step size. We pick the step size that generates the highest convergence index.
In Fig. 6, we analyze the performance of the reported scheme with respect to the number of translated patterns and different noise levels. Figures 6(a1)-6(a4) show the recovered object using different numbers of translated patterns. Figure 6(a5) quantifies the result using mean square error (MSE) and structural similarity (SSIM) index. We can see that more translated patterns lead to improved image quality of the reconstruction (lower MSE and higher SSIM). The achievable resolution, on the other hand, is determined by the speckle size and remains the same in Fig. 6(a1)-6(a4). In Fig. 6(b), we analyze the effect of additive noise. Different amounts of speckle noise are added into the simulated raw images. The reconstructed images are shown in Fig. 6(b1)-6(b4). The corresponding MSEs and SSIMs are quantified in Fig. 6(b5). Evidently, the reported scheme is robust against additive noise.
Fig. 6.
The performance of the reported scheme with different numbers of translated patterns and different noise levels. 81 by 81 raw images are used for recovery in this simulation. (a1)-(a4) Recovered object images with different numbers of translated patterns; the performance is quantified using SSIM and MSE in (a5). No noise is added into the raw images. (b1)-(b4) Recovered object images with different noise levels; the performance is quantified in (b5).
3. 13-fold resolution gain through turbid layers
Next we consider experimental results using the setup in Fig. 1(a), where the fluorescence object is sandwiched between two turbid layers (two scotch tapes as shown in the inset of Fig. 1(a)). A 532-nm laser diode is coupled to a single mode fiber and illuminates the object with turbid layers. The fiber is 1 cm away from the first turbid layer. The distance between the object and the first turbid layer is ~8 cm and the distance between the object and the second turbid layer is about ~2 cm. The 532-nm excitation light forms a random speckle pattern on the sample through the first turbid layer. The resulting fluorescence emission is low-pass filtered by the second turbid layer and detected by a camera with a 550-nm long-pass filter and a photographic lens (Nikon 50mm f/1.2). In our implementation, we mechanically moved the fiber to different positions with a 0.5-µm motion step size and generated slightly tilted wavefronts for illumination. Based on the memory effect, the tilted wavefront laterally translates the unknown speckle pattern on the fluorescence object (Visualization 1 (3.7MB, mov) ), resulting in the forward imaging model of Eq. (1).
In the first experiment, we use a fluorescence USAF target as the object. Figure 7(a) shows the raw fluorescence image through the turbid layer. Clearly no detail can be resolved from the fluorescence USAF resolution target. Figures 7(b) and 7(c) show the recovered image of the resolution target and Fig. 7(d) shows the recovered speckle patterns. Based on Fig. 7(a) and 7(c4), we achieve 13-fold resolution gain through the turbid layer using the reported strategy. In the second experiment, we draw some lines on a fluorescence microsphere slide and use it as the object. Figure 8(a) depicts the raw fluorescence image through the turbid layer. Figure 8(b) demonstrates the ground truth image by removing the two turbid layers. Figure 8(c) and 8(d) show the recovered images and speckle patterns. The line features of the fluorescence object are clearly resolved from the recovered images.
Fig. 7.
13-fold resolution gain through the turbid layer. (a) The captured raw image through the turbid layers. (b) The recovered object image using different numbers of translated speckle patterns (refer to the bottom textbox of (d)). (c) Magnified views of (b). (d) The recovered speckle patterns corresponding to (b).
Fig. 8.
Experimental demonstration of the reported strategy using a fluorescence object. (a) The captured raw image through the turbid layers. (b) The ground truth image of the fluorescence object. (c) The recovered object images using a different number translated patterns. (d) The recovered speckle patterns corresponding to (c).
4. Wide-field, high-resolution fluorescence imaging
For many microscopy imaging applications, it is important to get both wide field of view and high resolution at the same time [30]. The reported scheme provides a potential solution to achieve this goal, as we show next.
In Fig. 9(a), we use a low-NA objective lens (4X, 0.1 NA) to acquire raw images of a sample and use a high-NA condenser lens (0.9 NA) to generate a speckle pattern on the object. A diffuser is placed at the back focal plane of the condenser lens in the setup. We also place an aperture stop at the center of the back focal plane of the condenser lens to block the direct-transmitted light to the fluorescence detection system (Fig. 9(a)). In this experiment, we translate the sample to 30 by 30 different positions with 0.3 µm step size and capture the corresponding images through the 0.1 NA objective lens. There is no scattering layer between the sample and the objective lens. The captured images are then used to recover both the high-resolution object and the unknown speckle pattern. Figure 9(b1) shows the captured raw image of a fluorescence resolution target. Figure 9(b2) and (b3) show the recovered object and the speckle pattern. The resolution of the recovered images corresponds to a NA of 0.4. The resolution improvement factor in this experiment is 4, limited by the precision of the employed motorized stage (Newport LTA-HS).
Fig. 9.
Wide-field, high-resolution fluorescence imaging using the reported strategy. (a) The experimental setup where we generate a high-NA speckle pattern on the sample. (b1) The captured raw image of the fluorescence resolution target. (b2)-(b3) The recovered object and the recovered speckle pattern. (c1) The wide-field, high-resolution fluorescence image recovered using the reported strategy. (c2) The magnified view of the microspheres. (c3) The recovered speckle pattern corresponding to (c2). (c4) The raw image of (c2).
In Fig. 9(c), we demonstrate the use of the reported scheme to recover a wide-field, high-resolution fluorescence image of a microsphere sample. Figure 9(c1) depicts the recovered image where the field of view is determined by the employed 4X objective. Figure 9(c2) and 9(c3) show the recovered object image and the speckle pattern and Fig. 9(c4) shows the raw image captured using the 0.1 NA objective lens.
5. Discussion
In summary, we report a new strategy for improving fluorescence imaging resolution through a turbid layer with a large field of view. Instead of generating one focus spot on the sample via wavefront shaping, we use an unshaped beam to illuminate the turbid layer and generate an unknown speckle pattern on the sample. By tilting the input wavefront, we raster scan the unknown speckle pattern via the memory effect and capture the corresponding low-resolution fluorescence images through the turbid layer. Without direct access to the object plane or knowledge of the illumination pattern, we achieve 13-fold resolution gain using the reported strategy. While the idea of structured illumination is well-known for improving resolution in microscopy platform, previous demonstrations, to the best of our knowledge, are targeted at 2-fold resolution gain with a known system PSF. In this work we explore super resolution by relying on the memory effect which allows to obtain many images from a single unknown speckle pattern. This strategy is different from previous SI demonstrations which uses multiple speckle patterns [18, 21] and allows us to achieve more than one order of magnitude resolution gain without direct access to the object plane. Our work shares some roots with Refs [11, 12]. which recover the object from its autocorrelation measurements. In our work, we use a joint object-pattern recovery scheme to reconstruct both the object and the pattern. The scattering layer may not be needed in our scheme and we demonstrate the use of a 0.1 NA objective lens to obtain a 0.4-NA resolution with a large field of view.
The limitations of the reported strategy are threefold. First, it is based on the traditional memory effect where the target plane is at a distance from the diffusing layer. For imaging inside thick scattering media, we may need to exploit the translational memory effect [15] for the reported scheme. Second, we need a large number of acquisitions in the reconstruction process. This may be due to the low modulating efficiency for converting the high-frequency information to the low-frequency band, especially when we aim at one order of magnitude resolution gain. Third, we assume the PSF is shift-invariant in the recovery process. If needed, we can divide the captured images into many smaller segments, and jointly recover the object, the illumination pattern and the PSF for each segment. This is similar to the pupil recovery process in Fourier ptychographic microscopy, where the pupil aberrations are recovered at different spatial locations independently [30, 31].
There are also a few directions for improving the reported scheme. First, we can use a scanning galvo mirror to better control the tilted beam and achieve better positional accuracy. Second, we can employ motion correction [32] in the reconstruction process to address the positional error of the scanning process. Third, we may incorporate support constraints [22] including signal sparsity [33, 34] in the reconstruction to reduce the number of acquisitions. Fourth, multi-layer modeling [35] can be integrated into the reported scheme to handle 3D fluorescence sample.
Appendix
The simulation Matlab code consists of the following seven steps – 1) parameters and constants definition, 2) input object image preparation, 3) optical transfer function (OTF) generation, 4) ‘mother speckle pattern’ generation, 5) shifted speckle patterns generation, 6) low-resolution target images generation, and 7) iterative reconstruction.
In step 1, we define the experimental parameters in accordance with our experimental set-up, including the laser wavelength, the effective pixel size of the imaging system, the estimated NA caused by the diffuser, the estimated NA of the speckle patterns, the estimated step size of the speckle pattern’s shift, and the maximum shift along one direction.
%% Step 1: Set Parameters
-
1.
WaveLength = 0.632e-6; % Wave length(red)
-
2.
PixelSize = 54e-6; % Effective pixel size of imaging system
-
3.
DiffuserNA = 0.5 * 1e-3; % Low-pass filter of the diffuser
-
4.
IlluminationNA = 3 * 1e-3; % Numerical aperture of speckle patterns
-
5.
ShiftStepSize = 0.75; % Step size of pattern's shift
-
6.
SpiralRadius = 20; % Pattern number = (20*2 + 1)^2
-
7.
nIterative = 30;
-
8.
InputImgSize = 135; % Size of image (assumed to be square)
-
9.
nPattern = (SpiralRadius*2 + 1)^2; % Number of illumination patterns
-
10.
InputImgSizeHalf = floor(InputImgSize / 2);
-
11.
InputImgCenter = ceil(InputImgSize / 2);
-
12.
MaxShiftInPixel = round(ShiftStepSize * SpiralRadius) * 2;
In step 2, we use the ‘siemen star’ pattern as the input object image, as shown in Fig. 10
Fig. 10.
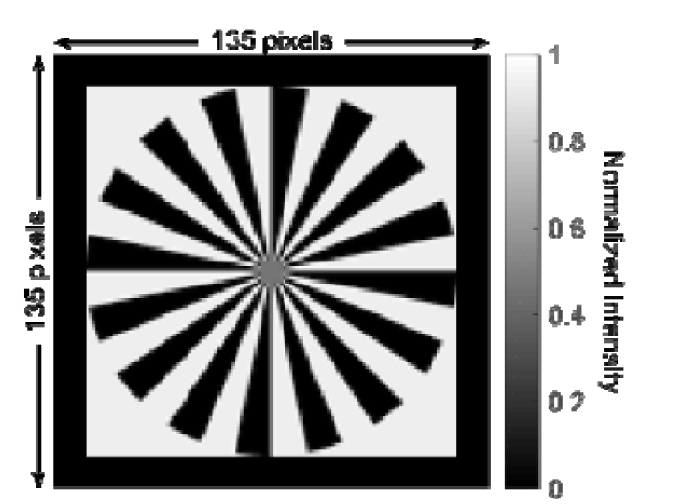
The simulated high-resolution input object image.
. The size of the image is 135 by 135 pixels. The intensity of the input object image is normalized. The prepared input object image is stored in ‘InputImg’.
%% Step 2: Input object image preparation
-
13.
InputImg = double(imread('siemensstar.png'));
-
14.
InputImg = InputImg./max(max(InputImg)); % Image intensity normalization
-
15.
InputImgFT = fftshift(fft2(InputImg));
-
16.
InputImgSizeX = size(InputImg, 1);
-
17.
InputImgSizeY = size(InputImg, 2);
-
18.
% Show prepared input object image and its Fourier transform
-
19.
figure;
-
20.
subplot(1,2,1); imshow(abs(InputImg),[]); title('Ground Truth');
-
21.
subplot(1,2,2); imshow(log(abs(InputImgFT) + 1),[]); title('Ground Truth FT');
In step 3, we generate the diffuser’s OTF and use it in the following generation of low-resolution target images through the diffuser. The imaging process through the diffuser is modeled as low-pass filtering of the ground truth object. In Fig. 11(a)
Fig. 11.
Simulated OTF of the diffuser for low-resolution target image generation. (a) The simulated round-shaped CTF of the diffuser. (b) The corresponding OTF. (c) The Fourier spectrum of the low-resolution image captured through the diffuser. (d) The low-resolution target image.
, we simulate the coherent transfer function (CTF) of the diffuser with an ideal low-pass filter, with cut-off frequency determined by the NA of the diffuser (‘DiffuserNA’). The CTF is then converted to the incoherent OTF in Fig. 11(b). The image captured through the diffuser can be generated by multiplying the OTF and the Fourier spectrum of the object, and then take the inverse Fourier transform of the result. Figure 11(c) and 11(d) show an example of the target image in the Fourier and spatial domain, respectively.
%% Step 3: Optical transfer function (OTF) and target object image generation
-
22.
CTF = ones(InputImgSizeX,InputImgSizeY);
-
23.
CutoffFreqX = DiffuserNA*(1/WaveLength)*InputImgSizeX*PixelSize;
-
24.
CutoffFreqY = DiffuserNA*(1/WaveLength)*InputImgSizeY*PixelSize;
-
25.
[GridX, GridY] = meshgrid(1:InputImgSizeX,1:InputImgSizeY);
-
26.
CTF = CTF.*(((GridY- (InputImgSizeY + 1)/2)/CutoffFreqY).^2 + ((GridX-(InputImgSizeX + 1)/2)/CutoffFreqX).^2< = 1);
-
27.
CTFSignificantPix = numel(find(abs(CTF)>eps(class(CTF))));
-
28.
ifftscale = numel(CTF)/CTFSignificantPix;
-
29.
aPSF = fftshift(ifft2(ifftshift(CTF)));
-
30.
iPSF = ifftscale*abs(aPSF).^2;
-
31.
OTF = fftshift(fft2(ifftshift(iPSF)));
-
32.
LRTempTargetImgFT = fftshift(fft2(imresize(InputImg,1))).* OTF; % Low resolution target image FT
-
33.
InputImgLR = abs(ifft2(ifftshift(LRTempTargetImgFT))); % Low resolution target image
-
34.
figure; subplot(1,2,1); imshow(InputImgLR,[]); title('Low-resolution input image');
-
35.
subplot(1,2,2); imshow(log(abs(LRTempTargetImgFT) + 1),[]); title('Low-resolution input image FT');
In step 4, we generate the ‘mother speckle pattern’ corresponding to Punknown(x,y) in the Main Text with which we obtain shifted speckle patterns in the next step. The ‘mother speckle pattern’ is a random intensity pattern of size 165 by 165. It is 30 pixels (‘MaxShiftInPixel’) larger than the object image in each direction, because we assume the maximum shifting distance in each direction is 30 (= 0.75 * (41-1)) pixels.
%% Step 4: Mother Speckle pattern generation
-
36.
% generate random speckle pattern
-
37.
MotherSpeckleSizeX = InputImgSizeX + MaxShiftInPixel;
-
38.
MotherSpeckleSizeY = InputImgSizeY + MaxShiftInPixel;
-
39.
randomAmplitude = imnoise(ones(MotherSpeckleSizeX,MotherSpeckleSizeY),'speckle',0.5);
-
40.
randomPhase = imnoise(ones(MotherSpeckleSizeX,MotherSpeckleSizeY),'speckle',0.5);
-
41.
randomPhase = 0.5*pi*randomPhase./max(max(randomPhase));
-
42.
randomSpeckle = randomAmplitude.*exp(1j.*randomPhase);
-
43.
randomSpeckleFT = fftshift(fft2(randomSpeckle));
-
44.
% speckle pattern lowpass filter
-
45.
specklePatternCTF = ones(MotherSpeckleSizeX,MotherSpeckleSizeY);
-
46.
CutoffFreqX = IlluminationNA * (1/WaveLength)*MotherSpeckleSizeX* PixelSize;
-
47.
CutoffFreqY = IlluminationNA * (1/WaveLength)*MotherSpeckleSizeY* PixelSize;
-
48.
[GridX, GridY] = meshgrid(1:MotherSpeckleSizeX,1:MotherSpeckleSizeY);
-
49.
specklePatternCTF = specklePatternCTF.*(((GridY-(MotherSpeckleSizeY + 1)/2) /CutoffFreqY).^2 + ((GridX-(MotherSpeckleSizeX + 1)/2)/CutoffFreqX).^2< = 1);
-
50.
% lowpassed speckle intensity
-
51.
aMotherSpeckle = ifft2(ifftshift(specklePatternCTF.*randomSpeckleFT));
-
52.
iMotherSpeckle = (abs(aMotherSpeckle)).^2;
-
53.
MotherSpeckle = iMotherSpeckle./max(max(iMotherSpeckle));
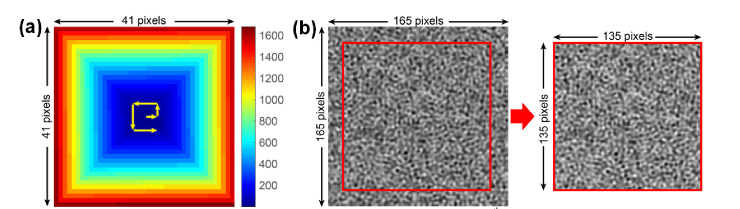
In step 5, we generate a sequence of shifted speckle patterns whose size is 135 by 135. Each shifted speckle pattern is generated by laterally shifting ‘mother speckle pattern’ and cropping the central 135-by-135-pixel area. The ‘mother speckle pattern’ is laterally shifted along a spiral path (which is represented by a 41-by-41 matrix, as shown in Fig. 12(a)
Fig. 12.
Generation of the speckle pattern. (a) The spiral path matrix. (b) The 9th shifted ‘mother speckle pattern’ and the resultant cropped shifted speckle pattern.
). The spiral path matrix can be easily obtained using the built-in function ‘spiral()’ by MATLAB. As shown in Fig. 12(a), the spiral path matrix consists of 1681 integers from 1 to 1681. To generate the nth shifted speckle pattern, for instance, we will search for the location of ‘n’ in the matrix. Assuming the number of ‘n’ is located at (LocationX, LocationY), the lateral shift will be ‘LocationX*ShiftStepSize’ along the x direction and ‘LocationY*ShiftStepSize’ along the y direction. The lateral shifting of the pattern is performed in the Fourier domain by multiplying an equivalent phase factor to the spectrum of the ‘mother speckle pattern’ (we use the function ‘subpixelshift()’). We get the final nth shifted speckle pattern by cropping the central 135-by-135-pixel area from the shifted ‘mother speckle pattern’. The number of shifted speckle patterns is 1681 (= 41 by 41) and we save them in ‘ShiftedPatterns’, which has dimension 135 by 135 by 1681. The relative lateral shifts along both directions are stored in arrays ‘ShiftX’ and ‘ShiftY’, respectively. Figure 12(b) shows the 9th shifted ‘mother speckle pattern’ and the cropped speckle pattern.
%% Step 5: Shifted speckle pattern generation
-
54.
LocationX = zeros(1, nPattern);
-
55.
LocationY = zeros(1, nPattern);
-
56.
ShiftY = zeros(1, nPattern);
-
57.
ShiftX = zeros(1, nPattern);
-
58.
SpiralPath = spiral(2*SpiralRadius + 1);
-
59.
SpiralPath = flipud(SpiralPath);
-
60.
for iShift = 1:nPattern
-
61.
[iRow, jCol] = find(SpiralPath = = iShift);
-
62.
LocationX(iShift) = iRow;
-
63.
LocationY(iShift) = jCol;
-
64.
end;
-
65.
ShiftedSpecklePatterns = zeros(size(InputImg,1), size(InputImg,2), nPattern);
-
66.
for iPattern = 1:nPattern
-
67.
ShiftedMotherSpeckle = subpixelshift(MotherSpeckle, ...
LocationX(1,iPattern) * ShiftStepSize * PixelSize,...
LocationY(1,iPattern) * ShiftStepSize * PixelSize,...
PixelSize); % Generate speckle pattern sequence
-
68.
ShiftedSpecklePatterns(:,:,iPattern) = ShiftedMotherSpeckle(MotherSpeckleSizeX/2-
InputImgSizeX/2:MotherSpeckleSizeX/2 + InputImgSizeX/2-1,
MotherSpeckleSizeX/2-InputImgSizeX/2:MotherSpeckleSizeX/2
+ InputImgSizeX/2-1);
-
69.
if iPattern < (nPattern)
-
70.
ShiftX(iPattern + 1) = (LocationX(1,iPattern + 1)-LocationX(1,iPattern))
.* ShiftStepSize;
-
71.
ShiftY(iPattern + 1) = (LocationY(1,iPattern + 1)-LocationY(1,iPattern))
.* ShiftStepSize;
-
72.
end
-
73.
disp(iPattern);
-
74.
end
-
75.
function output_image = subpixelshift(input_image,xshift,yshift,spsize)
-
76.
[m,n,num] = size(input_image);
-
77.
[FX,FY] = meshgrid(1:m,1:n);
-
78.
for i = 1:num
-
79.
Hs = exp(−1j*2*pi.*(FX.*(xshift(1,i)/spsize)/m + FY.*(yshift(1,i)/spsize)/n));
-
80.
output_image(:,:,i) = abs(ifft2(ifftshift(fftshift(fft2(input_image(:,:,i))).*Hs)));
-
81.
end
-
82.
end
In step 6, we generate the low-resolution images captured through the diffuser. We simulate these images by multiplying the true object image with a shifted speckle pattern and then applying the low-pass filter given by the OTF of the diffuser. The resultant low-resolution images are stored in the matrix ‘TargetImgs’ which is organized as an image stack with dimension 135 by 135 by 1681. Figure 13(a)
Fig. 13.
Simulation result of the resolution improvement. (a) The 9th generated low-resolution target image. (b) The reconstructed high-resolution object image and ‘mother speckle pattern’.
shows the 9th generated low-resolution target image.
%% Step 6: Low-resolution target image generation
-
83.
TargetImgs = zeros(size(ShiftedSpecklePatterns));
-
84.
nTargetImgs = nPattern;% Total number of target low-resolution images
-
85.
for iTargetImg = 1:nTargetImgs
-
86.
TargetImgs(:,:,iTargetImg) = abs(ifft2(ifftshift(fftshift(fft2(InputImg
.*ShiftedSpecklePatterns(:,:,iTargetImg))).*OTF)));
-
87.
disp(iTargetImg);
-
88.
end;
In step 7, we apply the iterative algorithm described in the Main Text to reconstruct both the high-resolution object image, the OTF, and the ‘mother speckle pattern’. In our iterations, ImgRecovered, OTF and MotherSpeckleRecovered correspond to Object, PSF and Punknown in the Main Text. The number of iterations are defined by variable ‘nIterative’. Assuming we have no any prior about the object image or the speckle pattern, we initialize the object by averaging all measurements and initialize the ‘mother speckle pattern’ using an all-ones matrix. Figure 13(b) shows the reconstructed high-resolution object image and ‘mother speckle pattern’ after 30 iterations.
%% Step 7: Iterative reconstruction
-
89.
ImgRecovered = mean(TargetImgs,3); % Initial guess of the object
-
90.
MotherSpeckleRecovered = ones(InputImgSizeX + MaxShiftInPixel, InputImgSizeY + MaxShiftInPixel); % Initial guess of the speckle pattern
-
91.
for iterative = 1:nIterative
-
92.
for iShift = 1:nPattern
-
93.
display([iterative iShift])
-
94.
MotherSpeckleRecovered = subpixelshift(MotherSpeckleRecovered,
ShiftX(1,iShift)*PixelSize, ShiftY(1,iShift)*PixelSize, PixelSize);
-
95.
MotherSpeckleRecoveredCropped =
MotherSpeckleRecovered(round(MotherSpeckleSizeX/2-
InputImgSizeX/2):round(MotherSpeckleSizeX/2 + InputImgSizeX/2-1),
round(MotherSpeckleSizeY/2 -InputImgSizeY/2):
round(MotherSpeckleSizeY/2 + InputImgSizeY/2-1));
-
96.
TempTargetImg = ImgRecovered .* MotherSpeckleRecoveredCropped;
-
97.
TempTargetImgCopy = TempTargetImg; % Use it to recover Itn
-
98.
TempTargetImgFT = fftshift(fft2(TempTargetImg)); % 2D Fourier transform
-
99.
LRTempTargetImgFT = OTF .* TempTargetImgFT; % Lowpass the image
-
100.
LRTempTargetImg = ifft2(ifftshift(OTF .* TempTargetImgFT)); % Inverse FT
-
101.
LRTempTargetImg_AmpUpdated = TargetImgs(:,:,iShift);
-
102.
LRTempTargetImg_AmpUpdated_FT =
fftshift(fft2(LRTempTargetImg_AmpUpdated));
-
103.
TempTargetImgFT =
TempTargetImgFT + conj(OTF)./(max(max((abs(OTF)).^2)))
.*(LRTempTargetImg_AmpUpdated_FT- LRTempTargetImgFT);
-
104.
% Update the target image
-
105.
if (iterative > 2)
-
106.
OTF = OTF + conj(TempTargetImgFT)
./(max(max((abs(TempTargetImgFT)).^2)))
.*(LRTempTargetImg_AmpUpdated_FT-LRTempTargetImgFT);
% Update the OTF in the Fourier domain; we may need to reinitialize the
object and pattern every 10 loops if we have a bad initial OTF estimate
-
107.
end
-
108.
TempTargetImg = ifft2(ifftshift(TempTargetImgFT));
-
109.
ImgRecovered = ImgRecovered + MotherSpeckleRecoveredCropped
.*(TempTargetImg-TempTargetImgCopy)./
(max(max(MotherSpeckleRecoveredCropped))).^2; % Update the object
-
110.
ImgRecovered = abs(ImgRecovered);
-
111.
MotherSpeckleRecoveredCropped = MotherSpeckleRecoveredCropped
+ ImgRecovered.*(TempTargetImg-
TempTargetImgCopy)./(max(max(ImgRecovered))).^2;
-
112.
MotherSpeckleRecoveredCropped = abs(MotherSpeckleRecoveredCropped);
-
113.
MotherSpeckleRecovered(round(MotherSpeckleSizeX/2 - InputImgSizeX/2):
round (MotherSpeckleSizeX/2 + InputImgSizeX/2-1),
round(MotherSpeckleSizeY/2-InputImgSizeY/2):round(MotherSpeckleSizeY/2
+ InputImgSizeY/2-1)) = abs(MotherSpeckleRecoveredCropped);
-
114.
end
-
115.
MotherSpeckleRecovered = subpixelshift(MotherSpeckleRecovered,
-sum(ShiftX)*PixelSize, -sum(ShiftY)*PixelSize, PixelSize);
-
116.
ImgRecoveredFT = fftshift(fft2(ImgRecovered));
-
117.
figure; subplot(1,2,1); imshow(abs(ImgRecovered),[]); title('Recovered image');
-
118.
subplot(1,2,2); imshow(log(abs(ImgRecoveredFT) + 1),[]); title('Recovered FT');
-
119.
pause(0.5)
-
120.
subplot(1,2,2); imshow(log(abs(ImgRecoveredFT)+1),[]); title('Recovered FT');
-
121.
pause(0.5)
-
122.
end
Funding
NSF 1555986, and NIH R21EB022378, NIH R03EB022144. Z. Zhang acknowledges the support of the China Scholarship Council.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References and links
- 1.Vellekoop I. M., Aegerter C. M., “Scattered light fluorescence microscopy: imaging through turbid layers,” Opt. Lett. 35(8), 1245–1247 (2010). 10.1364/OL.35.001245 [DOI] [PubMed] [Google Scholar]
- 2.Vellekoop I. M., “Feedback-based wavefront shaping,” Opt. Express 23(9), 12189–12206 (2015). 10.1364/OE.23.012189 [DOI] [PubMed] [Google Scholar]
- 3.Nixon M., Katz O., Small E., Bromberg Y., Friesem A. A., Silberberg Y., Davidson N., “Real-time wavefront shaping through scattering media by all-optical feedback,” Nat. Photonics 7(11), 919–924 (2013). 10.1038/nphoton.2013.248 [DOI] [Google Scholar]
- 4.Mosk A. P., Lagendijk A., Lerosey G., Fink M., “Controlling waves in space and time for imaging and focusing in complex media,” Nat. Photonics 6(5), 283–292 (2012). 10.1038/nphoton.2012.88 [DOI] [Google Scholar]
- 5.Xu X., Liu H., Wang L. V., “Time-reversed ultrasonically encoded optical focusing into scattering media,” Nat. Photonics 5(3), 154–157 (2011). 10.1038/nphoton.2010.306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang Y. M., Judkewitz B., Dimarzio C. A., Yang C., “Deep-tissue focal fluorescence imaging with digitally time-reversed ultrasound-encoded light,” Nat. Commun. 3, 928 (2012). 10.1038/ncomms1925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Katz O., Small E., Silberberg Y., “Looking around corners and through thin turbid layers in real time with scattered incoherent light,” Nat. Photonics 6(8), 549–553 (2012). 10.1038/nphoton.2012.150 [DOI] [Google Scholar]
- 8.Park J.-H., Park C., Yu H., Park J., Han S., Shin J., Ko S. H., Nam K. T., Cho Y.-H., Park Y., “Subwavelength light focusing using random nanoparticles,” Nat. Photonics 7(6), 454–458 (2013). 10.1038/nphoton.2013.95 [DOI] [Google Scholar]
- 9.Tang J., Germain R. N., Cui M., “Superpenetration optical microscopy by iterative multiphoton adaptive compensation technique,” Proc. Natl. Acad. Sci. U.S.A. 109(22), 8434–8439 (2012). 10.1073/pnas.1119590109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Popoff S. M., Lerosey G., Carminati R., Fink M., Boccara A. C., Gigan S., “Measuring the Transmission Matrix in Optics: An Approach to the Study and Control of Light Propagation in Disordered Media,” Phys. Rev. Lett. 104(10), 100601 (2010). 10.1103/PhysRevLett.104.100601 [DOI] [PubMed] [Google Scholar]
- 11.Bertolotti J., van Putten E. G., Blum C., Lagendijk A., Vos W. L., Mosk A. P., “Non-invasive imaging through opaque scattering layers,” Nature 491(7423), 232–234 (2012). 10.1038/nature11578 [DOI] [PubMed] [Google Scholar]
- 12.Katz O., Heidmann P., Fink M., Gigan S., “Non-invasive single-shot imaging through scattering layers and around corners via speckle correlations,” Nat. Photonics 8(10), 784–790 (2014). 10.1038/nphoton.2014.189 [DOI] [Google Scholar]
- 13.Kang S., Jeong S., Choi W., Ko H., Yang T. D., Joo J. H., Lee J.-S., Lim Y.-S., Park Q.-H., Choi W., “Imaging deep within a scattering medium using collective accumulation of single-scattered waves,” Nat. Photonics 9, 253–258 (2015). [Google Scholar]
- 14.Freund I., Rosenbluh M., Feng S., “Memory effects in propagation of optical waves through disordered media,” Phys. Rev. Lett. 61(20), 2328–2331 (1988). 10.1103/PhysRevLett.61.2328 [DOI] [PubMed] [Google Scholar]
- 15.Judkewitz B., Horstmeyer R., Vellekoop I. M., Papadopoulos I. N., Yang C., “Translation correlations in anisotropically scattering media,” Nat. Phys. 11(8), 684–689 (2015). 10.1038/nphys3373 [DOI] [Google Scholar]
- 16.Osnabrugge G., Horstmeyer R., Papadopoulos I. N., Judkewitz B., Vellekoop I. M., “Generalized optical memory effect,” Optica 4(8), 886–892 (2017). 10.1364/OPTICA.4.000886 [DOI] [Google Scholar]
- 17.Gustafsson M. G., “Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy,” J. Microsc. 198(2), 82–87 (2000). 10.1046/j.1365-2818.2000.00710.x [DOI] [PubMed] [Google Scholar]
- 18.Mudry E., Belkebir K., Girard J., Savatier J., Le Moal E., Nicoletti C., Allain M., Sentenac A., “Structured illumination microscopy using unknown speckle patterns,” Nat. Photonics 6(5), 312–315 (2012). 10.1038/nphoton.2012.83 [DOI] [Google Scholar]
- 19.Chakrova N., Rieger B., Stallinga S., “Deconvolution methods for structured illumination microscopy,” J. Opt. Soc. Am. A 33(7), B12–B20 (2016). 10.1364/JOSAA.33.000B12 [DOI] [PubMed] [Google Scholar]
- 20.Yilmaz H., van Putten E. G., Bertolotti J., Lagendijk A., Vos W. L., Mosk A. P., “Speckle correlation resolution enhancement of wide-field fluorescence imaging,” Optica 2(5), 424–429 (2015). 10.1364/OPTICA.2.000424 [DOI] [Google Scholar]
- 21.Yeh L.-H., Tian L., Waller L., “Structured illumination microscopy with unknown patterns and a statistical prior,” Biomed. Opt. Express 8(2), 695–711 (2017). 10.1364/BOE.8.000695 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Min J., Jang J., Keum D., Ryu S.-W., Choi C., Jeong K.-H., Ye J. C., “Fluorescent microscopy beyond diffraction limits using speckle illumination and joint support recovery,” Sci. Rep. 3(1), 2075 (2013). 10.1038/srep02075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chakrova N., Rieger B., Stallinga S., “Deconvolution methods for structured illumination microscopy,” J. Opt. Soc. Am. A 33(7), B12–B20 (2016). 10.1364/JOSAA.33.000B12 [DOI] [PubMed] [Google Scholar]
- 24.Chakrova N., Heintzmann R., Rieger B., Stallinga S., “Studying different illumination patterns for resolution improvement in fluorescence microscopy,” Opt. Express 23(24), 31367–31383 (2015). 10.1364/OE.23.031367 [DOI] [PubMed] [Google Scholar]
- 25.Dong S., Nanda P., Shiradkar R., Guo K., Zheng G., “High-resolution fluorescence imaging via pattern-illuminated Fourier ptychography,” Opt. Express 22(17), 20856–20870 (2014). 10.1364/OE.22.020856 [DOI] [PubMed] [Google Scholar]
- 26.Dong S., Nanda P., Guo K., Liao J., Zheng G., “Incoherent Fourier ptychographic photography using structured light,” Photon. Res. 3(1), 19–23 (2015). 10.1364/PRJ.3.000019 [DOI] [Google Scholar]
- 27.Maiden A. M., Rodenburg J. M., “An improved ptychographical phase retrieval algorithm for diffractive imaging,” Ultramicroscopy 109(10), 1256–1262 (2009). 10.1016/j.ultramic.2009.05.012 [DOI] [PubMed] [Google Scholar]
- 28.Hesse R., Luke D. R., Sabach S., Tam M. K., “Proximal heterogeneous block implicit-explicit method and application to blind ptychographic diffraction imaging,” SIAM J. Imaging Sci. 8(1), 426–457 (2015). 10.1137/14098168X [DOI] [Google Scholar]
- 29.Bian Z., Dong S., Zheng G., “Adaptive system correction for robust Fourier ptychographic imaging,” Opt. Express 21(26), 32400–32410 (2013). 10.1364/OE.21.032400 [DOI] [PubMed] [Google Scholar]
- 30.Zheng G., Horstmeyer R., Yang C., “Wide-field, high-resolution Fourier ptychographic microscopy,” Nat. Photonics 7(9), 739–745 (2013). 10.1038/nphoton.2013.187 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ou X., Zheng G., Yang C., “Embedded pupil function recovery for Fourier ptychographic microscopy,” Opt. Express 22(5), 4960–4972 (2014). 10.1364/OE.22.004960 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bian L., Zheng G., Guo K., Suo J., Yang C., Chen F., Dai Q., “Motion-corrected Fourier ptychography,” Biomed. Opt. Express 7(11), 4543–4553 (2016). 10.1364/BOE.7.004543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hojman E., Chaigne T., Solomon O., Gigan S., Bossy E., Eldar Y. C., Katz O., “Photoacoustic imaging beyond the acoustic diffraction-limit with dynamic speckle illumination and sparse joint support recovery,” Opt. Express 25(5), 4875–4886 (2017). 10.1364/OE.25.004875 [DOI] [PubMed] [Google Scholar]
- 34.Eldar Y. C., Kutyniok G., Compressed Sensing: Theory and Applications (Cambridge University Press, 2012). [Google Scholar]
- 35.Dong S., Guo K., Jiang S., Zheng G., “Recovering higher dimensional image data using multiplexed structured illumination,” Opt. Express 23(23), 30393–30398 (2015). 10.1364/OE.23.030393 [DOI] [PubMed] [Google Scholar]