Compact, multi-exposure speckle contrast optical spectroscopy (SCOS) device for measuring deep tissue blood flow

Abstract

Speckle contrast optical spectroscopy (SCOS) measures absolute blood flow in deep tissue, by taking advantage of multi-distance (previously reported in the literature) or multi-exposure (reported here) approach. This method promises to use inexpensive detectors to obtain good signal-to-noise ratio, but it has not yet been implemented in a suitable manner for a mass production. Here we present a new, compact, low power consumption, 32 by 2 single photon avalanche diode (SPAD) array that has no readout noise, low dead time and has high sensitivity in low light conditions, such as in vivo measurements. To demonstrate the capability to measure blood flow in deep tissue, healthy volunteers were measured, showing no significant differences from the diffuse correlation spectroscopy. In the future, this array can be miniaturized to a low-cost, robust, battery operated wireless device paving the way for measuring blood flow in a wide-range of applications from sport injury recovery and training to, on-field concussion detection to wearables.

1. Introduction

Blood flow supplies brain and other organs with oxygen and removes the by-products in order to maintain healthy functions of the organs. Chronic, transient poor or absent blood flow can lead to death or diminished functions [1] and alteration due to excessive or abnormal growth (e.g. tumors) of other biomarkers in healthy tissue, where the blood flow is affected both in large vessels, as in microvasculature. Thus, continuous, real-time, non-invasive, bedside monitoring of blood flow is necessary.

Optical imaging of blood flow (BF) in general, and cerebral blood flow (CBF) in particular, has many applications in studying both healthy and pathophysiological tissue [2] non-invasively. Diffuse correlation spectroscopy (DCS) [3], laser Doppler flowmetry (LDF) [4] and laser speckle contrast imaging (LSCI) [5] are some of the optical methods based on the spatio-temporal statistics of the laser speckles that are used to measure blood flow in the microvasculature.

Traditionally, LSCI uses two-dimensional detector arrays (CCD or CMOS) [5–8] with a relatively long exposure time to obtain information about superficial relative blood flow. This technique allows the use of a simple experimental setup with a relatively high spatio-temporal resolution, but with the use of a single exposure time it is prone to systematic error, due to deviations from the physical model in the presence of the static scatters (such as skull). This can be resolved by implementing multi-exposure speckle imaging (MESI) [9,10]. Although this method allows the measurement of absolute CBF, the serial acquisition of different exposure times reduces the possibility of imaging fast changes in the blood flow. Recently an improved acquisition speed was demonstrated with single-photon avalanche diode (SPAD) camera where full data set was acquired in a single-shot acquisition (sMESI) [11]. In parallel, others [12] developed a MESI acquisition by implementing a field-programmable gate array with one mega pixel CMOS camera. While both, MESI and sMESI, allow absolute blood flow measurements, they are still limited to imaging the superficial tissue (<1 mm) due to single or few scattering events.

On the other hand, diffuse correlation spectroscopy (DCS) is a non invasive, optical method that probes deep tissue blood flow up to several centimeters, [3,13,14]. However, the drawback of the DCS is that it samples each speckle independently with single mode fibers, limiting the collection area to the small diameter of fiber [3]. To obtain better signal-to-noise ratio (SNR) it is necessary to use a collection of detectors allowing the simultaneous acquisition of independent speckles [15], while increasing the complexity and the cost of the device. For example, the four detector array costs more than € 10,000.

Recently, a speckle contrast method called speckle contrast optical spectroscopy (SCOS) was developed for measuring deep tissue blood flow, [16–18]. SCOS merges deep tissue capabilities of DCS and relatively inexpensive (CCD or CMOS) detectors from LSCI. In general, SCOS takes advantage of a multi-distance [16–18] and/or a multi-exposure approach to measure absolute blood flow in vivo. Although, SCOS utilizes low-cost detectors, the technique was not implemented in commercial production. By implementing, faster, photon-counting detectors, with no readout noise, such as SPADs, it is possible to use a full multi-exposure approach to get information about absolute BF with the sMESI approach.

On the other hand, functional near-infrared spectroscopy (fNIRS) has been used for measuring oxy and de-oxy hemoglobin in multiple brain locations simultaneously, at a depth up to few centimeters non-invasively [19]. In the past few years fNIRS devices have been made more compact even wireless and battery operated. This has enabled measurements during cognitive tasks, sport activities, video games playing or walking [20–23]. These wearable systems allow longitudinal measurements, without disrupting basic daily activities, giving real time measurements of brain hemodynamics in microvasculature. Other applications such as monitoring muscle health and metabolism led to prosumer devices.

These successes of fNIRS are yet to be translated to blood flow as a biomarker due to limitations in technology when utilizing DCS for non-invasive measurements. However, the need to do so, is clearly identified [24]. SCOS promises to break this barrier. Here we have presented a novel, compact, custom 32 by 2 pixels SPAD array [25] for measuring deep tissue BF based on sMESI approach. The detectors are designed in a scaled, industry standard CMOS technology that allows low noise detectors, with low dead time, no readout noise and high-frame rate. In order to measure absolute blood flow during in vivo measurements under very low light conditions, such as encountered during most in vivo measurements, sensors with high sensitivity are of great importance. With future improvements, we believe that this device could be used for measuring blood flow in freely moving human subjects.

To demonstrate the SPAD array with the sMESI SCOS approach, we have measured deep tissue blood flow in twenty-one healthy volunteers, during arterial arm cuff occlusion, voluntary apnea (breath-hold) and working memory task. The results were compared to simultaneous measurement with the “gold standard” optical technique, DCS.

The paper is organized in three sections. First, we address the basic theory of SCOS, the SPAD array architecture and real time acquisition of the sMESI system. Followed by the results from three different experiments with a total of twenty-one subjects. In the end, we discuss our results in comparison to other techniques, we explain the novelty provided with the SPAD array and the potential future improvements.

2. Methods

2.1. Compact single-photon detection system

The SPAD array system, shown in Fig. 1, exploits an integrated circuit composed of 32 by 2 pixels with 50 μm active area diameter SPADs, designed in a 0.35μm CMOS technology, [26,27]. The whole system is enclosed in a typical 1″ diameter aluminum tube for the bench top optics (Thorlabs, Germany) with a coated glass (Thorlabs, Germany) protecting the sensor.

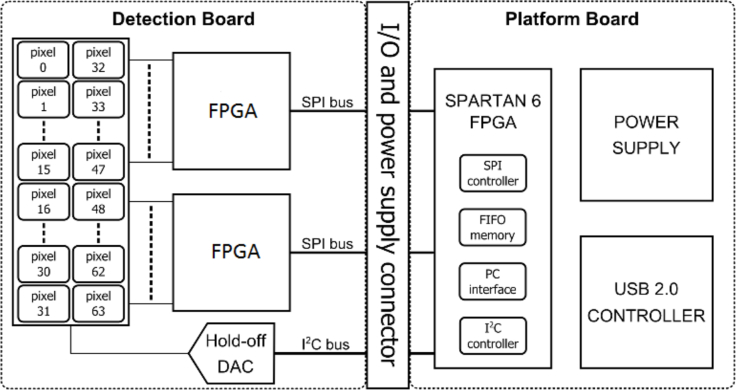
Fig. 1.

Detection block diagram. The detection board hosts the 32 by 2 SPAD array and two FPGAs, able to compute the speckle contrast. The platform board handles the serial interfaces and transfers data to the PC by means of USB 2.0 controller.

A SPAD is a p-n junction that is reverse-biased well above its breakdown voltage. At the bias, a single carrier is injected into the detection area that can trigger a self-sustaining avalanche current where an integrated sensing and quenching circuit [26] generates a pulse synchronous with the sensed current, in correspondence to the first detected photon with in the dead time. The digital nature of the signal, unlike CCD and CMOS imagers, avoids the contribution of readout noise. Furthermore, there is no fundamental limitation on the minimum integration time due to electronic signal-to-noise ratio (SNR) degradation. The array has a dark count rate (DCR) of a hundred counts-per-second (cps) at 25°C and a programmable minimum hold-off time from 50 ns up to few microseconds giving a maximum photon count rate of 20 MHz.

The detection board of the array is connected to two field-programmable gate arrays (FPGAs, MAX-10, Intel Corp. USA, 8000 logic elements with 47 kB memory) [25], where the speckle contrast is calculated in real time. The detection board is connected to the platform board, which consists of a power supply and a communication USB 2.0 controller.

2.2. Speckle contrast optical spectroscopy

A speckle pattern is a random interference pattern produced when light is scattered or reflected from an object illuminated with coherent light [6]. In the case of tissue, the incident light is multiply scattered, and the statistics of the speckle pattern is altered. Speckle contrast optical spectroscopy quantifies the statistics of the fluctuation of the speckle pattern as the variance of the measured intensity (${\sigma }_I^2$) over mean square of the measured intensity (< I >²) calculated in spatial or temporal domain [6], as

$${\kappa }^2(r,T)=\frac{{\sigma }_I^2(r,T)}{{<I(r,T)>}^2},$$ (1)

where r is source-detector separation, T is exposure time of the imager and κ² is speckle contrast whose value varies between zero and one, with higher values indicating slower fluctuations of the scatterers. When calculating speckle contrast it is necessary to account for contribution of the noise (shot, readout and dark noise, etc.) coming from the imager as explained in the Ref. [16]. In order to account for the dark signal, the mean of the dark intensity (I_D) is subtracted from the measured intensity (I), as I_C = I − I_D. Although the intensity is corrected, the variance of the dark noise is added to the variance of the intensity, thus it is necessary to subtract dark variance (${\sigma }_D^2$). More significant noise contribution is from the shot noise, whose variance is defined as ${\sigma }_S^2=<I_C>$. Implementing dark and shot noise corrections, the corrected speckle contrast (${\kappa }_C^2$) is written as

$${\kappa }_c^2=\frac{{\sigma }_{I_C}^2-{\sigma }_S^2-{\sigma }_D^2}{{<I_C>}^2}.$$ (2)

The speckle contrast can be related to the normalized electric field autocorrelation function, g₁(r, τ) as, [28],

$${\kappa }^2(\mathbf{r},T)=\frac{2\beta }{T}{\int }_0^T{\left|g_1(\mathbf{r},\tau )\right|}^2\left(1-\frac{\tau }{T}\right)d\tau ,$$ (3)

where β is a constant, whose value depends on the detection optics as well as the different optical modes in the measurement, and τ is the correlation delay time. The normalized autocorrelation function (g₁(r, τ)) is related to the dynamics of the scattering in the medium which is described by the mean square displacement, < Δr²(τ) >, of the scatterers. It has been shown that the blood flow index (BFI) in tissues can be extracted using an effective Brownian motion coefficient (D_B) where < Δr²(τ) >= 6D_Bτ [3,29].

2.3. Single-shot acquisition multi-exposure speckle contrast imaging

Single-shot acquisition multi-exposure speckle contrast imaging (sMESI) [11] takes advantage of noise free SPAD array detector. Where with the sMESI method, the exposure time of the device is always set to the minimal exposure time (T₁), allowing a single high-speed acquisition. During the post-processing, the frames are summed to obtain different equivalent exposure times ($T_N={\sum }_{i=0}^N{T}_1$), where N is number of frames and T_N is the exposure time, where speckle contrast is calculated in temporal domain. The sMESI acquisition method was previously demonstrated in Ref. [11].

2.4. Real-time computation of speckle contrast

The speckle contrast computation is carried out in real-time on the detection board (Fig. 2), taking into account the noise corrections (Eq. 2). The main challenge implementing the sMESI into a small-sized FPGA is the limited storage memory. Since the speckle contrast has an exponentially decaying trend, it is possible to acquire logarithmically (binary) spaced exposure times to save memory. In this way, given a minimum exposure time (T), a decorrelation time (τ_c) and a number of frames, it is possible to store a reduced number of values with respect to a linearly spaced approach without losing any significant information. Therefore, we generate logarithmically spaced exposure times to trigger the 18 bit SPAD counters with the minimum exposure time of 1μs. An exposure time generator has been implemented in the FPGA to gate the SPAD counters, and to generate the exposure times.

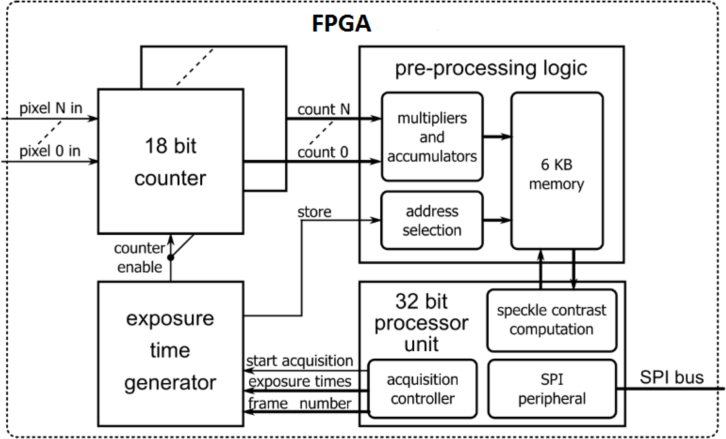
Fig. 2.

Simplified block diagram of the logic implemented into both FPGA devices. Each FPGA receives the 32 pixel outputs (16 by 2 pixels, half of the array) and employs 18 bit counters to measure the light intensity. The exposure time generator gates the counters to perform the measurement during proper exposure times. The pre-processing logic block computes a partial result of the mean intensity and the variance of the measured light, optimizing resources and processing time. Then a processor unit computes the speckle contrast and transfers the result to the PC through the SPI interface.

Furthermore, due to limited storage memory, it is not possible to store all the intensity values (for all pixels, exposure times and frames), thus only accumulated values of intensity (I_M) and the squared intensity ($I_M^2$) are stored for each pixel and exposure time in the pre-processing logic.

From the stored data, the variance can be calculated after acquisition of all exposure times and frames, according to the following formula:

$${\sigma }_M^2=<I_M^2>-{<I_M>}^2=\frac{{\sum }_{i=0}^{N_M}\left(I_{\mathit{Mi}}^2\right)}{N_M}-\frac{{\left({\sum }_{i=0}^{N_M}{I}_{\mathit{Mi}}\right)}^2}{N_M^2}$$ (4)

where N_M is the number of the captured images with the raw intensity (I_M).

In order to correct the SCOS signal for noise, a dark signal is acquired (I_D). This is done by keeping the detector in dark condition and measuring N number of frames (Eq. 5). Data is then stored in a dedicated memory area. Note that the exposure times for the dark and the intensity data are the same. The dark variance is then calculated as

$${\sigma }_D^2=<I_D^2>-{<I_D>}^2=\frac{{\sum }_{i=0}^{N_D}\left(I_{\mathit{Di}}^2\right)}{N_D}-\frac{{\left({\sum }_{i=0}^{N_D}{I}_{\mathit{Di}}\right)}^2}{N_D^2}.$$ (5)

The shot noise is calculated as

$${\sigma }_S^2=<I_M>-<I_D>=\frac{{\sum }_{i=0}^{N_M}{I}_{\mathit{Mi}}}{N_M}-\frac{{\sum }_{i=0}^{N_D}{I}_{\mathit{Di}}}{N_D}.$$ (6)

During the signal measurement, each FPGA measures and stores intensity values over the chosen exposure times and the number of frames. When the acquisition is completed, the FPGA processes the stored data, by computing the corrected speckle contrast (κ²) as:

$${\kappa }^2=\frac{N_D^2\left(N_M({\sum }_{i=0}^{N_M}{I}_{\mathit{Mi}}^2)-{({\sum }_{i=0}^{N_M}{I}_{\mathit{Mi}})}^2-N_M({\sum }_{i=0}^{N_M}{I}_{\mathit{Mi}})\right)}{{(N_D{\sum }_{i=0}^{N_M}{I}_{\mathit{Mi}}-N_M{\sum }_{i=0}^{N_D}{I}_{\mathit{Di}})}^2}-\frac{N_M^2(N_D({\sum }_{i=0}^{N_D}{I}_{\mathit{Di}}^2)-{({\sum }_{i=o}^{N_D}{I}_{\mathit{Di}})}^2-N_D({\sum }_{i=0}^{N_M}{I}_{\mathit{Di}}))}{{(N_D{\sum }_{i=0}^{N_M}{I}_{\mathit{Mi}}-N_M{\sum }_{i=0}^{N_D}{I}_{\mathit{Di}})}^2}.$$ (7)

This implementation of the speckle contrast calculation is suitable for real-time processing in an embedded system, such as the SPAD array. The summation operations are performed by hardware multiply-accumulate units (located in the pre-processing logic) during the intensity acquisition phase itself, the remaining operations (multiplication, division and integer additions) are performed when the measurement is in the microprocessor.

2.5. Experimental setup

The SCOS setup (Fig. 3(a)) consists of a continuous wave (785 nm) laser (Crystal laser, USA) and the SPAD array. To match pixel size to the speckle size in front of the SPAD array, we have placed an objective lens (Basler, Germany). The source was placed parallel to the SPAD array chip (allowing the averaging over all pixels) at a 2 cm distance from the central pixels as shown in Fig. 3(a).

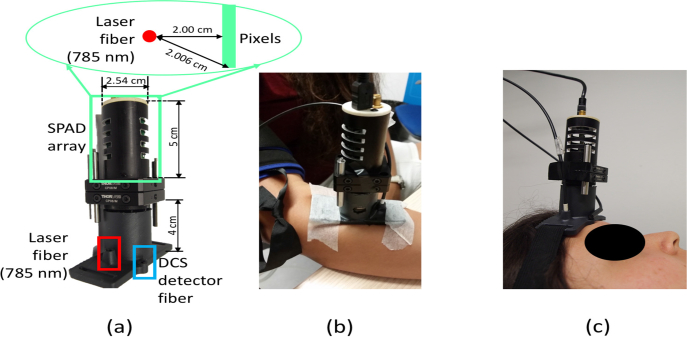
Fig. 3.

SCOS/DCS probe geometry (a), with laser source fiber (785 nm) placed at 2 cm distance from SPAD array and DCS detector. For the arm cuff occlusion (b) SCOS/DCS probe was placed on the flexor carpi ulnaris muscle of a right arm; For the cerebral blood flow measurement (c) the probe was placed on the frontal bone (frontal eminence) of the left hemisphere of the subject head during voluntary apnea measurement and verbal fluency task.

The DCS setup consisted of 4-in-1 detector array (AQ4C, Excellitas, USA) and the shared source that is used in SCOS setup. The source-detector separation was also 2 cm (Fig. 3 (a)).

For the acquisition of SCOS sMESI data, we have used 30 exposure times, ranging from 0.3 to 10 ms spaced in a binary logarithmic scale and the decorrelation time of 10 ms. Each data point was calculated over 200 frames, giving an acquisition time of 2.1 s per point where the speckle contrast was calculated in the temporal domain. To match SCOS sMESI acquisition time, we have used a 2.1 s averaging time for DCS.

2.6. In vivo measurements

The studies were approved by the ethical committee of Hospital Clinic in Barcelona. Each subject signed an informed consent and the study was conducted according to the principles of the Declaration of Helsinki. All protocols were done on healthy volunteers.

2.6.1. Arm cuff occlusion

Volunteers were asked to sit on a chair and place the right arm on a table (Fig. 3(b)). The SCOS/DCS probe was placed on the flexor carpi ulnaris muscle of the right arm. After baseline acquisition (3 min), the pressure cuff was inflated to 180 mmHg for 3 minutes. When the pressure cuff was released, the recovery of the blood flow was recorded for 4 minutes.

2.6.2. Voluntary apnea

Subjects were asked to lie in the supine position and the SCOS/DCS probe was placed on the left hemisphere on the frontal eminence bone Fig. 3(c). First baseline was acquired for 3 minutes. Afterwards, a voluntary apnea consisting of 30 s breath-hold, where the subjects were asked 6 s before the breath-hold to breath-in for 3 s, and to breath-out for 3 s and to stop breathing for 30 s was recorded. After the breath-hold subjects were asked to continue breathing normally for 2 minutes. In total five breath-hold repetitions were performed for each subject. Before the start of the protocol, one practice of the voluntary apnea was done.

To monitor physiological parameters (pulse rate (PR), respiration rate (RR), oxygen saturation (SpO₂), abdomen and thoracic movement), clinical monitor (Embletta, MPR PG, Natus, USA) was used. To check the quality of the breath-hold, we have looked at SpO₂, PR, RR, and abdominal/thoracic movement. Subjects that did not keep their breath-hold (as indicated by the RR, abdominal and/or thoracic movement) or did not have any change in the oxygen saturation after or alteration of the normal pulse rate during the breath-hold were excluded from the study [30,31].

2.6.3. Working memory task

For the verbal fluency task (VFT) the subjects were asked to lay in the supine position. Probe was placed on the left hemisphere on the frontal bone (Fig. 3(c)), and a 2 minutes baseline measurement was acquired. On the screen subjects were able to see a ’+’ sign during the baseline, displaced by a letter for 1 minute, during which subjects were asked to name as many nouns as they can remember. The protocol was repeated for four different letters with a 1 minute recovery during which a ’+’ sign was displayed. Through the whole protocol heart rate and oxygen saturation were monitored with a pulse-oximeter (Capnostream 20, Oridion, USA).

2.7. Data analysis

The corrected speckle contrast was calculated for each individual pixel, for every exposure time in the temporal domain over 200 frames on the board of the SPAD array. In the post-processing, we have averaged the calculated speckle contrast (64 independent values) over the 64 pixels. This approach is the so-called multiple speckle averaging approach which is a well-established and a reliable method to improve the signal-to-noise ratio. The multi-exposure speckle contrast data was fitted for the semi-infinitive medium solution for the correlation diffusion equation [3], and normalized to the baseline period.

The count rate for all the measurements was 30–80 kcps which is well below the maximum count rate of the array. This was monitored in real-time during all measurements, and, if needed, appropriate attenuation could have been introduced to ensure that we do not suffer from non-linearity.

To see if sMESI SCOS and DCS are correlated, Lin’s concordance correlation coefficient (ρ_c) with the Pearson’s (R) correlation coefficient and Bland-Altman analysis were done. Bland-Altman analysis was calculated as the percentage change between two methods as (SCOS − DCS)/ < SCOS, DCS > [%] [32] with the hypothesis that there is no significant difference between the methods for p-values higher than 0.05.

3. Results

3.1. Arm cuff occlusion

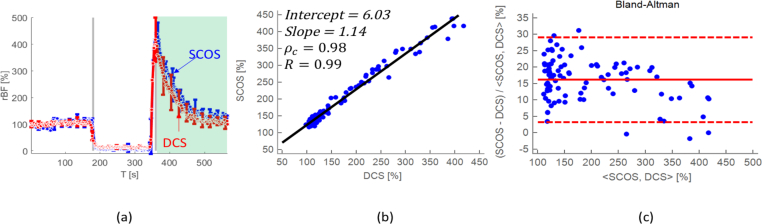
In total seven subjects, average age of (30 ± 5) years, were measured with arm cuff occlusion. The average blood flow for all the subjects is shown in Fig. 4(a), where the solid (blue) line is SCOS and the dashed (red) line is DCS data. During cuff inflation, a reduction of the blood flow to the baseline, was seen. Hyperemia was seen after releasing the pressure cuff for all subjects with both the SCOS and the DCS. The concordance coefficient, Pearson’s correlation coefficient and Bland-Altman analysis plot, are shown in Fig. 4(b) and (c) respectively, for shaded region in Fig. 4(a).

Fig. 4.

Averaged rBF with the mean standard deviation error for seven subjects during arm cuff occlusion is shown in panel (a). A concordance plot with the concordance correlation coefficient (ρ_c =0.98) and the Pearson’s correlation coefficient (R=0.96), including the slope (1.14) and the intercept (6.03) of a linear fit are shown in panel (b). The Bland-Altman (difference) plot is shown in panel (c) with a p-value of 0.1, showing that there is no significant difference between the SCOS and the DCS results for the shaded region in panel (a).

3.2. Voluntary apnea

From eleven measured subjects, average age (28 ± 4) years, four subjects were excluded from the study. Two subjects were excluded due to technical difficulties, and two did not have any reduction in the oxygen saturation (SpO₂) after the breath-hold or change in heart rate during the apnea.

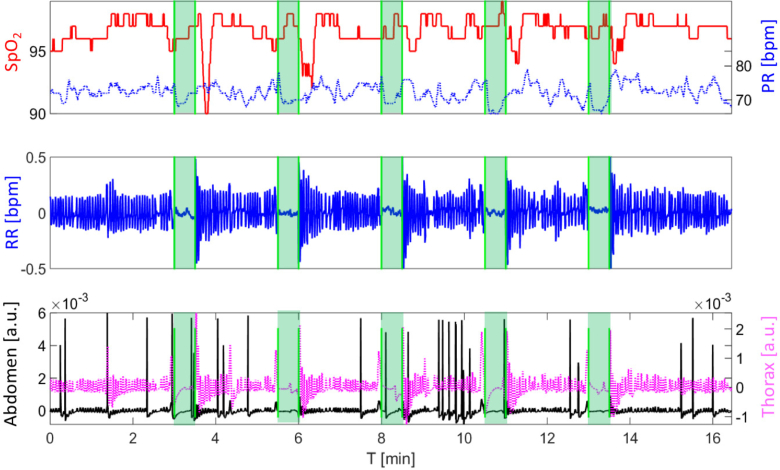
In Fig. 5, the Embletta result is shown for one subject. The oxygen saturation (solid line) and the pulse rate (dashed line) from the pulse-oximeter are shown in the top panel, where the shaded region presents the 30 s period during which the subject was asked to hold breath. Respiration rate measured with the thermistor can be seen in the middle panel. In the bottom panel, the thorax (dashed line) and the abdomen (solid line) movement are shown. The voluntary apnea (shaded region) shows no air flow or movement of the chest and the abdomen. With all seven subjects, we could see the drop of the SpO₂ just after the apnea and alteration of the heart rate during the apnea.

Fig. 5.

Embletta result for one representative subject during the whole voluntary apnea protocol. The oxygen saturation (SpO₂, left axis, solid line) and the pulse rate (PR, right axis, dotted line) are shown in the top panel. Shaded regions correspond to the 30 s breath-hold period. There is a decrease of the SpO₂ after the apnea challenge, and alteration of the PR during the challenge. In the second panel the respiration rate (RR) is shown. In the bottom plot the abdomen and the thorax movement are shown in left (solid line) and right (dotted line) axis respectively. During the breath-hold (shaded region) subject is not breathing (respiration panel), and there is no movement of the thorax and the abdomen (bottom panel).

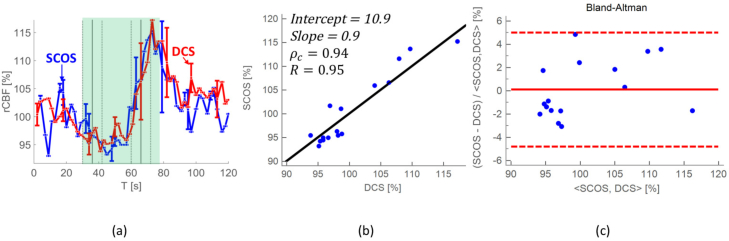
In the Fig. 6(a), averaged rCBF over seven subjects and all epochs is shown. As it can be seen there is an increase of the blood flow during the breath-hold, and a drop to normal CBF values after the challenge. This is seen with both techniques. To compare the SCOS and the DCS data, we computed the concordance correlation coefficient (ρ_c) and Pearson’s coefficient (R) (Fig. 6(b)) showing high agreement between the SCOS and the DCS. Furthermore, the Bland-Altman (difference) plot does not show significant difference (p > 0.05) between the techniques Fig. 6(c).

Fig. 6.

Averaged rCBF over seven subjects with the standard error of the mean computed for all epochs from all seven subjects is shown in panel (a); Concordance plot with Pearson’s correlation coefficient (R=0.95), linear regression fit (the slope (0.9) and the intercept (10.9)), and concordance coefficient (ρ_c =0.94) are shown in panel (b). The Bland-Altman plot, panel (c) with the p-value of 0.06, showing that there is no significant difference between two techniques for the shaded region in panel (a).

3.3. Working memory task

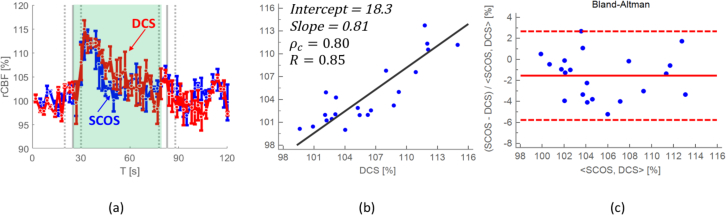
Three subjects, average age (29 ± 4) years underwent verbal fluency task. All subjects were able to complete the VFT with an average of 20 words per letter. In the Fig. 7, rCBF response was averaged over all subjects, for four different letters and the standard deviation of the mean error is shown in panel (a) where rCBF for the DCS and the SCOS are shown in dashed (red) and solid (blue) line respectively. Lin’s concordance correlation coefficient with the Pearson’s correlation coefficient and linear fit regression are shown in panel (b), showing high correlation between SCOS and DCS. In the Fig. 7(c) the Bland-Altman plot with the p-value higher than 0.05 shows no significant difference between the methods.

Fig. 7.

Averaged rCBF over three subjects and four letters with the standard deviation of the mean error is shown in panel (a). The concordance correlation coefficient (ρ_c = 0.80) with Pearson’s R-value (R=0.82) including the slope (0.81) and the intercept (18.3) of the linear regression fit are shown in panel (b). The Bland-Altman plot with the p-value of 0.05, showing that there is no significant difference between the SCOS and the DCS (c) during VTF (shaded region) is shown in panel (c).

4. Discussion

Single-shot acquisition multi-exposure speckle imaging (sMESI) was implemented with the SPAD array for the speckle contrast optical spectroscopy (SCOS) measurements of deep tissue blood flow in real time. The method was demonstrated by using point source measurement and acquiring simultaneously speckle measurements with 64 pixel array detector for a total of thirty different exposure times. We show that the method is comparable to the diffuse correlation spectroscopy (DCS), where sMESI SCOS method uses a CMOS SPAD array making the technique relatively low cost and fast. To demonstrate sMESI SPAD array with SCOS, we measured blood flow change during the arm cuff occlusion, voluntary apnea and working memory task in 21 healthy subjects.

To show that sMESI SCOS is able to probe deep tissue blood flow, an arm cuff occlusion was done in seven healthy subjects (Fig. 4(a)). High hyperemia after the release of the pressure cuff demonstrates that SCOS is capable of measuring deep tissue BF [33]. Furthermore, high correlation with the “gold standard” optical technique, DCS, shows that there is no significant difference between SCOS and DCS methods, for high BF changes Fig. 4.

To demonstrate that SCOS method is sensitive to small changes in cerebral blood flow, voluntary apnea and working memory task were performed in fourteen healthy subjects. First we present results from the voluntary apnea Fig. 6(a) showing that the sMESI SCOS is sensitive to measure small CBF change in seven healthy subjects. The increase in the blood flow at the end of the epoch is in agreement with the DCS measurement and literature [34,35].

In three healthy subjects we measured CBF change during the working memory task Fig. 7(a). Subjects showed high task performance during the verbal fluency task, generating on average (20 ± 3) words per letter [36]. Corresponding CBF change is in agreement with the DCS and the published literature [36,37].

We mention here that the goal of the paper was to quantitatively compare the two related methods (DCS and SCOS) for measuring deep tissue blood flow on equal footing, and based on the results presented, one could conclude that there are no significant differences between SCOS and DCS. The two techniques also share the same shortcomings such as those due to the partial volume effects. We note here that Eq. 3 is an integral over the field autocorrelation function (g₁(r, τ)), so SCOS does not resolve the fine-details like DCS measurements which are contained in the complete shape of the auto-correlation curve. This in not expected to be crucial for in vivo measurements for the relatively homogeneous tissue. It may become more relevant in multi-layered tissue with a large difference between the blood flow in layers. Furthermore, the integral implies loss of the sensitivity to very small changes in blood flow when using larger exposure times that are comparable to the correlation decay time (from hundreds of nano seconds). To overcome this, the exposure time could be more reduced but this decreases the SNR. Our ability to use SCOS for the common brain challenges shows that these issues are not relevant.

We note here that SPAD array provides a good SNR, even for the lowest exposure times (300 μs). Furthermore, we utilize the absence of the readout noise and the negligible dead-time to demonstrate single-shot acquisition MESI. In the current setup, maximum exposure time was 10 ms giving a maximum temporal resolution of 100 fps. We have chosen to calculate the speckle contrast over 200 frames in the temporal domain instead of the spatial (over multiple pixels), which has reduced the temporal resolution to 2 s. This could be improved in the future by calculating the speckle statistics over different pixels in the spatial domain. We note that this temporal resolution is similar to standard DCS approaches.

The current SPAD array has been designed in a CMOS scaled technology (0.35 μm) that allows low noise detectors and the integration of the readout circuitry on the chip. Pixels are based on a 50 μm diameter SPADs resulting in a 100 μm pitch, that limits the number of pixels to 64 in a 3.2 mm. In the future, the pixel pitch could be reduced to as low as 25 μm (with a 10 μm diameter of an active area), thus leading to an increased number of pixels achieving higher SNR while using the same array area. Moreover, the employed SPADs have a quantum efficiency peak of 50% at 420 nm, while only 8% at 785 nm. As result, an optimization of the SPAD quantum efficiency in the near-infrared range can improve the SNR and reduce the measurement time. Next generation of CMOS SPAD arrays are expected to provide a higher quantum efficiency in the near-infrared (700-900 nm) range which is a current limitation [38], and reduce the price with the large scale production.

In the current setup, for the source we have used a fiber coupled laser source (Fig. 3(a)), where in the future this can be remedied with a custom build source. The source could be minituarized and placed in the same box as the SPAD array, allowing the same power supply to be switched from the USB 2.0 to a battery, where the data transfer can be changed to wireless. Current SCOS setup requires commercial objective lens to match speckle to pixel size, making the device around 10 cm in length. In the future, custom made optics could be placed directly in front of each pixel, reducing the size of optics to few millimeters, making a scalable battery operated wireless, making wearable and cost efficient device. We believe that this new device format could be used as a multi unit device, measuring the blood flow longitudinally during different daily activities, such as walking, sport, injury recovery, or monitoring of cognitive tasks.

5. Conclusion

We have presented in vivo real time absolute blood flow measurements with speckle contrast optical spectroscopy (SCOS). SCOS was implemented with sMESI method with a SPAD array to measure deep tissue blood flow in twenty-one healthy volunteers. Results were compared with the “gold standard” optical technique, diffuse correlation spectroscopy, demonstrating capability of SCOS method to measure relative blood flow changes from few to hundreds percent changes. These results pave the way for developing wearable device for noninvasive blood flow measurement.

Funding

Fundació CELLEX Barcelona, Ministerio de Economía y Competitividad (PHOTODEMEN-TIA (DPI2015-64358-c1 and c2 (MINECO/FEDER)), Instituto de Salud Carlos III/FEDER (MEDPHOTAGE DTS16/00087), the “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV-2015-0522), the Obra social “la Caixa” Foundation (LlumMedBcn), LASERLAB-EUROPE IV. J.L. Hollmann acknowledges the Marie Curie COFUND (FP7-PEOPLE-2013-COFUND) fellowship.

Disclosures

ICFO has equity ownership in the spin-off company HemoPhotonics S.L. that commercializes DCS technology. Potential financial conflicts of interest and objectivity of research have been monitored by ICFO’s Knowledge & Technology Transfer Department. No financial conflicts of interest were identified or declared by the authors.