Correction of an adding-doubling inversion algorithm for the measurement of the optical parameters of turbid media

Abstract

We present broadband measurements of the optical properties of tissue-mimicking solid phantoms using a single integrating sphere to measure the hemispherical reflectance and transmittance under a direct illumination at the normal incident angle. These measurements are traceable to reflectance and transmittance scales. An inversion routine using the output of the adding-doubling algorithm restricted to the reflectance and transmittance under a direct illumination was developed to produce the optical parameters of the sample along with an uncertainty budget at each wavelength. The results for two types of phantoms are compared to measurements by time-resolved approaches. The results between our method and these independent measurements agree within the estimated measurement uncertainties.

1. Introduction

Well-characterized tissue-mimicking phantoms are essential to validate the performance and to calibrate measurement results in the development and clinical applications of biomedical instruments from the bench and to the bedside. The phantoms are fabricated from turbid materials to simulate tissue optical properties with desired absorption coefficient μ_a, scattering coefficient μ_s and anisotropy of scattering g.

A variety of measurement techniques with the aids of physics-based photon-transport models have been developed to measure these parameters. Measurements of the optical properties of turbid media in the time domain are based on the estimation of the temporal spreading of a light pulse subjected to scattering and absorption events as it travels through the sample. Analysis using the diffusion approximation of the radiative transfer equation (RTE) or Monte Carlo (MC)-based model were used to obtain μ_a and ${\mu }_s^{\prime }$ = μ_s(1 − g) (reduced scattering coefficient) of liquid [1,2] and solid phantoms [3]. In the scope of the diffusion approximation, frequency domain measurements techniques were used to measure the optical properties of turbid liquids [4–6]. Spatial domain measurement techniques either fiber-based [7, 8] or non-contact [9–11] were developed as well. Integrating sphere measurement techniques associated with a MC model or the adding-doubling (AD) algorithm [12] were also used to measure the optical properties of biomedical phantoms and tissues [13–15].

In the scope of the current effort to implement a national scale for the optical properties of turbid media at the National Institute of Standards and Technology (NIST), in previous studies [16,17] we have established an inversion routine of the AD algorithm that allowed for the computation of the absorption coefficient μ_a and the reduced scattering coefficient ${\mu }_s^{\prime }$ along with the total uncertainty budget at each measurement wavelength. The measurements were made following a procedure described in the inverse adding-doubling (IAD) manual [19] using a double integrating sphere setup with identical spheres and the substitution method. The details on how to make these measurements can be found elsewhere [13,18]. Contrary to the comparison method, in the substitution method the sphere efficiencies change when the sample is substituted for the reflectance standard used as reference in the measurements [20]. In his Phd. thesis [18], Moffitt presented the equation describing the sphere efficiency of a single sphere in terms of the geometrical parameters of the spheres, the reflectance of the sphere wall, the reflectance of the detector and $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ and further expressed the measured reflectance R_Meas and transmittance T_Meas for measurements with one integrating sphere and with double integrating spheres (for both measurements techniques the corresponding formulas are also presented in the documentation related to IAD source code that’s part of the IAD package). For double integrating sphere systems, cross talk between spheres lead to complex relationships between (R_Meas, T_Meas), the sample hemispherical reflectance and transmittance under a direct illumination, $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ and $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$, and the hemispherical reflectance and transmittance under a diffuse illumination, $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ and $T_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$.

Reflectance and transmittance measurements should be traceable to reflectance and transmittance scales. Under the substitution method, it’s easier using a single integrating sphere since the measurement equations are simpler. Measurements of diffuse samples using a single integrating sphere have been underway for at least a decade and has been coupled with IAD [13, 21] or inverse Monte Carlo routine [22, 23] to obtain the optical properties of the samples. Within the scope of IAD, whereas the measurements are made with one or two spheres, an important experimental step (so-called sphere calibration step) in the measurement procedure is to estimate the reflectance of the sphere wall for each sphere by aiming the incident beam toward the sphere wall and measuring the signal for (i) an empty sample port and (ii) a sample port blocked by a reference standard. Since the illumination is diffuse in that case, it’s possible to measure $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ by adding a measurement step where the sample is set at the sample port of the sphere, provided that the sphere model is valid. By measuring a set of samples with known reflectance under a diffuse illumination, this measurement step can then be used for the traceability to the reflectance scale and also provide a means of testing the IAD model.

In this study we measure $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ for a set of calibrated quasi-Lambertian reflectance standards in the 5 % to 99 % reflectance range. A discrepancy between the reflectance results and their expected values led us to modify our measurement procedure and move from measurements made with a double integrating sphere system to using a single integrating sphere to measure the hemispherical reflectance and transmittance under a direct illumination. The inversion algorithm of the AD routine is modified accordingly and the optical properties are accompanied by an uncertainty budget. For the first time, using a single integrating sphere, the hemispherical reflectance and transmittance under a direct illumination used as input to the AD inversion routine are traceable to reflectance and transmittance scales. The results include measurements of a commonly produced and a custom phantom that were also measured independently by a time-resolved method.

2. Material and methods

2.1. Experimental setup

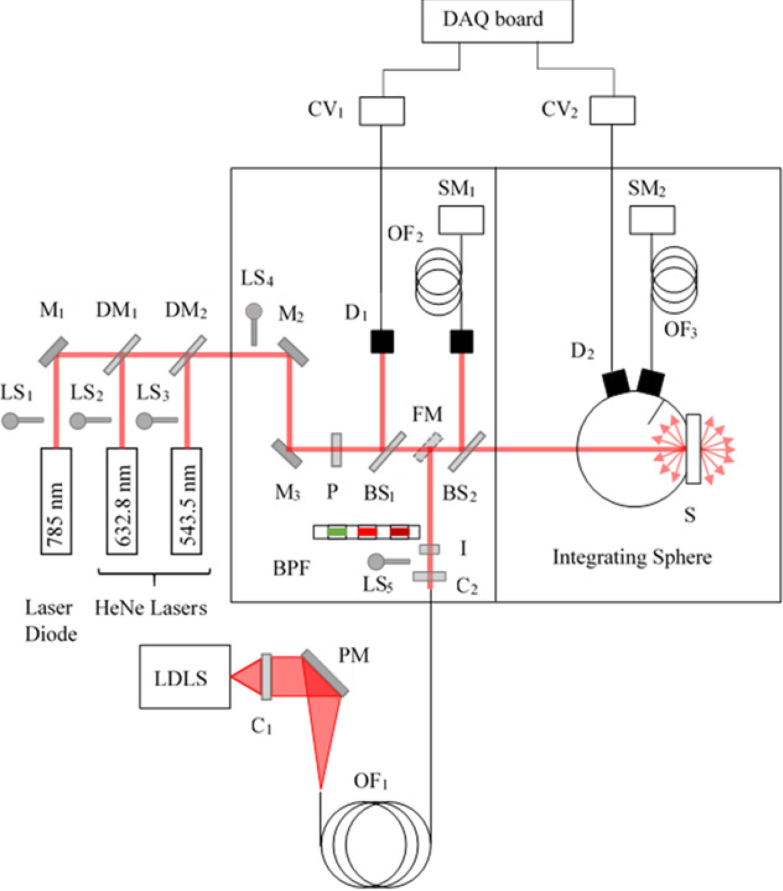
Figure 1 describes the experimental setup. It’s an evolution of what was already described in Ref. [16] with the notable difference that it only includes a single integrating sphere (UMBK-190, Gigahetrz Optik, Türkenfeld, Germany; 196 mm internal diameter coated with ODM98 synthetic material, 12 mm thick; all dimensions are nominal unless noted otherwise) instead of two for reasons explained in Section 2.4. The integrating sphere has an entrance port (diameter 25.1 mm), a sample port (diameter 63.5 mm reduced to 38.1 mm by an internally conical port reducer to get a knife-edge contact with the sample), a fiber port (diameter 12.7 mm), a photodiode port (diameter 12.7 mm) inside a cylindrical baffle (diameter 30 mm, height 18 mm, with a 10 mm diameter hole on the side of the cylinder) that prevents direct reflections from the sample to the photodiode. The other notable difference from our previous setup is that the illumination sources are now of two types: one laser-based from one of three options (HeNe laser: λ = 543 nm, JDS Uniphase Corporation, Milpitas, CA, USA; λ = 632 nm, Research Electro-Optics Inc., Boulder, CO, USA; laser diode: λ = 785 nm, Spectra-Physics, Santa Clara, CA, USA) and the other using a laser driven light source (LDLS, EQ 1500, Energetiq Technology Inc., MA, USA; broadband from 170 nm to 2100 nm). The choice of illumination source is made by blocking the unwanted illumination using a mechanical light shutter LS₄ (blocks the laser illumination) or LS₅ (blocks the broadband illumination) and by flipping the flipping mirror FM down (laser illumination) or up (broadband illumination).

Fig. 1.

Schematic layout of the integrating sphere instrument; LDLS: laser-driven light source; LS₁, LS₂, LS₃, LS₄ and LS₅: light shutters; M₁, M₂ and M₃: mirrors; DM₁ and DM₂: dichroic mirrors; PM, parabolic mirror; P, Glan-Taylor linear polarizer; BS₁ and BS₂: beam splitters; FM: folding mirror; C₁ and C₂: collimators; BPF: band bass filters; I: iris; D₁ and D₂: photodiodes; CV₁ and CV₂: current-voltage amplifiers; DAQ: data acquisition board; OF₁, OF₂ and OF₃: optical fibers; SM₁ and SM₂: spectrometers.

The selection of the laser wavelength is made by blocking unwanted laser beams using the manual light shutters LS₁, LS₂ or LS₃. The beam is directed toward the sample by a set of mirrors (M₁, M₂, M₃) and dichroic mirrors (DM₁, DM₂). The polarization of the laser beam is controlled by a linear polarizer P placed in front of a beam splitter BS₁ that diverts a portion of the beam for detection by a photodiode D₁ to simultaneously monitor power fluctuations. The remaining portion of the beam is normally incident to the front face of the sample set at the sample port of the integrating sphere (Fig. 1: reflectance measurement situation; the sphere is rotated 180° around the vertical axis perpendicular to the optical table for transmittance measurements). The signal of the corresponding diffuse hemispherical reflectance or hemispherical transmittance is detected by a second photodiode D₂. The photocurrents are amplified by two current-voltages amplifiers CV₁ and CV₂ and the corresponding voltages are acquired by a data acquisition board (DAQ).

The output of the LDLS source is collimated by C₁ (biconvex lens, f = 30 mm) and the beam is converged to the tip of an optical fiber OF₁ by a parabolic mirror PM. At the output of OF₁, the beam is collimated by C₂ (biconvex lens, f = 25 mm) and the beam diameter is adjusted by an iris I. A band pass filter BPF can be inserted in the the beam path for wavelength selection. The beam is directed by FM to a beam splitter BS₂ which diverts a portion of the beam to the tip of a fiber OF₂ connected to a spectrometer SM₁ for reference. The remaining part of the beam is directed to the sample and the reflectance (transmittance) signal is detected by a fiber OF₃ connected to a spectrometer SM₂ (detection range of the spectrometers: 350 nm to 1050 nm). In this paper, the measurements are made using the broadband source.

2.2. Samples

Two types of solid phantoms are measured in this study. The first type is a set of three polyurethane phantoms from the Institut National d’Optique (INO, Quebec, Canada) with titanium dioxide (TiO₂) as a scatterer and carbon black as an absorber (batch B0430). The nominal optical properties of these phantoms are: μ_a = 0.01 mm⁻¹ and ${\mu }_s^{\prime }$ = 1 mm⁻¹ at λ = 805 nm. The samples were cut to three different thicknesses t = 5 mm, 7 mm and 10 mm (nominal) and have the same lateral dimensions (100 mm × 100 mm). The surface aspect of their faces is smooth from machining by INO and present a diffuse reflectance. We used a dial gage micrometer to measure the actual thicknesses of the samples at nine locations set on a 3×3 grid with a center point near the center of the sample. The combined uncertainty associated with thickness, $u_t^2=s_t^2+u_{\text{dial}}^2$ was computed combining the variance of the measured thickness, $s_t^2$, with the variance attributable to the precision of the dial micrometer, $u_{\text{dial}}^2$. The measured thickness values are: t = 4.94 ± 0.04 mm, 6.95 ± 0.02 mm and 9.83 ± 0.04 mm (coverage factor k = 2, used in the rest of the paper unless noted). The second type of solid phantoms were fabricated at NIST [25]. They are made of polydimethylsiloxane (PDMS) and have different concentrations of TiO₂ (0.2 %, 0.1 % and 0.05 % in w/w of TiO₂/PDMS) but no absorber added. They were molded using Petri dishes (diameter 87 mm) and their measured thicknesses are: t = 4.85 ± 0.18 mm (TiO₂ = 0.2%), t = 4.39 ± 0.14 mm (TiO₂ = 0.1%), t = 4.32 ± 0.13 mm (TiO₂ = 0.05%). For comparison with time-resolved measurements at the Physikalisch-Technische Bundesanstalt (PTB, Berlin, Germany), samples of different dimensions (diameter 51.5 mm, nominal thickness 12 mm) were prepared from the same PDMS batch. The samples faces are specular, one from molding, the other from the air-PDMS interface.

2.3. Measurement of the index of refraction of the specular samples

The index of refraction of the base material of the specular samples was obtained by fitting the measurements of the Fresnel reflectance at an 8° incident angle with a Cauchy dispersion law over the measurement wavelengths. The instrument we used was a bench-top spectrophotometer equipped with an integrating sphere detector and a specular port (Lambda 1050, Perkin-Elmer, Waltham, MA, USA). The Fresnel reflectance was estimated by subtracting the diffuse hemispherical reflectance measured with the specular port open from the total hemispherical reflectance measured with the specular port blocked for λ = 400 nm to 1000 nm in steps of 10 nm. The index of refraction of PDMS was estimated from the mean value of the Fresnel reflectance of the three samples (uncertainty 0.015 at k = 1). A set of three specular phantoms from INO was measured to estimate the index of refraction of the polyurethane material [26]. We assume that the B0430 samples are made of an identical base material (uncertainty 0.015 at k = 1).

2.4. Test of the validity of the IAD model of the integrating spheres

IAD assumes an “ideal” integrating sphere with an entrance port, a sample port and a detector port, and neglects the area of the baffle but not its effect [19]. Since our spheres have a more complex internal geometry, we assumed in one of our previous papers [16] that we could use the IAD “ideal” sphere model by adjusting the diameter to basically get the same sphere gain as the real ones. This hypothesis put our system in conformity with the model used in IAD and not surprisingly, the results we obtained with our inversion of the adding-doubling algorithm were consistent with what was obtained with IAD with the additional benefit of getting the total uncertainty budget on the optical parameters μ_a and ${\mu }_s^{\prime }$.

Under the scope of the IAD sphere model (see Appendix), the diffuse hemispherical reflectance of the sample under a diffuse illumination (beam aimed at the sphere wall) $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}=R(d:d)$ (diffuse/diffuse geometry [24]) can be estimated using Eq. (A5)

$$R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}=R_{\mathit{\text{StdRef}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}({\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}-{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}})}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}({\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}-{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}})},$$ (1)

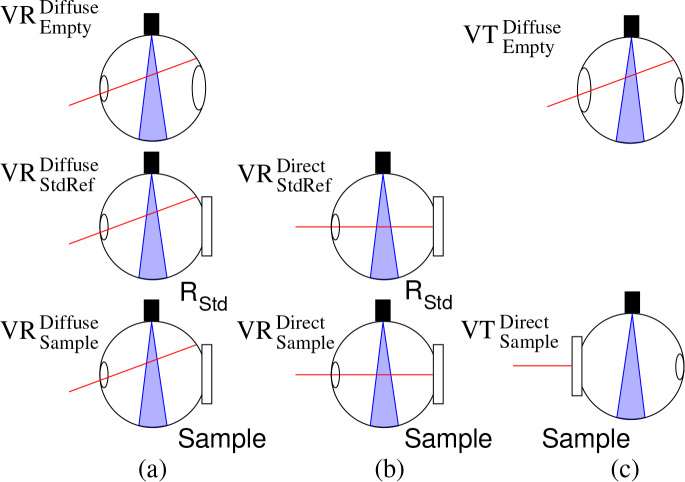
by successively measuring the voltages (i) ${\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}$, with no sample, (ii) ${\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}$, with a reference standard R_StdRef and (iii) ${\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$,with the sample, respectively set at the sample port of the sphere (Fig. 2(a)). This approach is known as the so-called first Taylor method [27,28].

Fig. 2.

Steps of the measurement procedure for estimating the hemispherical reflectance and transmittance at a 0° incident angle (detection by an optical fiber): (a) diffuse illumination, (b) sample reflectance under direct illumination at a 0° illumination angle and (c) sample transmittance under direct illumination at a 0° illumination angle.

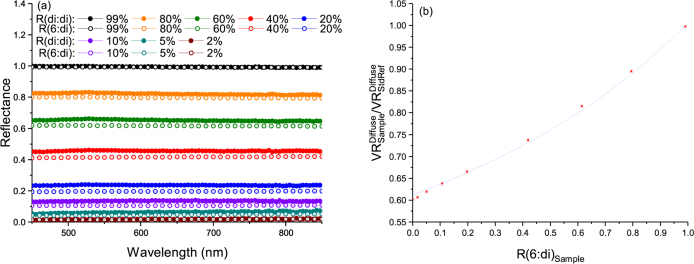
Using a NIST-traceable 99 % reflectance standard as a reference, we measured a set of calibrated quasi-Lambertian reflectance standards in the range [2 %, 5 %, 10 %, 20 %, 40 %, 60 %, 80 %, 99 %] (Avian Technologies LLC, Sunapee, NH, USA) and compared the values to the measurements from 400 nm to 1000 nm of the directional-hemispherical reflectance with specular component included at a 6° illumination angle, R(6 : di) [24], made using the integrating sphere instrument of NIST’s Spectral Tri-function Automated Reference Reflectometer (STARR) [29]. Figure 3(a) presents the results of this comparison from 450 nm to 850 nm. For both measurement techniques, the uncertainties are computed by propagation of a Gaussian distribution of uncertainties with a coverage factor k = 2. There is a discrepancy larger than the error bars between the measured reflectance R(d : d) and the reference reflectance R(6 : di) for the 20 % to 60 % reflectance standards. This shouldn’t be the case for these quasi-Lambertian reflectance standards and the results cast doubts on the validity of the IAD sphere model for the integrating sphere used in our experimental apparatus.

Fig. 3.

(a): Comparison of the measurements with a single integrating sphere of the hemispherical reflectance under a diffuse illumination, R(d : d) to the measurements of the hemispherical reflectance with a 6° illumination angle, R(6 : di), made using the integrating sphere instrument of NIST STARR for a set of calibrated reflectance standards in the range [2 %, 5 %, 10 %, 20 %, 40 %, 60 %, 80 %, 99 %]. The error bars (coverage factor k = 2) on R(6 : di) are smaller than the symbols used; (b): Measured voltage ratios $\frac{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}}$ as a function of R(6 : di) reflectance of the samples fitted using the IAD model for the integrating sphere (smallest rmse value 2.62 × 10⁻⁴ at λ = 794 nm).

Moreover, using Eq. (A3)

$$\frac{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}}=\frac{A_1+B_1{R}_{\mathit{\text{StdRef}}}}{A_1+B_1{R}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}},$$ (2)

where A₁ and B₁ are dependent of the geometrical and reflectance constants of the sphere, we can fit the measured voltage ratios $\frac{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}}$ for each wavelength as a function of the reference reflectance of the samples $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}=R(6:di)$. Figure 3(b) presents the results at λ = 794 nm (wavelength of the smallest root-mean-square error (rmse), 2.62 × 10⁻⁴). The IAD model doesn’t fit the measurements well, specifically in the 40 % to 80 % reflectance range. The IAD model of the integrating sphere is not adequate for our application since it leads to substantial errors in $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$. That’s also the case for the IAD model for a double integrating sphere system at a 0° incident angle using the substitution method since it is based on the model for a single integrating sphere. This invalidates the measurements made with our original double integrating sphere system [16,17]. However, it is crucial to perform this measurements step with a single integrating sphere to get the values of ${\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}$, ${\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}$ and ${\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ for the estimation of $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ and $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$.

2.5. Measurements of $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$

The measurement of the diffuse hemispherical reflectance of the sample under a direct illumination at a 0° incident angle with specular component excluded, $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}=R(0:de)$ [24], can be estimated using Eq. (A7)

$$R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}=R_{\mathit{\text{StdRef}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}}{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Direct}}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}},$$ (3)

by successively measuring the voltages (i) ${\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Direct}}}$, with a reference standard R_StdRef and (ii) ${\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$, with the sample, respectively set at the sample port of the sphere (Fig. 2(b)). One should note that the voltages ratio $\frac{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}$ formed from the measurements presented in Section 2.4 is essential to compute $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$.

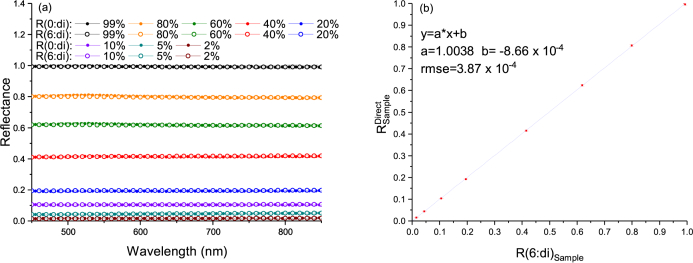
We measured $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ for the set of calibrated reflectance standards previously used and compared the results to their R(6 : di) values (Fig. 4(a)). The uncertainty on $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ are computed propagation of a Gaussian distribution of uncertainties with with a coverage factor k = 2. The measured values by our setup agree within the error bars with the calibrated values of the reflectance standards. Figure 4(b) presents a linear fit of the data at λ = 456 nm (wavelength of the largest rmse value 3.87 × 10⁻⁴). One should note that for a Lambertian reflectance standard, ${\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Direct}}}={\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}$ and Eq. (3) becomes $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}=R_{\mathit{\text{StdRef}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}$, i.e. the measurement procedure is identical to the comparison method with the sphere wall used as a reference (measurement steps (a) and (b) of Fig. 2 with the sample set at the sphere sample port).

Fig. 4.

(a) Comparison of the measurements with a single integrating sphere of the hemispherical reflectance at a 0° incident angle, R(0 : de), to the measurements of the hemispherical reflectance with a 6° illumination angle, R(6 : di), made using the integrating sphere instrument of NIST STARR for a set of calibrated reflectance standards in the range [2 %, 5 %, 10 %, 20 %, 40 %, 60 %, 80 %, 99 %]. The error bars (coverage factor k = 2) on R(6 : di) are smaller than the symbols used; (b) R(0 : de) as a function of R(6 : di) fitted with a linear model (largest rmse value = 3.87 × 10⁻⁴ at λ = 456 nm).

2.6. Measurements of $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$

The measurement of the diffuse hemispherical transmittance of the sample under a direct illumination at a 0° incident angle with specular component excluded [24], $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}=T(0:de)$, can be estimated using Eq. (A11)

$$T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}=\frac{{\mathit{\text{VT}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}}{{\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}},$$ (4)

by successively measuring the voltages (i) ${\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}$, no sample with the beam directed toward the sphere wall and (ii) ${\mathit{\text{VT}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$, with the sample set at the sample port of the sphere and the beam at a 0° incident angle (Fig. 2(c)). One should note that the voltages ratio $\frac{{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}$ formed from the measurements presented in Section 2.4 is essential to compute $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$.

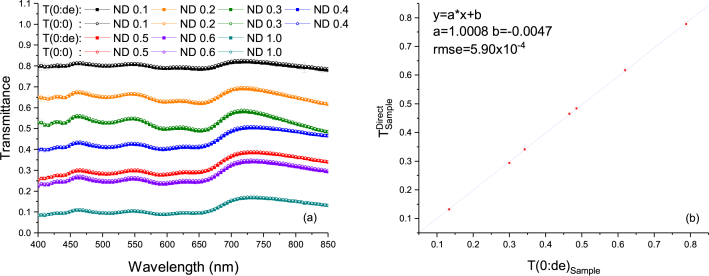
To validate this part of the experimental procedure, we measured $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ for a set of BK7-based neutral density filters with optical density OD = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 1.0] and compared the results to the transmittance coefficients T(0 : 0) (normal/normal geometry [24]) measured using NIST’s Reference Transmittance Spectrophotometer (RTS) between 400 nm and 1000 nm [30]. The filters are non-scattering and for a 0° incident angle the beam exits the sphere through the open exit port (see Fig. 2(c)) which cannot be blocked in order to maintain the sphere efficiency as measured in Fig. 2(a). In this situation, no signal is detected. Near a 0° incident angle, the differences in Fresnel transmittance values of BK7 are small. Hence, the angle of incidence is changed to 8° by tilting the sphere around the vertical axis of the setup so that the transmitted beam is reflected by the sphere wall and the transmitted signal is detected. One should note that for regular diffusive samples, the angle of incidence is maintained at 0°. Figure 5(a) shows that the results with our system are consistent with the results from RTS within the error bars for λ = 450 to 850 nm. For both measurement techniques, the uncertainty are computed propagation of a Gaussian distribution of uncertainties with with a coverage factor k = 2. Figure 5(b) presents a linear fit of the data at λ = 452 nm (wavelength of the largest rmse value 5.90 × 10⁻⁴). One should note that ${\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}$ and ${\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}$ are identical and that Eq. (4) becomes $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}=\frac{{\mathit{\text{VT}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}$ (measurement steps (a) and (c) of Fig. 2 with sample only).

Fig. 5.

(a) Comparison of the measurements with a single integrating sphere of the hemispherical transmittance at a 0° incident angle, T(0 : de), to the measurements of the collimated transmittance at a 0° incident angle, T(0 : 0), made with NIST RTS for a set of BK7-based neutral density filters with OD = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 1.0]. The error bars (coverage factor k = 2) are smaller than the symbols used for T(0 : 0) (uncertainty 0.5 %) and for most of T(0 : de); (b) T(0 : de) as a function of T(0 : 0) fitted with a linear model (largest rmse value = 5.90 × 10⁻⁴ at λ = 452 nm).

$R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ and $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ are measurable quantities using one integrating sphere with a beam incident at 0°. The measured values are traceable to reflectance and transmittance scales. Compared to our previous study [16], we modified our measurement routine following the measurements steps described in Fig. 2 and also the inversion algorithm we implemented to obtain μ_a and ${\mu }_s^{\prime }$.

3. Adding-doubling and modification of the inversion routine

Adding-doubling computes the total hemispherical reflectance and transmittance under a direct and a diffuse illumination using the incident angle θ, the thickness of the sample d, its index of refraction n, the anisotropy coefficient g and the optical parameters of the sample μ_a and μ_s as input parameters. It solves the RTE for samples with homogeneous optical properties, infinite plane-parallel slab geometry and smooth boundaries for a distribution of light independent of time and without considering polarization effects. The method gets its name from the fact that it uses a formal solution of the RTE for a thin layer of material in the single scattering approximation and computes the total reflectance and transmittance for a direct and a diffuse illumination by successively adding-doubling the values until the sample thickness is reached [31]. The inversion routine, either IAD or our previous work, computes an estimation of the measured reflectance R_Meas and transmittance T_Meas using the model of the spheres and the values of $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$, $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ and (i) $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ (measurements with one sphere) or (ii) $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ and $T_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ (measurements with two spheres) and further uses d, n, g, R_Meas and T_Meas as input parameters to estimate μ_a and ${\mu }_s^{\prime }$ by iteration.

The modified version of our inversion algorithm restricts the use of the output of the AD algorithm to $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ and $T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ since one only needs these two values to infer the two optical parameters μ_a and ${\mu }_s^{\prime }$. Hence

$$(R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}},T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}},d,n,g,\theta )\stackrel{\text{Inverse problem}}{\to }({\mu }_a,{\mu }_s^{\prime }).$$ (5)

From Eq. (3) and Eq. (4), the input parameters of the inversion routine are the measurement voltages ${\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$, ${\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Direct}}}$, ${\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$, ${\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}$, ${\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}$, ${\mathit{\text{VT}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$, ${\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}$, the reflectance standard R_StdRef, d, n, g and the incident angle θ.

One should note that in the case of the measurement of a specular sample at a 0° incident angle, $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ is not the total hemispherical reflectance since the Fresnel specular reflectance is rejected through the entrance port of the integrating sphere. This can be corrected by

$$R_{\mathit{\text{Sample}}}^{\mathit{\text{Total}},\mathit{\text{Direct}}}=R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}+R_{\mathit{\text{Fresnel}}}(n,\theta =0°).$$ (6)

In the case of smooth non specular samples, $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ is assumed to be equivalent to the total hemispherical reflectance needed by the inversion algorithm as an input even though the adding-doubling algorithm does not take the roughness of the interfaces into account.

As described in Ref. [16], we consider the uncertainty on the input parameters and the measured signals to compute the total uncertainty budget of (μ_a; ${\mu }_s^{\prime }$) by propagation of a Gaussian distribution of the input uncertainties. The type A uncertainty u_A and type B uncertainty u_B are estimated to produce the combined uncertainty u_C with $u_C^2=u_A^2+u_B^2$, following the Guide to the Estimation of Uncertainty in Measurement (GUM) [32]. The expanded uncertainty $U=k\sqrt{u_C^2}$ is estimated with a coverage factor k = 2.

4. Results

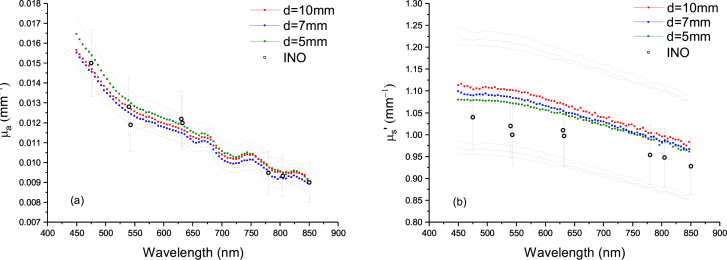
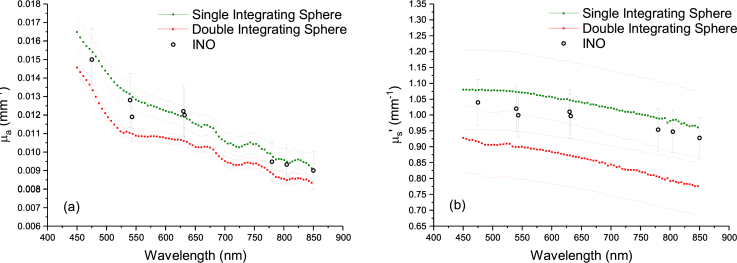
A NIST-traceable 99 % polytetrafluoroethylene (PTFE)-based reflectance standard R_StdRef = 0.99 ± 0.002 (k = 1) was used as a reference for the measurements. Figure 6 presents the measurements of μ_a and ${\mu }_s^{\prime }$ for the three B0430 samples from λ = 450 nm to 850 nm. The sample faces are smooth so no correction accounting for the Fresnel reflectance was considered in the analysis of the data. The values are compared to results by INO at λ = (475, 540, 543, 630, 632, 780, 805 and 850) nm on a 2 cm thick reference sample with smooth faces. INO uses a time-domain transmittance measurement [3] coupled to an analysis based on simulations using a modified version of the Monte Carlo modeling of light transport in Multi-Layered tissues (MCML) algorithm [33] that accounts for reflection by lateral boundaries. However, one should note that like MCML and AD their model does not take the roughness of the interfaces into account. INO does not provide an estimation of the uncertainties of their results so we used the uncertainty values computed for different samples at λ = 660 nm as presented in their reference paper (Ref. [3]). We also used their estimation of g = 0.621 ± 0.015 (k = 1) that was measured by non-scattered transmission of scattering-only thin wedges by retrieving the attenuation coefficient in the single scattering regime. With these considerations, our results for all three thicknesses are in good agreement with the ones from INO over the wavelength range (Fig. 6(a) and Fig. 6(b)). Typical uncertainty values for the integrating sphere instrument are about 4 % to 8 % on μ_a and about 12 % on ${\mu }_s^{\prime }$ compared to 11 % and 7 % for the INO results, respectively. The uniformity in the error bars is explained by the dominance of type B uncertainties. An example of uncertainty budget at λ = 632 nm for the 7 mm thick sample presented in Table 1 shows that n and g are dominant parameters for the uncertainties on μ_a and ${\mu }_s^{\prime }$. Table 2 presents our results and the ones obtained by INO at λ = [475, 540, 543, 630, 632, 780, 805, 850] nm. A comparison between the results obtained with our single integrating sphere setup, our previous double integrating sphere setup and the INO measurements is shown in Fig. 7 for one of the B0430 samples (nominal thickness t = 5 mm). The results for μ_a for both integrating sphere measurements techniques do not overlap for most wavelengths whereas there is an overlap over all wavelengths for ${\mu }_s^{\prime }$ (uncertainty at k = 2). The μ_a results from INO overlap with both integrating sphere measurements techniques due to higher uncertainty values. Less so for the ${\mu }_s^{\prime }$ results from INO that marginally overlap for higher wavelengths.

Fig. 6.

Measurements from λ = 450 nm to 850 nm of (a) the absorption coefficient μ_a and (b) the reduced scattering coefficient ${\mu }_s^{\prime }$ of the three the B0430 samples (nominal thicknesses t = 5 mm, 7 mm and 10 mm). Continuous lines are used to represent the upper and lower bounds of the uncertainties on the results by the single integrating sphere measurements. The results are compared to measurements by INO at λ = (475, 540, 543, 630, 632, 780, 805 and 850) nm (uncertainty at k = 2).

Table 1.

Uncertainty budget of the optical properties μ_a and ${\mu }_s^{\prime }$ of the B0430 sample (t = 6.95 mm) at λ = 632 nm. The standard deviation of the input experimental parameters is σ.

		Absolute uncertainties		Relative uncertainties
	σ	μa (mm−1)	${\mu }_s^{\prime }$ (mm−1)	μa(%)	${\mu }_s^{\prime }$(%)
Type B parameters
RStdRef	0.002	6.6 × 10−5	0.0034	0.58	0.33
d	0.02	9.3 × 10−5	0.0086	0.81	0.81
n	0.015	2.1 × 10−4	0.012	1.8	1.1
g	0.015	1.6 × 10−6	0.059	0.014	5.6
θ	0.0005	2.0 × 10−15	5.7 × 10−10	1.7 × 10−11	5.4 × 10−8
Total Type B uB		2.4 × 10−4	0.061	2.1	5.8
Repeatability		5.9 × 10−5	0.0033	0.51	0.31
Reproducibility sR		5.4 × 10−5	0.0028	0.47	0.27
Total type A uA		8.0 × 10−5	0.0043	0.69	0.41
Combined uc		2.5 × 10−4	0.061	2.2	5.8
Expanded U(k = 2)		5.0 × 10−4	0.12	4.4	12

Table 2.

Results and uncertainties (k = 2) of B0430, t = 6.95 mm: μ_a, the absorption coefficient of the sample; ${\mu }_s^{\prime }$ the reduced scattering coefficient of the sample. The uncertainties on the INO results were estimated from measurements made on different samples at λ = 600 nm as presented in Ref. [3].

λ(nm)	μa × 10−3 (mm−1)		${\mu }_s^{\prime }$ (mm−1)
	INO	NIST	INO	NIST
475	15.0 ± 1.7	14.6 ± 0.6	1.04 ± 0.07	1.09 ± 0.13
540	12.0 ± 1.5	12.5 ± 0.5	1.02 ± 0.07	1.09 ± 0.13
543	11.9 ± 1.3	12.5 ± 0.5	1.00 ± 0.07	1.08 ± 0.13
630	12.2 ± 1.4	11.5 ± 0.5	1.01 ± 0.07	1.06 ± 0.12
632	12.0 ± 1.4	11.5 ± 0.5	0.997 ± 0.070	1.05 ± 0.12
780	9.5 ± 1.1	9.5 ± 0.5	0.954 ± 0.067	1.00 ± 0.12
805	9.3 ± 1.1	9.2 ± 0.5	0.948 ± 0.066	0.98 ± 0.11
850	9.0 ± 1.0	8.9 ± 0.6	0.928 ± 0.065	0.97 ± 0.11

Fig. 7.

Measurements from λ = 450 nm to 850 nm of (a) the absorption coefficient μ_a and (b) the reduced scattering coefficient ${\mu }_s^{\prime }$ of a B0430 sample (nominal thickness t = 5 mm) using a single integrating sphere setup and a double integrating sphere setup [16]. Continuous lines are used to represent the upper and lower bounds of the uncertainties on the results. The results are compared to measurements by INO at λ = (475, 540, 543, 630, 632, 780, 805 and 850) nm (uncertainty at k = 2).

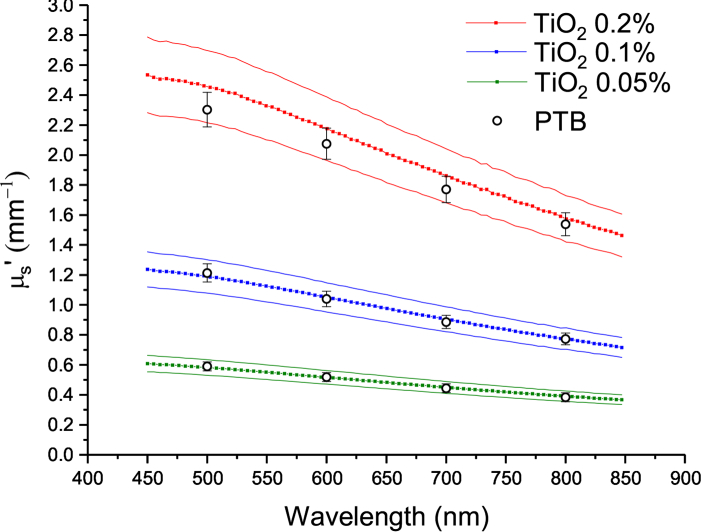
Figure 8 presents the measurements of ${\mu }_s^{\prime }$ for the three PDMS samples from λ = 450 nm to 850 nm. The faces of the samples are specular so the reflectance values were corrected for the Fresnel reflectance rejected through the entrance port of the sphere. The anisotropy factor g was set to 0.5 in the data analysis. The values of ${\mu }_s^{\prime }$ are compared to measurements on samples from the same batch at λ = (500, 600, 700 and 800) nm performed at PTB by means of time-resolved diffuse optical spectroscopy [34,35]. In this case the optical properties were derived from measurements of time-resolved diffuse transmittance and reflectance that were conducted independently using two systems based on fast detectors and time-correlated single photon counting. One system used a Ti:Sapphire laser, free-space optics and a microchannel plate photomultiplier. The second system employed a supercontinuum laser with acousto-optic filter, optical fibers to guide the light to and from the sample and a hybrid photodetector. The time resolution of these systems was about 35 ps and 125 ps, respectively. The fitting procedure for obtaining ${\mu }_s^{\prime }$ and μ_a was based on the Monte Carlo method for a slab-like turbid medium, with a database of photon time-of-flight distributions created for multiple ${\mu }_s^{\prime }$ values. The results presented here were obtained combining the data from both measurement systems. Instrumentation and analysis are described in more detail in Ref. [25]. It should be noted that the PDMS phantoms did not contain an added absorber and that μ_a was too small to be determined reliably. There is an agreement between both measurement techniques at the wavelengths of interest (Fig. 8). Table 3 presents the results by PTB and NIST results at λ = (500, 600, 700 and 800) nm.

Fig. 8.

Measurements and uncertainties (k = 2) from λ = 450 nm to 850 nm of the reduced scattering coefficient ${\mu }_s^{\prime }$ of three PDMS samples (TiO₂ concentrations 0.2 %, 0.1 % and 0.05 %). The results are compared to measurements by PTB at λ = (500, 600, 700 and 800) nm.

Table 3.

Results and uncertainties (k = 2) of the reduced scattering coefficient ${\mu }_s^{\prime }$ of the PDMS samples. The integrating sphere results are compared to time domain measurements by PTB.

λ (nm)		${\mu }_s^{\prime }$ (mm−1)
		PTB	NIST
TiO2 = 0.05%
	500	0.590 ± 0.030	0.582 ± 0.052
	600	0.518 ± 0.030	0.517 ± 0.045
	700	0.444 ± 0.030	0.449 ± 0.039
	800	0.384 ± 0.030	0.391 ± 0.035
TiO2 = 0.1%
	500	1.21 ± 0.06	1.19 ± 0.11
	600	1.04 ± 0.05	1.05 ± 0.10
	700	0.886 ± 0.044	0.904 ± 0.083
	800	0.773 ± 0.039	0.776 ± 0.071
TiO2 = 0.2%
	500	2.30 ± 0.12	2.46 ± 0.24
	600	2.07 ± 0.10	2.17 ± 0.21
	700	1.77 ± 0.09	1.86 ± 0.18
	800	1.54 ± 0.08	1.57 ± 0.15

5. Conclusion

We present the broadband measurements of the optical parameters of two types of tissue-mimicking solid phantoms, one polyurethane-based from INO and the other made at NIST using a PDMS base material. The optical parameters come with an uncertainty budget obtained by propagation of a Gaussian distribution of input uncertainties at each measurement wavelength. Our instrument measures the hemispherical reflectance and transmittance of the sample at a 0° incident by means of an integrating sphere and the substitution method. The data is analyzed using an inversion routine of the adding-doubling algorithm.

The non-validity of the IAD integrating sphere model is asserted by measuring the hemispherical reflectance under a diffuse illumination of a set of quasi-Lambertian reflectance standards and comparing the results to measurement made with the integrating sphere instrument of NIST STARR. We show that measuring the hemispherical reflectance and the hemispherical transmittance under a direct illumination (0° incident angle) is however possible with our setup. This is accomplished by measuring the same set of reflectance standards (reflectance under a direct illumination, comparison to results by NIST STARR facility) and a set of neutral density filters (transmittance under a direct illumination, comparison to results by NIST RTS). The measured reflectance are then traceable to reflectance and transmittance scales. We define our measurement procedure and restrict the use of the output of the adding-doubling algorithm to the hemispherical reflectance and transmittance under a direct illumination in our inversion routine. The optical properties of the measured sample are accompanied by an uncertainty budget.

A correction based on an independent measurement of the index of refraction is implemented to deal with the rejection of the Fresnel reflectance through the entrance port of the reflectance sphere while measuring specular samples. The optical parameters of the smooth and non specular samples are obtained with expanded uncertainties (k = 2) of about 5 % on μ_a and 12 % on ${\mu }_s^{\prime }$. They are compared to independent measurements by INO (k = 2 uncertainties: 12 % on μ_a, 7 % on ${\mu }_s^{\prime }$). The results for the PDMS samples show similar uncertainties and the ${\mu }_s^{\prime }$ values are compared to independent measurements by PTB (k = 2 uncertainties: 8 %).

Our future work plan toward the establishment of a reference scale is to develop an independent measurement of the anisotropy factor g and to define the range of optical properties values measurable by our system. A set of liquid phantoms with different concentration of intralipid and nigrosin are envisioned. A liquid cell has been fabricated for this purpose.

Appendix: IAD model of the integrating sphere

The mathematical description of this model can be found in Moffitt’s Ph.D. dissertation [18] and is further expanded here. The sphere has an entrance port (area A_e), a sample port (area A_s) and a detector port (area A_d). The area of the sphere wall is A and the fractional areas of interest are: $a_e=\frac{A_e}{A}$, $a_s=\frac{A_s}{A}$ and $a_d=\frac{A_d}{A}$. For a single sphere, the reflected optical power is

$$P(R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}},R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})=a_d(1-a_e)r_w[(1-f)R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}+f{r}_w]\mathit{\text{PG}}(R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}),$$ (A1)

with the sphere gain

$$G(R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})=\frac{1}{A_1+B_1{R}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}},$$ (A2)

where A₁ = 1 − a_wr_w − (1 − a_e)r_wa_dr_d, B₁ = (1 − a_e)r_wa_s, P is the incident optical power, r_w is the reflectance of the sphere wall, r_d is the reflectance of the detector, f = 0 for a direct incident illumination and f = 1 for a diffuse incident illumination.

Under a diffuse illumination, i.e. with the incident beam directed toward the sphere wall, two measurements can be made: (i) with the sample port blocked by a reference standard R_StdRef and (ii) with the sample set at the sample port of the sphere. The ratio of the reflected optical powers is

$$\begin{array}{lll}\frac{P(0,R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})}{P(0,R_{\mathit{\text{StdRef}}})}& =& \frac{G(R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})}{G(R_{\mathit{\text{StdRef}}})}\\ & =& \frac{A_1+B_1{R}_{\mathit{\text{StdRef}}}}{A_1+B_1{R}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}.\end{array}$$ (A3)

The measured voltages ${\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ and ${\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}$ are proportional to the optical powers P(0, $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$) and P(0, R_StdRef), respectively. With an additional measurement of ${\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}$ were no sample is set at the sample port of the sphere $\frac{{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}}$,

$$\frac{{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}}=\frac{A_1+B_1{R}_{\mathit{\text{StdRef}}}}{A_1}.$$ (A4)

Combining Eq.(A3) and Eq.(A4) and solving for $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ gives

$$R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}=R_{\mathit{\text{StdRef}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}({\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}-{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}})}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}({\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}-{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}})},$$ (A5)

which defines the diffuse hemispherical reflectance under a diffuse illumination from measurable quantities under the IAD model of the integrating sphere (see Fig. 2(a)).

Under a direct illumination, i.e. with the incident beam directed toward the sample, two measurements can be made: (i) with the sample set at the sample port of the sphere and (ii) with the sample port blocked by a reference standard R_StdRef (see Fig. 2(b)). The optical power is then proportional to the reflectance of the sample $R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}$ times the sphere gain $G(R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})$ for case(i) (R_StdRef times $G(R_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}})$ for case (ii)). Forming the ratio of the reflected optical powers, the proportionality factor cancels out and we have

$$\begin{array}{lll}\frac{P(R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}},R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})}{P(R_{\mathit{\text{StdRef}}},R_{\mathit{\text{StdRef}}})}& =& \frac{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}}{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Direct}}}}\\ & =& \frac{R_{\mathit{\text{Sample}}}^{\mathit{\text{direct}}}}{R_{\mathit{\text{StdRef}}}}\frac{G(R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})}{G(R_{\mathit{\text{StdRef}}})},\end{array}$$ (A6)

where the ratio of sphere gains is obtained as a ratio of voltages from the measurement of $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$, $\frac{G(R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})}{G(R_{\mathit{\text{StdRef}}})}=\frac{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}}$. So

$$R_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}=R_{\mathit{\text{StdRef}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}}{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Direct}}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{StdRef}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}},$$ (A7)

For a single sphere, the measurement of the transmittance under a direct illumination requires to rotate the sphere 180° around a vertical axis perpendicular to the plane of the optical bench, as compared to the previous experimental situation. The transmitted optical power is

$$P(T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}},R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})=a_d(1-a_e)r_w{T}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}\mathit{\text{PG}}(R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}).$$ (A8)

In that situation, two measurements can be made: (i) with an empty sample port, i.e. unit transmittance and (ii) with the sample set at the sample port of the sphere. Forming the ratio of the optical powers, the proportionality factor cancels out and

$$\begin{array}{lll}\frac{P(T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}},R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})}{P(1,0)}& =& \frac{{\mathit{\text{VT}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}}{{\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Direct}}}}\\ & =& T_{\mathit{\text{Sample}}}^{\mathit{\text{direct}}}\frac{G(R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})}{G(0)},\end{array}$$ (A9)

where $\frac{G(R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}})}{G(0)}=\frac{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}}$ (the exit port of the sphere is open so that the sphere gain does not change compared to the $R_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}$ measurement situation). So

$$T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}=\frac{{\mathit{\text{VT}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}}{{\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Direct}}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}.$$ (A10)

But ${\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Direct}}}$ is not measurable since the beam exits through the exit port of the sphere. It is then assumed that the signal for a unit transmittance is equivalent to the measured signal for an empty sample port when the beam hits the sphere wall. This experimental situation is obtained by tilting the sphere as shown in Fig. 2(c). Then ${\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Direct}}}={\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}$

$$T_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}=\frac{{\mathit{\text{VT}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Direct}}}}{{\mathit{\text{VT}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}}\frac{{\mathit{\text{VR}}}_{\mathit{\text{Empty}}}^{\mathit{\text{Diffuse}}}}{{\mathit{\text{VR}}}_{\mathit{\text{Sample}}}^{\mathit{\text{Diffuse}}}}.$$ (A11)

Disclosures

The authors declare that there are no conflicts of interest related to this article.