Quantitative observations on cytoskeleton changes of osteocytes at different cell parts using digital holographic microscopy

Abstract

Cytoskeletons such as F-actin have different distributions in different cell parts and they are the cause of different degrees of cell collapse when the F-actin is disrupted. It is challenging to use conventional methods such as fluorescence microscopy and atomic force microscopy to conduct real-time and three-dimensional observations on the dynamic processes at different cell parts due to the slow measuring speed and the need for live-cell staining. In this study, the morphological variations of different bone cell parts caused by F-actin disruption are dynamically measured by using digital holographic microscopy (DHM). We separately analyze local parameters (cell height and cell width) and global parameters (cell projected area and cell volume) of cells to address variations of specific cell areas and quantify the changing process of the whole cell. We found significant differences in temporal variations of both local and global cell parameters between the cell body and cell process, which is consistent with the qualitative observation by fluorescence staining. Our study not only validates the unique ability of DHM to simultaneously investigate the dynamic process at different cell parts, but also provides sufficient experimental bases for exploring the mechanism for F-actin disruption.

1. Introduction

Bone loss and osteoporosis are health-related issues, especially for the elderly and astronauts who have experienced extended stays in space [1–4]. Researchers have confirmed that bone loss is closely related to the cytoskeleton disruption of osteocytes [5,6]. As the load-bearing structure of osteocytes, the cytoskeleton plays an important role in the mechanotransduction process in the bone cell. A better understanding of the cytoskeleton-related force transmission from the membrane to the nucleus of the bone cell is important for the prevention and treatment of bone loss. In recent years, researchers have carried out much work to explore the mechanism of bone loss related to the cytoskeleton [7,8].

Nevertheless, the intrinsic mechanisms of the cytoskeleton-related force transmission from the membrane to the nucleus of bone cells are not well understood. One reason is that measurements of time-varying cellular changes during the cytoskeleton disruption of bone cells are challenging because of rapid and subtle changes in the related processes. The mechanosensitivity of osteocytes is often thought to develop accompanied by the F-actin reorganization during cell differentiation [9]. Furthermore, the F-actin cytoskeleton is found to display different distributions between the cell body and the rich cytoplasmic projections of the bone cell [10,11], which are also called the cell process. In a model developed by Han et al. [12], the different organization of F-actin in the cell process and cell body was thought to be responsible for the different mechanosensitivity of different cell parts. Correspondingly, the disruption of F-actin is often accompanied by a decrease in the mechanosensitivity of bone cells. In such situation, a better knowledge of the dynamic process during F-actin disrupting, especially the different processes happened in the cell process and cell body, will provide considerable help to investigate the intrinsic mechanisms of the cytoskeleton-related force transmission.

Much work has been done to explore these dynamic changes and the different processes in cell body and cell process. Rotsch et al. observed the drug-induced changes of cytoskeletal structure and mechanics according to the results from an atomic force microscope (AFM) [13]. Charras et al. observed the morphological changes of stained osteocytes by fluorescence microscopy (FM) and analyzed the mechanotransduction based on the AFM-observed images [14]. Kelly et al. measured the elasticity and morphology changes of bone cells during the cell cycle with an AFM and a confocal microscopy (CM) [15]. Kronlage et al. analyzed qualitatively the dynamic changes in the mechanical structure of bone cells using an AFM [16]. However, these researches failed to retrieve the dynamic process of cells changing due to the inability of these mentioned microscopes to provide dynamic quantitative three-dimensional measurements of the cell changes. Specifically, the FM can only provide the qualitative observation on the cytoskeleton. The AFM and CM need to scan the sample for obtaining morphological information, and are unable to catch the dynamic change of cytoskeletons. As such, the morphological changes of cytoskeletons at the cell body and cell process have not yet been dynamically observed and quantitatively studied. The different distributions between cell body and cell process poses a significant challenge to conventional methods such as the FM, AFM or CM, not to mention their subtle time-varying changes.

The quantitative phase-contrast microscopy provides an optimal method to carry out the measurements on the cellular morphological changing process. Here, we utilize a digital holographic microscopy (DHM) to perform quantitative measurements on the cytoskeleton-induced morphological changes of osteocytes for both the cell process and cell body. As an innovative quantitative phase-imaging approach [17–20], DHM is capable of recording the phase distributions of samples with just a single exposure, making it an ideal method to record dynamic processes, especially for living cells [21–25]. In recent years, there have been many attempts to apply DHM to biomedical research [26–31], and ways to improve the accuracy of the phase measurement for DHM are also fully analyzed and well studied [32–34]. Besides, owing to its robustness in long-term imaging, DHM has been validated for some special cases involving quantitative real-time measurements, such as micro-gravity environments [35,36] and below-zero environments [37]. DHM has also been shown to be capable of recording the dynamic process during special treatments on biomedical samples, e.g., the electroporation procedure [38] and photodynamic treatment [39] on cells.

In this study, we focus on quantitative measurement of the different dynamic morphological changes of MLO-Y4 cells between cell processes and cell bodies, which are caused mainly by F-actin disruption. Real-time monitoring of the osteocytes was achieved using an off-axis Mach-Zehnder DHM setup. We utilized Cytochalasin B and Jasplakinolide to disrupt and polymerize the F-actin as two counterproductive experimental groups, and in the control group, cells were treated under the same conditions but without any additional reagent. Local parameters, namely the cell height and cell width, were calculated and analyzed separately and synchronously at cell processes and cell bodies. We also compared the temporal variations of global parameters (cell projected area and cell volume) in experimental groups with the control group. A statistical analysis of the phase-based images was performed, and the results suggested that the change tendency and change rate of these local cell parameters were significantly different for cell processes and cell bodies. To our knowledge, this is the first time implementing both the real-time monitoring on the three-dimensional morphological changes of cytoskeletons induced by F-actin disruption and polymerization, and the quantitative analyzation on the different changing trends between the cell body and cell process. These results are consistent with those from qualitative observation by fluorescence staining. Supposed reasons for the results are discussed in section 4. Based on the results of our study, we described a “tent-like” structural model to better explain the mechanisms of the cytoskeleton-related force transmission from the membrane to the nucleus of bone cells.

2. Materials and methods

2.1 Cell culture and drug treatments

The MLO-Y4 cell osteocyte line was kindly provided by Prof. Lianwen Sun of Beihang University in Beijing, China. The cells were maintained in an alpha minimum essential medium (α-MEM) (Gibco, USA) supplemented with 2.5% (vol/vol) fetal bovine serum (FBS) (HyClone, South America) and 2.5% (vol/vol) calf serum (CS) (HyClone, New Zealand) on a culture flask (Nunc, Roskilde, Denmark) pre-coated with rat tail type I collagen (0.15 mg/Ml, Millipore, USA) at 37°C, 5% CO₂. Cells were passaged on a glass-bottom culture dish (NEST Biotechnology, China) at 80% confluency. Cytochalasin B (CB, Sigma-Aldrich, MO, USA) was used to depolymerize the F-actin. Jasplakinolide (Jas, ThermoFisher Scientific, USA) was used to induce actin polymerization. CB and JAS were both dissolved in DMSO as a stock solution and diluted to 20 μM and 200 nM for cell treatment. The cell viability after drug treatment was determined by MTT assays, and a DMSO control group was set.

2.2 Immunofluorescence

The F-actin of MLO-Y4 osteocytes was immunofluorescence-stained to enable the visualization of the microfilament cytoskeleton. After the CB/JAS treatments, the MLO-Y4 cells were briefly washed with PBS three times, and fixed with 4% paraformaldehyde for 20 min. Phalloidin-rhodamine (Invitrogen, USA) was used to label the F-actin (1:500 solution for 1 h), and 4',6-diamidino-2-phenylindole (DAPI, 1:1000) (Invitrogen, USA) was used to label the nucleus (1:1000 solution for 5 min). For the observation, we used a laser scanning confocal microscope (Leica Microsystems, Wetzlar, Germany).

2.3 DHM setup and experimental procedure

2.3.1 DHM setup

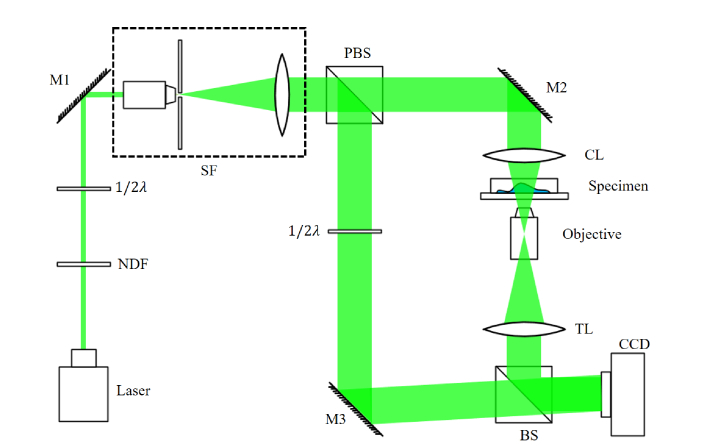
Figure 1 depicts the details of the transmission DHM utilized in this study, which is based on an off-axis Mach-Zehnder configuration. The light source was a 532 nm laser (Cobolt, Sweden) with an output power of 100 mW, and a neutral density filter (NDF) was used to control the light power transmitted through the cells. After propagating through the spatial filter (SF), the expanded laser beam was split into an object beam and reference beam by a polarizing beamsplitter (PBS). A half-wave plate (λ/2) was placed in conjunction with the PBS to adjust the intensity ratio of the object beam and reference beam. The object beam transmitted through the specimen after converged by the condenser lens (CL). An objective (Olympus UPLFLN, 20x, NA = 0.50) combined with a tube lens (TL) was used to obtain an optimal imaging resolution of 1.06 μm. In the reference beam, another half-wave plate was used to adjust the polarization direction of the reference beam, ensuring a high-fringe contrast. Then, the reference beam, which had a slight off-axis angle with the object beam, interfered with the object beam through a beam splitter (BS), and the holograms were recorded by a CCD camera (1920 × 1200 pixels, 5.86 μm, PointGrey, Canada). In this study, two holograms were obtained per second for 20 min in each experimental group, with an image size of 1024 × 1024 pixels.

Fig. 1.

Schematic of DHM system setup. NDF: neutral density filter; 1/2 : half-wave plate; M1-M3: mirrors; SF: spatial filter; BS: beamsplitter; PBS: polarizing beamsplitter; CL: condense lens; TL: tube lens.

Once the digital holograms were acquired, a series of necessary processes were conducted to the holograms before numerical reconstruction. The hologram apodization was firstly performed by multiplying the hologram with a two-dimensional window function [40] to avoid unwanted diffraction ripples on the wave front due to the non-infinite nature of the camera chip. Then, the spatial filtering was applied to remove the high-intensity zero order and the twin object image by computing the Fourier transform of the hologram [41]. Next, the tilt aberration due to the off-axis configure was compensated in the hologram plane by using the method of Numerical Parametric Lens (NPL) [42]. Finally, the angular spectrum reconstruction algorithm was employed to retrieve the complex amplitude of object wave with the reconstruction distance of 3.4 cm for all the experiments groups. Meanwhile, the approach of numerical aberration compensation was reused to compensate the phase aberrations of high order polynomials induced by the optical system, in particular by the MO [43,44].

After that, an offset procedure was applied to the reconstructed phase images, which made sure that the average of the background phase value was zero. In detail, for every experiment group, a background region was firstly chosen and the average phase value within the region was calculated, then the offset phase maps were obtained by subtracting the average value from all phase maps. Note that in the same experiment group, the background region to calculate the average value would be the same. Meanwhile, the background region would be re-chosen when the cell group changed. Thus, the offset phase maps were ready for the calculation of the cell parameters described in detail in section 2.5.

To assess the temporal stability of the DHM setup, a set of blank phases was recorded for 20 min with a frame rate of 2 fps. The standard deviation of the temporal optical path delay (OPD) fluctuation was calculated, and within a region of 3 × 3 pixels, it was 9.7 nm. This temporal stability is far less than the micron-scale cell morphological changes, and ensures a sufficient sensitivity of the DHM setup to detect the micron-scale cellular morphological changes.

2.3.2 Experimental procedure

In this study, we investigated three groups of cells: a control group with no drug (CON), a CB group with Cytochalasin B (CB), and a JAS group with Jasplakinolide (JAS), respectively. For the CB and JAS groups, the holographic recording of cells started immediately when the CB and JAS were added to the culture dish, and a 20-min continuous recording was implemented with a CCD frame rate of 2 fps in one experiment. The control group was subject to the same environmental conditions and frame rate without any drug. To reduce the potential effects of the DHM setup and environmental disturbances, we separately performed five experiments for each group, and the cells to be analyzed were randomly selected in these five sets of phase images.

2.4 Calculation of cell refractive index

For transmission DHM, the real cell height is calculated from the phase shift, which is coupled with the refractive index (RI) of the cell. Equation (1) exhibits the relationship between the real cell height at pixel $(x,y)$ and the phase shift coupled with the RI.

$$h\left(x,y\right)=\frac{\lambda }{2\pi }\times \frac{\Delta \phi \left(x,y\right)}{n\left(x,y\right)-{\overline{n}}_{medium}}.$$ (1)

In Eq. (1), $h(x,y)$ denotes the real cell height at pixel $(x,y)$, λ is the wavelength of the light source, $\Delta \phi \left(x,y\right)$ is the phase shift at pixel $(x,y)$, $n(x,y)$ is the RI correlated to the pixel $(x,y)$, and ${\overline{n}}_{medium}$ is the RI of the medium. It is obvious that without a priori knowledge of the RI, it is difficult to calculate the correlated real cell height from the phase map.

To solve this problem, we applied a decoupling procedure designed for DHM for calculating the RI of cell. Details of the decoupling procedure were presented in [45]. In summary, the cell phase maps were sequentially measured in two isosmotic solutions with different refractive indices. In this study, the RI of the solutions was measured by an Abbe refractometer at the wavelength of 532 nm. The RI of the standard perfused medium was$n_m=1.3401\pm 0.0002$ and RI of the mixed medium, which was produced by adding 400 mM Iohexol with a mass-to-volume ratio of 12.5% to the standard perfused medium, was$n_m^{\text{'}}=1.3584\pm 0.0002$. The first hologram was recorded for the cells in the standard perfused medium. Then the solution was immediately replaced by the mixed medium, which was full of the perfusion chamber as same as the standard perfused medium. Subsequently, the second hologram was recorded with the same field of view. Then the RI of cells and height of cells at the pixel can be calculated separately by solving the following equations

$$h\left(x,y\right)=\frac{\lambda }{2\pi }\times \frac{\Delta \phi {}_1\left(x,y\right)}{n\left(x,y\right)-{\overline{n}}_m}$$ (2)

$$h\left(x,y\right)=\frac{\lambda }{2\pi }\times \frac{\Delta \phi {}_2\left(x,y\right)}{n\left(x,y\right)-{\overline{n}}_m^{\text{'}}}.$$ (3)

In the above equations, $n(x,y)$ is the mean value of the intracellular RI along the cellular thickness at the pixel$(x,y)$. By averaging all the $n(x,y)$within a cell, the intracellular RI of the whole cell $n_{cell}$ was finally obtained.

We carried out the decoupling procedure five times to improve the measurement accuracy, and then we acquired an averaged RI of$n_{cell}=1.3720\pm 0.0020$. In addition, the differences in the RI between different cell parts are negligible according to [46,47]. Besides, the differences of RI between the medium and the cells are among 0.0339 ~0.0299. It is one order of magnitude more than the standard deviation of mean cellular RI 0.002. In such situation, the mean value can be used to represent the RI of whole cell. Therefore we utilized the mean RI of all the pixels within a cell to calculate the real height of the cell, and the range of cell heights obtained was 1.48~6.89 μm.

Actually, this study mainly focused on the different changing progress of cell parameters between different cell parts. Since we took the cellular RI as a constant for the observed cells, the change trends and rates of cell height and height-related cell parameters are proportional to the phase change.

2.5 Computations of local and global cell parameters

To quantitatively measure the morphological changes of MLO-Y4 cells induced by F-actin depolymerization at different cell parts, we calculated temporal variations of four parameters from phase images obtained from the 20-min measurements: cell height, cell width, cell projected area and cell volume. The first two, i.e., the cell height and cell width, were defined as local parameters that are used to address variations of specific areas of the cell, namely the cell process and cell body. Meanwhile, the latter two, i.e., the cell projected area and cell volume, were global parameters to quantify the changing process of the whole cell.

2.5.1 Local parameters: cell height and cell width

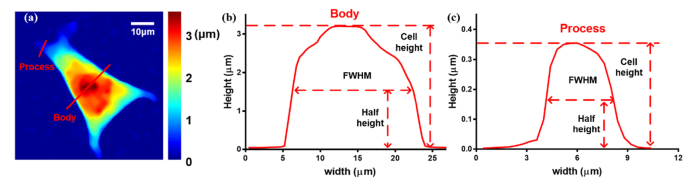
The cell height and cell width were extracted from the cell profile along the lines drawn across the cell, as shown in Fig. 2. These two parameters were defined as the maximum value and the full width at half maximum (FWHM) of the cell height profile along the line, respectively. In this study, we take FWHM as the cell width for convenient calculation and defined it as “cell width”. With the imaging resolution calibrated by a USAF 1951 resolution chart, the real size of the FWHM was computed simply by multiplying the real size of one pixel, which was 0.291μm, by the pixel numbers of the line related to the half-height (as seen in Figs. 2(b) and 2(c)). The lines were drawn across specific areas of the cell, which were mainly located at the cell process and cell body, as shown in Fig. 2(a). In cell body, the line was always selected across the maximum phase value. In cell process, the line was usually chosen in the middle at the obvious cell projections. Once a line was chosen, the profile at the line and the variation in the cell height and cell width at the line during the entire experimental period were automatically calculated using MATLAB code. In details, as the backgrounds of phase images were already offset to about zero (described in section 2.3.1), the cell heights were simply determined by the maximum phase value along the chosen line and were quantitatively calculated by Eq. (1). Once the maximum value along the line was fixed, the two points in the chosen line which correlated to the half maximum phase value can be given. Then the FWHM was calculated by multiplying the pixels numbers between these two points and the real size of one pixel.

Fig. 2.

Calculation of cell height and cell width at different cell parts: (a) cell height map; (b) cell body profile at the long red line; (c) cell process profile at the short red line.

2.5.2 Global parameters: cell projected area and cell volume

The cell projected area and cell volume are parameters that reflect both the transverse and three-dimensional (3D) morphology of the cell. Before calculating these two parameters, an automatic cell-edge detection procedure was conducted to determine the cell profile. Thereafter, the sum of the pixel areas within the cell profile was defined as the projected area of the cell, and the cell volume was equal to the product of the projected area and the mean height of the cell profile. The auto-detection procedure for the cell edge was realized using MATLAB codes, and is fully described in [48].

It is especially noteworthy that our method is different with some already-made ways to evaluate the cell volume, such as by summing the volumes above all of the pixels in the cell area [49]. By using our method, the cell volume is calculated by multiplying the average cell height with the cell area. It can reduce the influences by the unwanted and inevitable phase noises, such as floating particles in the medium, and particularly suitable for analysis of the change trends and change rates of cell volume.

3. Experiment results

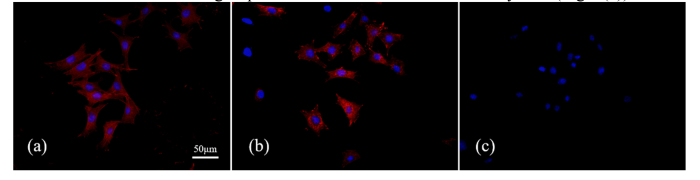
The structural changes of F-actin observed by immunofluorescence-staining are shown in Fig. 3. It can be seen that the F-actin was organized into strong fibers through the MLO-Y4 osteocytes in the CON group (Fig. 3(a)). After the 20-min treatment of the CB group, the filamentous structure was lost, and intense staining spots can be observed on the edge of MLO-Y4 osteocytes (Fig. 3(b)). In the JAS group, no Rhodamine staining of F-actin was observed because the binding of phalloidin to F-actin was inhibited by JAS (Fig. 3(c)).

Fig. 3.

The structural changes of F-actin by immunofluorescence-staining, 20 min after treatment: (a) CON group with no drug, (b) CB group, and (c) JAS group.

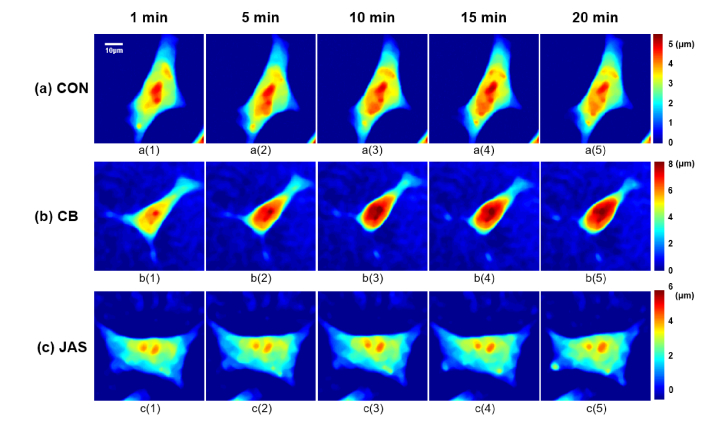
A movie in Visualization 1 ^{(2.9MB, mp4)} displays the phase maps of MLO-Y4 cells in the three groups obtained by DHM for 20 min and Fig. 4 demonstrates five frames of them, separately showing the phase map at the 1st, 5th, 10th, 15th, and 20th minute in the movie. In Fig. 4, there were significant changes for the CB group both in the cell process and in the cell body, while in the CON and JAS groups, variations in the cells were inconspicuous. For the JAS group, it should be noted that F-actin polymerization in the cell process was found 10 min after treatment (seen in Fig. 4 c(4) and Fig. 4 c(5)), while in the other two groups, no distinct F-actin aggregation could be observed.

Fig. 4.

Holographic phase images at the 1st, 5th, 10th, 15th, and 20th minute over a 20-min period measurement for a(1)–a(5): cells in CON group, b(1)–b(5): cells in CB group, and c(1)–c(5): cells in JAS group.

3.1 Variations in cell height and cell width

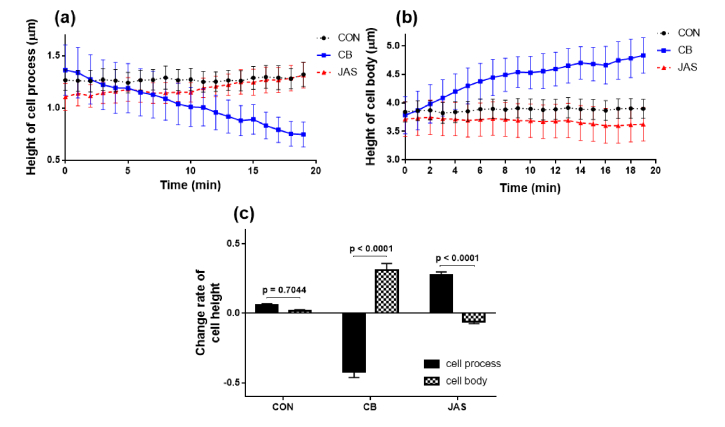
Figures 5(a) and 5(b) separately show curves of the different variations in the cell heights of the cell process and cell body after 20 min in the three groups. To investigate the changing process quantitatively, the change rates between the average heights at the first minute and the last minute were calculated, and they are demonstrated in Fig. 5(c). The p values of the change rates for the cell process and cell body are also shown in Fig. 5(c), and comparisons of the p values obtained for the three groups are listed in Table 1.

Fig. 5.

Temporal variations of average cell height at (a) cell process and (b) cell body. Black dashed lines with dots represent the CON group, blue solid lines with squares represent the CB group, and red dashed lines with triangles represent the JAS group. (c): change rates of cell height in the three groups.

Table 1. Comparison of p Values of Cell-height Change Rates for the Three Groups.

	CON vs. CB	CON vs. JAS	CB vs. JAS
Cell process	<0.0001 (Y)	0.1385 (N)	0.0008 (Y)
Cell body	<0.0001 (Y)	0.7202 (N)	<0.0001 (Y)

As seen in Fig. 5, the heights of the cell process and cell body in the CON group, which are represented by black dashed lines with dots in Figs. 5(a) and 5(b), showed the same varying tendency to become slightly larger, and they are nearly unchanged with increasing rates of 3.87% and 1.65%. However, the cell heights in the CB group (blue solid lines with squares in Figs. 5(a) and 5(b)) and JAS group (red dash line with triangles in Figs. 5(a) and 5(b)) exhibit completely different trends at the cell process and cell body. In the CB group, the heights of the cell process significantly reduced by 43.17% but the cell body heights meaningfully increased by 31.11% (p < 0.0001). However, in the JAS group, there was an increase of 27.91% for the cell process heights, but the heights of the cell body showed a downward trend of 2.01% (p < 0.0001). For the cell height, the CB group always displayed a statistical difference with the CON group and JAS, whether at the cell process or the cell body, and the p values between the three groups are shown in Table 1. It should be noted that the tendencies between the CB group and JAS group were also significantly opposite, as the heights of the cell process decreased in the CB group but increased in the JAS group (p = 0.0008), while the heights of the cell body increased in the CB group but decreased in the JAS group (p < 0.0001). The results indicated that the distributions of F-actin are different for cell processes and cell bodies, and these different distributions played opposite roles during the cell collapse, resulting in an inverse height-variation trend between the two cell parts.

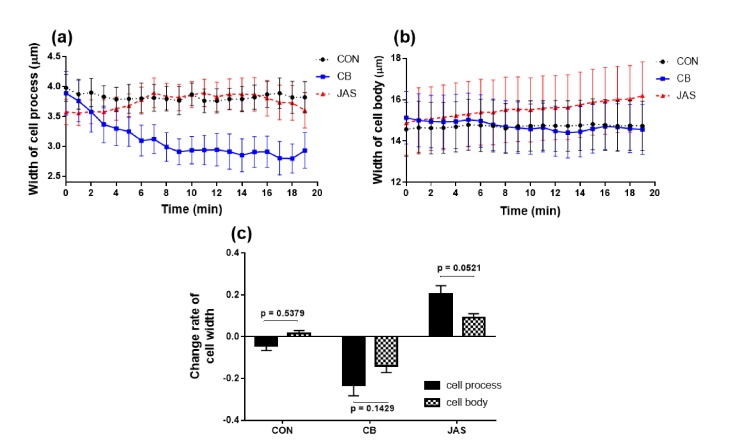
Figure 6 shows the variations of the cell widths for both cell processes and cell bodies in the three groups. The temporal changing curves in Figs. 6(a) and 6(b) indicated that the cell widths in the CB group at the cell process significantly decreased (as shown in Table 2, p = 0.0411 versus the CON group and p = 0.0047 versus the JAS group). Meanwhile, the cell widths for the cell process and cell body in the other groups displayed a relatively smaller variation for the entire time.

Fig. 6.

Temporal variations of average cell width at (a) cell process and (b) cell body. Black dashed lines with dots represent the CON group, blue solid lines with squares represent the CB group, and red dashed line with triangles represent the JAS group. (c): change rates of cell width in the three groups.

Table 2. Comparison of p Values of Cell-width Change Rates for the Three Groups.

	CON vs. CB	CON vs. JAS	CB vs. JAS
Cell process	0.0411 (Y)	0.5735 (N)	0.0047 (Y)
Cell body	0.6446 (N)	0.2399 (N)	0.0469 (Y)

The change rates of the cell widths for the three groups are presented in Fig. 6(c). The cell width in the CB group still has a significant reduction of 23.18% at the cell process, while at the cell body, it still decreased, but at a much lower rate of 2.98%. Besides, the cell widths of the cell body for the CB and JAS groups also displayed a statistically significant difference, but the cell widths in the JAS group showed no difference from the CON group for both the cell process and cell body.

3.2 Variation in cell projected area and cell volume

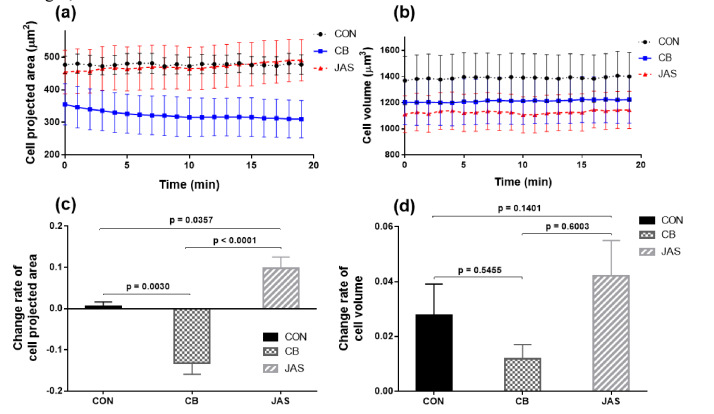
As opposed to the cell height and cell width, which were calculated using data from specific parts of cells, the cell projected area, and cell volume are parameters that are used to investigate variations of the whole cell. Ten cells in each group were randomly selected, and the averages of cell projected areas and cell volumes were calculated according to the method described in section 2.5.2. The temporal variations in these two parameters over 20 min are depicted in Figs. 7(a) and 7(b), and the change rate with the p values for the cell process and cell body are shown in Figs. 7(c) and 7(d). To better display the change process of the global parameters, a quasi 3D exhibition of temporal morphological evolutions of three cells in the three groups and temporal change progresses of their global parameters are shown in Visualization 2 ^{(2.7MB, mp4)} . The scale bars in Visualization 2 ^{(2.7MB, mp4)} are the same as Fig. 4.

Fig. 7.

Temporal variations of (a) cell projected area and (b) cell volume over 20 min. Black dashed lines with dots represent the CON group, blue solid lines with squares represent the CB group, and red dashed line with triangles represent the JAS group. (c): change rates of cell projected area and (d): change rates of cell volume in the three groups.

We observe that the control group remains nearly unchanged in the cell projected area for the whole 20 min. However, the cell projected areas in the CB and JAS groups displayed completely opposite trends. As can be seen in Fig. 7(c), the cell projected area in the CB group showed a decreasing trend of 12.40% during the entire period, while in the JAS group, the tendency was to increase by 9.02%. The p values of the cell projected area change rate for the three groups were all less than 0.05, indicating that the varying trends in all three groups were statistically significant.

The time-dependent variations of the cell volume and change rates in the three groups are shown in Figs. 7(b) and 7(d). The plots display almost unchanged trends in all three groups, which is completely different from the variation trends for other cell parameters. Noticeably, the p values of the cell volume between the three groups were all above 0.05, indicating that there were insignificant differences in the change rates of the cell volume. This was assumed to be because the cells in all three groups had few penetrations during the experimental period. The varying trends of the cell volume indicated that in terms of cellular morphological changes, variations in the F-actin distribution have little effect on the cell volume.

4. Discussion

In the present study, DHM was used to track the 3D morphological changes of osteocytes caused by F-actin polymerization and depolymerization. Several morphological parameters of MLO-Y4 osteocytes were quantified, and obvious changes in both cell body and cell process were observed. Specifically, the cell process was thinner while the cell body was swollen after the disruption of F-actin. It is known that the cell process of osteocyte is unique actin-rich [10] and the F-actin in the cell process is more organized than the F-actin in the cell body [50]. When disrupted by CB, there would be less support from the F-actin, resulting in a rapid collapse of the cell process. On the other hand, the MLO-Y4 osteocytes, which are a kind of adherent cell, are attached to the extracellular environment via a focal adhesion (FA) complex at the terminal ends of the F-actin fibers. There is a structural model to help understand the mechanism of the force transmission. A bone cell can be seen as a tent, and the FA complex is similar to the screw or welding spots of a tent. Meanwhile, the F-actin fibers are similar to the beams of the tent, and function as the tensile element of the cell. When the F-actin is disrupted, the FA-actin complex is also destroyed. It is like that the tent will collapse if the screws are broken. The FA was detached from the substrate, resulting in the contraction of MLO-Y4 osteocytes. JAS was used to increase the F-actin polymerization of MLO-Y4 osteocytes. The cell process became thicker and the projected area was expanded. It is notable that the cell adhesion formation was observed at the same time (Fig. 4c(1)-c(5)), which indicates a spread and migration of the MLO-Y4 osteocytes.

Researchers have previously demonstrated that the cell process of osteocytes is more mechanosensitive than the cell body, and the role of F-actin has been highlighted [51]. In this study, our results demonstrate that the cell process shows a more rapid and sensitive response to F-actin modification than the cell body, which indicates that a greater contribution is made by the F-actin of the cell process to sustain the tensegrity of MLO-Y4 osteocytes. Furthermore, with the reduction in the tension of the cell process, the mechanotransduction of osteocytes will also be affected. This may explain the dependence of the cell mechanosensitivity on the intact cytoskeleton [52]. These results could hardly be obtained by using the conventional microscopes, such as the FM or AFM.

However, we also focused on the real-time changes in the MLO-Y4 osteocyte, and some deductions can be made. With respect to the height of the cell process, the treatment of CB resulted in a continuous effect over 20 min, while for the height of the cell body and the width of the cell process, the effect was more obvious in the first 10 min, and then gradually became constant. In comparison, the effect of JAS was relatively constant for 20 min. These results may be useful in the time-point determination of chemical treatment on cells.

5. Conclusion

In this paper, the dynamic morphological changing process of osteocytes induced by F-actin depolymerization and reconstruction are integrally measured by DHM. The changing trends of morphological parameters after F-actin disruption are fully analyzed. Both specific cell parts, namely cell process and cell body, and the entire cell are investigated through the high-accuracy phase measurement provided by DHM. According to our results, F-actin distributions are significantly different between the cell body and cell process, which lead to the different dynamic changing processes on cell morphological parameters after F-actin disruption. These differences play an important role in the force transmission from the membrane to the nucleus of bone cells. Our study provides both a better understanding of these different dynamic processes and credible materials for a further study on the intrinsic mechanisms of the cytoskeleton-related force transmission from the membrane to the nucleus of bone cells.

Funding

The National Major Scientific Instruments Development Project of China (Grant No.2013YQ030595); National Natural Science Foundation of China (NSFC) (No. 11472033).

Disclosures

The authors declare that there are no conflicts of interest related to this article.