Abstract
Combining the ability to localize electromagnetic fields at the nanoscale with a directional response, plasmonic antennas offer an effective strategy to shape the far-field pattern of coupled emitters. Here, we introduce a family of directional multiresonant antennas that allows for polarization-resolved spectral identification of fluorescent emission. The geometry consists of a central aperture surrounded by concentric polygonal corrugations. By varying the periodicity of each axis of the polygon individually, this structure can support multiple resonances that provide independent control over emission directionality for multiple wavelengths. Moreover, since each resonant wavelength is directly mapped to a specific polarization orientation, spectral information can be encoded in the polarization state of the out-scattered beam. To demonstrate the potential of such structures in enabling simplified detection schemes and additional functionalities in sensing and imaging applications, we use the central subwavelength aperture as a built-in nanocuvette and manipulate the fluorescent response of colloidal-quantum-dot emitters coupled to the multiresonant antenna.
Keywords: surface plasmons, multiresonant, subwavelength aperture, nanoantenna, polarization control
Plasmonic nanoantennas have the capability to confine electromagnetic fields at the nanoscale as well as shape scattered light into the far field.1,2 Careful design of these nanostructures allows controlled in- and out-coupling of targeted wavelengths, propagation directions, and polarization states of light.3 Such properties can be used to engineer light–matter interactions in, for example, light-harvesting4,5 and light-emitting technologies.6 In addition, plasmonic nanoantennas have been extensively employed in spectroscopic and molecular sensing applications.7 Specifically, efficient near-field coupling between molecules and plasmonic antennas can lead to dramatically improved detection limits, enabling sensitivities down to the single-molecule level.8−11 At the same time, the antenna design can be used to structure and provide directionality to the far-field radiation pattern of the emission.12−15
A particularly successful example among directional plasmonic nanoantennas is the so-called bull’s-eye structure, which has the ability to generate a tightly confined beam of light in the out-of-plane direction.16−18 These antenna structures consist of concentric circular corrugations with a fixed periodicity. In a bull’s-eye with periodicity Λ, the out-scattering angle θ of a propagating surface plasmon is determined, for a specific wavelength λ, through the momentum matching condition:
| 1 |
where k0 is the momentum of the scattered light, m is an integer indicating the diffracted order, ksp is the momentum of the plasmon, kg is the additional momentum provided by the corrugations, and nsp is the effective refractive index seen by the propagating surface plasmon. From eq 1, it follows that light from the first diffraction order is scattered out in the direction normal to the metal surface when λ = Λnsp, generating the distinct resonant19 beaming behavior that is characteristic of these structures.20,21
Bull’s-eye antennas have been successfully employed to shape the far-field radiation profiles of dipole emitters, including colloidal quantum dots,22−25 molecular fluorophores,26,27 and nitrogen-vacancy centers in diamond.28 For example, the placement of dyes of different colors inside the central nanoaperture of a bull’s-eye results in efficient directional sorting and improved detection efficiency of fluorescence.29 Thanks to the on-resonant unidirectional emission imposed by the bull’s-eye antenna, single-molecule sensitivity can be achieved in such a system, even when using low numerical-aperture collection optics.30 An additional advantage of using nanoaperture bull’s-eyes in fluorescent sensing is the ability to provide selective excitation of small analyte volumes present inside the aperture, thereby significantly reducing background fluorescence.31
While providing excellent control over directionality, conventional bull’s-eyes are “single-resonant” structures, designed to provide beaming for only one color.19,32 However, in many sensing applications it is required to simultaneously probe multiple spectral features, for example, when distinguishing between different fluorescent labels33,34 or for dual-resonant enhancement of Raman signals.35−38 Such sensing applications would therefore benefit from a platform that can support resonances for more than one color, while providing directionality for each wavelength individually.
In this work, we present a family of compact multiresonant bull’s-eye antennas for spectral sorting of fluorescence, in which independent control over the directionality of the various resonant colors can be obtained. Our structures consist of concentric polygons that surround a central nanoaperture (see Figure 1). In contrast to the concentric circles of the traditional bull’s-eye aperture, a concentric polygonal structure can accommodate multiple resonances through variations in the periodicity along the different axes. Importantly, this allows independent directional control and parallel beaming of multiple wavelengths simultaneously. Moreover, benefiting from the breaking of symmetry in the concentric geometry, our multiresonant platform directly associates each resonance with a unique linear polarization.39−42 Combined with the controlled directionality of emission, it becomes possible to generate polarization-multiplexed parallel beams of light, in which spectral information is efficiently encoded in their polarization state. We will demonstrate that the subwavelength central nanoaperture of our structures can be used as a nanocuvette to probe the optical response of fluorescent emitters, such as colloidal quantum dots.
Figure 1.
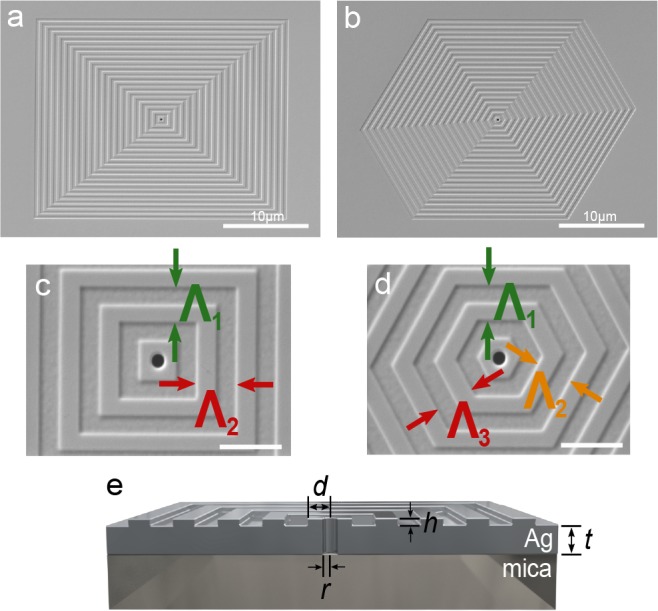
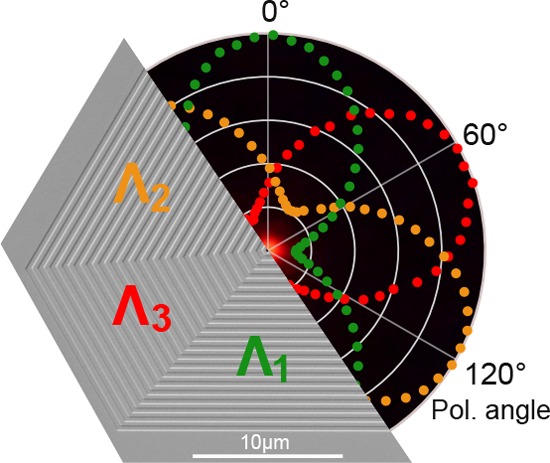
Design of concentric polygonal multiresonant antennas. (a–d) Scanning electron micrographs at different magnifications of a (a,c) rectangular and (b,d) hexagonal multiresonant antenna. The periodicity of the corrugations varies along the different axes of the structures. For the rectangle Λ1 = 515 nm and Λ2 = 635 nm. For the hexagon Λ1 = 515 nm, Λ2 = 575 nm, and Λ3 = 635 nm. (e) Cross-sectional schematic of the structure with distance from the center of the aperture to the first groove d = 300 nm, radius r of the aperture, height h of the corrugations, and thickness t of the film.
Results
Our multiresonant aperture antennas are fabricated using focused-ion-beam (FIB) milling of single-crystalline silver films grown on mica substrates (see Methods for details). High-resolution scanning electron micrographs of a concentric rectangle (Λ1 = 515 nm, Λ2 = 635 nm) and a concentric hexagon (Λ1 = 515 nm, Λ2 = 575 nm, Λ3 = 635 nm) are shown in Figure 1a,b, respectively. Around the circular central aperture, which is 210 nm in diameter, a total of 20 grooves with a depth of 60 nm were defined (see Figure 1e for the geometrical parameters of the structure and section 3 of the Supporting Information for more details on the structure performance and full-width-at-half-maximum of the resonances). The use of single-crystalline films has two main advantages. First, the reduced surface roughness and the absence of grain boundaries allow for increased plasmon propagation lengths.43,44 Second, it has been demonstrated that single-crystalline silver provides more homogeneous etching rates during focused-ion-beam milling and thus preserves the smooth surface after patterning, once more providing longer plasmon propagation lengths.44 These two effects should reduce random scattering and consequently lead to an improved control over the surface-plasmon out-scattering in our system.
To investigate the influence of our multiresonant concentric geometry on the angular and spectral scattering of light, we use k-space transmission microscopy. While illuminating the structure with quasi-monochromatic light (selected from a white light source using band-pass filters of 10 nm bandwidth, see Methods section for details) from the unpatterned back side, transmitted light is collected from the corrugated front side using a high-numerical-aperture (NA = 0.8) objective (see Figure 2a for a schematic). k-space microscopy images of the transmitted light are obtained by imaging the back focal plane of the collection objective. The measurement yields angularly resolved intensity maps across the ±53° collection cone of the objective.
Figure 2.
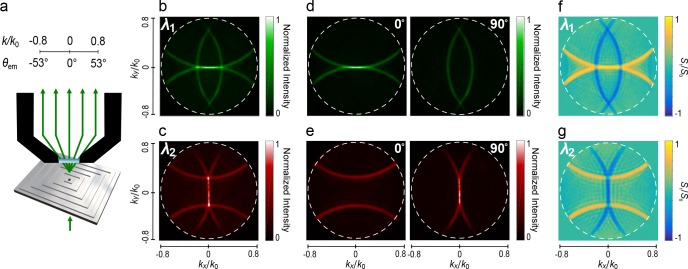
k-space microscopy and polarimetry of rectangular multiresonant antenna. (a) Schematic of k-space measurements where transmitted quasi-monochromatic light is collected using a high-NA objective (NA = 0.8). (b,c) Normalized k-space color maps for the rectangular structure of Figure 1a,c under (b) 550 ± 5 nm and (c) 650 ± 5 nm unpolarized excitation light. The diffraction patterns can be closely predicted using eq 1. (d,e) Corresponding k-space maps for selected polarization orientations. (f) The Stokes parameter S1 obtained using k-space polarimetry measurements for both 550 nm (top) and 650 nm (bottom) excitation quantifies the ability of the antenna to convert an unpolarized input into a polarized and directional beam. Dashed white lines indicate the numerical aperture of the objective.
Figure 2b,c shows the k-space maps for two different colors of quasi-monochromatic light transmitted through the aperture of the concentric rectangle shown in Figure 1a. Orthogonally oriented arc-like patterns of high transmission intensity are observed for each incident color. These arcs are characteristic of the dispersion relation for the two orthogonally oriented linear gratings where the scattering angle is dependent on the grating period (see eq 1). The variation in the periodicity of orthogonal corrugations results, for the rectangular case, in distinct positions of the arcs in k-space as further confirmed by numerical simulations (see the Supporting Information). For example, while green light (λ1 = 550 ± 5 nm) shows resonant out-coupling, via the x-axis periodicity (Λ1 = 515 nm), leading to high scattering intensity in the normal direction (kx/k0 and ky/k0 ≈ 0), light is scattered out at larger angles from the y axis (Λ2 = 635 nm). Conversely, red light (λ2 = 650 ± 5 nm) is off-resonant with the x axis, while on-resonant with the y axis. This clearly demonstrates the basic operation principle of the rectangular dual-resonant antenna where the structure’s geometry along the two axes can be controlled independently to satisfy the resonant condition for separate colors. Moreover, the high degree of angular control obtained through our structures is illustrated by the small width of the resonances at the center of k-space, measuring full-width-at-half-maxima (fwhm) of around ±2°.
A fundamental aspect of the surface-plasmon scattering by our multiresonant geometry is that the scattered-light polarization is acquired from the parallel polarization component of the propagating surface plasmons. It is therefore oriented along the respective axis of the polygon and parallel to the grating vector.45,46 To decompose the scattered patterns of Figure 2b,c into the different polarization components, we introduce a linear polarizer after the collection objective of Figure 2a. The horizontal and vertical polarization contributions are shown for green and red light in Figure 2d,e, respectively (for example, in the green case the 0° horizontal contributions are generated due to scattering from the vertically oriented periodicity of 515 nm and, correspondingly, the 90° contributions come from the orthogonally oriented horizontal grating periodicity which is not resonant with the green color). It is evident from these maps that the resonant conditions for the two colors occur at orthogonal polarization orientations and are separable using a linear polarizer.
To quantify the polarizing properties of our device, we perform k-space polarimetry using the combination of a quarter-wave plate followed by a linear polarizer as discussed in ref (47). By performing angle-resolved polarimetry of the transmitted light, we can retrieve the Stokes parameters to fully characterize the polarization state of the resulting optical beam (see Figure S1 in the Supporting Information for a schematic of the measurement setup and for the full polarimetric characterization of the rectangular multiresonant bull’s-eye). For example, the Stokes parameter S1, shown in Figure 2f,g for the two resonant wavelengths, quantifies the amount of linearly horizontal (LHP) and linearly vertical polarization (LVP) that our structure imposes on the scattered light (S1 = LHP – LVP).48−50S1 describes the ability of this multiresonant antenna to convert an unpolarized input into a polarized and directional beam. At the center of k-space, for both wavelengths, we find maxima of |S1| that reach >0.75, demonstrating that each wavelength has been efficiently mapped to a specific corresponding polarization.
Compared to the relatively simple orthogonal patterns generated by a concentric rectangle, more complex k-space patterns are obtained when using higher-order polygons. For example, using green (λ1 = 550 ± 5 nm), orange (λ2 = 600 ± 5 nm), and red (λ3 = 650 ± 5 nm) illumination colors, k-space maps for the hexagonal bull’s-eye of Figure 1b are shown in Figure 3. Resonant conditions can be observed every 60°, as imposed by the hexagonal geometry of our antenna for the different resonant colors (see Figure 3a–c). These resonant conditions become more apparent when using a linear polarizer, providing selective transmission of the three different beaming conditions (see Figure 3d–f). As for the rectangular case, each polarization contribution is obtained mainly via scattering from the orthogonally oriented axis of the structure. Similarly, polarization resolved k-space maps of the transmission of four different colors through an octagonal structure are presented in the Supporting Information, with resonant conditions in this case occurring with the expected 45° separations. Therefore, while the presence of additional diffraction arcs increases the complexity of the k-space maps, introducing a linear polarization analyzer provides an effective way to emphasize the individual resonances.
Figure 3.
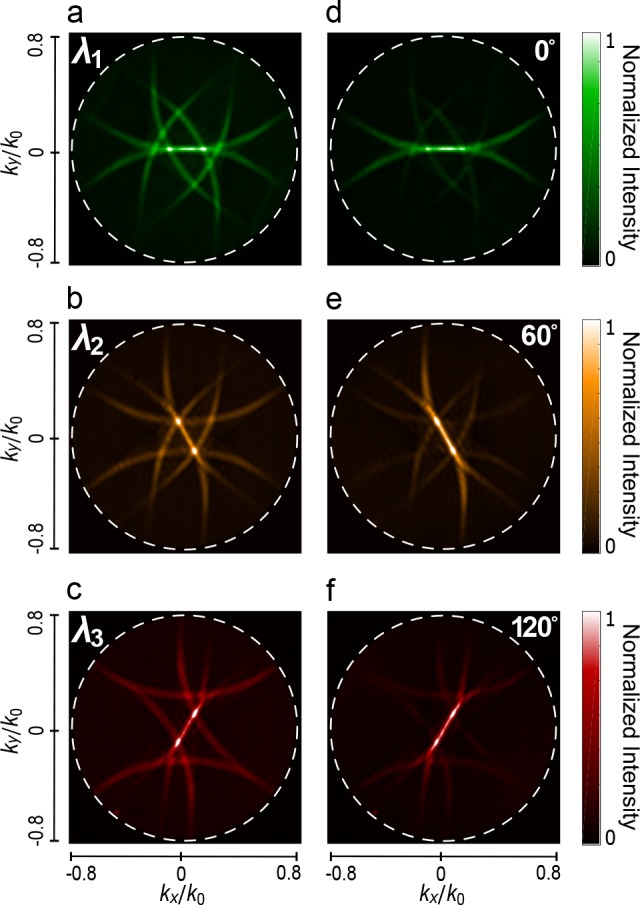
k-space measurements of hexagonal multiresonant antenna. Normalized k-space color maps for light scattered off the structure in Figure 1b. We use (a) 550 ± 5, (b) 600 ± 5, and (c) 650 ± 5 nm wavelength excitation. (d–f) From the patterns in parts (a–c), the different polarization components, for which a color-dependent beaming condition is satisfied, are separated. Due to the geometry of the structure, this occurs every 60°.
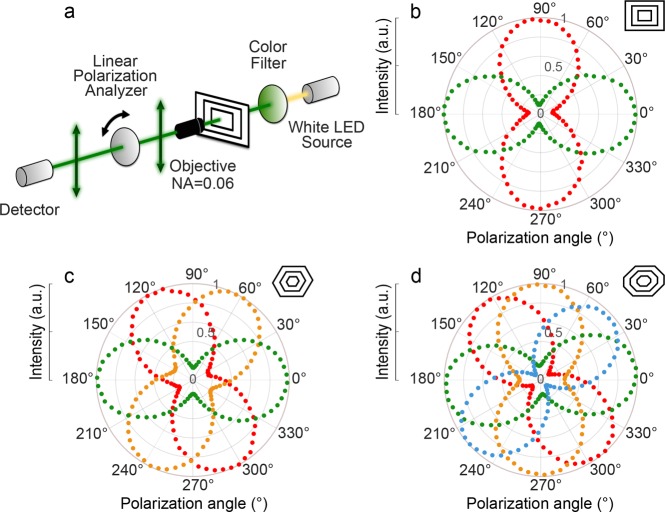
The presented direct mapping of each resonant color to a unique linear polarization, combined with the directional control over the out-scattering angle, provides us with the opportunity to generate multiplexed beams of light in which spectral information is encoded in the polarization state of the beam. To demultiplex and isolate the directional scattering of the resonant condition in the out-of-plane direction, we polarization-resolve the light collected with a low numerical aperture (NA = 0.06) objective that is sensitive only to a small cone of out-scattering angles (∼6.8°) (see schematic in Figure 4a). This angular selection is necessary to isolate a unique polarization for each color, filtering out the nonresonant arcs that are scattered out at larger angles from their corresponding nonresonant axes (see k-space maps in Figure 2 and Figure 3).
Figure 4.
Polarization-resolved spectroscopy. (a) Schematic of the detection scheme. A color filter is used to generate quasi-monochromatic light from a white-light source. Transmittance is collected using a numerical aperture of 0.06 and analyzed with a rotating linear polarizer. (b–d) Normalized transmitted intensity is measured as a function of polarization angle for different excitation wavelengths (red markers for λ = 650 ± 5 nm, orange for λ = 600 ± 5 nm, green for λ = 550 ± 5 nm, and blue for λ = 500 ± 5 nm) sent through a (b) rectangular, (c) hexagonal, and (d) octagonal multiresonant antenna.
The polarization-dependent response of our multiresonant structures to different excitation wavelengths is reported in polar coordinates in Figure 4b–d. In the case of the rectangular antenna, the highest transmitted intensity for two different excitation wavelengths (red and green) is found at orthogonal analyzer angles, as predicted by the k-space maps. In the case of a hexagonal structure, these maxima occur for angles shifted by 60°. To extend the multiresonant concept further, we also present the case of the octagonal configuration, in which resonances occur approximately at the expected 45° separation. Slight shifts in the estimated polarization angles can arise when the number of periodicities is significantly increased due to cross-talk of polarization components located at each individual axis. Generally, the measured behavior closely follows the numerical predictions obtained in simulations (see the Supporting Information for more details).
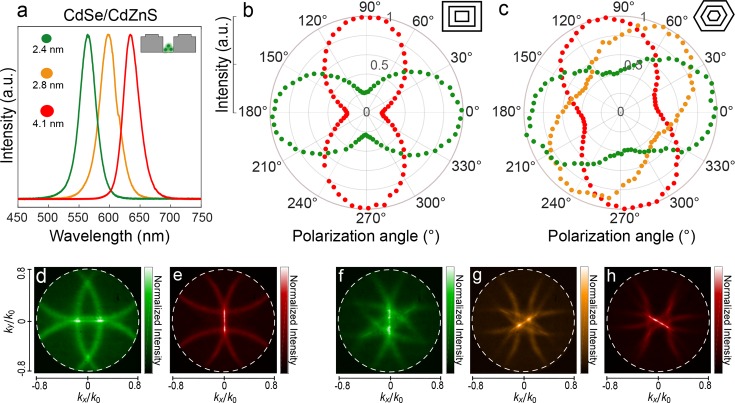
To demonstrate how our multiresonant antennas can be used to structure the emission of fluorescent labels, we place colloidal-quantum-dot emitters inside the central aperture. Colloidal quantum dots (cQDs) are commonly used in biological fluorescent labeling thanks to their size-tunable spectral properties as well as bright and photostable emission.51 Importantly, they exhibit narrow emission line widths, making them particularly suited for color-selective sensing. Here, we use a size series of CdSe/CdZnS core/shell QDs with emission colors in the green (λem = 565 nm), orange (λem = 600 nm), and red (λem = 635 nm), for which the emission spectra are shown in Figure 5a. Each antenna is coated with a single emitter color by drop-casting the QDs from dispersion. We excite the aperture from the unpatterned backside of our antenna using a 488 nm continuous wave (CW) laser (see schematics in Figure S9a,b). The subwavelength nature of the central nanoaperture and the presence of the optically thick Ag film around it, allow for spatially selective excitation of the emitters inside the aperture.22,33,52 The fluorescence is collected with a low-NA objective (NA = 0.06) from the corrugated side of the structure. In Figure 5b we show the polarization-dependent fluorescent intensity collected from a set of two rectangular structures, each coated with one of the two resonant emission-color QDs, in this case red and green. The expected orthogonal polarization for the two colors is indeed obtained. Similarly, Figure 5c shows the same measurement for a set of three hexagonal antennas, in this case coated with QDs of either green, orange, or red emission.
Figure 5.
Structuring of colloidal-quantum-dot fluorescence using multiresonant bull’s-eye antennas. Colloidal CdSe/CdZnS quantum dots (cQDs) are coupled to the aperture of the multiresonant antennas. (a) Normalized emission spectra of cQDs with core sizes of 2.4, 2.8, and and 4.1 nm. (b,c) Fluorescence intensity recorded using a NA = 0.06 as a function of polarization angle for (b) green and red cQDs on rectangular bull’s-eyes and (c) green, orange, and red cQDs on hexagonal bull’s-eyes. (d–h) Complete fluorescence k-space maps where (d,e) correspond to the measurements in part (b) and (f–h) to the measurements in (c) collected using a NA = 0.8.
From the corresponding measured fluorescence k-space maps for hexagonal antennas that are shown in Figure 5d–h, we can notice that, compared to the transmission measurements of Figure 4, the larger QD line width and smaller difference in the periodicities of the design (Λ1 = 522 nm and Λ2 = 602 nm due to the reduced spectral separation of the QD emission) introduce a slight broadening and overlap of the different sets of arcs increasing polarization cross-talk. This requires the use of small NAs in order to select only the resonant set of arcs of a color and reject the other polarizations. Nevertheless, in applications where high sensitivity is required, like single QD detection, higher numerical apertures can also be used to collect the structured light at the cost of reduced selectivity (see section 5 of the Supporting Information for a more detailed discussion).
Despite the occurrence of increased cross-talk in the hexagonal structure, causing a reduced on–off ratio in the polarization dependence and a slight shift from the expected 60° separation, the three colors obtain clearly distinct polarization angles (see Figure 5c). This demonstrates the ability of our antenna platform to structure the fluorescence of coupled emitters even in the hexagonal case. These characteristics of the fluorescent beam allow to resolve spectral components using linear polarization analysis and simplified detection schemes.
Conclusions
Combining multiresonant performance with controlled directionality and straightforward design principles, we have introduced a multiresonant plasmonic antenna that can efficiently tailor directionality and polarization of fluorescent emission. Through its built-in nanocuvette aperture, the presented antenna platform provides opportunities for next-generation sensing technologies toward single-emitter resolution.53 Specifically, polarization multiplexing of spectral information, as demonstrated through our polarization-resolved spectroscopy scheme, enables new concepts in molecular sequencing analysis. Polarization-resolved spectroscopy may benefit from high-speed signal modulation using, for example, photoelastic modulators, a strategy that may enable faster detection schemes in fluorescence-based sequencing techniques.52 Moreover, the high polarization dependence of our structure can add new functionalities to existing sequencing methods as well as be employed for dynamic color tuning54 or to generate multicolor or holographic on-chip sources.55
Methods
Fabrication of Ag Antennas
Highest quality grade mica disks with a diameter of 15 mm were freshly cleaved before deposition to reveal clean and flat faces. Silver (Ag) films of 250 nm thickness were epitaxially grown on the mica substrates via dc magnetron sputtering (Lesker PVD 75).44 Before deposition, a base pressure lower than 10–8 Torr was reached. Sputtering of Ag was performed at an argon pressure of 6 mTorr and a dc power of 400 W while the substrate temperature was maintained at 360 °C to yield single-crystalline films.
Focused-ion-beam milling (Helios 450, FEI) was used to pattern the desired geometries into the Ag films with an acceleration voltage of 30 kV and a beam current of 40 pA. Serial patterning of two different etching depths was performed to mill the corrugations and the hole, respectively.
Experimental Setups
Our transmission-angle-resolved setup is based on a Ti–U inverted microscope (Nikon) equipped with an optional Fourier transforming lens. Light from a white-light LED (Thorlabs MWWHLP1K) is collimated, filtered with 10 nm full-width-at-half-maximum (fwhm) bandpass filters (Thorlabs), and focused at the back of the sample using an excitation objective (NA = 0.6). The scattered light was measured using a collection objective with NA = 0.8. k-space polarimetry measurements were performed by introducing a quarter-wave plate and a linear polarization analyzer at the back of the collection objective. A pinhole was introduced at the microscope exit port focal plane. k-space maps were recorded using a charged-coupled device (PIXIS 256E, Princeton Instruments). To measure the polarization-dependent beaming of the multiresonant antennas, we used a collection objective with NA = 0.06 and a linear polarizer. Fluorescence images were recorded using a fiber coupled CW excitation laser operating at 488 nm (OBIS, Coherent).
Synthesis and Deposition of Core/Shell CdSe/CdZnS Quantum Dots
The synthesis of CdSe/CdZnS quantum dots was performed according to the method reported by Boldt et al.(56) (see the Supporting Information for details). The synthesis resulted in CdSe/CdZnS core/shell nanocrystals with an emission peak at 635 nm and fwhm of 29 nm for red-emitting quantum dots, 600 nm with fwhm of 35 nm for orange-emitting dots, and 565 nm with fwhm of 31 nm for green-emitting quantum dots.
The colloidal quantum dots were deposited on the patterned Ag films using drop-casting from 9:1 hexane/octane solutions. A volume of 20 μL of the dispersions was deposited on the 15 mm diameter disks to create a quantum dot film in the aperture of the antennas.
Numerical Simulations
Three-dimensional finite element modeling (FEM) of the structure was performed using COMSOL Multiphysics 5.2a. The simulated structure is composed of a 250 nm thick film with 5 periodic corrugations surrounding a central hole. The single-crystalline Ag optical properties used for calculations were measured from the fabricated films using spectroscopic ellipsometry (V-VASE, J. A. Woollam Co.). The model was excited with monochromatic TE and TM polarized fields and surrounded by cylindrical perfectly matched layers. For hexagonal bull’s-eye structures, the full geometry was simulated, whereas for the rectangular structure a quarter of the geometry with appropriate boundary conditions for the two orthogonal polarizations was sufficient. Far-field plots of a polarized input were obtained and postprocessed using Matlab to generate response for unpolarized or arbitrarily polarized inputs. Transmission versus polarization plots were obtained by selecting an NA = 0.06 from the calculated far-field plots.
Acknowledgments
We thank D. K. Kim and S. Jayanti for help with the preparation of single-crystalline silver films and S. Reidt for support using the FIB system. We acknowledge support by the Ambizione program of the Swiss National Science Foundation. L.V.P. was supported by the Swiss National Science Foundation (Award No. 200021-146747). B.l.F. acknowledges support from The Netherlands Organisation for Scientific Research (NWO, Rubicon Grant 680-50-1513).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b05269.
Further details related to the fabrication, characterization, measurement, and simulation of our structures (PDF)
Author Present Address
† F.P.: Condensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, Spain.
The authors declare no competing financial interest.
Supplementary Material
References
- Novotny L.; van Hulst N. Antennas for Light. Nat. Photonics 2011, 5, 83–90. 10.1038/nphoton.2010.237. [DOI] [Google Scholar]
- Schuller J. A.; Barnard E. S.; Cai W.; Jun Y. C.; White J. S.; Brongersma M. L. Plasmonics for Extreme Light Concentration and Manipulation. Nat. Mater. 2010, 9, 193–204. 10.1038/nmat2630. [DOI] [PubMed] [Google Scholar]
- Koenderink A. F.; Alù A.; Polman A. Nanophotonics: Shrinking Light-Based Technology. Science 2015, 348, 516–521. 10.1126/science.1261243. [DOI] [PubMed] [Google Scholar]
- Atwater H. A.; Polman A. Plasmonics for Improved Photovoltaic Devices. Nat. Mater. 2010, 9, 865–865. 10.1038/nmat2866. [DOI] [PubMed] [Google Scholar]
- Park J. H.; Han S. E.; Nagpal P.; Norris D. J. Observation of Thermal Beaming from Tungsten and Molybdenum Bull’s Eyes. ACS Photonics 2016, 3, 494–500. 10.1021/acsphotonics.6b00022. [DOI] [Google Scholar]
- Lozano G.; Rodriguez S. R.; Verschuuren M. A.; Gómez Rivas J. Metallic Nanostructures for Efficient LED Lighting. Light: Sci. Appl. 2016, 5, e16080. 10.1038/lsa.2016.80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brolo A. G. Plasmonics for Future Biosensors. Nat. Photonics 2012, 6, 709–713. 10.1038/nphoton.2012.266. [DOI] [Google Scholar]
- Zijlstra P.; Paulo P. M. R.; Orrit M. Optical Detection of Single Non-Absorbing Molecules Using the Surface Plasmon of a Gold Nanorod. Nat. Nanotechnol. 2012, 7, 379–382. 10.1038/nnano.2012.51. [DOI] [PubMed] [Google Scholar]
- Arroyo J. O.; Kukura P. Non-Fluorescent Schemes for Single-Molecule Detection, Imaging and Spectroscopy. Nat. Photonics 2015, 10, 11–17. 10.1038/nphoton.2015.251. [DOI] [Google Scholar]
- Punj D.; Mivelle M.; Moparthi S. B.; van Zanten T. S.; Rigneault H.; van Hulst N. F.; García-Parajó M. F.; Wenger J. A Plasmonic “Antenna-in-Box” Platform for Enhanced Single-Molecule Analysis at Micromolar Concentrations. Nat. Nanotechnol. 2013, 8, 512–516. 10.1038/nnano.2013.98. [DOI] [PubMed] [Google Scholar]
- Kinkhabwala A.; Yu Z.; Fan S.; Avlasevich Y.; Müllen K.; Moerner W. E. Large Single-Molecule Fluorescence Enhancements Produced by a Bowtie Nanoantenna. Nat. Photonics 2009, 3, 654–657. 10.1038/nphoton.2009.187. [DOI] [Google Scholar]
- Curto A. G.; Volpe G.; Taminiau T. H.; Kreuzer M. P.; Quidant R.; van Hulst N. F. Unidirectional Emission of a Quantum Dot Coupled to a Nanoantenna. Science 2010, 329, 930–933. 10.1126/science.1191922. [DOI] [PubMed] [Google Scholar]
- Li Z.; Shegai T.; Haran G.; Xu H. Multiple-Particle Nanoantennas for Enormous Enhancement and Polarization Control of Light Emission. ACS Nano 2009, 3, 637–642. 10.1021/nn800906c. [DOI] [PubMed] [Google Scholar]
- Shegai T.; Li Z.; Dadosh T.; Zhang Z.; Xu H.; Haran G. Managing Light Polarization via Plasmon-Molecule Interactions within an Asymmetric Metal Nanoparticle Trimer. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 16448–16453. 10.1073/pnas.0808365105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shegai T.; Brian B.; Miljković V. D.; Käll M. Angular Distribution of Surface-Enhanced Raman Scattering from Individual Au Nanoparticle Aggregates. ACS Nano 2011, 5, 2036–2041. 10.1021/nn1031406. [DOI] [PubMed] [Google Scholar]
- Lezec H. J.; Degiron A.; Devaux E.; Linke R. A.; Martin-Moreno L.; Garcia-Vidal F. J.; Ebbesen T. W. Beaming Light from a Subwavelength Aperture. Science 2002, 297, 820–822. 10.1126/science.1071895. [DOI] [PubMed] [Google Scholar]
- Garcia-Vidal F. J.; Martin-Moreno L.; Ebbesen T. W.; Kuipers L. Light Passing through Subwavelength Apertures. Rev. Mod. Phys. 2010, 82, 729–787. 10.1103/RevModPhys.82.729. [DOI] [Google Scholar]
- García-Vidal F. J.; Martín-Moreno L.; Lezec H. J.; Ebbesen T. W. Focusing Light with a Single Subwavelength Aperture Flanked by Surface Corrugations. Appl. Phys. Lett. 2003, 83, 4500–4502. 10.1063/1.1631384. [DOI] [PubMed] [Google Scholar]
- Please note that the term “resonant” in this context refers to the resonant nature of extraordinary optical transmission, not to be confused with a localized plasmon resonance.
- Martín-Moreno L.; García-Vidal F. J.; Lezec H. J.; Degiron A.; Ebbesen T. W. Theory of Highly Directional Emission from a Single Subwavelength Aperture Surrounded by Surface Corrugations. Phys. Rev. Lett. 2003, 90, 167401. 10.1103/PhysRevLett.90.167401. [DOI] [PubMed] [Google Scholar]
- Han S. E.; Norris D. J. Beaming Thermal Emission from Hot Metallic Bull’s Eyes. Opt. Express 2010, 18, 4829. 10.1364/OE.18.004829. [DOI] [PubMed] [Google Scholar]
- Jun Y. C.; Huang K. C. Y.; Brongersma M. L. Plasmonic Beaming and Active Control over Fluorescent Emission. Nat. Commun. 2011, 2, 283. 10.1038/ncomms1286. [DOI] [PubMed] [Google Scholar]
- Harats M. G.; Livneh N.; Zaiats G.; Yochelis S.; Paltiel Y.; Lifshitz E.; Rapaport R. Full Spectral and Angular Characterization of Highly Directional Emission from Nanocrystal Quantum Dots Positioned on Circular Plasmonic Lenses. Nano Lett. 2014, 14, 5766–5771. 10.1021/nl502652k. [DOI] [PubMed] [Google Scholar]
- Livneh N.; Harats M. G.; Yochelis S.; Paltiel Y.; Rapaport R. Efficient Collection of Light from Colloidal Quantum Dots with a Hybrid Metal-Dielectric Nanoantenna. ACS Photonics 2015, 2, 1669–1674. 10.1021/acsphotonics.5b00433. [DOI] [Google Scholar]
- Sapienza L.; Davanco M.; Badolato A.; Srinivasan K. Nanoscale Optical Positioning of Single Quantum Dots for Bright and Pure Single-Photon Emission. Nat. Commun. 2015, 6, 7833. 10.1038/ncomms8833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aouani H.; Itzhakov S.; Gachet D.; Devaux E.; Ebbesen T. W.; Rigneault H.; Oron D.; Wenger J. Colloidal Quantum Dots as Probes of Excitation Field Enhancement in Photonic Antennas. ACS Nano 2010, 4, 4571–4578. 10.1021/nn1009209. [DOI] [PubMed] [Google Scholar]
- Mohtashami A.; Osorio C. I.; Koenderink A. F. Angle-Resolved Polarimetry of Antenna-Mediated Fluorescence. Phys. Rev. Appl. 2015, 4, 54014. 10.1103/PhysRevApplied.4.054014. [DOI] [Google Scholar]
- Li L.; Chen E. H.; Zheng J.; Mouradian S. L.; Dolde F.; Schröder T.; Karaveli S.; Markham M. L.; Twitchen D. J.; Englund D. Efficient Photon Collection from a Nitrogen Vacancy Center in a Circular Bullseye Grating. Nano Lett. 2015, 15, 1493–1497. 10.1021/nl503451j. [DOI] [PubMed] [Google Scholar]
- Aouani H.; Mahboub O.; Devaux E.; Rigneault H.; Ebbesen T. W.; Wenger J. Plasmonic Antennas for Directional Sorting of Fluorescence Emission. Nano Lett. 2011, 11, 2400–2406. 10.1021/nl200772d. [DOI] [PubMed] [Google Scholar]
- Aouani H.; Mahboub O.; Bonod N.; Devaux E.; Popov E.; Rigneault H.; Ebbesen T. W.; Wenger J. Bright Unidirectional Fluorescence Emission of Molecules in a Nanoaperture with Plasmonic Corrugations. Nano Lett. 2011, 11, 637–644. 10.1021/nl103738d. [DOI] [PubMed] [Google Scholar]
- Wenger J.; Gérard D.; Aouani H.; Rigneault H.; Lowder B.; Blair S.; Devaux E.; Ebbesen T. W. Nanoaperture-Enhanced Signal-to-Noise Ratio in Fluorescence Correlation Spectroscopy. Anal. Chem. 2009, 81, 834–839. 10.1021/ac8024015. [DOI] [PubMed] [Google Scholar]
- Laux E.; Genet C.; Skauli T.; Ebbesen T. W. Plasmonic Photon Sorters for Spectral and Polarimetric Imaging. Nat. Photonics 2008, 2, 161–164. 10.1038/nphoton.2008.1. [DOI] [Google Scholar]
- Levene M. J.; Korlach J.; Turner S. W.; Foquet M.; Craighead H. G.; Webb W. W. Zero-Mode Waveguides for Single-Molecule Analysis at High Concentrations. Science 2003, 299, 682–686. 10.1126/science.1079700. [DOI] [PubMed] [Google Scholar]
- Aouani H.; Mahboub O.; Devaux E.; Rigneault H.; Ebbesen T. W.; Wenger J. Plasmonic Antennas for Directional Sorting of Fluorescence Emission. Nano Lett. 2011, 11, 2400–2406. 10.1021/nl200772d. [DOI] [PubMed] [Google Scholar]
- Chu Y.; Banaee M. G.; Crozier K. B. Double-Resonance Plasmon Substrates for Surface-Enhanced Raman Scattering with Enhancement at Excitation and Stokes Frequencies. ACS Nano 2010, 4, 2804–2810. 10.1021/nn901826q. [DOI] [PubMed] [Google Scholar]
- Turkmen M.; Aksu S.; Çetin A. E.; Yanik A. A.; Altug H. Multi-Resonant Metamaterials Based on UT-Shaped Nano-Aperture Antennas. Opt. Express 2011, 19, 7921–7928. 10.1364/OE.19.007921. [DOI] [PubMed] [Google Scholar]
- Cetin A. E.; Turkmen M.; Aksu S.; Etezadi D.; Altug H. Multi-Resonant Compact Nanoaperture with Accessible Large Nearfields. Appl. Phys. B: Lasers Opt. 2015, 118, 29–38. 10.1007/s00340-014-5950-7. [DOI] [Google Scholar]
- Hughes T. W.; Fan S. Plasmonic Circuit Theory for Multiresonant Light Funneling to a Single Spatial Hot Spot. Nano Lett. 2016, 16, 5764–5769. 10.1021/acs.nanolett.6b02474. [DOI] [PubMed] [Google Scholar]
- Sedoglavich N.; Sharpe J. C.; Künnemeyer R.; Rubanov S. Polarisation and Wavelength Selective Transmission through Nanohole Structures with Multiple Grating Geometry. Opt. Express 2008, 16, 5832–5837. 10.1364/OE.16.005832. [DOI] [PubMed] [Google Scholar]
- Sedoglavich N.; Künnemeyer R.; Sharpe J. C. Polarization Tunable Selective Polariton Generator. Appl. Phys. Lett. 2009, 94, 101111. 10.1063/1.3099040. [DOI] [Google Scholar]
- Jiao X.; Blair S. Polarization Multiplexed Optical Bullseye Antennas. Plasmonics 2012, 7, 39–46. 10.1007/s11468-011-9273-9. [DOI] [Google Scholar]
- Nazari T.; Kassani S. H.; Khazaeinezhad R.; Oh K. Polarization Dependent Transmission through a Sub-Wavelength Hexagonal Aperture Surrounded by Segmented Polygonal Grooves. Opt. Express 2013, 21, 32668. 10.1364/OE.21.032668. [DOI] [PubMed] [Google Scholar]
- Maier S. A.Plasmonics: Fundamentals and Applications; Springer Science & Business Media, 2007. [Google Scholar]
- Park J. H.; Ambwani P.; Manno M.; Lindquist N. C.; Nagpal P.; Oh S. H.; Leighton C.; Norris D. J. Single-Crystalline Silver Films for Plasmonics. Adv. Mater. 2012, 24, 3988–3992. 10.1002/adma.201200812. [DOI] [PubMed] [Google Scholar]
- Marquier F.; Arnold C.; Laroche M.; Greffet J. J.; Chen Y. Degree of Polarization of Thermal Light Emitted by Gratings Supporting Surface Waves. Opt. Express 2008, 16, 5305–5313. 10.1364/OE.16.005305. [DOI] [PubMed] [Google Scholar]
- Li L.; Li T.; Tang X.-M.; Wang S.-M.; Wang Q.-J.; Zhu S.-N. Plasmonic Polarization Generator in Well-Routed Beaming. Light: Sci. Appl. 2015, 4, e330. 10.1038/lsa.2015.103. [DOI] [Google Scholar]
- Osorio C. I.; Mohtashami A.; Koenderink a F. K-Space Polarimetry of Bullseye Plasmon Antennas. Sci. Rep. 2015, 5, 9966. 10.1038/srep09966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke D.; Grainger J. F. Measurement of the State of Polarization. In Polarized Light and Optical Measurement; Pergamon Press, 1971; pp 118–154. [Google Scholar]
- Berry H. G.; Gabrielse G.; Livingston A. E. Measurement of the Stokes Parameters of Light. Appl. Opt. 1977, 16, 3200–3205. 10.1364/AO.16.003200. [DOI] [PubMed] [Google Scholar]
- Collett E.Field Guide to Polarization; SPIE, 2005. [Google Scholar]
- Alivisatos P. The Use of Nanocrystals in Biological Detection. Nat. Biotechnol. 2004, 22, 47–52. 10.1038/nbt927. [DOI] [PubMed] [Google Scholar]
- Eid J.; Fehr A.; Gray J.; Luong K.; Lyle J.; Otto G.; Peluso P.; Rank D.; Baybayan P.; Bettman B.; et al. Real-Time DNA Sequencing from Single Polymerase Molecules. Science 2009, 323, 133–138. 10.1126/science.1162986. [DOI] [PubMed] [Google Scholar]
- Livneh N.; Harats M. G.; Istrati D.; Eisenberg H. S.; Rapaport R. Highly Directional Room-Temperature Single Photon Device. Nano Lett. 2016, 16, 2527–2532. 10.1021/acs.nanolett.6b00082. [DOI] [PubMed] [Google Scholar]
- Yun H.; Lee S.-Y.; Hong K.; Yeom J.; Lee B. Plasmonic Cavity-Apertures as Dynamic Pixels for the Simultaneous Control of Colour and Intensity. Nat. Commun. 2015, 6, 7133. 10.1038/ncomms8133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.; Li T.; Wang S.; Zhu S. Multiplexed Holograms by Surface Plasmon Propagation and Polarized Scattering. Nano Lett. 2017, 17, 5051–5055. 10.1021/acs.nanolett.7b02295. [DOI] [PubMed] [Google Scholar]
- Boldt K.; Kirkwood N.; Beane G. A.; Mulvaney P. Synthesis of Highly Luminescent and Photo-Stable, Graded Shell CdSe/CdxZn1-xS Nanoparticles by in Situ Alloying. Chem. Mater. 2013, 25, 4731–4738. 10.1021/cm402645r. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.