Reference correlations for the thermal conductivity of liquid copper, gallium, indium, iron, lead, nickel and tin

Abstract

The available experimental data for the thermal conductivity of liquid copper, gallium, indium, iron, lead, nickel, and tin has been critically examined with the intention of establishing thermal conductivity reference correlations. All experimental data have been categorized into primary and secondary data according to the quality of measurement specified by a series of criteria. The proposed standard reference correlations for the thermal conductivity of liquid copper, gallium, indium, iron, lead, nickel, and tin are respectively characterized by uncertainties of 9.8, 15.9, 9.7, 13.7, 16.9, 7.7, and 12.6% at the 95% confidence level.

1 INTRODUCTION

In recent years there has been an increasing use of mathematical models to simulate a variety of processes involving liquid metals such as shape-casting; primary and secondary metal production; powder production by spray-forming; and welding. In order to model any of these processes, there is a need for density, viscosity, and thermal conductivity data for the relevant alloys. For these reasons, a project was initiated in 2009 by the International Association for Transport Properties, IATP (former Subcommittee on Transport Properties of the International Union of Pure and Applied Chemistry, IUPAC), initially, to critically evaluate the density and the viscosity of selected liquid metals. Subsequently, reference correlations for the density and the viscosity of liquid aluminum and iron were published in 2006 [1], of liquid copper and tin in 2010 [2], of liquid antimony, bismuth, lead, nickel, and silver in 2012 [3], of liquid cadmium, cobalt, gallium, mercury, indium, silicon, thallium, and zinc in 2012 [4], and finally of liquid eutectic alloys (Al+Si), (Pb+Bi), and (Pb+Sn), also in 2012 [5].

The present work, also carried out under the auspices of IATP, continues the aforementioned task by proposing reference correlations for the thermal conductivity of copper, gallium, indium, iron, lead, nickel, and tin. These are based on critically-assessed measurements of the thermal conductivity. Values of the thermal conductivity calculated via the Wiedermann-Franz law, from the measurement of the electrical conductivity, were not considered here. Although the Wiedermann-Franz law [6] was first published in 1853, its basis is a simple theory of one mechanism of thermal conduction in a specific group of solid metals. Thus its application to the liquid phase of a wider group of metals is of uncertain pedigree [7–9].

In 1970 Touloukian et al. [10] published a review of thermal-conductivity data, and reference values for the thermal conductivity of some liquid metals. Following this, in 1996, Mills et al. [11] also proposed reference equations for some liquid metals. In addition to these references from 1996, new, more accurate measurements which emerged since then, allow us to make a better proposal for reference correlations. In particular, because we also describe which measurements were considered or what weight was attached with justification to different results.

2 PRIMARY AND SECONDARY DATA

According to the recommendation adopted by IATP, experimental data can be placed into two categories according to the quality of the data: primary and secondary data. The primary data are characterised by the following criteria [12]:

1. Measurements must have been made with a primary experimental apparatus, i.e., one for which a working equation, based on a full theory, is available.

2. The form of the working equation should be such that the sensitivity of the property measured to the principal variables does not magnify the random errors of measurement.

3. All principal variables should be measurable to a high degree of precision.

4. The published work should include some description of purification methods and a guarantee of the purity of the sample.

5. The data reported must be unsmoothed. Whilst graphs and fitted equations are useful summaries for the reader, they are not sufficient for standardization purposes.

6. The lack of accepted values of the thermal conductivity of standard reference materials of liquid metals implies that only absolute and not relative measurement results can be considered.

7. Explicit quantitative estimates of the uncertainty of reported values should be given, taking into account the precision of experimental measurements and possible systematic errors.

8. Owing to the desire to produce low-uncertainty reference values, limits must be imposed on the uncertainty of the primary data sets. These limits are determined after critical evaluation of the existing data sets.

These criteria have been successfully employed to propose standard reference values for the viscosity and thermal conductivity of fluids over a wide range of conditions, with uncertainties in the region of 1–2% [13–16].

In the case, however, of the liquid metals, it was felt and agreed that these criteria needed to be relaxed slightly, primarily because the uncertainty of almost all of the measurements is much higher than for organic liquids. This is principally due to (i) the difficulties associated with the techniques that must be employed for the high temperatures and high reactivity of the samples involved and (ii) the purity of the liquid metal sample which can be strongly affected by the surrounding atmosphere and the container used for the melt.

3 THERMAL CONDUCTIVITY

3.1 Experimental

Molten metals, such as copper, are highly reactive at high temperature. Hence, it is difficult to find an appropriate container for the materials during the measurement of thermophysical properties. Moreover, convection induced by a non-uniform temperature field in molten metals at high temperatures is exceedingly difficult to avoid completely, so that the measurement of thermal conductivity is generally contaminated by convective flows of heat.

A large number of techniques have been employed to measure the thermal conductivity of molten copper, gallium, indium, iron, lead, nickel, and tin. Methods employed include: transient hot wire, guarded heat flow, laser flash, electromagnetic levitation, temperature wave, and hot disk. These will briefly be described in the following paragraphs.

Transient hot wire

In this technique, a current is applied to a fine wire (or strip) of known length which acts as both a heating element and a resistance thermometer. The wire is immersed in the melt, a current is applied, and the temperature rise of the wire is measured as a function of time. The thermal conductivity is derived from the reciprocal of the slope of the linear portion of the plot of the temperature rise versus the logarithm of the time. Convective contributions to heat transfer can be detected as departures from the linear relation and normally the current is applied for less than 1 s, in order to avoid influences of buoyancy-driven convection. Experiments have also been carried out in a micro-gravitational field using a drop tower to minimize all forms of convection [17].

The main problem associated with the application of the technique to the measurement of the thermal conductivity of metals is the necessity to insulate the metallic wire from the melt. For this reason, the wire is insulated using a coating of Al₂O₃ or other metal oxides applied to the wire. For the most accurate work, the effect of the insulating coating on the temperature rise of the wire must be evaluated through a suitable theory either analytically or numerically for the one-dimensional (radial) heat transfer problem. Recent work has shown that if a thin metal strip is embedded in the mid-plane of two ‘green’ alumina sheets hot pressed to form a rigid sensor, an appropriate numerical analysis of the corresponding two-dimensional heat transfer problem is possible [18–20]. An appropriate choice of the dimensions of the sensor allows the thermal conductivity values for liquid metals that surround the composite sensor to be determined with good accuracy. The technique has an essentially exact working equation with a full set of theoretical corrections that can be applied experimentally and precisely [18–20].

Guarded heat flow

This is a steady-state technique, where a known heat input is applied to one end of the sample and removed at the other through a heat sink [9]. This method is very similar to the guarded hot-plate method [21], and the only difference is that the temperature drop through the sample in the direction of the heat flux is measured by thermocouples immersed in the specimen and not simply placed in the heating plates. The technique can be divided into two categories according to the geometry used, i.e., radial and axial heat flow method.

The radial heat flow instruments require a sufficiently large ratio of the specimen length to its diameter in order to ensure that all heat flow in the specimen is radial. The radial heat flow technique is also known as the concentric-cylinders technique. The largest advantage of the guarded heat flow instruments is the simple geometry and the relatively simple setup once the problem of containment is solved. The major problems are the avoidance of convective flows within the melt. The basic working equation for the method is simply a one-dimensional Fourier law, but the deviations of most instruments from the ideal to which this basic equation applies are frequently substantial, and the corrections seldom have precise theories.

Laser flash

The principle of the method involves the irradiation of the front surface of a small specimen of the test material in the form of a thin disk, by a short-duration, high-intensity uniform pulse from a high-power laser source [22, 23]. The radiation absorbed at the front face causes a thermal pulse which diffuses through the sample. The resulting temperature rise of the rear face of the disk is monitored as a function of time using a suitable detector and data acquisition system. The temperature rise detector can be an infrared detector, an optical pyrometer, or even a thermocouple. The technique produces the thermal diffusivity from an analysis of the temperature history observed, using a theory which is soundly based for the ideal case. The uncertainty of the technique as applied to molten metals at high temperatures is debatable, because there is a chance of convective flow within the sample (especially if times over 2 s are employed for irradiation) because the heated front face is often below the liquid surface for practical purposes. Because the surface of the liquid metal is not always observed directly by the detector, there are possible systematic errors introduced into the results by intermediate surfaces. Nevertheless, the technique is widely used for the measurement of the thermal conductivity of melts.

Electromagnetic levitation

In the electromagnetic levitation (EML) technique, the upper part of an electromagnetically levitated droplet is periodically heated by a modulated light source, i.e., a modulated semiconductor laser, and then the temperature variation at the lower part of the droplet is detected by a pyrometer. The thermal conductivity is obtained from the phase lag between the modulated laser heating and the temperature variation, measured at various frequencies of the modulated light. Details of the model are given by Tsukada et al.[24] and Baba et al.[25]. The technique is containerless, so that it removes the risk of heterogeneous nucleation from the wall of the container.

The convection caused by the electromagnetic force in the molten droplet, together with buoyancy and Marangoni convective effects, may affect the thermal field and consequently the measurement of the thermal conductivity of the molten metal. To suppress convective heat transfer, sometimes a static magnetic field is employed [25].

Temperature wave

The basic idea of this method is the creation of a heat pulse in the center of a hemispherical crucible filled with the material under test, into which is placed a temperature sensor (for example, a thermocouple) at a fixed and measured distance from the center. Measurement of the temperature pulse delay time between the source and the sensor gives information on the materials’ thermal diffusivity. In the case of measuring the thermal diffusivity of a molten metal, the specimen is melted in a porcelain crucible, and a local heat extraction was created by the evaporation of a drop of water falling into a thin walled steel hemisphere at the center of the surface of the melt. Chromel-alumel thermocouples were located at various distances from the center and their temperature measured as a function of time. A full mathematical model is described by Zinovyev et al.[26]. The thermal conductivity is obtained indirectly, through the thermal diffusivity which is the quantity measured directly.

It could be argued that convectional contributions would tend to be small due to the short duration of the experiment, but this assumption may not be valid since circulation flows could arise from buoyancy and thermocapillary forces caused by the large temperature gradients. The technique is also known as the plane temperature-wave, or the radial temperature-wave, or the modulated-beam technique.

Hot disk

In this method, a resistive element is used both as a heat source and as a temperature sensor and, in the ideal case, is placed within an infinite sample of the test material. In practice, attempts are made to make everything small so as to limit the amount of liquid metal required [27]. This first implies that the heat source should be very thin and secondly that its electrical resistance should be as large as possible, in order to provide application to small samples and high sensitivity to temperature measurements.

The planar heat source is often a resistive element created in a prescribed pattern by deposition techniques on an insulating material or by using thin metal foils. In both cases, the resistive element should be sandwiched between thin electrical insulating layers. It is immersed in the melt and a constant current is applied to it sufficient to increase the sensor temperature by 1 to 2 K. As the sensor’s temperature varies, so does its resistance. Consequently, monitoring the resistance change versus time yields the thermal history for the sensor from which the thermal conductivity of the sample can be obtained. Despite the fact that the resistive element of the heat source can have any form, for reasons of experimental and theoretical convenience the arrangements used are in the form of “hot plate/square” or “hot disks”.

Although the method is widely used for measurements on a great variety of materials, it is not an absolute technique and instruments depart so much from the simplest ideal model that it does not have a theoretical analytical solution of the heat transfer process. The majority of the commercial plane source devices are supplied with suitable software, which numerically solves the partial differential heat transfer equations. It is usually unclear the extent to which the modelling of the experiment accords with physical reality, and calibration is essential. In the case of molten metals, where there are no high quality standard reference values for calibration, this is problematic.

3.2 Data compilation

Tables 1 to 7 present, to the best of our knowledge, all the data sets for the measurement of the thermal conductivity of liquid copper, gallium, indium, iron, lead, nickel, and tin, reported in the literature. These measurements of the thermal conductivity as a function of temperature are shown in Figures 1 to 7. In these tables, the purity of the sample, the technique employed and the uncertainty quoted by the authors, and the temperature range covered, are also presented. Furthermore, the form in which the data are presented (diagram, equation or table), is noted. The data sets have been classified into primary and secondary sets according to the criteria presented in Section 2 and in conjunction with the techniques employed. As mentioned earlier, the entire set of data for these molten metals do not allow the rigorous application of the criteria we have mentioned. Importantly, we note that, as can be seen in the tables, we have been forced to use data taken from graphical presentations of results, counter to our preference. If this step were not taken, the data available to us would have been severely limited. In any event, because the uncertainties claimed for such data are usually quite large, little extra error is introduced in reading them from the diagrams provided.

TABLE 1.

Data sets considered for the thermal conductivity of liquid copper at 0.1 MPa

First author	Publ. year	Ref.	Puritya (mass %)	Technique employedb	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datac
Previous reference correlation/values
Mills	1996	[11]				-	1348–1780	E
Touloukian	1970	[10]			3–5	10	1355–2400	P
Primary data
Baba	2012	[25]	99.99	Electromagnetic levitation	10	24	1382–1665	D
Cusco	2002	[22]	99.98	Laser flash (TD)	12	132	1356–1435	D
Zinovyev	1994	[62]	99.99	Temperature wave (TD)	5	4	1364–1425	D
Tye	1979	[9]	HP	Guarded heat flow	10	7	1373–1673	P
Secondary data
Shibata	2002	[55]	-	Laser flash (TD)	30	1	1408	D
Filippov	1973	[63]	-	Temperature wave (TD)	-	6	1367–1760	D
Fieldhouse	1956	[43]	99.99	Guarded heat flow	2	7	1361–1761	P

^aHP = High Purity grade

^bTD = thermal diffusivity measurement,

^cD = diagram, E = equation, P = table data

TABLE 7.

Data sets considered for the thermal conductivity of liquid tin at 0.1 MPa

First author	Publ. year	Ref.	Purity (mass %)	Technique employeda	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datab
Previous reference correlation/values
Mills	1996	[11]				8	506–2073	E
Touloukian	1970	[10]			5–15	9	505–1300	P
Primary data
Savchenko	2011	[50]	99.996	Laser flash (TD)	2.5–3.5	21	513–1173	D
Bilek	2006	[19]	99.999	Transient hot wire	3	9	628–872	P
Nagai	2006	[27]	99.999	Hot disk	-	5	531–990	D
Peralta-Martinez	2006	[18]	99.99	Transient hot wire	2	8	534–731	P
Sklyarchuk	2005	[35]		Guarded heat flow	7	16	508–610	D
Hemminger	1985	[33]	99.999	Guarded heat flow	5	17	512–769	P
Otter	1978	[54]	99.90	Laser flash (TD)	5	9	1261–2068	D
Zinovyev	1973	[26]	-	Temperature wave (TD)	10	7	506–592	D
Osipenko	1970	[38]	-	Guarded heat flow	-	8	538–898	D
Dutchak	1967	[37]	-	Guarded heat flow	-	5	526–775	D
Kineke	1967	[32]	99.00	Guarded heat flow	2	5	552–594	D
Nikolsky	1959	[39]	-	Guarded heat flow	-	29	579–834	D
Brown	1923	[41]	-	Guarded heat flow	-	3	537–621	P
Konno	1920	[42]	-	Guarded heat flow	-	3	565–772	P
Secondary data
Yamasue	2003	[7]	99.90	Transient hot wire	4	10	573–1473	D
Shibata	2002	[55]	-	Laser flash (TD)	30	2	623,829	D
Banchila	1973	[66]	99.995	Temperature wave (TD)	6	14	1153–1970	D
Filippov	1973	[63]	-	Temperature wave (TD)	-	10	507–1609	D
Yurchak	1965	[64]	-	Temperature wave (TD)	6–8	22	868–1226	D
Pashaev	1961	[44]	99.94	Guarded heat flow	5	5	513–608	D
Bidwell	1940	[47]	-	Guarded heat flow	-	2	505–745	D

^aTD = thermal diffusivity measurement

^bD = diagram, E = equation, P = table data

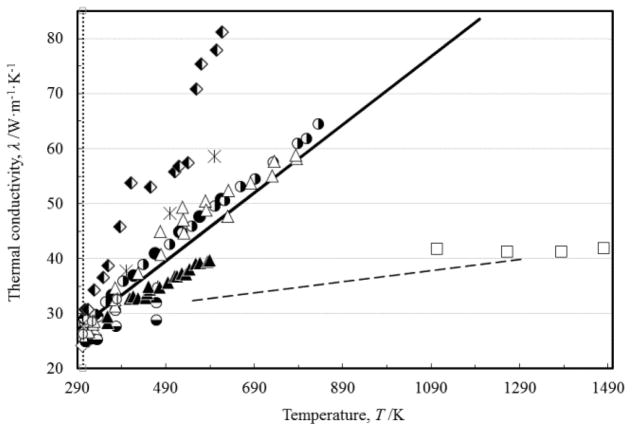
FIGURE 1.

Measurements of the thermal conductivity of liquid copper as a function of the temperature: (○) Baba et al. [25]; (△) Cusco and Monaghan [22]; (+) Shibata et al. [55]; (▲) Zinovyev et al. [62]; (◆) Tye and Hayden [9]; (- -) Filippov [63]; (■) Fieldhouse et al. [43]. Previous reference correlation of Mills et al. [11], (▬), and reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

FIGURE 7.

Measurements of the thermal conductivity of liquid tin as a function of the temperature: (◐) Savchenko et al. [50]; (□) Nagai et al. [27]; (◒) Bilek et al. [19]; (●) Peralta et al. [18]; (■) Sklyarchuk and Plevachuk [35]; (+) Yamasue et al. [7]; (⏃) Shibata et al. [55]; (▲) Hemminger [33]; (⦵) Otter and Arles [54]; (- -) Banchila and Filippov [66]; (□ -) Filippov [63]; (×) Zinovyev et al. [26]; (◇) Osipenko [38]; (⏀) Dutchak and Panasyuk [37]; (○) Kineke [32]; (◨) Yurchak and Filippov [64]; (⬖) Pashaev [44]; (△) Nikolskii et al. [39]; (◑) Bidwell [47]; (◆) Brown [41]; (⬙) Konno [42]. Previous reference correlation of Mills et al. [11], (▬), and estimated reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

We discuss the categorization of individual works among the complete set of data available to us on the thermal conductivity of the liquids below for each individual technique.

The transient hot-wire technique has recently been employed by Peralta et al. [18] and Bilek et al. [19, 20] with an uncertainty of 2 and 3%. These measurements, performed with two wires embedded in an alumina substrate, are believed to be the best measurements existing today, as they are backed by a rigorous, full theory; thus are part of the primary data set for each metal they studied. The same technique has also been employed, but with higher uncertainty, by Miyamura and Susa [28] and Fukuyama et al. [29], with corresponding uncertainties 15 and 18%. These measurements were also included in the primary data set, but with a lower weight. The 2003 measurements of Yamasue et al. [7] and Nagata et al. [17] were not included in the primary data set, because their results were much lower than the results of all the other measurements. This observation was attributed to problems with the insulation of the wire (corrected in their 2006 paper [29]). Finally, the transient hot-wire measurements of Nakamura et al. [30] were also included in the primary data set.

The guarded heat-flow technique, in different variations, is the most common technique for the measurement of the thermal conductivity of liquid metals. The measurements of Goldratt and Greenfield [31], Kineke [32], Hemminger [33, 34], Sklyarchuk and Plevachuk [35], and Tye and Hayden [9], performed with corresponding uncertainties of 1, 2–5, 3–5, 7, and 10%, respectively were all included in the primary data set, because in each case a detailed description of their instrument and the procedures adopted was included. The measurements of Magmedov [36], Dutchak and Panasyuk [37], Osipenko [38], Nikolski et al. [39], Powell [40], Brown [41], and Konno [42], were included in the primary data set, but with a lower weight because they did not discuss the uncertainty of their results. Finally, among work with this technique, the measurements of Fieldhouse et al. [43], Pashaev [44], Duggin [45, 46], and Bidwell [47] were excluded from the primary data set because they deviated far too much from the consensus of all the other measurements (see e.g. Fieldhouse et al.[43] in Figure 1, Pashaev [44] in Figure 2, Duggin [45, 46] in Figure 5, and Bidwell [47] in Figure 5).

As already discussed, the laser-flash technique directly measures the thermal diffusivity, α (m²·s⁻¹), of the sample and not the thermal conductivity, λ (W·m⁻¹·K⁻¹). The two are related through the equation

$$\alpha =\frac{\lambda }{\rho C_P},$$ (1)

where ρ (kg·m⁻³) is the density of the melt and C_P (J·kg⁻¹·K⁻¹) its isobaric heat capacity. For the liquid metals considered here, we have already published density reference correlations [1–4], and the heat capacity is readily available in the literature (e.g., [48]), so that the conversion we have performed is straightforward, although it introduces a small additional uncertainty in the thermal conductivity values. The recent measurements of Savchenko et al. [49–51] performed with uncertainties of 2.5–5% satisfy most of the criteria for primary data, and were thus included in the primary data set.

Measurements with the laser-flash technique were also performed by Nishi et al. [52], Cusco and Monaghan [22], Schriempf [53], and Otter and Arles [54], with corresponding estimated uncertainties of 3.3, 12, 5, and 5%, and these also formed part of the primary data set. The 2002 measurements of Shibata et al. [55], performed with an uncertainty of 30%, were considered as secondary data. Their technique was improved in their paper in 2003 [52]. Finally, the measurements of Khusainova and Palova [56] were also considered as secondary, because no assessment of uncertainty was given in the paper, and the results were consistently lower than all the others.

The electromagnetic-levitation technique was employed by Baba et al. [25] and Sugie et al. [57] with corresponding uncertainties of 10 and 5%. These two sets were included in the primary data set. The measurements of Kobatake et al. [58], although they do not quote an uncertainty, were also included in the primary data set, because they are from the same research group who provided reliable results [25, 57].

The temperature-wave technique was employed by Wittenberg [59], Ilinykh et al. [60], and Zinovyev et al. [61, 62] to measure the thermal diffusivity of lead and tin in 1973 [59], of iron in 1984 [60], iron and nickel in 1986 [61], and of copper in 1994 [62]. Their results, obtained with an estimated 5–10% uncertainty were included in the primary data set. The 1973 measurements of Filippov [63] however, include no discussion of uncertainty and the values deviate considerably from the consensus of all other measurements. Hence this set was not included among the primary data. The measurements of Yurchak and Filippov [64] were also excluded from the primary data set, because they deviated considerably from all other measurements at high temperatures. Using the same instrument, thermal diffusivity values at very high temperatures were published by Atalla et al. [65] and Banchila and Filippov [66]; they were also excluded from the primary data set.

Finally, the measurements of Nagai et al. [27], performed in a hot-disk instrument, were also included in the primary data set, but with a lower weight because no discussion of their uncertainty was included. We should also mention that in three cases it was not possible to obtain any information on the technique employed [67–69], and thus these measurements were considered as secondary data.

3.3 Thermal conductivity reference correlation

The primary thermal conductivity data for liquid copper, gallium, indium, iron, lead, nickel, and tin, shown in Tables 1 to 7 respectively, were employed in linear regression analyses to represent the thermal conductivity at 0.1 MPa, as a function of the temperature. A linear representation was adequate considering the uncertainties quoted for the data. The quoted uncertainties differed considerably, and the data were primarily weighted in inverse proportion to their uncertainty. In the case where the number of data of a particular investigator was very large in relation to the others, the aforementioned weight was reduced (by a factor equal to the average number of data of the other investigators divided by the number of data of the particular investigator). The following equation was used for the thermal conductivity, λ (W·m⁻¹·K⁻¹), as a function of the absolute temperature, T (K):

$$\lambda =c_1+c_2(T-T_{\mathrm{m}}),$$ (2)

where the coefficients c₁ (W·m⁻¹·K⁻¹), c₂ (W·m⁻¹·K⁻²), and the normal melting point T_m (K) are shown in Table 8. In the same table, the reference for the melting point and the temperature range of applicability are included. Finally, the expanded uncertainty, 2σ (%), of the above equation at the 95% confidence level is also shown.

Table 8.

Coefficients and ranges of Eq. (2)

	Trange (K)	c1 (W·m−1·K−1)	c2 (W·m−1·K−2)	Tm (K)	Tm Ref.	2σ, 95% (%)
Copper	1358 – 1700	150.49	0.070410	1357.77	[2]	9.8
Gallium	303 – 850	28.403	0.071896	302.914	[1]	15.9
Indium	430 – 1300	36.493	0.029185	429.748	[4]	9.7
Iron	1815 – 2050	36.349	0.0096207	1811	[1]	13.7
Lead	602 – 1150	16.093	0.0078526	600.61	[3]	16.9
Nickel	1730 – 2000	54.182	0.020970	1728	[3]	7.7
Tin	507 – 2000	28.037	0.023397	505.8	[2]	12.6

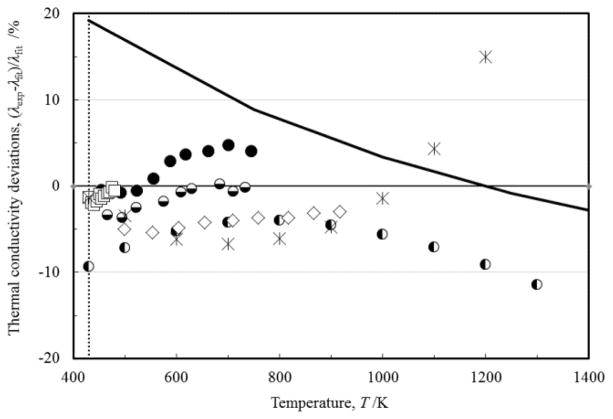
In Figs 8 to 14, the percentage deviations of the primary data employed for the derivation of Eq. (2) from the above equation for liquid copper, gallium, indium, iron, lead, nickel, and tin are shown respectively. All deviations shown in these figures are within the mutual uncertainty stated by each researcher and the standard deviation of Eq. (2).

FIGURE 8.

Percentage deviations of the primary thermal-conductivity data of liquid copper as a function of the temperature: (○) Baba et al. [25]; (△) Cusco and Monaghan [22]; (▲) Zinovyev et al. [62]; (◆) Tye and Hayden [9]. Previous reference correlation of Mills et al. [11], (▬), and reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

FIGURE 14.

Percentage deviations of the primary thermal-conductivity data of liquid tin as a function of the temperature: (◐) Savchenko et al. [50]; (□) Nagai et al. [27]; (◒) Bilek et al. [19]; (●;) Peralta et al. [18]; (■) Sklyarchuk and Plevachuk [35]; (▲) Hemminger [33]; (⦵) Otter and Arles [54]; (×) Zinovyev et al. [26]; (◇) Osipenko [38]; (⏀) Dutchak and Panasyuk [37]; (○) Kineke [32]; (△) Nikolskii et al. [39]; (◆) Brown [41]; (⬙) Konno [42]. Previous reference correlation of Mills et al. [11], (▬), and estimated reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

We note that for some of the metals, namely, gallium, indium, lead and tin, the results of Peralta et al.[18] and Bilek et al.[19, 20] have a significantly lower uncertainty than the standard deviation of the fit derived for the whole correlation. It may well be that the estimated uncertainty of the correlation in the lower temperature region which they covered could be reduced. However, the absence of any corroborative measurements by another technique suggests that it may be best to apply some caution until their work is supported by other accurate studies.

Thermal conductivity values calculated from Eq. (2) are listed in Table 9.

Table 9.

Recommended reference thermal-conductivity values for liquid metals at 0.1 MPa

	Copper	Gallium	Indium	Iron	Lead	Nickel	Tin
T (K)	Thermal conductivity, λ (W·m−1·K−1)
350		31.8
400		35.4
450		39.0	37.1
500		42.6	38.5
550		46.2	40.0				29.1
600		49.8	41.5				30.2
650		53.4	42.9		16.5		31.4
700		57.0	44.4		16.9		32.6
750		60.5	45.8		17.3		33.8
800		64.1	47.3		17.7		34.9
850		67.7	48.8		18.1		36.1
900			50.2		18.4		37.3
950			51.7		18.8		38.4
1000			53.1		19.2		39.6
1050			54.6		19.6		40.8
1100			56.1		20.0		41.9
1150			57.5		20.4		43.1
1200			59.0				44.3
1250			60.4				45.4
1300			61.9				46.6
1350							47.8
1400	153.5						49.0
1450	157.0						50.1
1500	160.5						51.3
1550	164.0						52.5
1600	167.5						53.6
1650	171.1						54.8
1700	174.6						56.0
1750						54.6	57.1
1800						55.7	58.3
1850				36.7		56.7	59.5
1900				37.2		57.8	60.7
1950				37.7		58.8	61.8
2000				38.2		59.9	63.0
2050				38.6

4 CONCLUSIONS

The available experimental data for the thermal conductivity of liquid copper, gallium, indium, iron, lead, nickel, and tin have been critically examined with the intention of establishing thermal-conductivity reference correlations at 0.1 MPa. All experimental data have been categorized into primary and secondary data according to the quality of measurement specified by a series of criteria. The proposed standard reference correlations for the thermal conductivity of liquid copper, gallium, indium, iron, lead, nickel, and tin are characterized by uncertainties of 9.8, 15.9, 9.7, 13.7, 16.9, 7.7, and 12.6% at the 95% confidence level, respectively.

FIGURE 2.

Measurements of the thermal conductivity of liquid gallium as a function of the temperature; (●) Peralta et al. [18]; (◇) Fukuyama et al. [29]; (◒) Miyamura and Susa (Abs) [28]; (◓) Miyamura and Susa (Rel) [28]; (- -) Okada and Ozoe [67]; (□ -) Gamazov et al. [68]; (◑) Magmedov [36]; (□) Filippov [63]; (△) Schriempf [53]; (⏀) Dutchak and Panasyuk [37]; (▲) Duggin [45]; (⬖) Pashaev [44]. Previous reference correlation of Mills et al. [11], (▬), and reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

FIGURE 3.

Measurements of the thermal conductivity of liquid indium as a function of the temperature: (◐) Savchenko et al. [49]; (◒) Bilek et al. [19]; (●) Peralta et al. [18]; (□) Goldratt and Greenfield [31]; (■) Khusainova and Palova [56]; (▲) Duggin (Pyrex cell) [46]; (△) Duggin Pyrex (SS cell) [46]; (◆) Atalla et al. [65]; (◇) Osipenko [38]. Previous reference correlation of Mills et al. [11], (▬), and estimated reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

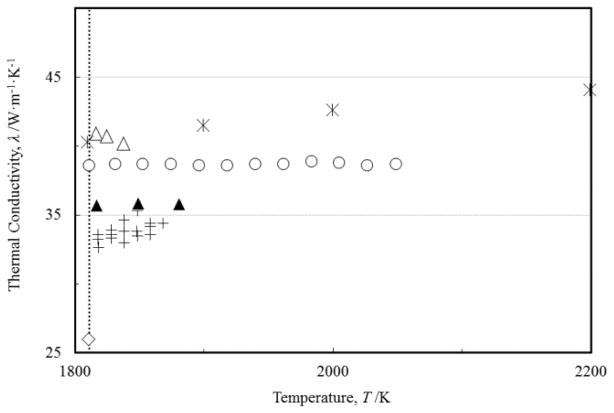
FIGURE 4.

Measurements of the thermal conductivity of liquid iron as a function of the temperature: (○) Sugie et al. [57]; (+) Nishi et al. [52]; (▲) Zinovyev et al. [61]; (△) Ilinykh et al. [60]; (◇) Ostrovskii et al. [69]. Previous reference values of Touloukian et al. [10], ( ) up to 2200 K, are also shown. (....) melting point.

FIGURE 5.

Measurements of the thermal conductivity of liquid lead as a function of the temperature: (○) Savchenko et al. [51]; (●) Bilek et al. [20]; (◆) Sklyarchuk and Plevachuk [35]; (+) Yamasue [7]; (▲) Nakamura et al. [30]; (■) Hemminger [34]; (- - ) Banchila and Filippov [66]; (□ -) Filippov [63]; (□) Wittenberg [59]; (◭) Duggin [46]; (◇) Osipenko [38]; (⏀) Dutchak and Panasyuk [37]; (◨) Yurchak and Filippov [64]; (△) Nikolskii et al. [39]; (◐) Powell and Tye [40]; (◑) Bidwell [47]; (⬙) Konno [42]. Previous reference correlation of Mills et al. [11], (▬), and estimated reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

FIGURE 6.

Measurements of the thermal conductivity of liquid nickel as a function of the temperature: (●) Kobatake et al. [58]; ( ) Nagata et al. [17]; (○) Nishi et al. [52]; (▲) Zinovyev et al. [61]; (◇) Ostrovskii et al. [69]. Previous reference value of Mills et al. [11], (▬), is also shown. (....) melting point.

FIGURE 9.

Percentage deviations of the primary thermal-conductivity data of liquid gallium as a function of the temperature: (●) Peralta et al. [18]; (◇) Fukuyama et al. [29]; (◒) Miyamura and Susa (Abs) [28]; (◓) Miyamura and Susa (Rel) [28]; (◑) Magmedov [36]; (△) Schriempf [53]; (⏀) Dutchak and Panasyuk [37]. Previous reference correlation of Mills et al. [11], (▬), and reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

FIGURE 10.

Percentage deviations of the primary thermal-conductivity data of liquid indium as a function of the temperature: (◐) Savchenko et al. [49]; (◒) Bilek et al. [19]; (●) Peralta et al. [18]; (□) Goldratt and Greenfield [31]; (▲) Duggin (Pyrex cell) [46]; (△) Duggin Pyrex (SS cell) [46]; (◇) Osipenko [38]. Previous reference correlation of Mills et al. [11], (▬), and estimated reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

FIGURE 11.

Percentage deviations of the primary thermal-conductivity data of liquid iron as a function of the temperature: (○) Sugie et al. [57]; (+) Nishi et al. [52]; (▲) Zinovyev et al. [61]; (△) Ilinykh et al. [60]. Previous reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

FIGURE 12.

Percentage deviations of the primary thermal-conductivity data of liquid lead as a function of the temperature: (○) Savchenko et al. [51]; (●) Bilek et al. [20]; (◆) Sklyarchuk and Plevachuk [35]; (▲) Nakamura et al. [30]; (■) Hemminger [34]; (□) Wittenberg [59]; (◇) Osipenko [38]; (⏀) Dutchak and Panasyuk [37]; (△) Nikolskii et al. [39]; (◐) Powell and Tye [40]; (⬙) Konno [42]. Previous reference correlation of Mills et al. [11], (▬), and estimated reference values of Touloukian et al. [10], ( ), are also shown. (....) melting point.

FIGURE 13.

Percentage deviations of the primary thermal-conductivity data of liquid nickel as a function of the temperature: (●) Kobatake et al. [58]; (○) Nishi et al. [52]; (▲) Zinovyev et al. [61]. Previous reference value of Mills et al. [11], (▬), is also shown. (....) melting point.

TABLE 2.

Data sets considered for the thermal conductivity of liquid gallium at 0.1 MPa

First author	Publ. year	Ref.	Puritya (mass %)	Technique employedb	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datac
Previous reference correlation/values
Mills	1996	[11]				-	303–1200	E
Touloukian	1970	[10]			10–15	4	303–600	P
Primary data
Peralta-Martinez	2006	[18]	99.99	Transient hot wire	2	7	321–615	P
Fukuyama	2006	[29]	99.99	Transient hot wire	18	3	301–330	D
Miyamura	2002	[28]	99.9999	Transient hot wire (Abs)	15	6	309–471	D
Miyamura	2002	[28]	99.9999	Transient hot wire (Rel)	15	6	308–471	D
Magmedov	1978	[36]	HP	Guarded heat flow	-	16	314–836	D
Schriempf	1973	[53]	99.99	Laser flash (TD)	5	21	316–785	D
Dutchak	1967	[37]	-	Guarded heat flow	-	4	305–474	D
Secondary data
Okada	1992	[67]	-	ns	2.5	-	306–312	E
Gamazov	1979	[68]	-	ns	-	-	550–1300	E
Filippov	1973	[63]	-	Temperature wave (TD)	-	4	1102–1480	D
Duggin	1969	[45]	Pure	Guarded heat flow	2.5	20	357–589	D
Pashaev	1961	[44]	99.999	Guarded heat flow	5	15	308–618	D

^aHP = High Purity

^bAbs = absolute, Rel = relative, TD = thermal diffusivity measurement, ns = not stated.

^cD = diagram, E = equation, P = table data

TABLE 3.

Data sets considered for the thermal conductivity of liquid indium at 0.1 MPa

First author	Publ. year	Ref.	Purity (mass %)	Technique employeda	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datab
Previous reference correlation/values
Mills	1996	[11]				-	430–2000	E
Touloukian	1970	[10]			4–10	9	430–1200	P
Primary data
Savchenko	2010	[49]	99.996	Laser flash (TD)	3.5–5	10	429–1300	P
Peralta-Martinez	2006	[18]	99.99	Transient hot wire	2	9	453–744	P
Bilek	2006	[19]	99.999	Transient hot wire	3	9	467–734	P
Goldratt	1980	[31]	99.999	Guarded heat flow	1	11	430–482	D
Osipenko	1970	[38]	-	Guarded heat flow	-	9	498–917	D
Secondary data
Khusainova	1976	[56]	-	Laser flash (TD)		14	766–1259	D
Atalla	1972	[65]	-	Temperature wave (TD)	8	20	1170–2045	D
Duggin	1972	[46]	99.999	Guarded heat flow (SScell)	5	22	455–843	D
Duggin	1972	[46]	99.999	Guarded heat flow (Pyrex)	3	25	442–633	D

^aTD = thermal diffusivity measurement

^bD = diagram, E = equation, P = table data

TABLE 4.

Data sets considered for the thermal conductivity of liquid iron at 0.1 MPa

First author	Publ. year	Ref.	Purity (mass %)	Technique employeda	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datab
Previous reference values
Touloukian	1970	[10]			3–8	8	1810–3000	P
Primary data
Sugie	2011	[57]	99.98	Electromagnetic levitation	5	12	1811–2049	D
Nishi	2003	[52]	99.80	Laser flash (TD)	3.3	16	1818–1869	D
Zinovyev	1986	[61]	99.99	Temperature wave (TD)	5	3	1817–1881	D
Ilinykh	1984	[60]	-	Temperature wave (TD)	5	3	1816–1838	D
Secondary data
Ostrovskii	1980	[69]	99.90	ns	20	1	1811	D

^aTD = thermal diffusivity measurement, ns = not stated,

^bD = diagram, P = table data

TABLE 5.

Data sets considered for the thermal conductivity of liquid lead at 0.1 MPa

First author	Publ. year	Ref.	Puritya (mass %)	Technique employedb	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datac
Previous reference correlation/values
Mills	1996	[11]				-	601–2100	E
Touloukian	1970	[10]			6–10	5	601–1000	P
Primary data
Savchenko	2013	[51]	99.992	Laser flash (TD)	3.5–5.0	5	608–1007	D
Bilek	2007	[20]	99.99	Transient hot wire	3	3	620–730	P
Sklyarchuk	2005	[35]	-	Guarded heat flow	7	19	607–1001	D
Nakamura	1990	[30]	-	Transient hot wire	-	9	620–973	D
Hemminger	1989	[34]	99.994	Guarded heat flow	3	5	616–773	P
Wittenberg	1973	[59]	99.999	Temperature wave (TD)	10	5	724–924	D
Osipenko	1970	[38]	-	Guarded heat flow	-	6	669–973	D
Dutchak	1967	[37]	-	Guarded heat flow	-		628–872	D
Powell	1958	[40]	99.995	Guarded heat flow	-	10	625–887	D
Nikolsky	1959	[39]	-	Guarded heat flow	-	47	699–1130	D
Konno	1920	[42]	99.90	Guarded heat flow	-	3	628–874	D
Secondary data
Yamasue	2003	[7]	-	Transient hot wire	8	8	671–1373	D
Banchila	1973	[66]	99.9995	Temperature wave (TD)	6	9	1159–2081	D
Filippov	1973	[63]	-	Temperature wave (TD)	-	6	600–1312	D
Duggin	1972	[46]	Spectr.	Guarded heat flow	5	157	626–875	D
Yurchak	1965	[64]	-	Temperature wave (TD)	6–8	29	828–1255	D
Bidwell	1940	[47]	-	Guarded heat flow	-	2	607–894	D

^aSpectr. = Spectroscopy grade

^bTD = thermal diffusivity measurement

^cD = diagram, E = equation, P = table data

TABLE 6.

Data sets considered for the thermal conductivity of liquid nickel at 0.1 MPa

First author	Publ. year	Ref.	Purity (mass %)	Technique employeda	Uncertainty quoted (%)	No. of data	Temp. Range (K)	Form of datab
Previous reference value
Mills	1996	[11]				1	1728	P
Primary data
Kobatake	2010	[58]	-	Electromagnetic levitation	-	15	1711–1983	D
Nishi	2003	[52]	-	Laser flash(TD)	3.3	34	1728–1868	D
Zinovyev	1986	[61]	99.90	Temperature wave (TD)	5	3	1739–1769	D
Secondary data
Nagata	2003	[17]	-	Transient hot wire	-	2	1789,1822	D
Ostrovskii	1980	[69]	99.90	ns	26	1	1728	P

^aTD = thermal diffusivity measurement, ns = not stated

^bD = diagram, P = table data