Measurements of Enthalpy of Sublimation of Ne, N₂, O₂, Ar, CO₂, Kr, Xe, and H₂O using a Double Paddle Oscillator

Abstract

We report precise experimental values of the enthalpy of sublimation (ΔH_s) of quenched condensed films of neon (Ne), nitrogen (N₂), oxygen (O₂), argon (Ar), carbon dioxide (CO₂), krypton (Kr), xenon (Xe), and water (H₂O) vapor using a single consistent measurement platform. The experiments are performed well below the triple point temperature of each gas and fall in the temperature range where existing experimental data is very limited. A 6 cm² and 400 µm thick double paddle oscillator (DPO) with high quality factor (Q ≈ 4 × 10⁵ at 298K) and high frequency stability (33 parts per billion) is utilized for the measurements. The enthalpies of sublimation are derived by measuring the rate of mass loss during temperature programmed desorption. The mass change is detected due to change in the resonance frequency of the self-tracking oscillator. Our measurements typically remain within 10% of the available literature, theory, and National Institute of Standards and Technology (NIST) Web Thermo Tables (WTT) values, but are performed using an internally consistent method across different gases.

1. Introduction

The intermolecular interaction of the condensed solid phase is a critical thermodynamic property and measured as the enthalpy of sublimation (ΔH_s). A variety of techniques have been developed to experimentally determine the sublimation energies and are broadly categorized as either direct or indirect [4–6]. Direct techniques, utilizing appropriate calorimeters, involve the measurement of heat during the sublimation process [9; 10]. Indirect methods measure the vapor pressure at different temperatures and assume that the sublimation enthalpies remain constant in the experimental temperature range [8; 11–13]. The sublimation vapor pressure measurements are typically carried out by either using standard manometers or non-traditional resonant base micro-sensors. Resonant micro-sensors such as quartz crystal microbalances (QCMs) [15–17] and silicon micro-machined double paddle oscillators (DPOs) [7; 18–20] are two methods utilized to measure the sublimation vapor pressures and enthalpies of different atmospheric gases. The change in mass of the deposited solid film is measured as a change in the resonance frequency of the micro-sensor. Subsequently, the evaluation of sublimation enthalpy is carried out during a temperature programmed desorption (TPD) of the film. Compared to DPO measurements, QCM measurements have the advantage of being able to operate in air and liquid environments. However, DPOs can provide better mass sensitivity (≈0.027 ng/cm²) and frequency stability (33 parts per billion) [18; 22] under ultra-high vacuum and at cryogenic temperature conditions. QCMs have been able to measure vapor pressures between 10⁻¹ Pa and 10⁻⁷ Pa for H₂O, N₂O and CO₂ films [16] while DPOs have been able to reach vapor pressures down to 4.8 ×10⁻¹¹ Pa for quenched condensed films of neon [20].

Despite a large number of experiments performed over the last century to experimentally evaluate enthalpies of sublimation of common atmospheric gases, we found limited experimental data for enthalpy values well-below the triple point temperatures. For example, in the National Institute of Standards and Technology (NIST) Web Thermo Tables (WTT) [1], no data are included for sublimation experiments of neon below 10 K, nitrogen below 35 K, and oxygen below 36 K. Consequently, the sublimation energies reported on the WTT [1] at these temperatures for each film are extrapolated from their respective triple point values and therefore have both large absolute and relative uncertainties. According to the WTT [1], the enthalpy of sublimation of neon at 10 K is (2.16 ± 0.22) kJ · mol⁻¹, nitrogen at 36 K is (6.9 ± 4.6) kJ · mol⁻¹ and oxygen at 36 K is (8.7 ± 3.7) kJ · mol⁻¹. Experiments have shown that nitrogen, CO₂, and water films exist in different solid phases [8; 28] below their triple points and thus can have different activation energies. Therefore, a thorough experimental study is required to benchmark the enthalpies of different atmospheric gases well below their triple point temperatures.

To address this need, we employed a single 400 µm thick DPO (for all the experiments presented) which was excited in the 2^nd anti-symmetric (AS2) torsional mode with a resonant frequency around 7.2 kHz. The AS2 mode of the DPO shows extremely high intrinsic quality factors both at room temperature (Q ≈ 4 ×10⁵) and 5 K (Q ≈ 8 × 10⁷). In general, the mass sensitivity of an oscillator is proportional to its mechanical quality factor. Therefore, a DPO excited in the AS2 mode provides an ideal measurement platform to study the evaporative mass loss during the sublimation process. In this study, we determined the enthalpy of sublimation for eight different atmospheric gases including Ne, N₂, O₂, Ar, CO₂, Kr, Xe, and H₂O with the 400 µm thick DPO. During the course of the current study, the same sensor was used for all measurements and was never removed from the chamber. The method presented here provides a single consistent measurement platform which reduces any systematic uncertainties that could be introduced during loading and unloading of the sensor. In the subsequent sections, we explain the theoretical background, apparatus, detailed example experiment using nitrogen, sources of uncertainties, and compile all results.

2. Theoretical Background

2.A. DPO Mechanics

The basic equation for the resonance frequency of the DPO in the torsional mode is given by

$$f=\frac{1}{2\pi }\sqrt{\frac{k}{I}}$$ (1)

where k is the torsional spring (elastic) constant and I is the moment of inertia of the paddle. Mass loading on the surface of the DPO will change both the elastic constant and the moment of inertia in equation (1). The resulting change in the resonance frequency upon mass loading is the primary mechanism used to quantitatively derive different properties (thickness, elastic modulus, porosity, internal friction and heat of sublimation [7; 19; 20; 30–34]) of the deposited material. The frequency shift for the AS2 mode for a film laden DPO relative to a bare DPO is mathematically approximated by equation (2) [20].

$${\frac{\mathrm{\Delta }f}{f}|}_{\mathit{\text{total}}}={\frac{\mathrm{\Delta }f}{f}|}_{\mathit{\text{elastic}}}+{\frac{\mathrm{\Delta }f}{f}|}_{\mathit{\text{mass}}}=\frac{3G_{\mathit{\text{film}}}{h}_{\mathit{\text{film}}}}{2G_{\mathit{\text{DPO}}}{h}_{\mathit{\text{DPO}}}}-\frac{{\rho }_{\mathit{\text{film}}}{h}_{\mathit{\text{film}}}}{2{\rho }_{\mathit{\text{DPO}}}{h}_{\mathit{\text{DPO}}}}$$ (2)

Where subscript "DPO" stands for the bare paddle with metal electrodes, “film” refers to the film of the gas molecules adsorbed onto the DPO, Δf is the resulting frequency shift, G are the shear moduli, h is the thickness, and ρ are the densities. The total change in the resonance frequency of the paddle can be attributed to the change in the shear modulus (first term) and mass loading (second term) of the deposited film. Analysis of the contribution from each mechanism is discussed below.

2. B. Fundamental Sublimation Mechanism

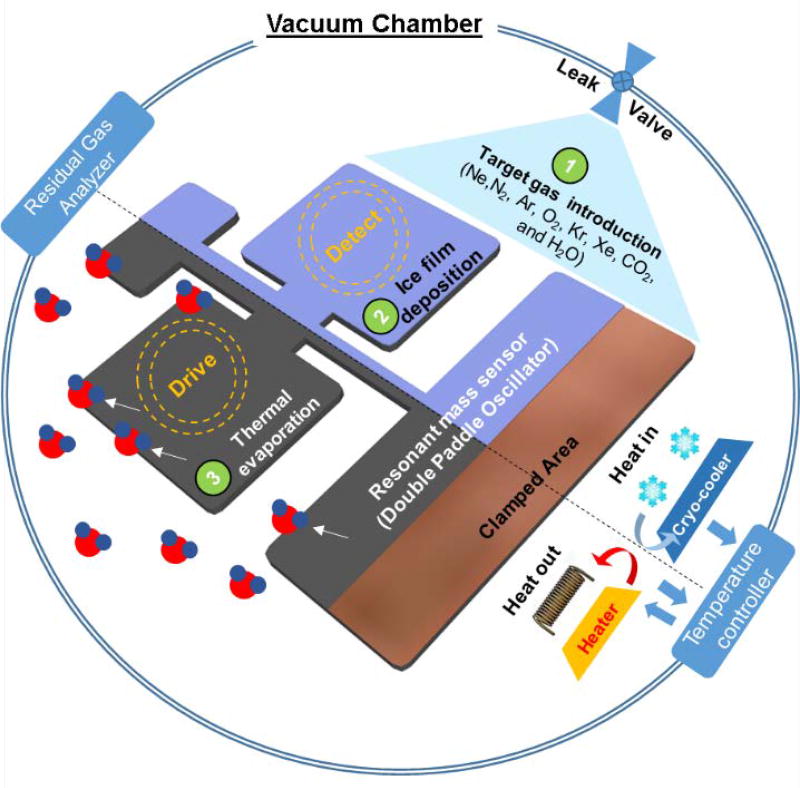
Determination of the enthalpy of sublimation is based on the principle of mass conservation and involves three main steps. This three step process is pictorially depicted in Figure 1 and explained in detail below.

Figure 1.

Schematic of the experimental process utilizing fundamental adsorption and desorption mechanisms inside an ultra-high vacuum chamber. (From right to left) Step 1 shows the introduction of the target gases from a leak valve, step 2 depicts the growth of the solid film on the surface of DPO held at temperatures well-below the triple point temperature of each gas and the last step (3) shows the thermal evaporation of gas molecules as the DPO is heated allowing some gas to release.

2.B.1. Mass Loading

The gas atoms/molecules arriving at the surface of the DPO (kept below the triple-point temperature of the target gas) result in a highly disordered solid film. The random distribution of the adsorbed gas molecules initially results in a highly porous film with a very small shear modulus [37]. In order to estimate the thickness of the deposited material, typically bulk values of shear modulus and density of the film are used in equation (2). For example, for bulk neon G_film/G_DPO ≅ 0.01 [20] and ρ_film/ρ_DPO ≅ 0.65.[2]. Therefore, the contribution of the elastic term in equation (2) is small compared to the mass term. The following linear frequency-mass relationship, relative to the base resonance frequency of the paddle, is typically used to estimate the thickness of the deposited film [20; 38].

$${\frac{\mathrm{\Delta }f}{f}|}_{\mathit{\text{total}}}\approx {\frac{\mathrm{\Delta }f}{f}|}_{\mathit{\text{mass}}}=-\frac{{\rho }_{\mathit{\text{film}}}{h}_{\mathit{\text{film}}}}{2{\rho }_{\mathit{\text{DPO}}}{h}_{\mathit{\text{DPO}}}}$$ (3)

The thickness of a film is computed using the bulk density values in equation (3). The negative sign in equation (3) signifies that during mass loading the resonance frequency of the paddle decreases. The estimation of the film thickness is only used as a control parameter during different experimental runs performed for the same target gas and not used for the enthalpy measurements.

2.B.2. Relaxation

The as-deposited ice films are initially highly disordered and porous [37]. Once the temperature of the DPO is increased, the atoms/molecules start to rearrange themselves into a more ordered form. This rearrangement leads to atomic relaxations and increases both the stiffness (G_film) and the density (ρ_film) of the film. The rise in the resonance frequency is due to the stiffening of the film (G_filmh_film increases) and a small amount of evaporative mass loss (ρ_filmh_film decreases) as the temperature rises. Earlier studies carried out on neon and argon solid films have shown [20] that these two mechanisms can be separated (to some extent) by controlling the DPO temperature. The rise in resonance frequency is mainly due to the increasing film stiffness at temperatures above the deposition temperature but where the vapor pressure is still low. In order to reduce the effect of the changing elastic term during the sublimation experiment, each film is annealed at temperatures where evaporative mass loss is small for 35 minutes to 50 minutes.

2.B.3. Desorption

The time reversal process of adsorption is desorption (sublimation) and studied here. The enthalpies of sublimation are derived from the apparent vapor pressures (P_a) of each gas during desorption and measured in narrow temperature ranges where the sublimation enthalpies can be treated as constants [20]. In principle, all the thermally activated molecules should escape, however, experimentally, a constant of proportionality (condensation coefficient) is used to account for difference between absolute and apparent vapor pressures. We are not able to independently determine the condensation coefficient. Therefore, we report the measured “apparent” vapor pressures in this work. We also see uncontrolled variations in the absolute value of the apparent vapor pressures from different experimental runs. We assume the differences are due to a change in condensation coefficient resulting from some surface changes. However, the temperature dependence of the apparent vapor pressure from run to run change little resulting in consistent heat of sublimation values. Therefore, the data supports the conclusion that the condensation coefficient is a temperature independent constant within the range of our data sets. The sublimation of gas molecules by sequentially heating the DPO is determined by monitoring the mass loss. In our study, the run to run variations between the apparent vapor pressures do not affect the measurement of heat of sublimation.

The mass per unit area (m_film) of the film on the surface of the oscillator is ρ_filmh_film. Given that the atomic mass of the gas is M, the total number of atoms/molecules (N) on the surface per unit area is

$$N=\frac{m_{\mathit{\text{film}}}}{M}$$ (4)

The time derivative of the equation (4) is the flux F (number of atoms/molecules leaving per unit area and time) and is given by

$$F=\frac{1}{M}\times \frac{d}{\mathit{\text{dt}}}{m}_{\mathit{\text{film}}}$$ (5)

The flux F of the leaving atoms/molecules is given by the modified Hertz-Knudsen formula [39]

$$F=\frac{P_a}{\sqrt{2\pi {\mathit{\text{Mk}}}_{B}T}}$$ (6)

Where, P_a is the apparent vapor pressure of gas given by condensation coefficient (α) times the absolute vapor pressure (P), M is the atomic/molecular mass of gas, k_B is the Boltzmann’s constant and T is the temperature. Combining equations (5) and (6)

$$P_a=\sqrt{\frac{2\pi k_{B}T}{M}}\times \frac{d}{\mathit{\text{dt}}}{m}_{\mathit{\text{film}}}$$ (7)

The rate of evaporative mass loss of the film (dm_film/dt) at each temperature is correlated to the change in oscillator frequency using equation (2) and given by

$$\frac{d}{\mathit{\text{dt}}}{m}_{\mathit{\text{film}}}=\frac{1}{f}{(\frac{3G_{\mathit{\text{film}}}^0}{2G_{\mathit{\text{DPO}}}{\rho }_{\mathit{\text{film}}}^0{h}_{\mathit{\text{DPO}}}}-\frac{1}{2{\rho }_{\mathit{\text{DPO}}}{h}_{\mathit{\text{DPO}}}})}^{-1}\times \frac{d(\mathrm{\Delta }f)}{\mathit{\text{dt}}}$$ (8)

where $G_{\mathit{\text{film}}}^0$ stands for the bulk shear modulus and ${\rho }_{\mathit{\text{film}}}^0$ represents the bulk density of the film. For each film we use the bulk values ( $G_{\mathit{\text{film}}}^0$ and ${\rho }_{\mathit{\text{film}}}^0$) gathered from the available literature. Equation 8 provides the rate of evaporative mass loss per unit area of the film at a particular temperature.

Substituting equation (8) into equation (7) yields the apparent sublimation vapor pressure of the target gas

$$P_a=\sqrt{\frac{2\pi k_B{T}_{\mathit{\text{DPO}}}}{M}}\frac{1}{f}{(\frac{3G_{\mathit{\text{film}}}^0}{2G_{\mathit{\text{DPO}}}{\rho }_{\mathit{\text{film}}}^0{h}_{\mathit{\text{DPO}}}}-\frac{1}{2{\rho }_{\mathit{\text{DPO}}}{h}_{\mathit{\text{DPO}}}})}^{-1}\times \frac{d(\mathrm{\Delta }f)}{\mathit{\text{dt}}}$$ (9)

The vapor pressure of the condensed phase is an important thermodynamic property that can be utilized to derive other fundamental physical properties like the heat of sublimation. In this study, we quantitatively derive the enthalpy of sublimation of different atmospheric gases by correlating their apparent vapor pressures to the shift in the resonance frequency during TPD. The vapor pressure of the gas is given by the famous Clausis-Clapeyron equation and approximated using an Arrhenius law. This approximation assumes that the sublimation enthalpy does not change with temperature over the range of the experiment and the ideal gas law holds [6].

$$P_a=C·\text{exp }(-\frac{\mathrm{\Delta }{H}_s}{k_B{T}_{\mathit{\text{DPO}}}})$$ (10)

where, C is a constant, ΔH_S is the enthalpy of sublimation, and T_DPO is the temperature of DPO. We can evaluate the heat of sublimation of the target gas by combining equations (9) and (10) and using a linear form of the resulting equation as

$$\mathrm{\Delta }{H}_s=k_B{T}_{\mathit{\text{DPO}}}\times [\text{ln }C-\text{ln}\{\sqrt{\frac{2\pi k_B{T}_{\mathit{\text{DPO}}}}{M}}\frac{1}{f}{(\frac{3G_{\mathit{\text{film}}}^0}{2G_{\mathit{\text{DPO}}}{\rho }_{\mathit{\text{film}}}^0{h}_{\mathit{\text{DPO}}}}-\frac{1}{2{\rho }_{\mathit{\text{DPO}}}{h}_{\mathit{\text{DPO}}}})}^{-1}\times \frac{d(\mathrm{\Delta }f)}{\mathit{\text{dt}}}\left\}\right]$$ (11)

The rate of shift in the resonance frequency (d(Δf)/dt) with respect to the base frequency (f) and the corresponding DPO temperature (T_DPO) are experimentally measured during each TPD step. The apparent sublimation vapor pressure of the evaporating gas is calculated at each temperature using equation (9). The enthalpy of sublimation of each target gas is calculated from equation (11) using a simple linear fit of the logarithm of the measured apparent vapor pressure against the inverse temperature. The units of energy (ΔH_s) are converted using the universal gas constant (R) value of 8.31446 J · mol⁻¹K⁻¹ [38]. The following sections explain in detail the experimental procedure used in this study to precisely measure the enthalpy values.

3. Experimental Section

3.A. Materials

The 400 µm thick DPO was fabricated from a 100-mm-wide, double side polished, un-doped, float zone and a (100) oriented single crystal silicon wafer with a high resistivity at room temperature (>10 k ohm-cm). All the gases (Table 1), except for neon, used in the experiments were of research grade purity (99.9999 %). Neon was purchased as an ultra-high purity grade (99.999 %) gas. Water was degasified using a freeze-vacuum-thaw method [3] for at least three cycles.

Table 1.

Source and purification details of the gases used in experiments

Chemical Name	Supplier	Purity Level	Purification Method	Analysis Method
Neon	MATHESONa	99.999 %	-	Provided by supplier
Nitrogen	MATHESONa	99.9999 %	-	Provided by supplier
Argon	MATHESONa	99.9999 %	-	Provided by supplier
Oxygen	MATHESONa	99.9999 %	-	Provided by supplier
Krypton	MATHESONa	99.9999 %	-	Provided by supplier
Xenon	MATHESONa	99.9999 %	-	Provided by supplier
Carbon dioxide	MATHESONa	99.9999 %	-	Provided by supplier
Water	-	-	Freeze vacuum thawb	-

^aCertain commercial products are identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology (NIST), nor does it imply that the products identified are necessarily the best available for the purpose.

^bRef [3]

3.B. Apparatus

Because the apparatus utilized in the current study has been explained in detail elsewhere [18], we will only summarize its important features here. The foot of the wet etched DPO is clamped to a mount assembly as shown in Figure 2. The mount assembly is attached to the second-stage of a 4.2 K cryogenic refrigerator. Afterwards, an outer heat shield is installed on the top of the DPO clamp assembly to reduce the radiative heat load. The sensor is housed in an ultra-high vacuum chamber with a typical base pressure of ≈ 6.6 ×10⁻⁷ Pa at room temperature. The system is equipped with an adjustable gas leak valve, a residual gas analyzer (RGA) and an ion gauge. Multiple low-temperature sensors and a closed-loop PID temperature controller are used to monitor and control temperature. The drive and detect signals are monitored and conditioned using a frequency counter, a current and a voltage amplifier and a lock-in amplifier. Additionally, a 10 MHz rubidium frequency standard with one second Allan Variance of < 2×10⁻¹¹ provides a clock source to different instruments enabling highly stable frequency measurements.

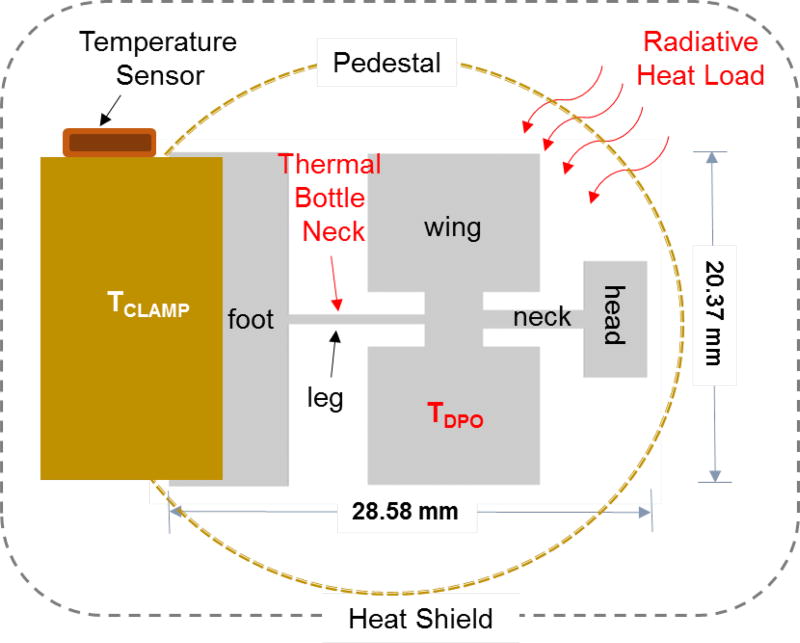
Figure 2.

Schematic representation of the 400 µm-thick DPO (right) installed on a clamp assembly (left) attached to the pedestal and the temperature sensor close to the foot of DPO. The leg (7.98 mm × 0.58 mm × 0.4 mm) of the DPO acts as a thermal bottle neck due to the poor thermal conductance of silicon below 10 K. This creates a temperature difference (T_DPO-T_CLAMP) between the DPO and the temperature sensor resulting in an under estimation of the sublimation enthalpy of Ne. The outer dashed box represents the heat shield installed to reduce the radiative heat load on the DPO during cryogenic operations.

The 400 µm thick DPO utilized in the current experiments was fabricated using well-established lithography and wet etching processes [40]. One side of the DPO has a T-patterned thin metal film of chrome (≈ 3 nm) and gold (≈ 50 nm) and is capacitively coupled to two electrodes used for excitation and detection purposes. An AC signal super-imposed onto a 200 V DC signal (coupled through a 1 µF capacitor) is used to linearize the driving force and enables the operation of the DPO at its fundamental resonance frequency. The detect signal is further processed (amplified and phase shifted) and used as a feedback to drive the oscillator in a self-tracking closed-loop. The frequency of the self-tracking sensor is constantly monitored using a high resolution frequency counter. Out of the different identifiable mechanical vibration modes, the sensor is operated in the AS2 mode.

3.C. Detailed Experiment

As explained earlier, each experiment used to evaluate the enthalpy values can be broadly categorized into three distinct steps or processes (mass loading, relaxation and thermal desorption as shown in Figure 3). We are going to use the sublimation of a thin solid nitrogen film and corresponding plots as an example to explain each of these processes in detail.

Figure 3.

The three steps (1. mass loading from start till 0.5 hr; 2. annealing/relaxation between 1.2 hr and 1.8 hr; 3. TPD from 2.6 hr to 3.6 hr) involved to determine the enthalpy of sublimation explained using N₂ gas as an example experiment.

3.C.1. Mass Loading

For nitrogen measurements, the system is first cooled down to ≈ 9 K (temperature measured at the foot of DPO as shown in Figure 2). The deposition temperature is well-below the triple point temperature ((63.148 ± 0.005) K) of nitrogen as reported in the NIST WTT [1]. Both the deposition temperature and a very low chamber pressure (≈5 ×10⁻⁷ Pa) ensure that during the TPD the solid film transitions directly into the gas phase (sublimation). Typical system cool-down to 10 K takes around 3 hours, Figure 3 only represents the data after the system has reached the desired temperature. Afterwards, nitrogen gas is slowly leaked into the chamber and the chamber pressure is constantly monitored through an ion gauge and a RGA. The rate of film deposition can be easily controlled through a high-precision adjustable gas leak valve. The partial pressure of nitrogen during deposition remained below ≈6.66 × 10⁻⁴ Pa. As the gas molecules start to deposit onto the cold sensor surface, the resonance frequency drops (Figure 3). After the desired film thickness (estimated from equation 3) is achieved, the leak valve is closed. The resonance frequency no longer drops and slowly rises as the film relaxes. The sensor is held at the deposition temperature for approximately an hour to equilibrate. The solid nitrogen film on the DPO is deposited at a rate of ≈ 0.3 nm/second for 15 minutes with the final film thickness of ≈266 nm estimated using equation 3.

3.C.2. Thermal Relaxation

As explained in the previous section, the nitrogen ice film formed after the deposition is highly porous with a small or a negligible elastic modulus. As the temperature rises, the molecules start to rearrange resulting in a more condensed film with an increasing shear modulus. The increase in the shear modulus along with the reducing film mass during warm-up is seen (equation 2) as a non-linear rise in the resonance frequency (Figure 4 a). Both the shear modulus and the film density can increase to a point where the relaxation levels off. Afterwards, the rise in the resonance frequency of the paddle increases linearly with time. The relaxed film is no stiffer and no denser than the bulk; giving an upper bound for both the shear modulus and the density of the relaxed film. After relaxation, the relationship between mass loss and frequency becomes linear. The solid nitrogen film (Figure 4 a) is heated at 23 K and ensures a significantly small evaporative mass loss. The two Gaussian fits (Figure 4 b) of the residuals (f_meas−f_fit) demonstrate the cut-off time (≈2.2 hours) in this case for a linear frequency-time relationship. The first Gaussian fit of the residuals from 1.55 hr to 2.2 hr (Figure 4 b₁) is skewed and represents an asymmetric frequency-time relationship. This shows that the solid nitrogen film is not completely relaxed. The second residual plot (Figure 4 b₁), between 2.2 hr and 2.55 hr, is highly symmetric demonstrating the rate of change of the resonance frequency (df/dt) is linearly related to the rate of change of mass (dm/dt). This shows that the solid film is properly relaxed after annealing at 23 K for more than 40 minutes. Therefore, we can utilize equation 11 (using the bulk values of shear modulus and density) to experimentally evaluate the enthalpies. It is pertinent to note that the relaxation time and temperature are different for the different materials studied in this work.

Figure 4.

Thermal relaxation of solid nitrogen film at 23 K (a) and the plot of residuals (b). The insets in plot (b) show the Gaussian plots that help to determine the minimum time required (shown as the vertical green dashed lines at 2.2 hr in both plots) to sufficiently anneal the film. The skewed Gaussian plot on the left (b₁) for the residuals between 1.53 hr and 2.2 hr shows the nonlinear frequency-time relationship, while the symmetric Gaussian plot on the right (b₂) shows a linear frequency-time dependence.

3.C.3. Thermal desorption

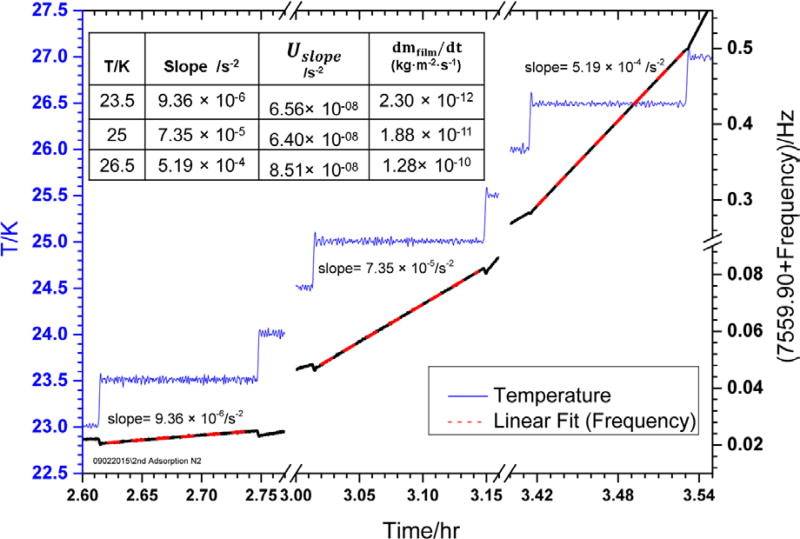
After the solid nitrogen film is sufficiently annealed, the next process is the step-by-step thermal desorption of the relaxed film. Figure 5 shows selected desorption data (starting immediately after the annealing step at 23 K). The temperature is increased by 0.5 K/step at a typical ramp rate of 5 K/minute and held at this temperature for about five minutes. The elastic modulus of silicon decreases with increasing temperature and the softening of silicon causes a small reduction in frequency at the start of each step (Figure 5), which we account for during final uncertainty analysis. The linear rise in the resonance frequency of the paddle held at a constant temperature is used to extract the evaporative mass loss. As the temperature rises to the next level, the rate of the evaporative mass loss increases (Figure 5); increasing the slope of each line (9.36 × 10⁻⁶ s⁻² at 23.5 K, 7.35 × 10⁻⁵ s⁻² at 23.5 K, and 5.19 × 10⁻⁴ s⁻² at 26.5 K). The evaporation rate remains constant at each temperature. The slope of each line at a particular temperature is determined using a simple linear fitting model. The rate of evaporative mass loss per unit area of the film at each temperature is listed in Figure 5 and calculated from equation 9. The total surface area of the DPO (both sides) is approximately 6.17 cm² and the thickness of the deposited N₂ film is ≈266 nm with total mass of ≈168 ng (using ρ_N2 = 1027 kg · m⁻³). The rate of mass loss from the DPO surface at 23.5 K is ≈1.42 × 10⁻³ ng/s and increases to ≈7.90 × 10⁻² ng/s at 26.5 K. The apparent sublimation vapor pressure corresponding to each desorption temperature is calculated from equation 9. The apparent vapor pressure for each temperature is plotted against the inverse of temperature (Figure 6). From Figure 6 and equation 11, the Arrhenius slope of the line is the enthalpy of sublimation of nitrogen.

Figure 5.

Determination of the rate of change of frequency at each temperature step using a simple linear line fitting (red line) after film relaxation performed at 23 K (Figure 4). The slope of each line is also mentioned on top. The table shows the corresponding evaporative mass loss (dm_film/dt) of the film per unit area per second at each temperature and the fitting error (U_slope) in the slope of each line.

Figure 6.

Linear Arrhenius plot of the apparent vapor pressures (P_a) of nitrogen between 24 K to 27 K to extract the sublimation enthalpy. The corresponding uncertainties in pressure and temperature are also plotted.

This was an example of the experiment performed to measure the enthalpy of sublimation of nitrogen film between 23 K to 27 K. Similarly, the same three step process (mass loading, relaxation, and thermal desorption) is also used for the measurement of apparent sublimation vapor pressures and the corresponding enthalpies of Ne, Ar, O₂, Kr, Xe, CO₂, and H₂O.

3.D. Sources of Uncertainty

We have broadly considered many sources of uncertainties (including systematic) that can affect the measurements. As explained later, some of the sources do not have significant contributions but nonetheless are still included in our final analysis. Our complete list of the identified uncertainties with values are provided in Table 2. These apparent vapor pressure uncertainties are propagated directly according to the NIST guidelines [41] and the propagation of error formula [42] from equation 9. The uncertainties for the heat of sublimation values are reported as the heat of sublimation uncertainties from the individual runs added in quadrature along with the standard deviation of the heat of sublimation values from all the runs. The evaluation of the source of each uncertainty is described in detail below

Table 2.

Magnitude of different sources of uncertainties for the solid films used in this study to calculate the enthalpy of sublimation (ΔH_s).

Gas	ΔHs /kJ·mol−1	uΔHsa /kJ·mol−1	σrb /kJ·mol−1	uTc /mK	uΔMd /kg ×10–28	ufe /µHz 298 K	uslopef /s−2 × 10−3	uGfilmg /MPa	uρSih /Kg·m−3	uGSii /MPa
Ne	1.90	0.29	0.06	42	3.35	<86	55	40	1	<<6.2
N2	7.34	0.48	0.13	33	0.23		1.5	51
Ar	7.79	0.24	0.03	63	2.98		4.6	96
O2	9.26	0.42	0.05	19	1.78		54	32
Kr	11.53	0.40	0.14	48	6.12		5.3	160
Xe	15.79	0.29	0.04	4	3.27		5.3	177
CO2	28.84	1.05	0.32	4	5.44		5.7	120
H2O	54.46	5.28	0.57	7	10.17		5	216		6.2

All uncertainties listed in the table are standard uncertainties u (0.68 confidence interval).

^au_ΔHs, combined standard uncertainty in ΔH_s of each gas

^bσ_r, standard deviation of ΔH_s values determined independently from each experimental run

^cu_T, combined maximum standard uncertainty values in temperature including the corrections from radiative heat load

^du_ΔM, standard uncertainty in atomic/molecular mass of the gas

^eu_f, standard uncertainty in the resonance frequency

^fu_slope, standard fitting error (maximum values) in the slope of line (Figure 5)

^gu_Gfilm, standard uncertainty in the shear modulus of each solid film

^hu_ρSi, standard uncertainty in the density of silicon

ⁱu_GSi, standard uncertainty in the shear modulus of silicon

3.D.1. DPO Temperature

The temperature of the film laden DPO is directly related to the apparent vapor pressure of the sublimating gas molecules according to equation 7. Therefore, precise measurement of the apparent sublimation vapor pressure and the corresponding sublimation enthalpy of the target gas are dependent on our ability to tightly control (within mK range) and precisely measure the paddle temperature. The control and monitoring of temperature at different locations (cold-head, heater and the foot of DPO) inside the chamber is carried out using silicon-diode sensors. Moreover, a temperature controller, equipped with a temperature heater, is used in a closed-loop PID configuration to maintain sample stage temperature within a tight control band. The estimation of the uncertainty at each temperature step is carried out through direct repetitions of measurements. Due to the timing constraints during data acquisition imposed by other instruments, data is recorded through our program every 1.3 s. Each temperature value is averaged over at least a minute including the cases where the condensed solid film of each gas evaporates completely to ensure enough sample size and consistency between the measurements. The temperature deviations in our experiments typically ranges from 1 mK to 62 mK for the experiments performed from 5 K to 160 K.

3.D.2. Thermal Conductance of Silicon at Low Temperatures

The thermal conductance of single crystal silicon below 10 K is primarily determined by phonon collisions at the crystal surfaces [43]. The reduction in thermal conductivity of silicon at 6 K (almost 10 times smaller than the maximum value at ≈22 K)[43] can create a temperature difference (T_DPO-T_CLAMP) of 1 K [20] between the active area of the DPO (wings, neck and head) and the temperature sensor (Figure 2), if constantly exposed to a radiative heat flux of ≈10 mW. Therefore, measurement of the actual paddle temperature (T_DPO), especially for neon measurements (performed below 10 K), is not possible. The temperature difference (T_DPO-T_CLAMP) of 1 K can result in the under estimation of enthalpy of sublimation (equation 10) for neon by almost 50 %. The temperature difference (T_DPO-T_CLAMP) reduces significantly (< 25 mK) above 20 K and is subsequently propagated during the final error analysis for the measurements performed with the original heat shield configuration. For neon measurements, the heat shield was modified to reduce the incident radiative heat load from milli-watts to micro-watts. The heat shield modification results in significantly reducing the temperature difference (T_DPO-T_CLAMP) to less than a mK (see Section 2 in supporting information).

3.D.3. Re-deposition

Re-deposition of the gas molecules onto the paddle surface during desorption (sublimation) could significantly change the extracted enthalpies. In order to significantly reduce re-deposition, all the surface temperatures inside the vacuum chamber are either kept well-below the deposition temperature (DPO pedestal) or are at a much higher temperature (outer heat shield). For example, during neon sublimation experiments, the DPO is kept at 6 K during film deposition and TPD is performed from 8 K to 9.75 K. Meanwhile, the pedestal (Figure 2) temperature remains below 5 K and the heat shield (Figure 2) temperature is ≈35.5 K during the experiment. The evaporation rate of sublimating gas molecules from the pedestal surface (below 5 K) remains significantly smaller than the evaporation rate of gas from the surface of the DPO during TPD (8 K to 9.75 K). Therefore, the re-deposition of gas molecules sublimating from the pedestal surface is significantly small (<< 0.01%). Moreover, the evaporating molecules are directly pumped out of the chamber by a turbo molecular pump at a rate of 480 L/s (N₂ gas molecules).

3.D.4. Gas purities

In order to reduce the contribution of any unwanted or unknown material deposition onto the surface of paddle, we undertook a number of important steps. First, research grade gases with purity of 99.9999 % (except neon and water) were used for all the experiments. An ultra-high purity (99.999 %) neon gas source was used due to the shortage of neon when experiments were conducted. In order to study the sublimation of pure water ice film, a well-established freeze-vacuum-thaw method [3] was used for a minimum of three cycles for water degasification. Although this method was highly effective to degasify water, the background concentration of unwanted gases (in situ confirmed through a RGA) was slightly higher compared to the other commercially purchased gas sources. The source of impurities, especially for water films, has been accounted for through an uncertainty in the mass (u_M) of deposited material (Table 2). The uncertainty U_M is estimated through the total partial pressure of residual gases, evaporating during the sublimation process, using a RGA. Secondly, all the experiments were performed inside an ultra-high vacuum chamber with a base pressure close to 5 ×10⁻⁷ Pa and the partial pressure of residual gases are well below the 10⁻⁸ Pa or 10⁻⁹ Pa range. To give readers some perspective, it will take ≈4.5 hours to deposit a single monolayer of nitrogen film (10⁻⁸ Pa) due to background gas, which is considerably smaller compared to the thickness of the target gas films (typically greater than 100 nm). We also performed regular in situ mass scans using a RGA to confirm that the partial pressure of any residual gas remains below 10⁻⁸ Pa during the whole experiment.

3.D.5. Frequency Stability

As described earlier, the intrinsically high quality factor of DPO in a torsional mode, along with interfacing instrumentation, provides very high frequency stability. In order to account for the frequency uncertainty in our measurements, we measured the standard error in the resonance frequency of the DPO held at room temperature (298 K) for ≈30 minutes using repetitive measurements. The uncertainty (u_f) in frequency as listed in Table 2 was ≈86 µHz. Similarly, another set of measurements performed at 10 K for 60 minutes yielded uncertainty (u_f) of <1 µHz. This clearly demonstrates that frequency stability increases with decreasing temperature as silicon becomes less sensitive to changes in the elastic properties. The magnitude of frequency shift observed during thermal evaporation (typically a few mHz), performed between 6 K and 160 K across all experiments, is significantly larger than the error in frequency (<12 parts per billion) even at room temperature and therefore ignored for analysis.

3.D.6. Relaxation/elastic part

The initial rise in frequency of the film-laden DPO upon heating (before relaxation) is the combination of evaporative mass loss (ρ_filmh_film decreases) and film stiffness (G_filmh_film increases). The contribution of a change in the elastic term (G_filmh_film) during warm-up is minimized by sufficiently annealing the disordered film at a high enough temperature [7; 19; 33]. In order to account for the uncertainty in elastic modulus of the film, two previous studies conducted with argon and water ice films are used. The change in the shear modulus of argon film after annealing is shown to be reversible during subsequent cool-down/warm-up cycles and remains about 6 % of the bulk values [20]. On the other hand, the shear modulus of as deposited water ice films at 142 K remains just 3 % below the bulk values [33]. Therefore, as a conservative estimate, we have used 6 % uncertainty in the shear moduli (u_Gfilm) of all films for the error analysis.

3.D.7. Temperature dependence of density and elastic modulus of silicon

The density and the shear modulus of silicon both show a strong temperature dependence. The magnitude of variation of these two values is small but nonetheless included in our final analysis. The shear modulus of silicon at 77 K (G_sub=62 GPa) [44] and the density at room temperature (ρ_sub=2330 kg · m⁻³) have been used [7] in our analysis. In order to account for the changing shear modulus of silicon with temperature, we first measured Δf (data not shown) of the bare paddle during the cool-down from 298 K to 6 K. Afterwards, third-order polynomials were used to fit the data in three different temperature ranges (6 K to 50 K, 50 K to 85 K and 100 K to165 K) overlapping with our experiments. The deviation in the shear modulus of silicon (u_GSi) from 62 GPa is calculated in these three temperature ranges and subsequently propagated. Similarly, the uncertainty in the density of silicon (u_ρSi) is also included using data for thermal expansion coefficient of a high-purity silicon sample [45] from room temperature to 6 K.

4. Results and Discussion

The apparent sublimation vapor pressures of all the target gases, after accounting for different sources of uncertainty listed in Table 2, are plotted in Figure 7. The error bars in the figure are smaller than the symbols. The enthalpies of sublimation for each gas are determined by averaging the fitted values from the individual experimental runs. The various uncertainties from each run are then added in quadrature along with the standard deviation of variations between each experimental run. The final enthalpies of sublimation along with the corresponding uncertainties are reported in Table 2 and Table 3. The apparent sublimation vapor pressures of all gases (Table S3 in supporting information) are fitted to an Arrhenius law and the fit parameters along with the corresponding uncertainties are listed in the supporting information (see Table S2 in supporting information). An extensive literature search was performed to compare values from the current study with previously reported numbers. In order to minimize any bias towards data selection, a three prong strategy was utilized for this selection. 1) The experiments performed by other groups using DPO for the measurement of sublimation enthalpies of neon [7] and argon [19] were used as a benchmark for our measurements.2) The temperature at which the measurements were performed was used as the primary selection criteria. It is well-established that different phases of solid films like N₂, O₂, and CO₂ [8; 26] exist at different deposition/measurement temperatures resulting in different enthalpy values. For example, an α-phase of N₂ ice film exists between 35.61 K to 63.14 K and below 35.61 K another phase known as a β-phase exists [8]. Correspondingly, the enthalpy of sublimation of N₂ ice film increases from 6.9 kJ · mol⁻¹ for the α-phase at ≈63 K [1] to 7.53 kJ · mol⁻¹ for the β-phase at 20 K [21]. The reported enthalpy of transition of solid nitrogen from α-phase to β-phase is 0.24 kJ · mol⁻¹ at 35.61 K [14]. Moreover, α, β and γ phases of solid oxygen exist between 54.33 K (triple point) to 20 K [8]. The enthalpy of transition of solid oxygen from α to β phase is 0.094 kJ · mol⁻¹ at 23.9 K [26] and that of β to γ phase is 0.74 kJ · mol⁻¹ at 43.8 K [26]. In our measurements, we are not able to independently determine the phase of ices and compare our results with the literature values in the same temperature range as our experiments. 3) Finally, the experiments that report uncertainties in the enthalpy values were also preferred. Theoretical enthalpy of sublimation values (presented in Table 3) were also extracted in an appropriate temperature range from the empirical relationships published in a review article [8], except for the values for water ice that were taken from the work by Feistel and Wagner [28]. The small uncertainty in the theoretical values stem from the fitting error (except water). The uncertainty in theoretical values of heat of sublimation of water is calculated from the experimental uncertainties of heat capacities of ice and vapor [28]. Similarly, the bulk values of density and shear modulus of each solid film were also selected based on the deposition temperature (only if available). The NIST WTT values [1] provided here for each solid film are extrapolated to the lowest possible temperatures listed in the database and consequently the uncertainties get very large. The lowest temperature values available from WTT do not overlap with our experiments as seen in this reference table [1].

Figure 7.

Compendium of Arrhenius plots of the Ne, Ar, N₂, O₂, Kr, Xe, CO₂, and H₂O used to extract the sublimation enthalpies of each gas. Experimental temperatures range from 8 K to 162 K (right to left) and the enthalpies range from (1.90 ± 0.29) kJ · mol⁻¹ for Ne to (54.44 ± 5.28) kJ · mol⁻¹ for H₂O.

Table 3.

Comparison of sublimation enthalpies (ΔH_s) and the corresponding temperatures (T) from current study with the literature, theoretical, and original/adjusted ( $\mathrm{\Delta }{H}_s^{\mathit{\text{adj}}}$) NIST WTT (Web Thermo Tables) values. DPO stands for double paddle oscillator, QCM represents quartz crystal microbalance, G⁰ is bulk shear modulus and ρ⁰ is bulk density. All uncertainties listed in the table are standard uncertainties u (0.68 confidence interval). Enthalpy of sublimation for water was calculated by summing the enthalpies of vaporization at 273.16 K (45.1 ± 1.4) kJ · mol⁻¹) and fusion ((6.014 ± 0.07) kJ · mol⁻¹)) listed in the NIST WTT [1].

Gas	aG0 /Gpa (T/K)	bρ0 /kg·m−3 (T/K)	Literature Values			Theoretical	NIST WTT		Current Study DPO
			ΔHs /kJ ·mol−1	T /K	Method	ΔHs /kJ·mol−1 (Phase)	Originalu ΔHs /kJ·mol−1	T /K	ΔHs /kJ·mol−1 (Expected Phase)w	T /K
							Adjustedv $\mathrm{\Delta }{H}_s^{\mathit{\text{adj}}}$
Ne	0.60c	1507c	1.88d	5.98–9.13	DPO	2.04 ± 0.07e	2.16 ± 0.22	10	1.90 ± 0.29	8–9.78
	(6)	(6)				(N/A)	N/A	N/A	(N/A)
N2	0.79f	1023f	7.53g	20	Manometer	7.65 ± 0.04e	6.9 ± 4.7	35.63	7.34 ± 0.48	23–27.5
	(24)	(24)				(α)e	7.20	27.14	(α)w
Ar	1.43h	1753i	7.83j	20.9–28.2	DPO	8.10 ± 0.09e	7.88 ± 0.05	75	7.79 ± 0.24	27.5–31
	(30)	(30)				(N/A)	8.07	30	(N/A)
O2	0.53k	1525k	9.23–9.24l	28–34		9.24 ± 0.06e	8.7 ± 2.1	44	9.26 ± 0.42	29–33
	(23.5)	(23.5)			Manometer	(β)e	9.54	29	(β)w
Kr	2.35m	3040i	11.63n			11.45 ± 0.02e	10.834 ± 0.062	103.73	11.54 ± 0.40	38.5 – 42.5
	(40)	(40)		54.7–73.8	Manometer	(N/A)	11.26	40	(N/A)
Xe	2.95i	3706i	14.22 ± 0.42o	53.7–59.5		16.09 ± 0.03e	15.9 ± 1.9	55	15.79 ± 0.29	50–57
	(4)	(55)			QCM	(N/A)	N/A	N/A	(N/A)
CO2	2p	1560q	27.19 ± 0.42o	69.7–102.5		27.19 ± 0.1e	28.3 ± 1.6	80	28.84 ± 1.05	80–84.5
	(217)	(194)			QCM	(N/A)	N/A	N/A	(N/A)
H2O	3.60d	820r	51.04 ± 0.42o	153–187		50.68 ± 0.01s	51.11 ± 1.4	273	54.46 ± 5.28	155–161.5
	(79)	(140)			QCM	(N/A)	50.97	155	(N/A)

All uncertainties listed in the table are standard uncertainties u. Enthalpy of sublimation for water was calculated by summing the enthalpies of vaporization at 273.16 K (45.1 ± 1.4) kJ·mol⁻¹) and fusion ((6.014 ± 0.07) k·mol⁻¹)) listed in the NIST WTT [1].

^aG⁰, bulk shear modulus

^bρ⁰, bulk density

^cTaken from Ref. [2]

^dTaken from Ref. [7]

^eTaken from Ref. [8]

^fTaken from Ref. [14]

^gTaken from Ref. [21]

^hTaken from Ref. [23]

ⁱTaken from Ref. [24]

^jTaken from Ref. [19]

^kTaken from Ref. [25]

^lTaken from Ref. [26]

^mTaken from Ref. [27]

ⁿTaken from Ref. [12]

^oTaken from Ref. [16]

^pTaken from Ref. [29]

^qTaken from Ref. [35]

^rTaken from Ref. [36]

^sTaken from Ref. [28]

^tTaken from Ref. [18]

^uTaken from Ref. [1]

^vadjustments performed to the NIST WTT values using the molar heat capacities and the transition enthalpies (see section 3 in supporting information).

^wbased on expectation from literature, phases were not independently determined in this study.

All the previous experiments, presented in Table 3, carried out to study the sublimation enthalpies of the target gases either do not report uncertainties [7; 12; 19; 21; 26] or do not report an extensive analysis for the identification of different uncertainty sources [16]. For example, the conventional manometer based sublimation experiments listed in Table 3 for N₂ [21] and O₂ [26] are without uncertainties. Similarly, the apparent sublimation vapor pressure experiments for neon, argon, and water ice films [7; 19; 20; 33; 37], carried out using 300 µm thick DPOs, were reported without uncertainties. The experiments performed with QCM for Xe, CO₂, and water ice report the same uncertainty (± 0.42 kJ · mol⁻¹) [16] for all three gases. The uncertainty (± 0.42 kJ · mol⁻¹) was assumed by comparisons of deviation of the apparent sublimation vapor pressures of water from QCM with the conventional pressure measurement methods.

The sublimation enthalpy for both neon and argon films from our experiments is consistent with the earlier reported results also using DPOs. The average enthalpy of sublimation of neon from our experiments is (1.90 ± 0.29) kJ · mol⁻¹ (8 K to 9.78 K) compared to 1.88 kJ · mol⁻¹ (5.98 K to 9.13 K) [7]. The average sublimation enthalpy from the current study for argon is (7.79 ± 0.24) kJ · mol⁻¹ (27.5 K to 31 K) compared to 7.83 kJ · mol⁻¹ (20.9 K to 28.2 K) [19]. The sublimation measurements performed with the conventional manometer based methods for nitrogen and oxygen ice films show that our values remain within ≈2.5 % of 7.53 kJ · mol⁻¹ (20 K) [21] and 0.2 % of 9.24 kJ · mol⁻¹ (28 K to 33 K) [26] respectively (Figure 8). The range of measurement temperature plays an important role on the enthalpy values as described earlier. The current study for N₂ ice film was performed at a slightly higher temperature range (23 K to 28K) compared to the listed value of 7.53 kJ · mol⁻¹ at 20 K [21] and results in a slightly lower enthalpy value of 7.34 ± 0.48 kJ · mol⁻¹ (Table 3). The enthalpy of sublimation of krypton (11.54 ± 0.40 kJ · mol⁻¹) from our measurements performed between 38.5 K to 42.5 K remains less 1% of the previous experimental value of 11.63 kJ · mol⁻¹ (54.7 K to 73.8 K) [12] measured using a conventional manometer apparatus. The sublimation enthalpies for Xe, CO₂, and water evaluated from our study is higher than the QCM experiments [16] (Table 3, Figure 8). This could be due to the difference in the range of experimental temperatures (Table 3). The relatively higher deviation (<7 %, Figure 8b), from theoretical [28] (150 K to 162 K) and prior experimental values (153 K to 187 K) [16], in our enthalpy values (154 K to 161.5K) for water ice films and the corresponding higher uncertainty (± 5.28 kJ · mol⁻¹) could be attributed to the presence of higher level of residual gases (confirmed through a RGA). Our enthalpy values for Xe and CO₂ show less than 6 % deviation (Figure 8 b) if compared to the theoretical [8] and NIST WTT values. A complete deviation plot between our values with prior experiments, NIST WTT and theoretical extrapolations is shown in Figure 8 b. Even after considering different sources of uncertainty, a systematic trend moving from low to higher enthalpies/temperatures is observed (Figure 8 b). The trend shows that we may be underestimating the sublimation enthalpies of Ne, N₂ and Ar measured between 8 K to 33 K and over-estimating the enthalpies of O₂, Kr, Xe, CO₂, and H₂O measured between 38 K to 160 K. The trend is amplified by the NIST WTT enthalpy values that are typically extrapolated at much higher temperatures compared to our measurements (Table 3). This trend could be the result of either inconsistencies in the previously reported measurement techniques [16; 21; 26] or difference in the experimental temperature ranges between our measurements and the earlier studies [16; 21; 26].We have also performed adjustments to the NIST WTT values to account for the difference in temperature and phase when possible. The reference heat capacities and the enthalpies of transitions are presented in Table S5 in supporting information. The final adjusted enthalpies of sublimation $(\mathrm{\Delta }{H}_s^{\mathit{\text{adj}}})$ of nitrogen, argon, oxygen, krypton, and water are included in Table 3 and shown in Figure 8. More importantly, our enthalpy of sublimation values for all gases (except neon and water) remain within 6 % (Figure 8b) of the extrapolated theoretical values (evaluated in the same temperature ranges as our experiments) [8; 28]. For both neon and water, our enthalpy values remain within 7.5 % (Figure 8b) of the theoretical values [8; 28]. Moreover, the theoretical sublimation enthalpies for both neon (2.04 ±0.07) kJ · mol⁻¹ [8] and water (50.68 ±0.01) kJ · mol⁻¹ [28] overlap with our enthalpy values for neon (1.90 ± 0.29) kJ · mol⁻¹ and water (54.46 ± 5.23) kJ · mol⁻¹. It is important to note that our enthalpy values for all target gases, except for water, still remain within 5 % of at least one of the three values (prior experiments, NIST WTT or theoretical) as seen in Figure 8 b.

Figure 8.

Comparison of the enthalpy of sublimation of Ne, N₂, Ar, O₂, Kr, Xe, CO₂, and H₂O (in the increasing order of enthalpies and experimental temperatures) determined from the current study $(\mathrm{\Delta }{H}_s^{\mathit{\text{current}}})$ with the corresponding literature values (a). The dashed line in (a) is only for a guide to the eye. Percentage deviation of the $\mathrm{\Delta }{H}_s^{\mathit{\text{current}}}$ from the prior experimental, original/adjusted NIST WTT and theoretical values (b). The error bars in (b) are from original NIST WTT and prior experimental values.

5. Conclusions

According to the NIST thermodynamic reference data, the sublimation enthalpies of Ne, Ar, N₂, O₂, Kr, Xe, CO₂, and H₂O below their triple point temperatures are unavailable, limited or imprecise. We utilized a single 400 µm thick DPO, providing extremely high quality factors and mass sensitivity, for the precise determination of the sublimation enthalpies of target atmospheric gases. The use of a single DPO across all experiments provides an internal consistency among the measurements carried out in a wide temperature range from 8 K to 162 K. The experimental process for measuring enthalpy of sublimation involves three steps; mass loading, annealing, and temperature programmed desorption. The enthalpy of sublimation of each gas is extracted by fitting the natural logarithm of the apparent sublimation vapor pressures against the inverse DPO temperature using a simple Arrhenius form. The precise enthalpy measurements for all eight target gases also involved treatment of different sources of statistical and systematic uncertainties. Standard error in temperature, due to random fluctuations (<65 mK), is a major source of uncertainty in our experiment. Moreover, difficulties in accurately measuring the DPO temperature below 10 K for neon measurements (systematic error), arising from the poor thermal conductance of silicon, was also mitigated by modifying the heat shield to reduce the radiative heat load on the DPO. The effect of gas re-deposition during sublimation is minimized by monitoring temperatures of critical surfaces inside the vacuum chamber. Gas purity is ensured by using research and ultra-high purity grade gas sources (except for water). The magnitude of error in measurements of the resonance frequency (<12 parts per billion) is significantly small and therefore ignored. Based on the previous studies [20; 33], a 6 % uncertainty is assumed to account for the uncertainty in the shear modulus of each solid film during temperature desorption. The contributions of temperature dependent shear modulus and density of silicon, though very small, are also included in our final analysis. In the end, we compared our results with existing literature, theoretical and NIST WTT values in comparable temperature ranges.