A Mathematical Model of Countercurrent Exchange of Oxygen Between Paired Arterioles and Venules

Abstract

A mathematical model is formulated for diffusive countercurrent exchange of oxygen between paired arterioles and venules. A closed form solution of the problem is obtained by linearizing the nonlinear oxyhemoglobin dissociation curve at the inlet P_O2 in the vessel. The closed form solution is compared with the corresponding numerical solution of the nonlinear problem. Under normal conditions, longitudinal gradients of venular P_O2 are found to be small. Examples are presented where the model predicts significant gradients of venular P_O2 when the blood flow rate in the venule is several times smaller than that in the arteriole.

INTRODUCTION

One of the main functions of the blood is to supply adequate amounts of oxygen (O₂) to the tissues. Until recently, O₂ was believed to be exchanged exclusively at the level of the blood capillaries, but a number of investigators have demonstrated experimentally that oxygen tension (P_O2) and hemoglobin saturation with oxygen (S_O2) decrease gradually along the arteriolar network [2, 12, 13, 7, 3, 8, 19]. Mathematical models suggest that observed longitudinal gradients in oxygen tension (P_O2) are qualitatively consistent with a diffusional mechanism of O₂ transport from arterioles [15, 17]. Therefore, the site of O₂ transport may not be restricted to capillaries, as was previously assumed, but includes precapillary vessels. However, it is not known at present how the oxygen lost from the arterioles is distributed or how universal this phenomenon is in different tissues and different physiologic states.

Even less information is available on the participation of venules in O₂ exchange, although the question of countercurrent exchange has been discussed extensively in the literature [6]. There are numerous observations in many tissues that larger arterioles and venules run side by side, parallel to each other in countercurrent fashion. These vessels are henceforth termed paired. Pittman and Duling [14] and Swain and Pittman [19] observed that O₂ may be gained by the venular blood as it proceeds from smaller to larger vessels. The question of the magnitude of countercurrent exchange has an important implication: if this effect is significant, then the oxygen tension (P_O2) in the venous blood cannot be considered an accurate measure of either end-capillary or tissue P_O2.The assumption that the venous P_O2 is an indicator of tissue P_O2 is commonly made in interpretation of whole organ experiments. Another mechanism that would lead to dissociation of the venous and capillary P_O2 levels has to do with the kinetics of O₂-hemoglobin binding [5].

Popel and Gross [15] formulated a mathematical model of O₂ diffusion from noncapillary vessels to tissue and computed longitudinal P_O2 gradients in a simplified vascular network using the characteristics of the hamster check pouch microcirculation. Roth and Wade [17] presented a compartmental model of organ circulation. In their model several generations of vessels are represented by vascular compartments; in addition, there is a tissue compartment and a connective tissue compartment. Each vascular compartment can exchange O₂ with one of the tissue compartments. For the purpose of calculation of exchange coefficients, each noncapillary vessel is modeled as a cylinder surrounded by two concentric layers of finite thickness representing the vascular wall and a tissue. Piiper et al. [11] presented estimates of the effect of countercurrent exchange of oxygen between arterioles and venules using essentially a compartmental model. They concluded that the effect should be much smaller for O₂ than for inert gases, due to the chemical binding of oxygen to hemoglobin.

The aim of the present study is to formulate a model of O₂ transport between paired arterioles and venules. The model of Popel and Gross [15] is extended, and the O₂ fluxes between the arterioles, tissue, and venules are calculated. A systematic analysis of arteriovenous O₂ exchange in physiological situations will be presented elsewhere.

MATHEMATICAL MODEL

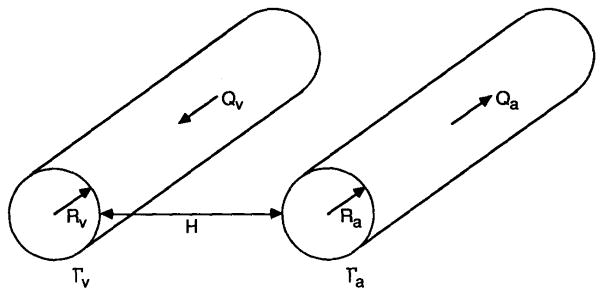
Consider a pair of circular parallel unbranched vessels of radii R_a and R_v at a distance H apart (Figure 1). The subscripts a and v refer to arteriolar and venular segments, respectively.

Fig. 1.

Schematic diagram of the model.

The problem of simulating O₂ transport in the vicinity of the arteriolar and venular vessels, taking into account the specific local geometry and hemodynamics of the capillary bed, does not seem to be mathematically tractable at present. Also, the necessary experimental information on the capillary geometry in relation to arteriolar and venular vessels is not available. Popel and Gross [15] have treated this problem by formulating a phenomenological model for the O₂ transport around the arteriolar vessel. The formulation is based on the following requirements: (a) the model should not include the heterogeneities of P_O2 at the scale of single capillaries and cells; (b) the model should be concerned with “large scale” diffusional processes in the vicinity of sources or sinks of oxygen such as arteriolar and venular vessels and the external boundary of the tissue; (c) far from such sources or sinks, the model should give an average P_O2 level, denoted as P_∞, which is solely determined by capillary-tissue O₂ exchange. The P_O2 distribution in the extravascular space satisfying the above requirements is governed by the diffusion equation:

$${\nabla }^{2}P-\frac{1}{l_t^2}(P-P_{\infty })=0,$$ (1)

where P is the oxygen tension in the tissue, l_t is the penetration depth, and P_∞ is a given oxygen tension at “infinity.” We consider the diffusion only in the x-y plane perpendicular to the arteriole-venule axes; diffusion parallel to the axes, in the z direction, is neglected. The parameter l_t characterizes the depth of penetration of oxygen from a “large scale” source or sink, e.g., arteriole, venule, or tissue surface; in the model the value of this parameter has to be specified. In the absence of the macroscopic oxygen tension gradients, equation (1) yields P = P_∞; thus P_∞ is the mean oxygen tension determined by the capillary-tissue exchange.

Equation (1) is subject to the boundary conditions

$${P\mid }_{{\mathrm{\Gamma }}_a}=P_a,{P\mid }_{{\mathrm{\Gamma }}_v}=P_v,$$ (2)

and

$$P\to P_{\infty }\text{as}r\to \infty .$$ (3)

Here P_a and P_v are the P_O2’s on the surface of the arteriole and the venule, respectively. We ignore the effect of the vascular wall.

The diffusive fluxes of O₂ from the arteriole and venule are

$$J_a=-D\alpha {\int }_{{\mathrm{\Gamma }}_a}\frac{\partial P}{\partial n}d\mathrm{\Gamma },J_v=-D\alpha {\int }_{{\mathrm{\Gamma }}_v}\frac{\partial P}{\partial n}d\mathrm{\Gamma },$$ (4)

where n is the unit outward normal to the arteriolar or venular surfaces, D is the diffusion coefficient, and α is the solubility coefficient of O₂ in the tissue. The integrals in (4) are taken over the corresponding circuits, Γ_a and Γ_v, which are the intersections of the arteriole and venule with a plane z = const.

DIFFUSION CONDUCTANCES

Equation (1) and the boundary conditions (2)–(4) are linear; thus, the flux of oxygen from the arteriole, J_a, can be expressed as a linear combination of oxygen tensions P_a, P_v, and P_∞. There is also a constraint that the flux must vanish when all three oxygen tensions are equal (P_a = P_v = P_∞). From these conditions it follows that flux can be expressed as

$$J_a^{\ast }=-\frac{J_a}{D\alpha }=F_1(P_a-P_{\infty })+F_2(P_a-P_v),$$ (5)

where F₁ and F₂ are coefficients that depend only on the vascular geometry, (i.e. on R_a, R_v, and H) and the penetration depth l_t. Similarly, the net flux from the venule, J_v, is

$$J_v^{\ast }=-\frac{J_v}{D\alpha }=G_1(P_a-P_v)+G_2(P_v-P_{\infty }),$$ (6)

where G₁ and G₂ are geometrical coefficients.

It can be shown that G₁ = −F₂. Therefore, the second term in Equation (5) represents the amount of oxygen transferred from the arteriole to the venule, whereas the first term represents the amount transferred from the arteriole to the surrounding tissue less the amount transferred to the venule. The two terms in Equation (6) are interpreted accordingly. Hence counter-current exchange of oxygen is quantitatively expressed by the terms F₂(P_a − P_v) = −G₁(P_a − P_v) in Equations (5) and (6).

The coefficients F₁, F₂, G₁, and G₂ can be determined numerically for each set of parameters R_a, R_v, H, and l_t. The details of the numerical procedure are given in the Appendix.

OXYGEN TRANSPORT IN THE BLOOD

Oxygen is transported in the blood by convective motion of red blood cells and plasma in both longitudinal and radial directions and by molecular diffusion. It is known that at higher rates of shear the transport can be significantly augmented, the effect being attributed to pseudorandom radial motion of red blood cells [1, 20]. Recently, Ellsworth and Pittman [4] measured oxygen hemoglobin saturation profiles in arterioles and venules and found that the profiles in some cases are nonuniform and asymmetric; the sources of nonuniformity or asymmetry have not been identified, but upstream vascular bifurcations and noncircular vessel shapes were implicated. To describe these effects, a careful analysis of O₂ distribution in the vascular lumen is necessary. For the purpose of the present analysis we introduce “mixing cup” P_O2 in the blood, P_b; i.e., we assume that O₂ flow through the vessel cross section is given by the expression

$$Q[{\alpha }_b{P}_b+CS(P_b)]$$

where Q is the volumetric blood flow rate, α_b is the oxygen solubility coefficient in blood, C is the oxygen-carrying capacity of the blood, and S is the fractional saturation of hemoglobin with O₂. It is assumed that the chemical reaction between hemoglobin and oxygen is in equilibrium, which yields the relationship S(P_b).

Oxygen balance in a vessel can be expressed in the form

$$Q{\alpha }_b\frac{\partial }{\partial z}\left[P_b+\frac{C}{{\alpha }_b}S(P_b)\right]=-J,$$ (7)

where J is the O₂ flux from the vessel per unit length.

Using Equations (5), (6), and (7), the O₂ transport in a paired arteriole and venule is given by the following simultaneous differential equations:

$$Q_a{\alpha }_b[1+\mathrm{\Phi }(P_a)]\frac{\partial P_a}{\partial z}=-D\alpha [F_1(P_a-P_{\infty })+F_2(P_a-P_v)],$$ (8)

$$Q_v{\alpha }_b[1+\mathrm{\Phi }(P_v)]\frac{\partial P_v}{\partial z}=-D\alpha [G_1(P_a-P_v)+G_2(P_v-P_{\infty })],$$ (9)

where the variables with subscripts a and v, respectively, pertain to the arteriolar and venular vessels. Φ is proportional to the slope of the oxyhemoglobin dissociation curve (ODC):

$$\mathrm{\Phi }(P)=\frac{C}{{\alpha }_b}\frac{dS}{dP}.$$ (10)

The equation (8) and (9) are subject to the boundary conditions, which are specified at the respective inlets of the vessels:

$$z=0:P_a=P_a^{\text{in}},$$ (11)

$$z=L:P_v=P_v^{\text{in}},$$ (12)

where L is the length of each vessel.

ANALYSIS

The saturation function for the ODC is nonlinear. Thus, Equations (8) and (9) with the boundary conditions (11)–(12) form a nonlinear system of differential equations. This system can be solved numerically. In the analysis of O₂ transport in arterioles [15], it was found that the P_O2 falls almost linearly in a given vessel. The experimental studies [14, 19] suggest that there are no large variations in the O₂ saturation in a single vessel. Hence we obtain an analytical solution of the problem by approximating the slope of the ODC along the length of the vessel as that determined at the entry point. Thus, the variables Φ for the arteriolar and venular vessels are given by

$${\mathrm{\Phi }}_a={\frac{C}{{\alpha }_b}\frac{dS}{d{P}_a}|}_{P_a=P_a^{\text{in}}}$$ (13)

and

$${\mathrm{\Phi }}_v={\frac{C}{{\alpha }_b}\frac{dS}{d{P}_v}|}_{P_v=P_v^{\text{in}}}.$$ (14)

Any form of the equation can be used to represent the ODC in the present model. We use the Hill equation:

$$S(P)=\frac{{(P/P_{50})}^n}{1+{(P/P_{50})}^n},$$ (15)

where P₅₀ is the partial pressure of O₂ at 50% saturation and n is the Hill parameter. Note that the Hill equation is accurate in the range of hemoglobin saturation S = 0.2–0.8 and is not valid at low values of P_O2.

Introducing dimensionless variables z^* = z/l_t, L^* = L/l_t, and using (13) and (14), we recast Equations (8) and (9):

$$\frac{d{P}_a}{d{z}^{\ast }}=-[f_1(P_a-P_{\infty })+f_2(P_a-P_v)]$$ (16)

and

$$\frac{d{P}_v}{d{z}^{\ast }}=-[g_1(P_a-P_v)+g_2(P_v-P_{\infty })],$$ (17)

in which

$$\begin{gathered} f_1=\frac{D\alpha l_t{F}_1}{Q_a{\alpha }_b(1+{\mathrm{\Phi }}_a)},f_2=\frac{D\alpha l_t{F}_2}{Q_a{\alpha }_b(1+{\mathrm{\Phi }}_a)}; \\ {g}_1=\frac{D\alpha l_t{G}_1}{Q_v{\alpha }_b(1+{\mathrm{\Phi }}_v)},g_2=\frac{D\alpha l_t{G}_2}{Q_v{\alpha }_b(1+{\mathrm{\Phi }}_v)}. \end{gathered}$$ (18)

The boundary condition (12) becomes

$$z^{\ast }=L^{\ast }:P_v=P_v^{\text{in}}.$$ (19)

Equations (16) and (17) are linear. The following two cases are considered:

Case 1: No countercurrent exchange

When there is no countercurrent exchange between the paired arteriole and venule, F₂ = 0 and G₁ = 0. From (18), f₂ = 0 and g₁ = 0. In this case, the solution of Equations (16) and (17) with the boundary conditions (11) and (19) is

$$\begin{gathered} P_a=\left(P_a^{\text{in}}-P_{\infty }\right)e^{-f_1{z}^{\ast }}+P_{\infty }, \\ {P}_v=\left(P_v^{\text{in}}-P_{\infty }\right)e^{-g_2(z^{\ast }-L^{\ast })}+P_{\infty }. \end{gathered}$$ (20)

Case 2: With countercurrent exchange

The solution of (16) and (17) with the boundary conditions (11) and (19) is given by

$$\begin{gathered} P_a=A{e}^{m_1{z}^{\ast }}+B{e}^{{m_t}^{\ast }}+P_{\infty }, \\ {P}_v=\frac{A}{f_2}(f_1+f_2+m_1)e^{m_1{z}^{\ast }}+\frac{B}{f_2}(f_1+f_2+m_2)e^{m_{2}z\ast }+P_{\infty }, \end{gathered}$$ (21)

where

$$\begin{gathered} A=\frac{1}{\beta }\left[f_2\left(P_v^{\text{in}}-P_{\infty }\right)-\left(f_1+f_2+m_2\right)\left(P_a^{in}-P_{\infty }\right)e^{m_2{L}^{\ast }}\right], \\ B=-\frac{1}{\beta }\left[f_2\left(P_v^{\text{in}}-P_{\infty }\right)-\left(f_1+f_2+m_1\right)\left(P_a^{\text{in}}-P_{\infty }\right)e^{m_1{L}^{\ast }}\right], \end{gathered}$$ (22)

in which

$$\begin{gathered} \beta =(f_1+f_2+m_1)e^{m_1{L}^{\ast }}-(f_1+f_2+m_2)e^{m_2{L}^{\ast }}, \\ {m}_1=\frac{1}{2}\left[-(f_1+f_2-g_1+g_2)+{\left\{{(f_1+f_2+g_1-g_2)}^2-4f_2{g}_1\right\}}^{1/2}\right], \\ {m}_2=\frac{1}{2}\left[-(f_1+f_2-g_1+g_2)-{\left\{{(f_1+f_2+g_1-g_2)}^2-4f_2{g}_1\right\}}^{1/2}\right]. \end{gathered}$$ (23)

It can be easily verified that the solution (21) with countercurrent exchange tends toward that without countercurrent exchange when f₂ = 0 and g₁ = 0.

PARAMETERS OF THE MODEL

For the computation of P_O2 in the blood flowing through the arteriole and venule, we have chosen the parameters corresponding to the hamster cheek pouch microcirculation: arteriolar diameter D_a = 60 μm and length L = 0.75 cm [9]; arteriolar velocity v = 0.25 cm/s [18]. The penetration depth l_t is 100 μm, the same as was assumed in the previous theoretical study on O₂ transport in the arteriolar networks [15]. The values of Hill’s parameters are P₅₀ = 26.0 mmHg and n = 2.55, and the diffusion and solubility coefficients D = 1.5 × 10⁻⁵ cm²/s and α = α_b ≈ 3 × 10⁻⁵ (cm³ O₂)/cm³ mmHg [15]. Unless otherwise specified, the following values of the parameters are assumed: C = 0.2 (cm³ O₂)/(cm³ blood), P_∞ = 8 mmHg, H = 25 μm, Q_v = Q_a, $P_a^{\text{in}}=60\text{mmHg},P_v^{\text{in}}=20\text{mmHg}$, and D_v = 90 μm.

RESULTS AND DISCUSSION

The coefficients F₁, F₂, G₁ and G₂ depend only on the geometrical factors and the penetration depth. Once these coefficients are known, the diffusive flux from the arteriole and venule can be computed from the relations (5) and (6).

First we show the results of numerical solution, and then we compare them with the analytical solution. In Table 1 the diffusion conductance coefficients are presented for different values of vessel diameters; the coefficients decrease as the vessel diameter decreases. In Table 2 the diffusion conductance coefficients are presented for different values of the distance H between the arteriole and venule. For the computation, the diameters of the paired arteriole and venule are chosen as D_a = 60 μm and D_v = 90 μm. The coefficients F₂ and G₁, which determine the countercurrent exchange, increase as the distance between the paired vessels decreases. If H = 1000 μm, there is no diffusional interaction between the arteriole and venule, and the venules do not affect the transport of O₂ from the arterioles to the surrounding tissue. Popel and Gross [15] have derived an expression for the diffusion conductance for the arteriole without countercurrent exchange, based on the phenomenological model (1). The diffusion conductances computed from the present model for large values of H coincide, within the 1% accuracy of our numerical solution, with those obtained from the model of Popel and Gross [15].

TABLE 1.

Diffusion Conductance Coefficients for the Paired Arterioles and Venules Separated by H = 100 μm^a

Da (μm)	Dv (μm)	F1	F2	G1	G2
800	1200	25.57	3.03	−3.03	36.7
120	160	5.48	1.05	−1.05	6.84
60	90	3.59	0.73	−0.73	4.50
40	40	2.99	0.51	−0.51	2.99
7	10	1.61	0.22	−0.22	1.81

^aPenetration depth l_t = 100 μm.

TABLE 2.

Diffusion Conductance Coefficients for the Paired Arteriole and Venule with Variation of the Distance H between Them^a

H (μm)	F1	F2	G1	G2
25	2.89	2.68	−2.68	4.09
50	3.18	1.55	−1.55	4.33
100	3.59	0.73	−0.73	4.50
150	3.85	0.38	−0.38	4.94
250	4.08	0.12	−0.12	5.17
500	4.19	0.74 ×10−2	−0.74×10−2	5.28
1000	4.21	0.39×10−4	−0.39×10−4	5.30
2000	4.21	0.2×10−4	−0.2×10−4	5.30

^aD_a = 60 μm, D_v = 90 μm, l_t = 100 μm.

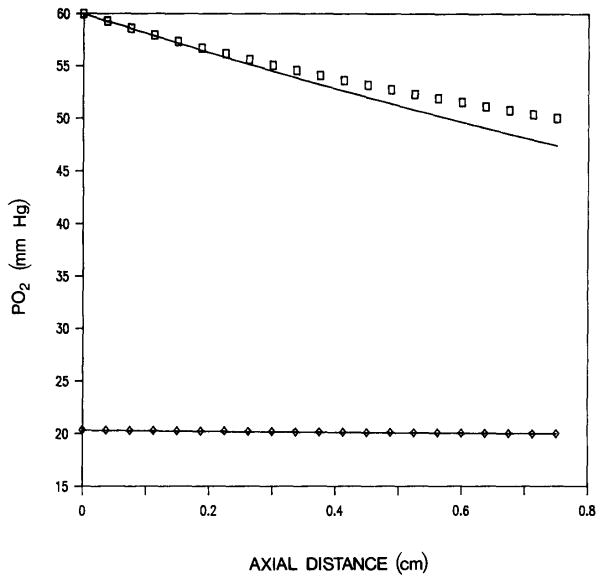
In the analytical calculations, we have approximated the slope of the oxyhemoglobin dissociation curve [Equation (10)] by the value determined at the inlet of the vessel. The equations then become linear, which makes possible a closed form analytical solution (21). Equations (8) and (9) with nonlinear slope have also been solved numerically. Figure 2 shows the P_O2 in an arteriolar-venular pair computed from the analytical solution (21) and also numerically using the nonlinear dissociation curve. There is reasonably good agreement between the solutions except for a discrepancy toward the outlet in the arteriole. This difference reflects the change in the slope of the oxygen dissociation curve in the range of oxygen tensions 60 to 49 mmHg. The error introduced by the linearization of the ODC may become substantial when the solution is applied to vascular networks, where the error from individual vascular segments can accumulate. In this case, the numerical solution should be used.

Fig. 2.

Axial P_O2 distribution in an arteriolar (upper curve) and a venular (lower curve) vessel. Analytical solution (solid curve), and numerical solutions for arteriole (□) and venule (◇).

Table 3 shows the effect of the distance H between the paired arteriole and venule on their outlet P_O2. The outlet P_O2 in the venule increases with decreasing distance H. At H = 1000 μm, P_O2 corresponds to that of no countercurrent exchange. The diffusion conductance coefficients F₂ and G₁, proportional to the diffusive flux from the arteriole to the venule, increase significantly with decreasing H (Table 2), but not enough to significantly affect the venular P_O2 (Table 3). Because the change in venular P_O2 from inlet to outlet is so small, it appears that there is no countercurrent exchange. This may not be the case, however. To estimate the contribution of counter-current exchange, we average oxygen fluxes (5) and (6) over the length of the vessel:

$${\overline{J}}_a^{\ast }=F_1\left({\overline{P}}_a-P_{\infty }\right)+F_2\left({\overline{P}}_a-{\overline{P}}_v\right),$$ (24)

$${\overline{J}}_v^{\ast }=G_1\left({\overline{P}}_a-{\overline{P}}_v\right)+G_2\left({\overline{P}}_v-P_{\infty }\right).$$ (25)

TABLE 3.

Effect of the distance H between the Paired Arteriole and Venule on Their Outlet P_O2^a

H (μm)	Outlet PO2 (mmHg)
	Arteriole	Venule
1000	48.9	19.5
250	49.0	19.5
100	49.1	19.7
50	48.6	20.0
25	47.4	20.3
10	44.5	20.9

^aD_a = 60 μm, D_v = 90 μm, Q_v = Q_a, $P_a^{\text{in}}=60\text{mmHg},P_v^{\text{in}}=20\text{mmHg}$. H = 1000 μm corresponds to no countercurrent exchange.

An overbar denotes spatial averaging. The longitudinal distributions of arteriolar and venular P_O2are nearly linear within a vessel (Figure 2); thus, we can replace average values P_a and P_v with the corresponding arithmetic averages of inlet and outlet values. For example, consider the case H = 50 μm. From Table 3 we obtain p̄_a = 54.3 mmHg, p̄_v = 20.0 mmHg. Taking the values of the diffusion conductance coefficients from Table 2, we obtain for the fluxes (24) and (25)

$${\overline{J}}_a^{\ast }=147.2+53.2=200.4,{\overline{J}}_v^{\ast }=-53.2+52.0=-\mathrm{1.2.}$$

Thus about 27% of the total oxygen flux from the arteriole (53.2/200.4) is transferred to the venule. The total flux from the venule is approximately zero, since the amount received from the arteriole (−53.2) is nearly balanced by the amount transferred to the surrounding tissue (52.0). For H = 25 μm, according to Table 3, p̄_a = 53.7 mmHg and p̄_v = 20.2 mmHg; hence

$${\overline{J}}_a^{\ast }=132.1+89.8=221.9,{\overline{J}}_v^{\ast }=-89.8+49.9=-\mathrm{39.9.}$$

In this case, 41% of the total flux from the arteriole is transferred to the venule, and the amount received by the venule (−89.8) is larger than the amount transferred to the surrounding tissue (49.9); as a result, the venule is gaining oxygen. In the case of a larger separation between the arteriole and venule, H = 100 μm, the values from Table 2 and 3 yield p̄_a = 54.6 mmHg, p̄_v = 19.9 mmHg, and

$${\overline{J}}_a^{\ast }=167.3+25.3=192.6,{\overline{J}}_v^{\ast }=-25.3+53.6=\mathrm{28.2.}$$

The flux from the arteriole into the venule (−25.3) is smaller than the flux from the venule to the surrounding tissue; thus there is a net loss of oxygen from the venule.

From this analysis we conclude that venular P_O2 can remain constant while a substantial amount of oxygen is received from the paired arteriole, i.e. in the presence of countercurrent exchange, if the venule loses an equal amount of oxygen to the surrounding tissue. Thus, the magnitude of arteriovenular countercurrent exchange should be judged not by the venular longitudinal P_O2 profile, but by the relative contribution of the four terms in the relationships (24) and (25).

It should also be kept in mind that due to nonlinearity of the oxyhemoglobin dissociation curve (15), equal changes in arteriolar and venular P_O2 correspond to unequal changes in hemoglobin saturation; e.g., a change ΔP_O2 = 1 mmHg at P_O2 = 45 mmHg corresponds to ΔS_O2 = 0.9%, whereas at P_O2 = 20 mmHg it corresponds to ΔS_O2 =1.5%. Thus, even small changes in venular P_O2 may correspond to substantial changes in hemoglobin saturation.

Table 4 shows that the P_O2 at the venular outlet increases as the blood flow rate in the venule decreases. The venular S_O2 rises by 7.5% when its blood flow rate is reduced to 10% of the arteriolar blood flow rate. The ratio of venular to arteriolar diameter does not have appreciable effect on venular P_O2 (Table 5). The difference in the P_O2 between the outlet and inlet of the venule decreases as the inlet venular P_O2 increases (Table 6). Also, Table 7 shows that the outlet venular P_O2 decreases as the inlet P_O2 in the arteriole decreases.

TABLE 4.

P_O2 at the Outlet of the Paired Arteriole and Venule with Variation of the Ratio of Blood Flow Rates (Q_v/Q_a)^a

Qv/Qa	Outlet PO2 (mmHg)
	Arteriole	Venule
1	417.4	20.3
0.5	47.4	20.6
0.25	47.5	21.2
0.1	47.5	22.7

^aH = 25 μm, $P_a^{\text{in}}=60\text{mmHg},P_v^{\text{in}}=20\text{mmHg}$.

TABLE 5.

P_O2 at the Outlet of the Paired Arteriole and Venule with Variation of the Ratio of Their Diameters, D_v/D_a^a

Dv/Da	Outlet PO2 (mmHg)
	Arteriole	Venule
1	47.5	20.4
1.2	47.5	20.4
1.5	47.4	20.3

^aH = 25 μm, D_a = 60 μm.

TABLE 6.

Effect of Inlet Venular P_O2 on the Outlet P_O2 in the Paired Arteriole and Venule^a

$P_v^{\text{in}}(\text{mmHg})$	Outlet PO2 (mmHg)
	Arteriole	Venule
30	48.7	29.7
20	47.4	20.3
15	46.8	15.6

^a $P_a^{\text{in}}=60\text{mmHg}$.

TABLE 7.

Effect of Inlet Arteriolar P_O2 on the Outlet P_O2 in the Paired Arteriole and Venule^a

$P_a^{\text{in}}(\text{mmHg})$	Outlet PO2 (mmHg)
	Arteriole	Venule
70	47.8	20.4
60	47.4	20.3
50	43.7	20.2

^a $P_v^{\text{in}}=20\text{mmHg}$.

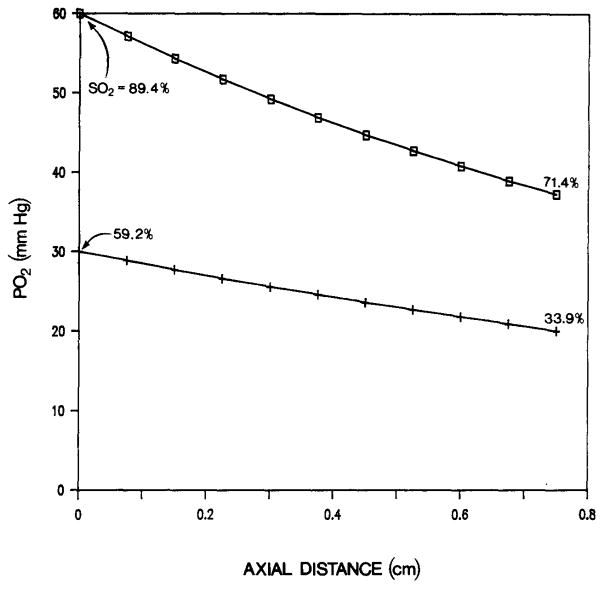
The following example shows that under certain conditions venular P_O2 can significantly increase due to countercurrent exchange. We take D_a = 60 μm, D_v = 90 μm, L = 0.75 cm, C = 0.1 (cm³ O₂)/(cm³ blood) (a low value of C can be a result of anemia), v = 0.25 cm/s, Q_v = Q_a/10, P_∞ = 12 mmHg, and H = 10 μm. For these parameters, the venous P_O2 increases from 20 mmHg at the inlet to 30 mmHg at the outlet (Figure 3). The venous O₂ saturation increases from 33.9 to 59.2%, i.e., by about 25.3%, as a result of countercurrent exchange.

Fig. 3.

Axial P_O2 distribution in arteriolar (□) and venular (+) vessels. The numbers at the end points of the curve are the values of the O₂ saturation. Low flow in the venule, Q_v = Q_a/10.

CONCLUSIONS

We have formulated a mathematical model for the O₂ transport between a paired arteriole and venule. To obtain an analytical solution to the problem, we evaluated the nonlinear O₂ dissociation curve at the inlet of the vessel. Using this approximation, we were able to obtain the solution in closed form. Reasonably good agreement is found between the exact solution of the linearized system and the numerical solution of the corresponding nonlinear system, but the error can accumulate if the solution is applied to vascular networks. We have found that the diffusive countercurrent exchange can contribute significantly to the total flux of oxygen from the venule, even though the effect on venular P_O2 may be small. However, there are cases where the model predicts significant rise of venular P_O2.

It is also possible that oxygen that diffuses from arterioles is carried to the venules convectively by the capillaries. This mechanism is not included in the present model.

APPENDIX. COMPUTATION OF THE DIFFUSION CONDUCTANCE COEFFICIENTS

Consider a plane z = const perpendicular to the vessel axes. In this plane we introduce the bipolar coordinates (ξ, θ) [10]:

$$\begin{gathered} x=\frac{asinh\xi }{cosh\xi +cos\theta }, \\ y=\frac{asin\theta }{cosh\xi +cos\theta } \end{gathered}$$ (A1)

with scale factors

$$h_{\xi }=h_{\theta }=\frac{1}{cosh\xi +cos\theta },$$ (A2)

where (± a, 0) are the coordinates of the foci which will be expressed below.

The radii of the vessels are expressed as

$$\begin{gathered} R_a=\frac{a}{sinh{\xi }_a}, \\ {R}_v=-\frac{a}{sinh{\xi }_v}, \end{gathered}$$ (A3)

and the coordinates of their centers (vessel axes) are

$$\left(\frac{a}{tanh{\xi }_a},0\right),\left(\frac{a}{tanh{\xi }_v},0\right).$$ (A4)

Notice that ξ_a > 0 and ξ_v < 0.

The distance R between the centers of the vessels is

$$R=R_a+R_v+H.$$ (A5)

From (A3), (A4), and (A5), the focus coordinate a is expressed as:

$$a=\sqrt{{\left(\frac{R^2+R_v^2+R_a^2}{2R}\right)}^2-R_v^2}.$$ (A6)

The transformation (Al) maps the region outside the circles onto a rectangular region in the ξ-θ plane. The boundaries Γ_a and Γ_v are mapped to lines ξ = ξ_a and ξ = ξ_v; θ varies from 0 to 2π.

Equation (1) and the boundary conditions (2) become

$$\frac{{\partial }^{2}P}{\partial {\xi }^2}+\frac{{\partial }^{2}P}{\partial {\eta }^2}-\frac{a^2}{l_t^2{\left(cosh\xi +cos\theta \right)}^2}\left(P-P_{\infty }\right)=0,$$ (A7)

$$\xi ={\xi }_a:P=P_a;\xi ={\xi }_v:P=P_v.$$ (A8)

We introduce the periodic boundary condition for θ:

$$P\left(\xi ,0\right)=P\left(\xi ,2\pi \right).$$ (A9)

Using the transformed coordinates, we obtain

$$J_a^{\ast }={\int }_0^{2\pi }{\left(\frac{\partial P}{\partial \xi }\right)}_{\xi ={\xi }_a}d\theta ,$$ (A10)

$$J_v^{\ast }={\int }_0^{2\pi }{\left(\frac{\partial P}{\partial \xi }\right)}_{\xi ={\xi }_v}d\theta .$$ (A11)

Equation (A7) with boundary conditions (A8) and (A9) is solved numerically by the finite difference method. The second derivatives are approximated by the central difference operator with second order accuracy. The resulting system of algebraic equations is solved by the successive overrelaxation method [16].

The derivatives at the boundary are computed from three points to retain the second order accuracy. Finally, the integrals (A10) and (A11) are computed numerically using Simpson’s rule [16].

Once $J_a^{\ast }$ and $J_v^{\ast }$ are computed, the parameters F₁ and F₂ are calculated as

$$F_1={\frac{J_a^{\ast }}{P_a-P_{\infty }}|}_{P_v\to P_a}$$ (A12)

and

$$F_2={\frac{J_a^{\ast }}{P_a-P_v}|}_{P_a\to P_{\infty }}$$ (A13)

G₁ and G₂ are obtained in a similar way.